Selection of the Bandwidth Matrix in Spatial Varying Coefficient Models to Detect Anisotropic Regression Relationships
Abstract
:1. Introduction
2. Selection and Estimation of Bandwidth of Spatial Varying Coefficient Model
2.1. Spatial Varying Coefficient Model
2.2. Selection of Bandwidth Matrix
3. Simulation Experiment
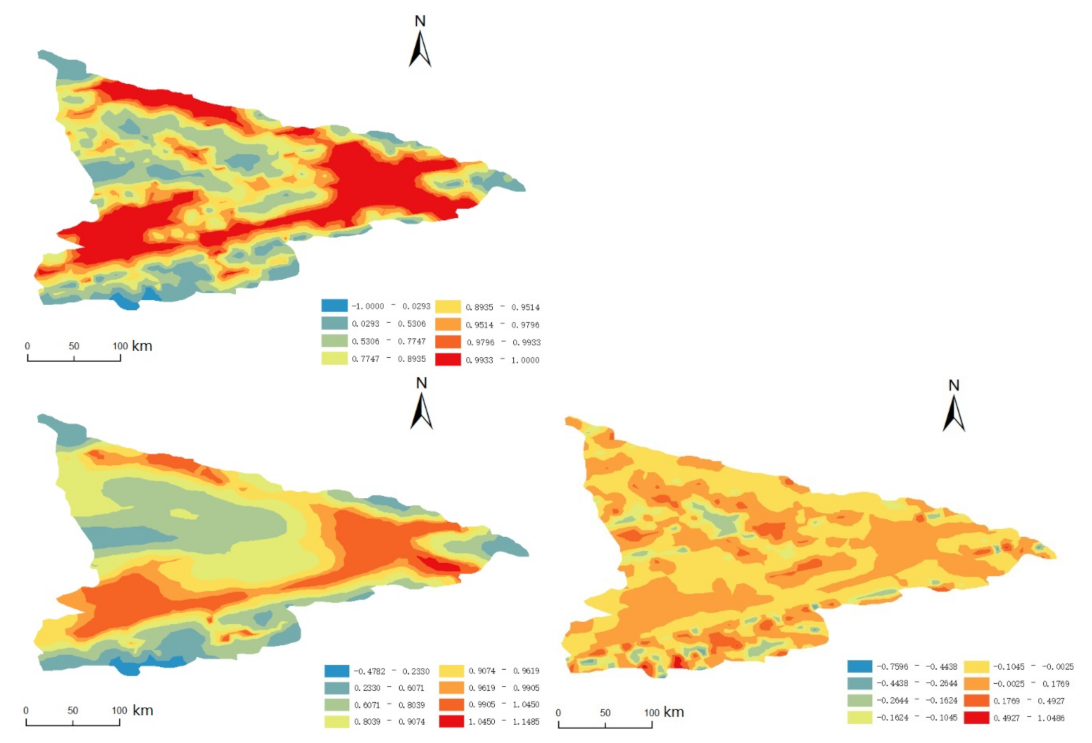
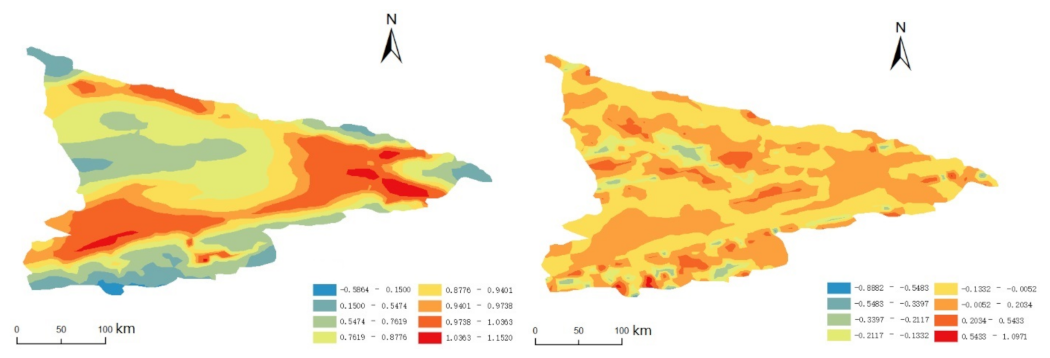
4. Empirical Research
4.1. Data Sources
4.2. Modelling
4.3. Results and Analysis
4.3.1. Results of Unary Bandwidth and Bandwidth Matrix
4.3.2. Results of Bandwidth Matrix and Adaptive Bandwidth Matrix
5. Summary and Prospect
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically weighted regression: A method for exploring spatial nonstationarity. Geogr. Anal. 1996, 28, 281–298. [Google Scholar] [CrossRef]
- Brunsdont, C.; Fotheringham, S.; Charlton, M.E. Geographically weighted regression—Modelling spatial non-stationarity. J. R. Stat. Soc. Ser. D Stat. 1998, 47, 431–443. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Charlton, M.E.; Brunsdon, C. Geographically Weighted Regression: A Natural Evolution of The Expansion Method for Spatial Data Analysis. Environ. Plan. A 1998, 30, 1905–1927. [Google Scholar] [CrossRef]
- Wang, N.; Mei, C.L.; Yan, X.D. Local linear estimation of spatial varying coefficient models: An improvement on the geographically weighted regression technique. Environ. Plan. A 2008, 40, 986–1005. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Leong, Y.Y.; Yue, J.C. A Modification to Geographically Weighted Regression. Int. J. Health Geogr. 2017, 16, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yu, H.; Fotheringham, A.S.; Li, Z.; Oshan, T.; Kang, W.; Wolf, L.J. Inference in multiscale geographically weighted regression. Geogr. Anal. 2020, 52, 87–106. [Google Scholar] [CrossRef]
- Loftsgaarden, D.O.; Quesenberry, C.P. A Nonparametric Estimate of a Multivariate Density Function. Ann. Math. Stat. 1965, 36, 1049–1051. [Google Scholar] [CrossRef]
- Breiman, L.; Meisel, W.; Purcell, E. Variable kernel estimates of multivariate densities. Technometrics 1977, 19, 135–144. [Google Scholar] [CrossRef]
- Abramson, I.S. On bandwidth variation in kernel estimates-a square root law. Ann. Stat. 1982, 10, 1217–1223. [Google Scholar] [CrossRef]
- Fan, J.; Gijbels, I. Data-driven bandwidth selection in local polynomial fitting: Variable bandwidth and spatial adaptation. J. R. Stat. Soc. Ser. B Methodol. 1995, 57, 371–394. [Google Scholar] [CrossRef]
- Tian, M.Z. Selection and Application of bandwidth in Modern Nonparametric Statistics; Science Press: Beijing, China, 2019; pp. 206–260. [Google Scholar]
- Gramacki, A. Nonparametric Kernel Density Estimation and Its Computational Aspects; Springer International Publishing: Cham, Switzerland, 2018; pp. 63–83. [Google Scholar]
- Chacón, J.E.; Duong, T. Multivariate Kernel Smoothing and Its Applications; CRC Press: Boca Raton, FL, USA, 2018; pp. 43–66. [Google Scholar]
- Wand, M.P.; Jones, M.C. Multivariate plug-in bandwidth selection. Comput. Stat. 1994, 9, 97–116. [Google Scholar]
- Duong, T.; Hazelton, M. Plug-in bandwidth matrices for bivariate kernel density estimation. J. Nonparametric Stat. 2003, 15, 17–30. [Google Scholar] [CrossRef]
- Chacón, J.E.; Duong, T. Multivariate plug-in bandwidth selection with unconstrained pilot bandwidth matrices. Test 2010, 19, 375–398. [Google Scholar] [CrossRef]
- Brewer, M. Bayesian model for local smoothing in kernel density estimation. Stat. Comput. 2000, 10, 299–309. [Google Scholar] [CrossRef]
- Zhang, X.; King, M.L.; Hyndman, R.J. A Bayesian approach to bandwidth selection for multivariate kernel density estimation. Comput. Stat. Data Anal. 2006, 50, 3009–3031. [Google Scholar] [CrossRef] [Green Version]
- Zougab, N.; Adjabi, S.; Kokonendji, C. Bayesian estimation of adaptive bandwidth matrices in multivariate kernel density estimation. Comput. Stat. Data Anal. 2014, 75, 28–38. [Google Scholar] [CrossRef]
- Belaid, N.; Adjabi, S.; Kokonendji, C.C.; Zougab, N. Bayesian adaptive bandwidth selector for multivariate discrete kernel estimator. Commun. Stat.-Theory Methods 2018, 47, 2988–3001. [Google Scholar] [CrossRef]
- Gramacki, A.; Gramacki, J. FFT-based fast computation of multivariate kernel density estimators with unconstrained bandwidth matrices. J. Comput. Graph. Stat. 2017, 26, 459–462. [Google Scholar] [CrossRef]
- Sain, S.R.; Baggerly, K.A.; Scott, D.W. Cross-validation of multivariate densities. J. Am. Stat. Assoc. 1994, 89, 807–817. [Google Scholar] [CrossRef]
- Wu, T.; Chen, C.; Chen, H. A variable bandwidth selector in multivariate kernel density estimation. Stat. Probab. Lett. 2007, 77, 462–467. [Google Scholar] [CrossRef]
- Xu, J. Generalized Spatial Variable Coefficient Model. Ph.D. Thesis, Hunan Normal University, Changsha, China, 2009. [Google Scholar]
- Wand, M.P.; Jones, M.C. Comparison of smoothing parameterizations in bivariate kernel density estimation. J. Am. Stat. Assoc. 1993, 88, 520–528. [Google Scholar] [CrossRef]
- Mei, C.L.; Wang, N. Modern Regression Analysis Method; Science Press: Beijing, China, 2012; pp. 163–190. [Google Scholar]
- Feng, J.; Zhang, H.; Hu, X. Spatial non-stationary characteristics of the impacts of precipitation and temperature on FVC: A case study of Yili River Valley, Xinjiang. Chin. J. Ecol. 2016, 36, 4626–4634. [Google Scholar]
- Leung, Y.; Mei, C.L.; Zhang, W.X. Statistical Tests for Spatial Nonstationarity Based on the Geographically Weighted Regression Model. Environ. Plan. A 2000, 32, 9–32. [Google Scholar] [CrossRef]
- Mei, C.L.; Wang, N.; Zhang, W.X. Testing the importance of the explanatory variables in a mixed geographically weighted regression model. Environ. Plan. A Econ. Space 2006, 38, 587–598. [Google Scholar] [CrossRef]
- Wei, C.H.; Qi, F. On the estimation and testing of mixed geographically weighted regression models. Econ. Model. 2012, 29, 2615–2620. [Google Scholar] [CrossRef]
- Mei, C.L.; Xu, M.; Wang, N. A bootstrap test for constant coefficients in geographically weighted regression models. Int. J. Geogr. Inf. Sci. 2016, 30, 1622–1643. [Google Scholar] [CrossRef]
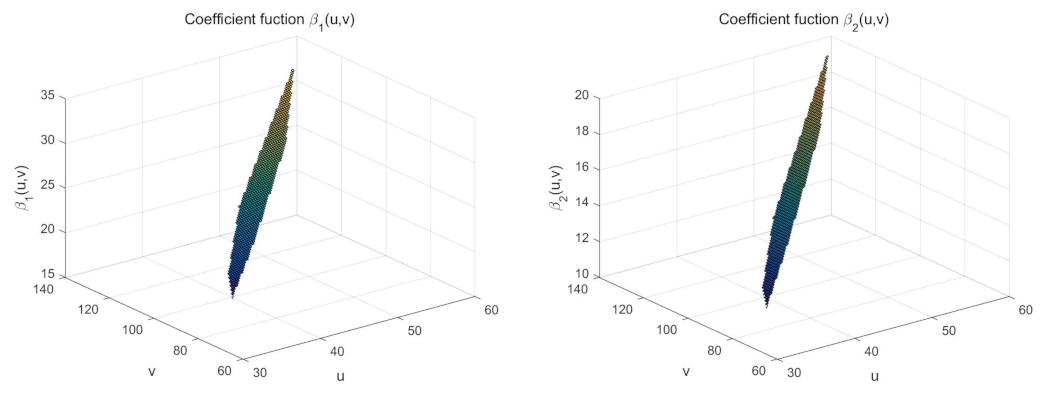
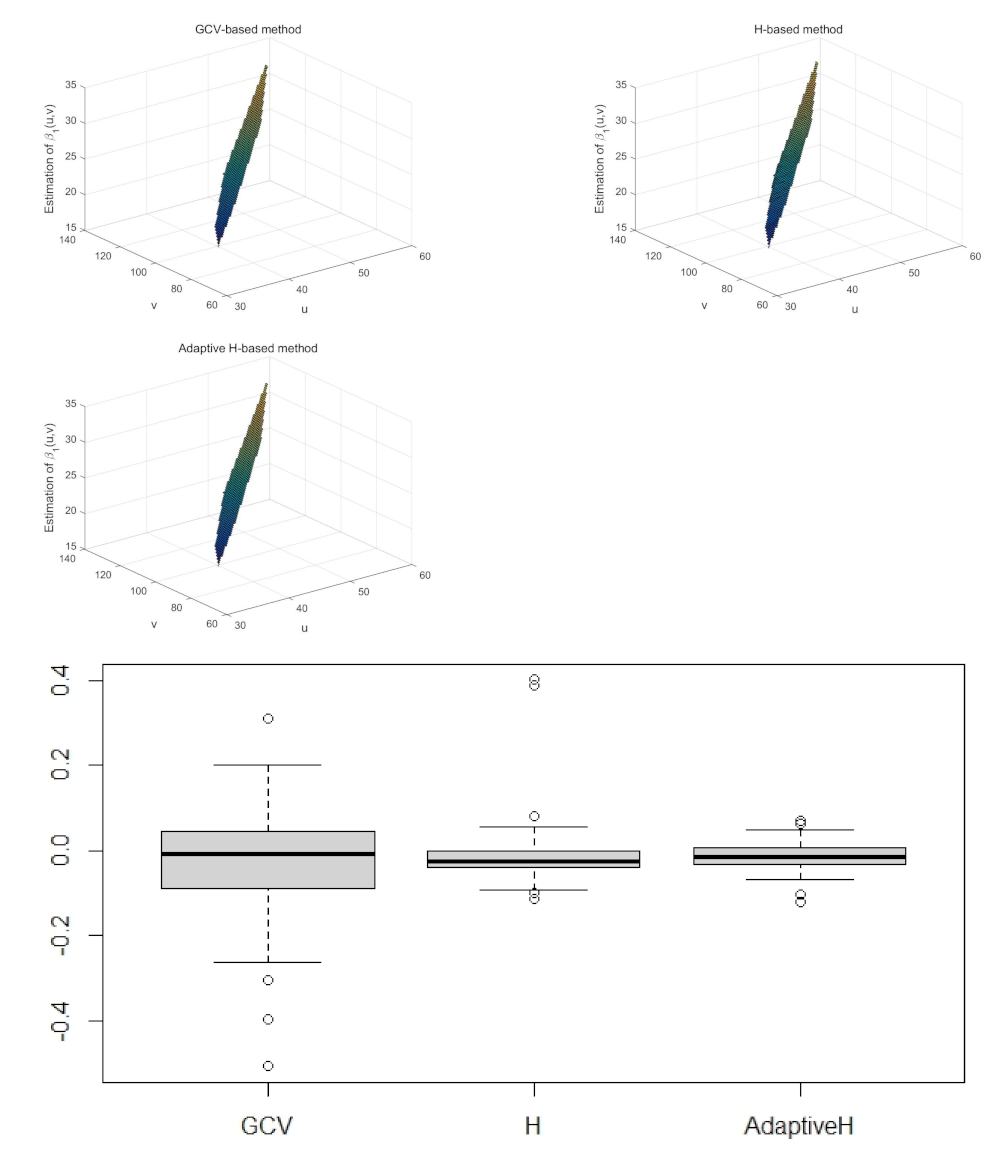
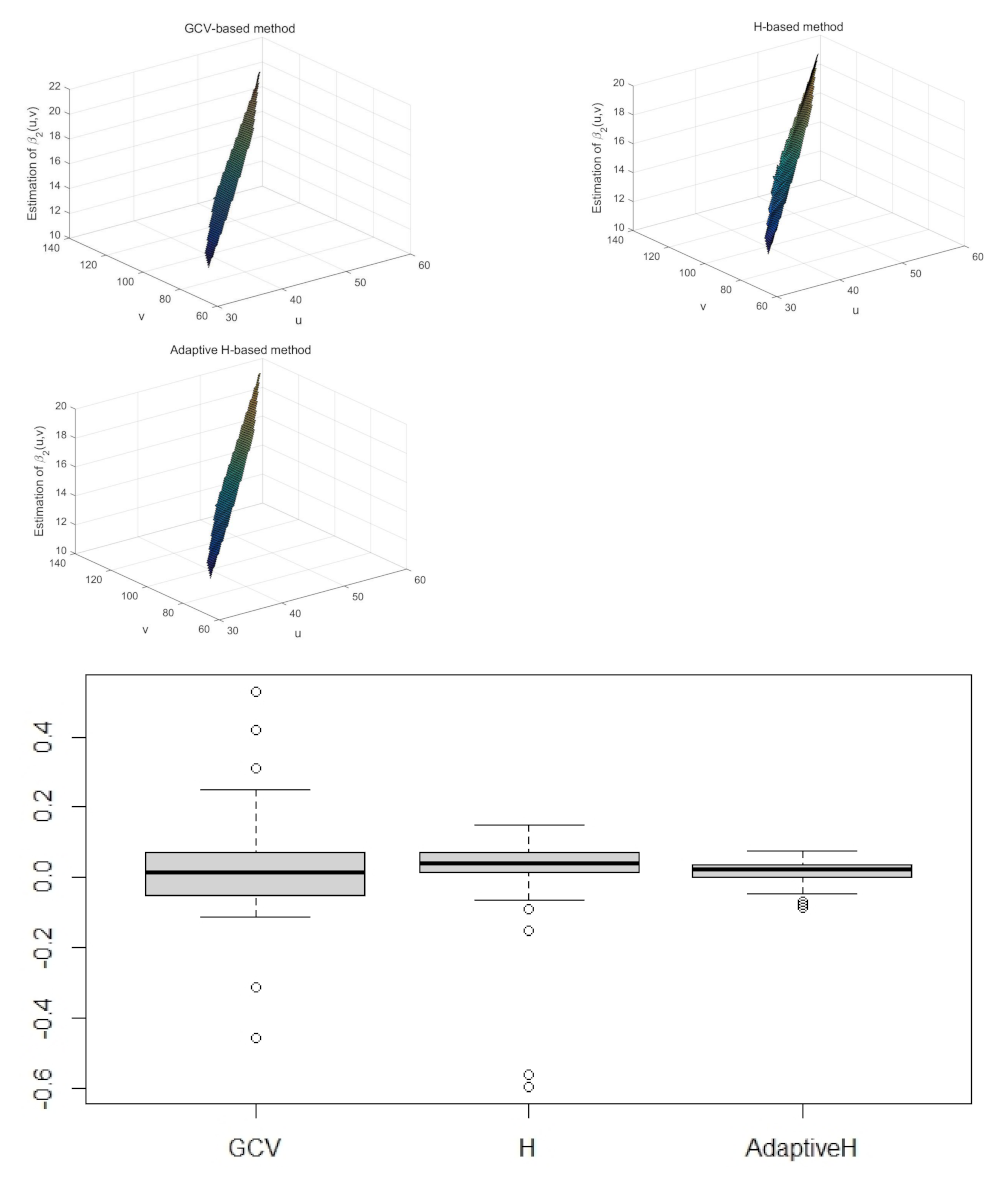
| Bandwidth Type | GCV-Based | Matrix H-Based | Adaptive Matrix H-Based |
|---|---|---|---|
| MSE(Y) | 3.0298 | 2.3928 | 0.6633 |
| MSE() | 0.0048 | 0.0136 | 0.0011 |
| MSE() | 0.0105 | 0.0137 | 0.0012 |
| Running time | 14.24 s | 2.38 s | 5.67 s |
| Bandwidth Type | Bandwidth h | Bandwidth Matrix H |
|---|---|---|
| MSE(Y) | 0.074 | 0.039 |
| Running time | 33.69 min | 1.32 min |
| Regression Coefficients | Minimum | 1/4 Quantile | Median | 3/4 Quantile | Maximum |
|---|---|---|---|---|---|
| −10.5274 | −0.0085 | 0.8041 | 1.3285 | 12.5262 | |
| −0.0349 | −0.0017 | 0.0003 | 0.0021 | 0.0358 | |
| −0.0788 | 0.0013 | 0.0155 | 0.0566 | 0.3834 |
| Regression Coefficients | Minimum | 1/4 Quantile | Median | 3/4 Quantile | Maximum |
|---|---|---|---|---|---|
| −5.3196 | 0.3858 | 0.8049 | 1.1690 | 6.6727 | |
| −0.0207 | −0.0011 | 0.0002 | 0.0013 | 0.0196 | |
| −0.0288 | −0.0008 | 0.0141 | 0.0520 | 0.2599 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Lu, Y.; Zhang, H.; Jiang, H.; Shi, Q. Selection of the Bandwidth Matrix in Spatial Varying Coefficient Models to Detect Anisotropic Regression Relationships. Mathematics 2021, 9, 2343. https://doi.org/10.3390/math9182343
Hu X, Lu Y, Zhang H, Jiang H, Shi Q. Selection of the Bandwidth Matrix in Spatial Varying Coefficient Models to Detect Anisotropic Regression Relationships. Mathematics. 2021; 9(18):2343. https://doi.org/10.3390/math9182343
Chicago/Turabian StyleHu, Xijian, Yaori Lu, Huiguo Zhang, Haijun Jiang, and Qingdong Shi. 2021. "Selection of the Bandwidth Matrix in Spatial Varying Coefficient Models to Detect Anisotropic Regression Relationships" Mathematics 9, no. 18: 2343. https://doi.org/10.3390/math9182343





