Spatio-Temporal Spread Pattern of COVID-19 in Italy
Abstract
:1. Introduction
2. Concerns Related to the Italian COVID-19 Data
- Delays in reporting cases. These occur because counts are updated on the notification day rather than aligned to a more appropriate date. Deaths may be counted on the day of the reporting instead of on the day of the outcome, and positive status may also be counted when test results are received, with swabs being done from one day to weeks after symptoms’ onset. Moreover, the reporting procedure may differ from area to area, making the data not comparable in space;
- Lack of comparable data. In Italy, up to the end of April 2020, only the total number of daily positive swabs were available, with neither information on swabs or tested individuals. This information would have been essential to use the swabs’ count to model the whole first pandemic wave;
- Time-varying under-reporting of COVID-19 cases. It is well established that people diagnosed with COVID-19 disease are only a tiny fraction of the infected ones. the swabs’ count changes over time since the tracking was highly symptoms’ driven in the first phase of the outbreak, and it continued to change following the different policies adopted. in particular, the swabs’ count has continued to increase significantly due to the increased availability of swabs since they became crucial for determining local government actions.
3. Spatial and Spatio-Temporal Models for Disease Mapping
- Type I assumes that the two unstructured effects and , give rise to the structure matrix , because both u and do not have a spatial or temporal structure. Consequently, we assume no spatial or temporal structure on the interaction either and, therefore, ;
- Type II combines the structured temporal main effect and the unstructured spatial effect . We write the structure matrix as where and is the neighborhood structure specified for instance through a first- or second-order random walk. This leads to the assumption that for the i-th area the parameter vector has an autoregressive structure on the time component, which is independent from the ones of the other areas;
- Type III combines the unstructured temporal effect and the spatially structured main effect . We write the structure matrix as , where and is a neighboring structure defined through the CAR specification. This leads to the assumption that the parameters of the t-th time point have a spatial structure independent from the other time points.
- Finally, Type IV is the most complex type of interaction, assuming that the spatially and temporally structured effects and interact. the structure matrix can be written as , which basically assumes that the temporal dependency structure for each area is not independent from all the other areas anymore, but depends on the temporal pattern of the neighboring areas as well.
4. Modeling COVID-19 Infection Spread
4.1. Lockdown Effectiveness in Northern Italy
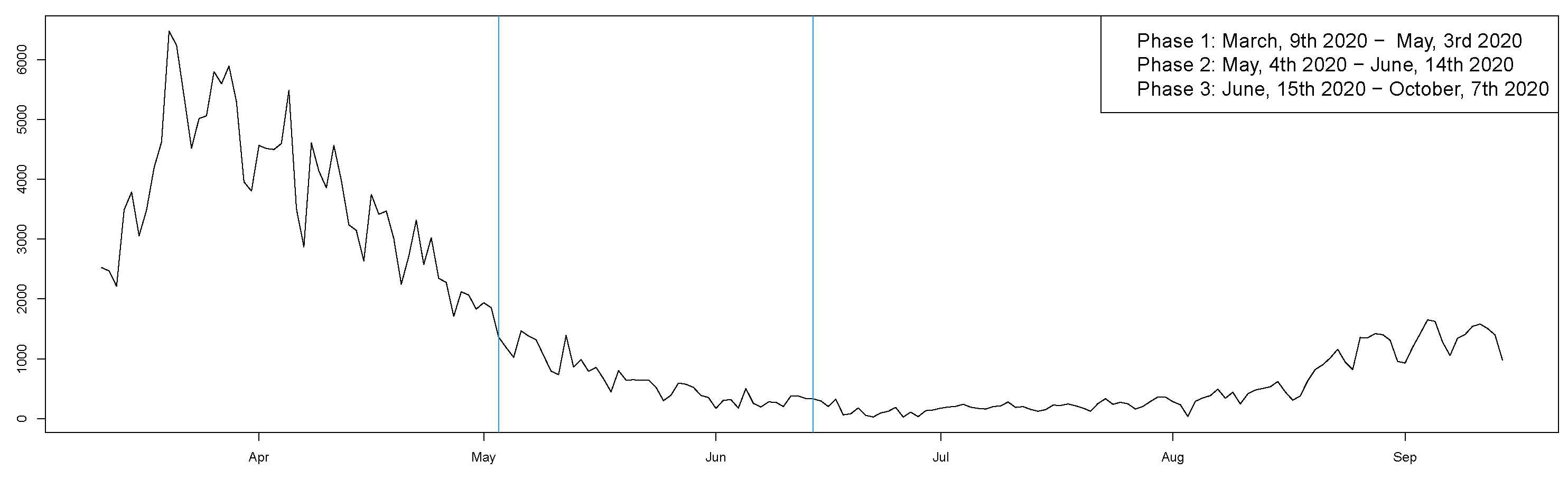
4.2. Spatio-Temporal Spread of COVID-19 in the Whole Italian Territory during the First Wave
- Phase 1: lockdown (9 March 2020–3 May 2020);
- Phase 2: easing of containment measures (4 May 2020–14 June 2020);
- Phase 3: coexistence with COVID-19 (15 June 2020–7 October 2020).
5. Conclusions
- During the pre-lockdown period, the spread of the COVID-19 in the provinces under study could be ascribable to the spatial arrangement of provinces, the same conclusion can not be drawn for the post-lockdown period, since the decreasing number of people moving among provinces;
- The selected spatio-temporal model suggests that the temporal evolution of cases that occurred in each province is independent of the temporal evolution of the other provinces. This means that the number of contagions and their temporal trends may not be caused by the spatial movements of people, but by some aspects that are specific of the considered provinces. That is, for a better comprehension of this spreading phenomenon, point process, even accounting for external information, would be more appropriate;
- The proposed models are our best option for dealing with aggregated data at the district level. Indeed, starting from this low-detailed scale dataset and the absence of geocoded health data, our study still shows the proposed BYM models’ advantages;
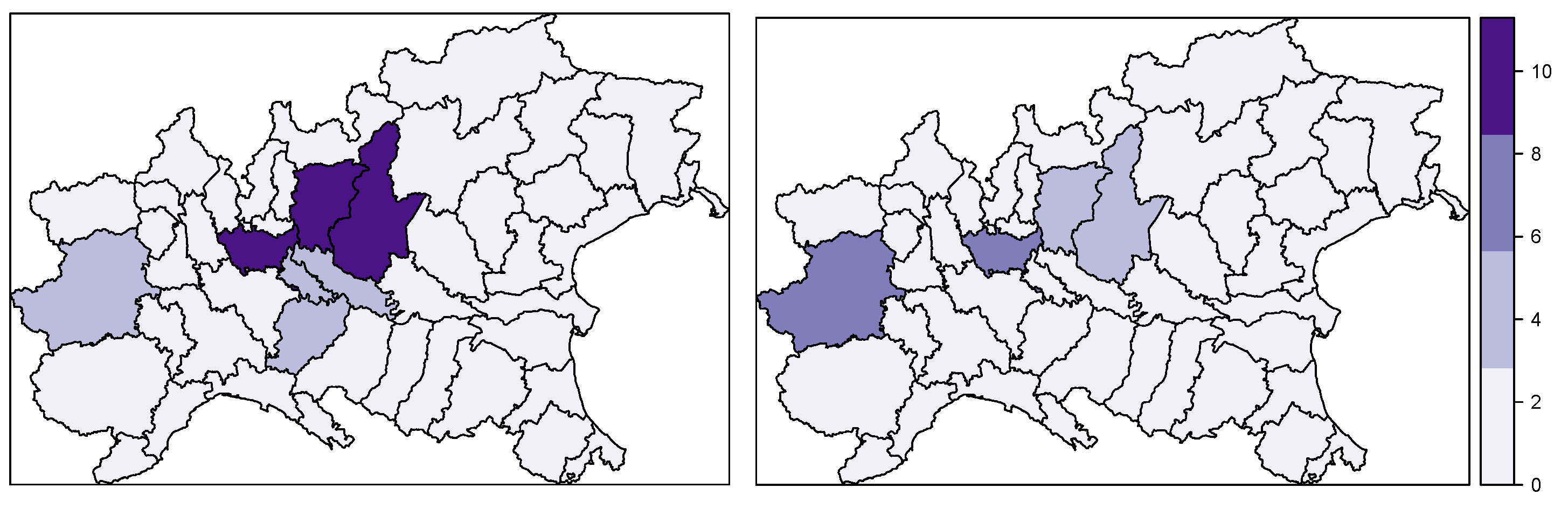
- The estimated posterior means of the district-specific relative risk identified the highest-risk areas, confirming that the most at-risk provinces are in Lombardy (i.e., Milan, Bergamo and Brescia) and Piedmont (Turin).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Guliyev, H. Determining the spatial effects of COVID-19 using the spatial panel data model. Spat. Stat. 2020, 38, 100443. [Google Scholar] [CrossRef]
- Mollalo, A.; Vahedi, B.; Rivera, K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total Environ. 2020, 728, 138884. [Google Scholar] [CrossRef] [PubMed]
- Arauzo-Carod, J.M. A first insight about spatial dimension of COVID-19: Analysis at municipality level. J. Public Health 2021, 43, 98–106. [Google Scholar] [CrossRef] [PubMed]
- Cordes, J.; Castro, M.C. Spatial analysis of COVID-19 clusters and contextual factors in New York City. Spat. Spatio-Temporal Epidemiol. 2020, 34, 100355. [Google Scholar] [CrossRef] [PubMed]
- Desjardins, M.; Hohl, A.; Delmelle, E. Rapid surveillance of COVID-19 in the United States using a prospective space-time scan statistic: Detecting and evaluating emerging clusters. Appl. Geogr. 2020, 118, 102202. [Google Scholar] [CrossRef] [PubMed]
- Hohl, A.; Delmelle, E.M.; Desjardins, M.R.; Lan, Y. Daily surveillance of COVID-19 using the prospective space-time scan statistic in the United States. Spat. Spatio-Temporal Epidemiol. 2020, 34, 100354. [Google Scholar] [CrossRef] [PubMed]
- Kang, D.; Choi, H.; Kim, J.H.; Choi, J. Spatial epidemic dynamics of the COVID-19 outbreak in China. Int. J. Infect. Dis. 2020, 94, 96–102. [Google Scholar] [CrossRef] [PubMed]
- Liao, H.; Marley, G.; Si, Y.; Wang, Z.; Xie, Y.; Wang, C.; Tang, W. A Tempo-geographic Analysis of Global COVID-19 Epidemic Outside of China. medRxiv 2020. [Google Scholar] [CrossRef]
- Ramírez-Aldana, R.; Gomez-Verjan, J.C.; Bello-Chavolla, O.Y. Spatial analysis of COVID-19 spread in Iran: Insights into geographical and structural transmission determinants at a province level. PLoS Neglected Trop. Dis. 2020, 14, e0008875. [Google Scholar] [CrossRef]
- Chen, Y.C.; Lu, P.E.; Chang, C.S.; Liu, T.H. A Time-Dependent SIR Model for COVID-19 With Undetectable Infected Persons. IEEE Trans. Netw. Sci. Eng. 2020, 7, 3279–3294. [Google Scholar] [CrossRef]
- Giordano, G.; Blanchini, F.; Bruno, R.; Colaneri, P.; Di Filippo, A.; Di Matteo, A.; Colaneri, M. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat. Med. 2020, 26, 855–860. [Google Scholar] [CrossRef]
- Gatto, M.; Bertuzzo, E.; Mari, L.; Miccoli, S.; Carraro, L.; Casagrandi, R.; Rinaldo, A. Spread and dynamics of the COVID-19 epidemic in Italy: Effects of emergency containment measures. Proc. Natl. Acad. Sci. USA 2020, 117, 10484–10491. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 2020, 369, eabb9789. [Google Scholar] [CrossRef]
- Ioannidis, J.P.; Cripps, S.; Tanner, M.A. Forecasting for COVID-19 has failed. Int. J. Forecast. 2020. [Google Scholar] [CrossRef] [PubMed]
- D’Angelo, N.; Adelfio, G.; Abbruzzo, A. Spatio-temporal analysis of the Covid-19 spread in Italy by Bayesian hierarchical models. In Book of Short Papers—SIS 2021; Pearson: New York, NY, USA, 2021; pp. 1016–1020. [Google Scholar]
- Wu, X.; Nethery, R.C.; Sabath, M.B.; Braun, D.; Dominici, F. Air pollution and COVID-19 mortality in the United States: Strengths and limitations of an ecological regression analysis. Sci. Adv. 2020, 6, eabd4049. [Google Scholar] [CrossRef] [PubMed]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- Abellan, J.J.; Richardson, S.; Best, N. Use of space–time models to investigate the stability of patterns of disease. Environ. Health Perspect. 2008, 116, 1111–1119. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Møller, J.; Syversveen, A.R.; Waagepetersen, R.P. Log gaussian cox processes. Scand. J. Stat. 1998, 25, 451–482. [Google Scholar] [CrossRef]
- Konstantinoudis, G.; Schuhmacher, D.; Rue, H.; Spycher, B.D. Discrete versus continuous domain models for disease mapping. Spat. Spatio-Temporal Epidemiol. 2020, 32, 100319. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Brown, P.; Gesink, D.C.; Rue, H. Log Gaussian Cox processes and spatially aggregated disease incidence data. Stat. Methods Med. Res. 2012, 21, 479–507. [Google Scholar] [CrossRef]
- Loro, P.A.D.; Divino, F.; Farcomeni, A.; Lasinio, G.J.; Lovison, G.; Maruotti, A.; Mingione, M. Nowcasting COVID-19 incidence indicators during the Italian first outbreak. arXiv 2020, arXiv:2010.12679. [Google Scholar]
- Briz-Redón, Á. The impact of modelling choices on modelling outcomes: A spatio-temporal study of the association between COVID-19 spread and environmental conditions in Catalonia (Spain). Stoch. Environ. Res. Risk Assess. 2021, 1–13. [Google Scholar] [CrossRef]
- Elliot, P.; Wakefield, J.C.; Best, N.G.; Briggs, D.J. Spatial Epidemiology: Methods and Applications; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Lesaffre, E.; Lawson, A.B. Bayesian Biostatistics; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Tiefelsdorf, M.; Griffith, D.A.; Boots, B. A variance-stabilizing coding scheme for spatial link matrices. Environ. Plan. A 1999, 31, 165–180. [Google Scholar] [CrossRef]
- Kelejian, H.H.; Prucha, I.R. Specification and estimation of spatial autoregressive models with autoregressive and heteroskedastic disturbances. J. Econom. 2010, 157, 53–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sørbye, S.H.; Rue, H. Scaling intrinsic Gaussian Markov random field priors in spatial modelling. Spat. Stat. 2014, 8, 39–51. [Google Scholar] [CrossRef]
- MacNab, Y.C. On Gaussian Markov random fields and Bayesian disease mapping. Stat. Methods Med. Res. 2011, 20, 49–68. [Google Scholar] [CrossRef]
- Riebler, A.; Sørbye, S.H.; Simpson, D.; Rue, H. An intuitive Bayesian spatial model for disease mapping that accounts for scaling. Stat. Methods Med. Res. 2016, 25, 1145–1165. [Google Scholar] [CrossRef] [Green Version]
- Dean, C.; Ugarte, M.; Militino, A. Detecting interaction between random region and fixed age effects in disease mapping. Biometrics 2001, 57, 197–202. [Google Scholar] [CrossRef] [PubMed]
- Simpson, D.; Rue, H.; Riebler, A.; Martins, T.G.; Sørbye, S.H. Penalising model component complexity: A principled, practical approach to constructing priors. Stat. Sci. 2017, 32, 1–28. [Google Scholar] [CrossRef]
- Moraga, P. Geospatial Health Data: Modeling and Visualization with R-INLA and Shiny; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Best, N.; Richardson, S.; Thomson, A. A comparison of Bayesian spatial models for disease mapping. Stat. Methods Med. Res. 2005, 14, 35–59. [Google Scholar] [CrossRef]
- Anderson, C.; Lee, D.; Dean, N. Bayesian cluster detection via adjacency modelling. Spat. Spatio-Temporal Epidemiol. 2016, 16, 11–20. [Google Scholar] [CrossRef] [Green Version]
- Bernardinelli, L.; Clayton, D.; Pascutto, C.; Montomoli, C.; Ghislandi, M.; Songini, M. Bayesian analysis of space—Time variation in disease risk. Stat. Med. 1995, 14, 2433–2443. [Google Scholar] [CrossRef]
- Knorr-Held, L. Bayesian modelling of inseparable space-time variation in disease risk. Stat. Med. 2000, 19, 2555–2567. [Google Scholar] [CrossRef] [Green Version]
- Clayton, D.G. Generalized linear mixed models. Markov Chain Monte Carlo Pract. 1996, 1, 275–302. [Google Scholar]
- Blangiardo, M.; Cameletti, M. Spatial and Spatio-Temporal Bayesian Models with R-INLA; John Wiley-Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Goicoa, T.; Adin, A.; Ugarte, M.; Hodges, J. In spatio-temporal disease mapping models, identifiability constraints affect PQL and INLA results. Stoch. Environ. Res. Risk Assess. 2018, 32, 749–770. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Diggle, P.; Guttorp, P.; Fuentes, M. Handbook of Spatial Statistics; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Allard, D. Handbook of Spatial Statistics. Book Review; Gelfand, A.E., Diggle, P.J., Fuentes, M., Peter Guttorp, Eds.; CRC Press: Boca Raton, FL, USA, 2011; Volume 21, pp. 293–294. [Google Scholar]
- Hastings, W.K. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B Stat. Methodol. 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Martins, T.G.; Simpson, D.; Lindgren, F.; Rue, H. Bayesian computing with INLA: New features. Comput. Stat. Data Anal. 2013, 67, 68–83. [Google Scholar] [CrossRef] [Green Version]
- Blangiardo, M.; Cameletti, M.; Baio, G.; Rue, H. Spatial and spatio-temporal models with R-INLA. Spat. Spatio-Temporal Epidemiol. 2013, 4, 33–49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lindgren, F.; Rue, H.; Lindström, J. An explicit link between Gaussian fields and Gaussian Markov random fields: The stochastic partial differential equation approach. J. R. Stat. Soc. Ser. B Stat. Methodol. 2011, 73, 423–498. [Google Scholar] [CrossRef] [Green Version]
- Bisanzio, D.; Giacobini, M.; Bertolotti, L.; Mosca, A.; Balbo, L.; Kitron, U.; Vazquez-Prokopec, G.M. Spatio-temporal patterns of distribution of West Nile virus vectors in eastern Piedmont Region, Italy. Parasites Vectors 2011, 4, 230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schrödle, B.; Held, L. Spatio-temporal disease mapping using INLA. Environmetrics 2011, 22, 725–734. [Google Scholar] [CrossRef]
- Schrödle, B.; Held, L.; Rue, H. Assessing the Impact of a Movement Network on the Spatiotemporal Spread of Infectious Diseases. Biometrics 2012, 68, 736–744. [Google Scholar] [CrossRef]
- Cameletti, M.; Lindgren, F.; Simpson, D.; Rue, H. Spatio-temporal modeling of particulate matter concentration through the SPDE approach. AStA Adv. Stat. Anal. 2013, 97, 109–131. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Rubio, V.; Bivand, R.; Rue, H. A New Latent Class to Fit Spatial Econometrics Models with Integrated Nested Laplace Approximations. Procedia Environ. Sci. 2015, 27, 116–118. [Google Scholar] [CrossRef] [Green Version]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Adin, A.; Goicoa, T.; Ugarte, M.D. Online relative risks/rates estimation in spatial and spatio-temporal disease mapping. Comput. Methods Programs Biomed. 2019, 172, 103–116. [Google Scholar] [CrossRef] [Green Version]
- Haug, N.; Geyrhofer, L.; Londei, A.; Dervic, E.; Desvars-Larrive, A.; Loreto, V.; Pinior, B.; Thurner, S.; Klimek, P. Ranking the effectiveness of worldwide COVID-19 government interventions. Nat. Hum. Behav. 2020, 4, 1303–1312. [Google Scholar] [CrossRef]
- Richardson, S.; Thomson, A.; Best, N.; Elliott, P. Interpreting posterior relative risk estimates in disease-mapping studies. Environ. Health Perspect. 2004, 112, 1016–1025. [Google Scholar] [CrossRef]
- Meyer, S.; Held, L.; Höhle, M. Spatio-temporal analysis of epidemic phenomena using the R package surveillance. arXiv 2014, arXiv:1411.0416. [Google Scholar] [CrossRef] [Green Version]
- Adelfio, G.; Chiodi, M. Including covariates in a space-time point process with application to seismicity. Stat. Methods Appl. 2021, 30, 947–971. [Google Scholar] [CrossRef]


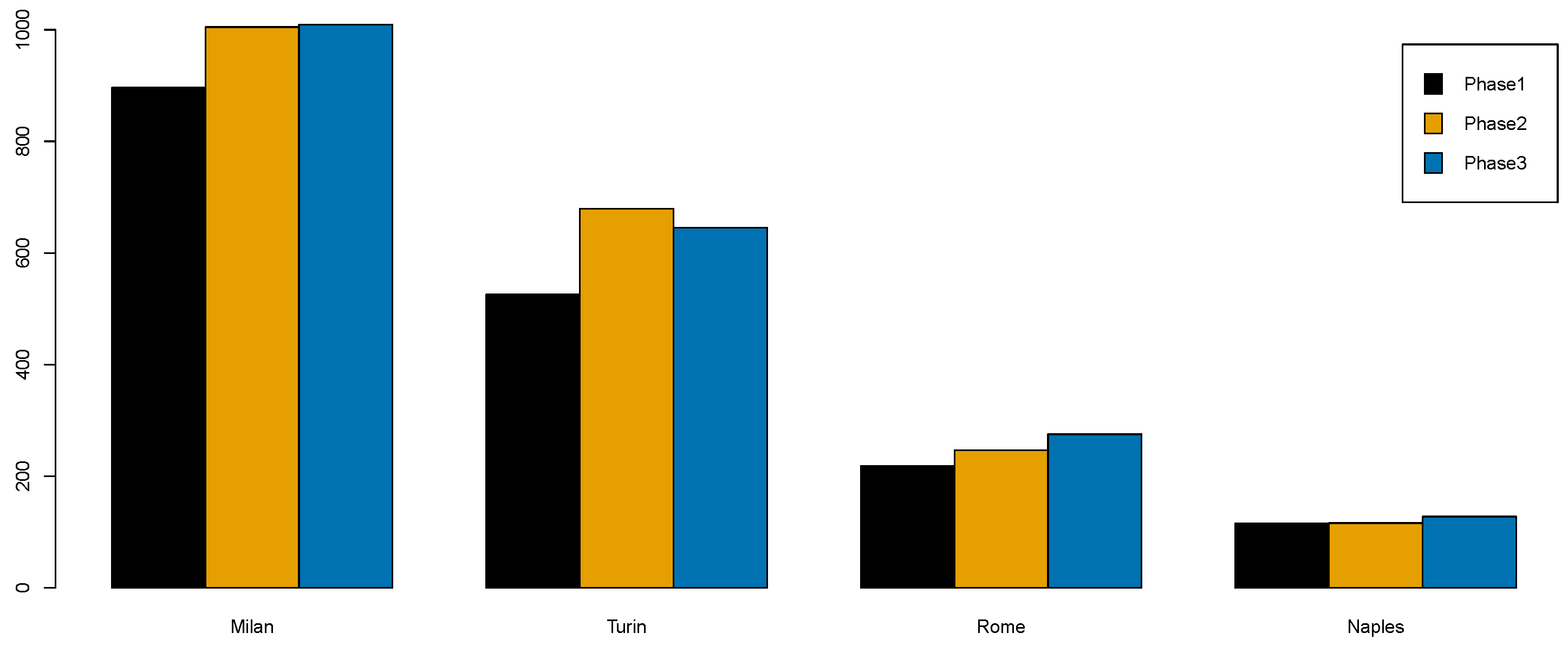
| Model | Interactions | Spatial Correlation | Temporal Correlation | DIC |
|---|---|---|---|---|
| BYM | – | – | – | 135,642.433 |
| Linear T | – | – | – | 52,002.912 |
| Type I | and | – | – | 4695.569 |
| Type II | and | – | ✓ | 4695.264 |
| Type III | and | ✓ | – | 4695.281 |
| Type IV | and | ✓ | ✓ | 5441.607 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Angelo, N.; Abbruzzo, A.; Adelfio, G. Spatio-Temporal Spread Pattern of COVID-19 in Italy. Mathematics 2021, 9, 2454. https://doi.org/10.3390/math9192454
D’Angelo N, Abbruzzo A, Adelfio G. Spatio-Temporal Spread Pattern of COVID-19 in Italy. Mathematics. 2021; 9(19):2454. https://doi.org/10.3390/math9192454
Chicago/Turabian StyleD’Angelo, Nicoletta, Antonino Abbruzzo, and Giada Adelfio. 2021. "Spatio-Temporal Spread Pattern of COVID-19 in Italy" Mathematics 9, no. 19: 2454. https://doi.org/10.3390/math9192454






