Analytical Stress Solution and Numerical Mechanical Behavior of Rock Mass Containing an Opening under Different Confining Stress Conditions
Abstract
:1. Introduction
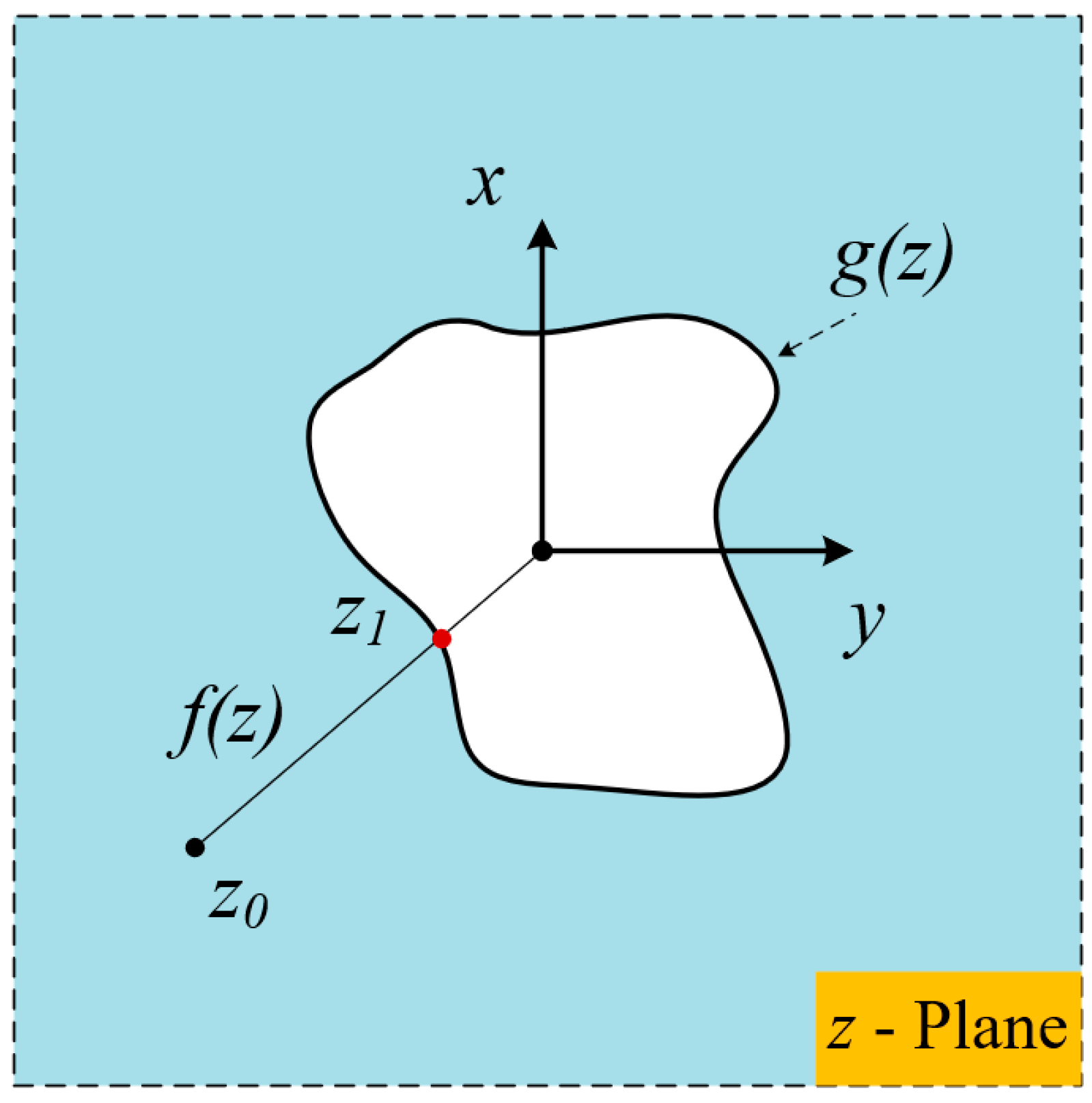
2. Determination of Mapping Function
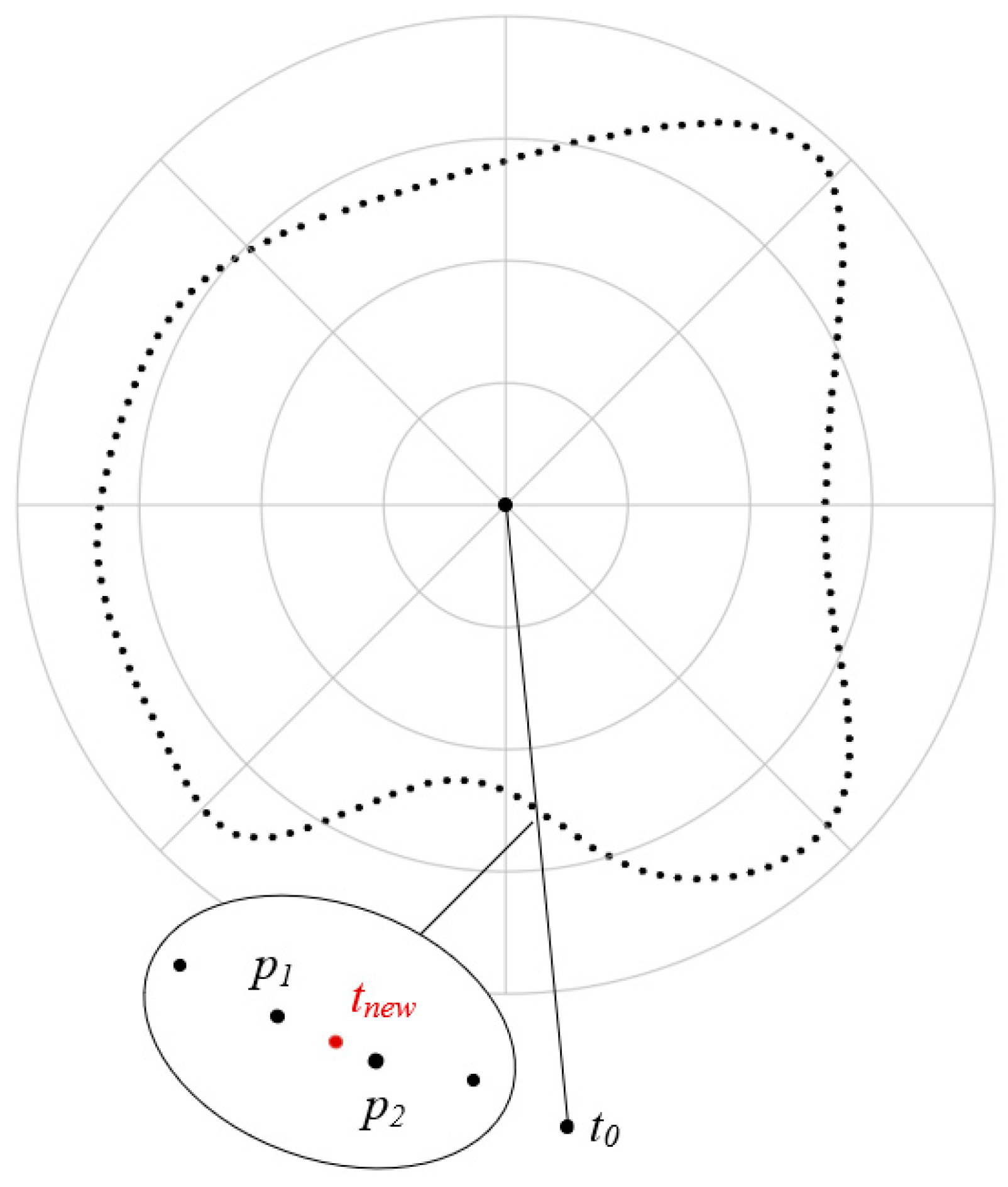
2.1. Principles of Triangle Interpolation
2.2. The Determination of Mapping Functions
3. Stress Solution of Plates Containing a Single Opening
3.1. Calculation Models
3.2. Stress Calculation for Plates
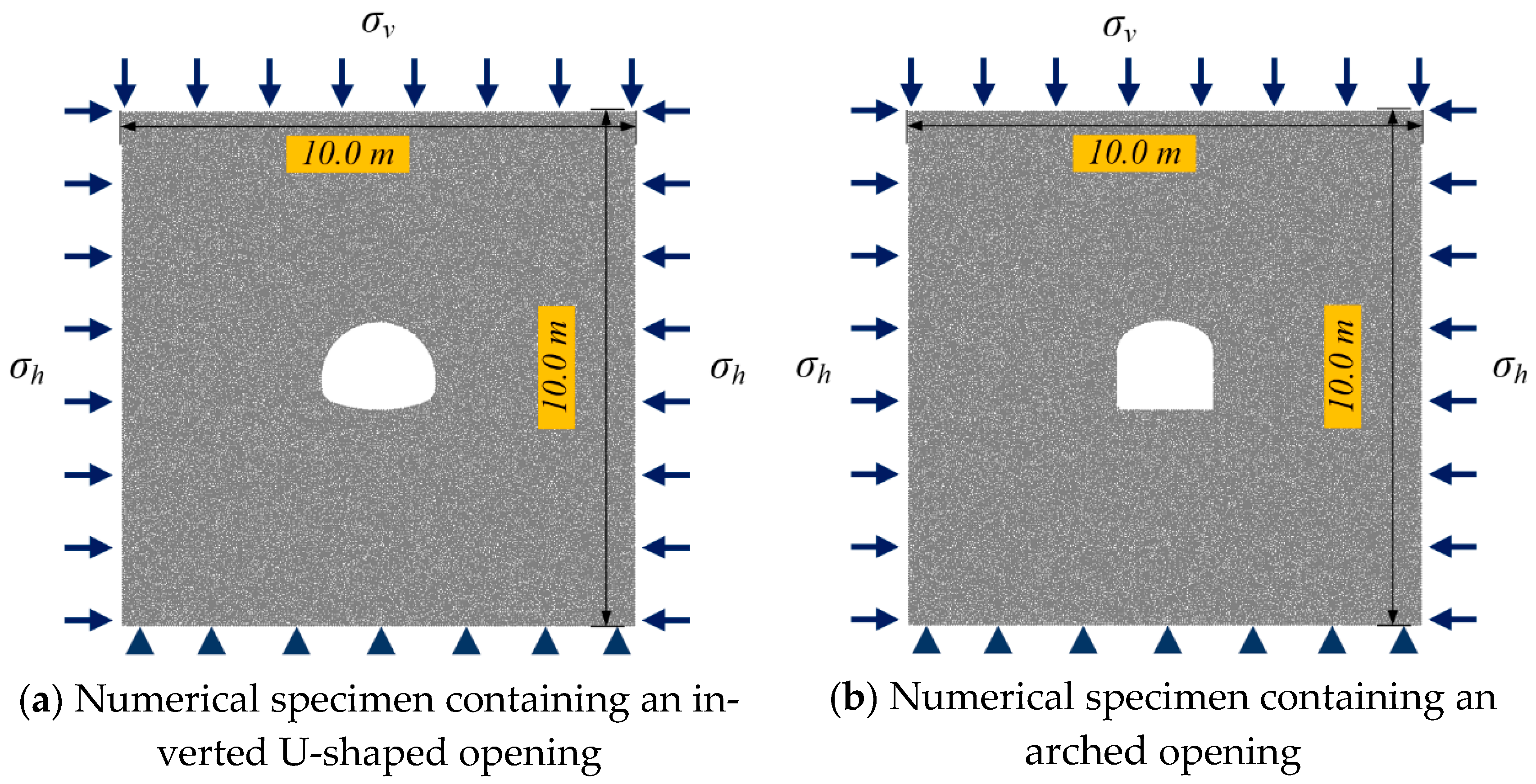
4. DEM Numerical Simulation
4.1. Numerical Modelling
4.2. Mechanical Properties
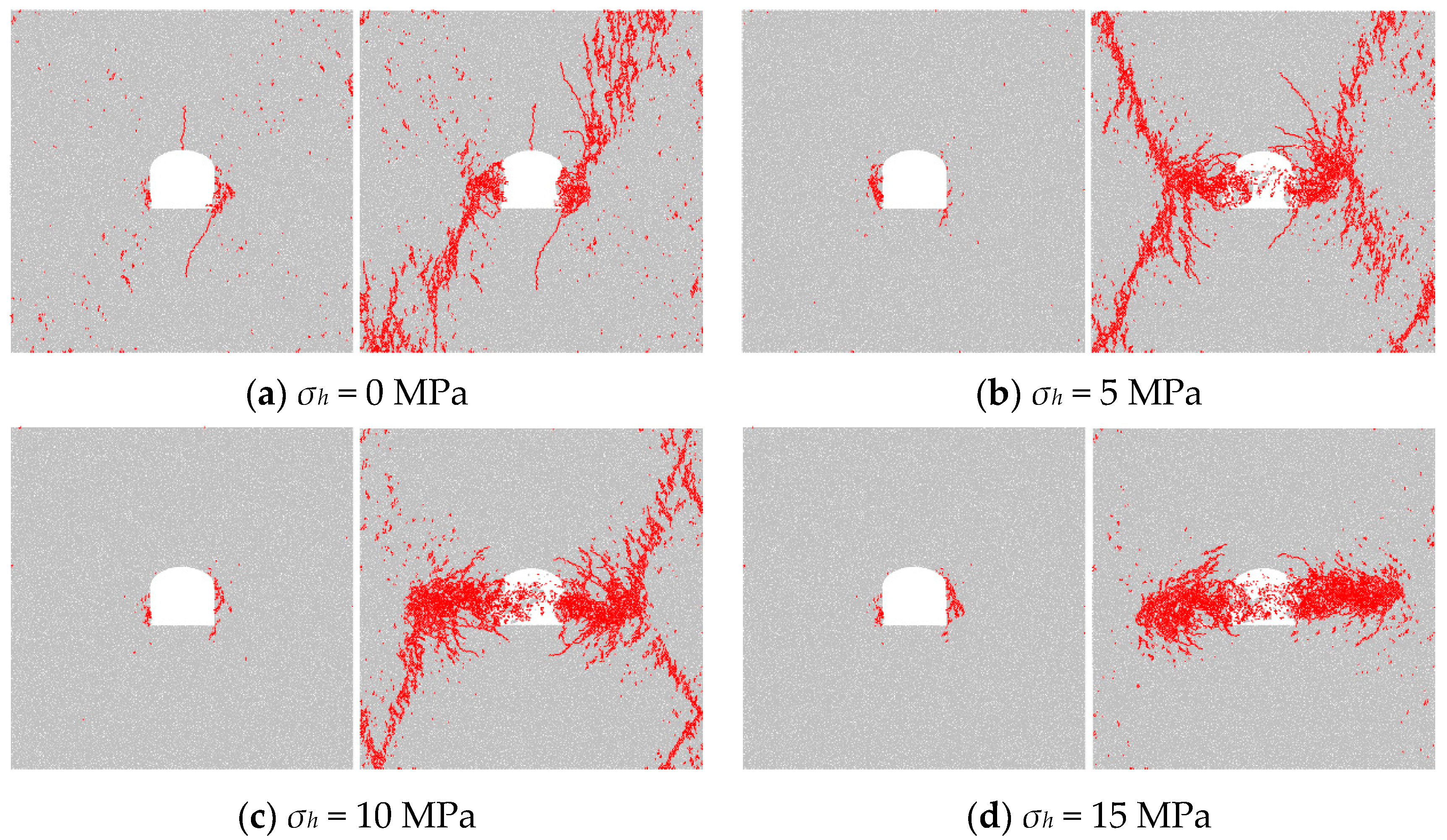
4.3. Failure Patterns
5. Discussion
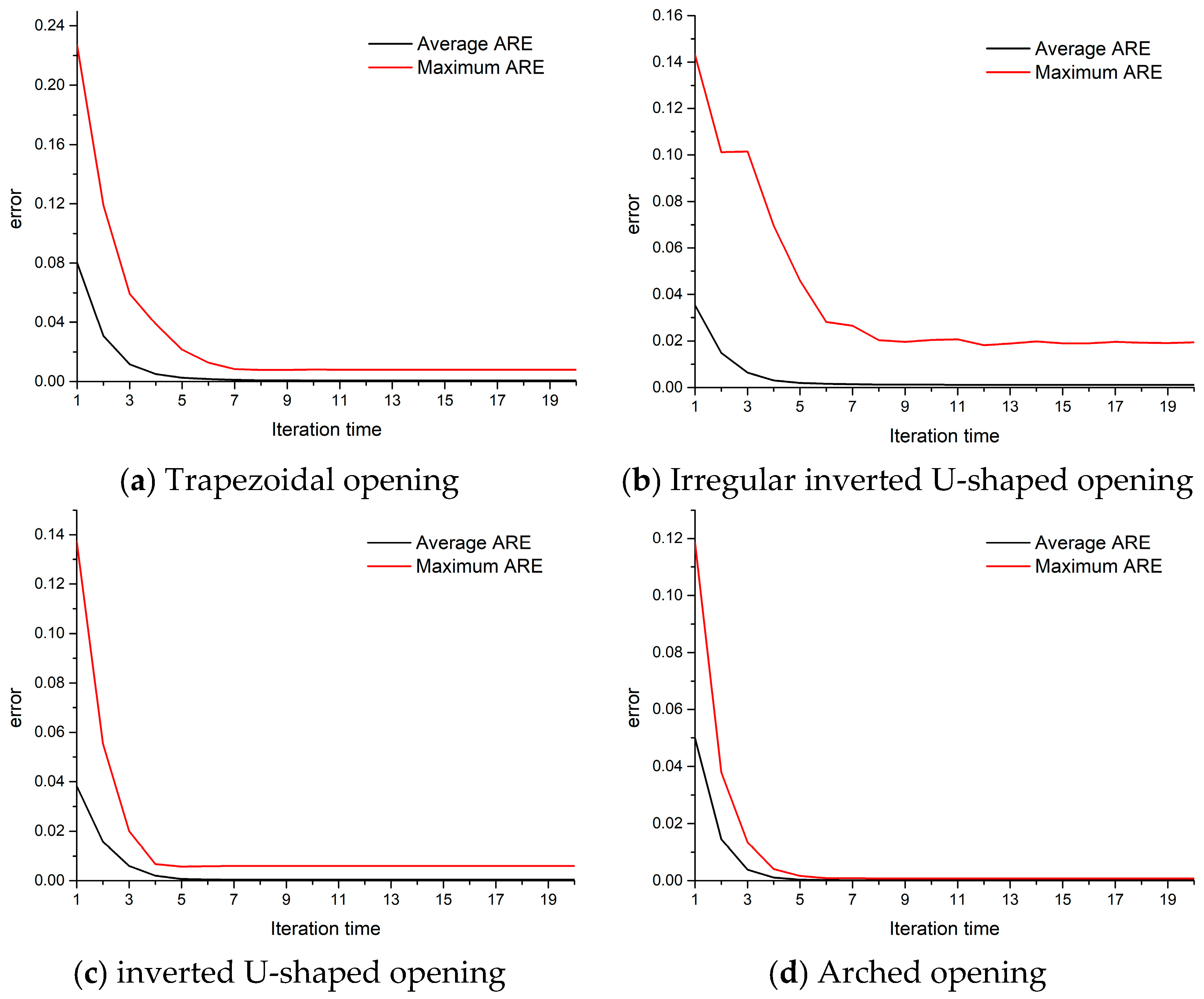
5.1. Generality of the Improved Triangle Interpolation Method for the Determination of Mapping Function
5.2. Influence of Opening Shape and Confining Stress on the Mechanical Behaviour of Specimens
6. Conclusions
- (1)
- Mapping function is essential for the stress solution of rock mass around underground openings. By keeping even and odd interpolation points iterating each other repeatedly, the mapping function for a given opening can be effectively determined by the triangle interpolation method. The key point of this method is to move the calculated mapping points into the opening boundary during each iteration. Compared with boundary curve function, the method of sampling reference points at the boundary combined with linear interpolation is suggested for this adjustment as it is easy to conduct and promise high accuracy.
- (2)
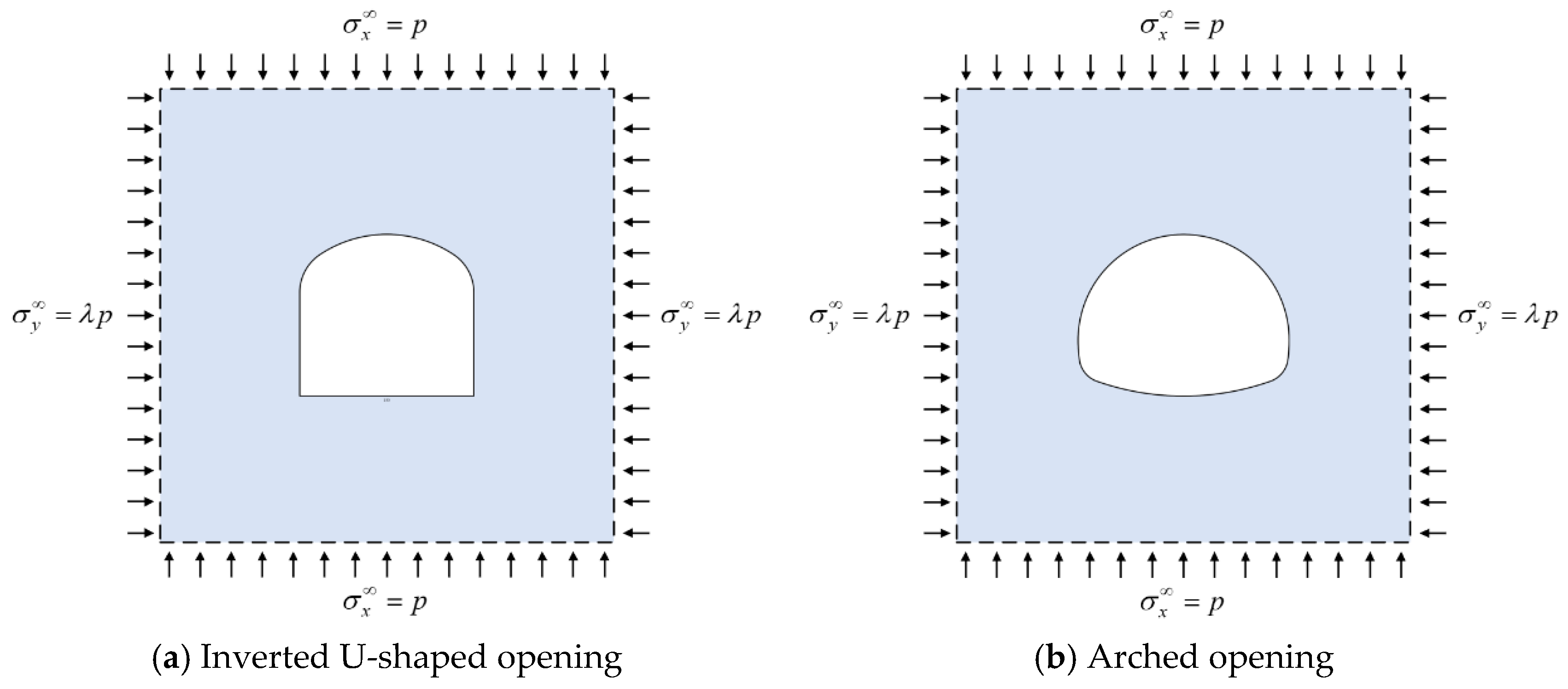
- Stress distribution characteristics around the opening are significantly affected by the opening shape, which further affects the stability and failure pattern of the rock mass. The maximum hoop stress at the boundary of the inverted U-shaped opening is much higher than that at the boundary of the arched opening under the same far-field stress condition and shows a linear increasing trend with the increase in lateral pressure coefficient. However, the sensitivity of the maximum hoop stress of the later one to the lateral pressure coefficient is much less, remaining at a stable level despite of the varying lateral pressure coefficient.
- (3)
- Combining the analytical stress solution and DEM numerical tests shows that the failure patterns of specimens in the pre-peak stage agree well with the analytical elastic stress solution. Under uniaxial stress conditions, initial failure is characterized by tensile cracks from the roof and floor of the openings, where there are tensile stress concentration areas, then failure from the sidewalls and corners caused by concentrated compressive stress is observed. Under biaxial stress conditions, the analytical stress solution reveals that tensile stress around the openings gradually decreases and finally coverts into compressive stress with the increase in the lateral pressure coefficient. Accordingly, the tensile failure is suppressed in the corresponding numerical cases.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhou, Z.; Cai, X.; Li, X.; Cao, W.; Du, X. Dynamic Response and Energy Evolution of Sandstone Under Coupled Static–Dynamic Compression: Insights from Experimental Study into Deep Rock Engineering Applications. Rock Mech. Rock Eng. 2020, 53, 1305–1331. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, Z.; Zang, H.; Song, Z. Water saturation effects on dynamic behavior and microstructure damage of sandstone: Phenomena and mechanisms. Eng. Geol. 2020, 276, 105760. [Google Scholar] [CrossRef]
- Wang, S.-F.; Tang, Y.; Li, X.-B.; Du, K. Analyses and predictions of rock cuttabilities under different confining stresses and rock properties based on rock indentation tests by conical pick. Trans. Nonferr. Met. Soc. China 2021, 31, 1766–1783. [Google Scholar] [CrossRef]
- Wang, S.-F.; Tang, Y.; Wang, S.-Y. Influence of brittleness and confining stress on rock cuttability based on rock indentation tests. J. Cent. South. Univ. 2021, 1–15. [Google Scholar] [CrossRef]
- Song, Z.; Konietzky, H.; Cai, X. Modulus degradation of concrete exposed to compressive fatigue loading: Insights from lab testing. Struct. Eng. Mech. 2021, 78, 281–296. [Google Scholar]
- Tan, L.; Ren, T.; Yang, X.; He, X. A numerical simulation study on mechanical behaviour of coal with bedding planes under coupled static and dynamic load. Int. J. Min. Sci. Technol. 2018, 28, 791–797. [Google Scholar] [CrossRef]
- Cao, R.-H.; Yao, R.; Hu, T.; Wang, C.; Li, K.; Meng, J. Failure and mechanical behavior of transversely isotropic rock under compression-shear tests: Laboratory testing and numerical simulation. Eng. Fract. Mech. 2021, 241, 107389. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, Z.; Du, X. Water-induced variations in dynamic behavior and failure characteristics of sandstone subjected to simulated geo-stress. Int. J. Rock Mech. Min. Sci. 2020, 130, 104339. [Google Scholar] [CrossRef]
- Zhou, Z.; Tan, L.; Cao, W.; Zhou, Z.; Cai, X. Fracture evolution and failure behaviour of marble specimens containing rectangular cavities under uniaxial loading. Eng. Fract. Mech. 2017, 184, 183–201. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Cai, X.; Yang, X.; Zhou, Q. Dynamic response and fracture evolution of marble specimens containing rectangular cavities subjected to dynamic loading. Bull. Eng. Geol. Environ. 2021. [Google Scholar] [CrossRef]
- Wu, H.; Zhao, G.; Liang, W. Mechanical properties and fracture characteristics of pre-holed rocks subjected to uniaxial loading: A comparative analysis of five hole shapes. Theor. Appl. Fract. Mech. 2020, 105, 102433. [Google Scholar] [CrossRef]
- Wang, M.; Wan, W.; Zhao, Y. Experimental study on crack propagation and the coalescence of rock-like materials with two preexisting fissures under biaxial compression. Bull. Eng. Geol. Environ. 2020, 79, 3121–3144. [Google Scholar] [CrossRef]
- Zhou, K.; Dou, L.; Gong, S.; Li, J.; Zhang, J.; Cao, J. Study of Rock Burst Risk Evolution in Front of Deep Longwall Panel Based on Passive Seismic Velocity Tomography. Geofluids 2020, 2020, 8888413. [Google Scholar] [CrossRef]
- Ukadgaonker, V.; Awasare, P. A novel method of stress-analysis of an infinite-plate with rounded corners of a rectangular hole under uniform edge loading. Indian J. Eng. Mater. 1994, 1, 17–25. [Google Scholar]
- Ukadgaonker, V.; Awasare, P. A novel method of stress analysis of an infinite plate with elliptical hole with uniform loading at infinity. J. Inst. Eng. (India) 1993, 73, 309–311. [Google Scholar]
- Ukadgaonker, V.; Awasare, P. A novel method of stress-analysis of infinite-plate with circular hole with uniform loading at infinity. Indian J. Eng. Mater. Sci. 1994, 1, 17–25. [Google Scholar]
- Ukadgaonker, V.; Rao, D. Stress distribution around triangular holes in anisotropic plates. Compos. Struct. 1999, 45, 171–183. [Google Scholar] [CrossRef]
- Sharma, D.S. Stress distribution around circular/elliptical/triangular holes in infinite composite plate. Eng. Lett. 2012, 20, 1. [Google Scholar]
- Wu, H.; Ma, D. Fracture response and mechanisms of brittle rock with different numbers of openings under uniaxial loading. Geomech. Eng. 2021, 25, 481–493. [Google Scholar]
- Zhao, G.; Yang, S. Analytical solutions for rock stress around square tunnels using complex variable theory. Int. J. Rock Mech. Min. Sci. 2015, 80, 302–307. [Google Scholar] [CrossRef]
- Lu, A.-z.; Zhang, N.; Kuang, L. Analytic solutions of stress and displacement for a non-circular tunnel at great depth including support delay. Int. J. Rock Mech. Min. Sci. 2014, 70, 69–81. [Google Scholar] [CrossRef]
- Setiawan, N.B.; Zimmerman, R.W. A unified methodology for computing the stresses around an arbitrarily-shaped hole in isotropic or anisotropic materials. Int. J. Solids Struct. 2020, 199, 131–143. [Google Scholar] [CrossRef]
- Melentiev, P. Several New Methods and Devices for Approximate Computations; Nordhoff: Groningen, The Netherlands, 1953. [Google Scholar]
- Sharma, D.S. Stress distribution around polygonal holes. Int. J. Mech. Sci. 2012, 65, 115–124. [Google Scholar] [CrossRef]
- Balakrishnan, A.; Joines, W.T.; Wilson, T.G. Air-gap reluctance and inductance calculations for magnetic circuits using a Schwarz-Christoffel transformation. IEEE Trans. Power Electron. 1997, 12, 654–663. [Google Scholar] [CrossRef]
- Lv, A.Z.; Wang, Q.W. New Method of Determination for the Mapping Function of Tunnel with Arbitrary Boundary Using Optomozation Techniques. Chin. J. Rock Mech. Eng. 1995, 014, 269–274. [Google Scholar]
- Holland, J.H. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence; The University of Michigan Press: Ann Arbor, MI, USA, 1975. [Google Scholar]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Qiao, M.; Peng, H. Analytical stress solution and mechanical properties for rock mass containing a hole with complex shape. Theor. Appl. Fract. Mech. 2021, 114, 103002. [Google Scholar] [CrossRef]
- Tan, L.; Ren, T.; Dou, L.; Yang, X.; Cai, X.; Qiao, M. Analytical stress solution for rock mass containing two holes based on an improved Schwarz alternating method. Theor. Appl. Fract. Mech. 2021, 116, 103092. [Google Scholar] [CrossRef]
- Zhu, J.H.; Yang, J.H.; Shi, G.P.; Wang, J.; Cai, J.P. Calculating method on the conformal mapping from the exterior of unit circle to the exterior of cavern with the arbitrary excavation cross section. Rock Soil Mech. 2014, 35, 175–183. [Google Scholar]
- Wu, H.; Kulatilake, P.H.S.W.; Zhao, G.; Liang, W.; Wang, E. A comprehensive study of fracture evolution of brittle rock containing an inverted U-shaped cavity under uniaxial compression. Comput. Geotech. 2019, 116, 103219. [Google Scholar] [CrossRef]
- Itasca, C. PFC (particle flow code in 2 and 3 dimensions), version 5.0 [User’s manual]. Numer. Anal. Methods Geomech. 2014, 32, 189–213. [Google Scholar]
- Wu, N.; Liang, Z.; Zhou, J.; Zhang, L. Energy evolution characteristics of coal specimens with preformed holes under uniaxial compression. Geomech. Eng. 2020, 20, 55–66. [Google Scholar]
- Vahab, S.; Tabaroei, A. Numerical simulation of the influence of interaction between Qanat and tunnel on the ground settlement. Geomech. Eng. 2020, 23, 455–466. [Google Scholar] [CrossRef]
- Fan, H.; Sun, S.; Wei, J.; Le, H.; Zhu, F.; Wang, W.; Liu, Y.; Wang, J. Shear Behavior of Soil–Rock Mixture Composed of Diorite-Porphyrite Considering Weathering Sequence. Int. J. Geomech. 2021, 21, 04021122. [Google Scholar] [CrossRef]
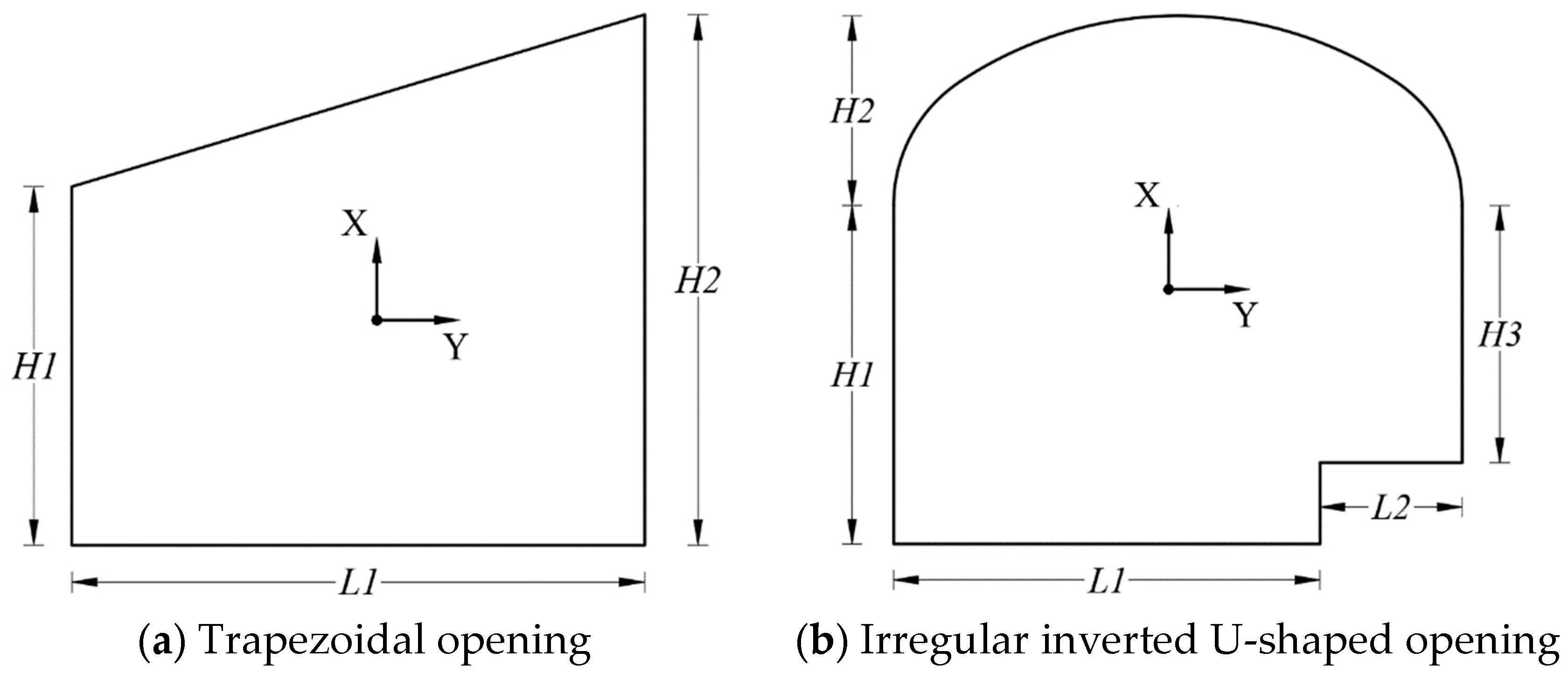

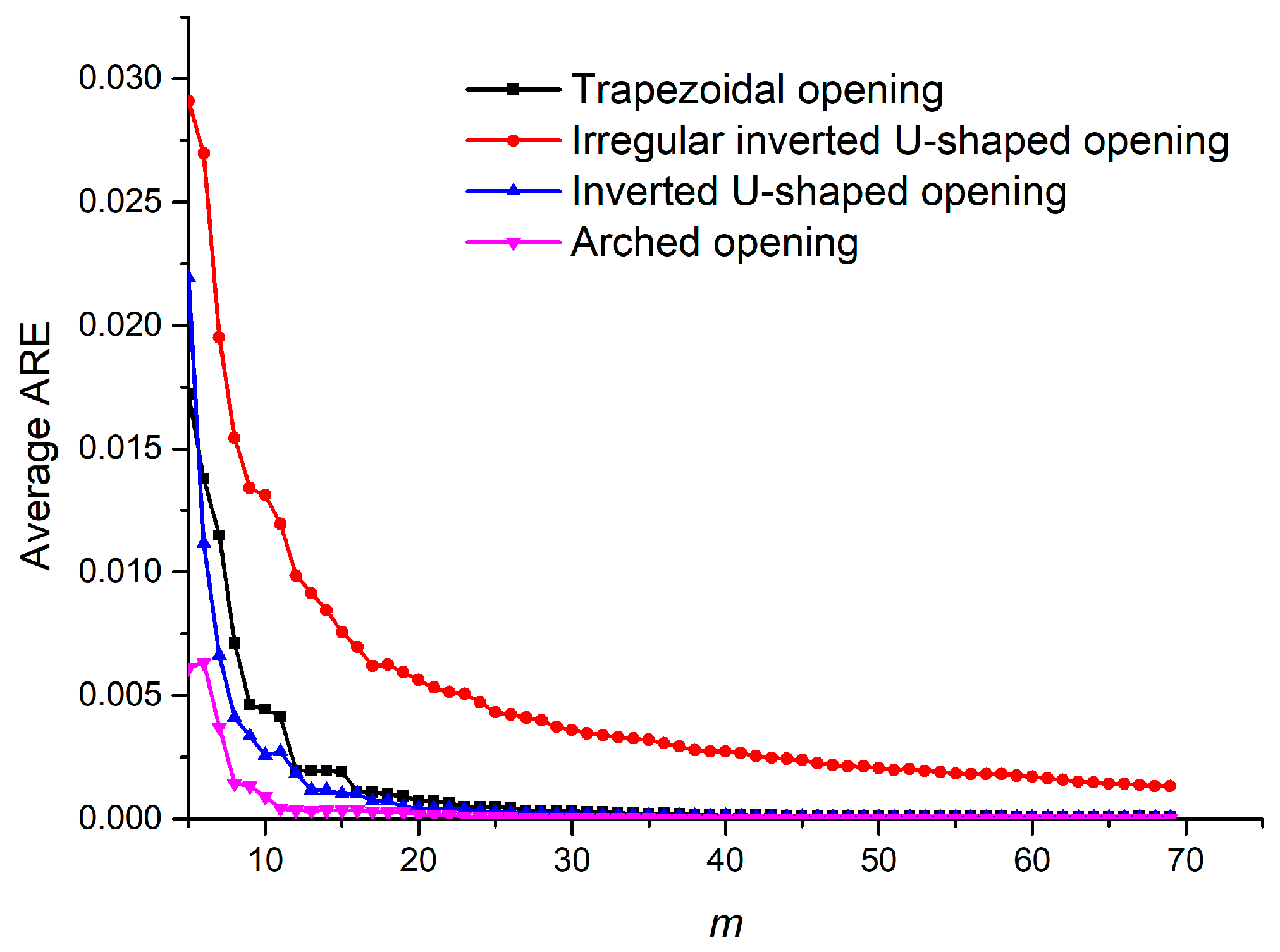

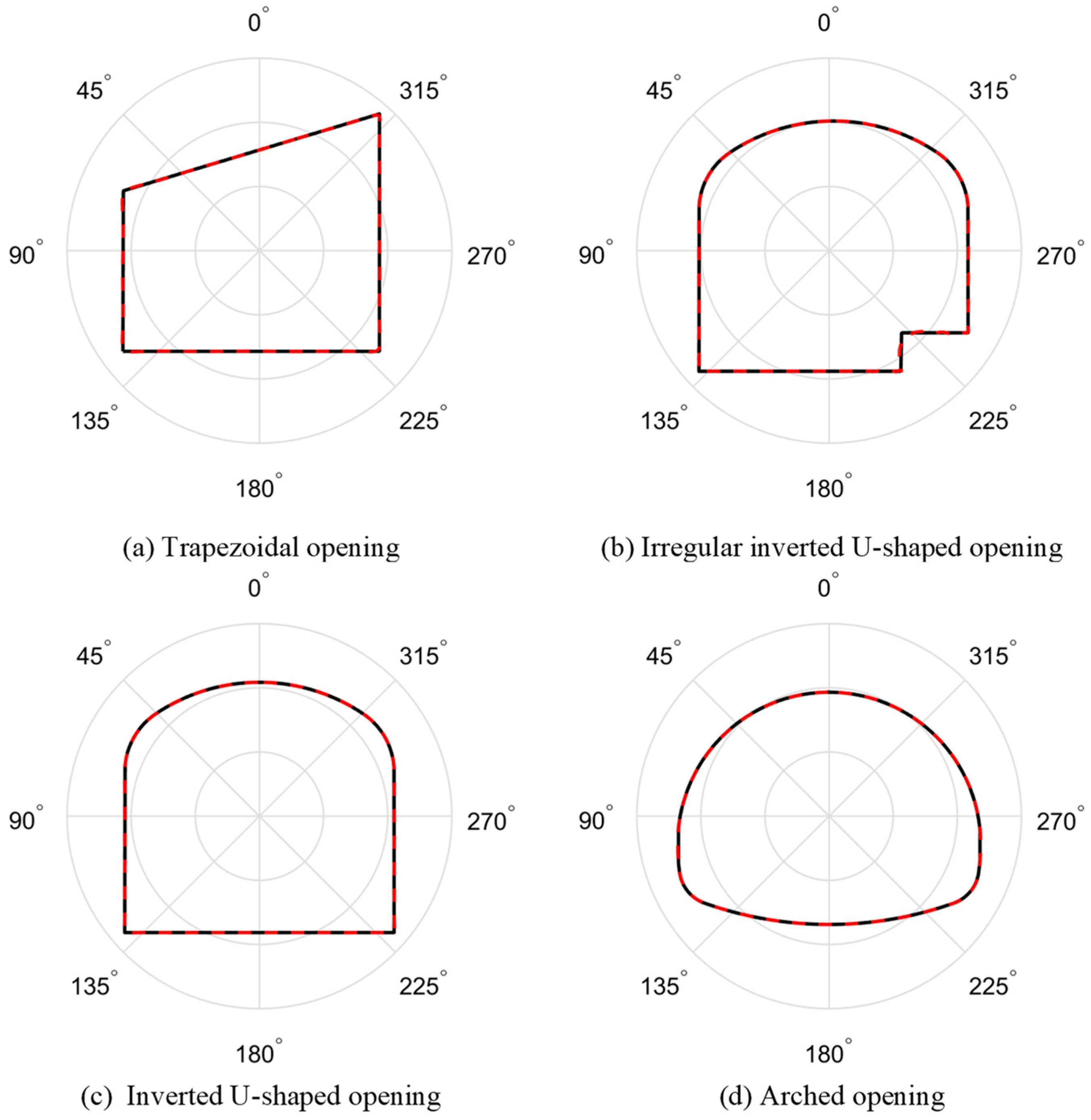





| Trapezoidal Opening | Inverted U-Shaped Opening | Arched Opening | ||
|---|---|---|---|---|
| k | Ak | Bk | Ck | Ck |
| 1 | 2.108 | −0.016 | 2.252 | 5.689 |
| 2 | 0.022 | −0.027 | −0.061 | −0.071 |
| 3 | −0.190 | −0.233 | −0.105 | −0.760 |
| 4 | 0.054 | −0.209 | 0.147 | 0.421 |
| 5 | −0.295 | −0.102 | −0.237 | −0.152 |
| 6 | 0.026 | −0.035 | 0.073 | −0.003 |
| 7 | 0.022 | 0.009 | 0.032 | 0.049 |
| 8 | −0.016 | 0.026 | −0.022 | −0.033 |
| 9 | 0.017 | 0.014 | 0.013 | 0.004 |
| 10 | −0.007 | 0.003 | −0.008 | 0.009 |
| 11 | −0.004 | −0.005 | −0.003 | −0.007 |
| 12 | 0.010 | −0.007 | 0.008 | 0.001 |
| 13 | −0.001 | −0.001 | −0.006 | 0.000 |
| 14 | 0.001 | 0.001 | −0.001 | 0.001 |
| 15 | 0.000 | 0.001 | 0.002 | 0.000 |
| 16 | −0.005 | 0.001 | −0.002 | −0.002 |
| 17 | 0.000 | −0.001 | 0.003 | 0.003 |
| 18 | 0.001 | 0.000 | 0.000 | −0.001 |
| 19 | 0.000 | 0.001 | −0.002 | −0.001 |
| 20 | 0.002 | 0.000 | 0.001 | 0.002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tan, L.; Ren, T.; Dou, L.; Yang, X.; Wang, G.; Peng, H. Analytical Stress Solution and Numerical Mechanical Behavior of Rock Mass Containing an Opening under Different Confining Stress Conditions. Mathematics 2021, 9, 2462. https://doi.org/10.3390/math9192462
Tan L, Ren T, Dou L, Yang X, Wang G, Peng H. Analytical Stress Solution and Numerical Mechanical Behavior of Rock Mass Containing an Opening under Different Confining Stress Conditions. Mathematics. 2021; 9(19):2462. https://doi.org/10.3390/math9192462
Chicago/Turabian StyleTan, Lihai, Ting Ren, Linming Dou, Xiaohan Yang, Gaofeng Wang, and Huaide Peng. 2021. "Analytical Stress Solution and Numerical Mechanical Behavior of Rock Mass Containing an Opening under Different Confining Stress Conditions" Mathematics 9, no. 19: 2462. https://doi.org/10.3390/math9192462






