ABS-Based Direct Method for Solving Complex Systems of Linear Equations
Abstract
:1. Introduction
2. The Scaled Complex ABS (scABS) Algorithm
2.1. Basic Properties of the Scaled Complex ABS Algorithm
| Algorithm 1: Scaled complex ABS (scABS) algorithm. |
 |
2.2. Special Choice of the Scaling Vector
- the scaling vectors defined by (13) are mutually orthogonal, i.e.,for and .
- the search vectors are conjugate if A is square and nonsingular matrix.
- the algorithm generates an implicit factorization of A into the product of an orthogonal and an upper triangular matrix if is a multiple of and (unit matrix). The algorithm with these selections can be considered as an alternative method of the classic QR factorization.
- by the choice of , , the required number of multiplication is .
| Algorithm 2: Orthogonally scaled complex ABS (oscABS) algorithm. |
 |
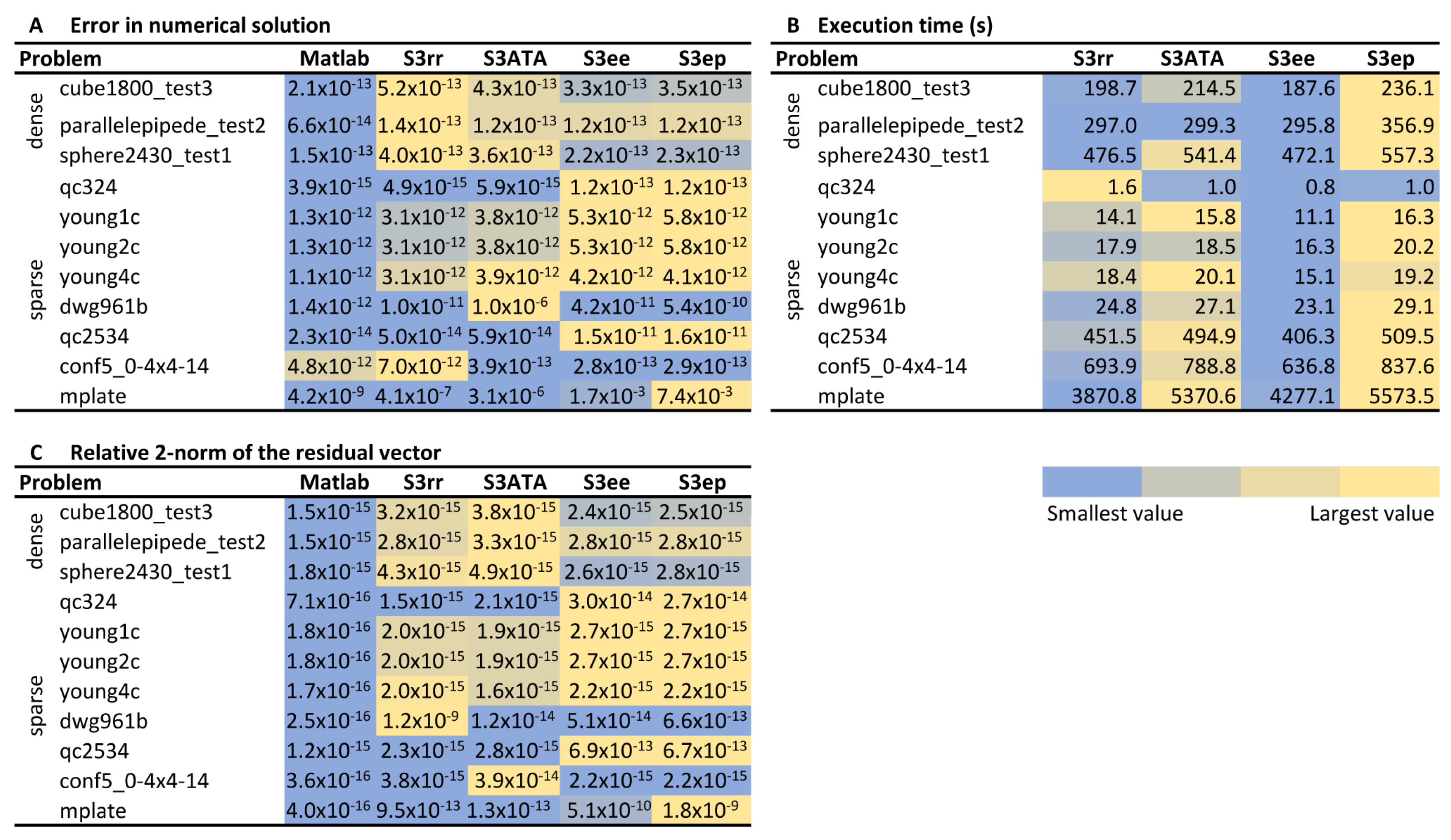
3. Numerical Experiments
- S3rr: and are selected such that , .
- S3ATA: and are selected such that , .
- S3ee: and are selected such that , .
- S3ep: and are selected such that , .
- Matlab: the built-in mldivide (\) function of Matlab.
3.1. Randomly Generated Problems
3.2. Chosen Test Problems from MATLAB Gallery
3.3. Real-Life Problems
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| transpose of the matrix A | |
| the conjugate of the matrix A | |
| conjugate transpose of the matrix A |
References
- Wong, S.S.M. Computational Methods in Physics and Engineering; World Scientific Publishing Co Pte Ltd.: Hackensack, NJ, USA, 1992. [Google Scholar]
- Metzler, L.A. Taxes and subsidies in Leontief’s input-output model. Q. J. Econ. 1951, 65, 433–438. [Google Scholar] [CrossRef]
- Bar-On, I.; Ryaboy, V. Fast diagonalization of large and dense complex symmetric matrices, with applications to quantum reaction dynamics. SIAM J. Sci. Comput. 1997, 18, 1412–1435. [Google Scholar] [CrossRef] [Green Version]
- Nesemann, J. PT-Symmetric Schrödinger Operators with Unbounded Potentials; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lancaster, P. Inverse spectral problems for semisimple damped vibrating systems. SIAM J. Matrix Anal. Appl. 2007, 29, 279–301. [Google Scholar] [CrossRef]
- Keller, J.B.; Givoli, D. Exact non-reflecting boundary conditions. J. Comput. Phys. 1989, 82, 172–192. [Google Scholar] [CrossRef]
- Van Dijk, W.; Toyama, F. Accurate numerical solutions of the time-dependent Schrödinger equation. Phys. Rev. E 2007, 75, 036707. [Google Scholar] [CrossRef] [Green Version]
- Benia, Y.; Ruggieri, M.; Scapellato, A. Exact solutions for a modified Schrödinger equation. Mathematics 2019, 7, 908. [Google Scholar] [CrossRef] [Green Version]
- Obaidat, S.; Mesloub, S. A New Explicit Four-Step Symmetric Method for Solving Schrödinger’s Equation. Mathematics 2019, 7, 1124. [Google Scholar] [CrossRef] [Green Version]
- Biddlecombe, C.; Heighway, E.; Simkin, J.; Trowbridge, C. Methods for eddy current computation in three dimensions. IEEE Trans. Magn. 1982, 18, 492–497. [Google Scholar] [CrossRef]
- Arridge, S.R. Optical tomography in medical imaging. Inverse Probl. 1999, 15, R41. [Google Scholar] [CrossRef] [Green Version]
- Benzi, M.; Bertaccini, D. Block preconditioning of real-valued iterative algorithms for complex linear systems. IMA J. Numer. Anal. 2008, 28, 598–618. [Google Scholar] [CrossRef]
- Day, D.; Heroux, M.A. Solving complex-valued linear systems via equivalent real formulations. SIAM J. Sci. Comput. 2001, 23, 480–498. [Google Scholar] [CrossRef] [Green Version]
- Gu, X.M.; Clemens, M.; Huang, T.Z.; Li, L. The SCBiCG class of algorithms for complex symmetric linear systems with applications in several electromagnetic model problems. Comput. Phys. Commun. 2015, 191, 52–64. [Google Scholar] [CrossRef]
- Wang, J.; Guo, X.P.; Zhong, H.X. Accelerated GPMHSS method for solving complex systems of linear equations. East Asian J. Appl. Math. 2017, 7, 143–155. [Google Scholar] [CrossRef]
- Li, L.; Huang, T.Z.; Ren, Z.G. A preconditioned COCG method for solving complex symmetric linear systems arising from scattering problems. J. Electromagn. Waves Appl. 2008, 22, 2023–2034. [Google Scholar] [CrossRef]
- Gu, X.M.; Huang, T.Z.; Li, L.; Li, H.B.; Sogabe, T.; Clemens, M. Quasi-minimal residual variants of the COCG and COCR methods for complex symmetric linear systems in electromagnetic simulations. IEEE Trans. Microw. Theory Tech. 2014, 62, 2859–2867. [Google Scholar] [CrossRef]
- Jacobs, D.A. A generalization of the conjugate-gradient method to solve complex systems. IMA J. Numer. Anal. 1986, 6, 447–452. [Google Scholar] [CrossRef]
- Saad, Y. Iterative Methods for Sparse Linear Systems; SIAM: Philadelphia, PA, USA, 2003. [Google Scholar]
- Fischer, B.; Reichel, L. A stable Richardson iteration method for complex linear systems. Numer. Math. 1989, 54, 225–242. [Google Scholar] [CrossRef]
- Bai, Z.Z.; Benzi, M.; Chen, F. Modified HSS iteration methods for a class of complex symmetric linear systems. Computing 2010, 87, 93–111. [Google Scholar] [CrossRef]
- Li, X.; Yang, A.L.; Wu, Y.J. Lopsided PMHSS iteration method for a class of complex symmetric linear systems. Numer. Algorithms 2014, 66, 555–568. [Google Scholar] [CrossRef]
- Puzyrev, V.; Koric, S.; Wilkin, S. Evaluation of parallel direct sparse linear solvers in electromagnetic geophysical problems. Comput. Geosci. 2016, 89, 79–87. [Google Scholar] [CrossRef] [Green Version]
- Koric, S.; Lu, Q.; Guleryuz, E. Evaluation of massively parallel linear sparse solvers on unstructured finite element meshes. Comput. Struct. 2014, 141, 19–25. [Google Scholar] [CrossRef]
- Abaffy, J.; Spedicato, E. ABS Projection Algorithms: Mathematical Techniques for Linear and Nonlinear Equations; Prentice-Hall, Inc.: Chichester, UK, 1989. [Google Scholar]
- Spedicato, E.; Xia, Z.; Zhang, L. ABS algorithms for linear equations and optimization. J. Comput. Appl. Math. 2000, 124, 155–170. [Google Scholar] [CrossRef] [Green Version]
- Fodor, S. Symmetric and non-symmetric ABS methods for solving Diophantine systems of equations. Ann. Oper. Res. 2001, 103, 291–314. [Google Scholar] [CrossRef]
- Abaffy, J.; Fodor, S. Solving Integer and Mixed Integer Linear Problems with ABS Method. Acta Polytech. Hung. 2013, 10, 81–98. [Google Scholar] [CrossRef]
- Galántai, A. Parallel ABS projection methods for linear and nonlinear systems with block arrowhead structure. Comput. Math. Appl. 1999, 38, 11–17. [Google Scholar] [CrossRef] [Green Version]
- Fodor, S.; Németh, Z. Numerical analysis of parallel implementation of the reorthogonalized ABS methods. Cent. Eur. J. Oper. Res. 2019, 27, 437–454. [Google Scholar] [CrossRef]
- Abaffy, J.; Fodor, S. Reorthogonalization methods in ABS classes. Acta Polytech. Hung. 2015, 12, 23–41. [Google Scholar]
- Broyden, C. On the numerical stability of Huang’s and related methods. J. Optim. Theory Appl. 1985, 47, 401–412. [Google Scholar] [CrossRef]
- Hegedüs, C.J. Reorthogonalization Methods Revisited. Acta Polytech. Hung. 2015, 12, 7–26. [Google Scholar]
- Parlett, B. The Symmetric Eigenvalue Problem, Republished amended version of original published by Prentice-Hall; SIAM: Philadelphia, PA, USA; Prentice-Hall: Englewood Cliffs, NJ, USA, 1980; p. 1980. [Google Scholar]
- Attaway, D.C. Matlab: A Practical Introduction to Programming and Problem Solving; Butterworth-Heinemann Elsevier Ltd.: Oxford, UK, 2013. [Google Scholar]
- Golub, G.H.; Van Loan, C.F. Matrix Computations, 4th ed.; Johns Hopkins University Press: Baltimore, MD, USA, 2012; Volume 3. [Google Scholar]
- Davis, T.A.; Hu, Y. The University of Florida sparse matrix collection. ACM Trans. Math. Softw. (TOMS) 2011, 38, 1–25. [Google Scholar] [CrossRef]
- Gu, X.M.; Carpentieri, B.; Huang, T.Z.; Meng, J. Block variants of the COCG and COCR methods for solving complex symmetric linear systems with multiple right-hand sides. In Numerical Mathematics and Advanced Applications ENUMATH 2015; Springer: Berlin/Heidelberg, Germany, 2016; pp. 305–313. [Google Scholar]
- Jing, Y.F.; Huang, T.Z.; Zhang, Y.; Li, L.; Cheng, G.H.; Ren, Z.G.; Duan, Y.; Sogabe, T.; Carpentieri, B. Lanczos-type variants of the COCR method for complex nonsymmetric linear systems. J. Comput. Phys. 2009, 228, 6376–6394. [Google Scholar] [CrossRef]
- Zhong, H.X.; Gu, X.M.; Zhang, S.L. A Breakdown-Free Block COCG Method for Complex Symmetric Linear Systems with Multiple Right-Hand Sides. Symmetry 2019, 11, 1302. [Google Scholar] [CrossRef] [Green Version]





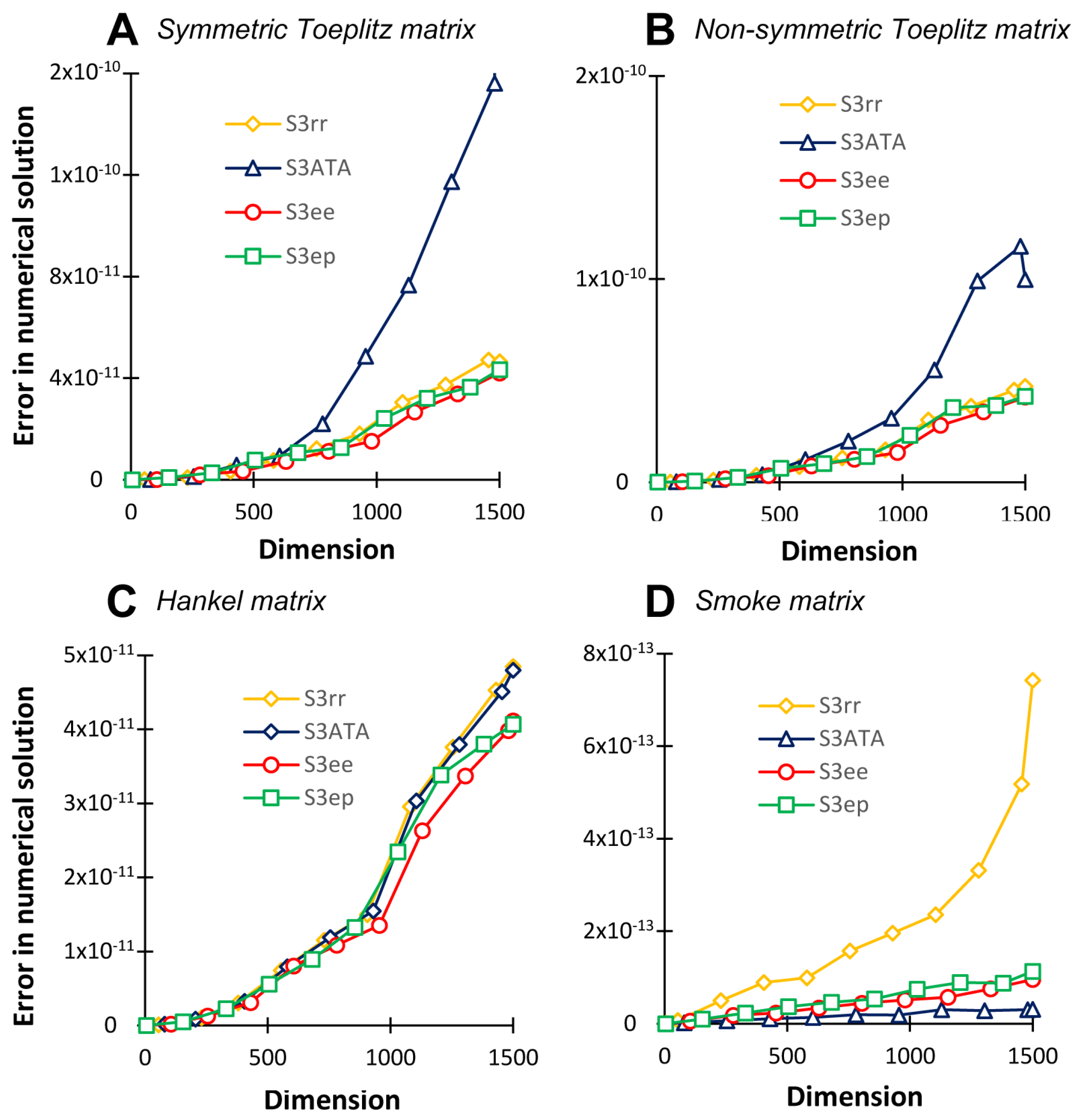


| Name | Description |
|---|---|
| Symmetric Toeplitz | Diagonal-constant matrix |
| using Matlab toeplitz(r) function where r is the first row. | |
| The vector r was randomly generated in this experiment. | |
| Non-symmetric Toeplitz | Diagonal-constant matrix |
| using Matlab toeplitz(c,r) function where c is first column, | |
| r is the first row of the matrix. | |
| The vector c, and the vector r were generated randomly. | |
| Hankel | Symmetric and constant across the anti-diagonals matrix |
| using Matlab hankel(c) function where c | |
| defines the first column of the matrix. | |
| The c column was generated randomly in this experiment. | |
| Smoke | Complex matrix with a ‘smoke ring’ pseudospectrum |
| using Matlab gallery(‘smoke’,n) function | |
| where n is the dimension of the matrix. |
| Matrix Name | n | m | Condition Number | Application Area |
|---|---|---|---|---|
| qc324 | 324 | 324 | 7.38 × | Electromagnetics |
| young1c | 841 | 841 | 9.91 × | Acoustics |
| young2c | 841 | 841 | 9.91 × | Duplicate Acoustics |
| young4c | 841 | 841 | 5.55 × | Acoustics |
| dwg961b | 961 | 961 | 3.35 × | Electromagnetics |
| cube1800_test3 | 1800 | 1800 | 4.98 × | Electromagnetics |
| parallelepipede_test2 | 2016 | 2016 | 8.43 × | Electromagnetics |
| sphere2430_test1 | 2431 | 2431 | 4.32 × | Electromagnetics |
| qc2534 | 2534 | 2534 | 5.19 × | Electromagnetics |
| conf5_0-4x4-14 | 3072 | 3072 | 9.17 × | Quantum Chemistry |
| mplate | 5962 | 5962 | 4.83 × | Acoustics |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abaffy, J.; Fodor, S. ABS-Based Direct Method for Solving Complex Systems of Linear Equations. Mathematics 2021, 9, 2527. https://doi.org/10.3390/math9192527
Abaffy J, Fodor S. ABS-Based Direct Method for Solving Complex Systems of Linear Equations. Mathematics. 2021; 9(19):2527. https://doi.org/10.3390/math9192527
Chicago/Turabian StyleAbaffy, József, and Szabina Fodor. 2021. "ABS-Based Direct Method for Solving Complex Systems of Linear Equations" Mathematics 9, no. 19: 2527. https://doi.org/10.3390/math9192527






