Hierarchical Cognitive Control for Unknown Dynamic Systems Tracking

Abstract

A general control system tracking learning framework is proposed, by which an optimal learned tracking behavior called ‘primitive’ is extrapolated to new unseen trajectories without requiring relearning. This is considered intelligent behavior and strongly related to the neuro-motor cognitive control of biological (human-like) systems that deliver suboptimal executions for tasks outside of their current knowledge base, by using previously memorized experience. However, biological systems do not solve explicit mathematical equations for solving learning and prediction tasks. This stimulates the proposed hierarchical cognitive-like learning framework, based on state-of-the-art model-free control: (1) at the low-level L1, an approximated iterative Value Iteration for linearizing the closed-loop system (CLS) behavior by a linear reference model output tracking is first employed; (2) an experiment-driven Iterative Learning Control (EDILC) applied to the CLS from the reference input to the controlled output learns simple tracking tasks called ‘primitives’ in the secondary L2 level, and (3) the tertiary level L3 extrapolates the primitives’ optimal tracking behavior to new tracking tasks without trial-based relearning. The learning framework relies only on input-output system data to build a virtual state space representation of the underlying controlled system that is assumed to be observable. It has been shown to be effective by experimental validation on a representative, coupled, nonlinear, multivariable real-world system. Able to cope with new unseen scenarios in an optimal fashion, the hierarchical learning framework is an advance toward cognitive control systems.

1. Introduction

Cognitive control systems are characterized by perception, learning, planning and memorization, defining a clear path toward general intelligent systems that are able to optimally handle new, unseen before situations and display adaptability. The best examples of collections of such complex control systems are offered by certain biological systems (living organisms, humans in particular) who intelligently solve complex tasks by combining knowledge gathered through experience via learning and planning mechanisms that are encoded in the brain. As such, the brain acts as a processing unit that is able, at a higher level, to project future strategies in order to achieve goals through reasoning and planning, decompose complex strategies into well-known possibly simpler strategies (planning), memorize new experiences to augment the current knowledge base, and process feedback signals by fusing visual, tactile, auditory, and olfactory information for task execution improvement through learning. Finally, it guides the lower-level neuromuscular control system to act in the environment to achieve higher-level goals.

This intelligence of living organisms has developed without solving explicit mathematical equations; therefore, this kind of complex intelligence serves as inspiration for developing model-free control, learning, and planning techniques. One suitable paradigm for explaining the above techniques is the process of learning neuromotor skills, which rely on well-acknowledged control formulations such as those found in feed-forward- and feedback-based control and predictive-based control. A common trait of all these techniques is that they are almost always posed and solved in optimization-based settings [1]. In such settings (e.g., taking error-based learning), the error gradient is exploited to improve the control solutions. Alternatively, use-dependent learning addresses the permanent compromise between repeatable tasks whose improved execution is improvable for high-performance and non-repeatable tasks that require a significant relearning effort.

One illustrative natural behavior for some of the above concepts is the imitating behavior of biological systems: the first execution of an imitation task is nearly optimal. The brain can analyze, memorize, and decompose the imitation task into subtasks for each limb and plan for corresponding immediate future tracking tasks. The control of each limb is already encoded in the neuromuscular system through an inverse dynamical model that is not explicitly represented. Another illustrative situation occurs when new neuromotor tasks are solved by first decomposing them into tasks with known solutions and then recomposing the new solution from existing ones. The previously described behavior unites several concepts that can be formally called a primitive-based learning framework [1].

Primitive-based control has been researched for at least two decades, in various forms, by transforming the time scale [2,3], concatenation-based mechanisms [4,5,6], and decomposition/re-composition in time [7,8]. More recently, primitive-based control has been studied in [9,10,11,12,13], mostly as part of hierarchical learning frameworks [14,15,16,17,18]. However, the application of the Iterative Learning Control (ILC, a full list of the acronyms used in the paper is presented in abbreviations part) technique [19,20,21,22,23,24,25] over linearized feedback closed-loop control systems (CLSs) as a primer mechanism for primitive-based learning was proposed in [8]. An experiment-driven ILC (EDILC) variant was crafted in a norm-optimal tracking setting to learn reference-input controlled output pairs called primitives. Such a primitive tuple contains a reference input to the CLS (called the input primitive) coupled with its paired control system output (called the output primitive). Subsequently, the output primitive is usually shaped as a Gaussian function, but it can be any shape suitable for approximation purposes. Delayed copies of the output primitives are used to approximate a new trajectory that must be tracked. The coefficients that combine the output primitives linearly to approximate the new trajectory are used to combine the delayed and copied input primitives to obtain the optimal reference input. For the assumed linear CLS, this reconstructed reference input is optimal with respect to the criterion by which the original primitives are learned; therefore, when set as input to the CLS, it leads to theoretically perfect new trajectory tracking. It does this without repetitive-based relearning using the EDILC.

The primitive-based approach is sensible to the CLS’s linearity assumption; therefore, a control that makes the CLS as linear as possible has to be learned. One framework to ensure this linearization is the approximate (adaptive) dynamic programming (ADP) [26,27,28,29,30], also known as reinforcement learning (RL) [31,32,33,34,35], designed for the output reference model (ORM) paradigm. Specifically, a model-free iterative Value Iteration (IVI) algorithm as a representative ADP/RL approach can serve this goal by using general function approximators such as neural networks (NNs). Hence, it is called the approximated IVI (AIVI).

With a linear ORM’s output well tracked by the CLS output, an approximate linearized CLS from the reference input to the controlled output is ensured in a wide range, together with some inherent disturbance attenuation ability. Two major problems with ADP/RL are exploration and state knowledge [36,37,38,39,40]. The former is still an open issue, although much research is underway. Enhanced and accelerated exploration is achievable with pre-stabilizing controllers, which can also be designed based on the unknown dynamics assumption principles. The state availability was solved with virtual state-space models constructed from input-output (I/O) samples of general unknown but assumed observable nonlinear systems [41,42]. Using historical I/O samples from the system as an alternate system, state representation has been used in more complex but unformalized environments, such as video games [43].

This work aims to integrate the learning control techniques and machine learning techniques previously presented in a hierarchical cognitive-based control framework tailored to extrapolate optimally learned tracking control to novel tracking tasks. Tracking should be achievable without relearning through trials by exploiting the already learned optimal tracking skills. It is obtained through a hierarchical learning architecture where (a) the closed-loop system at a lower level (called L1 level herein) is first linearized using the ORM principle. This is achieved through nonlinear state-feedback control, where a virtual state is built from finite sequences of I/O system data samples. Learning such a controller is performed using AIVI; (b) an EDILC is used at the secondary upper L2 level to learn the optimal tracking skills called primitives, by repetitions; (c) the tertiary and last L3 level is dedicated to extrapolating the optimally learned tracking skills, without repetitions, to new tracking tasks.

Progress and contributions with respect to work [8] are:

• At level L1, CLS linearization is strongly ensured using a virtual state-feedback neuro-controller learned by AIVI. The new state-space representation relies on a virtual transformation empowered by observability theory.
• At level L2, the model-free EDILC dedicated to primitive learning is improved in several aspects: (1) the gradient information is extracted using a single gradient experiment in the vicinity of the current iteration nominal trajectory, irrespective of the CLS’s number of controlled outputs; (2) EDILC monotonic convergence is derived by optimally selecting the learning rate parameter in order to trade-off learning speed and robustness. This is achieved using two approximate CLS models for a double-safe mechanism; (3) proper initialization of the gradient-based search specific to EDILC results in fewer iterations for convergence.
• The primitive-based mechanism at level L3, for optimally predicting the reference input ensuring theoretical perfect tracking of a previously unseen desired trajectory, is designed to: (1) handle desired trajectories longer than the learned primitives, and (2) indirectly handle constraints on the CLS’s output.

The following bottom-up presentation of the proposed hierarchical learning framework results in an effective validation of a hybrid software-electrical system that is coupled, multivariable, and has a delay. The case study is representative of many mechatronic systems.

2. The Linear ORM Tracking for Observable Systems with Unknown Dynamics

A common and general representation for a deterministic controlled system model in a discrete-time state space is

$$\{\begin{array}{l}{\mathit{s}}_{k+1}^{ext}=\mathit{E}\left({\mathit{s}}_k^{ext},{\mathit{a}}_k\right),\\ {\mathit{y}}_k={\mathit{v}}_{k,1}, {\mathit{y}}_k^{ORM}=\mathit{L}{\mathit{s}}_k^{ORM},\end{array}$$

(1)

where E() is a partially known nonlinear state map, $k$ is the sample index, ${\mathit{a}}_k={[a_{k,1},\dots ,a_{k,m_u}]}^T\in {\mathsf{\Omega }}_A\subset {\Re }^{m_u}$ lumps the m_u control action inputs of the system within a known domain ${\mathsf{\Omega }}_A$. A number of p measurable system outputs are formally collected in the partial output vector ${\mathit{y}}_k={[y_{k,1},\dots ,y_{k,p}]}^T\in {\mathsf{\Omega }}_Y\subset {\Re }^p$ with known domain ${\mathsf{\Omega }}_Y$. Another p measurable system outputs formally complete the remaining output as ${\mathit{y}}_k^{ORM}={[y_{k,1}^{ORM},\dots ,y_{k,p}^{ORM}]}^T\in {\mathsf{\Omega }}_{Y_{ORM}}\subset {\Re }^p$ with known domain ${\mathsf{\Omega }}_{Y_{ORM}}$, to be contextualized later on. The state ${\mathit{s}}_k^{ext}={\left[{\mathit{v}}_k^T,{\left({\mathit{s}}_k^{ORM}\right)}^T,{\mathit{\rho }}_k^T\right]}^T$ lumps three types of state variables stemming from three independent systems. First, a virtual state-space system is defined as follows:

$$\{\begin{array}{l}{\mathit{v}}_{k+1}=\mathit{F}\left({\mathit{v}}_k,{\mathit{a}}_k\right),\\ {\mathit{y}}_k={\mathit{v}}_{k,1},\end{array}$$

(2)

which is a transformation of the true state–space system

$$\{\begin{array}{l}{\mathit{s}}_{k+1}=\mathit{f}\left({\mathit{s}}_k,{\mathit{a}}_k\right),\\ {\mathit{y}}_k=\mathit{g}\left({\mathit{s}}_k\right),\end{array}$$

(3)

where ${\mathit{s}}_k={[s_{k,1}\dots s_{k,n}]}^T\in {\mathsf{\Omega }}_S\subset {\Re }^n$ gathering the n (which is unknown) true system states that cannot be measured, a_k are the control action inputs of the true system, and the measurable true system outputs are y_k. The system functions as nonlinear maps $\mathit{f}\left({\mathit{s}}_k,{\mathit{a}}_k\right):{\mathsf{\Omega }}_S\times {\mathsf{\Omega }}_A\to {\mathsf{\Omega }}_S$, $\mathit{g}\left({\mathit{s}}_k\right):{\mathsf{\Omega }}_S\to {\mathsf{\Omega }}_Y$ are unknown and are assumed to be continuously differentiable. Some assumptions regarding (1) were introduced. The pair ($\mathit{f},\mathit{g}$) is entirely state observable, meaning that the true state ${\mathit{s}}_k$ from (3) is recoverable from the present and past I/O measurements of ${\mathit{a}}_k,{\mathit{y}}_k$. The observability property is used in the sense defined for linear systems. Further, (3) is assumed to be controllable, and the system’s relative degree (delay included) is known and constant.

With unknown system functions ($\mathit{f},\mathit{g}$), observability and controllability can only be inferred from the working experience with the system, from technical manuals, or from the literature. The system’s relative degree and its non-minimum phase (NMP) type are recognizable from historical I/O response data.

Relying on the system’s (3) complete observability, using Lemma 1 from [41] shows how to build transformation (2) whose virtual state vector is defined in terms of I/O samples of (3): ${\mathit{v}}_k=[({\mathit{Y}}_{\overline{k,k-\tau }}{)}^T,({\mathit{A}}_{\overline{k-1,k-\tau }}{)}^T{]}^T\stackrel{∆}{=}[({\mathit{v}}_{k,1}{)}^T,({\mathit{v}}_{k,2}{)}^T,\dots ,({\mathit{v}}_{k,2\tau +1}{)}^T{]}^T\in \underset{\tau +1 \mathit{times}}{\underbrace{{\mathsf{\Omega }}_Y\times \dots \times {\mathsf{\Omega }}_Y}}\times \underset{\tau \mathit{times}}{\underbrace{{\mathsf{\Omega }}_A\times \dots \times {\mathsf{\Omega }}_A}}\stackrel{∆}{=}{\mathsf{\Omega }}_v\subset {\Re }^{p(\tau +1)+m_u\tau }$. For a more detailed element-wise correspondence, the indexing ${\mathit{Y}}_{\overline{k,k-\tau }}={[{({\mathit{y}}_k)}^T\dots {({\mathit{y}}_{k-\tau })}^T]}^T\stackrel{\Delta }{=}{[{({\mathit{v}}_{k,1})}^T\dots ,{({\mathit{v}}_{k,\tau +1})}^T]}^T, {\mathit{A}}_{\overline{k-1,k-\tau }}={[{({\mathit{a}}_{k-1})}^T\dots {({\mathit{a}}_{k-\tau })}^T]}^T\stackrel{\Delta }{=}[{({\mathit{v}}_{k,\tau +2})}^T\dots {({\mathit{v}}_{k,2\tau +1})}^T{]}^T$ is utilized. Remarkably, knowing ${\mathsf{\Omega }}_Y, {\mathsf{\Omega }}_A,$ makes ${\mathsf{\Omega }}_v$ known. The $\tau \in \mathbb{N}$ (ℕ is the set of positive integers) indexes the historical I/O measurements, and its value is related to the order of (3); therefore, it is also correlated with the unknown observability index of (3).

Definition 1.

The unknown observability index of (3) is the minimal value τ_min of τ for which state s_k is fully recoverable from the I/O measurements ${\mathit{Y}}_{\overline{k,k-\tau }}, {\mathit{A}}_{\overline{k-1,k-\tau }}$. The role of this index is similar to that of linear systems.

Under the observability assumption, there exists a minimal value $\tau ={\tau }_{min}$ which makes ${\mathit{s}}_k$ fully recovered from I/O data and uniquely associated with ${\mathit{v}}_k$ which is a sort of alias for ${\mathit{s}}_k$, but in a different dimensional space [41]. For $\tau >{\tau }_{min}$, the size increase of ${\mathit{v}}_k$ does not add valuable information about ${\mathit{s}}_k$. In practice, $\tau$ should be as large as possible without negatively affecting the computational complexity of the subsequent learning of state-feedback control based on high-dimensional ${\mathit{v}}_k$.

Based on transformation (2), system (2) is also I/O controllable, having the same I/O as (1). The main feature of (2) is its complete state availability, making it fully state observable but without entirely known dynamics because the map $\mathit{F}(.)$ is partially unknown. Input delay (dead-time) systems also hold transforms such as (2) to render them fully state observable.

The second component of ${\mathit{s}}_k^{ext}$ is the state ${\mathit{s}}_k^{ORM}$ of the ORM model which will be matched by the CLS by proper control design; let this known ORM state-space model be

$$\{\begin{array}{l}{\mathit{s}}_{k+1}^{ORM}=\mathit{G}{\mathit{s}}_k^{ORM}+\mathit{H}{\mathit{\rho }}_k,\\ {\mathit{y}}_k^{ORM}=\mathit{L}{\mathit{s}}_k^{ORM},\end{array}$$

(4)

where ${\mathit{s}}_k^{ORM}={[s_{k,1}^{ORM},\dots ,s_{k,n_m}^{ORM}]}^T\in {\mathsf{\Omega }}_{S_{ORM}}\subset {\Re }^{n_m}$ gathers the n_m ORM states in known domain ${\mathsf{\Omega }}_{S_{ORM}}$, ${\mathit{\rho }}_k={[{\rho }_{k,1},\dots ,{\rho }_{k,p}]}^T\in {\mathsf{\Omega }}_{\mathit{\rho }}\subset {\Re }^p$ lumps the ORM’s inputs in their known domain ${\mathsf{\Omega }}_{\mathit{\rho }}$; ${\mathit{\rho }}_k$ will also serve as CLS input. The ORM outputs are collected in ${\mathit{y}}_k^{ORM}$ introduced in the first place. Note that ${\mathit{\rho }}_k$ completes the definition of ${\mathit{s}}_k^{ext}$ in (1).

The tuple $\left(\mathit{G},\mathit{H},\mathit{L}\right)$ characterizes the linear ORM for which an I/O pulse transfer matrix (t.m.) is ${\mathit{y}}_k^{ORM}={\mathit{T}}_{ORM}\left(q\right){\mathit{\rho }}_k$ (q is the unit time step advance operator). Information about (3), such as relative degree, non-minimum phase character, and bandwidth, must be synthesized within the ORM (4), as dictated by classical control rules. Commonly, this selection is better reflected in a ${\mathit{T}}_{ORM}\left(q\right)$, as it is more straightforward and easier to interpret (bandwidth, overshoot).

To fulfill the Markovian property of (1), the exogenous reference input signal ${\mathit{\rho }}_k$ is described by the known generation model dynamics ${\mathit{\rho }}_{k+1}=\Gamma \left({\mathit{\rho }}_k\right)$, where ${\mathit{\rho }}_k$ acts as a measurable state variable. Note that the extended model (1) has two outputs stemming from (3) and (4). In summary, the dynamics $\mathit{E}(.)$ will be partially unknown owing to the partially unknown dynamics of its component $\mathit{F}(.)$. The main feature of (1) is its full state observability, that is, the state is fully measurable, and the domain of ${\mathit{s}}_k^{ext}$ is known as ${\mathsf{\Omega }}_{S_{ext}}={\mathsf{\Omega }}_v\times {\mathsf{\Omega }}_{S_{ORM}}\times {\mathsf{\Omega }}_{\mathit{\rho }}$.

The ORM tracking problem finally poses as the optimal control search over an infinite-horizon cost $V_{ORM}^{\infty }$:

$$\begin{gathered} {\mathit{a}}_k^{*}=\mathit{arg} \underset{{\mathit{a}}_k}{min} V_{ORM}^{\infty }\left({\mathit{a}}_k\right), V_{ORM}^{\infty }\left({\mathit{a}}_k\right)={{\displaystyle \sum }}_{k=0}^{\infty }\parallel {\mathit{y}}_k\left({\mathit{a}}_k\right)-{\mathit{y}}_k^{ORM}{\parallel }_2^2, \\ s.t. dynamics \left(1\right). \end{gathered}$$

(5)

The norm $\parallel .{\parallel }_2$ defined as the vector-wise Euclidean distance, penalizes at each sampling instant the CLS’s output deviation from the ORM’s output. Problem (5) is a type of imitation (or apprentice) learning with the ORM (3) acting as a teacher (or expert or supervisor) and with system (1) trying to mimic (or follow) the ORM dynamics. Assuming that (5) is solvable in the following, ADP/RL techniques are well suited for finding closed-form optimal control laws of the type ${\mathit{a}}_k=\mathit{C}\left({\mathit{s}}_k^{ext}\right)$ with the control action input as a nonlinear mapping of the extended state. An AIVI is in fact employed to solve (5) as a competitive alternative to the recently proposed Virtual State-Feedback Reference Tuning (VSFRT) [42]. This is considered the L1 level control and is presented next.

3. The L1 Level—ORM Tracking AIVI-Based Solution

AIVI is a type of model-free offline batch reinforcement Q-learning that is used to find the optimal control solution to (5). AIVI most often uses NNs as function approximators because of their easily customizable architecture, training software availability, and generalization capacity. As such, AIVI uses one NN to parameterize the nonlinear control action as ${\mathit{a}}_k=\mathit{C}\left({\mathit{s}}_k^{ext},\mathit{\psi }\right)$ and another NN to parameterize the well-known Q-function as $Q\left({\mathit{s}}_k^{ext},{\mathit{a}}_k,\mathit{\pi }\right)$. Here, $\mathit{\psi }$ and $\mathit{\pi }$ formally gather all the NN tunable weights corresponding to some generic NN architectures. Starting from some initial solutions ${\mathit{\psi }}^0$ and ${\mathit{\pi }}^0$, two AIVI-specific steps are called iteratively, and in this particular order, the Q-function update and controller improvement. The steps are formally expressed as

$${\mathit{\pi }}_{}^j=\mathit{arg} \underset{\mathit{\pi }}{min}\frac{1}{B}{\displaystyle \sum }_{i=1}^B{[Q\left({\mathit{s}}_k^{ext\left[i\right]},{\mathit{u}}_k^{\left[i\right]},\mathit{\pi }\right)-r\left({\mathit{s}}_k^{ext\left[i\right]},{\mathit{a}}_k^{\left[i\right]}\right)-Q\left({\mathit{s}}_{k+1}^{ext\left[i\right]},\mathit{C}\left({\mathit{s}}_{k+1}^{ext\left[i\right]},{\mathit{\psi }}^{j-1}\right),{\mathit{\pi }}_{}^{j-1}\right)]}^2,$$

(6)

$${\mathit{\psi }}^j=\mathit{arg} \underset{\mathit{\psi }}{min}\frac{1}{B}{\displaystyle \sum }_{i=1}^{B}Q\left({\mathit{s}}_k^{ext\left[i\right]},\mathit{C}\left({\mathit{s}}_k^{ext\left[i\right]},\mathit{\psi }\right),{\mathit{\pi }}_{}^j\right),$$

(7)

respectively, with penalty $r\left({\mathit{s}}_k^{ext\left[i\right]},{\mathit{a}}_k^{\left[i\right]}\right)={\mathit{y}}_k\left({\mathit{a}}_k\right)-\parallel {\mathit{y}}_k^{ORM}{\parallel }_2^2$, over a batch consisting of B transition samples (also known tuples or experiences) of the form $\left\{\left({\mathit{s}}_k^{ext\left[i\right]},{\mathit{a}}_k^{\left[i\right]},{\mathit{s}}_{k+1}^{ext\left[i\right]}\right)\right\},i=\overline{1,B}$. Here, j indexes the AIVI iteration. It is easily shown that (6) and (7) are equivalent to the NN training of the Q-function and controller, respectively. The transition samples set is collectable from the controlled system (5) under any sufficiently exploratory (i.e., it visits many state-action combinations which uniformly span their space) controller. Even a random control strategy may be suitable for this purpose; however, a priori stabilizing controllers accelerate the exploration process: faster visiting more state-action combinations while simultaneously dealing with operational (e.g., safety) constraints. This off-policy offline is more data efficient than online on-policy reinforcement learning, where the exploration-exploitation dilemma throughout learning, combined with the lower data efficiency, is a major challenge. When all (or a random subset) of the transition samples are used in each AIVI step, the approach ensures the so-called experience replay.

The AIVI steps converge to the optimal virtual state feedback controller, ensuring that the CLS tracks the ORM in terms of reference input-controlled output at the L1 level [31,32,40,41]. It is assumed that the CLS is indirectly linearized in the ORM tracking sense. Thus, it is prepared to receive the L2 level learning phase, next presented.

4. The L2 Level—EDILC for Learning Primitives

The L2 level aims to learn pairs of reference inputs and CLS outputs called primitive pairs or simply primitives, where the CLS outputs have a basis function shape (e.g., Gaussian), to be used later for function approximation. To this end, we search for ${\mathit{\rho }}_k$ which makes ${\mathit{y}}_k$ track a desired trajectory ${\mathit{y}}_k^d$. The CLS is assumed to be reset with each ILC iteration to zero initial conditions. The CLS response to non-zero (but constant) initial conditions and repeated disturbances is easily absorbed into ${\mathit{y}}_k^d$. At the given ILC iteration j, the CLS reference input-controlled output relationship is written in lifted (or supervector) notation over an N-length experiment, as in

$${\mathit{Y}}^j=\mathit{T}{\mathit{P}}^j,$$

(8)

where the reference input at iteration j is ${\mathit{P}}^j={[{({\mathit{P}}_1^j)}^T{({\mathit{P}}_2^j)}^T\dots {({\mathit{P}}_p^j)}^T]}^T\in {\Re }^{pN\times 1}$, ${\mathit{P}}_l^j={[{\rho }_{0,l}^j, {\rho }_{1,l}^j,\dots , {\rho }_{N-1,l}^j]}^T \in {\Re }^{N\times 1}, l=\overline{1,p}$, the CLS output at iteration j is ${\mathit{Y}}^j={[{({\mathit{Y}}_1^j)}^T{({\mathit{Y}}_2^j)}^T\dots {({\mathit{Y}}_p^j)}^T]}^T\in {\Re }^{pN\times 1}$, ${\mathit{Y}}_l^j={[y_{0,l}^j,y_{1,l}^j,\dots ,y_{N-1,l}^j]}^T\in {\Re }^{N\times 1}, l=\overline{1,p}$. The impulse response terms of the pulse transfer matrix (t.m.) operator $\mathit{T}\left(q\right)$ characterizing the CLS are used to build the matrix T. To see how T emerges, the $p\times p$ causal CLS at the current iteration j is (in time notation)

$$\left[\begin{array}{l}{y}_{k,1}^j\\ y_{k,2}^j\\ \dots \\ y_{k,p}^j\end{array}\right]=\underset{\mathit{T}\left(q\right)}{\underbrace{\left[\begin{array}{l}{T}^{1,1}\left(q\right)T^{2,1}\left(q\right)\dots T^{p,1}\left(q\right)\\ T^{1,2}\left(q\right)T^{2,2}\left(q\right)\dots T^{p,2}\left(q\right)\\ \dots \\ T^{1,p}\left(q\right)T^{2,p}\left(q\right)\dots T^{p,p}\left(q\right)\end{array}\right]}}\left[\begin{array}{l}{\rho }_{k,1}^j\\ {\rho }_{k,2}^j\\ \dots \\ {\rho }_{k,p}^j\end{array}\right],$$

(9)

where $j=0,1,2,\dots$ is the iteration index, $k=0,1,\dots$ is the discrete-time index, $y_{k,l}^j$ is the l^th output at time k in iteration j, ${\rho }_{k,l}^j$ is the l^th input at time k in iteration j, and $T^{i,l}\left(q\right)$ are the pulse transfer functions (t.f.) from input i to output l. The t.m. $\mathit{T}(q)$ encompasses the feedback CLS with some kind of a multiple input multiple output (MIMO) (possibly nonlinear) feedback controller over a MIMO (possibly nonlinear) controlled system. The feedback CLS is square; that is, each reference input drives one controlled output. In general, $\mathit{T}\left(q\right)$ was coupled.

With each rational t.f. $T^{i,l}\left(q\right)$ admitting an infinite $T^{i,l}\left(q\right)=\cdots +t_{-2}^{i,l}{q}^2+t_{-1}^{i,l}q+t_0^{i,l}+t_1^{i,l}{q}^{-1}+t_2^{i,l}{q}^{-2}+\cdots$ power series expansion, a truncated lifted notation of length N for the ILC system is

$$\left[\begin{array}{c}{y}_{0,1}^j\\ y_{1,1}^j\\ ⋮\\ y_{N-1,1}^j\\ ---\\ ⋮\\ ---\\ y_{0,p}^j\\ y_{1,p}^j\\ ⋮\\ y_{N-1,p}^j\end{array}\right]=\underset{\mathit{T}}{\underbrace{\left[\begin{array}{l}{\mathit{T}}^{1,1}{\mathit{T}}^{2,1}\dots {\mathit{T}}^{p,1}\\ --------\\ ⋮\\ --------\\ {\mathit{T}}^{1,p}{\mathit{T}}^{2,p}\dots {\mathit{T}}^{p,p}\end{array}\right]}}\left[\begin{array}{c}{\rho }_{0,1}^j\\ {\rho }_{1,1}^j\\ ⋮\\ {\rho }_{N-1,1}^j\\ ---\\ ⋮\\ ---\\ {\rho }_{0,p}^j\\ {\rho }_{1,p}^j\\ ⋮\\ {\rho }_{N-1,p}^j\end{array}\right]\equiv {\mathit{Y}}^j=\mathit{T}{\mathit{P}}^j,$$

(10)

where each ${\mathit{T}}^{i,l}=\left[\begin{array}{cccc}{t}_0^{i,l}& t_{-1}^{i,l}& \dots & t_{1-N}^{i,l}\\ t_1^{i,l}& t_0^{i,l}& \dots & t_{2-N}^{i,l}\\ ⋮& ⋮& \ddots & ⋮\\ t_{N-1}^{i,l}& t_{N-2}^{i,l}& \dots & t_0^{i,l}\end{array}\right]\in {\Re }^{N\times N}$ is built from the impulse response coefficients of $T^{i,l}\left(q\right)$ and all the ${\mathit{T}}^{i,l}$ build the $\mathit{T}\in {\Re }^{pN\times pN}$ (note the difference between T and $\mathit{T}\left(q\right)$).

Let the desired output trajectory be ${\mathit{Y}}^d={[{({\mathit{Y}}_1^d)}^T {({\mathit{Y}}_2^d)}^T \dots {({\mathit{Y}}_p^d)}^T]}^T\in {\Re }^{pN\times 1}$, ${\mathit{Y}}_l^d = {[y_{0,l}^d, y_{1,l}^d, \dots , y_{N-1,l}^d]}^T\in {\Re }^{N\times 1}, l=\overline{1,p}$. The learning goal is formally expressed as an optimization problem without constraints as:

$${\mathit{P}}^{*}=\mathit{arg} \underset{\mathit{P}}{min}J\left(\mathit{P}\right), J\left(\mathit{P}\right)=\frac{1}{N}\parallel \mathit{E}\left(\mathit{P}\right){\parallel }_2^2=\frac{1}{N}\parallel \mathit{T}\mathit{P}-{\mathit{Y}}^d{\parallel }_2^2+\frac{\lambda }{N}\parallel \mathit{P}{\parallel }_2^2,$$

(11)

where the tracking error in the current iteration is ${\mathit{E}}^j={\mathit{Y}}^d-\mathit{T}{\mathit{P}}^j$. The non-zero regularization coefficient $\lambda$ may be useful in cases where, for example, ${\mathit{Y}}^d$ does not acknowledge a possible NMP $\mathit{T}\left(q\right)$. For simplicity, no regularization is used next ($\lambda =0$). Directly working with T in practice raises several numerical difficulties: ill-conditioning, large size, and its identification is costly. A convenient numerical solution to (11) is ${\mathit{P}}^{*}={({\mathit{T}}^T\mathit{T})}^{-1}{\mathit{T}}^T{\mathit{Y}}^d$. However, without using T explicitly, (11) is solved based on an ILC-specific iterative update law as a gradient descent search starting from an initial ${\mathit{P}}^0$:

$$\left[\begin{array}{c}{\mathit{P}}_1^{j+1}\\ {\mathit{P}}_2^{j+1}\\ \dots \\ {\mathit{P}}_p^{j+1}\end{array}\right]=\left[\begin{array}{c}{\mathit{P}}_1^j\\ {\mathit{P}}_2^j\\ \dots \\ {\mathit{P}}_p^j\end{array}\right]-\mathit{\xi }{\left[\begin{array}{l}\frac{\partial J\left(\mathit{P}\right)}{\partial {\mathit{P}}_1}\\ ⋮\\ \frac{\partial J\left(\mathit{P}\right)}{\partial {\mathit{P}}_p}\end{array}\right]|}_{\mathit{P}={\mathit{P}}^j}=\left[\begin{array}{c}{\mathit{P}}_1^j\\ {\mathit{P}}_2^j\\ \dots \\ {\mathit{P}}_p^j\end{array}\right]-\mathit{\xi }\frac{\partial J\left({\mathit{P}}^j\right)}{\partial \mathit{P}},$$

(12)

with a positive-definite matrix $\mathit{\xi }=diag\left({\xi }_i\right), i=\overline{1,p}$ is a user-selectable learning rate. The gradient in (12) computed according to the cost in (11) is $\frac{2}{N}·{\mathit{T}}^T{\mathit{E}}^j$ and is based on an unknown T. The next EDILC Algorithm 1 extracts this gradient information experimentally, and its steps are:

Algorithm 1

Step 0. Initialize ${\mathit{P}}^0={\mathit{Y}}^d$, then for each $j=\overline{0,ϵ}$ call the subsequent steps.

Step 1. In a nominal experiment, with the current iteration reference input Pj, measure Ej. Flip Ej to obtain udf(Ej): the upside-down flipped version of Ej.

Step 2. In a so-called gradient experiment, use μ·udf(Ej) (with scaling factor μ) as an additive disturbance on the current iteration Pj. With the disturbed reference input, the CLS output ${\mathit{Y}}_G^j$. It is valid that ${\mathit{Y}}_G^j=\mathit{T}\left({\mathit{P}}^j+\mu ·udf\left({\mathit{E}}^j\right)\right)={\mathit{Y}}^j+\mu \mathit{T}udf\left({\mathit{E}}^j\right)$. Irrespective of the number of control channels p, a single gradient experiment was performed.

Step 3. Calculate $\frac{\partial J\left({\mathit{P}}^j\right)}{\partial \mathit{P}}=\frac{2}{N}·udf\left(\frac{{\mathit{Y}}_G^j-{\mathit{Y}}^j}{\mu }\right)$, since ${\mathit{T}}^T{\mathit{E}}^j=udf\left(\mathit{T}udf\left({\mathit{E}}^j\right)\right)$ provably holds.

Step 4. Call (8) to update ${\mathit{P}}^j$.

Step 5. Go to Step 1 if j < ϵ, otherwise exit with ${\mathit{P}}^{ϵ}$.

The output of the model-free EDILC algorithm is the primitive pair $\left\{{\mathit{P}}^{ϵ}\stackrel{\Delta }{=}{\tilde{\mathit{P}}}_{}^{*},\mathit{Y}\right\}$ where the input primitive is ${\tilde{\mathit{P}}}^{*}$, the output primitive is Y. Several such pairs can be learned, and they can be indexed $\left\{{\tilde{\mathit{P}}}_{}^{*\left[\delta \right]},{\mathit{Y}}^{\left[\delta \right]}\right\}$. Note that $\mathit{Y}$ is used instead of ${\mathit{Y}}^d$ in the primitive because of the following reasons: after the algorithm, $\mathit{Y}$ and ${\mathit{Y}}^d$ are close; it is the pair $\left\{{\tilde{\mathit{P}}}_{}^{*},\mathit{Y}\right\}$ that intrinsically encodes the behavior $\mathit{T}\left(q\right)$. In addition, ${\tilde{\mathit{P}}}^{*}$ is not exactly the ${\mathit{P}}^{*}$ solving (11) because EDILC stops after a finite number of iterations. Algorithm 1 runs in a mixed-mode: each iteration requires two real-time experiments which are proportional to the number N of samples of the desired trajectory. These computations are repeated for a number of iterations $ϵ$. We conclude that this algorithm complexity is $O\left(N^2\right)$. Note that the gradient computation has been greatly optimized: it requires a single gradient experiment than the previous variants of the EDILC algorithm in [8] which required a number of gradient experiments equal to the number of CLS inputs, in which case the complexity would have been $O\left(N^3\right)$.

Monotonic convergence is desirable for EDILC and is ensured by the proper selection of step size $\mathit{\xi }$. The learning level L1 makes the CLS match ${\mathit{T}}_{ORM}\left(q\right)$ to some extent; however, a mismatch is expected. The I/O samples from the EDILC trajectories used to learn $\left\{{\tilde{\mathit{P}}}_{}^{*},\mathit{Y}\right\}$ offer the opportunity to identify a linear lower-order model for the CLS, which commonly has low-pass behavior. We denote the model identified from the I/O data as $\tilde{\mathit{T}}\left(q\right)$. Then, ${\mathit{T}}_{ORM}\left(q\right)$ and $\tilde{\mathit{T}}\left(q\right)$ are both rough CLS estimates, which can be used to derive suitable step sizes for monotonic EDILC convergence. The most conservative selection of $\mathit{\xi }$ is selected by solving the subsequent optimization:

$$\begin{array}{l}{\mathit{\xi }}_1^{*}=\mathit{arg} \underset{\mathit{\xi }}{max}{{\displaystyle \sum }}_{i=1}^p{\xi }_{1,i}, s.t.{\xi }_{1,i}>0, \parallel {\mathit{I}}_{p\times p}-\frac{2}{N}{\mathit{T}}_{ORM}\left(q\right){\mathit{\xi }}_1{\mathit{T}}_{ORM}^T\left(\frac{1}{q}\right){\parallel }_{\infty }<1;\\ {\mathit{\xi }}_2^{*}=\mathit{arg} \underset{\mathit{\xi }}{max}{{\displaystyle \sum }}_{i=1}^p{\xi }_{2,i}, s.t.{\xi }_{2,i}>0, \parallel {\mathit{I}}_{p\times p}-\frac{2}{N}\tilde{\mathit{T}}\left(q\right){\mathit{\xi }}_2{\tilde{\mathit{T}}}^T\left(\frac{1}{q}\right){\parallel }_{\infty }<1;\\ {\mathit{\xi }}^{*}=diag\left[{\xi }_i\right], {\xi }_i=\mathit{min}\left({\xi }_{1,i},{\xi }_{2,i}\right), i=\overline{1,p},\end{array}$$

(13)

where $\parallel .{\parallel }_{\infty }$ is the norm calculated as the greatest singular value of a t.m. over the frequency domain, while the identity transfer matrix is ${\mathit{I}}_{p\times p}$. Derivation of the convergence condition for the t.m. norm inequality constraints in (13) is presented in Appendix A.

${\mathit{T}}_{ORM}\left(q\right)$ is usually selected diagonally to ensure decoupling between the control channels through controller design, at least in the steady state, for example, by including integral action in the controllers. For example, for a first-order square reference model of size 2-by-2, the continuous-time unitary-gain t.m. is selected as ${\mathit{T}}_{ORM}\left(s\right)=diag\left(\frac{e^{-s{T}_{m1}}}{1+s{T}_1},\frac{e^{-s{T}_{m2}}}{1+s{T}_2}\right)$ (s is the continuous-time Laplace complex argument), where T₁ and T₂ are the time constants that impose the transient behavior, $T_{m1},T_{m2}$ are delays. The real achieved behavior in continuous time can be modeled as $\tilde{\mathit{T}}\left(s\right)=\left[{\tilde{T}}_{11}{\tilde{T}}_{12};{\tilde{T}}_{21}{\tilde{T}}_{22}\right]$ with ${\tilde{T}}_{11}\left(s\right)=\frac{k_{11}\left(T_{11}s+1\right)e^{-s{T}_{m11}}}{s^2+b_{11}s+c_{11}}$, ${\tilde{T}}_{21}\left(s\right)=\frac{k_{21}s\left(T_{21}s+1\right)e^{-s{T}_{m21}}}{s^2+b_{21}s+c_{21}}$, ${\tilde{T}}_{12}\left(s\right)=\frac{k_{12}s\left(T_{12}s+1\right)e^{-s{T}_{m12}}}{s^2+b_{12}s+c_{12}}$, ${\tilde{T}}_{22}\left(s\right)=\frac{k_{22}\left(T_{22}s+1\right)e^{-s{T}_{m22}}}{s^2+b_{22}s+c_{22}}$ where the second-order t.f.s on the anti-diagonal capture any coupling transient that possibly vanishes in time and oscillates at most, while the second-order t.f.s from the main diagonal captures any transient responses that are oscillatory at most and may or may not achieve the desired unit gains. Time delay and NMP zeros must be included in the ORM definition without difficulty, if present. The equivalent discretized causal behavior model $\tilde{\mathit{T}}\left(q\right)$ of the CLS $\tilde{\mathit{T}}\left(s\right)$, identifiable from I/O data, is (where $m_{ij}\in \mathbb{N}$ are the delay steps)

$$\tilde{\mathit{T}}\left(q\right)=\left[\begin{array}{cc}\frac{b_{11}^1{q}^{-1}+b_{11}^2{q}^{-2}}{1+a_{11}^1{q}^{-1}+a_{11}^2{q}^{-2}}{q}^{-m11}& \frac{b_{12}^0+b_{12}^1{q}^{-1}+b_{12}^2{q}^{-2}}{1+a_{12}^1{q}^{-1}+a_{12}^2{q}^{-2}}{q}^{-m12}\\ \frac{b_{21}^0+b_{21}^1{q}^{-1}+b_{21}^2{q}^{-2}}{1+a_{21}^1{q}^{-1}+a_{21}^2{q}^{-2}}{q}^{-m21}& \frac{b_{22}^1{q}^{-1}+b_{22}^2{q}^{-2}}{1+a_{22}^1{q}^{-1}+a_{22}^2{q}^{-2}}{q}^{-m22}\end{array}\right].$$

(14)

During ILC operation, $\tilde{\mathit{T}}\left(q\right)$ is identified using I/O data either from the nominal or gradient experiment, or from both. The model can be re-estimated or can be continuously refined with every ILC iteration, with no computational burden, owing to the offline experimental nature of ILC. Model precision is not crucial because uncertainty only affects the monotonic convergence condition, and more cautious learning can be attempted. In any case, using low-order models such as (14) is recommended because the ORM control ensures that the CLS approximately matches ${\mathit{T}}_{ORM}\left(q\right)$.

A better initial value than ${\mathit{P}}^0={\mathit{Y}}^d$ in the EDILC law (12) could theoretically be found based on the desired ORM ${\mathit{T}}_{ORM}\left(q\right)$. This could further improve the convergence speed of the subsequent EDILC. The initialization is expressed as:

$${\mathit{P}}^0=\mathit{arg} \underset{\mathit{P}}{min}\frac{1}{N}{({\mathit{T}}_{ORM}\mathit{P}-{\mathit{Y}}^d)}^T\left({\mathit{T}}_{ORM}\mathit{P}-{\mathit{Y}}^d\right)+\frac{\lambda }{N}{\mathit{P}}^T\mathit{P},$$

(15)

where the term ${\mathit{T}}_{ORM}\mathit{P}$ is evaluated by simulation, based on ${\mathit{T}}_{ORM}\left(q\right)$, on a finite-time scenario with length N. However, experimental investigations reveal that this initialization renders oscillatory ${\mathit{P}}^0$ near its ends because of noncausal filtering involved in the model-based solution of (15).

The EDILC learns primitives under constraints imposed on the operational variables, such as on the control action ${\mathit{a}}_k$ (and also on its derivative) and on the system (and also the CLS) output ${\mathit{y}}_k$ (and also on its derivative). The reference input constraints are not of interest in this type of tracking problem. These constraints are mostly of the inequality type owing to the underlying dynamical system. They can be directly handled either as hard constraints appended to (7) or as soft constraints by additional terms in the cost function of the optimization (7). It was shown [44] that inequality-type hard constraint handling is still possible with EDILC in an experimental-driven fashion with unknown system dynamics. For primitive-based learning with EDILC, inequality-type constraints on ${\mathit{a}}_k$ are possible, but generally not an issue, as long as the CLS operates in the linearized range resulting from the level L1 learning phase. Any constraints on ${\mathit{a}}_k$ (and possibly on its derivative) may negatively impact the level of L2 learning trajectory tracking performance. Therefore, the constraints on ${\mathit{y}}_k$ are more interesting, mainly for safety reasons such as saturation, which when violated in mechanical systems could lead to permanent damage. The constraints on ${\mathit{y}}_k$ will not be handled explicitly at this level L2, but rather indirectly at the next level L3 and deferred to a later section.

Concluding the level L2 learning aspects discussion, the final tertiary learning level L3 is presented next.

5. The L3 Level—New Desired Trajectories Optimally Tracked by Extrapolating Primitives’ Behavior

Suppose a new desired trajectory ${\mathit{Y}}_{}^d$ is to be tracked; this time, without relearning by EDILC. This amounts to finding the optimal reference input ${\mathit{P}}_{}^{*}$ to obtain a CLS output that perfectly tracks ${\mathit{Y}}_{}^d$. A solution to use and extrapolate the behavior of learned primitive pairs was proposed in [8]. Because the solution uses delayed copies of the output primitives from the learned pairs serving as basis functions for approximating ${\mathit{Y}}_{}^d$, the reason for using EDILC to learn output primitives that have good approximation capability is transparent. Among others, Gaussian shapes are well-known in function approximation theory; therefore, primitive pairs $\left\{{\tilde{\mathit{P}}}_{}^{*\left[\delta \right]},{\mathit{Y}}^{\left[\delta \right]}\right\}$ where the output primitives ${\mathit{Y}}^{\left[\delta \right]}$ have a Gaussian-like shape, are commonly learned with EDILC.

In the following, the desired trajectory ${\mathit{Y}}_{}^d$ is assumed to start from zero and end in non-zero values, component-wise. To accommodate for fine approximations whenever ${\mathit{Y}}_{}^d$ ends in a non-zero value and starts from zero with a non-zero slope, both ${\mathit{Y}}_{}^d$ and the copied primitive pairs $\left\{{\tilde{\mathit{P}}}_{}^{*\left[\delta \right]},{\mathit{Y}}^{\left[\delta \right]}\right\}$ will undergo a time-extension process. The length of ${\mathit{Y}}_{}^d$ is N (same as the primitives’ length), and with no generality loss, N is assumed even. A longer desired trajectory was deferred to a later discussion. The optimal reference input calculation Algorithm 2 is summarized below.

Algorithm 2

Step 0. Initialize ${\mathit{P}}^0={\mathit{Y}}^d$, then for each $j=\overline{0,ϵ}$ call the subsequent steps.

Step 1. Let $y_{k,1}^d,y_{k,2}^d,\dots ,y_{k,p}^d$ be the components of ${\mathit{Y}}_{}^d$. In lifted notation, these trajectories are ${\mathit{Y}}_1^d,{\mathit{Y}}_2^d,\dots ,{\mathit{Y}}_p^d$.

Step 2. Extend each ${\mathit{Y}}_1^d,\dots ,{\mathit{Y}}_p^d$ to size 2N, padding with the first and last sample of ${\mathit{Y}}_1^d,\dots ,{\mathit{Y}}_p^d$, respectively with N/2 values to the right and to the left, respectively. We denote the extended trajectories ${\mathit{Y}}_1^{d\left[e\right]},{\mathit{Y}}_2^{d\left[e\right]},\dots ,{\mathit{Y}}_p^{d\left[e\right]}$.

Step 3. Arrange ${\mathit{Y}}^{d\left[e\right]}={[{\mathit{Y}}_1^{d{[e]}^T},{\mathit{Y}}_2^{d{[e]}^T},\dots ,{\mathit{Y}}_p^{d{[e]}^T}]}^T\in {\Re }^{2pN}$.

Step 4. The N-length input primitives $\left({\tilde{\mathit{P}}}_1^{*\left[\delta \right]}\right),\left({\tilde{\mathit{P}}}_2^{*\left[\delta \right]}\right),\dots ,\left({\tilde{\mathit{P}}}_p^{*\left[\delta \right]}\right)$ and N-length output primitives $\left({\mathit{Y}}_1^{\left[\delta \right]}\right),\left({\mathit{Y}}_2^{\left[\delta \right]}\right),\dots ,\left({\mathit{Y}}_p^{\left[\delta \right]}\right)$, from the δth  learned pair, are extended to size 2N by padding to the left and right N/2 zeros, respectively. Padding with zeros is employed because both ${\tilde{\mathit{P}}}_{}^{*\left[\delta \right]},{\mathit{Y}}^{\left[\delta \right]}$ start and end at zero, owing to the Gaussian-like shape of ${\mathit{Y}}^{\left[\delta \right]}$. We denote $\left\{{\tilde{\mathit{P}}}_{}^{*\left[\delta e\right]},{\mathit{Y}}^{\left[\delta e\right]}\right\}$ as the extended primitives.

Step 5. Make M copies of the randomly occurring δ extended pairs $\left\{{\tilde{\mathit{P}}}_{}^{*\left[\delta e\right]},{\mathit{Y}}^{\left[\delta e\right]}\right\}$, let them be called as $\left\{{\tilde{\mathit{P}}}_{}^{*\left[\pi e\right]},{\mathit{Y}}^{\left[\pi e\right]}\right\}, \pi =\overline{1,M}$.

Step 6. Delay each component ${\tilde{\mathit{P}}}_1^{*\left[\pi e\right]},\dots ,{\tilde{\mathit{P}}}_p^{*\left[\pi e\right]}$ and ${\mathit{Y}}_1^{\left[\pi e\right]},\dots ,{\mathit{Y}}_p^{\left[\pi e\right]}$ of the π pairs by an integer uniform number $\theta \in \left[-N,N\right]$. Because the delay is a non-circular shift, padding is again required to either end, based on the sign of θ. The value used for padding for a number of |θ| samples is the first or last sample value of the unshifted signals. Let ${\tilde{\mathit{P}}}_1^{*\left[{\theta }_{\pi }e\right]},\dots ,{\tilde{\mathit{P}}}_p^{*\left[{\theta }_{\pi }e\right]},{\mathit{Y}}_1^{\left[{\theta }_{\pi }e\right]},\dots ,{\mathit{Y}}_p^{\left[{\theta }_{\pi }e\right]}$ be the notation for the delayed input and output primitive of each of the π pairs.

Step 7. Obtain ${\tilde{\mathit{P}}}_{}^{*\left[{\theta }_{\pi }e\right]}={[{\tilde{\mathit{P}}}_1^{*{[{\theta }_{\pi }e]}^T},\dots ,{\tilde{\mathit{P}}}_p^{*{[{\theta }_{\pi }e]}^T}]}^T\in {\Re }^{2pN}$ and ${\mathit{Y}}_{}^{\left[{\theta }_{\pi }e\right]}={[{\mathit{Y}}_1^{{[{\theta }_{\pi }e]}^T},\dots ,{\mathit{Y}}_p^{{[{\theta }_{\pi }e]}^T}]}^T\in {\Re }^{2pN}$. The basis function matrix is ${\mathit{Y}}_{}^{\left[b\right]}=\left[{\mathit{Y}}_{}^{\left[{\theta }_{1}e\right]},\dots ,{\mathit{Y}}_{}^{\left[{\theta }_{M}e\right]}\right]\in {\Re }^{2pN\times M}$. A visual summary of the extension with padding, delay with padding, and final concatenation is shown for the output primitives in Figure 1.

Step 8. Compute $\mathit{w}={[w_1,\dots ,w_M]}^T\in {\Re }^M$ as the minimizer of $\parallel {\mathit{Y}}_{}^{\left[b\right]}\mathit{w}-{\mathit{Y}}_{}^{d\left[e\right]}{\parallel }_2$ with linear least-squares. Each component of w multiplies a specific ${\mathit{Y}}_{}^{\left[{\theta }_{\pi }e\right]}$.

Step 9. Based on Theorem 1 from [8], the optimal reference to ensure the tracking of ${\mathit{Y}}^d$ is: $${\tilde{\mathit{P}}}_{}^{*}={\displaystyle \sum }_{\pi =1}^M{w}_{\pi }{\tilde{P}}_{}^{*\left[{\theta }_{\pi }e\right]},$$ (16)

Step 10. In (16), ${\tilde{\mathit{P}}}_{}^{*}={[{\tilde{\mathit{P}}}_1^{*}{}^T{\tilde{\mathit{P}}}_2^{*}{}^T\dots {\tilde{\mathit{P}}}_p^{*}{}^T]}^T\in {\Re }^{2pN}$. To obtain N-length channel-wise optimal reference inputs, the p components are clipped in the middle of their intervals.

Step 11. The clipped optimal references are set as CLS inputs, and the CLS output tracks ${\mathit{Y}}_{}^d$. The algorithm ends.

Algorithm 2 is entirely performed offline, not impacting the real-time control task. Of course, the planner is allowed sufficient computation time. If the trajectories to be tracked on each subinterval are very long, this may impact performance, but we have tried to solve this particular issue by dividing the longer trajectories in shorter, manageable trajectories. Essentially, Algorithm 2 has two complexity components: the least squares matrices preparation part which has complexity $O\left(N^3\right)$ and the least squares regression solution which combines matrix multiplication and the SVD factorization. For this numerical solution, the complexity is $O\left(M^{2}X\right)$ where $M$ is the size of the regression vector $\mathit{w}$ and $X=2\mathit{pN}$ is the number of examples ($N$ is the experiment length and $p$ is the number of CLS inputs and outputs). Hence, the complexity of Algorithm 2 is $O\left(N^4\right)$ but since p is usually a small constant, it can be approximated to $O\left(N^3\right)$.

The optimality of ${\tilde{\mathit{P}}}_{}^{*}$ in (16) with respect to the tracking performance and its relation to the true optimal solution ${\mathit{P}}_{}^{*}$ of (11) is analyzed next.

Theorem 1.

When ${\mathit{Y}}^{d\left[e\right]}$ is approximated with a bounded reconstruction error ζ, then ${\mathit{P}}^{*}$ can be computed with arbitrary precision.

Proof. 

The desired trajectory is decomposed as in ${\mathit{Y}}^{d\left[e\right]}={{\displaystyle \sum }}_{\pi =1}^M{w}_{\pi }{\mathit{Y}}^{\left[{\theta }_{\pi }e\right]}+\mathit{\zeta }$, where ζ is the bounded reconstruction error. The optimal reference input ensuring perfect tracking is ${\mathit{P}}_{}^{*}={({\mathit{T}}^T\mathit{T})}^{-1}{\mathit{T}}^T{\mathit{Y}}^{d\left[e\right]}$ and is expressed as ${\mathit{P}}_{}^{*}={({\mathit{T}}^T\mathit{T})}^{-1}{\mathit{T}}^T\left({{\displaystyle \sum }}_{\pi =1}^M{w}_{\pi }{\mathit{Y}}^{\left[{\theta }_{\pi }e\right]}+\mathit{\zeta }\right)={{\displaystyle \sum }}_{\pi =1}^M{w}_{\pi }{\tilde{\mathit{P}}}^{*\left[{\theta }_{\pi }e\right]}+{({\mathit{T}}^T\mathit{T})}^{-1}{\mathit{T}}^T\mathit{\zeta }$. As ${\parallel \mathit{\zeta }\parallel }_2\to 0$, then $\parallel {({\mathit{T}}^T\mathit{T})}^{-1}{\mathit{T}}^T\mathit{\zeta }{\parallel }_2\le \parallel {({\mathit{T}}^T\mathit{T})}^{-1}{\mathit{T}}^T{\parallel }_2 {\parallel \mathit{\zeta }\parallel }_2\to 0$ follows, where ${\parallel •\parallel }_2$ applied to a matrix is the induced 2-norm by a vector, which represents the matrix’s largest singular value, ${\parallel •\parallel }_2$ applied to a vector is the Euclidean norm. □

Theorem 1 shows that a good approximation of the desired trajectory in terms of a small error leads to a reference input close to the optimal one. This ensures good tracking performance. To achieve a small approximation error, the number of basis functions can be adjusted along with the desired shape.

Managing Longer Desired Trajectories

Suppose that each signal component $y_{k,1}^d,y_{k,2}^d,\dots ,y_{k,p}^d$ of Y^d has length Ω as a multiple of N (padding is again usable when Ω is not a multiple of N). One solution to obtain the desired optimal reference input that achieves CLS output tracking of Y^d is to extend the primitive pairs $\left\{{\tilde{\mathit{P}}}_{}^{*\left[\delta e\right]},{\mathit{Y}}^{\left[\delta e\right]}\right\}$ to length Ω with appropriate padding. In addition, proportionally more M copies of these extended pairs were used. This will increase the size of w and the ill-condition the least squares. An intuitive mitigation is to perform tracking experiments on subintervals of length N as divisions of Y^d.

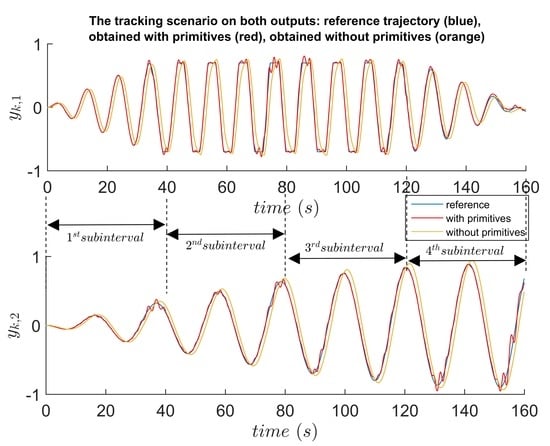
For example, a longer trajectory of length 2N, comprising two shorter trajectories of length N, is displayed in Figure 2 for a single input single output (SISO) system. The end of trajectory $\overline{{00}^{\prime }}$ is the start of trajectory $\overline{0^{\prime }B}$. A base reference frame in discrete-time is $<k0y^d>$ with a discrete-time index k.

One solution is to translate the origin of the base reference frame $<k0y^d>$ to the starting point of each piece of the desired trajectory of length N. In Figure 2, $<k0y^d>$ is translated to $<k^{\prime }{0}^{\prime }{y}^{d\prime }>$. This is equivalent to having the desired trajectory $\overline{0^{\prime }B}$ starting from the origin. Thus, the planner always computes the optimal reference inputs for a desired trajectory starting in zero initial conditions. Considering that the tracked trajectory $\overline{0A}$ does not perfectly track the desired one $\overline{{00}^{\prime }}$ and there exists a vertical distance $\epsilon$ between the endpoints of $\overline{0A}$ and $\overline{{00}^{\prime }}$, then in the translated reference frame $<k^{\prime }{0}^{\prime }{y}^{d^{\prime }}>$ the closed-loop CS will have a non-zero initial condition in the $\epsilon$-vicinity near $0^{\prime }$. In practice, $\epsilon$ is expected to be small. The CS response due to the non-zero initial condition vanishes over time.

After executing the tracking task on the second subinterval with desired trajectory $\overline{0^{\prime }B}$, the execution is translated back in the base frame $<k0y^d>$ for visualization; afterwards, the reference frame $<k^{\prime }{0}^{\prime }{y}^{d\prime }>$ is moved in the start of the desired trajectory of the third subinterval, and the entire process repeats itself for all subintervals. After all subinterval tracking tasks are executed, the actual obtained trajectories are translated back to the base reference frame and then concatenated to be presented as a longer tracking task.

Inequality-type constraints on $\mathit{Y}$ can be handled indirectly at the tertiary learning level. The aim of this learning level is to ensure the theoretical perfect tracking of ${\mathit{Y}}_{}^d$, meaning that $\mathit{Y}={\mathit{Y}}_{}^d$. This implies that any constraint on ${\mathit{Y}}_{}^d$ is imposed on $\mathit{Y}$ also. We note that inequality constraints on the rate of $\mathit{Y}$ are again not of particular interest when trajectory tracking is aimed; therefore, the magnitude constraints are more feasible in the lifted form as ${\mathit{Y}}_{low}^d\le {\mathit{Y}}_{}^d\le {\mathit{Y}}_{up}^d$. As a result, the constraints on $\mathit{Y}$ are softly handled.

With the discussed aspects of the L3 learning level, the entire hierarchical three-level framework shown in Figure 3 was validated on a real-world system.

6. Validation Case Study

6.1. The Hybrid Software-Electrical Controlled System

Figure 4 shows the proposed multivariable nonlinear controlled system. The USB-based communication between an Arduino-based board and a computer (PC) manages the pulse-width modulated interface (PWM) used for voltage input action setting and for the analog-to-digital interface to read controlled voltages. Here, the PWM duty cycles are the system’s input actions, $\mathit{a}={[a_1,a_2]}^T$. Their domain [0;1] is shifted to [−0.5,0.5] for symmetric operation. Let V_o1 and V_o2 be the capacitors C₁ and C₂ voltages, respectively. The system controlled outputs are shifted to $\left[–2.5;2.5\right] V$ for symmetric operation; therefore, they are calculated on the PC as $y_1=V_{o1}-2.5$, $y_2=V_{o2}-2.5$. All communication, processing and control tasks are performed using MATLAB software package.

Part of this Hammerstein-like system is electrical (circuit parameters are $C1=C2=47 \mathsf{\mu }\mathrm{F}$,$C3=16.5 \mathsf{\mu }\mathrm{F}, R1=R2= 10\mathrm{k}\Omega$,), while the input nonlinearities (characterized by a hyperbolic tangent function) and a linear t.f. on the first input action (which has a resonant mode at approximately 7.3 rad/s) run on a PC. The system is zero-order-hold sampled at $T_s=0.1 s$, rendering the I/O as ${\mathit{a}}_k={[a_{k,1},a_{k,2}]}^T$ and y_k = [y_k,1, y_k,2]^T. Prior experiments reveal a unit step delay $T_s$ to be included when defining the ORM for level L1 learning and also in defining ${\mathit{y}}_k^d$ for level L2 learning [45].

6.2. ORM Tracking Learned for Feedback Linearization (Level L1)

First, a PI-type controller of the form $a_{k,1}=\left[0.15+0.1T_s/\left(q-1\right)\right]\left({\rho }_{k,1}-y_{k,1}\right)$, $a_{k,2}=[0.35+0.25T_s/\left(q-1\right)$ $]\left({\rho }_{k,2}-y_{k,2}\right)$ is employed to collect transition sample experiences from the CLS under noisy additive disturbances on the control action inputs [45]. These disturbances were used to enhance exploration. For a prescribed time of 1500 s, sequences of piecewise constant reference inputs with random amplitudes within some tunable domains drive the CLS dynamics. The state of a transition tuple $\left({\mathit{s}}_k^{ext},{\mathit{a}}_k,{\mathit{s}}_{k+1}^{ext}\right)$ is ${\mathit{s}}_k^{ext}={[y_{k,1}, y_{k,2}, \dots , y_{k-5,1}, y_{k-5,2}, a_{k-1,1}, a_{k-1,2}, \dots , a_{k-5,1}, a_{k-5,2}, s_{k,1}^m, s_{k,2}^m, {\rho }_{k,1}, {\rho }_{k,2} ]}^T$. Transitions from the time steps when ${\mathit{\rho }}_{k+1}={\mathit{\rho }}_k$ were considered. Approximately 14,000 transitions were formed and used for AIVI learning.

At the same time, to achieve indirect CLS linearization by ORM tracking, level L1 learning requires the selection of a linear ORM model as ${\mathit{T}}_{ORM}\left(s\right)=diag\left(e^{-s{T}_s}/\left(s+1\right),e^{-s{T}_s}/\left(s+1\right)\right)$, in the easy-interpretable continuous-time. Before discretizing ${\mathit{T}}_{ORM}\left(s\right)$, note that it acknowledges the dead-time of one sampling period observed for the system, in addition to the relative degree one induced by the zero-order hold. This is read from the discrete-time I/O sample acquisition of the transition collection phase. The discretized t.f. ${\mathit{T}}_{ORM}\left(q\right)=diag\left(\frac{0.0952q^{-2}}{1-0.9048q^{-1}},\frac{0.0952q^{-2}}{1-0.9048q^{-1}}\right)$ is then expressed as a state-space model resulting from an observable canonical transformation. The resulting 4^th order state-space uses two extra states denoted with $\varpi$, owing to the time delay of each t.f. from the ${\mathit{T}}_{ORM}\left(q\right)$. The model used is ([45]):

$$\{\begin{array}{l}\left[\begin{array}{l}{s}_{k+1,1}^m\\ {\varpi }_{k+1,1}\\ s_{k+1,2}^m\\ {\varpi }_{k+1,2}\end{array}\right]=\left[\begin{array}{cccc}0.9048& 0.0952& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0.9048& 0.0952\\ 0& 0& 0& 0\end{array}\right]\left[\begin{array}{l}{s}_{k,1}^m\\ {\varpi }_{k,1}\\ s_{k,2}^m\\ {\varpi }_{k,2}\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 1& 0\\ 0& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}{\rho }_{k,1}\\ {\rho }_{k,2}\end{array}\right],\\ {\mathit{y}}_k^m=[y_{k,1}^m{y}_{k,2}^m{]}^T=[1,0,1,0]\times [s_{k,1}^m{\varpi }_{k,1}{s}_{k,2}^m{\varpi }_{k,2}{]}^T.\end{array}$$

(17)

A single hidden layer feed-forward controller NN of size 28–15–2 is learned to output ${\mathit{a}}_k$ for the input ${\mathit{s}}_k^{ex}$, using the AIVI iteration steps, which implies NN training for both the controller and for a Q-function approximator NN, having a similar architecture but size 30–100–1. The CLS with the converged AIVI NN controller after six iterations of the AIVI approach is shown the ORM tracking ability in Figure 5. To check this convergence, the controller resulting after each iteration of the AIVI is tested on a scenario in which sequences of piecewise constant reference inputs drive the CLS. The ORM tracking performance was measured with a regularized finite-length version of $V_{ORM}^{\infty }$, defined as $V_{test}=1/N·V_{ORM}^N$, with $N=2000$. The convergence is illustrated in Figure 6. It occurs relatively quickly, and the best controller is shown in Figure 5.

This concludes the L1 level indirect CLS linearization by matching the behavior of ${\mathit{T}}_{ORM}\left(q\right)$. The subsequent EDILC L2 level learning benefits from this assumption.

6.3. Two Primitives Learned with EDILC (Level L2)

A number of $\delta =2$ primitives of length $N=400$ samples are learned using the EDILC Algorithm 1 with ${\mathit{P}}_{}^0={\mathit{Y}}_{}^d$, $\mu =0.01$, $ϵ=30$, and the learning rate $\mathit{\xi }=diag(299.13, 281.35)$ was determined by solving (13) using ${\mathit{T}}_{ORM}\left(q\right)$ and an approximate CLS t.f. identified as [45]

$$\tilde{\mathit{T}}\left(q\right)=\left[\begin{array}{cc}\frac{0.1278q^{-2}}{1-0.77258q^{-1}-0.1126q^{-2}}& \frac{0.02189q^{-2}-0.02101q^{-3}}{1-1.213q^{-1}+0.2206q^{-2}}\\ \frac{0.0756q^{-2}-0.05602q^{-3}}{1-0.8129q^{-1}+0.7474q^{-2}}& \frac{0.1554q^{-2}}{1-0.4374q^{-1}-0.422q^{-2}}\end{array}\right].$$

(18)

For the first primitive $\left\{{\tilde{\mathit{P}}}_{}^{*\left[1\right]},{\mathit{Y}}^{\left[1\right]}\right\}$, the desired trajectory spanning N = 400 time steps ($k=\overline{0,399}$) is $y_{k,1}^{d\left[1\right]}={\chi }_1\mathit{exp}({\chi }_2\left(k-{\chi }_3{)}^2\right)$, (${\chi }_1=2$, ${\chi }_2=-0.002$, ${\chi }_3=200$) and $y_{k,2}^{d\left[1\right]}=0$, whereas the second primitive $\left\{{\tilde{\mathit{P}}}_{}^{*\left[2\right]},{\mathit{Y}}^{\left[2\right]}\right\}$ is characterized by the same length and by $y_{k,1}^{d\left[2\right]}=0$, $y_{k,2}^{d\left[2\right]}=y_{k,1}^{d\left[1\right]}$. That is, for each primitive, one desired output is Gaussian, while the other is zero. The first primitive $\left\{{\tilde{\mathit{P}}}_{}^{*\left[1\right]},{\mathit{Y}}^{\left[1\right]}\right\}$ learned using EDILC is shown in Figure 7.

6.4. Optimal Tracking Predicted from Primitives (Level L3)

At level L3, it is desired to track $y_{k,1}^d=\mathit{max}\{-0.7,\mathit{min}[0.7,{\chi }_1\mathit{sin}({\chi }_{2}k{T}_s)\mathit{sin}({\chi }_{3}k{T}_s)]\}$ (${\chi }_1=1.1$, ${\chi }_2=0.6$, ${\chi }_3=0.02$) and $y_{k,2}^d={\chi }_1\mathit{sin}({\chi }_{2}k{T}_s)\mathit{sin}({\chi }_{3}k{T}_s)$, (${\chi }_1=-0.9$, ${\chi }_2=0.01$, ${\chi }_3=0.3$) for $k=\overline{0,\mathsf{\Omega }-1}$, where $\mathsf{\Omega }=1600=4\times N$. Trajectory $y_{k,1}^d$ is clipped in amplitude with min/max operators to induce an output constraint. Then, the CLS output $\mathit{Y}$ will be constrained because, by the primitive-based mechanism, level L3 ensures that $\mathit{Y}={\mathit{Y}}_{}^d$. Then, ${\mathit{Y}}_{}^d$ is divided into four subintervals, and the optimal reference input calculation by the primitive-based approach together with the trajectory tracking takes place on one subinterval of length N at a time. Each subinterval is offset to start the tracking at zero intervals. The parameters in Algorithm 2 are $N=400$, $\delta =2$ primitive pairs, $M=400$ copies of the two primitives are employed, $\theta \in \left[-400,400\right]$, to fulfill Theorem 1.

Figure 8 displays the extended, padded, delayed, once-again padded, and concatenated output primitives ${\mathit{Y}}_1^{\left[{\theta }_{\pi }e\right]},{\mathit{Y}}_2^{\left[{\theta }_{\pi }e\right]}$. Notably, the basis function matrix is ${\mathit{Y}}_{}^{\left[b\right]}\in {\Re }^{1600\times 400}$. The tracking results for each subinterval are re-offset in the original reference frame and displayed in Figure 9 where, for comparisons, the tracking results obtained with ${\mathit{P}}_1={\mathit{Y}}_1^d,{\mathit{P}}_2={\mathit{Y}}_2^d$ are also plotted. It is obvious that tracking is more accurate with the primitive-based approach (red line vs. blue line) than with respect to the case when it is not used (black line vs. blue line). The latter case corresponds to using only the CLS linearized with L1 level, with the reference inputs being set as usually, leaving the control system to reactively ensure trajectory tracking. Primitive-based tracking also better satisfies the constraints (in a soft, not a hard sense), which is enforced on the first axis only.

The tracking MSEs obtained with the primitive-based mechanism for the first and second axes are 0.44·10^–3 and 0.31·10^–3, respectively. When ${\mathit{P}}_1={\mathit{Y}}_1^d, {\mathit{P}}_2={\mathit{Y}}_2^d$, the tracking MSEs for the first and second axis are 6.50·10^–3 and 3.75·10^–3, respectively. A ten-fold improvement in tracking was realized using the primitive-based approach.

The observed improvement is of no surprise, since the primitive-based tracking solution behaves in an anticipative manner, whereas the tracking based on the L1 control only is “reactive” and only decides based on the provided reference input. The anticipative behavior of the primitive-based solution inherits its character from the level L2 subjected to the ILC concept. It proves that an optimal behavior can be extrapolated successfully to new trajectories to be tracked, without requiring learning by repetitions with ILC.

7. Implementation Issues and Analysis of the Primitive-Based Framework

One of the most important aspects affecting the entire hierarchical learning performance is the CLS linearity assumption achieved at level L1. Therefore, it is critical to ensure that the CLS matches the linear ORM as accurately as possible. While the mismatch does not affect the L2 level too much because the EDILC displays good learning ability even for some nonlinear CLS (the perturbation-based gradient experiment performed in the vicinity of the nominal trajectory where linearity holds), the level L3 operations have proven to be more sensitive to this mismatch because the optimal reference reconstruction relies on the superposition principle. Therefore, all efforts in learning AIVI NN controllers are justified, both in terms of NN complexity and in terms of the required database size and exploration effort. Better parameterization (more specifically, a linear one using polynomials as basis functions, as opposed to a more generic, such as, e.g., a NN) of the Q-function may need fewer transition samples for learning; however, the downside is that it requires more insight about the underlying controlled system. This insight is still needed in terms of relative degree, system order, minimum-phase character, and in matching the system bandwidth with the linear ORM’s bandwidth. Together, these impact the virtual state size (hence the learning space complexity and the function approximators architectural complexity). With careful AIVI design, the NN should be preferred because the underlying training management (e.g., early stopping) allows the more complex NN architectures to use just as much as needed in terms of approximation capacity. Another advantage is automatic feature selection, which is inherently encoded in the NN layers. Yet another aspect of offline AIVI learning is that it does not require online computational power (as in e.g., [46]). The resulting NN controllers take up to a few hours to learn offline; however, they are easily implementable afterwards on hardware with no special computing requirements for typical mechatronic systems. The efforts needed for this L1 level control, also regarded as limitations, are:

−

a good estimation of the controlled system’s relative degree. A too small degree is equivalent to partial observability and will incur a performance degradation in achieving linearized ORM tracking behavior. A higher degree will add information redundancy which is not a real issue except for the computational costs involving the resulted controller.

−

some additional required information leading to a degree of subjectiveness in the design: the underlying system’s minimum-phase character, and its bandwidth to be matched with the linear ORM’s bandwidth. This information quantification necessitates some experience from the designer and some insight into the process phenomena.

−

the controller computational complexity is not seen as an important issue. Indeed, there is more complexity than with a PI/PID controller with few parameters; however, the used NN architectures are shallow, allowing for less than 1ms inference time on a wide range of embedded devices, which would extend the application range of the control. The benefits in terms of nonlinear control performance well balance the costs.

Concerning level L2 learning, it should be used mostly in cases where ${\mathit{P}}^0={\mathit{Y}}^d$ does not render the output $\mathit{Y}$ close to the basis function shape imposed by ${\mathit{Y}}^d$. Otherwise, the impact on level L3 is not damaging, since essentially just about any shape of $Y$ will eventually have some approximation capacity. The major question at this stage is how to learn primitives to be useful for level L3. This is discussed among the aspects of the next and final learning levels. The L2 level design is dependent only on the initial solution ${\mathit{P}}^0$ and the linaerity assumption. The limitations associated with these are

−

the L2 level CLS requires resetting conditioned which for some system may be more restrictive. ILC solutions for systems without perfect resetting such stochastic resetting exists, but not in a model-free style. However, for most mechatronic systems, this is not an issue.

−

The initialization for ${\mathit{P}}^0$ can be optimized using, e.g., (15), for a neal-optimal approximate model-based initialization. This would require fewer EDILC iterations. On the other hand, model-based initialization based on non-causal filtering showed some oscillations at the beginning and at the end of ${\mathit{P}}^0$ hence it was not applied here.

−

The linearity assumption about the CLS. This must be ensured with the L1 level virtual state-feedback control. There is a certain degree of tolerance, as EDILC was applied before on smooth nonlinear systems and the underlying linear system’s theory showed effectiveness and learnability.

Most aspects concern level L3 implementation details. The discussion about how to learn the proper primitives starts backward, with the new desired trajectory ${\mathit{Y}}^d$. From Algorithm 2’s steps, ${\mathit{Y}}^d$ undergoes a transformation process (extrapolation plus padding, then concatenation), resulting in ${\mathit{Y}}^{d\left[e\right]}$ as a single signal. The same is valid when obtaining ${\mathit{Y}}_{}^{[{\theta }_{\pi }e]}={[{\mathit{Y}}_1^{{[{\theta }_{\pi }e]}^T},\dots ,{\mathit{Y}}_p^{{[{\theta }_{\pi }e]}^T}]}^T$, except for the additional delay process involved. It is obvious that the final ${\mathit{Y}}_{}^{\left[{\theta }_{\pi }e\right]}$ should resemble a basis function (here, Gaussians were used, also known as radial basis functions), which means that only one output channel should be Gaussian and the rest should be zero. Therefore, the practical rule is that if the CLS has p channels, then a number of p primitives should be learned, each time with a different output channel being a Gaussian, while the other outputs are zero.

Learning Gaussian-like shapes as output primitive trajectories is advantageous because a Gaussian is described with only two design parameters: mean (center) and variance (width). With the function approximation, the width of the Gaussian-like output primitive influences the approximation capacity in relation to the shape of ${\mathit{Y}}^d$: if ${\mathit{Y}}^d$ is non-smooth, more copies of output primitives should be used when their widths are small. Conversely, when ${\mathit{Y}}^d$ is smooth, a good approximation is achievable with fewer copied, wider output primitives. The Gaussian polarity (pointing upward or downward) is not important as long as the CLS linearity holds, because a negative weighting coefficient suitably reverses polarity and helps with the approximation.

Typically, the number of copies (parameter M) does not significantly affect the approximation quality. The number of delay/advance steps for each copied primitive (parameter $\theta$) should be chosen from an interval such that the copied and time-shifted output primitives span the entire approximation range of interest for ${\mathit{Y}}^d$. In summary, the limitations at this particular L3 level include:

−

correlating the shape of the basis functions with the shape of the desired trajectory to be tracked on each subinterval.

−

selecting the adequate number of copies for the learned primitives. While more is better in the sense that the approximation quality does not increase past a certain number M of copies, it could increase the computational cost for the underlying regression and reference input recomposition. We still argue that the computations are performed online and manageable.

−

the tracking has to be of good quality for each subinterval, to avoid large deviations at the end, since this would shift the initial point for trajectory tracking of the next subinterval. This was found to depend largely on the ORM matching (CLS linearization quality) at the level L1.

Concluding, the discussed aspects also reveal the sensitive issues across the proposed framework. At level L1, it is important to ensure exceptional ORM matching for level L3 to accept behavior extrapolation. This is related to AIVI learning, which is strongly tied to exploration quality. This is an open issue in ADP/RL and requires further investigation. At level L2, with an impact on level L3, the basis function shape of the output primitives with respect to the desired trajectory shape is another trade-off and an open issue.

8. Conclusions

The three-level hierarchical cognitive-based learning framework validated here uses several tools from control systems and from machine learning to extrapolate an optimal tracking behavior to new tracking situations by avoiding explicit knowledge of the underlying system dynamics. This framework, inspired by intelligent life, could make progress toward more autonomous and adaptive learning control systems, as required by modern paradigms. It includes all traits of intelligence: memorization and learning from past experiences, generalizing behavior outside of the current knowledge base, and self-improvement in terms of specified performance. The framework’s validation on more complex and different systems will prove its potential and may lead to faster adoption and industrial implementation.