Abstract
In order to take into account cost and timeliness and enhance accuracy testing, this study developed the fuzzy number and membership function, using the confidence interval of ratio operating performance index. Subsequently, according to the statistical test rules and the application of the fuzzy number and membership function, a fuzzy evaluation decision model for the operating performance index is proposed, to evaluate if the business performance reaches the needed level. Based on the abovementioned, the evaluation model in this study took into account not only timeliness but also accuracy, so that it could grasp the opportunity of improvement for operating organizations with poor operating performance after being evaluated. This fuzzy evaluation decision model for the operating performance index constructs a fuzzy membership function retrieved from an index’s confidence interval, reducing the chance of miscalculation due to sampling mistakes and improving the efficiency of evaluation. Finally, in order to facilitate the application of readers and the industry, this paper uses cases to explain the proposed fuzzy verification method. On the whole, the model proposed in this paper is a data-based auxiliary tool for the service operating performance improvement strategy.
1. Introduction
Quite a few people in the service industry are discussing evaluation methods of service performance, hoping to find a good evaluation model for the service operating performance as an auxiliary tool for the service operating improvement strategy to identify key service elements that need to improve, so as to grasp the opportunity of improvement [1,2,3,4,5]. In particular, the related methods of the customer satisfaction performance evaluation matrix mainly use questionnaires to conduct a satisfaction survey for each provided service item and adopt the performance evaluation matrix to find out the service items that need to be improved [6,7,8,9,10]. This study targeted and improved the service items that needed to improve to increase the total customer satisfaction, as well as to further raise the customer arrival rate of a store, to enhance its operating performance. Kurosu [11] and Shreve et al. [12] noted that store customers’ arrivals provide a company with a good solution to the performance measurement, as they instantly affect the company’s profitability and costs of operation. Chen and Yang [13] considered the number of customers’ store visits through a quantifiable Poisson process. This paper uses the random variable X in the next section, to explain, in detail, how customers arrive at the store and follow the Poisson’s distribution. Therefore, based on the Smaller-the-Better type of six-sigma quality index proposed by Chen et al. [14], this study brings up an operating performance index (OPI) containing a one-to-one mathematical relationship with the performance compliance ratio, viewed as a store-operating-performance evaluation tool.
According to numerous scholars, indicators are simple and unitless management tools. Therefore, under reasonable conditions, the simpler they are, the more easily they are managed [15,16,17]. Based on this point of view, this study revises the operating performance index to be a more concise ratio operating performance index (ROPI). Its numerator represents the maximum of the expected store customer arrival times, indicating that the operating performance of the store is quite satisfactory, while its denominator is the average interval time between customers’ arrivals at the store. The shorter the average interval time between customers’ arrivals at the store is, the greater the number of customers entering the store per unit time is.
In fact, the new indicator ROPI proposed by this study has a one-to-one mathematical relationship with the operating performance compliance ratio. In addition, when the ROPI value is greater than or equal to 1, then the operating performance is good. When the value is greater than 1, then its operating performance is better. Conversely, when the ROPI value is less than 1, then the average interval time between customers’ arrivals at the store is long, indicating that the store’s service operating performance has not met the requirements.
Obviously, it is more effective to evaluate a store’s operating performance by means of the time interval between customers’ arrivals than to collect the number of customers’ arrivals per unit time [13,18,19]. In addition, some studies have pointed out that, based on cost considerations and practicality, the sample size, n, is usually not too large in practice, so it will affect the accuracy of statistical inference [20,21,22]. This study first derived index estimates based on sample data, to find out the best estimation formula of the index as the testing statistic. In order to take into account timeliness and enhance testing accuracy, the confidence interval of ROPI was employed to construct the fuzzy number and membership function of ROPI. Next, according to the statistical test rules and the application of the fuzzy number and membership function of ROPI, this study proposes a fuzzy evaluation decision model of the operating performance index, to evaluate if the operating performance reaches the standard. Based on Yu et al. [23] and Chen [19], the collection of fuzzy data is more complicated and time-consuming than the measurement data, but it is more accurate and stable, while the fuzzy evaluation method developed by the application of confidence interval is to maintain the use of simple and non-time-consuming direct measurement data and then to develop the fuzzy membership function through the confidence interval, so it has the advantages of simplicity, non-time-consuming, accuracy and stability. Therefore, this study will apply this method to establish a fuzzy evaluation method for ROPI. According to the abovementioned, the evaluation model in this study not only makes the indicators more practical, accurate and stable but also has the following advantages:
- Evaluating the performance of service operations in a quantitative manner is more scientific than using questionnaires [23].
- For the proposed indicators, developing a fuzzy evaluation model based on confidence intervals can avoid the chance of misjudgment due to sampling errors.
- According to the research of Luo et al. [24], this method integrates experts’ accumulated experiences of data analysis, which can solve the problems of too small sample size and too large error due to timeliness and cost considerations.
- Based on the previous three points, this method not only has timeliness and small errors but also can lower the probability of misjudgment, so it can grasp the opportunity for improvement, as well as reduce the yield of defective products.
According to the abovementioned, the fuzzy evaluation model is more reasonable and advantageous in use than the traditional statistical testing model, which is identical to the conclusions of some related studies [25,26,27,28]. Finally, in order to facilitate the application of readers and the industry, this paper uses cases to explain the proposed fuzzy testing method. On the whole, the proposed model in this paper is a data-based auxiliary tool for the service operating improvement strategy.
2. Ratio Operating Performance Index and Statistical Hypothesis Testing
Following the Introduction, this paper lets random variable denote the number of customers’ arrivals at a store per unit time. Chen and Yang [13] noted that random variable is allocated as Poisson distribution with rate ; the sequence of inter-arrival times is also distributed as an exponential distribution with mean ( ), that is, . Then, it is learned that the probability density function of is as follows:
Concerning an exponential distribution, since mean and standard deviation both equal , Chen and Yang [13] defined the operating performance index (OPI) directly based on the quality index of the Six Sigma process. In fact, OPI is based on whether the difference between the maximum expected customer inter-arrival times of a store (U) and mean is greater than zero, viewed as an evaluation criterion. Obviously, when , then 0 and OPI 1. As noted above, indicators are simple and unitless management tools. Consequently, under reasonable circumstances, the simpler they are, the more easily managed they are. Therefore, this study considered whether the ratio of the maximum expected inter-arrival times to mean is greater than 1 as an evaluation criterion and defined the ratio operating performance index (ROPI) as follows:
Obviously, when , then 1 and ROPI 1. Let denote that the time interval, , between customer arrivals is lower than the maximum of expected inter-arrival times, U, and then and have a one-to-one mathematical relationship, where .
It is supposed that is the required performance value of index . Then, the problem of the hypothesis test is that the null hypothesis, : = , is considered to be against the alternative hypothesis : at the desired level of significance . Let be independent identity distribution (i.i.d.) random variables with . Next, an unbiased estimator of is put forward, as displayed below:
in which and denotes the mean of inter-arrival times of customers at a store. Then, random variable is designated as . Furthermore, we assume the following:
where W is designated as , and the critical regain can be expressed as follows:
To meet a significant level of with sample size, n, value is determined by the following:
Hence, we have the following:
Similarly, value is determined by the following:
Hence, we have the following:
Therefore, the critical regain can be rewritten as follows:
It is assumed that when , then and
in which is the observed value of random variable , while is the observed value of . As noted above, : is against the alternative hypothesis, : , at the desired level of significance, . Then, the rules of statistic testing decision can be illustrated as shown below:
- (1)
- If , will be rejected and will be concluded. Thus, the operation needs to improve.
- (2)
- If , will be rejected and will be concluded. Thus, the operation needs to maintain the status quo or set a higher goal.
- (3)
- If , will not be rejected and will be concluded. Thus, the operation needs to maintain the status quo.
3. Two-Tailed Fuzzy Testing Decision Rules Based on Confidence Intervals
Many studies have pointed out that the sample size, n, is usually not too large when considering cost and timeliness. Moreover, if the sample size, n, is not large enough, it will affect the result of statistical inference [18,19]. Therefore, this section of the paper proposes a fuzzy testing method on the basis of the confidence interval, using the abovementioned statistical testing decision rules, so as to assess if the operating performance reaches the required level. First, this paper derives the confidence interval of ROPI. denotes a lower confidence limit whereas denotes an upper confidence limit for with confidence coefficient 1 as follows:
Therefore, we obtain the following:
and
Let the observed value of be and the observed value of be , where
and
Based on Chen [19], the -cuts of triangular-shaped fuzzy number are expressed as for , where
and
We suppose the -cuts of the triangular-shaped fuzzy number for all equal . When , then . Based on Chen [19], for the convenience in practice, we allow the following:
As a result, the -cuts of transformed triangular fuzzy number are expressed as for , where
and
Recall that the -cut of triangular-shaped fuzzy number for all equal . When , then . Therefore, the new transformation triangular-shaped fuzzy number is expressed as , where we have the following:
Furthermore, the membership function of is as follows:
where and .
Let set be the area in the graph of , such that we obtain the following:
Based on Chen [18], we suppose , and then for , in which shows that the value of maximum integer is lower than or equal to . Let and , indicating that is divided into 100 trapezoid-like blocks with 101 horizontal lines. Consequently, the jth block can be displayed in the following:
Therefore, the jth horizontal line distance can be expressed as shown below:
Obviously, , and let the area of set be , and then we get the following:
Due to the two-tailed test, the following two cases are considered:
Case 1:
Similar to , when , the -cuts of the new transformation triangular fuzzy critical value number are expressed as for , where
and
It is assumed that the -cuts of the new transformation triangular fuzzy critical value number for all equal . When , then . Therefore, we learn the new transformation triangular-shaped fuzzy number is , where we get the following:
Moreover, the membership function of is expressed as follows:
where and .
The membership functions and can be expressed in Figure 1 as shown below:
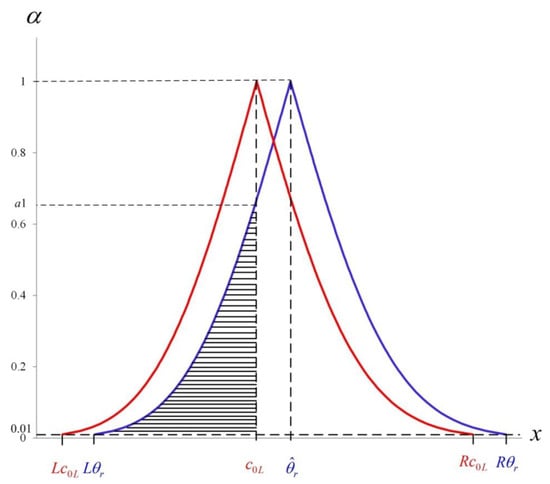
Figure 1.
The figure of membership functions and .
It is supposed that is the area in the graph of to the left of the vertical line , and then we have the following:
Similar to , let . It is learned that for , where is the maximum integer which is lower than or equal to 100 . Obviously, 0.01 and horizontal lines with divide into trapezoid-like blocks. The intersection point lies between the jth horizontal line and vertical line . The jth block of is expressed below:
Therefore, the length () of the jth horizontal line is denoted below:
Obviously, , and let the area of set be , and then we get the following:
As noted by Buckley [29], we let 0 0.5, and then we formulate fuzzy evaluation rules and operating performance improvement strategies as follows:
- (1)
- If , then reject and conclude that . Thus, the operation needs to improve.
- (2)
- If , then do not reject and conclude that .
Thus, the operation Case 2 is as follows: .
Similar to , when , the -cut of the new transformation triangular fuzzy critical value number denote for , where
and
It is assumed that the -cuts of the new transformation triangular fuzzy critical value number for 0 0.01 all equal . When , then . Therefore, we learn the new transformation triangular-shaped fuzzy number , where we have the following:
Moreover, the membership function of is as follows:
where and .
The membership functions and are illustrated in Figure 2 as shown below:
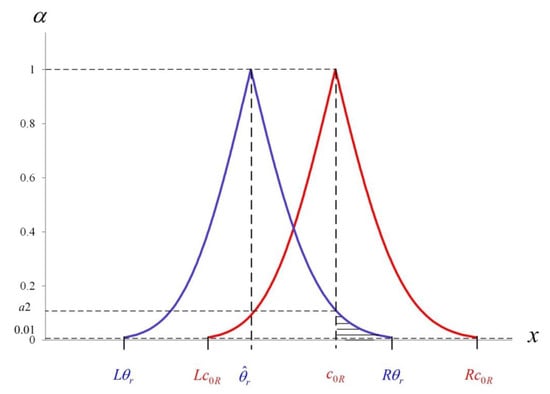
Figure 2.
The figure of membership functions and .
Suppose is the area in the graph of to the right of the vertical line , and then we get the following:
Similar to , let . It is learned that for , where is the maximum integer lower than or equal to 100 . Apparently, 0.01 and horizontal lines with divide into trapezoid-like blocks. The intersection point lies between the jth horizontal line and vertical line . Then, the jth block of can be illustrated as shown below:
where . Thus, the length of the jth horizontal line, , can be described as follows:
Obviously, , and let the area of set be . Then, we obtain the following:
As noted by Buckley [29], we let 0 0.5, and then we may set fuzzy evaluation rules and operating performance improvement strategies as follows:
- (1)
- If , will be rejected and will be concluded. Thus, the operation needs to maintain the status quo or set a higher goal.
- (2)
- If , will not be rejected and will be concluded. Thus, the operation needs to maintain the status quo.
4. Numerical Example
A numerical example, in this section, is used to demonstrate the rules of fuzzy testing decision made in Section 3. At the same time, through this example, we can understand the difference between the method proposed in this paper and the traditional statistical method and learn that this model is more reasonable and practical than the traditional statistical method.
It is assumed that a goal set at 6 is applied to assess a store’s operating performance. This is identical to the following hypotheses:
Null Hypothesis : 6,
Alternative Hypothesis : 6.
To meet a significant level of with sample size n 261, 230.29, 293.6, and the critical region is as follows:
where
Thus, we can derive that 486 and set U 10 and the value
In fact, we have 260.67, 221.27 and 304.49. Therefore, we learn the triangular-shaped fuzzy number , where
Furthermore, 48.72x, and the membership function of is expressed below:
Obviously, 5.35 6, so we can calculate the values of , and as follows:
Therefore, the new transformation triangular-shaped fuzzy number , 49.09x and the membership function of are displayed below:
Due to the fact that 5.35 6, the conditions of Case 1 ( ) continue. Therefore, the membership functions and with 5.35 and 5.31 are displayed in Figure 3 as shown below:
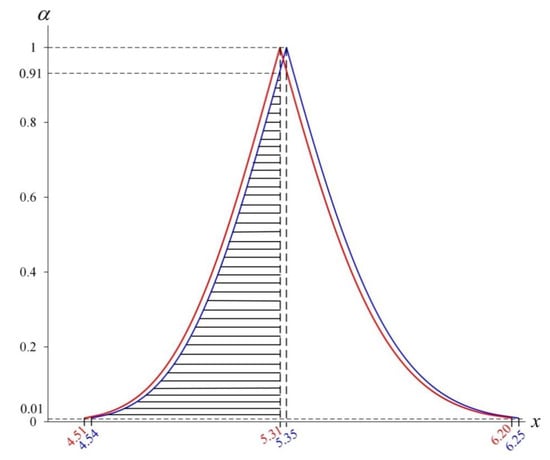
Figure 3.
Membership functions and for a numerical example.
The area of , that is, , can be expressed below:
On the other hand, when such that 5.31, then , and , the area of , can be calculated as follows:
Thus, 0.415. Let , and then will be rejected, and 6 will be concluded. Thus, the operation needs to improve. If the traditional statistical testing method is adopted, due to the large error, there is a high probability of misjudgment and miss the opportunity to improve the process. As a result, products with poor or bad quality will be produced, which will lead to certain losses. Based on the statistical inference, will not be rejected, and 6 will be concluded. Nevertheless, 5.35 is much less than 6. Based on Chen [18], a large sampling error takes place because the sample size is not large enough. Some studies highlighted that timeliness is extremely critical in a competitive market, and samples are rarely oversized [20,21,22]. Moreover, that is why we came up with a two-tailed fuzzy testing method. The proposed fuzzy testing method suggests that be rejected and 6 be concluded. From a practical point of view, the outcome seems applicable, reasonable and consistent with the recent research [25,26,27,28].
5. Conclusions
This study proposes a ratio operating performance indicator to evaluate the operating performance conducted in the service industry. The ratio of the ROPI to the time interval, , between customer arrivals less than U has a one-to-one mathematical relationship. Then, the proposed two-tailed fuzzy testing method is built on ROPI as an improved decision rule. The sample size is usually not too large, owing to the consideration of cost and timeliness, so it will affect the accuracy of statistical inference [20,21,22,24,25]. In addition to cost and timeliness, the advantage of this approach is not only to minimize the chance of miscalculations resulting from the sample errors but also to enhance the accuracy of testing. Furthermore, this conventional measurement method can be employed during the confidence interval of ROPI and then adopted to develop a fuzzy membership function for fuzzy tests. Furthermore, simple calculation models are offered in this paper, to obtain the approximate values of , and , which represent a valuable contribution in practice. This paper further presents a numerical example to explain the proposed decision rule of two-tailed fuzzy testing and instantly grasp opportunities of improvement. Moreover, this example demonstrates that the proposed approach receives more reasonable results than statistical ones, from a practical perspective, and it is also consistent with the recent studies [25,26,27,28].
Author Contributions
Conceptualization, M.L. and K.-S.C.; methodology, M.L. and K.-S.C.; software, C.-M.Y. (Chun-Min Yu); validation, C.-M.Y. (Chun-Ming Yang); formal analysis, M.L. and K.-S.C.; resources, M.L. and C.-M.Y. (Chun-Ming Yang); data curation, C.-M.Y. (Chun-Ming Yang); writing—original draft preparation, M.L., K.-S.C., C.-M.Y. (Chun-Min Yu) and C.-M.Y. (Chun-Ming Yang); writing—review and editing, M.L. and K.-S.C.; visualization, C.-M.Y. (Chun-Ming Yang); supervision, K.-S.C.; project administration, C.-M.Y. (Chun-Min Yu). All authors have read and agreed to the published version of the manuscript.
Funding
This work was financially supported by National Natural Science Foundation of China, under grant No. 71762008, and Quality and Brand Development Research Center in Dongguan University of Technology, under Grant No. GB200101.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ghosh, P.; Ojha, M.K.; Geetika. Determining passenger satisfaction out of platform-based amenities: A study of Kanpur Central Railway Station. Transp. Policy 2017, 60, 108–118. [Google Scholar] [CrossRef]
- Li, Y.; Wang, L.; Li, F. A data-driven prediction approach for sports team performance and its application to national basketball association. Omega (UK) 2021, 98, 102123. [Google Scholar] [CrossRef]
- Mustafa, H.; Omar, B.; Mukhiar, S.N.S. Measuring destination competitiveness: An importance-performance analysis (IPA) of six top island destinations in south east asia. Asia Pac. J. Tour. Res. 2020, 25, 223–243. [Google Scholar] [CrossRef]
- Wu, J.; Wang, Y.; Zhang, R.; Cai, J. An approach to discovering product/service improvement priorities: Using dynamic importance-performance analysis. Sustainability 2018, 10, 3564. [Google Scholar] [CrossRef]
- Wong, R.C.P.; Szeto, W.Y. An alternative methodology for evaluating the service quality of urban taxis. Transp. Policy 2018, 69, 132–140. [Google Scholar] [CrossRef]
- Chen, K.S.; Chen, H.T. Applying importance-performance analysis with simple regression model and priority indices to assess hotels’ service performance. J. Test. Eval. 2014, 42, 455–466. [Google Scholar] [CrossRef]
- Feng, M.; Mangan, J.; Wong, C.; Xu, M.; Lalwani, C. Investigating the different approaches to importance-performance analysis. Serv. Ind. J. 2014, 34, 1021–1041. [Google Scholar] [CrossRef]
- Hung, Y.H.; Huang, M.L.; Chen, K.S. Service Quality Evaluation by Service Quality Performance Matrix. Total Qual. Manag. Bus. Excel. 2003, 14, 79–89. [Google Scholar] [CrossRef]
- Martínez-Caro, E.; Cegarra-Navarro, J.G.; Cepeda-Carrión, G. An application of the performance-evaluation model for e-learning quality in higher education. Total Qual. Manag. Bus. Excel. 2015, 26, 632–647. [Google Scholar] [CrossRef]
- Nam, J.H.; Lee, T.J. Foreign travelers’ satisfaction with traditional Korean restaurants. Int. J. Hosp. Manag. 2011, 30, 982–989. [Google Scholar] [CrossRef]
- Kurosu, S. Effects of fluctuations in the quantity of work arriving on waiting time, idle time and rate of losing customers. Int. J. Prod. Res. 1986, 24, 611–622. [Google Scholar] [CrossRef]
- Kruk, L.; Lehoczky, J.; Ramanan, K.; Shreve, S. Heavy traffic analysis for EDF queues with reneging. Ann. Appl. Probab. 2011, 21, 484–545. [Google Scholar] [CrossRef]
- Chen, K.S.; Yang, C.M. Developing a performance index with a Poisson process and an exponential distribution for operations management and continuous improvement. J. Comput. Appl. Math. 2018, 343, 737–747. [Google Scholar] [CrossRef]
- Chen, K.S.; Chen, H.T.; Chang, T.C. The construction and application of Six Sigma quality indices. Int. J. Prod. Res. 2017, 55, 2365–2384. [Google Scholar] [CrossRef]
- Gutierrez, D.M.; Scavarda, L.F.; Fiorencio, L.; Martins, R.A. Evolution of the performance measurement system in the logistics department of a broadcasting company: An action research. Int. J. Prod. Econ. 2015, 160, 1–12. [Google Scholar] [CrossRef]
- Rodriguez, R.R.; Saiz, J.J.A.; Bas, A.O. Quantitative relationships between key performance indicators for supporting decision-making processes. Comput. Ind. 2009, 60, 104–113. [Google Scholar] [CrossRef]
- Kucukaltan, B.; Irani, Z.; Aktas, E. A decision support model for identification and prioritization of key performance indicators in the logistics industry. Comput. Hum. Behav. 2016, 65, 346–358. [Google Scholar] [CrossRef]
- Chen, K.S. Fuzzy testing of operating performance index based on confidence intervals. Ann. Oper. Res. 2019. [Google Scholar] [CrossRef]
- Chen, K.S. Two-tailed Buckley fuzzy testing for operating performance index. J. Comput. Appl. Math. 2019, 361, 55–63. [Google Scholar] [CrossRef]
- Chen, K.S.; Yu, C.M. Fuzzy test model for performance evaluation matrix of service operating systems. Comput. Ind. Eng. 2020, 140, 106240. [Google Scholar] [CrossRef]
- Yu, C.H.; Liu, C.C.; Chen, K.S.; Yu, C.M. Constructing fuzzy hypothesis methods to determine critical-to-quality service items. Mathematics 2020, 8, 573. [Google Scholar] [CrossRef]
- Yu, C.M.; Chen, K.S.; Lai, K.K.; Hsu, C.H. Fuzzy supplier selection method based on smaller-the-better quality characteristic. Appl. Sci. 2020, 10, 3635. [Google Scholar] [CrossRef]
- Yu, C.M.; Chang, H.T.; Chen, K.S. Developing a performance evaluation matrix to enhance the learner satisfaction of an e-learning system. Total Qual. Manag. Bus. Excel. 2018, 29, 272–745. [Google Scholar] [CrossRef]
- Luo, W.J.; Chen, K.S.; Yu, C.M.; Hsu, T.H. The Fuzzy Process Quality Evaluation Model for the STB Quality Characteristic of Machining. Appl. Sci. 2020, 10, 8272. [Google Scholar] [CrossRef]
- Yu, C.M.; Luo, W.J.; Hsu, T.H.; Lai, K.K. Two-Tailed Fuzzy Hypothesis Testing for Unilateral Specification Process Quality Index. Mathematics 2020, 8, 2129. [Google Scholar] [CrossRef]
- Chen, K.S. Fuzzy testing decision-making model for intelligent manufacturing process with Taguchi capability index. J. Intell. Fuzzy Syst. 2020, 38, 2129–2139. [Google Scholar] [CrossRef]
- Chen, K.S.; Chang, T.C. Construction and fuzzy hypothesis testing of Taguchi Six Sigma quality index. Int. J. Prod. Res. 2020, 58, 3110–3125. [Google Scholar] [CrossRef]
- Chen, K.S.; Wang, C.H.; Tan, K.H. Developing a fuzzy green supplier selection model using Six Sigma quality indices. Int. J. Prod. Econ. 2019, 212, 1–7. [Google Scholar] [CrossRef]
- Buckley, J.J. Fuzzy statistics: Hypothesis testing. Soft Comput. 2005, 9, 512–518. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).