Estimating Copula-Based Extension of Tail Value-at-Risk and Its Application in Insurance Claim
Abstract
:1. Introduction
2. The Dependent Tail Value-at-Risk
3. The Estimation of DTVaR
4. The Dependent Conditional Tail Variance and Confidence Intervals
4.1. The Estimation of DCTV
4.2. Confidence Intervals for DTVaR
5. Parametric Estimation under FGM Copula
- Derive the expression of the DTVaR for the Pareto distribution;
- Calculate the parametric estimates of the distribution parameters of random samples and , each of which is assumed to be a Pareto distribution.
6. Data Analysis
6.1. Parametric Preliminary Results
6.2. Backtesting
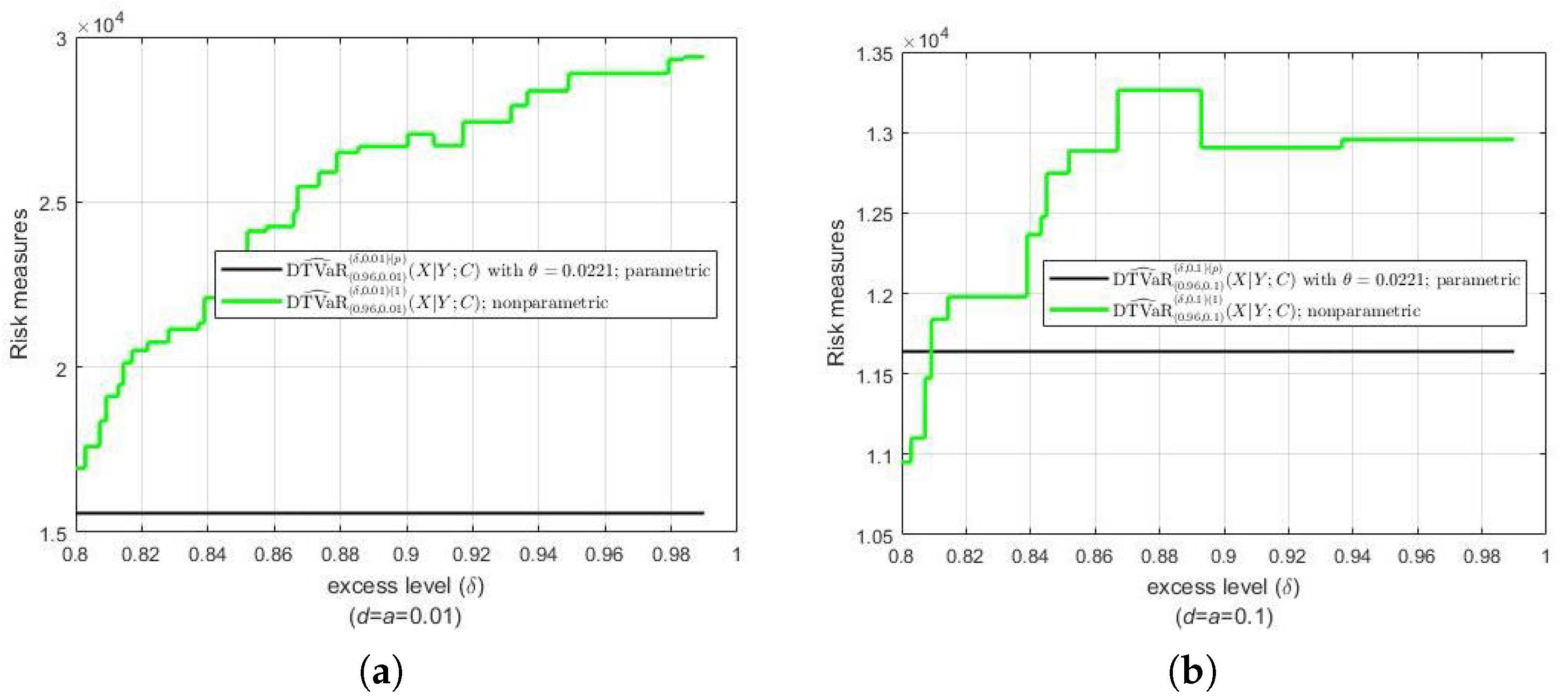
6.3. Result Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- (*)
- If , then
- (**)
- If , then
- Step 1. Assuming that the random variables are i.i.d. with distribution function , Brazauskas et al. (2008) argued that the bi-implication—the statement (A3) below—is true if and only if the following two statements (weak convergence) and hold. The first statement follows from the classical Glivenko–Cantelli theorem, which says that the supremum distance between and converges almost surely to 0.
- Step 2. Similarly to Brazauskas et al. (2008), we argue that the statement (A2) is true if the following two statements and almost surely hold. However, previously, we know the fact that (weak convergence) and almost surely hold from Step 1. Then, we haveHence, the statement (A2) holds. Thus, the estimator is consistent for .
| 1 | In description we use the terms loss(es) and risk(s) interchangeably. |
References
- Artzner, Philippe, Freddy Delbaen, Jean-Marc Eber, and David Heath. 1999. Coherent measures of risk. Mathematical Finance 9: 203–28. [Google Scholar] [CrossRef]
- Bairakdar, Roba, Lu Cao, and Melina Mailhot. 2020. Range value-at-risk: Multivariate and extreme values. arXiv arXiv:2005.12473. [Google Scholar]
- Bargès, Mathieu, Hélène Cossette, and Etienne Marceau. 2009. Tvar-based capital allocation with copulas. Insurance: Mathematics and Economics 45: 348–61. [Google Scholar] [CrossRef] [Green Version]
- Bernard, Carole, Rodrigue Kazzi, and Steven Vanduffel. 2020. Range value-at-risk bounds for unimodal distributions under partial information. Insurance: Mathematics and Economics 94: 9–24. [Google Scholar] [CrossRef]
- Brahim, Brahimi, Benatia Fatah, and Yahia Djabrane. 2018. Copula conditional tail expectation for multivariate financial risks. Arab Journal of Mathematical Sciences 24: 82–100. [Google Scholar] [CrossRef]
- Brazauskas, Vytaras, Bruce L. Jones, Madan L. Puri, and Ričardas Zitikis. 2008. Estimating conditional tail expectation with actuarial applications in view. Journal of Statistical Planning and Inference 138: 3590–604. [Google Scholar] [CrossRef]
- Chadjiconstantinidis, Stathis, and Spyridon Vrontos. 2014. On a renewal risk process with dependence under a farlie–gumbel–morgenstern copula. Scandinavian Actuarial Journal 2014: 125–58. [Google Scholar] [CrossRef] [Green Version]
- Chang, Yi-Ping, Ming-Chin Hung, and Yi-Fang Wu. 2003. Nonparametric estimation for risk in value-at-risk estimator. Communications in Statistics-Simulation and Computation 32: 1041–64. [Google Scholar] [CrossRef]
- Cheung, Ka Chun, K. C. J. Sung, Sheung Chi Phillip Yam, and Siu Pang Yung. 2014. Optimal reinsurance under general law-invariant risk measures. Scandinavian Actuarial Journal 2014: 72–91. [Google Scholar] [CrossRef]
- Dutta, Santanu, and Suparna Biswas. 2018. Nonparametric estimation of 100(1 − p)% expected shortfall: p → 0 as sample size is increased. Communications in Statistics-Simulation and Computation 47: 338–52. [Google Scholar] [CrossRef]
- Furman, Edward, and Zinoviy Landsman. 2006. Tail variance premium with applications for elliptical portfolio of risks. ASTIN Bulletin: The Journal of the IAA 36: 433–62. [Google Scholar] [CrossRef] [Green Version]
- Jadhav, Deepak, Thekke Variyam Ramanathan, and Uttara Naik-Nimbalkar. 2013. Modified expected shortfall: A new robust coherent risk measure. Journal of Risk 16: 69–83. [Google Scholar] [CrossRef]
- Jiang, Wuyuan, and Zhaojun Yang. 2016. The maximum surplus before ruin for dependent risk models through farlie–gumbel–morgenstern copula. Scandinavian Actuarial Journal 2016: 385–97. [Google Scholar] [CrossRef]
- Josaphat, Bony Parulian, and Khreshna Syuhada. 2021. Dependent conditional value-at-risk for aggregate risk models. Heliyon 7: e07492. [Google Scholar] [CrossRef]
- Josaphat, Bony Parulian, Moch Fandi Ansori, and Khreshna Syuhada. 2021. On optimization of copula-based extended tail value-at-risk and its application in energy risk. IEEE Access 9: 122474–85. [Google Scholar] [CrossRef]
- Kaiser, Thomas, and Vytaras Brazauskas. 2006. Interval estimation of actuarial risk measures. North American Actuarial Journal 10: 249–68. [Google Scholar] [CrossRef]
- Kang, Yao, Dehui Wang, and Jianhua Cheng. 2019. Risk models based on copulas for premiums and claim sizes. Communications in Statistics-Theory and Methods 50: 2250–69. [Google Scholar] [CrossRef]
- Krätschmer, Volker, Alexander Schied, and Henryk Zähle. 2014. Comparative and qualitative robustness for law-invariant risk measures. Finance and Stochastics 18: 271–95. [Google Scholar] [CrossRef] [Green Version]
- Macquarie University. 2005. The Data of One-Year Vehicle Insurance Policies from Department of Applied Finance and Actuarial Studies, Macquarie University. Available online: http://www.businessandeconomics.mq.edu.au (accessed on 24 March 2021).
- Methni, Jonathan El, Laurent Gardes, and Stephane Girard. 2014. Non-parametric estimation of extreme risk measures from conditional heavy-tailed distributions. Scandinavian Journal of Statistics 41: 988–1012. [Google Scholar] [CrossRef] [Green Version]
- Pham, Minh H., Chris Tsokos, and Bong-Jin Choi. 2019. Maximum likelihood estimation for the generalized pareto distribution and goodness-of-fit test with censored data. Journal of Modern Applied Statistical Methods 17: 11. [Google Scholar] [CrossRef]
- Righi, Marcelo Brutti, and Paulo Sergio Ceretta. 2015. A comparison of expected shortfall estimation models. Journal of Economics and Business 78: 14–47. [Google Scholar] [CrossRef]
- Shen, Zhiyi, Yukun Liu, and Chengguo Weng. 2019. Nonparametric inference for var, cte, and expectile with high-order precision. North American Actuarial Journal 23: 364–85. [Google Scholar] [CrossRef]
- Wang, Ruodu, and Yunran Wei. 2020. Characterizing optimal allocations in quantile-based risk sharing. Insurance: Mathematics and Economics 93: 288–300. [Google Scholar] [CrossRef]
- Zhang, Yiying, Peng Zhao, and Ka Chun Cheung. 2019. Comparisons of aggregate claim numbers and amounts: A study of heterogeneity. Scandinavian Actuarial Journal 2019: 273–90. [Google Scholar] [CrossRef]
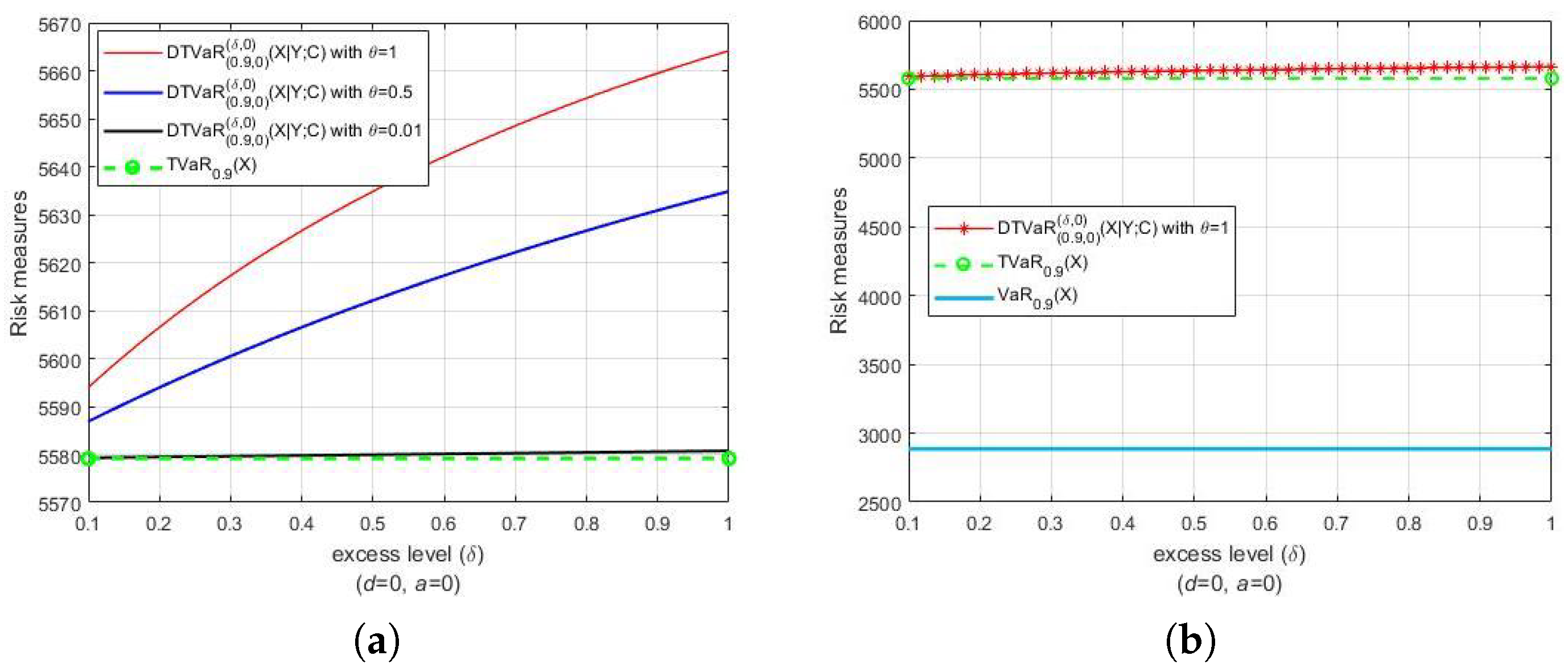
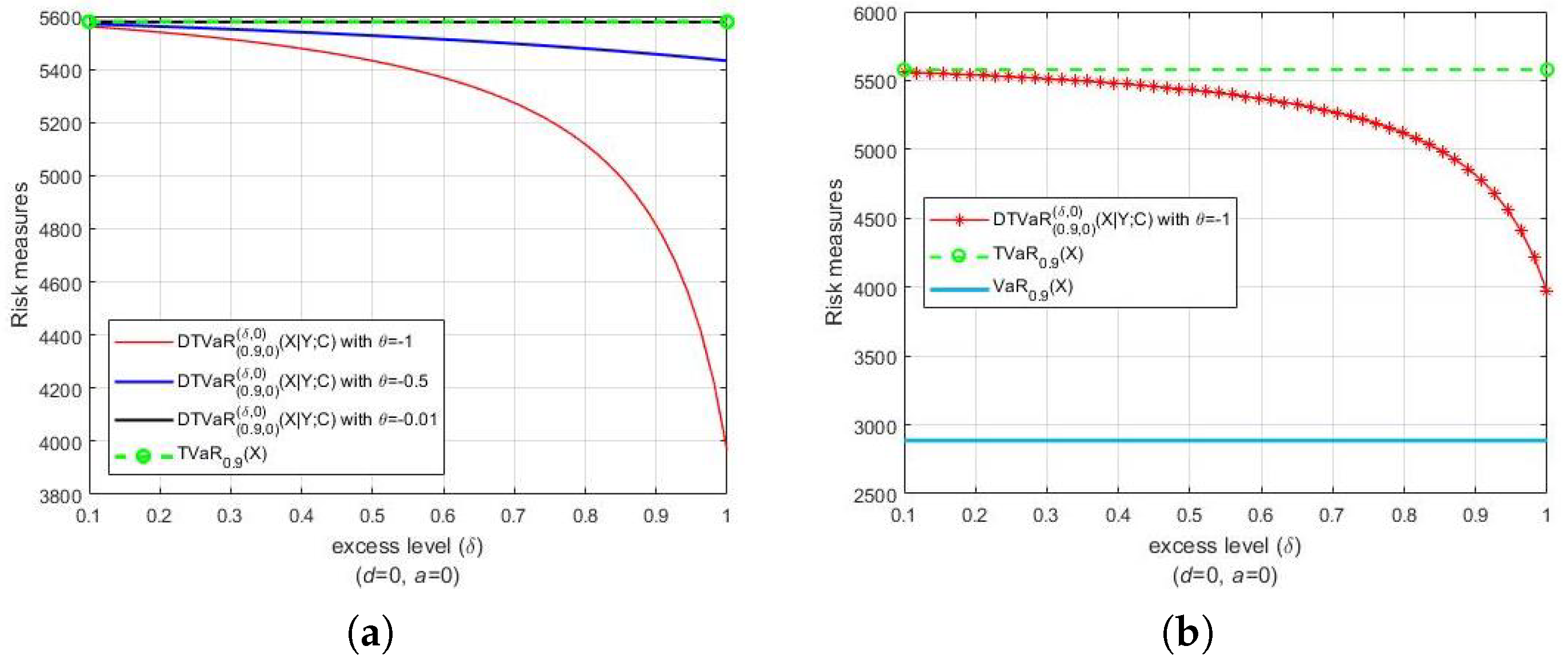

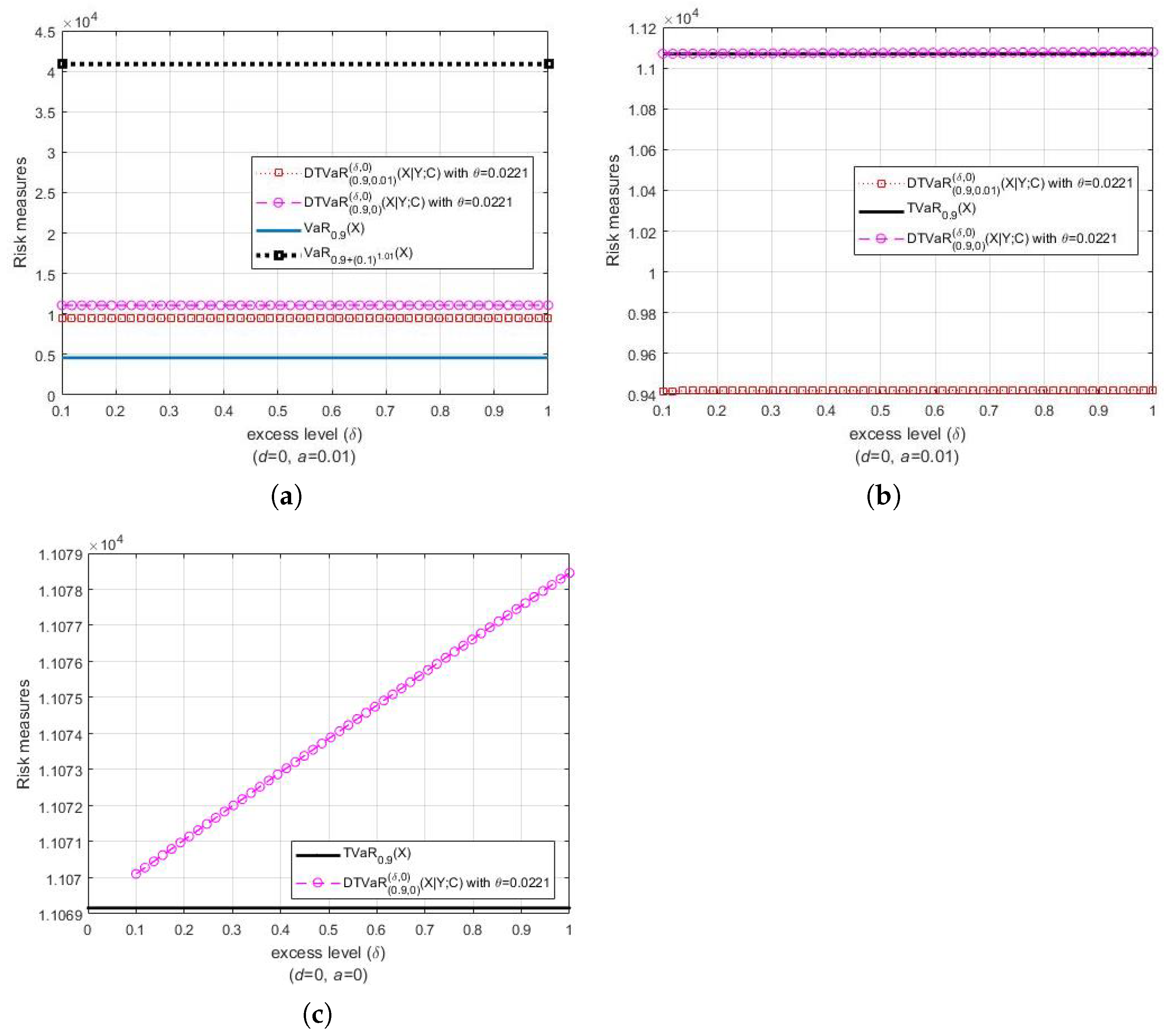
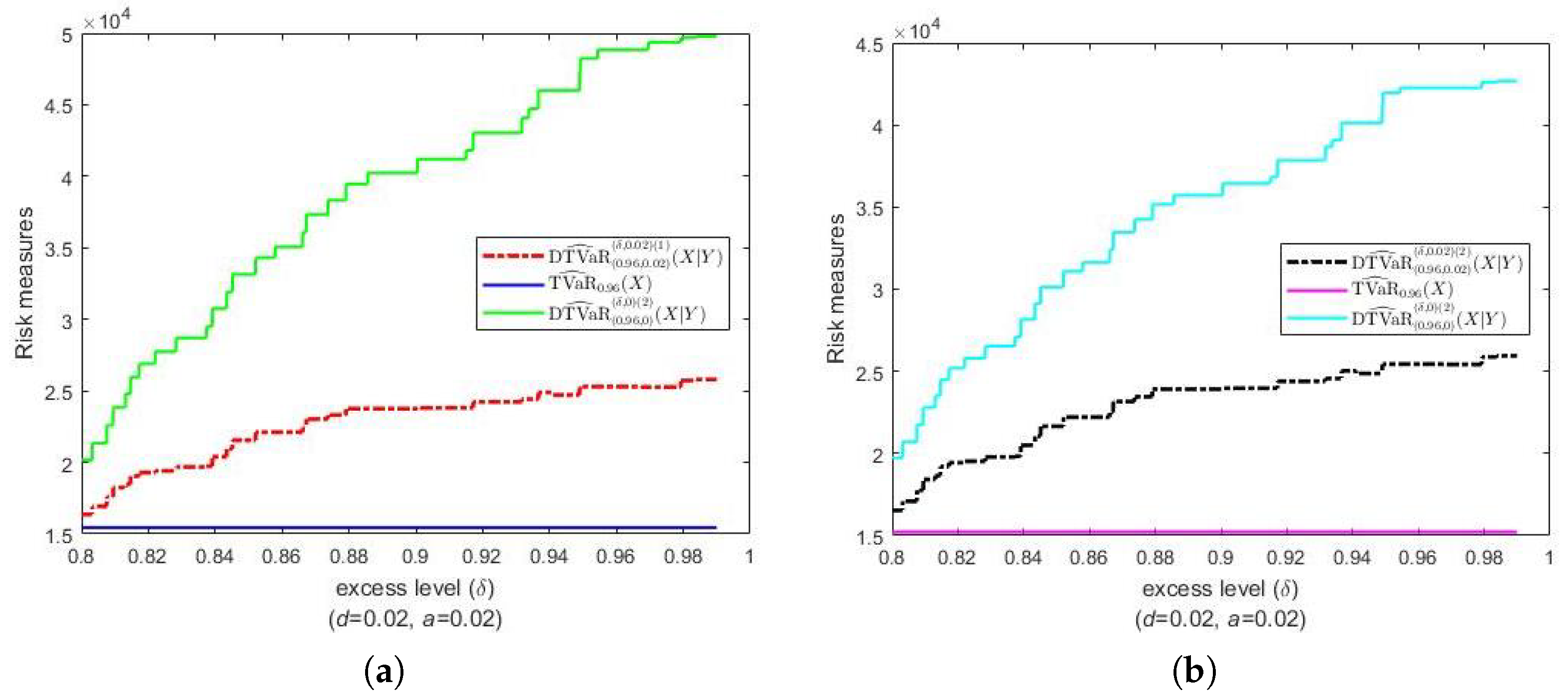

| Statistics | Claim Amount (X) | Vehicle Value (Y) |
|---|---|---|
| Sample number | 4618 | 4618 |
| Mean | 1.8616 | |
| Standard deviation | 1.1584 | |
| Skewness | 5.0470 | 1.8614 |
| Kurtosis | 43.3102 | 9.9344 |
| Method of Estimations | Estimators | 0.9 j.s.l. (%) | No. viol. (%) | Estimators | 0.92 j.s.l. (%) | No. viol. (%) | Estimators | 0.94 j.s.l. (%) | No. viol. (%) | Estimators | 0.96 j.s.l. (%) | No. viol. (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Nonparametric | DTVaR | 0.95 | 62 | DTVaR | 0.76 | 44 | DTVaR | 0.57 | 29 | DTVaR | 0.38 | 19 |
| (15,601) | (1.34) | (18,216) | (0.95) | (20,880) | (0.63) | (23,693) | (0.41) | |||||
| DTVaR | 65 | DTVaR | 49 | DTVaR | 33 | DTVaR | 20 | |||||
| (14,890) | (1.41) | (17,420) | (1.06) | (20,002) | (0.71) | (22,785) | (0.43) | |||||
| Parametric | ||||||||||||
| (Pareto, FGM Copula) | DTVaR | 130 | DTVaR | 103 | DTVaR | 65 | DTVaR | 41 | ||||
| (10,557) | (2.81) | (12,132) | (2.23) | (14,423) | (1.41) | (18,229) | (0.89) | |||||
| Nonparametric | DTVaR | 0.76 | 59 | DTVaR | 0.61 | 40 | DTVaR | 0.45 | 26 | DTVaR | 0.30 | 18 |
| (15,920) | (1.28) | (18,744) | (0.87) | (21,468) | (0.56) | (24,143) | (0.39) | |||||
| DTVaR | 65 | DTVaR | 47 | DTVaR | 33 | DTVaR | 20 | |||||
| (15,029) | (0.76) | (17,741) | (1.02) | (20,366) | (0.69) | (23,011) | (0.43) | |||||
| Parametric | ||||||||||||
| (Pareto, FGM Copula) | DTVaR | 130 | DTVaR | 103 | DTVaR | 65 | DTVaR | 41 | ||||
| (11,052) | (2.81) | (12,586) | (2.23) | (14,825) | (1.41) | (18,565) | (0.89) | |||||
| Nonparametric | DTVaR | 0.57 | 52 | DTVaR | 0.45 | 36 | DTVaR | 0.34 | 20 | DTVaR | 0.23 | 17 |
| (16,715) | (1.12) | (19,184) | (0.78) | (22,811) | (0.43) | (25,298) | (0.37) | |||||
| DTVaR | 63 | DTVaR | 47 | DTVaR | 27 | DTVaR | 18 | |||||
| (15,554) | (1.36) | (17,902) | (1.02) | (21,391) | (0.58) | (23,864) | (0.39) | |||||
| Parametric | ||||||||||||
| (Pareto, FGM Copula) | DTVaR | 130 | DTVaR | 103 | DTVaR | 65 | DTVaR | 41 | ||||
| (11,052) | (2.81) | (12,585) | (2.23) | (14,824) | (1.41) | (18,564) | (0.89) | |||||
| Nonparametric | DTVaR | 0.38 | 51 | DTVaR | 0.30 | 34 | DTVaR | 0.23 | 17 | DTVaR | 0.15 | 15 |
| (17,159) | (1.10) | (19,622) | (0.74) | (24,876) | (0.37) | (26,802) | (0.32) | |||||
| DTVaR | 63 | DTVaR | 47 | DTVaR | 20 | DTVaR | 18 | |||||
| (15,472) | (1.36) | (17,744) | (1.02) | (22,720) | (0.43) | (24,638) | (0.39) | |||||
| Parametric | ||||||||||||
| (Pareto, FGM Copula) | DTVaR | 130 | DTVaR | 103 | DTVaR | 65 | DTVaR | 41 | ||||
| (11,051) | (2.81) | (12,584) | (2.23) | (14,824) | (1.41) | (18,564) | (0.89) | |||||
| Nonparametric | DTVaR | 0.19 | 93 | DTVaR | 0.15 | 74 | DTVaR | 0.11 | 53 | DTVaR | 0.08 | 41 |
| (13,143) | (2.01) | (14,053) | (1.60) | (16,639) | (1.15) | (18,459) | (0.89) | |||||
| DTVaR | 92 | DTVaR | 74 | DTVaR | 52 | DTVaR | 40 | |||||
| (13,253) | (1.99) | (14,184) | (1.60) | (16,790) | (1.12) | (18,656) | (0.87) | |||||
| Parametric | ||||||||||||
| (Pareto, FGM Copula) | DTVaR | 130 | DTVaR | 103 | DTVaR | 65 | DTVaR | 41 | ||||
| (11,050) | (2.81) | (12,584) | (2.23) | (14,823) | (1.41) | (18,564) | (0.89) | |||||
| Estimators | ||||||
|---|---|---|---|---|---|---|
| DTVaR | 15,601 | 18,216 | 20,880 | 23,693 | 28,982 | |
| 12,826 | 13,189 | 13,233 | 13,057 | 11,630 | ||
| LCL | −0.3261 | −0.3585 | −0.3877 | −0.4408 | −0.5043 | |
| UCL | 0.3567 | 0.3937 | 0.4476 | 0.4860 | 0.5720 | |
| DTVaR | 14,890 | 17,420 | 20,002 | 22,785 | 28,059 | |
| 11,908 | 12,250 | 12,270 | 12,079 | 10,468 | ||
| LCL | −0.2784 | −0.3119 | −0.3598 | −0.4069 | −0.4719 | |
| UCL | 0.4462 | 0.4820 | 0.5410 | 0.5867 | 0.7214 | |
| DTVaR | 15,920 | 18,744 | 21,468 | 24,143 | 29,369 | |
| 13,366 | 13,789 | 13,841 | 13,672 | 12,346 | ||
| LCL | −0.3435 | −0.3869 | −0.4406 | −0.4784 | −0.5490 | |
| UCL | 0.3895 | 0.4422 | 0.4776 | 0.5228 | 0.6402 | |
| DTVaR | 15,029 | 17,741 | 20,366 | 23,011 | 28,218 | |
| 12,278 | 12,691 | 12,732 | 12,565 | 11,103 | ||
| LCL | −0.3017 | −0.3428 | −0.3844 | −0.4296 | −0.4988 | |
| UCL | 0.5095 | 0.5619 | 0.6233 | 0.6564 | 0.7848 | |
| DTVaR | 16,715 | 19,184 | 22,811 | 25,298 | 30,409 | |
| 14,148 | 14,530 | 14,567 | 14,291 | 12,954 | ||
| LCL | −0.3840 | −0.4233 | −0.4862 | −0.5222 | −0.6004 | |
| UCL | 0.4388 | 0.4971 | 0.5523 | 0.5970 | 0.6761 | |
| DTVaR | 15,554 | 17,902 | 21,391 | 23,864 | 28,987 | |
| 12,881 | 13,280 | 13,346 | 13,098 | 11,684 | ||
| LCL | −0.3358 | −0.3568 | −0.4303 | −0.4519 | −0.5566 | |
| UCL | 0.5700 | 0.6423 | 0.7151 | 0.7514 | 0.8861 | |
| DTVaR | 17,159 | 19,622 | 24,876 | 26,802 | 31,595 | |
| 15,074 | 15,541 | 15,540 | 15,205 | 13,923 | ||
| LCL | −0.4296 | −0.4775 | −0.5689 | −0.6046 | −0.6908 | |
| UCL | 0.5107 | 0.5495 | 0.6413 | 0.6918 | 0.8115 | |
| DTVaR | 15,472 | 17,744 | 22,720 | 24,638 | 29,412 | |
| 13,337 | 13,848 | 13,987 | 13,708 | 12,490 | ||
| LCL | −0.3640 | −0.4029 | −0.4832 | −0.5196 | −0.5904 | |
| UCL | 0.6988 | 0.7635 | 0.9066 | 0.9198 | 1.0359 | |
| DTVaR | 13,143 | 14,053 | 16,639 | 18,459 | 20,468 | |
| 6773.1 | 6644.3 | 5665.9 | 4318.5 | 1769.9 | ||
| LCL | −0.6585 | −0.6870 | −0.8201 | −0.9703 | −0.9887 | |
| UCL | 0.6671 | 0.6957 | 0.7464 | 0.7341 | 0.8679 | |
| DTVaR | 13,253 | 14,184 | 16,790 | 18,656 | 20,637 | |
| 6849.2 | 6,16.6 | 5715.9 | 4316.7 | 1711.9 | ||
| LCL | −0.6502 | −0.7013 | −0.8250 | −1.0162 | −1.1208 | |
| UCL | 0.6390 | 0.6518 | 0.7331 | 0.6889 | 0.7987 |
| Estimators | |||||||
|---|---|---|---|---|---|---|---|
| DTVaR | 15,910 | 19,014 | 22,145 | 25,388 | 30,139 | ||
| 13,783 | 14,325 | 14,403 | 14,114 | 12,694 | |||
| LCL | −0.3248 | −0.3862 | −0.4613 | −0.5435 | −0.5979 | ||
| UCL | 0.3840 | 0.4108 | 0.4380 | 0.4291 | 0.5628 | ||
| DTVaR | 14,939 | 17,907 | 20,928 | 24,151 | 28,936 | ||
| 12,657 | 13,207 | 13,297 | 13,033 | 11,482 | |||
| LCL | −0.2875 | −0.3471 | −0.4074 | −0.5003 | −0.5566 | ||
| UCL | 0.4912 | 0.5206 | 0.5557 | 0.5757 | 0.7132 | ||
| DTVaR | 16,242 | 19,801 | 22,439 | 26,026 | 31,517 | ||
| 14,197 | 14,767 | 14,829 | 14,509 | 12,651 | |||
| LCL | −0.3512 | −0.4359 | −0.4773 | −0.5801 | −0.6906 | ||
| UCL | 0.3453 | 0.3377 | 0.4072 | 0.3706 | 0.4660 | ||
| DTVaR | 15,189 | 18,594 | 21,139 | 24,711 | 30,312 | ||
| 13,049 | 13,649 | 13,739 | 13,474 | 11,457 | |||
| LCL | −0.2909 | −0.3844 | −0.4107 | −0.5234 | −0.6754 | ||
| UCL | 0.4593 | 0.4547 | 0.5226 | 0.5022 | 0.5964 | ||
| DTVaR | 17,580 | 20,330 | 26,482 | 28,849 | 31,595 | ||
| 15,440 | 15,908 | 15,573 | 14,912 | 13,923 | |||
| LCL | −0.4515 | −0.5125 | −0.6770 | −0.7624 | −0.6662 | ||
| UCL | 0.4726 | 0.4952 | 0.5424 | 0.5672 | 0.7846 | ||
| DTVaR | 15,801 | 18,342 | 24,243 | 26,648 | 29,412 | ||
| 13,712 | 14,252 | 14,113 | 13,507 | 12,490 | |||
| LCL | −0.3748 | −0.4290 | −0.5916 | −0.6701 | −0.5855 | ||
| UCL | 0.6643 | 0.7088 | 0.7794 | 0.8211 | 1.0668 | ||
| DTVaR | 17,308 | 20,218 | 27,083 | 29,875 | 33,249 | ||
| 15,909 | 16,553 | 16,419 | 15,676 | 14,387 | |||
| LCL | −0.4237 | −0.4849 | −0.6829 | −0.7833 | −0.7663 | ||
| UCL | 0.4719 | 0.4938 | 0.4801 | 0.4499 | 0.6182 | ||
| DTVaR | 15,375 | 18,031 | 24,598 | 27,461 | 30,994 | ||
| 14,097 | 14,846 | 15,054 | 14,430 | 13,158 | |||
| LCL | −0.3363 | −0.3979 | −0.5754 | −0.6828 | −0.6794 | ||
| UCL | 0.6686 | 0.7002 | 0.6862 | 0.6770 | 0.8527 | ||
| Estimators | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| DTVaR LCL UCL DTVaR LCL UCL | 12,500 6665.3 −0.0647 2.3908 12,595 6748.8 −0.0804 2.3226 | 12,500 6665.3 −0.0719 2.3684 12,595 6748.8 −0.0469 2.3294 | 11,406 6116.2 0.1294 2.7870 11,505 6223.1 0.1060 2.6779 | 18,301 4615.1 −0.1676 4.0913 18,476 4654.9 −0.1869 4.0551 | 18,301 4615.1 −0.1319 4.1357 18,476 4654.9 −0.1846 4.0480 | 18,301 4615.1 −0.1520 4.0711 18,476 4654.9 −0.1944 4.0487 | 20,468 1769.9 0.8529 12.3001 20,637 1711.9 0.8545 12.6727 | 20,468 1769.9 0.9921 12.6703 20,637 1711.9 0.7986 12.7271 | 20,468 1769.9 0.9070 12.5987 20,637 1711.9 0.7832 12.6842 | ||
| DTVaR LCL UCL DTVaR LCL UCL | 11,481 6243.5 0.1043 2.6871 11,576 6341.7 0.0759 2.6477 | 11,481 6243.5 0.1172 2.7063 11,576 6341.7 0.1068 2.6221 | 10,123 5222.3 0.3885 10,222 5362.1 0.3889 3.3928 | 17,459 4804.0 0.0013 4.1230 17,653 4867.9 −0.0120 4.0887 | 17,459 4804.0 −0.0240 4.1619 17,653 4867.9 −0.0516 4.0430 | 17,459 4804.0 −0.0054 4.1322 17,653 4867.9 −0.0019 4.0177 | 20,068 1880.4 10,297 118,503 20,264 1830.7 1.0705 12.2409 | 20,068 1880.4 1.1467 12.0218 20,264 1830.7 0.8565 12.0540 | 20,068 1880.4 1.1327 11.8399 20,264 1830.7 0.9883 12.0647 | ||
| DTVaR LCL UCL DTVaR LCL UCL | 11,481 6243.5 0.0971 2.6883 11,576 6341.7 0.1104 2.6320 | 11,481 6243.5 0.0969 2.7121 11,576 6341.7 0.1038 2.6449 | 10,123 5222.3 0.3918 3.4545 10,222 5362.1 0.3510 3.4162 | 17,459 4804.0 −0.0014 4.0688 17,653 4867.9 −0.0625 4.0382 | 17,459 4804.0 −0.0212 4.0664 17,653 4867.9 −0.0243 3.9866 | 17,459 4804.0 −0.0049 4.1201 17,653 4867.9 −0.0441 4.0767 | 20,068 1880.4 1.1327 11.8503 20,264 1830.7 0.9883 12.2752 | 20,068 1880.4 1.0817 11.8451 20,264 1830.7 0.9955 11.9624 | 20,068 1880.4 1.0736 11.8207 20,264 1830.7 1.0935 11.9624 | ||
| DTVaR LCL UCL DTVaR LCL UCL | 14,572 6950.0 −0.7380 0.5712 14,701 7030.0 −0.7490 0.5444 | 14,572 6950.0 −0.7253 0.5648 14,701 7030.0 −0.7425 0.5659 | 13,277 6679.9 −0.5678 0.8019 13,417 6790.9 −0.5666 0.7660 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | ||
| DTVaR LCL UCL DTVaR LCL UCL | 14,572 6950.0 −0.7264 0.5789 14,701 7030.0 −0.7534 0.5714 | 14,572 6950.0 −0.7496 0.5870 14,701 7030.0 −0.7474 0.5659 | 13,277 6679.9 −0.5777 0.8008 13,417 6790.9 −0.5846 0.7533 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | ||
| DTVaR LCL UCL DTVaR LCL UCL | 14,572 6950.0 −0.7504 0.5906 14,701 7030.0 −0.7474 0.5572 | 14,572 6950.0 −0.7370 0.6010 14,701 7030.0 −0.7294 0.5752 | 13,277 6679.9 −0.5672 0.8118 13,417 6790.9 −0.5914 0.7590 | 20,468 1769.9 −3.5026 0.5803 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −3.5026 0.6560 20,678 1687.6 −3.7977 0.5639 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | 20,468 1769.9 −0.9887 0.8679 20,637 1711.9 −1.1208 0.7987 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Syuhada, K.; Neswan, O.; Josaphat, B.P. Estimating Copula-Based Extension of Tail Value-at-Risk and Its Application in Insurance Claim. Risks 2022, 10, 113. https://doi.org/10.3390/risks10060113
Syuhada K, Neswan O, Josaphat BP. Estimating Copula-Based Extension of Tail Value-at-Risk and Its Application in Insurance Claim. Risks. 2022; 10(6):113. https://doi.org/10.3390/risks10060113
Chicago/Turabian StyleSyuhada, Khreshna, Oki Neswan, and Bony Parulian Josaphat. 2022. "Estimating Copula-Based Extension of Tail Value-at-Risk and Its Application in Insurance Claim" Risks 10, no. 6: 113. https://doi.org/10.3390/risks10060113






