Flexible Design and Operation of Multi-Stage Flash (MSF) Desalination Process Subject to Variable Fouling and Variable Freshwater Demand
Abstract
:1. Introduction
2. Dynamic Freshwater Demand
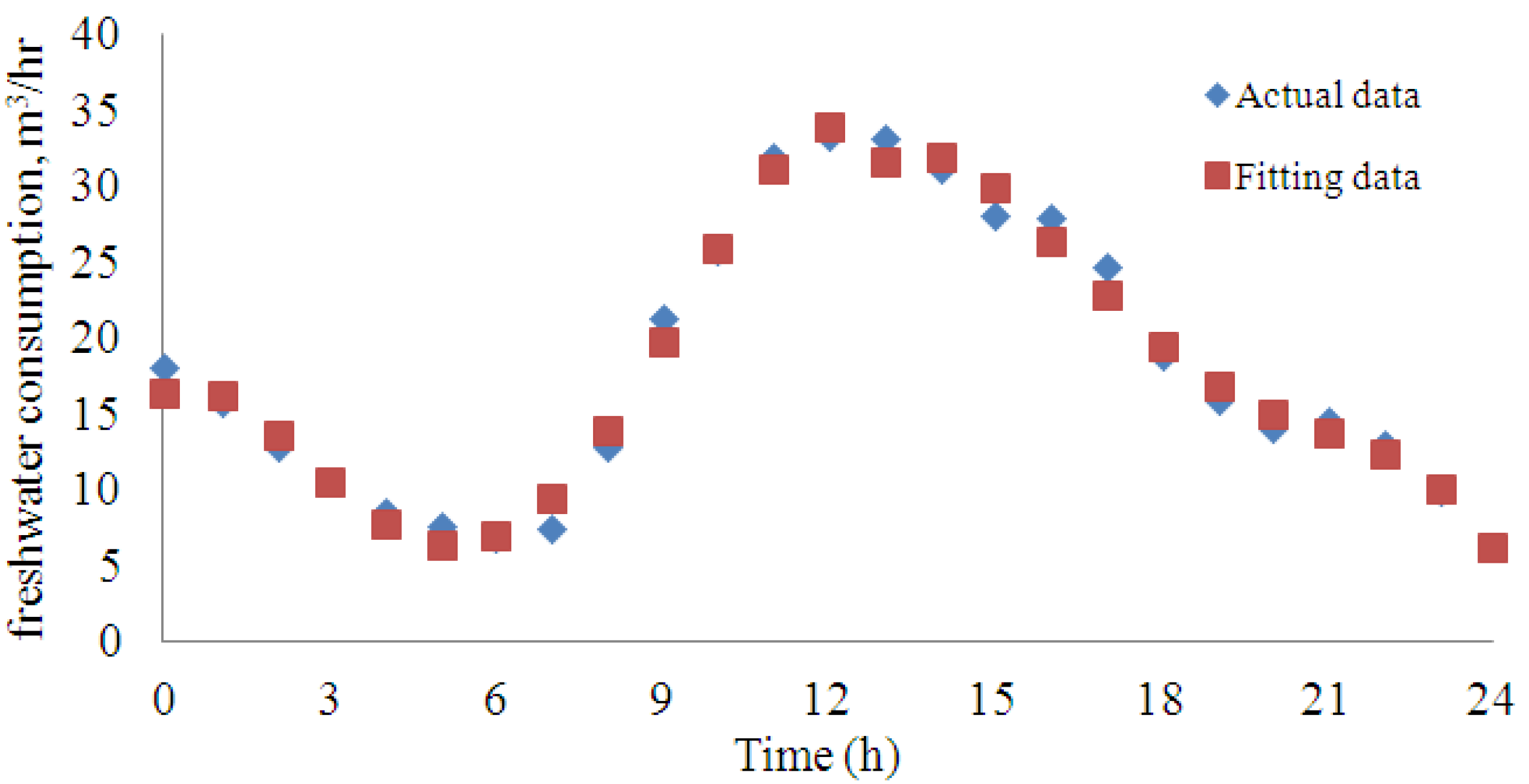
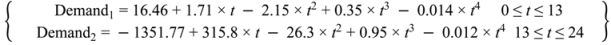
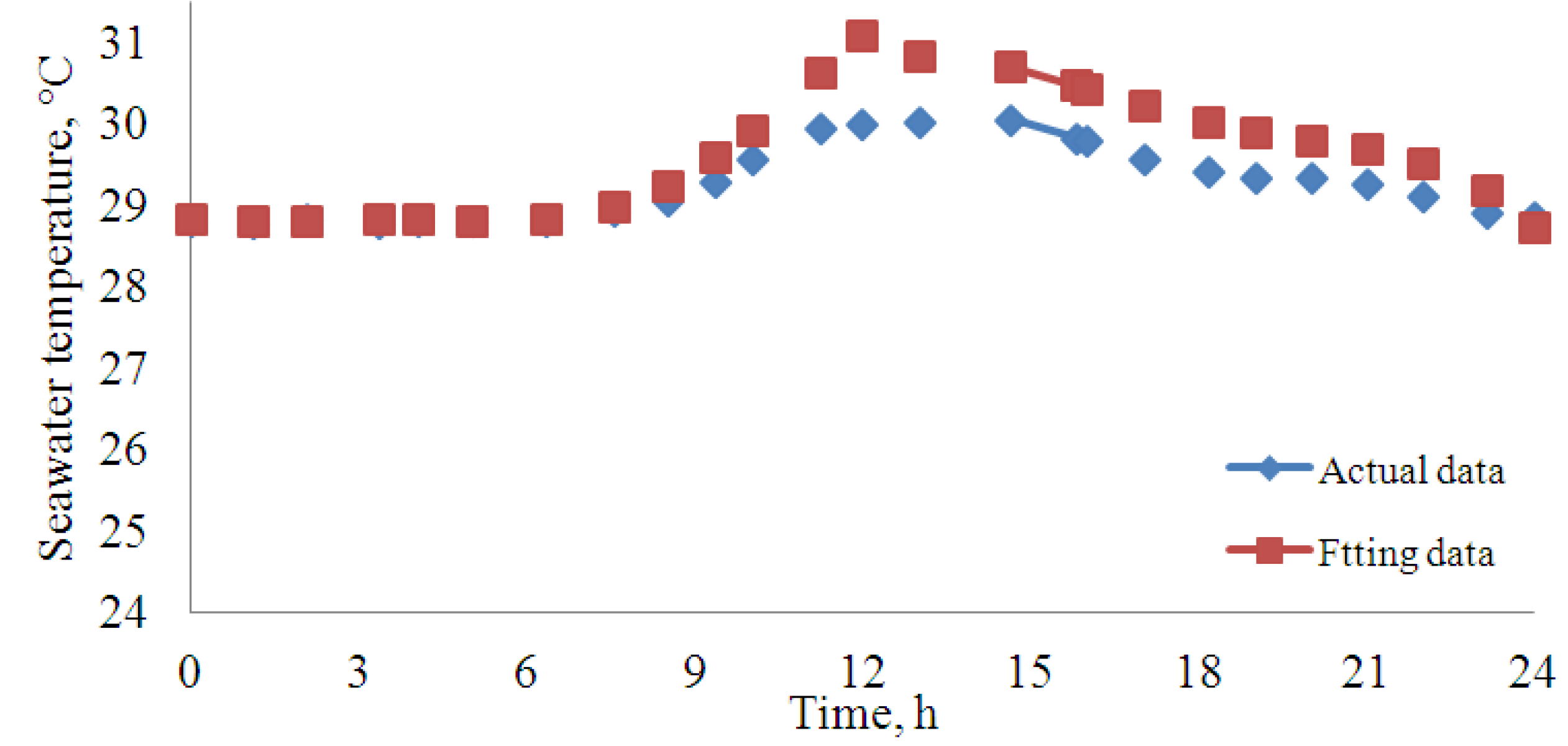
3. Seawater Temperature Dynamic Profiles
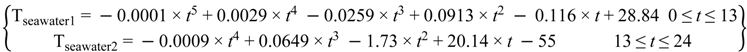
4. MSF Process Model
4.1. MSF Process Description
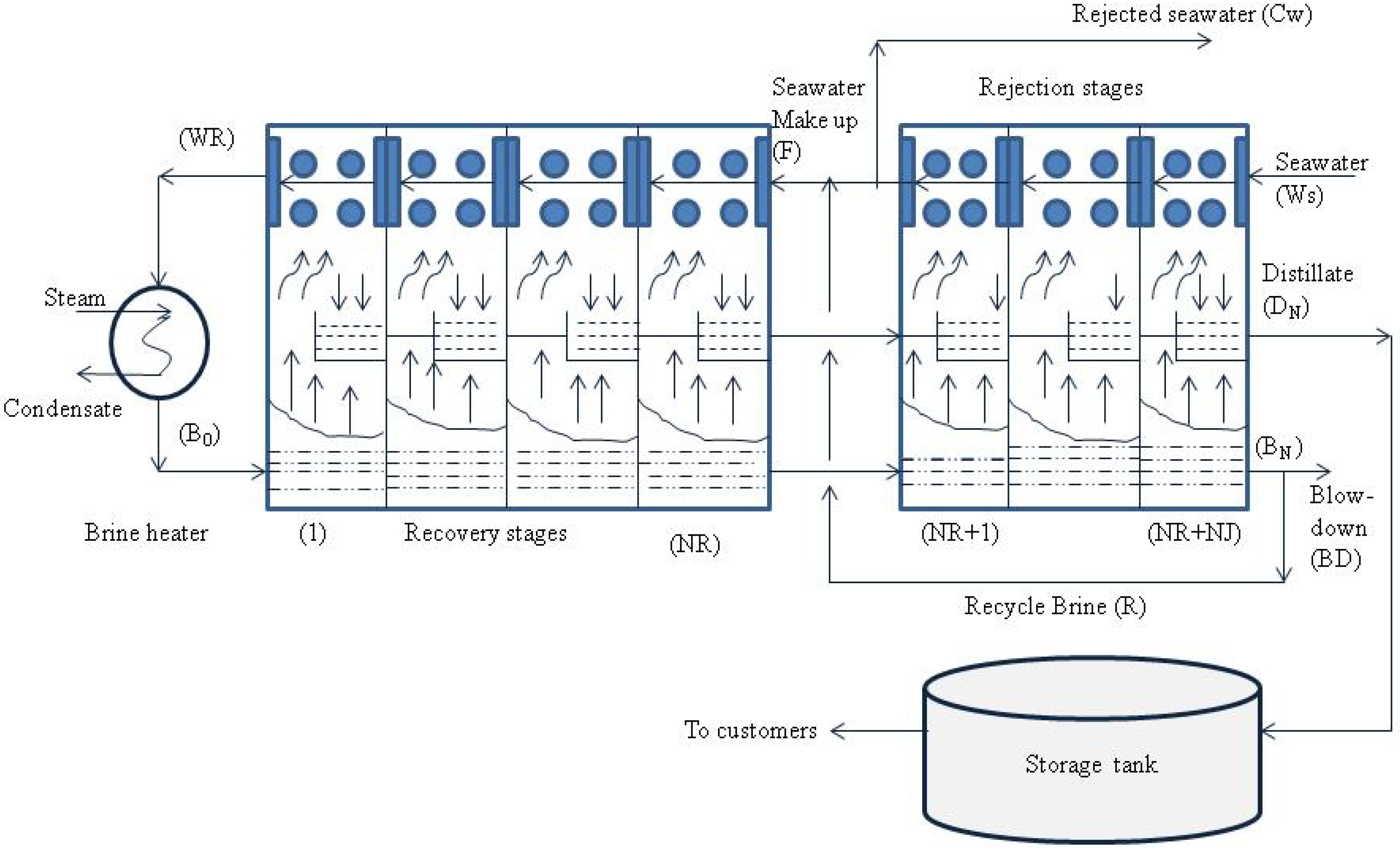
4.2. Steady State MSF Process Model
- The distillated from any stage is salt free
- Heat of mixing are negligible
- No sub cooling of condensate leaving the brine heater
- There are no heat losses and
- There is no entrainment of mist by the flashed vapour.
4.2.1. Stage Model
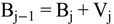
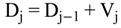
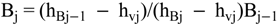
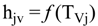
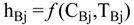
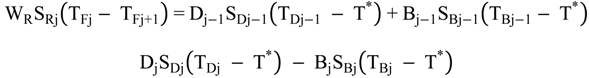
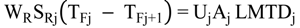
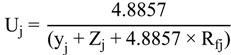
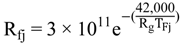
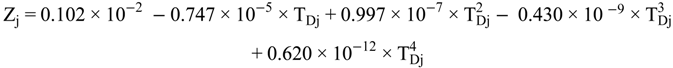
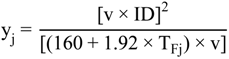
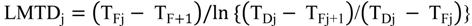
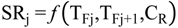
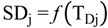
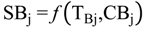
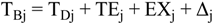
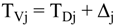
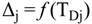
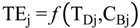
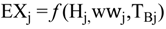
4.2.2. Brine Heater Model
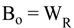
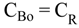
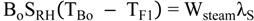
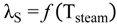
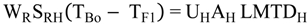
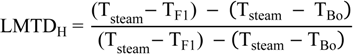
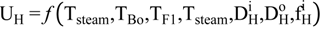
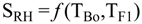
4.2.3. Splitter Model
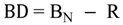
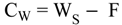
4.2.4. Mixers Model
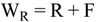
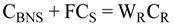
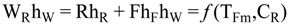
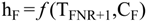
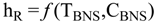
5. Storage Tank and Level Control Models
5.1. Storage Tank Model
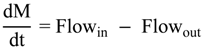
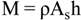
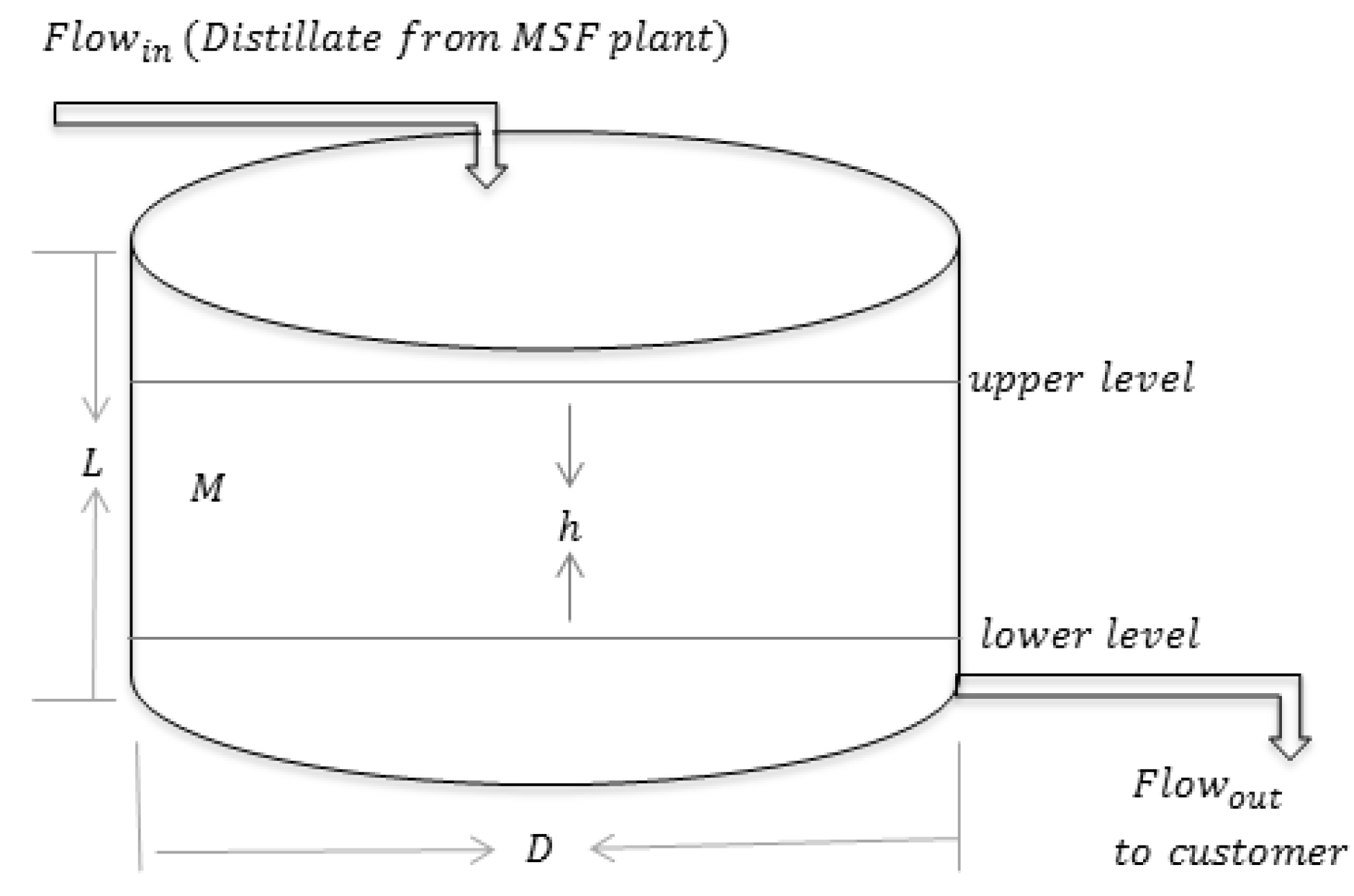
5.2. Storage Tank Level Control Model
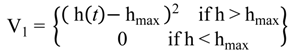
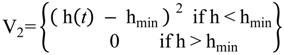
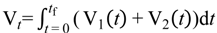
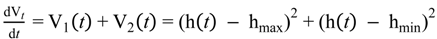
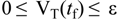
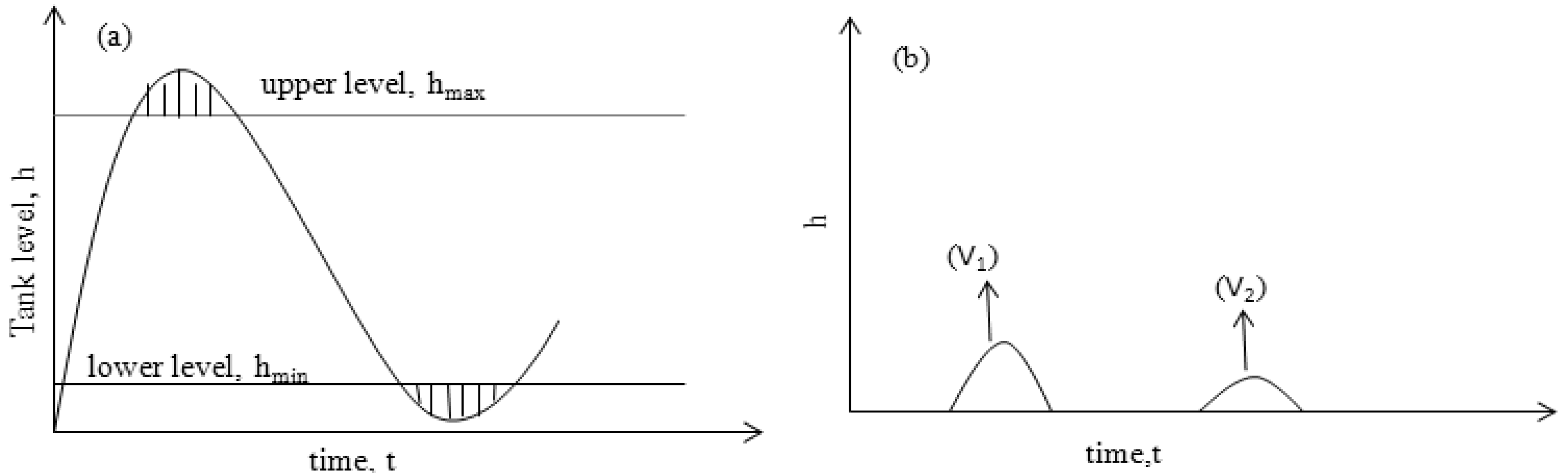
6. Optimisation of MSF Parameters
Optimisation Problem Formulation

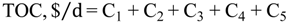
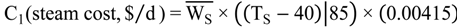
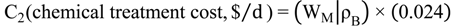
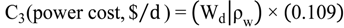
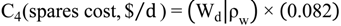
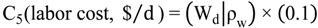
7. Case Study
| Unit | Aj/AH | Dji/DHi | Dj0/DH0 | wj/Lj/LH | Hj |
|---|---|---|---|---|---|
| Brine heater | 3530 | 0.022 | 0.0244 | 12.2 | |
| Recovery stage | 3995 | 0.022 | 0.0244 | 12.2 | 0.457 |
| Rejection stage | 3530 | 0.024 | 0.0254 | 10.7 | 0.457 |
| Case | N | C1, $/d | C2, $/d | C3, $/d | C4, $/d | C5, $/d | TOC, $/d |
|---|---|---|---|---|---|---|---|
| 1 | 16 | 46,184,583 | 37,498,047 | 17,220,256 | 12,954,688 | 15,798,400 | 129,655,973 |
| 2 | 17 | 44,026,301 | 37,597,628 | 17,358,817 | 13,058,927 | 15,925,521 | 127,967,194 |
| 3 | 18 | 41,403,746 | 37,222,956 | 17,250,642 | 12,977,547 | 15,826,277 | 124,681,167 |
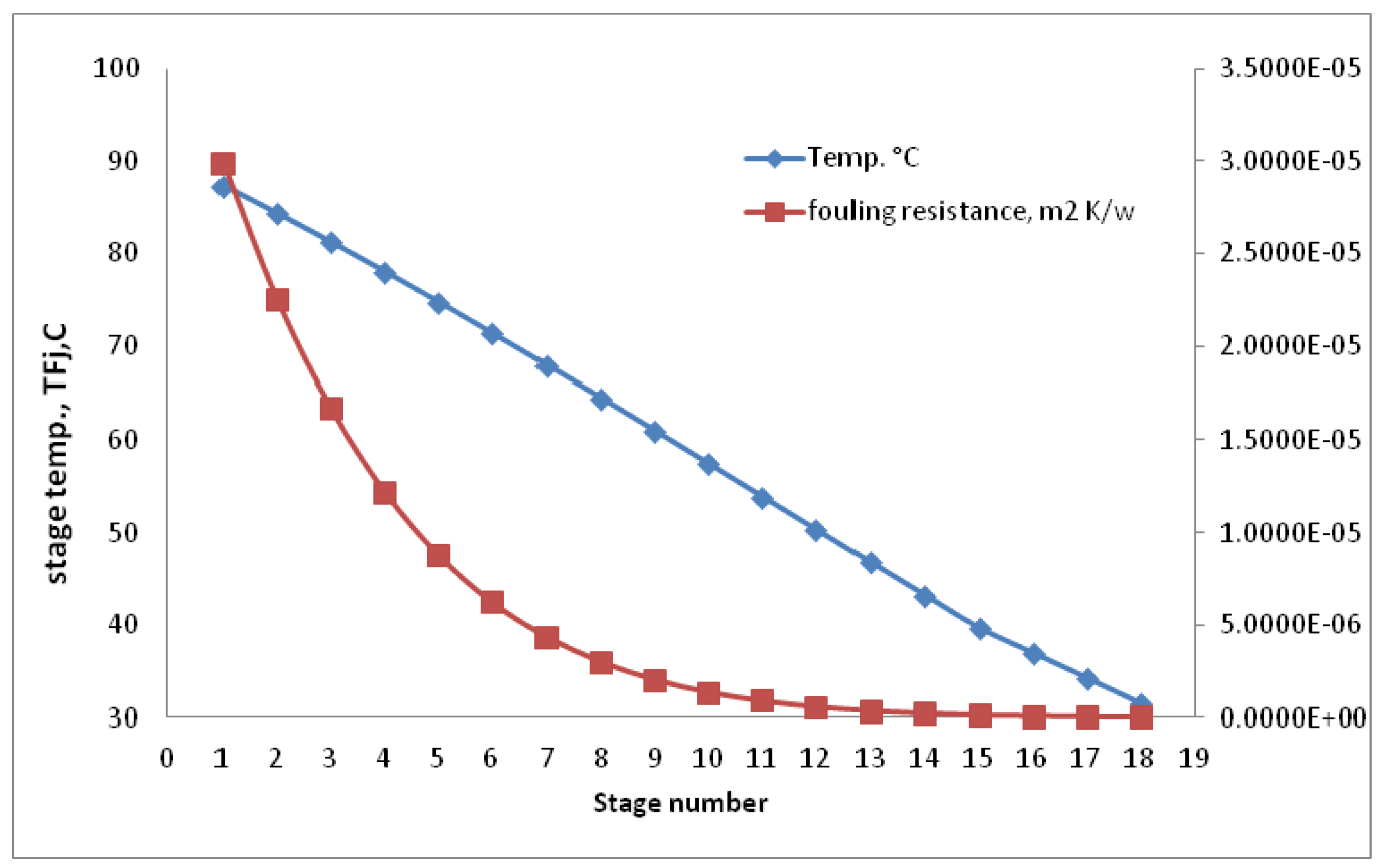
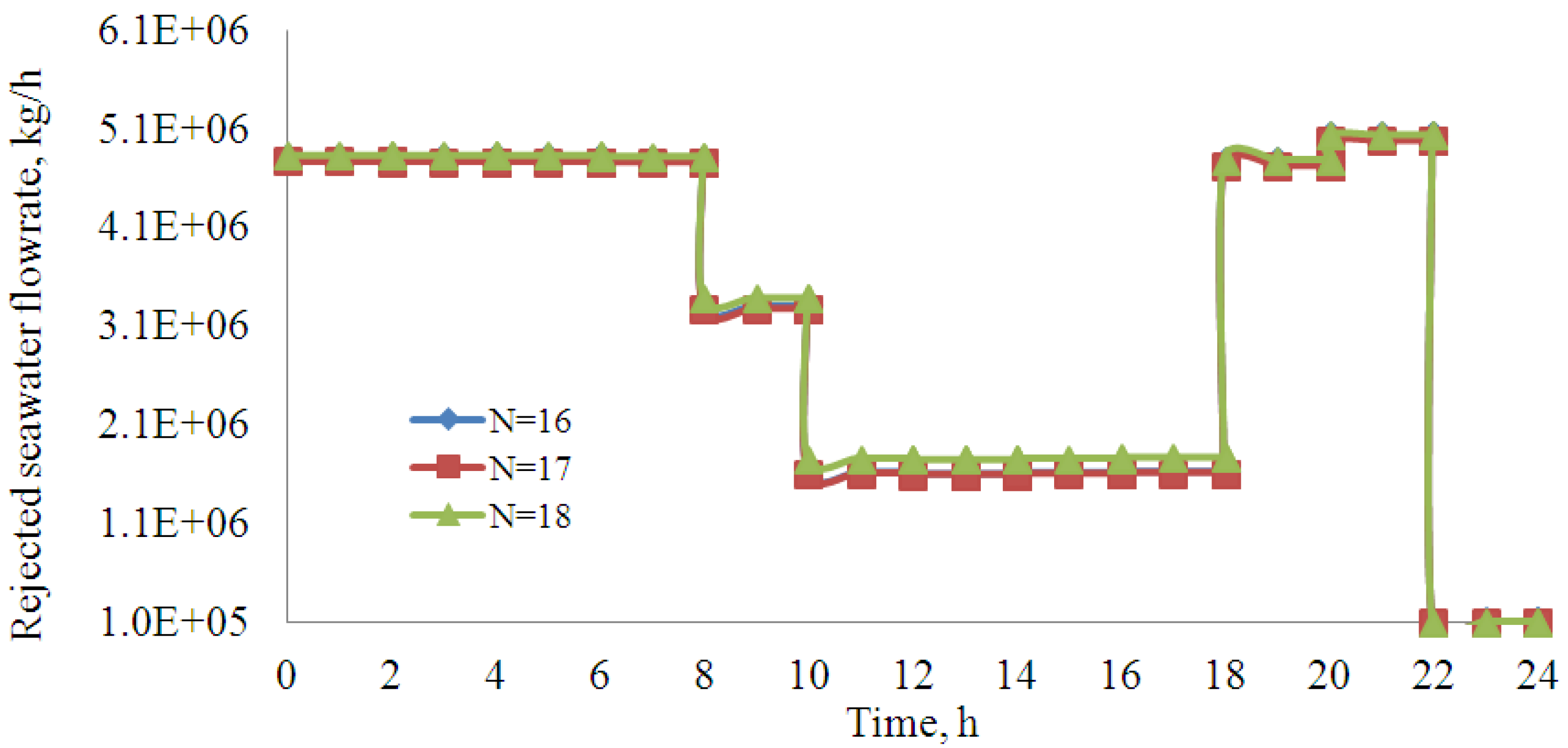
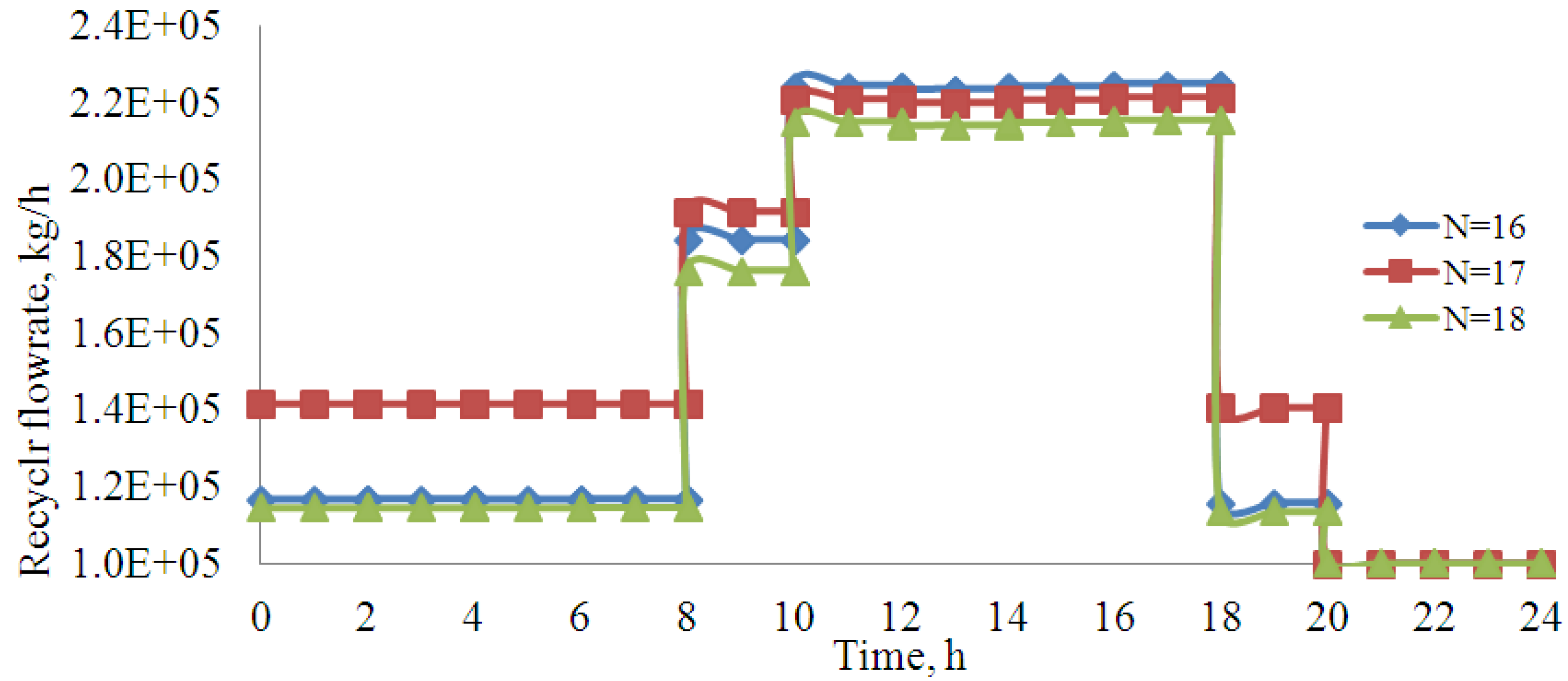
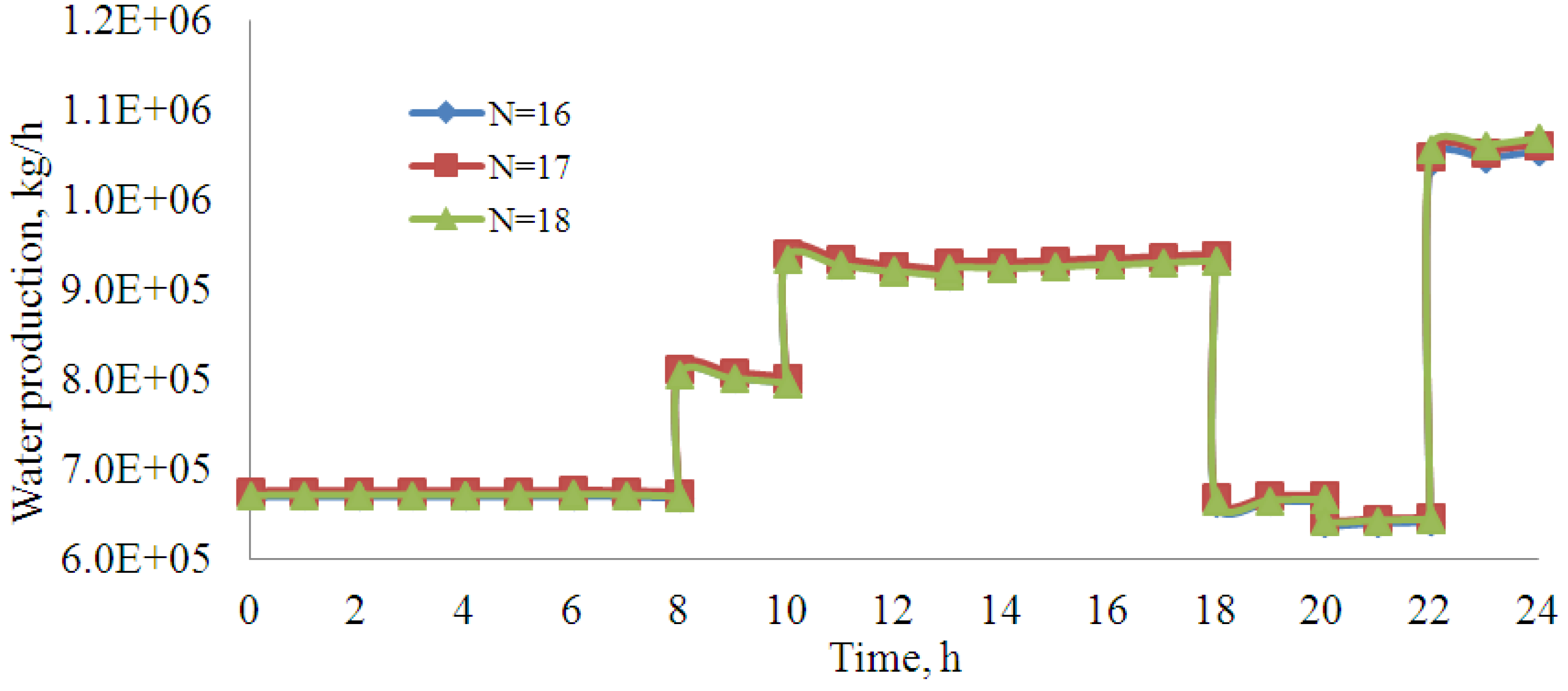
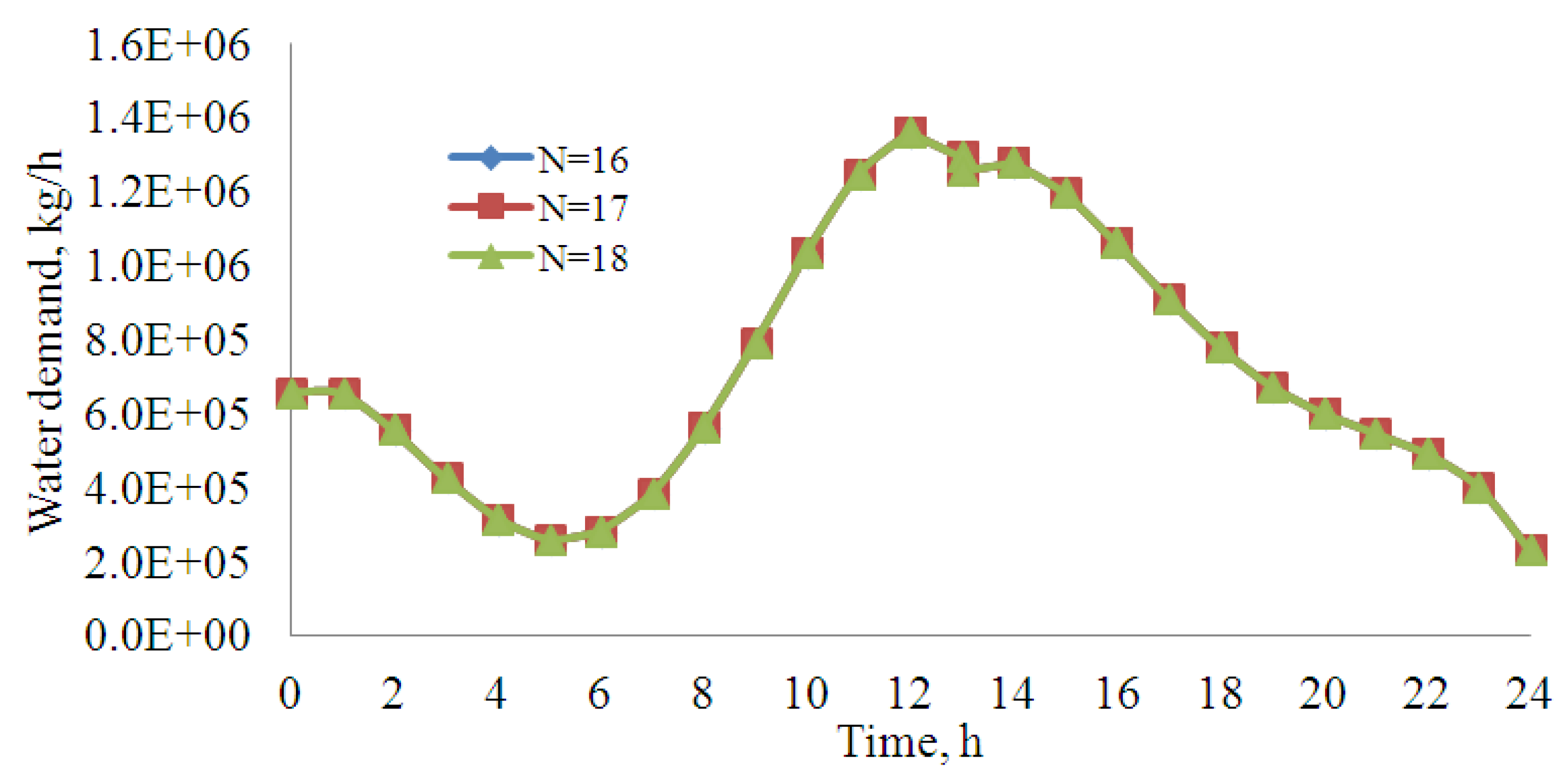
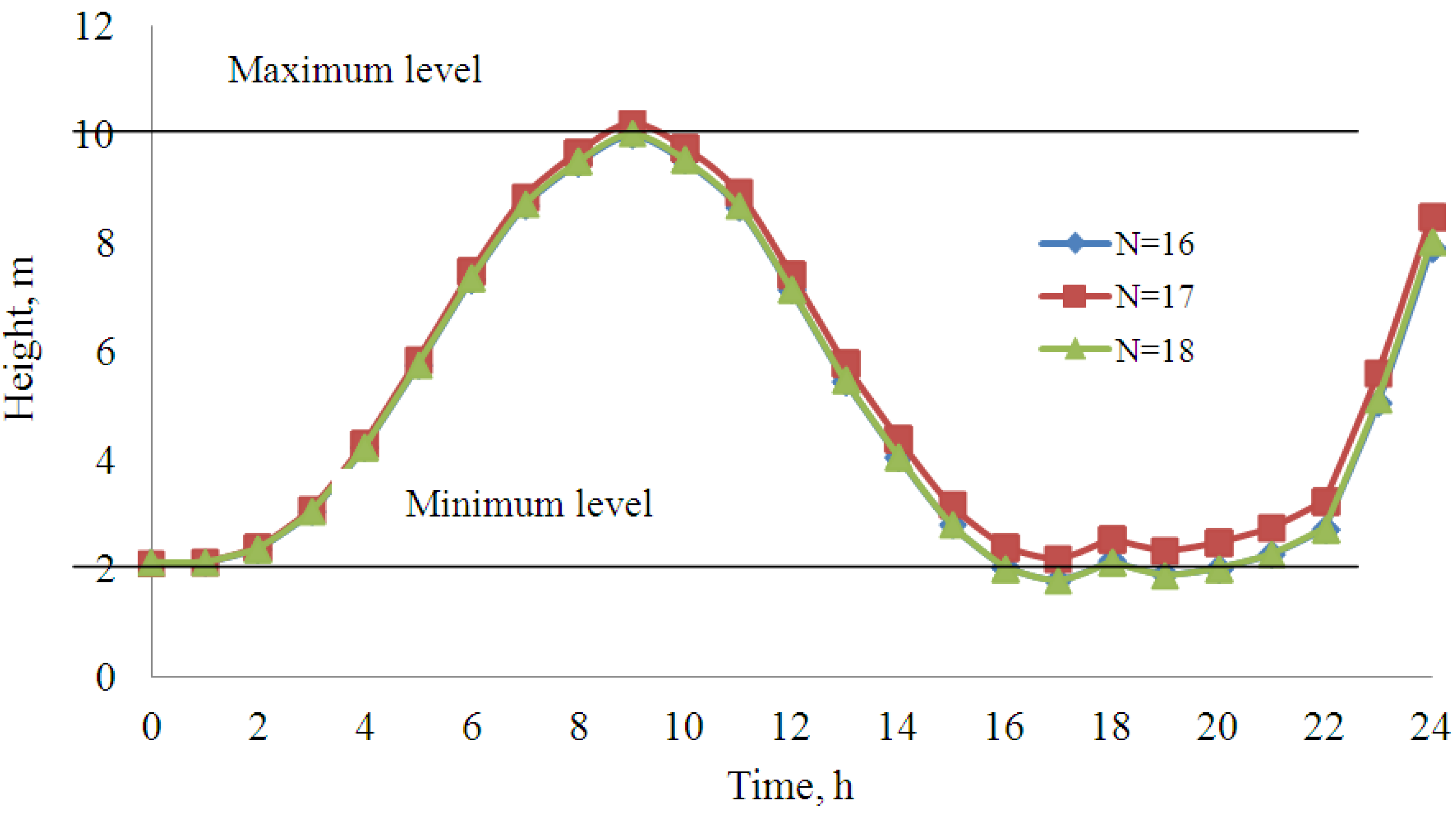
8. Conclusions
Nomenclature
| AH | Heat transfer area of brine heater (m2) |
| Aj | Heat transfer area of stage j (m2) |
| AS | cross sectional area of storage tank (m2) |
| B0 | Flashing brine mass flow rate leaving brine heater (kg/h) |
| BBT | Bottom brine temperature (°C) |
| BD | Blow-down mass flow rate (kg/h) |
| Bj | Flashing brine mass flow rate leaving stage j (kg/h) |
| CB0 | Salt concentration in flashing brine leaving brine heater (wt. %) |
| CBj | Salt concentration in flashing brine leaving stage j (wt. %) |
| CBNS | Salt concentration in brine recycle (R) (wt. %) |
| CR | Salt concentration in feed seawater (WR) (wt. %) |
| CS | Salt concentration in makeup seawater (F) (wt. %) |
| CW | Rejected seawater mass flow rate (kg/h) |
| Dj | Distillate flow rate leaving stage j (kg/h) |
| D | Diameter of storage tank (m) |
| EXj | Non-equilibrium allowance at stage j |
| F | Make-up seawater mass flow rate (kg/h) |
| fjH | Brine heater fouling factor ( h m2 °C/kcal) |
| fji | Fouling factor at stage j ( h m2 °C/kcal) |
| h | freshwater level in the storage tank (m) |
| hBj | Specific enthalpy of flashing brine at stage j (kcal/kg) |
| hR | Specific enthalpy of flashing brine at TF (kcal/kg) |
| hvj | Specific enthalpy of flashing vapor at stage j (kcal/kg) |
| hW | Specific enthalpy of brine at TF (kcal/kg) |
| Hj | Height of brine pool at stage j (m) |
| LH | Length of brine heater tubes (m) |
| L | Length of storage tank (m) |
| Lj | length of tubes at stage j (m) |
| M | storage tank holdup |
| ID | Internal diameter of tubes (m) |
| OD | External diameter of tubes (m) |
| Wsteam | Steam mass flow rate (kg/h) |
| R | Recycle stream mass flow rate (kg/h) |
| SBj | Heat capacity of flashing brine leaving stage j (kcal/kg/°C) |
| SDj | Heat capacity of distillate leaving stage j (kcal/kg/°C) |
| SRj | Heat capacity of cooling brine leaving stage j (kcal/kg/°C) |
| TBT | Top brine temperature (°C) |
| TBj | Temperature of flashing brine leaving stage j (°C) |
| TBNS | Temperature of the brine in the recycle flowrate (°C) |
| TBO | Temperature of flashing brine leaving brine heater (°C) |
| TDj | Temperature of distillate leaving stage j (°C) |
| TEj | Boiling point elevation at stage j (°C) |
| TFj+1 | Temperature of cooling brine leaving stage j (°C) |
| TFNR+1 | Temperature of makeup flowrate (F) (°C) |
| TFm | Temperature of the brine in feed entering recovery stage (°C) |
| TVj | Temperature of flashed vapour at stage j (°C) |
| Tsteam | Steam temperature (°C) |
| Tseawater | Seawater temperature (°C) |
| UH | Overall heat transfer coefficient at brine heater (Kcal/m2 h K) |
| Uj | Overall heat transfer coefficient at stage j (Kcal/m2 h K) |
| wwj | Width of stage j (m) |
| WS | Seawater mass flow rate (kg/h) |
| X | LMTD, logarithmic mean temperature difference at stages |
| Y | LMTD, logarithmic mean temperature difference at brine heater |
| Δj | Temperature loss due to demister (°C) |
| ρj | Brine density (kg/h) |
| λs | Latent heat of steam to the brine heater (kcal/kg) |
IDEX
| H | Brine heater |
| j | Stage index |
| * | Reference value |
Conflicts of Interest
References
- Assiry, A.M.; Gaily, M.H.; Alsamee, M.; Sarifudin, A. Electrical conductivity of seawater during ohmic heating. Desalination 2010, 260, 7–19. [Google Scholar]
- El-Dessouky, H.T.; Eltouney, H.M. Fundamentals of Salt Water Desalination; Elsevier Science, Ltd.: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Alasfour, F.N.; Abdulrahim, H.K. Rigorous steady state modeling of MSF-BR desalination system. Desalin. Water Treat. 2009, 1, 259–276. [Google Scholar] [CrossRef]
- Tanvir, M.S.; Mujtaba, I.M. Optimisation of MSF desalination process for fixed water demand using gPROMS. Comput. Aided Chem. Eng. 2007, 24, 763. [Google Scholar] [CrossRef]
- Tanvir, M.S.; Mujtaba, I.M. Optimisation of design and operation of MSF desalination process using MINLP technique in gPROMS. Desalination 2008, 222, 419–430. [Google Scholar] [CrossRef]
- Hawaidi, E.A.; Mujtaba, I.M. Freshwater production by MSF desalination process: Coping with variable demand by flexible design and operation. Comput. Aided Chem. Eng. 2011, 29, 1180–1184. [Google Scholar] [CrossRef]
- Yasunaga, K.; Fujita, M.; Ushiyama, T.; Yoneyama, K.; Takayabu, Y.N.; Yoshizaki, M. Diurnal variations in precipitable water observed by shipborne GPS over the tropical indian ocean. SOLA 2008, 4, 97–100. [Google Scholar] [CrossRef]
- Alvisi, M.A.; Franchini, M.; Marinelli, A. A short-term pattern-based model for water-demand forecasting. J. Hydroinform. 2007, 91, 39–50. [Google Scholar]
- Hawaidi, E.A.; Mujtaba, I.M. Meeting variable freshwater demand by flexible design and operation of the Multistage Flash Desalination process. Ind. Eng. Chem. Res. 2011, 50, 10604–10614. [Google Scholar] [CrossRef]
- Herrera, M.; Torgo, L.; Izquierdo, J.; Perez-Garcıa, R. Predictive models for forecasting hourly urban water demand. J. Hydrol. 2010, 387, 141–150. [Google Scholar] [CrossRef]
- Said, S.; Mujtaba, I.M.; Emtir, M. Effect of Fouling Factors on the Optimisation of MSF Desalination Process for Fixed Water Demand Using gPROMS. In Proceeding of the 9th International Conference on Computational Management, London, UK, 18–20 April 2012.
- Said, S.A. MSF Process Modelling, Simulation and Optimisation: Impact of Noncondensable Gases and Fouling Factor on Design and Operation. Ph.D. Thesis, University of Bradford, Yorkshire, UK, 2012. [Google Scholar]
- Said, S.; Mujtaba, I.M.; Emtir, M. Modelling and simulation of the effect of non-condensable gases on heat transfer in the MSF desalination plants using gPROMS software. Comput. Aided Process Eng. 2010, 28, 25–30. [Google Scholar] [CrossRef]
- gPROMS. In gPROMS User Guide 2005; Process System Enterprise, Ltd. (PSE): London, UK, 2005.
- Rosso, M.; Beltramini, A.; Mazzotti, M.; Morbidelli, M. Modelling of multistage flash desalination plants. Desalination 1996, 108, 365–374. [Google Scholar]
- Helal, A.; Medani, M.; Soliman, M.; Flower, J. Tridiagonal matrix model for multistage flash desalination plants. Comput. Chem. Eng. 1986, 10, 327–342. [Google Scholar] [CrossRef]
- Hussain, A.; Hassan, A.; Al-Gobaisi, D.; Al-Radif, A.; Woldai, A.; Sommariva, C. Modeling, simulation, optimization and control of multistage flash (MSF) desalination plants Part2: Modeling and simulation. Desalination 1993, 92, 21–41. [Google Scholar] [CrossRef]
- Helal, A.M.; El-Nashar, A.M.; Al-Kahtheeri, E.; Al-Malek, S. Optimal design of hybrid RO/MSF desalination plants Part I: Modeling and algorithms. Desalination 2003, 154, 43–66. [Google Scholar] [CrossRef]
- Sowgath, T.; Mujtaba, I.M. Less of the foul play: Flexible design and operation can cut fouling and shutdown of desalination plants. tce 2008, June, 28–29. [Google Scholar]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Said, S.A.; Emtir, M.; Mujtaba, I.M. Flexible Design and Operation of Multi-Stage Flash (MSF) Desalination Process Subject to Variable Fouling and Variable Freshwater Demand. Processes 2013, 1, 279-295. https://doi.org/10.3390/pr1030279
Said SA, Emtir M, Mujtaba IM. Flexible Design and Operation of Multi-Stage Flash (MSF) Desalination Process Subject to Variable Fouling and Variable Freshwater Demand. Processes. 2013; 1(3):279-295. https://doi.org/10.3390/pr1030279
Chicago/Turabian StyleSaid, Said Alforjani, Mansour Emtir, and Iqbal M. Mujtaba. 2013. "Flexible Design and Operation of Multi-Stage Flash (MSF) Desalination Process Subject to Variable Fouling and Variable Freshwater Demand" Processes 1, no. 3: 279-295. https://doi.org/10.3390/pr1030279





