Investigation of Performance Enhancements of Savonius Wind Turbines through Additional Designs
Abstract
:1. Introduction
2. Designs and Method
2.1. Savonius Wind Turbine Aerodynamics
2.2. Exterior Design Studies
2.3. Interior Design Studies
3. Results and Discussions
4. Conclusions
- It has been determined that the turbine’s performance can be increased by structural design changes on the Savonius wind turbine as well as with the assemblies added to the outside of the turbine without making any changes to the turbine.
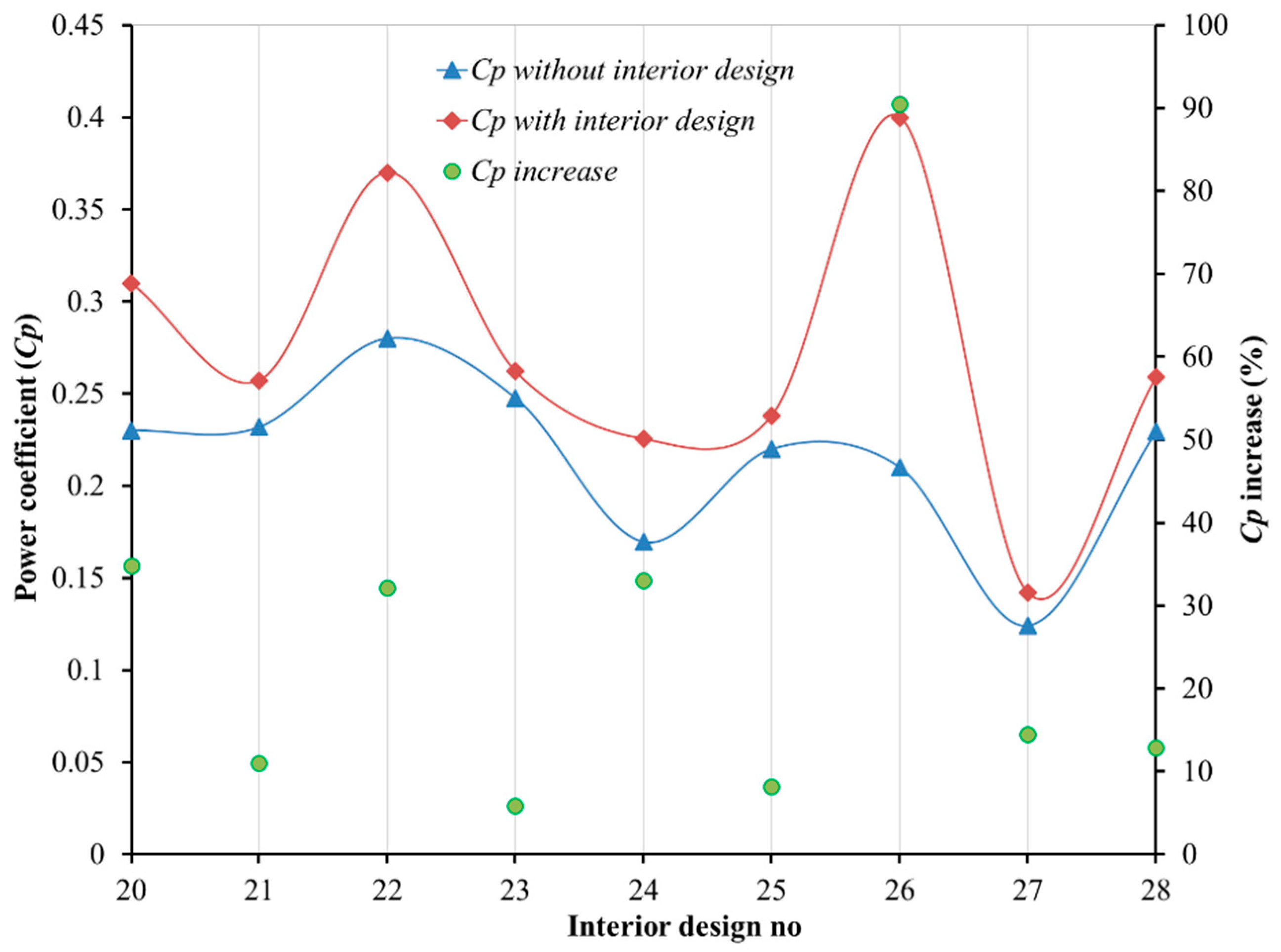
- It has been determined that the power coefficient values of Savonius wind turbines have been increased up to 0.400 levels with interior design changes.
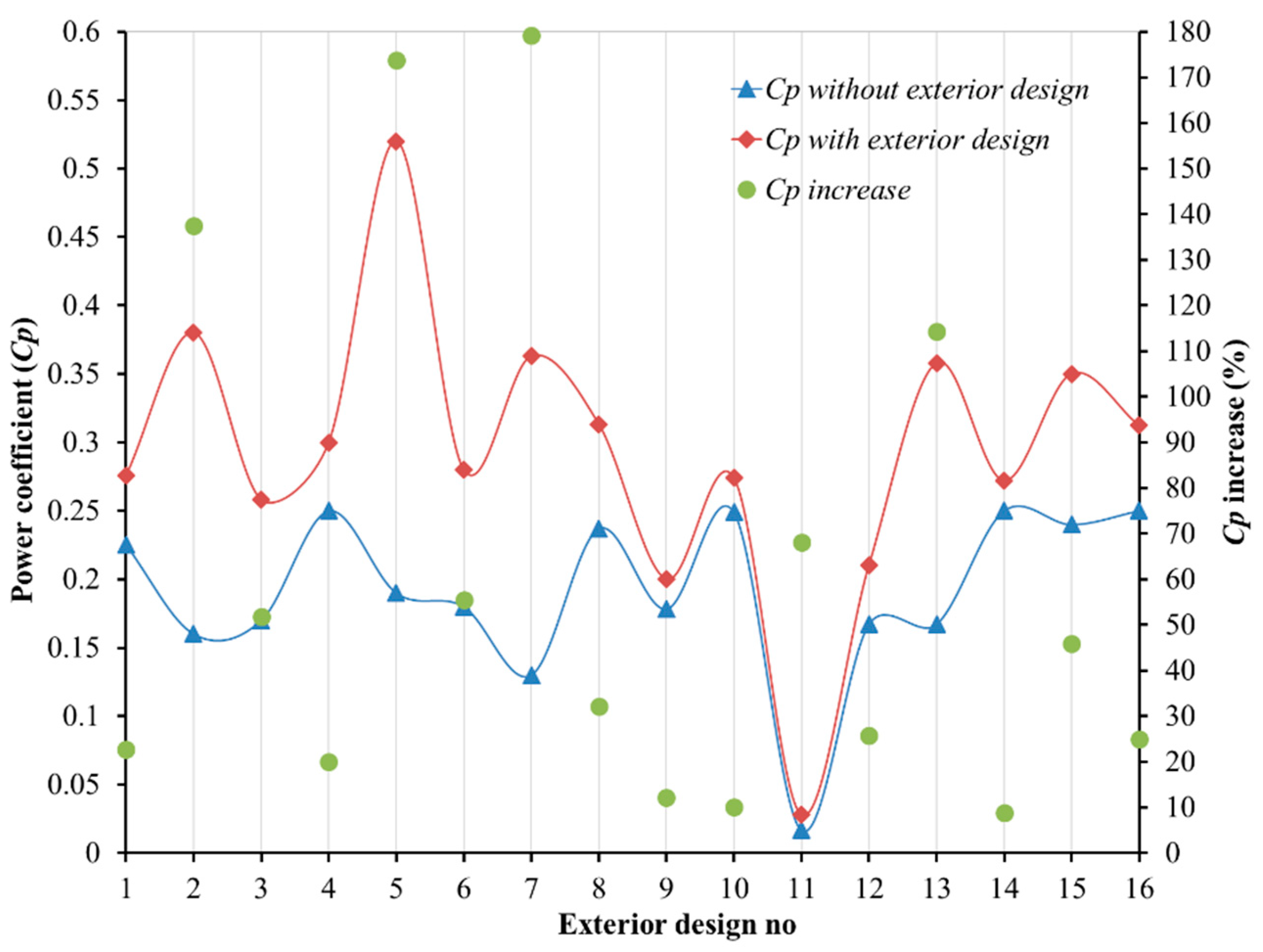
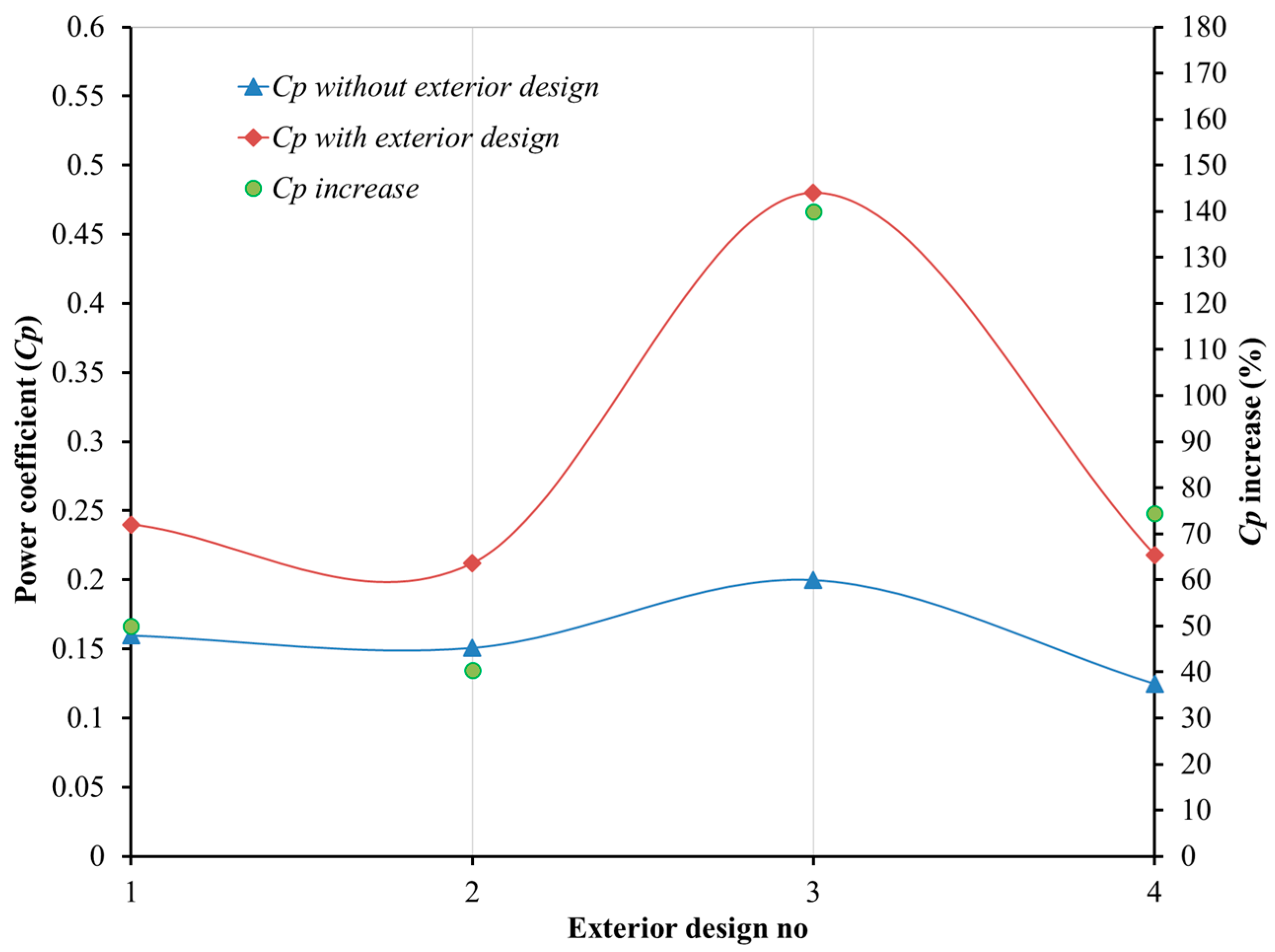
- It has been determined that the power coefficient values of Savonius wind turbines with exterior designs have been increased up to 0.520 levels.
- According to the studies reviewed in this study, the average power coefficient increases in Savonius wind turbines are around 33% for interior design modifications and around 64% for exterior design modifications. This indicates that the impact of exterior designs on the power coefficient of Savonius wind turbines is greater compared to interior design.
- It has been determined that the Savonius wind turbine’s ability to receive wind from all directions has been reduced or destroyed due to exterior design additions. An additional wind direction sensor mechanism can be used to regain this ability. In the case of turbines with interior designs, there is no need for an additional sensor mechanism as the ability of the turbine to receive wind from all directions is preserved.
- The inclusion of exterior design additions and additional equipment, such as direction sensors, in turbines with exterior design results in additional manufacturing and cost compared to turbines with interior design.
- Turbines with exterior design additions occupy a larger space compared to turbines with interior design, which can lead to a wind blockage effect in collective uses such as wind farms. Therefore, for meeting personal energy needs, especially in rural areas, it is more efficient to utilize turbines with exterior designs.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sridhar, S.; Zuber, M.; Shenoy, B.S.; Kumar, A.; Ng, E.Y.; Radhakrishnan, J. Aerodynamic comparison of slotted and non-slotted diffuser casings for Diffuser Augmented Wind Turbines (DAWT). Renew. Sustain. Energy Rev. 2022, 161, 112316. [Google Scholar] [CrossRef]
- Deda Altan, B.; Gungor, A. Investigation of the turbine performances in the case of dual usage of Savonius wind turbines. Proc. Inst. Mech. Eng. Part E J. Proc. Mech. Eng. 2022. [Google Scholar] [CrossRef]
- Sridhar, S.; Joseph, J.; Radhakrishnan, J. Implementation of tubercles on Vertical Axis Wind Turbines (VAWTs): An Aerodynamic Perspective. Sustain. Energy Technol. Assess. 2022, 52, 102109. [Google Scholar] [CrossRef]
- Irabu, K.; Roy, J.N. Characteristics of wind power on Savonius rotor using a guide-box tunnel. Exp. Therm. Fluid Sci. 2007, 32, 580–586. [Google Scholar] [CrossRef]
- Altan, B.D.; Atılgan, M.; Özdamar, A. An experimental study on improvement of a Savonius rotor performance with curtaining. Exp. Therm. Fluid Sci. 2008, 32, 1673–1678. [Google Scholar] [CrossRef]
- Zhou, T.; Rempfer, D. Numerical study of detailed flow field and performance of Savonius wind turbines. Renew. Energy 2013, 51, 373–381. [Google Scholar] [CrossRef]
- Altan, B.D.; Gungor, A. Examination of the Effect of Triangular Plate on the Performances of Reverse Rotating Dual Savonius Wind Turbines. Processes 2022, 10, 2278. [Google Scholar] [CrossRef]
- Gultekin, G.S. Investigation of Savonius Turbines in Terms of Performance. Master’s Thesis, Akdeniz University Institute of Natural and Applied Sciences, Antalya, Türkiye, 2022. [Google Scholar]
- Dorel, S.F.; Mihai, G.A.; Nicusor, D. Review of Specific Performance Parameters of Vertical Wind Turbine Rotors Based on the SAVONIUS Type. Energies 2021, 14, 1962. [Google Scholar] [CrossRef]
- Altan, B.D.; Atılgan, M. A Study on Increasing the performance of Savonius wind rotors. J. Mech. Sci. Technol. 2012, 26/5, 1493–1499. [Google Scholar] [CrossRef]
- Le Gourieres, D. Wind Power Plants Theory and Design; Pergamon Press Ltd.: Oxford, UK, 1982. [Google Scholar]
- Shaughnessy, B.; Probert, S. Partially-blocked Savonius rotor. Appl. Energy 1992, 43, 239–249. [Google Scholar] [CrossRef]
- Altan, B.D.; Atılgan, M. The use of a curtain design to increase the performance level of a Savonius wind rotors. Renew. Energy 2010, 35, 821–829. [Google Scholar] [CrossRef]
- El-Deen, A.E.S.; Nawar, M.A.A.; Attai, Y.A.; El-Maksoud, R.M.A. On the enhancement of Savonius Bach-type rotor performance by studying the optimum stator configuration. Ocean Eng. 2020, 217, 107954. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xin, D.; Zhan, J. Improvement of Aerodynamic Performance of Savonius Wind Rotor Using Straight-Arc Curtain. Appl. Sci. 2020, 10, 7216. [Google Scholar] [CrossRef]
- Mohamed, M.H.; Alqurashi, F.; Thévenin, D. Performance enhancement of a Savonius turbine under effect of frontal guiding plates. Energy Rep. 2021, 7, 6069–6076. [Google Scholar] [CrossRef]
- Alom, N. Influence of curtain plates on the aerodynamic performance of an elliptical bladed Savonius rotor (S-rotor). Energy Syst. 2021, 13, 265–280. [Google Scholar] [CrossRef]
- Shouman, M.R.; Helal, M.M.; El-Haroun, A.A. Numerical prediction of improvement of a Savonius rotor performance with curtaining and fin addition on blade. Alex. Eng. J. 2022, 61, 10689–10699. [Google Scholar] [CrossRef]
- Mohamed, M.; Janiga, G.; Pap, E.; Thévenin, D. Optimization of Savonius turbines using an obstacle shielding the returning blade. Renew. Energy 2010, 35, 2618–2626. [Google Scholar] [CrossRef]
- Tartuferi, M.; D’Alessandro, V.; Montelpare, S.; Ricci, R. Enhancement of Savonius wind rotor aerodynamic performance: A computational study of new blade shapes and curtain systems. Energy 2015, 79, 371–384. [Google Scholar] [CrossRef]
- El-Askary, W.; Nasef, M.; AbdEL-Hamid, A.; Gad, H. Harvesting wind energy for improving performance of Savonius rotor. J. Wind. Eng. Ind. Aerodyn. 2015, 139, 8–15. [Google Scholar] [CrossRef]
- Kalluvila, J.B.S.; Sreejith, B. Numerical and experimental study on a modified Savonius rotor with guide blades. Int. J. Green Energy 2018, 15, 744–757. [Google Scholar] [CrossRef]
- Mohammadi, M.; Ramadan, A.; Mohamed, M. Numerical investigation of performance refinement of a drag wind rotor using flow augmentation and momentum exchange optimization. Energy 2018, 158, 592–606. [Google Scholar] [CrossRef]
- Hesami, A.; Nikseresht, A.H.; Mohamed, M.H. Feasibility study of twin-rotor Savonius wind turbine incorporated with a wind-lens. Ocean Eng. 2022, 247, 110654. [Google Scholar] [CrossRef]
- Layeghmand, K.; Tabari, N.G.; Zarkesh, M. Improving efficiency of Savonius wind turbine by means of an air-foil-shaped deflector. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 528. [Google Scholar] [CrossRef]
- Yuwono, T.; Sakti, G.; Aulia, F.N.; Wijaya, A.C. Improving the performance of Savonius wind turbine by installation of a circular cylinder upstream of returning turbine blade. Alex. Eng. J. 2020, 59, 4923–4932. [Google Scholar] [CrossRef]
- Nimvari, M.E.; Fatahian, H.; Fatahian, E. Performance improvement of a Savonius vertical axis wind turbine using a porous deflector. Energy Convers. Manag. 2020, 220, 113062. [Google Scholar] [CrossRef]
- Yahya, W.; Ziming, K.; Juan, W.; Qurashi, M.S.; Al-Nehari, M.; Salim, E. Influence of tilt angle and the number of guide vane blades towards the Savonius rotor performance. Energy Rep. 2021, 7, 3317–3327. [Google Scholar] [CrossRef]
- Fatahian, H.; Hosseini, E.; Nimvari, M.E.; Fatahian, R.; Jouybari, N.F.; Fatahian, E. Performance enhancement of Savonius wind turbine using a nanofiber-based deflector. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 1–15. [Google Scholar] [CrossRef]
- Marinić-Kragić, I.; Vučina, D.; Milas, Z. Robust optimization of Savonius-type wind turbine deflector blades considering wind direction sensitivity and production material decrease. Renew. Energy 2022, 192, 150–163. [Google Scholar] [CrossRef]
- Tian, W.; Bian, J.; Yang, G.; Ni, X.; Mao, Z. Influence of a passive upstream deflector on the performance of the Savonius wind turbine. Energy Rep. 2022, 8, 7488–7499. [Google Scholar] [CrossRef]
- Yao, Y.; Tang, Z.; Wang, X. Design based on a parametric analysis of a drag driven VAWT with a tower cowling. J. Wind. Eng. Ind. Aerodyn. 2013, 116, 32–39. [Google Scholar] [CrossRef]
- Manganhar, A.L.; Rajpar, A.H.; Luhur, M.R.; Samo, S.R.; Manganhar, M. Performance analysis of a Savonius vertical axis wind turbine integrated with wind accelerating and guiding rotor house. Renew. Energy 2019, 136, 512–520. [Google Scholar] [CrossRef]
- Kacprzak, K.; Liskiewicz, G.; Sobczak, K. Numerical investigation of conventional and modified Savonius wind tur-bines. Renew. Energy 2013, 60, 578–585. [Google Scholar] [CrossRef]
- Mao, Z.; Tian, W. Effect of the blade arc angle on the performance of a Savonius wind turbine. Adv. Mech. Eng. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Alom, N.; Saha, U.K. Performance evaluation of vent-augmented elliptical-bladed Savonius rotors by numerical simulation and wind tunnel experiments. Energy 2018, 152, 277–290. [Google Scholar] [CrossRef]
- Ramadan, A.; Yousef, K.; Said, M.; Mohamed, M. Shape optimization and experimental validation of a drag vertical axis wind turbine. Energy 2018, 151, 839–853. [Google Scholar] [CrossRef]
- El-Askary, W.; Saad, A.S.; AbdelSalam, A.M.; Sakr, I. Investigating the performance of a twisted modified Savonius rotor. J. Wind. Eng. Ind. Aerodyn. 2018, 182, 344–355. [Google Scholar] [CrossRef]
- Damak, A.; Driss, Z.; Abid, M. Optimization of the helical Savonius rotor through wind tunnel experiments. J. Wind. Eng. Ind. Aerodyn. 2018, 174, 80–93. [Google Scholar] [CrossRef]
- Zemamou, M.; Toumi, A.; Mrigua, K.; Lahlou, Y.; Aggour, M. A novel blade design for Savonius wind turbine based on polynomial bezier curves for aerodynamic performance enhancement. Int. J. Green Energy 2020, 17, 652–665. [Google Scholar] [CrossRef]
- Ramarajan, J.; Jayavel, S. Performance Improvement in Savonius Wind Turbine by Modification of Blade Shape. J. Appl. Fluid Mech. 2022, 15, 99–107. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, R.K. Performance improvement of Savonius rotor using multiple quarter blades—A CFD investigation. Energy Convers. Manag. 2016, 127, 43–54. [Google Scholar] [CrossRef]
- Altan, B.D.; Altan, G.; Kovan, V. Investigation of 3D printed Savonius rotor performance. Renew. Energy 2016, 99, 584–591. [Google Scholar] [CrossRef]
- Sharma, S.; Sharma, R.K. CFD investigation to quantify the effect of layered multiple miniature blades on the performance of Savonius rotor. Energy Convers. Manag. 2017, 144, 275–285. [Google Scholar] [CrossRef]
- Tian, W.; Mao, Z.; Zhang, B.; Li, Y. Shape optimization of a Savonius wind rotor with different convex and concave sides. Renew. Energy 2018, 117, 287–299. [Google Scholar] [CrossRef]
- Ostos, I.; Ruiz, I.; Gajic, M.; Gómez, W.; Bonilla, A.; Collazos, C. A modified novel blade configuration proposal for a more efficient VAWT using CFD tools. Energy Convers. Manag. 2018, 180, 733–746. [Google Scholar] [CrossRef]
- Haddad, H.Z.; Elsayed, K.; Shabana, Y.M.; Mohamed, M.H. Comprehensive influence of the additional inner blades with different configurations on the performance of a Savonius wind turbine. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Gallo, L.A.; Chica, E.L.; Flórez, E.G.; Obando, F.A. Numerical and Experimental Study of the Blade Profile of a Savonius Type Rotor Implementing a Multi-Blade Geometry. Appl. Sci. 2021, 11, 10580. [Google Scholar] [CrossRef]
- Al Absi, S.M.; Jabbar, A.H.; Mezan, S.O.; Al-Rawi, B.A.; Al_Attabi, S.T. An experimental test of the performance enhancement of a Savonius turbine by modifying the inner surface of a blade. Mater. Today Proc. 2021, 42, 2233–2240. [Google Scholar] [CrossRef]
- Roy, S.; Saha, U.K. Wind tunnel experiments of a newly developed two-bladed Savonius-style wind turbine. Appl. Energy 2015, 137, 117–125. [Google Scholar] [CrossRef]
- Tian, W.; Song, B.; VanZwieten, J.H.; Pyakurel, P. Computational Fluid Dynamics Prediction of a Modified Savonius Wind Turbine with Novel Blade Shapes. Energies 2015, 8, 7915–7929. [Google Scholar] [CrossRef]
- Roy, S.; Ducoin, A. Unsteady analysis on the instantaneous forces and moment arms acting on a novel Savonius-style wind turbine. Energy Convers. Manag. 2016, 121, 281–296. [Google Scholar] [CrossRef]
- Zhang, B.; Song, B.; Mao, Z.; Tian, W.; Li, B.; Li, B. A Novel Parametric Modeling Method and Optimal Design for Savonius Wind Turbines. Energies 2017, 10, 301. [Google Scholar] [CrossRef]
- Chan, C.M.; Bai, H.L.; He, D.Q. Blade shape optimization of the Savonius wind turbine using a genetic algorithm. Appl. Energy 2018, 213, 148–157. [Google Scholar] [CrossRef]
- Marinić-Kragić, I.; Vučina, D.; Milas, Z. Concept of flexible vertical-axis wind turbine with numerical simulation and shape optimization. Energy 2018, 167, 841–852. [Google Scholar] [CrossRef]
- Sobczak, K.; Obidowski, D.; Reorowicz, P.; Marchewka, E. Numerical Investigations of the Savonius Turbine with Deformable Blades. Energies 2020, 13, 3717. [Google Scholar] [CrossRef]
- Lajnef, M.; Mosbahi, M.; Chouaibi, Y.; Driss, Z. Performance improvement in a helical Savonius wind rotor. Arab. J. Sci. Eng. 2020, 45, 9305–9323. [Google Scholar] [CrossRef]
- Imeni, S.Z.H.; Kaabinejadian, A.; Ahmadi, H.A.; Moghimi, M. Optimal design and sensitivity analysis of airfoil-shaped rotor blade for Savonius wind turbine by using response surface methodology. Wind. Eng. 2022, 46, 1203–1223. [Google Scholar] [CrossRef]
- Saeed, H.A.H.; Elmekawy, A.M.N.; Kassab, S.Z. Numerical study of improving Savonius turbine power coefficient by various blade shapes. Alex. Eng. J. 2019, 58, 429–441. [Google Scholar] [CrossRef]
- Halmy, M.S.M.; Didane, D.H.; Afolabi, L.O.; Al-Alimi, S. Computational Fluid Dynamics (CFD) Study on the Effect of the Number of Blades on the Performance of Double-Stage Savonius Rotor. CFD Lett. 2021, 13, 1–10. [Google Scholar] [CrossRef]
- Sheldahl, R.E.; Blackwell, B.F.; Feltz, L.V. Wind-tunnel performance data for 2-bucket and 3-bucket Savonius rotors. J. Energy 1978, 2, 160–164. [Google Scholar] [CrossRef]
- Ogawa, T.; Yoshida, H. The Effects of a Deflecting Plate and Rotor End Plates on Performances of Savonius-type Wind Turbine. Bull. JSME 1986, 29, 2115–2121. [Google Scholar] [CrossRef]
- Fujisawa, N. On the torque mechanism of Savonius rotors. J. Wind. Eng. Ind. Aerodyn. 1992, 40, 277–292. [Google Scholar] [CrossRef]
- Nasef, M.; El-Askary, W.; AbdEL-Hamid, A.; Gad, H. Evaluation of Savonius rotor performance: Static and dynamic studies. J. Wind. Eng. Ind. Aerodyn. 2013, 123, 1–11. [Google Scholar] [CrossRef]
- Kamoji, M.; Kedare, S.; Prabhu, S. Experimental investigations on single stage modified Savonius rotor. Appl. Energy 2009, 86, 1064–1073. [Google Scholar] [CrossRef]
- Akwa, J.V.; da Silva Júnior, G.A.; Petry, A.P. Discussion on the verification of the overlap ratio influence on performance coefficients of a Savonius wind rotor using computational fluid dynamics. Renew. Energy 2012, 38, 141–149. [Google Scholar] [CrossRef]
- Mohammadi, M.; Lakestani, M.; Mohamed, M. Intelligent parameter optimization of Savonius rotor using Artificial Neural Network and Genetic Algorithm. Energy 2018, 143, 56–68. [Google Scholar] [CrossRef]
- Alexander, A.I.; Holownia, B.P. Wind-tunnel tests on a Savonius rotor. J. Ind. Aerodyn. 1978, 3, 343–351. [Google Scholar] [CrossRef]
- Saha, U.; Rajkumar, M.J. On the performance analysis of Savonius rotor with twisted blades. Renew. Energy 2006, 31, 1776–1788. [Google Scholar] [CrossRef]
- Jeon, K.S.; Jeong, J.I.; Pan, J.-K.; Ryu, K.-W. Effects of end plates with various shapes and sizes on helical Savonius wind turbines. Renew. Energy 2015, 79, 167–176. [Google Scholar] [CrossRef]
- Fujisawa, N.; Gotoh, F. Visualization study of the flow in and around a Savonius rotor. Exp. Fluids 1992, 12, 407–412. [Google Scholar] [CrossRef]
- Premkumar, T.M.; Sivamani, S.; Kirthees, E.; Hariram, V.; Mohan, T. Data set on the experimental investigations of a helical Savonius style VAWT with and without end plates. Data Brief 2018, 19, 1925–1932. [Google Scholar] [CrossRef]
- Goodarzi, M.; Salimi, S. Numerical assessment of the effect of different end-plates on the performance of a finite-height Savonius turbine. Energy Sources Part A Recover. Util. Environ. Eff. 2021, 1–20. [Google Scholar] [CrossRef]
- Kamoji, M.A.; Kedare, S.B.; Prabhu, S.V. Experimental investigations on single stage, two stage and three stage conventional Savonius rotor. Int. J. Energy Res. 2008, 32, 877–895. [Google Scholar] [CrossRef]
- Menet, J.L. Adouble-step Savonius rotor for local production of electricity: A design study. Renew. Energy 2004, 29, 1843–1862. [Google Scholar] [CrossRef]
- Frikha, S.; Driss, Z.; Ayadi, E.; Masmoudi, Z.; Abid, M.S. Numerical and experimental characterization of multi-stage Savonius rotors. Energy 2016, 114, 382–404. [Google Scholar] [CrossRef]
- Kothe, L.B.; Möller, S.V.; Petry, A.P. Numerical and experimental study of a helical Savonius wind turbine and a comparison with a two-stage Savonius turbine. Renew. Energy 2019, 148, 627–638. [Google Scholar] [CrossRef]
- Bhayo, B.A.; Al-Kayiem, H.H. Experimental characterization and comparison of performance parameters of S-rotors for standalone wind power system. Energy 2017, 138, 752–763. [Google Scholar] [CrossRef]
- Saha, U.; Thotla, S.; Maity, D. Optimum design configuration of Savonius rotor through wind tunnel experiments. J. Wind. Eng. Ind. Aerodyn. 2008, 96, 1359–1375. [Google Scholar] [CrossRef]
- Mrigua, K.; Toumib, A.; Zemamoua, M.; Ouhmmoua, B.; Lahloua, Y.; Aggoura, M. CFD Investigation of a new elliptical-bladed multistage Savonius rotors. Int. J. Renew. Energy Dev. 2020, 9, 383–392. [Google Scholar] [CrossRef]
- Saad, A.S.; Elwardany, A.; El-Sharkawy, I.I.; Ookawara, S.; Ahmed, M. Performance evaluation of a novel vertical axis wind turbine using twisted blades in multi-stage Savonius rotors. Energy Convers. Manag. 2021, 235, 114013. [Google Scholar] [CrossRef]







| (a) | ||||||
|---|---|---|---|---|---|---|
| E.d. No | Reference | Study Type | Exterior Design Name | Cp without e.d. | Cp with e.d. | Exterior Design |
| 1 | Irabu and Roy [4] | Experimental | Guide-box tunnel | 0.225 | 0.276 |  |
| 2 | Deda Altan et al. [5] | Experimental | Curtain arrangement | 0.160 | 0.380 | 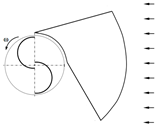 |
| 3 | Mohamed et al. [19] | Validated numerical Optimization | Shielding obstacle | 0.170 | 0.258 | 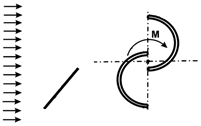 |
| 4 | Tartuferi et al. [20] | Experimental Numerical | Conveyor-deflector curtain system | 0.250 | 0.300 | 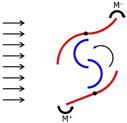 |
| 5 | El-Askary et al. [21] | Validated numerical | Guide plates design | 0.190 | 0.520 | 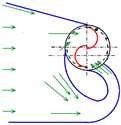 |
| 6 | Kalluvila and Sreejith [22] | Experimental Numerical | Guide blade arrangement | 0.180 | 0.280 | 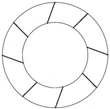 |
| 7 | Mohammadi et al. [23] | Validated numerical | Nozzle design | 0.130 | 0.363 | 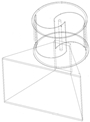 |
| 8 | Layeghmand et al. [25] | Validated numerical | Airfoil-shaped deflector | 0.237 | 0.313 | 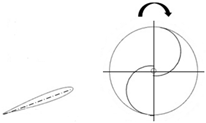 |
| (b) | ||||||
| E.d. No | Reference | Study Type | Exterior Design Name | Cp without e.d. | Cp with e.d. | Exterior Design |
| 9 | Yuwono et al. [26] | Experimental | Circular cylinder | 0.178 | 0.200 | 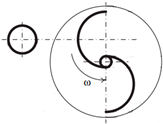 |
| 10 | Nimvari et al. [27] | Validated numerical | Porous deflector | 0.249 | 0.274 |  |
| 11 | Yahya et al. [28] | Experimental | Guide vane | 0.017 | 0.028 |  |
| 12 | Hesami et al. [24] | Validated numerical | Wind-lens | 0.167 | 0.210 |  |
| 13 | Hesami et al. [24] | Validated numerical | Wind-lens (with a dual turbine) | 0.167 | 0.358 |  |
| 14 | Fatahian et al. [29] | Validated numerical | Nanofiber-based deflector | 0.250 | 0.272 | 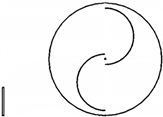 |
| 15 | Marinic-Kragic et al. [30] | Validated numerical Optimization | Deflector blades | 0.240 | 0.350 | 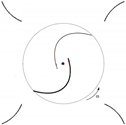 |
| 16 | Tian et al. [31] | Validated numerical | Passive deflector | 0.250 | 0.313 | 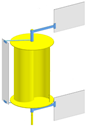 |
| E.d. No | Reference | Study Type | Exterior Design Name | Cp without e.d. | Cp with e.d. | Exterior Design |
|---|---|---|---|---|---|---|
| 1 | Irabu and Roy [4] | Experimental | Guide-box tunnel | 0.160 | 0.240 | 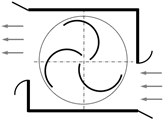 |
| 2 | Mohamed et al. [19] | Validated numerical Optimization | Shielding obstacle | 0.151 | 0.212 |  |
| 3 | Yao et al. [32] | Numerical Experimental | Tower cowling | 0.200 | 0.480 | 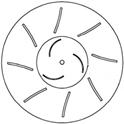 |
| 4 | Manganhar et al. [33] | Experimental | Rotor house | 0.125 | 0.218 | 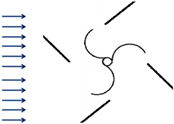 |
| I.d. No | Reference | Study Type | Interior Design Name | Cp without i.d. | Cp with i.d. |
|---|---|---|---|---|---|
| 1 | Zhou and Rempfer [6] | Compared numerical | Bach-type | 0.189 | 0.264 |
| 2 | Kacprzak et al. [34] | Compared numerical | Bach-type | 0.155 | 0.180 |
| 3 | Kacprzak et al. [34] | Compared numerical | Elliptical blade | 0.155 | 0.170 |
| 4 | Mao and Tian [35] | Validated numerical | Blade arc angle | 0.262 | 0.284 |
| 5 | Alom and Saha [36] | Experimental Numerical | Vented elliptical blade | 0.112 | 0.146 |
| 6 | Alom and Saha [36] | Experimental Numerical | Non-vented elliptical blade | 0.112 | 0.134 |
| 7 | Ramadan et al. [37] | Experimental Numerical Genetic algorithm | S-shaped optimum blade design | 0.140 | 0.280 |
| 8 | El-Askary et al. [38] | Experimental Numerical | Twisted modified design | 0.140 | 0.220 |
| 9 | Damak et al. [39] | Experimental Numerical | Helical Bach design | 0.180 | 0.200 |
| 10 | Zemamou et al. [40] | Validated numerical Optimization Taguchi method | Bezier curved blade | 0.270 | 0.350 |
| 11 | Ramarajan and Jayavel [41] | Validated numerical | Three-fourth modified blade | 0.230 | 0.250 |
| I.d. No | Reference | Study Type | Interior Design Name | Cp without i.d. | Cp with i.d. |
|---|---|---|---|---|---|
| 12 | Sharma and Sharma [42] | Validated numerical | Multiple quarter blades | 0.208 | 0.227 |
| 13 | Deda Altan et al. [43] | Experimental Numerical | Additional design | 0.099 | 0.119 |
| 14 | Sharma and Sharma [44] | Validated numerical | Multiple miniature blades | 0.192 | 0.213 |
| 15 | Tian et al. [45] | Validated numerical Optimization | Optimal design | 0.247 | 0.258 |
| 16 | Ostos et al. [46] | Validated numerical | Two-quarters conventional blade | 0.214 | 0.252 |
| 17 | Haddad et al. [47] | Validated numerical | Additional inner blade | 0.196 | 0.243 |
| 18 | Gallo et al. [48] | Experimental Numerical | Multi-blade geometry | 0.195 | 0.295 |
| 19 | Al Absi et al. [49] | Experimental Numerical | Zigzag surface blade | 0.260 | 0.292 |
| I.d. No | Reference | Study Type | Interior Design Name | Cp without i.d. | Cp with i.d. |
|---|---|---|---|---|---|
| 20 | Roy and Saha [50] | Experimental Numerical | Newly developed blade | 0.230 | 0.310 |
| 21 | Tian et al. [51] | Validated numerical | Fullness of the blade | 0.232 | 0.257 |
| 22 | Roy and Ducoin [52] | Validated numerical | New blade design with moment arms | 0.280 | 0.370 |
| 23 | Zhang et al. [53] | Validated numerical Optimization | Optimal design | 0.247 | 0.262 |
| 24 | Chan et al. [54] | Numerical Genetic algorithm | Optimized blade | 0.169 | 0.225 |
| 25 | Marinic-Kragic et al. [55] | Validated numerical Optimization Genetic algorithm | Flexible-blade | 0.220 | 0.238 |
| 26 | Sobczak et al. [56] | Validated numerical | Deformable blade | 0.210 | 0.400 |
| 27 | Lajnef et al. [57] | Experimental Numerical | Novel delta-bladed | 0.124 | 0.142 |
| 28 | Imeni et al. [58] | Validated numerical | Airfoil-shaped blade | 0.229 | 0.259 |
| I.d. No | Reference | Study Type | Interior Design Name | Cp without i.d. | Cp with i.d. |
|---|---|---|---|---|---|
| 1 | Ramadan et al. [37] | Experimental Numerical Genetic algorithm | 3 blades | 0.140 | 0.110 |
| I.d. No | Reference | Study Type | Design Remarks | Cp without i.d. | Cp with i.d. |
|---|---|---|---|---|---|
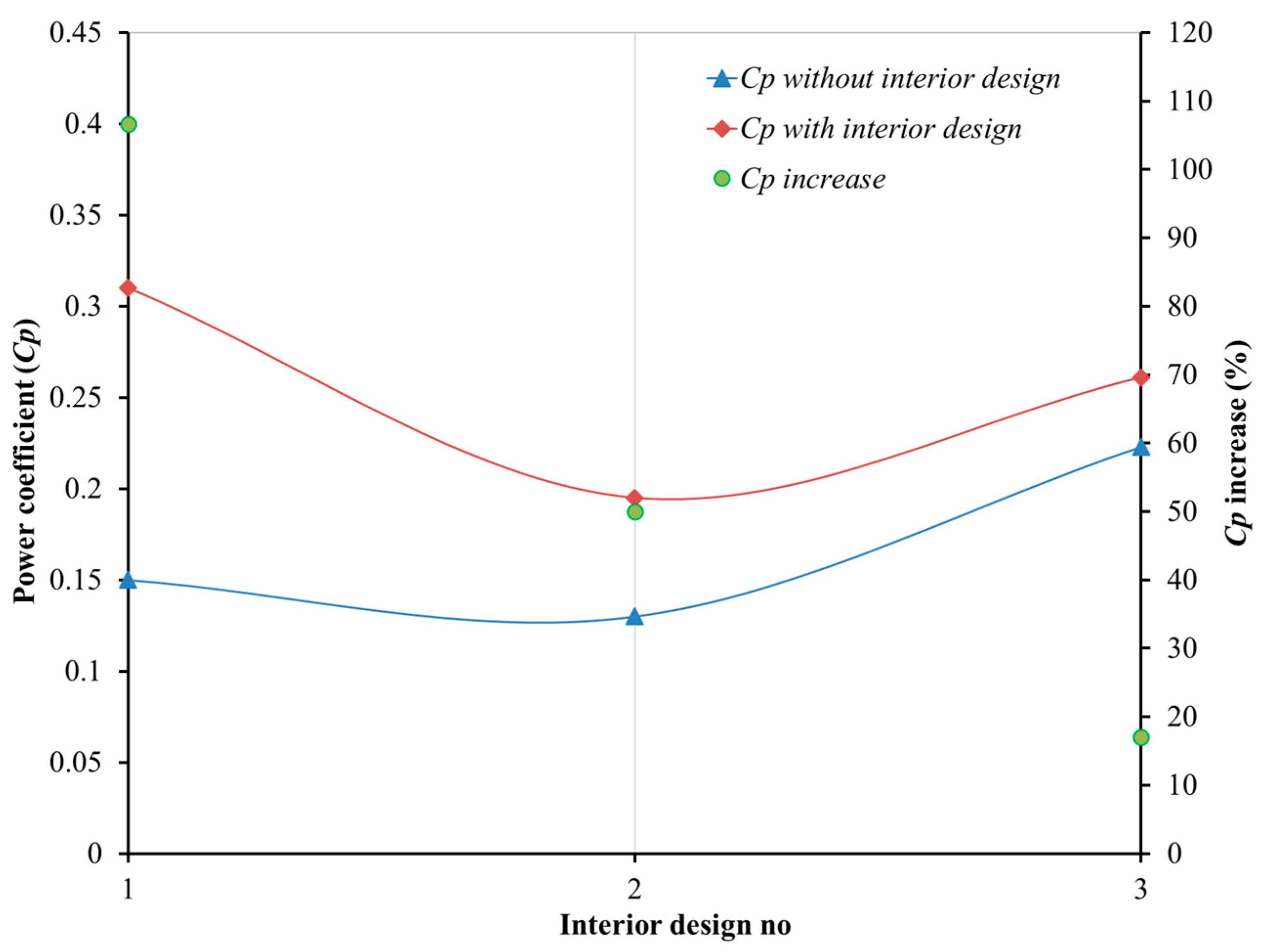
| 1 | Kamoji et al. [65] | Experimental | Overlap ratio = 0 Aspect ratio = 0.7 Blade arc angle = 124° Blade shape factor (p/q) = 0.2 End plate ratio = 1.1 | 0.175 | 0.210 |
| 2 | Akwa et al. [66] | Validated numerical | Overlap ratio (0–0.6) Overlap ratio = 0.15 | 0.200 | 0.316 |
| 3 | Nasef et al. [64] | Experimental Numerical | Overlap ratios; 0, 0.15, 0.2, 0.3, 0.5 (Max. Overlap ratio = 0.15) | 0.170 | 0.210 |
| 4 | Mohammadi et al. [67] | Validated numerical Optimization Genetic algorithm Artificial neural network | Overlap ratio = 0.159 Aspect ratio = 0.89 | 0.196 | 0.222 |
| I.d. No | Reference | Study Type | Design Remarks | Cp without i.d. | Cp with i.d. |
|---|---|---|---|---|---|
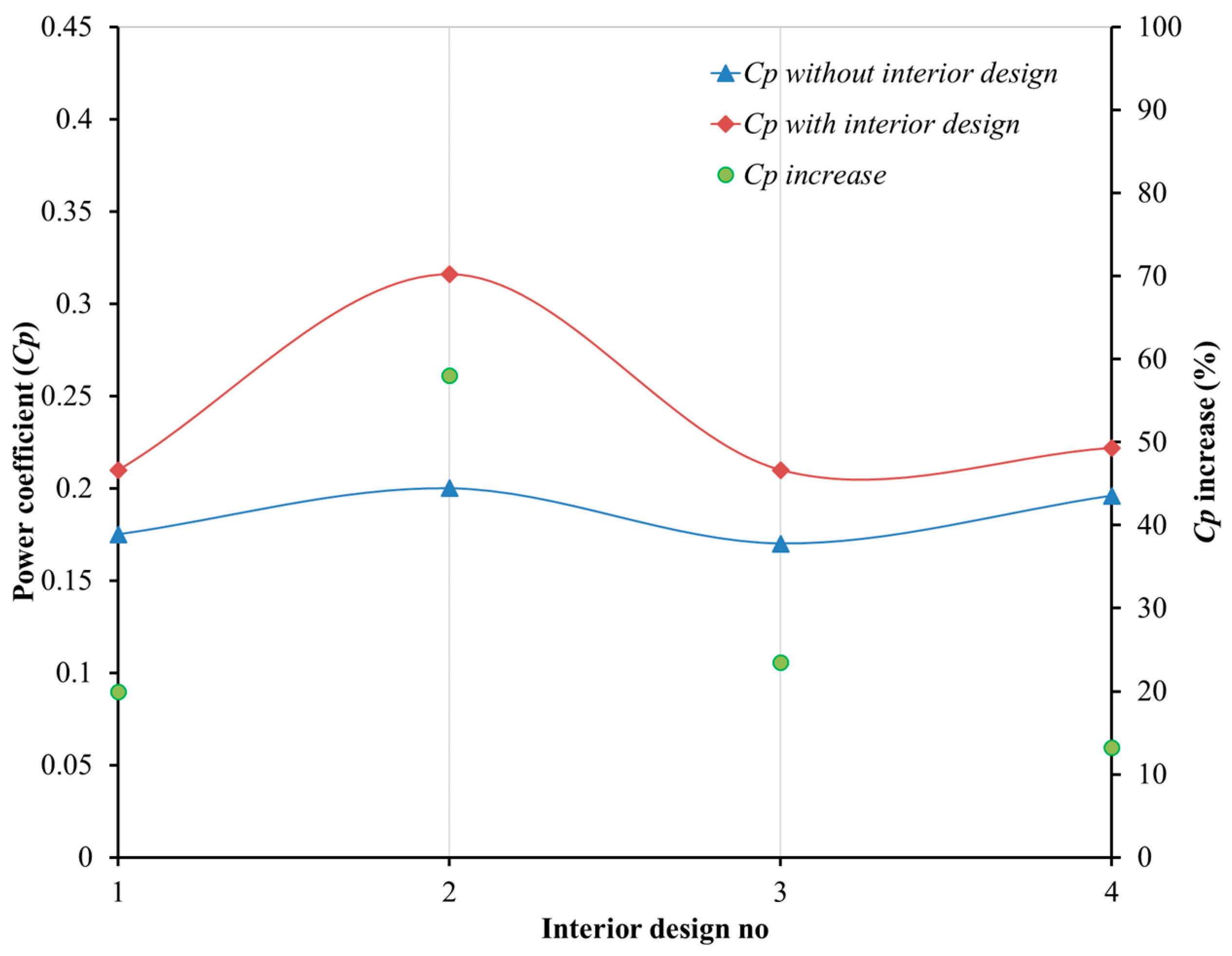
| 1 | Jeon et al. [70] | Experimental | Helical Savonius | 0.060 | 0.082 |
| 2 | Premkumar et al. [72] | Experimental | Helical Savonius | 0.042 | 0.054 |
| 3 | Goodarzi and Salimi [73] | Validated numerical | Conventional Savonius Quarter-spherical end-plate, Semi-circular end-plate, Circular end-plate | 0.047 | 0.163 |
| I.d. No | Reference | Study Type | Design Remarks | Cp without i.d. | Cp with i.d. |
|---|---|---|---|---|---|
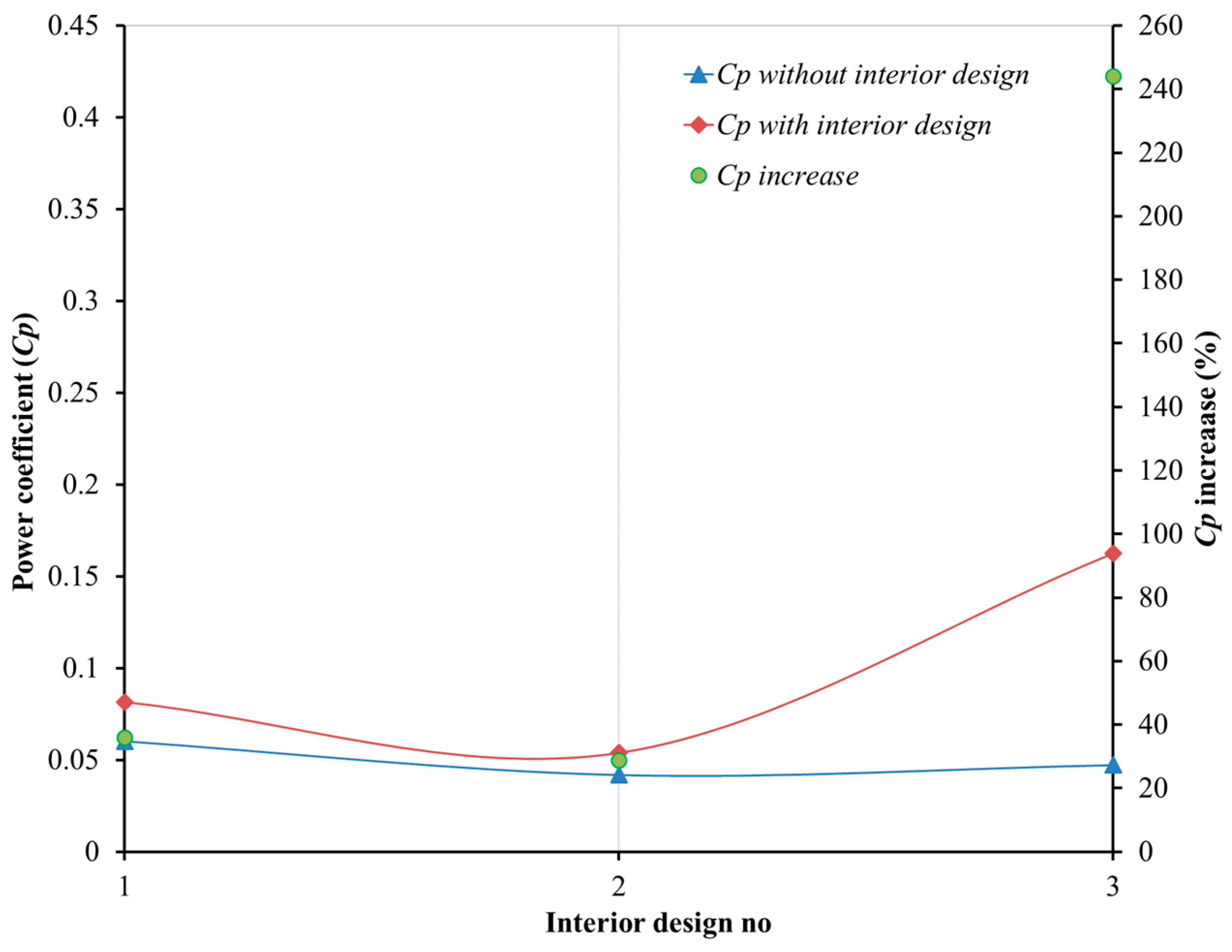
| 1 | Saha et al. [79] | Experimental | Single-, two- and three-stage (max. two-stage) Semicircular and twisted blade (max. twisted blade) Two and three bladed (max. two-bladed) | 0.150 | 0.310 |
| 2 | Mrigua et al. [80] | Numerical | Elliptical-bladed multistage (one, two, three-stage) (max. two-stage) | 0.130 | 0.195 |
| 3 | Saad et al. [81] | Numerical | Multi-stage turbines with twisted blades (a) single-stage, (b) two-stage, (c) three-stage, (d) four-stage (max. four-stage) | 0.223 | 0.261 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deda Altan, B.; Gultekin, G.S. Investigation of Performance Enhancements of Savonius Wind Turbines through Additional Designs. Processes 2023, 11, 1473. https://doi.org/10.3390/pr11051473
Deda Altan B, Gultekin GS. Investigation of Performance Enhancements of Savonius Wind Turbines through Additional Designs. Processes. 2023; 11(5):1473. https://doi.org/10.3390/pr11051473
Chicago/Turabian StyleDeda Altan, Burcin, and Gursel Seha Gultekin. 2023. "Investigation of Performance Enhancements of Savonius Wind Turbines through Additional Designs" Processes 11, no. 5: 1473. https://doi.org/10.3390/pr11051473






