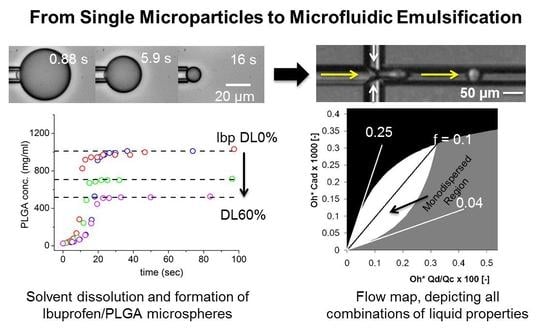
From Single Microparticles to Microfluidic Emulsification: Fundamental Properties (Solubility, Density, Phase Separation) from Micropipette Manipulation of Solvent, Drug and Polymer Microspheres
Abstract
:1. Introduction
1.1. The Micropipette Technique
1.2. Microfluidics
1.3. Ibuprofen Formulations
1.4. The Main Aims of This Work
2. Materials and Methods
2.1. Materials
2.2. Preparation and Recrystallization of Ibuprofen H
2.3. Thermal Characterization of Ibuprofen
2.4. The Micropipette Technique
2.5. Microdroplet Dissolution: Calculation of Diffusion Coefficient of Solvent or Drug in the Aqueous Phase
2.6. Formation and Investigation of Microdroplets/Microparticles
2.6.1. Preparation of Samples
2.6.2. Solvent Microdroplet Formation and Dissolution
2.6.3. Polymer Microsphere and Polymer Microsphere-Drug Formation
2.6.4. Formation and Dissolution of Pure Ibuprofen Microdroplets
2.7. Microfluidic Emulsification for PLGA Microsphere Production
2.7.1. Single Channel System
2.7.2. Multichannel System
3. Results and Discussion
3.1. Solvent Droplet-Dissolution
3.2. PLGA Microsphere Formation in PBS
3.3. Ibuprofen Encapsulation in PLGA Microparticles
3.4. Ibuprofen Phase-Separation from DCM/PLGA
3.5. New Measure of Ibp Diffusion Coefficient and Dissolution Time from DCM/Ibp Microparticle Dissolution into PBS
3.6. Ibuprofen Dissolution into a Micellar Sink
3.7. Micromanipulation and DSC Showed That Ibp Microparticles Are Possibly Supercooled Liquids
3.8. Microfluidic Single Channel Scale-Up
3.9. Multichannel Microfluidic Scale-Up
4. Summary and Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kinoshita, K.; Parra, E.; Needham, D. New sensitive micro-measurements of dynamic surface tension and diffusion coefficients: Validated and tested for the adsorption of 1-octanol at a microscopic air-water interface and its dissolution into water. J. Colloid Interface Sci. 2017, 488, 166–179. [Google Scholar] [CrossRef] [PubMed]
- Duncan, P.B.; Needham, D. Test of the epstein-plesset model for gas microparticle dissolution in aqueous media: Effect of surface tension and gas undersaturation in solution. Langmuir 2004, 20, 2567–2578. [Google Scholar] [CrossRef] [PubMed]
- Rickard, D.L.; Brent, D.; David, N. Hydration potential of lysozyme: Protein dehydration using a single microparticle technique. Biophys. J. 2010, 1075–1084. [Google Scholar] [CrossRef] [PubMed]
- Su, J.T.; Duncan, P.B.; Momaya, A.; Jutila, A.; Needham, D. The effects of hydrogen bonding on the diffusion of water in n-alkanes and n-alcohols measured with a novel single microdroplet method. J. Chem. Phys. 2010, 132, 044506. [Google Scholar] [CrossRef] [PubMed]
- De Bruijn, R.; Van Der Schaaf, J.; Narendra, P.; Schouten, J.C. Process for Preparing Monodispersed Emulsions. US20110165311 A1, 25 March 2010. [Google Scholar]
- Hochmuth, R.M.; Worthy, P.R.; Evans, E.A. Red-cell extensional recovery and the determination of membrane viscosity. Biophys. J. 1979, 26, 101–114. [Google Scholar] [CrossRef]
- Bagatolli, L.A.; Needham, D. Quantitative optical microscopy and micromanipulation studies on the lipid bilayer membranes of giant unilamellar vesicles. Chem. Phys. Lipids 2014, 181, 99–120. [Google Scholar] [CrossRef] [PubMed]
- Needham, D.; Zhelev, D. The mechanochemistry of lipid vesicles examined by micropipet manipulation techniques. In Vesicles; Rosoff, M., Ed.; Marcell Dekker: New York, NY, USA, 1996; Volume 62, p. 373. [Google Scholar]
- Needham, D.; Zhelev, D. Use of micropipet manipulation techniques to measure the properties of giant lipid vesicles. In Giant Vesicles; Luisi, P.L., Walde, P., Eds.; John Wiley & Sons Ltd.: Chichester, UK, 2000; pp. 103–147. [Google Scholar]
- Parra, E.; Needham, D. Mechanic assays based on micropipette aspiration. In The Giant Vesicle Book; Dimova, R., Marques, C., Eds.; CRC Taylor & Francis: Boca Raton, FL, USA, 2016; in press. [Google Scholar]
- Mitchison, J.; Swann, M. The mechanical properties of the cell surface I. The cell elastimeter. J. Exp. Biol. 1954, 31, 443–460. [Google Scholar]
- Mitchison, J.; Swann, M. The mechanical properties of the cell surface iii. The sea-urchin egg from fertilization to cleavage. J. Exp. Biol. 1955, 32, 734–750. [Google Scholar]
- Rand, R.; Burton, A. Mechanical properties of the red cell membrane: I. Membrane stiffness and intracellular pressure. Biophys. J. 1964, 4, 115. [Google Scholar] [CrossRef]
- Evans, E.; Skalak, R. Mechanics and Thermodynamics Biomembranes; CRC Press: Boca Raton, FL, USA, 1980. [Google Scholar]
- Evans, E.; Hochmuth, R.M. Mechanochemical properties of membranes. In Current topics in Membranes and Transport; Bonner, F., Kleinzeller, A., Eds.; Academic Press: New York, NY, USA, 1978; Volume 10, p. 1. [Google Scholar]
- Meiselman, H.J.; Lichtman, M.A.; LaCelle, P.L. White cell mechanics: Basic science and clinical aspects. In Proceedings of the a symposium held at the Kroc Foundation, Santa Ynez Valley, CA, USA, 12–16 September 1984.
- Tran-Son-Tay, R.; Needham, D.; Yeung, A.; Hochmuth, R.M. Time-dependent recovery of passive neutrophils after large deformation. Biophys. J. 1991, 60, 856–866. [Google Scholar] [CrossRef]
- Needham, D.; McIntosh, T.; Evans, E. Thermomechanical and transition properties of dimyristoylphosphatidylcholine/cholesterol bilayers. Biochemistry 1988, 27, 4668–4673. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Kwok, R. Mechanical calorimetry of large dimyristoylphosphatidylcholine vesicles in the phase transition region. Biochemistry 1982, 21, 4874–4879. [Google Scholar] [CrossRef] [PubMed]
- Kwok, R.; Evans, E. Thermoelasticity of large lecithin bilayer vesicles. Biophys. J. 1981, 35, 637–652. [Google Scholar] [CrossRef]
- Evans, E.; Needham, D. Physical-properties of surfactant bilayer-membranes—Thermal transitions, elasticity, rigidity, cohesion, and colloidal interactions. J. Phys. Chem. 1987, 91, 4219–4228. [Google Scholar] [CrossRef]
- Evans, E.; Rawicz, W.; Smith, B.A. Back to the future: Mechanics and thermodynamics of lipid biomembranes. Faraday Discuss 2013, 161, 591–611. [Google Scholar] [CrossRef] [PubMed]
- Kiser, P.F.; Wilson, G.; Needham, D. A synthetic mimic of the secretory granule for drug delivery. Nature 1998, 394, 459–462. [Google Scholar] [PubMed]
- Kiser, P.F.; Wilson, G.; Needham, D. Lipid-coated microgels for the triggered release of doxorubicin. J. Control. Release 2000, 68, 9–22. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D.H.; Needham, D. Equilibrium and dynamic interfacial tension measurements at microscopic interfaces using a micropipet technique. 2. Dynamics of phospholipid monolayer formation and equilibrium tensions at the water-air interface. Langmuir 2001, 17, 5544–5550. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D.H.; Needham, D. Equilibrium and dynamic interfacial tension measurements at microscopic interfaces using a micropipet technique. 1. A new method for determination of interfacial tension. Langmuir 2001, 17, 5537–5543. [Google Scholar] [CrossRef]
- Duncan, P.B.; Needham, D. Microdroplet dissolution into a second-phase solvent using a micropipet technique: Test of the epstein-plesset model for an aniline-water system. Langmuir 2006, 22, 4190–4197. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.; Plackett, D.; Needham, D.; Burt, H.M. Plga and phbv microsphere formulations and solid-state characterization: Possible implications for local delivery of fusidic acid for the treatment and prevention of orthopaedic infections. Pharm. Res. 2009, 26, 1644–1656. [Google Scholar] [CrossRef] [PubMed]
- Gilchrist, S.E.; Rickard, D.L.; Letchford, K.; Needham, D.; Burt, H.M. Phase separation behavior of fusidic acid and rifampicin in plga microspheres. Mol. Pharm. 2012, 9, 1489–1501. [Google Scholar] [CrossRef] [PubMed]
- Su, J.T.; Needham, D. Mass transfer in the dissolution of a multicomponent liquid droplet in an immiscible liquid environment. Langmuir 2013, 29, 13339–13345. [Google Scholar] [CrossRef] [PubMed]
- Gaul, D.A.; Rickard, D.L.; Needham, D. Microglassificationtm: A novel technique for protein dehydration. J. Pharm. Sci. 2014, 103, 810–820. [Google Scholar]
- Kinoshita, K.; Parra, E.; Utoft, A.; Needham, D. Saturation and supersaturation measurement of hydrophobic solute with micropipette manipulation technique. In Proceedings of the 29th Conference of the European Colloid and Interface Society, Bordeaux, France, 4–9 September 2015.
- Bitterfield, D.; Anders, U.; Needham, D. Dissolution rates of solute-containing microdroplets: An activity-based dissolution model. Langmuir 2016, in press. [Google Scholar] [CrossRef] [PubMed]
- Kinoshita, K.; Parra, E.; Utoft1, A.; Hussein, A.; Muala, T.; Mohamud, H.; Walke, P.; Needham, D. New single microparticle technique for forming and characterizing polymer microsphere-drug encapsulation and dissolution: Initial tests for ibuprofen-PLGA-DCM. In Presented at Annual Meeting & Exposition of the Controlled Release Society, Seattle, WA, USA, 17–20 July 2016.
- Parra, E.; Hervella, P.; Needham, D. Real-time visualization of the precipitation and phase behavior of octaethylporphyrin in lipid microparticles. J. Pharm. Sci. 2016, in press. [Google Scholar]
- Kinoshita, K.; Parra, E.; Needham, D. Saturation and supersaturation measurement of cholesterol and cholesteryl ester with micropipette manipulation technique. Langmuir 2016, in press. [Google Scholar]
- Parra, E.; Kinoshita, K.; Needham, D. Micropipette technique study of natural and synthetic lung surfactants at the air-water interface: Presence of a sp-b analog peptide promotes membrane aggregation, formation of tightly stacked lamellae, and growth of myelin figures. Langmuir 2016, 32, 10570–10581. [Google Scholar] [CrossRef] [PubMed]
- Yeung, A.; Dabros, T.; Masliyah, J.; Czarnecki, J. Micropipette: A new technique in emulsion research. Coll. Surf. A Physicochem. Eng. Asp. 2000, 174, 169–181. [Google Scholar] [CrossRef]
- Thorssen, T.; Roberts, R.W.; Arnold, F.H.; Quake, S.R. Dynamic pattern formation in a vesicle-generating microfluidic device. Phys. Rev. Lett. 2001, 86, 4163–4166. [Google Scholar] [CrossRef] [PubMed]
- Herrero-Vanrell, R.; Bravo-Osuna, I.; Andrés-Guerrero, V.; Vicario-de-la-Torre, M.; Molina-Martínez, I.T. The potential of using biodegradable microspheres in retinal diseases and other intraocular pathologies. Prog. Retin. Eye Res. 2014, 42, 27–43. [Google Scholar] [CrossRef] [PubMed]
- Okada, H. One- and three-month release injectable microspheres of the lh-rh superagonist leuprorelin acetate. Adv. Drug Deliv. Rev. 1997, 28, 43–70. [Google Scholar] [CrossRef]
- Hirota, K.; Doty, A.C.; Ackermann, R.; Zhou, J.; Olsen, K.F.; Feng, M.R.; Wang, Y.; Choi, S.; Qu, W.; Schwendeman, A.S.; et al. Characterizing release mechanisms of leuprolide acetate-loaded plga microspheres for ivivc development i: In vitro evaluation. J. Control. Release 2016. [Google Scholar] [CrossRef] [PubMed]
- Uhrich, K.E.; Cannizzaro, S.M.; Langer, R.S.; Shakesheff, K.M. Polymeric systems for controlled drug release. Chem. Rev. 1999, 99, 3181–3198. [Google Scholar] [CrossRef] [PubMed]
- Davies, N.M. Clinical pharmacokinetics of ibuprofen-the first 30 years. Clin. Pharm. 1998, 34, 101–154. [Google Scholar] [CrossRef] [PubMed]
- Wiegand, T.J. Nonsteroidal Anti-Inflammatory Agent Toxicity. Available online: http://emedicine.medscape.com/article/816117-overview. (accessed on 30 November 2016).
- Bédouet, L.; Pascale, F.; Moine, L.; Wasse, M.; Ghegediban, S.H.; Nguyen, V.-N.; Bonneau, M.; Labarre, D.; Laurent, A. Intra-articular fate of degradable poly(ethyleneglycol)-hydrogel microspheres as carriers for sustained drug delivery. Int. J. Pharm. 2013, 456, 536–544. [Google Scholar] [CrossRef] [PubMed]
- Bedouet, L.; Moine, L.; Pascale, F.; Nguyen, V.N.; Labarre, D.; Laurent, A. Synthesis of hydrophilic intra-articular microspheres conjugated to ibuprofen and evaluation of anti-inflammatory activity on articular explants. Int. J. Pharm. 2014, 459, 51–61. [Google Scholar] [CrossRef] [PubMed]
- Bedouet, L.; Pascale, F.; Bonneau, M.; Laurent, A. In vitro evaluation of s-(+)-ibuprofen as drug candidate for intra-articular drug delivery system. Drug Dev. Ind. Pharm. 2015, 41, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Gerwin, N.; Hops, C.; Lucke, A. Intraarticular drug delivery in osteoarthritis. Drug Deliv. Degener. Jt. Dis. 2006, 58, 226–242. [Google Scholar]
- Larsen, C.; Østergaard, J.; Larsen, S.W.; Jensen, H.; Jacobsen, S.; Lindegaard, C.; Andersen, P.H. Intra-articular depot formulation principles: Role in the management of postoperative pain and arthritic disorders. J. Pharm. Sci. 2008, 97, 4622–4654. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Carballido, A.; Herrero-Vanrell, R.; Molina-Martinez, I.T.; Pastoriza, P. Biodegradable ibuprofen-loaded plga microspheres for intraarticular administration. Effect of labrafil addition on release in vitro. Int. J. Pharm. 2004, 279, 33–41. [Google Scholar] [CrossRef] [PubMed]
- Bonelli, P.; Tuccillo, F.M.; Federico, A.; Napolitano, M.; Borrelli, A.; Melisi, D.; Rimoli, M.G.; Palaia, R.; Arra, C.; Carinci, F. Ibuprofen delivered by poly(lactic-co-glycolic acid) (plga) nanoparticles to human gastric cancer cells exerts antiproliferative activity at very low concentrations. Int. J. Nanomed. 2012, 7, 5683–5691. [Google Scholar] [CrossRef] [PubMed]
- Epstein, P.S.; Plesset, M.S. On the stability of gas bubbles in liquid-gas solutions. J. Chem. Phys. 1950, 18, 1505. [Google Scholar] [CrossRef]
- Dudognon, E.; Danede, F.; Descamps, M.; Correia, N.T. Evidence for a new crystalline phase of racemic ibuprofen. Pharm. Res. 2008, 25, 2853–2858. [Google Scholar] [CrossRef] [PubMed]
- Williams, P.A.; Hughes, C.E.; Harris, K.D.M. New insights into the preparation of the low-melting polymorph of racemic ibuprofen. Cryst. Growth Des. 2012, 12, 5839–5845. [Google Scholar] [CrossRef]
- Olbrich, K.C. Water Permeability and Mechanical Properties of Unsaturated Lipid Membranes and Sarcolemmal Vesicles; Duke University: Durham, NC, USA, 1997. [Google Scholar]
- Schneider, C.A.; Rasband, W.S.; Eliceiri, K.W. Nih image to imagej: 25 years of image analysis. Nat. Methods 2012, 9, 671–675. [Google Scholar] [CrossRef] [PubMed]
- Nunes, J.K.; Tsai, S.S.H.; Wan, J.; Stone, H.A. Dripping and jetting in microfluidic multiphase flows applied to particle and fibre synthesis. J. Phys. D Appl. Phys. 2013, 46, 114002–114021. [Google Scholar] [CrossRef] [PubMed]
- Christopher, G.F.; Anna, S.L. Microfluidic methods for generating continuous droplet streams. J. Phys. D Appl. Phys. 2007, 40, R319–R336. [Google Scholar] [CrossRef]
- Anna, S.L.; Bontoux, N.; Stone, H.A. Formation of dispersions using “flow focusing” in microchannels. Appl. Phys. Lett. 2003, 82, 364–366. [Google Scholar] [CrossRef]
- Dreyfus, R.; Tabeling, P.; Willaime, H. Ordered and disordered patterns in two-phase flows in microchannels. Phys. Rev. Lett. 2003, 90, 14505. [Google Scholar] [CrossRef] [PubMed]
- Utada, A.S.; Fernandez-Nieves, A.; Stone, H.A.; Weitz, D.A. Dripping to jetting transitions in coflowing liquid streams. Phys. Rev. Lett. 2007, 99, 094502. [Google Scholar] [CrossRef] [PubMed]
- Herrada, M.A.; Ganan-Calvo, A.M.; Guillot, P. Spatiotemporal instability of a confined capillary jet. Phys. Rev. E 2008, 78, 1398–1411. [Google Scholar] [CrossRef] [PubMed]
- Utada, A.S.; Lorenceau, E.; Link, D.R.; Kaplan, P.D.; Stone, H.A.; Weitz, D.A. Monodisperse double emulsions generated from a microcapillary device. Science 2005, 308, 537–541. [Google Scholar] [CrossRef] [PubMed]
- Nisisako, T.; Okushima, S.; Torii, T. Controlled formulation of monodisperse double emulsions in a multiple-phase microfluidic system. Soft Matter 2005, 1, 23–27. [Google Scholar] [CrossRef]
- Gu, H.; Duits, M.H.G.; Mugele, F. Droplets formation and merging in two-phase flow microfluidics. Int. J. Mol. Sci. 2011, 12, 2572–2597. [Google Scholar] [CrossRef] [PubMed]
- Martin-Banderas, L.; Flores-Mosquera, M.; Riesco-Chueca, P.; Rodriguez-Gil, A.; Cebolla, A.; Chavez, S.; Ganan-Calvo, A.M. Flow focusing: A versatile technology to produce size-controlled and specific-morphology microparticles. Small 2005, 1, 688–692. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.F.; Yue, P.T.; Feng, J.J. Formation of simple and compound drops in microfluidic devices. Phys. Fluids 2006, 18, 092105. [Google Scholar] [CrossRef]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977–1026. [Google Scholar] [CrossRef]
- Donahue, D.J.; Bartell, F.E. The boundary tension at water-organic liquid interfaces. J. Phys. Chem. 1952, 56, 480–484. [Google Scholar] [CrossRef]
- Lyman, W.J.; Reehl, W.F.R. Handbook of Chemical Property Estimation Methods: Environmental Behavior of Organic Compounds; American Chemical Society: Washington, DC, USA, 1990. [Google Scholar]
- Arnold, M.M.; Gonnan, E.M.; Schieber, L.J.; Munson, E.J.; Berkland, C. Nanocipro encapsulation in monodisperse large porous plga microparticles. J. Control. Release 2007, 121, 100–109. [Google Scholar] [CrossRef] [PubMed]
- Derrick, T.S.; McCord, E.F.; Larive, C.K. Analysis of protein/ligand interactions with nmr diffusion measurements: The importance of eliminating the protein background. J. Magn. Reson. 2002, 155, 217–225. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; de la Torre, T.Z.G.; Forsgren, J.; Bergstrom, C.A.S.; Stromme, M. Diffusion-controlled drug release from the mesoporous magnesium carbonate upsalite. J. Pharm. Sci. 2016, 105, 657–663. [Google Scholar] [CrossRef] [PubMed]
- Rangel-Yagui, C.O.; Hsu, H.W.L.; Pessoa, A., Jr.; Tavares, L.C. Micellar solubilization of ibuprofen—Influence of surfactant head groups on the extent of solubilization. Rev. Bras. Ciênc. Farm. 2005, 41, 237–246. [Google Scholar] [CrossRef]
- Shaw, L.R.; Irwin, W.J.; Grattan, T.J.; Conway, B.R. The effect of selected water-soluble excipients on the dissolution of paracetamol and ibuprofen. Drug Dev. Ind. Pharm. 2005, 31, 515–525. [Google Scholar] [CrossRef] [PubMed]
- Rangel-Yagui, C.O.; Pessoa, A.; Tavares, L.C. Micellar solubilization of drugs. J. Pharm. Pharm. Sci. 2005, 8, 147–163. [Google Scholar] [PubMed]
- Stephenson, B.C.; Rangel-Yagui, C.O.; Pessoa, A.; Tavares, L.C.; Beers, K.; Blankschtein, D. Experimental and theoretical investigation of the micellar-assisted solubilization of ibuprofen in aqueous media. Langmuir 2006, 22, 1514–1525. [Google Scholar] [CrossRef] [PubMed]
- Ridell, A.; Evertsson, H.; Nilsson, S.; Sundelöf, L.O. Amphiphilic association of ibuprofen and two nonionic cellulose derivatives in aqueous solution. J. Pharm. Sci. 1999, 88, 1175–1181. [Google Scholar] [CrossRef] [PubMed]
- Rub, M.A.; Azum, N.; Kumar, D.; Asiri, A.M.; Marwani, H.M. Micellization and microstructural studies between amphiphilic drug ibuprofen with non-ionic surfactant in aqueous urea solution. J. Chem. Thermodyn. 2014, 74, 91–102. [Google Scholar] [CrossRef]
- Prakash, P.; Sayyed-Ahmad, A.; Zhou, Y.; Volk, D.E.; Gorenstein, D.G.; Dial, E.; Lichtenberger, L.M.; Gorfe, A.A. Aggregation behavior of ibuprofen, cholic acid and dodecylphosphocholine micelles. Biochim. Biophys. Acta 2012, 1818, 3040–3047. [Google Scholar] [CrossRef] [PubMed]
- Bras, A.R.; Noronha, J.P.; Antunes, A.M.M.; Cardoso, M.M.; Schonhals, A.; Affouard, F.; Dionisio, M.; Correia, N.T. Molecular motions in amorphous ibuprofen as studied by broadband dielectric spectroscopy. J. Phys. Chem. B 2008, 112, 11087–11099. [Google Scholar] [CrossRef] [PubMed]
- Johari, G.P.; Kim, S.; Shanker, R.M. Dielectric relaxation and crystallization of ultraviscous melt and glassy states of aspirin, ibuprofen, progesterone, and quinidine. J. Pharm. Sci. 2007, 96, 1159–1175. [Google Scholar] [CrossRef] [PubMed]
- Descamps, M.; Dudognon, E. Crystallization from the amorphous state: Nucleation-growth decoupling, polymorphism interplay, and the role of interfaces. J. Pharm. Sci. 2014, 103, 2615–2628. [Google Scholar] [CrossRef] [PubMed]
















© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kinoshita, K.; Parra, E.; Hussein, A.; Utoft, A.; Walke, P.; De Bruijn, R.; Needham, D. From Single Microparticles to Microfluidic Emulsification: Fundamental Properties (Solubility, Density, Phase Separation) from Micropipette Manipulation of Solvent, Drug and Polymer Microspheres. Processes 2016, 4, 49. https://doi.org/10.3390/pr4040049
Kinoshita K, Parra E, Hussein A, Utoft A, Walke P, De Bruijn R, Needham D. From Single Microparticles to Microfluidic Emulsification: Fundamental Properties (Solubility, Density, Phase Separation) from Micropipette Manipulation of Solvent, Drug and Polymer Microspheres. Processes. 2016; 4(4):49. https://doi.org/10.3390/pr4040049
Chicago/Turabian StyleKinoshita, Koji, Elisa Parra, Abdirazak Hussein, Anders Utoft, Prasad Walke, Robin De Bruijn, and David Needham. 2016. "From Single Microparticles to Microfluidic Emulsification: Fundamental Properties (Solubility, Density, Phase Separation) from Micropipette Manipulation of Solvent, Drug and Polymer Microspheres" Processes 4, no. 4: 49. https://doi.org/10.3390/pr4040049
APA StyleKinoshita, K., Parra, E., Hussein, A., Utoft, A., Walke, P., De Bruijn, R., & Needham, D. (2016). From Single Microparticles to Microfluidic Emulsification: Fundamental Properties (Solubility, Density, Phase Separation) from Micropipette Manipulation of Solvent, Drug and Polymer Microspheres. Processes, 4(4), 49. https://doi.org/10.3390/pr4040049