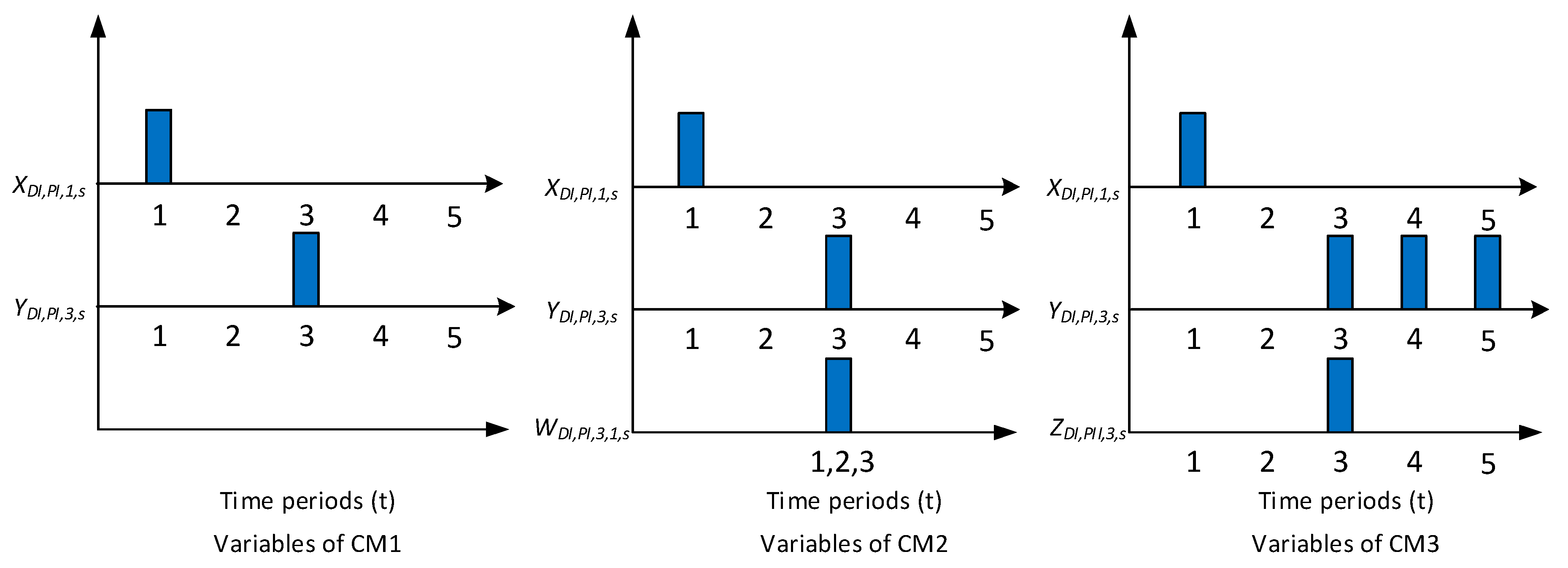1. Introduction
Pharmaceutical industry is a global business with over one trillion U.S. dollars per year market with extensive supply chains throughout the world [
1]. A potential drug identified at discovery stage has to go through pre-clinical testing, generally laboratory and animal model studies, before applying for approval by regulatory bodies, such as The Food and Drug Administration (FDA) in USA. The goal of these laboratory and animal model studies is to understand how the drug works and assess its safety. The potential drugs that successfully complete pre-clinical trials enter clinical trial phase. Clinical trials aim to demonstrate the safety and efficacy of the potential drug and are designed with and carried out under strict guidelines and supervision of regulatory bodies. If a drug successfully completes the clinical trials and is approved by the regulatory bodies, the drug is manufactured and distributed to the market. Pharmaceutical manufacturers are under pressure to improve the efficiency of the pharmaceutical R&D pipeline, partially because the patent protections of a number of significant brand-name drugs will soon expire [
2].
Scheduling and planning of clinical trials is one of the efficient ways to reduce the cost of developing new drugs. There are three phases in clinical trials. The goal of Phase I clinical trials is to assess the safety and dosage of the drug and to understand how it is metabolized in the body. The lengths of Phase I clinical trials are several months. Approximately 70% of drugs will move to the next phase. Phase II clinical trials are used to evaluate the drug’s effectiveness and short-term side effects on a limited number of target patient volunteers. Phase II may take from several months to two years. Approximately 33% of drugs pass Phase II clinical trials and move to the next stage. Phase III clinical trials aim to assess the benefit-risk ratio of the drug using a large number of target patient volunteers (in the order of thousands). Phase III takes one to four years to complete and approximately 25–30% of drugs pass Phase III [
3,
4]. Clinical trial planning is complicated due to its highly stochastic nature: pharmaceutical companies do not know which drugs will successfully complete clinical trials
a priori. The outcomes of clinical trials significantly influence drug development plan, the investments and overall profits. Clinical trial planning is a series of trade-offs between maximizing expected economic returns and minimizing risk and maintaining a diverse portfolio of drugs under the limited drug development dollars available. The plan tries to accomplish these goals by selecting which potential drugs to push through the clinical trial pipeline and when to start the clinical trials of selected drugs. This is a challenging problem due to its strong combinatorial character and impact of uncertainty.
Stochastic programming is a framework for modeling optimization problems that involve uncertainty [
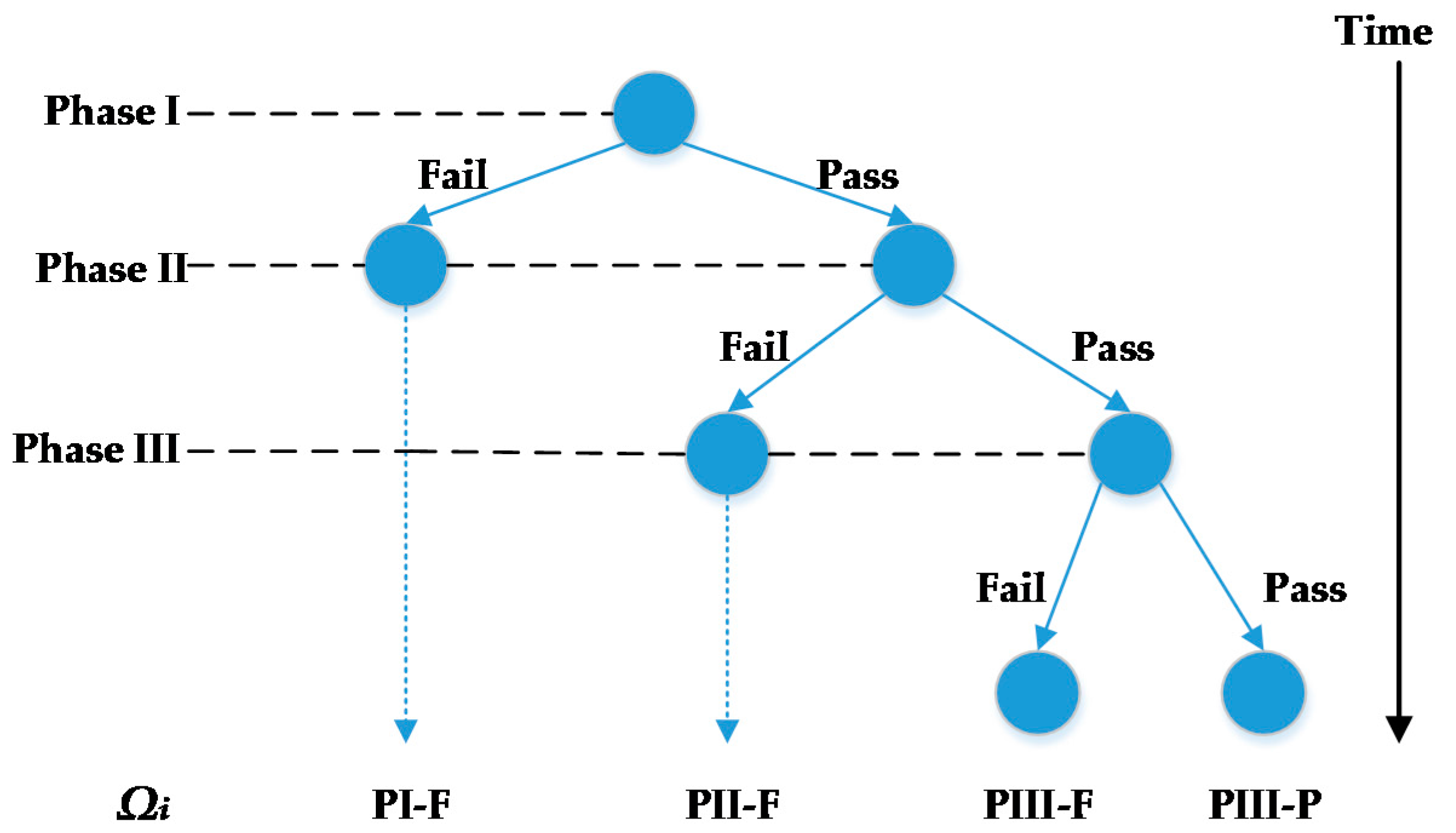
5]. Stochastic programming optimizes the expected value of the decisions over all possible realizations of uncertain parameters. A set of scenarios describes all possible realizations of uncertain parameters. In clinical trial planning problem, the uncertain parameter is the outcome of a clinical trial and it is an endogenous uncertain parameter because the decisions of whether or not and when to start clinical trials influence when the outcomes are realized. We assume that there are two discrete outcomes of a drug starting and completing a clinical trial: (1) the drug may successfully pass the clinical trial; or (2) the drug may fail the clinical trial. Because the outcomes are discrete, all combinations of possible realizations can be used to form a finite set of scenarios for the clinical trial planning problem. To consider recourse action in multiple stages after realizations of uncertainty, one of the widely used approaches employs multistage stochastic programming (MSSP). To avoid making decisions that anticipate the values of uncertain parameters that have not been realized, a set of constraints, called non-anticipativity constraints (NACs), are introduced to MSSPs.
Multistage stochastic programming is a scenario-based approach that considers recourse actions in multiple stages after realization of uncertainty. In the MSSP formulations of problems with endogenous uncertainty, decision variables are defined independently for each scenario. For formulations whose objective function and constraints are all linear and include integer variables, the deterministic equivalent of the MSSP can be constructed as a mixed-integer linear programming (MILP) model.
The general formulation of a MSSP with endogenous uncertainty can be written as follows:
where
are differentiable functions,
is the index for the set of scenario-specific constraints,
is the index for the set of discrete time periods,
is the index of the set of scenarios and
is the probability of scenario
. The variable
is the decision variable associated with endogenous uncertain parameter
at time
in scenario
. The variable
is recourse-action variable at time
(
) in scenario
. The objective is to minimize the expected value of
. Functions
define the scenario-specific constraints. At the first time period, the values of decision variables must be identical because all scenarios are indistinguishable (Equation (3)). The variable
is a Boolean variable, which indicates when scenarios s and s’ are indistinguishable. If
is True, then the decision variables and recourse actions for these scenarios should be identical (Equation (4)). The value of the Boolean variable depends on the decision variable values, as shown in Equation (5). If functions
are all linear, the deterministic equivalent of MSSP can be formulated as a MILP model.
There have been a number of studies that introduced stochastic programing models for solving pharmaceutical clinical trial planning problem. Here, we limit our review to the ones that explicitly incorporated the impact of clinical trial outcome uncertainty. Gatica et al. [
6] developed a model that integrates the production planning and investment strategy simultaneously in pharmaceutical industries considering the impact of uncertainty in the outcome of clinical trials. The case studies considered in the paper included only two phases of the clinical trials with three products yielding 64 scenarios. However, if all stages of clinical trials were considered, the size of the resulting model would have become prohibitively large and would require heuristic approaches to solve. Colvin and Maravelias [
7] developed a MSSP model for clinical trial planning and included the impact of endogenous clinical-trial outcome uncertainty. In a later study, they exploited the structure of the problem to reduce the number of scenarios and extended their model to account for resource planning by introducing outsourcing decisions [
8]. In Reference [
9], they introduced a number of theoretical properties, which reduce the problem size and tighten the formulation, and developed a novel branch and cut algorithm to solve the resulting problem efficiently. Sundaramoorthy et al. [
10] proposed a stochastic programming formulation that integrates the capacity planning and clinical trial planning and that takes into account uncertainty in the outcomes of clinical trials. The proposed formulation was solved for problems with a total of 256 scenarios in 1127 CPUs. The solution time increases significantly for problems with more than 256 scenarios.
Multistage stochastic programs and their deterministic equivalent forms quickly become computationally intractable because the number of scenarios and the corresponding decision trees grow exponentially as the number of uncertain parameters increases. Furthermore, for discrete-time MSSPs, the problem size increases rapidly especially in numbers of variables and NACs with increases in the length of the planning horizon. Thus, solving any large-scale MSSP model, especially with endogenous uncertainty, requires significant computational effort. Most recent work on MSSPs with endogenous uncertainty focuses on developing new algorithms or decomposition frameworks for solving these problems.
Solak et al. [
11] developed a sample average approximation (SAA) algorithm to solve the optimization problem of R&D project portfolio. The proposed algorithm approximates the MSSP formulation with smaller MSSPs constructed using a random sample of scenarios selected from the full set. For the case studies considered, the SAA algorithm obtained a solution within 3.4–8.3% of the optimal. Gupta and Grossmann [
12] proposed an improved lagrangean decomposition framework, which decomposed the original problem into individual scenario groups. For process synthesis and oilfield planning problems, the improved lagrangean decomposition framework obtained tighter bounds with fewer iterations. Christian and Cremaschi [
13] developed a knapsack-problem based decomposition algorithm (KDA) for solving pharmaceutical clinical trial planning problem. The KDA obtains feasible solutions by decomposing the original MSSP problem into a series of knapsack problems. Instead of characterizing all realizations as scenarios, the KDA generates knapsack problems at time periods when outcomes are realized. Solutions obtained by KDA were within three percent of the optimum for the case studies considered. Christian and Cremaschi [
14] presented a branch and bound algorithm to solve large-scale MSSPs with endogenous uncertainty. The algorithm generates dual bounds using progressive hedging (PH) and primal bounds using the KDA [
14]. Although the algorithm required considerable time to converge, it reduced the memory requirements considerably. Apap and Grossmann [
15] proposed a sequential scenario decomposition (SSD) approach for solving MSSPs with endogenous and exogenous uncertainties. The algorithm starts at the initial time period and selects one scenario from each exogenous scenario group. A sub-problem is constructed by removing all NACs associated with the exogenous uncertain parameters. The scenarios in the sub-problem are only connected by first-time period NACs and NACs associated with the endogenous uncertain parameter. The solution of the sub-problem is used to fix the variables of the original MSSP at first-time period. The algorithm repeats this process until the end of the planning horizon. At termination, all decisions are fixed in original MSSPs yielding a feasible solution. For the oilfield development planning problem [
15], the SSD solution was within 0.2% of the optimum.
Most of these algorithms decompose the original problem into smaller sub-problems to generate a feasible solution. No recent literature studied the impact of different decision variable definitions and corresponding sequencing and non-anticipativity constraints on the size and solution times of the resulting MSSP formulations constructed for clinical trial planning.
Motivated by the above, we propose two new MSSP formulations, CM1 and CM2, for pharmaceutical clinical trial planning problem. The first formulation, CM1, employs two decision variables, which separately track the start and end time points of clinical trials. The second formulation, CM2, introduces an additional binary variable, which tracks both start and end time points of a clinical trial. We applied both formulations to solve 42 instances of clinical trial planning problem [
16]. For comparison, all instances were also solved using the MSSP formulation of [
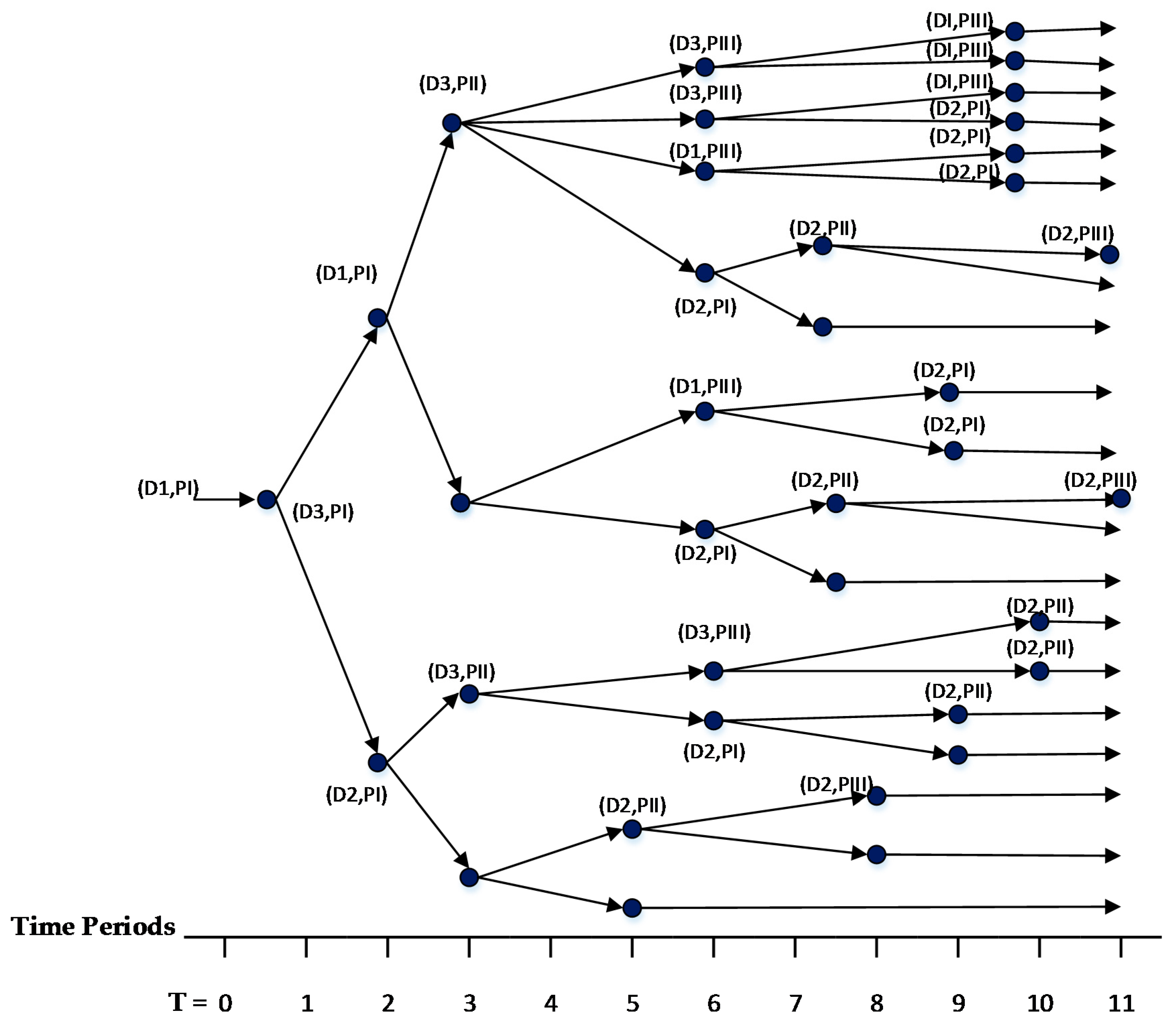
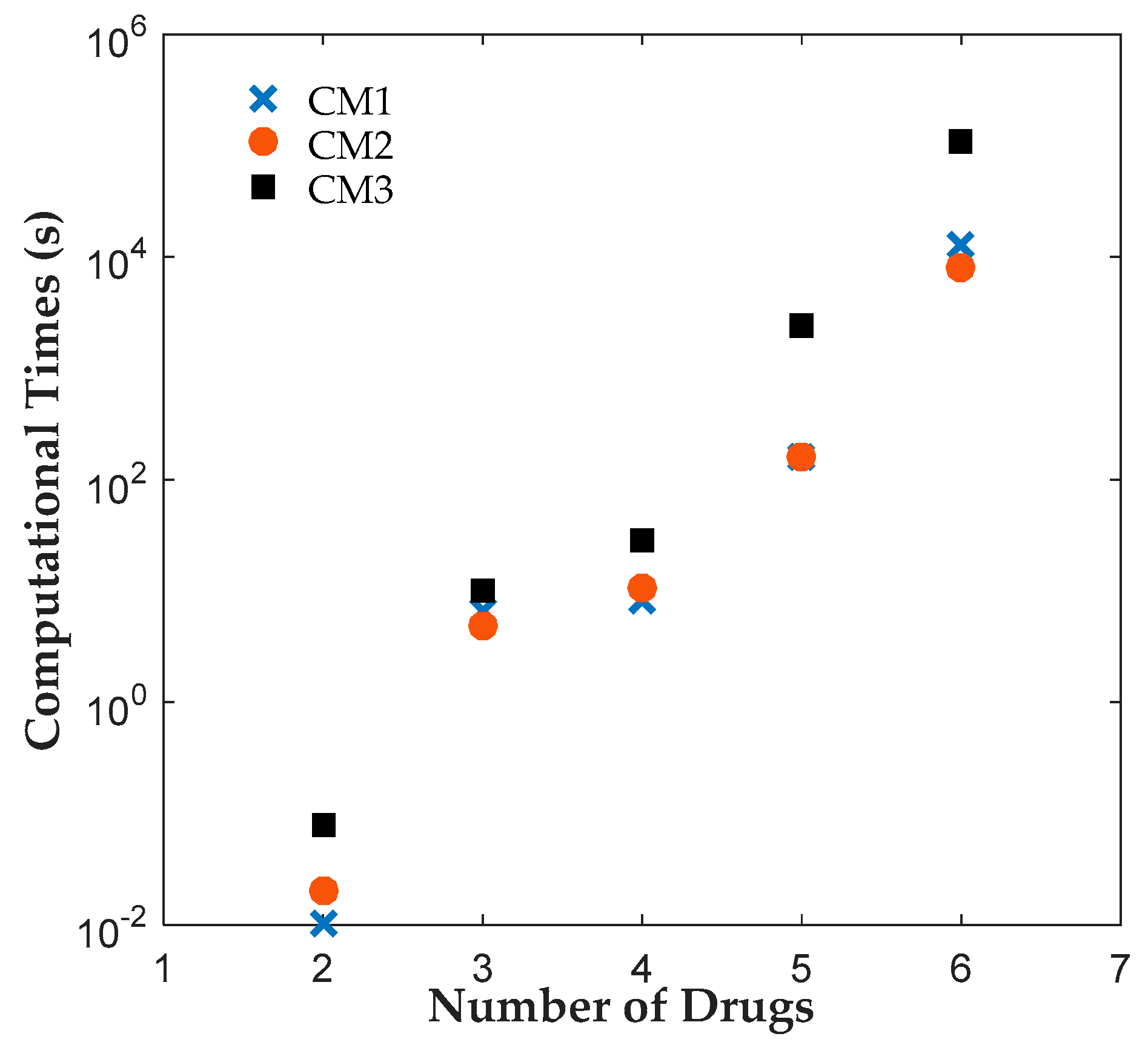
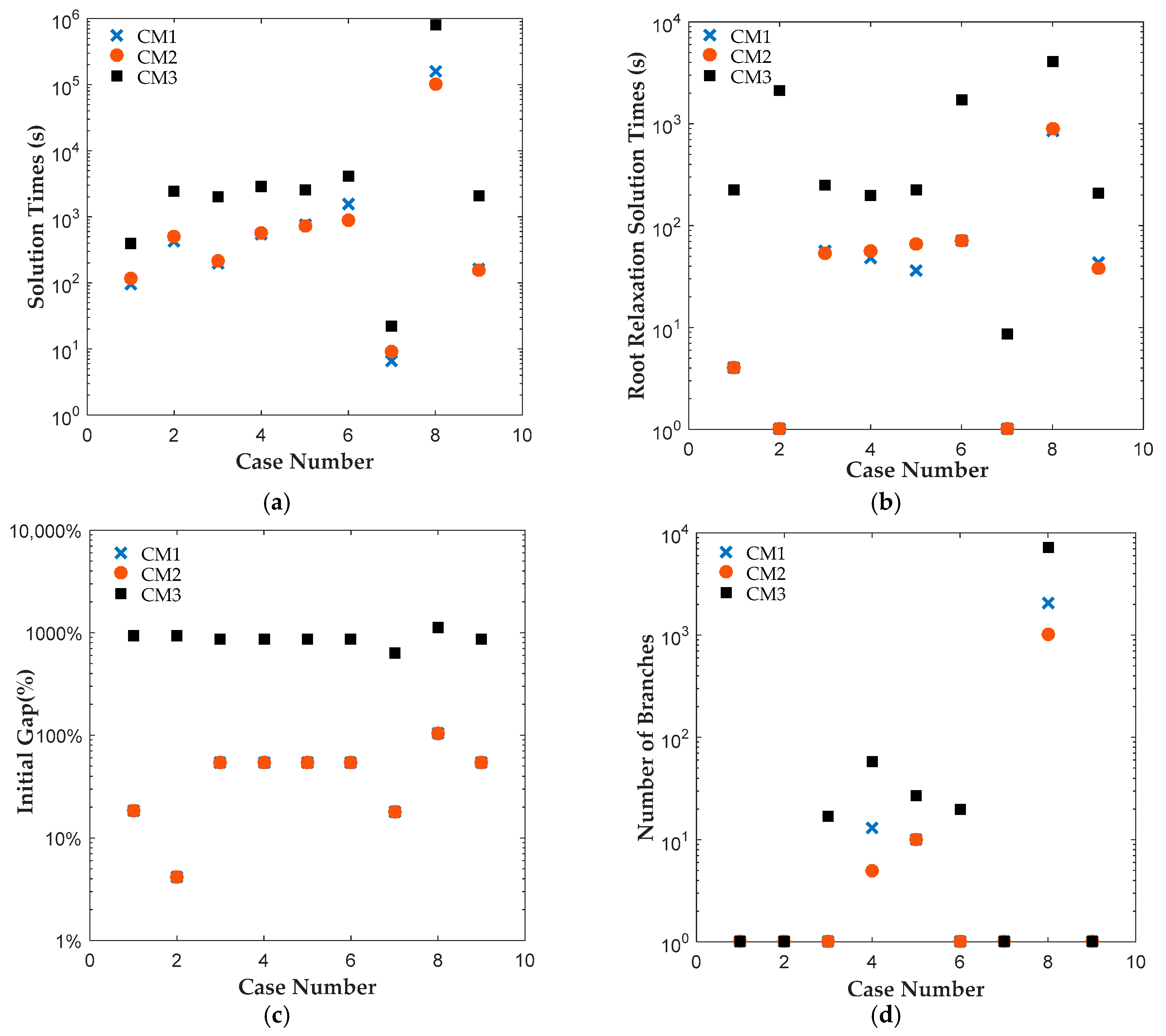
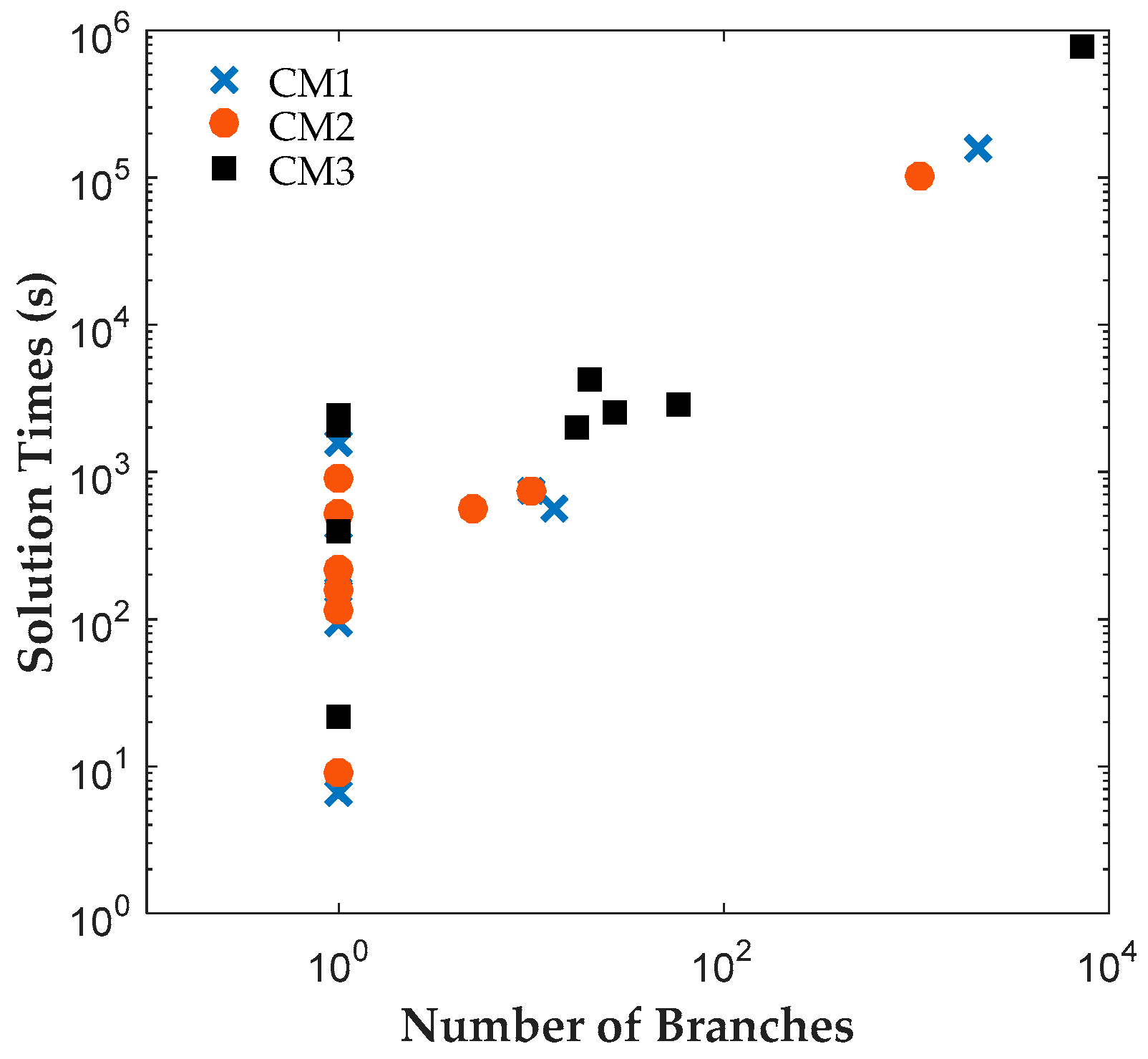
7], which will be referred to as CM3 here. All instances were solved to 0.1% optimality gap using ILOG CPLEX Optimization Studio (Version 12.6.3.0, IBM, Armonk, NY, USA). The results reveal that CM1 and CM2 were consistently solved up to two orders of magnitude faster than CM3 for all cases. A closer look at the branching trees indicates that the optimum was obtained with fewer branches for CM1 or CM2 than CM3.
Section 2 gives the clinical trial planning problem statement. New MSSP formulations are presented in
Section 3.
Section 4 summarizes and discusses the results of the computational studies. Conclusion are summarized in
Section 5.
5. Conclusions
This paper presented two new MSSP formulations, CM1 and CM2, for pharmaceutical clinical trial planning problems. The first formulation, CM1, uses two binary variables to track the beginning and the end of clinical trials. The second formulation, CM2, introduces an additional binary variable that tracks both the beginning and the end of clinical trials. We compare the sizes and solution times of CM1 and CM2 to each other and to CM3, an MSSP presented in [
7] for clinical trial planning problem, for different instances.
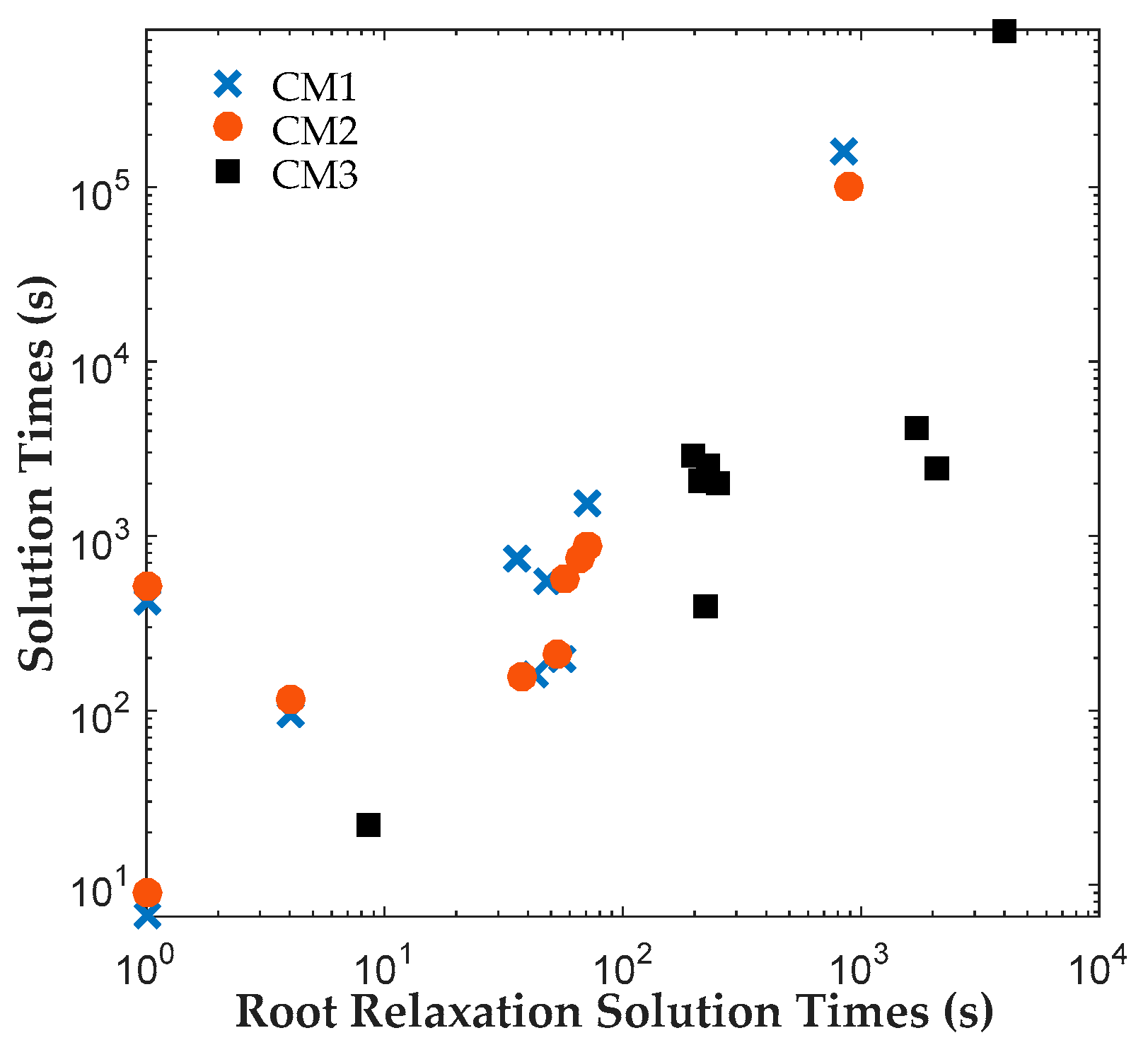
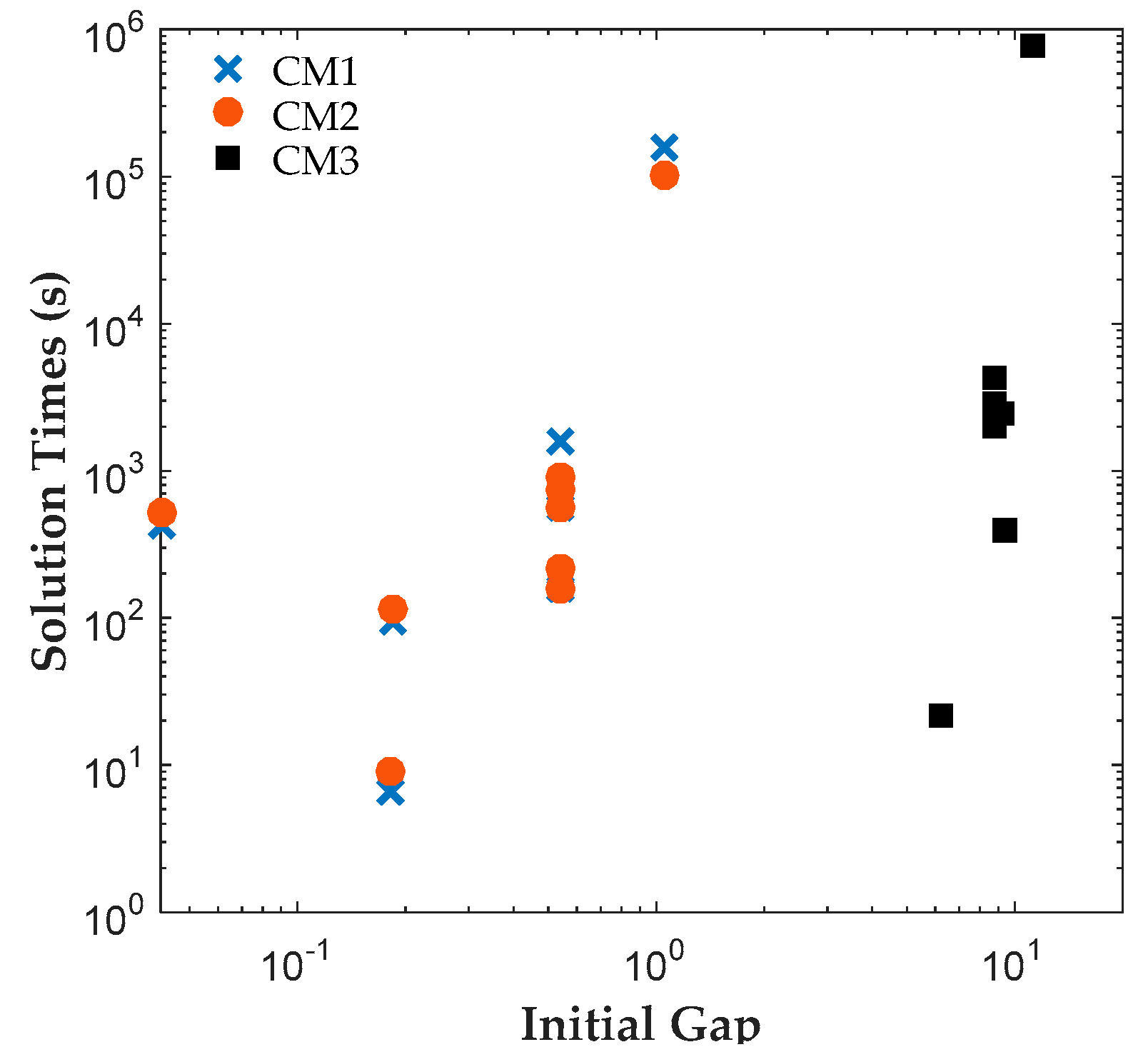
The results reveal that both CM1 and CM2 provide tighter formulations than CM3 and are solved faster by ILOG CPLEX Optimization Studio. The proposed binary variables in CM1 and CM2 contribute to shorter root relaxation solution times and generate much tighter initial gaps. It is worth noting that for all formulations, most problems were solved at the root node. For instances with branches, CM1 and CM2 consistently required fewer branches than CM3, which suggest that the binary variables in CM1 and CM2 provided ILOG CPLEX Optimization Studio a more efficient branching variable. The correlation coefficients between the solution time and root relaxation solution time, initial gap and number of branches, respectively, revealed that all three have strong positive relationship to solution times. When the root relaxation solution time, initial gap and number of branches of a case increase, so does its solution time. For all formulations, the correlations suggest that the root relaxation solution time and number of branches have stronger impact on solution time than the initial gap. We also investigated the sensitivity of solution times and problem sizes to the parameters of the clinical trial planning problem. The results revealed that the resource constraints and length of planning horizon contribute most to the computational complexity of this problem. It is worth noting that ILOG CPLEX Optimization Studio was not able to solve any of the formulations for a seven-drug case study. The future work will focus on developing decomposition approaches to generate valid upper and lower bounds quickly to solve large instances of the clinical trial planning problem.
In this paper, the outcomes of clinical trials of different drugs are assumed to be independent. This assumption may not be valid when the pipeline contains drugs that are being developed for treating similar conditions or that have similar formulations and characteristics. In such cases, the outcomes of the events for these drugs may not be independent, i.e., may be correlated. Then, the decision to start any clinical trial of these drugs will not only affect the timing of realizations of their endogenous uncertain parameters (clinical trial outcomes), but also affect the probability distributions of these uncertain parameters. For instance, let’s assume that drugs D1 and D2 have similar formulations and their outcomes are correlated and that the solution recommends starting drug trial pair (D1, PI) at period one. When the outcome of (D1, PI) is realized, the probability distribution of outcome space for D2 would be different if drug D1 passes PI or fails it. This will make the resulting problem a MSSP with both Type I and Type II endogenous uncertainty, which is a more difficult formulation to solve with limited approaches available to address it. We left this as future study.