Higher Order Accurate Transient Numerical Model to Evaluate the Natural Convection Heat Transfer in Flat Plate Solar Collector
Abstract
:1. Introduction
2. Methodology
2.1. Governing Equations for Natural Convection Flow in Enclosures
2.2. Validation
- Differentially heated square cavity—Turbulent Behavior (Ra = 107 to 108)
- Differentially heated vertical cavity—Transient & Periodic Behavior
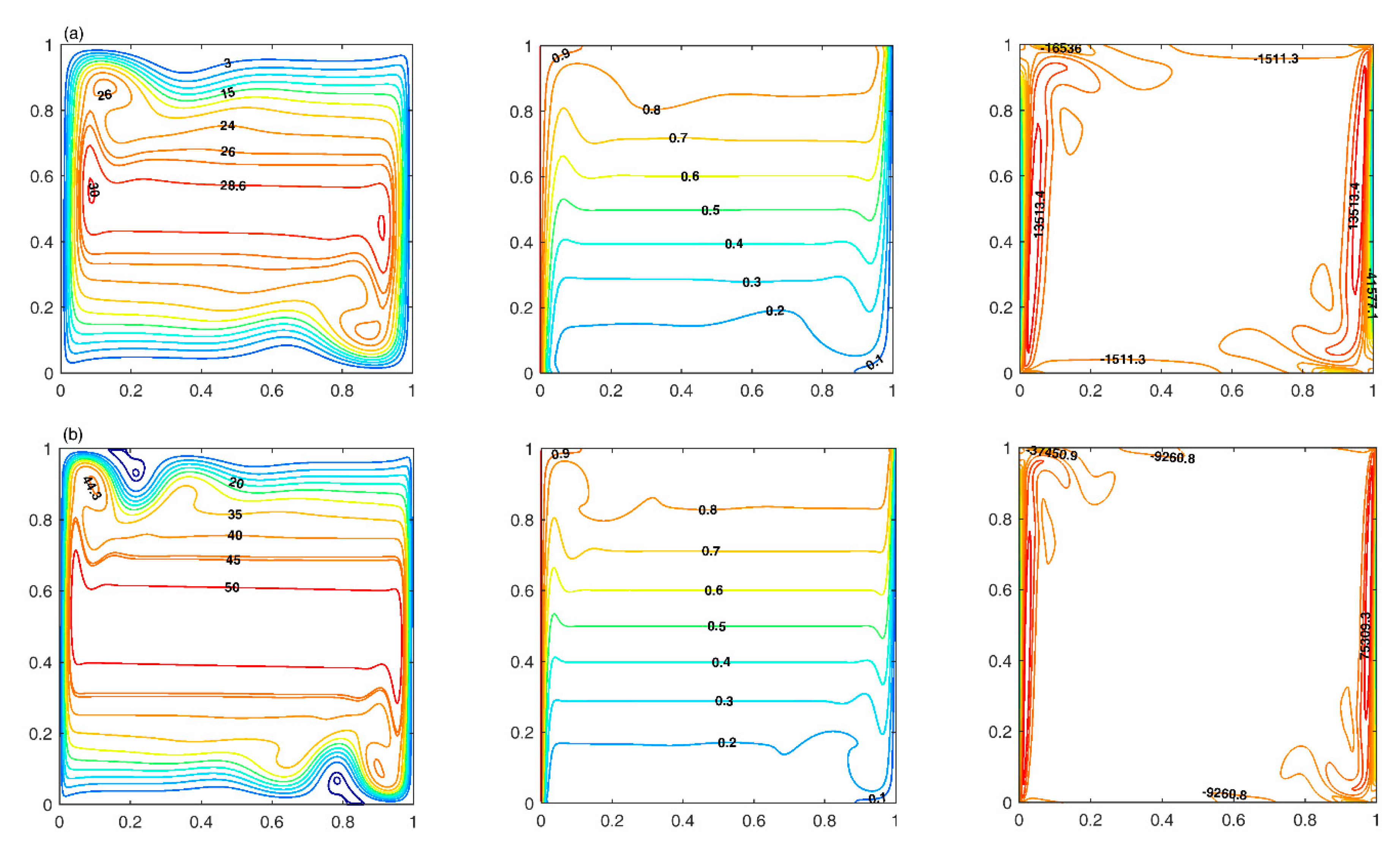
2.2.1. Differentially Heated Square Cavity
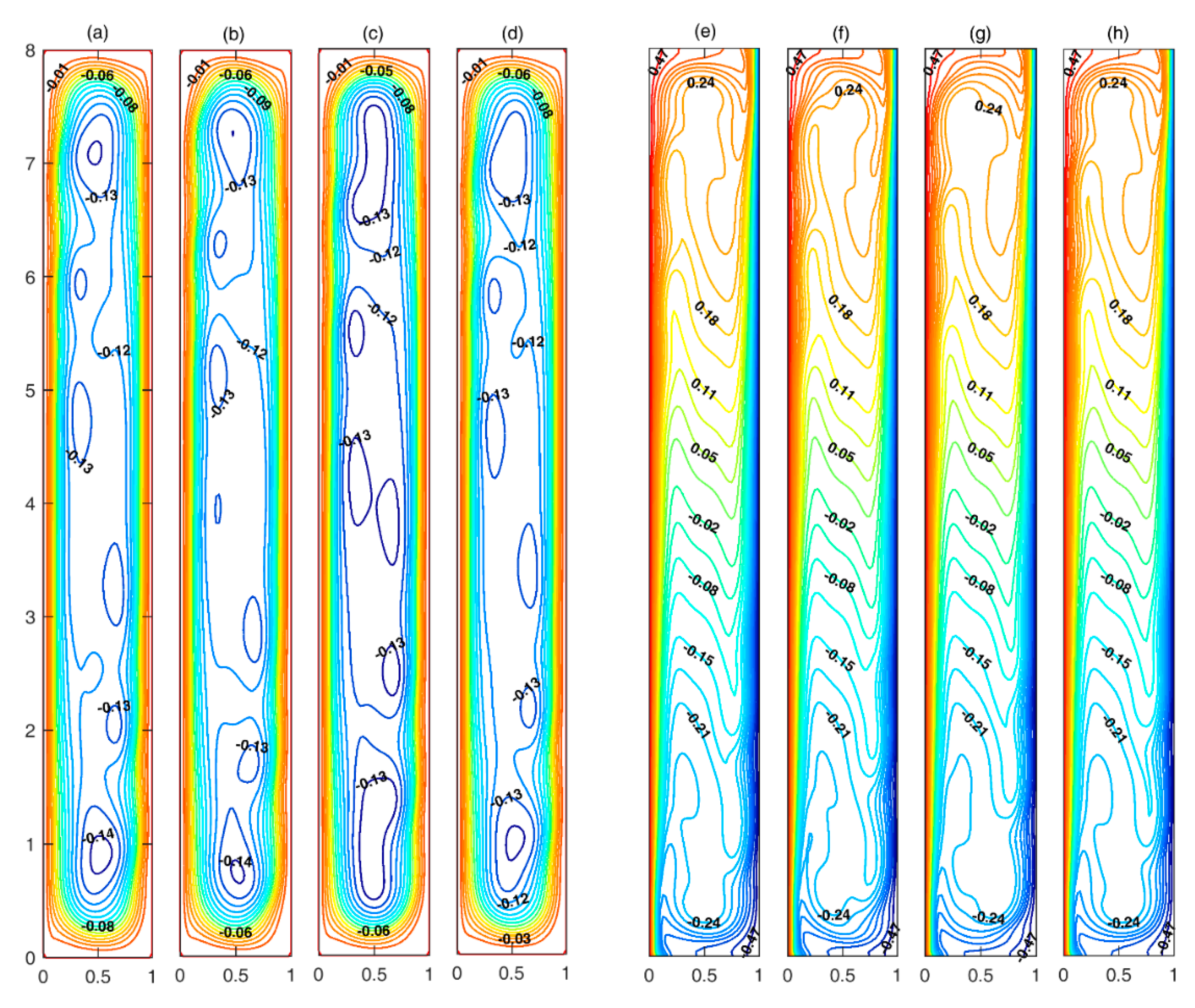
2.2.2. Buoyancy Driven Convection in Rectangular Cavity
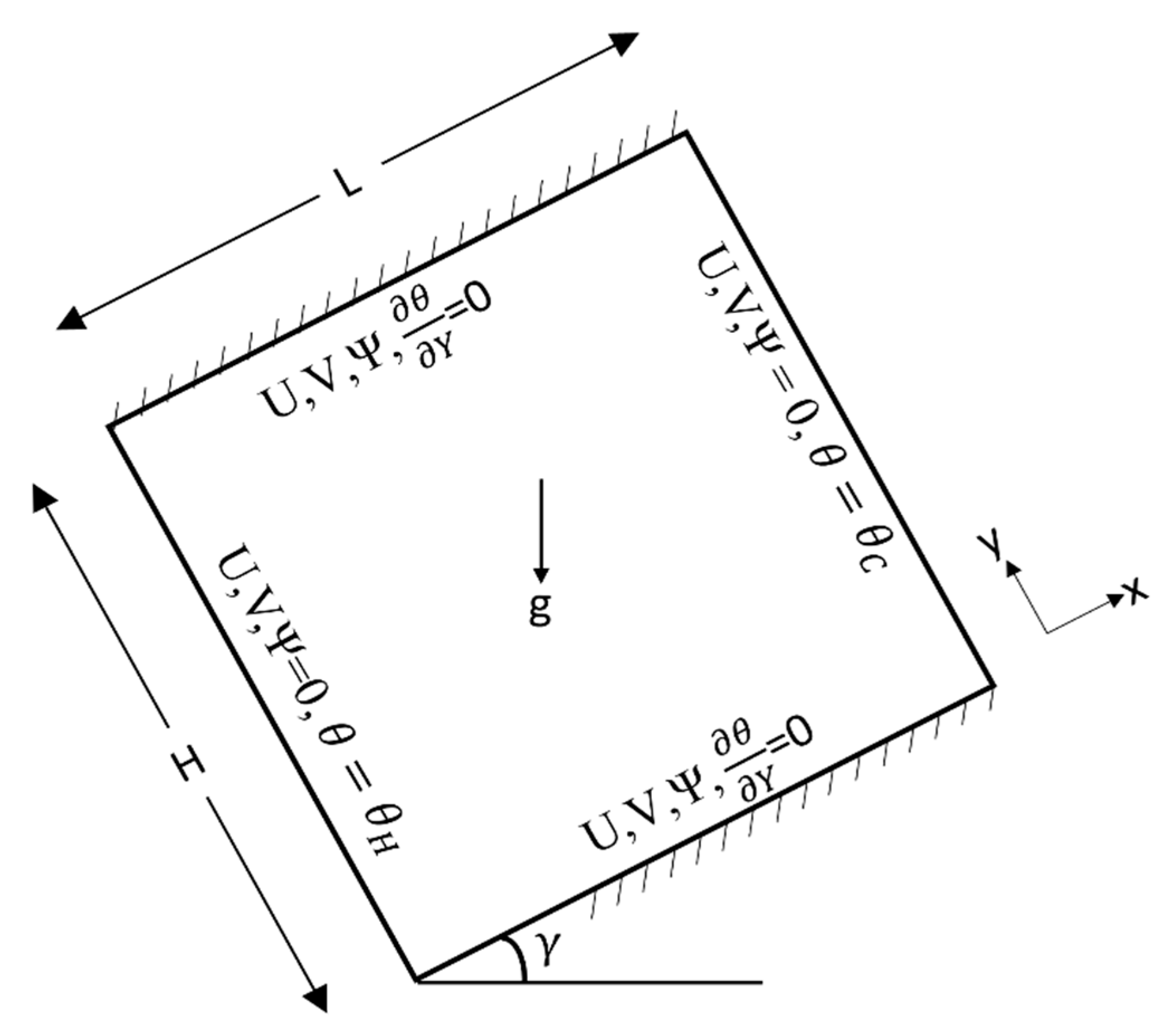
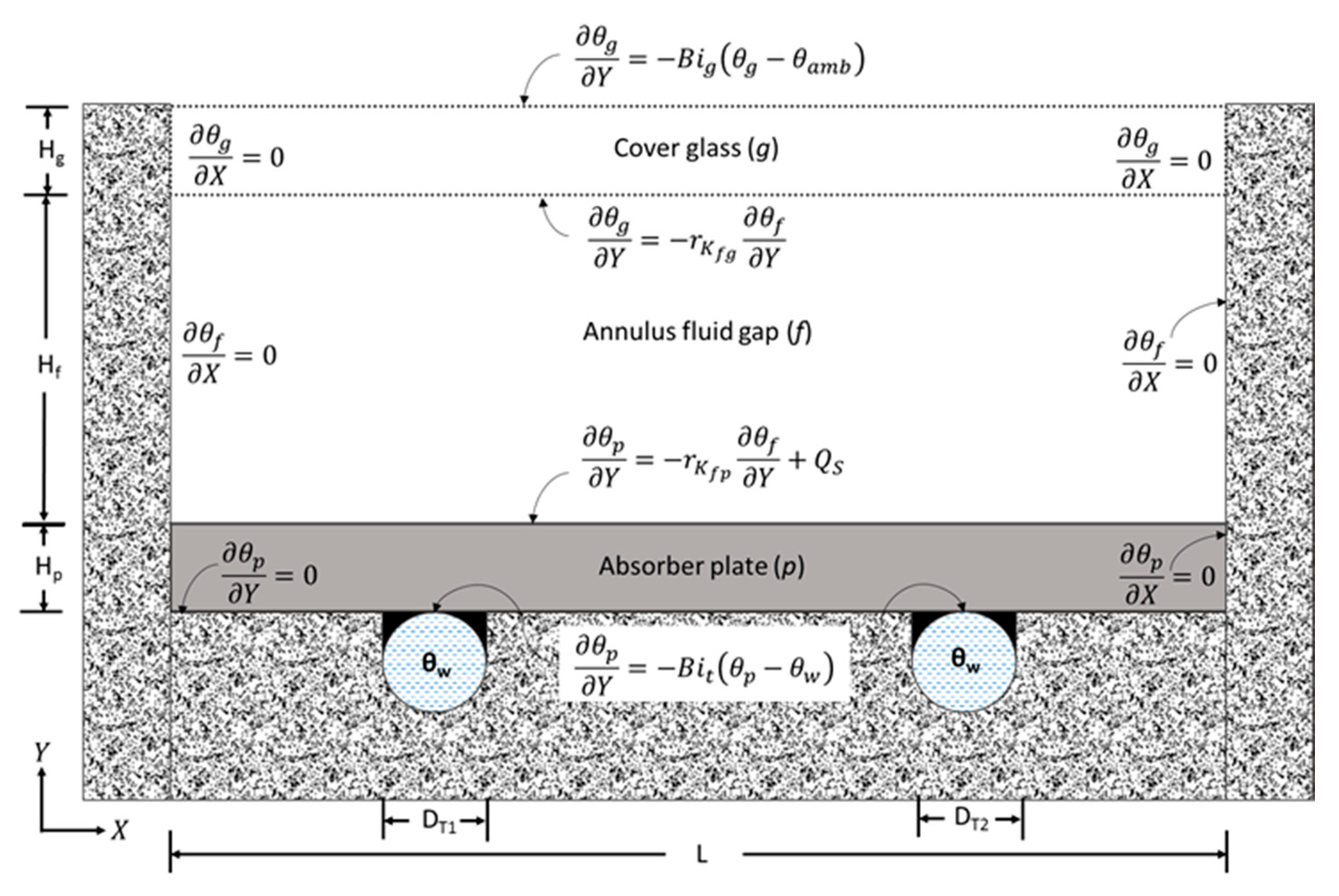
2.3. Extension of the Developed Numerical Method to Solar Thermal Collector
2.3.1. Assumptions
- Two dimensional flow in X and Y directions only;
- The temperature of the heat transfer fluid in the tube is constant;
- No radiation heat transfer;
- Fluid and material properties are evaluated as a function of constant temperature throughout the transient simulation;
- Side and bottom heat transfer losses are neglected by considering perfectly insulated.
2.3.2. Governing Equations
2.3.3. Numerical Implementation
| Algorithm 1 |
|---|
|
2.3.4. Validation
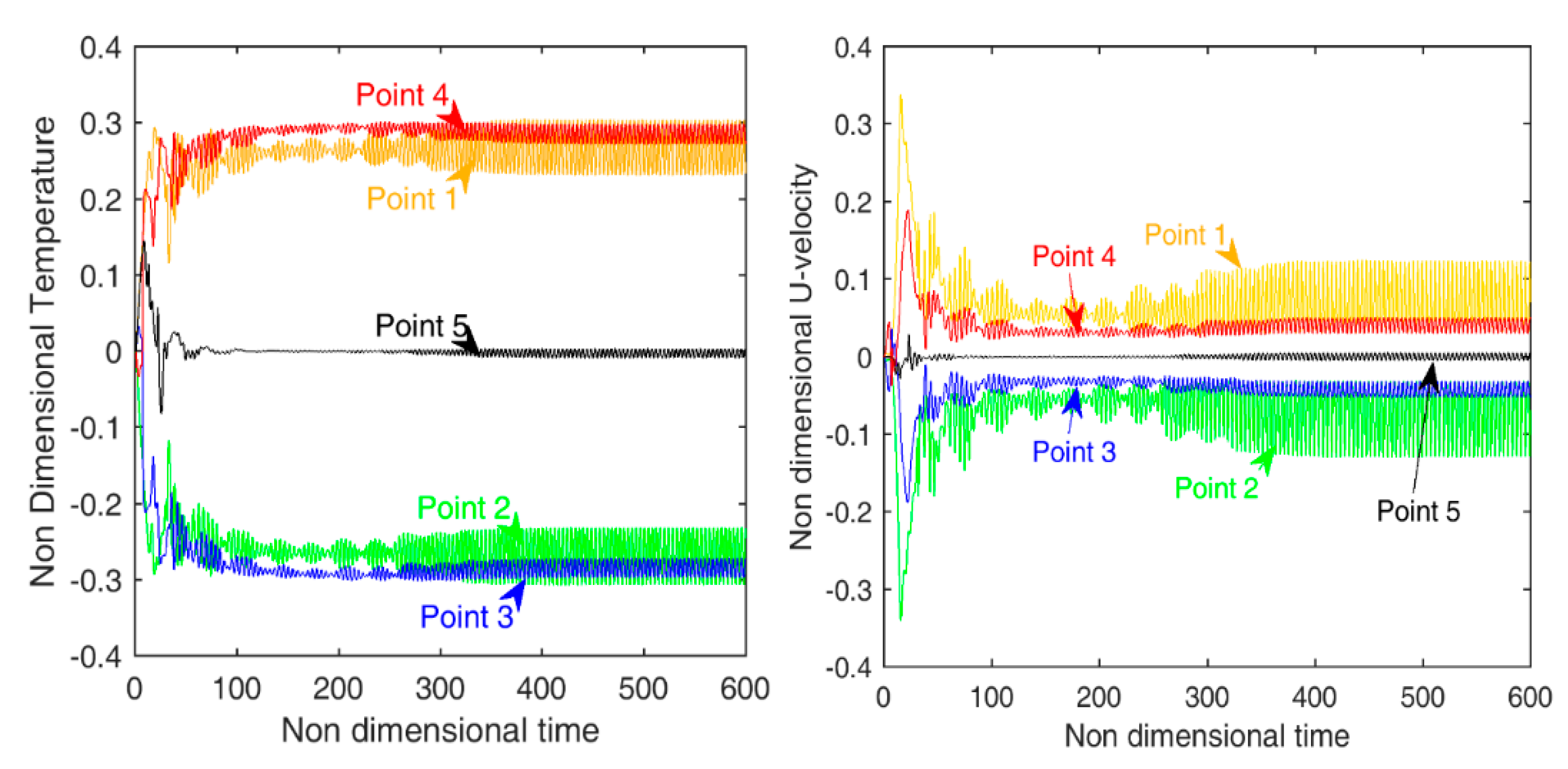
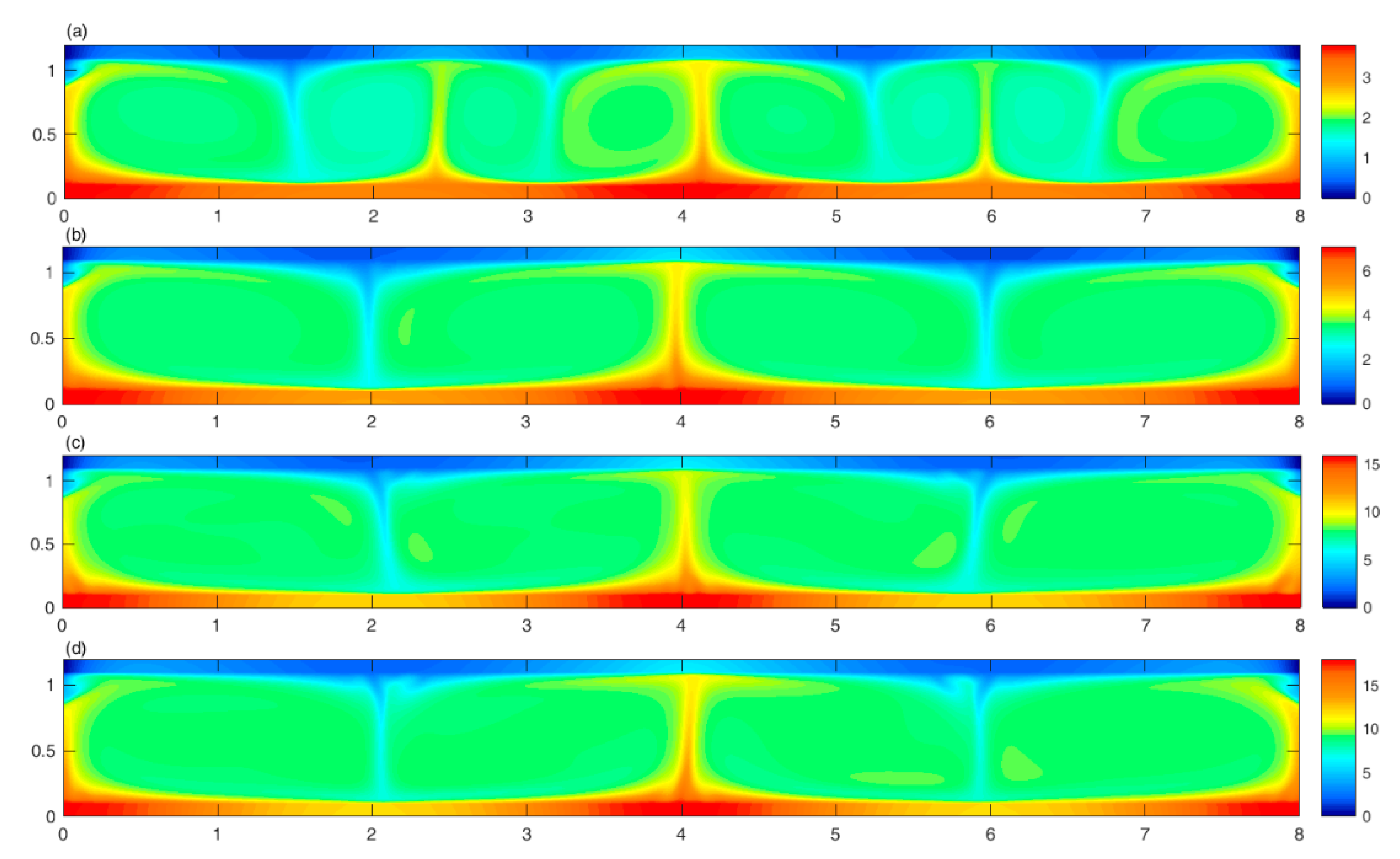
3. Results
- Flow development stage;
- Flow mode transition stage;
- Fully developed stage.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Ar | Aspect Ratio (L/H) | X,Y | Non dimensional coordinates |
| Bi | Biot number | α | Thermal diffusivity, m2/s |
| Cp | Specific heat capacity, J/kg·K | β | Thermal expansion coefficient, 1/K |
| g | Gravitational force, m/s2 | γ | Angle of inclination of enclosure, °deg |
| Gr | Grashof number | ε | Numerical tolerance limit |
| h | Convective heat transfer coef., W/(m2·K) | θ | Non dimensional temperature |
| H | Height of respective domain | ν | Kinematic viscosity, m2/s |
| L | Length of enclosure | ρ | Density, kg/m3 |
| K | Thermal conductivity, W/(m·K) | τ | Non dimensional time |
| KΦ | Diffusion coefficient | ψ | Stream function |
| n | Time step | Ψ | Non dimensional streamfunction |
| N | Number of tubes | ω | vorticity |
| Nu | Nusselt number | Ω | Non dimensional vorticity |
| p | Pressure, N/m2 | Φ | General conservation variable |
| Pr | Prandtl number | ∇2 | Laplacian operator |
| q” | Heat flux, W/m2 | Order of discretisation | |
| Q | Non dimensional Heat flux | Subscripts/Superscripts | |
| R | Residual | o | Reference condition |
| Ra | Rayleigh number | amb | Ambient |
| SΦ | Transport eqn. source term | f | fluid |
| t | Time, sec | fp | fluid to plate |
| T | Temperature, K | fg | fluid to glass |
| Velocity vector, m/s | g | glass | |
| u,v | Velocity components, m/s | p | plate |
| Non dimensional velocity, m/s | S | Solar | |
| U,V | Non dimensional v components, m/s | t | tube |
| x,y | coordinates | w | water |
References
- Duffie, J.A.; Beckman, W.A. Solar Engineering of Thermal Processes; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Smith, J.G. Comparison of Transient Models for Flat-Plates and Trough Concentrators. J. Sol. Energy Eng. 1986, 108, 341–344. [Google Scholar] [CrossRef]
- Tagliafico, L.A.; Scarpa, F.; De Rosa, M. Dynamic thermal models and CFD analysis for flat-plate thermal solar collectors—A review. Renew. Sustain. Energy Rev. 2014, 30, 526–537. [Google Scholar] [CrossRef]
- Close, D. A design approach for solar processes. Sol. Energy 1967, 11, 112–122. [Google Scholar] [CrossRef]
- Klein, S. Calculation of flat-plate collector loss coefficients. Sol. Energy 1975, 17, 79–80. [Google Scholar] [CrossRef]
- Morrison, G.; Ranatunga, D. Transient response of thermosyphon solar collectors. Sol. Energy 1980, 24, 55–61. [Google Scholar] [CrossRef]
- Oliva, A.; Costa, M.; Segarra, C. Numerical simulation of solar collectors: The effect of nonuniform and nonsteady state of the boundary conditions. Sol. Energy 1991, 47, 359–373. [Google Scholar] [CrossRef]
- Ouzzane, M.; Galanis, N. Numerical Analysis Of Mixed Convection In Inclined Tubes With External Longitudinal Fins. Sol. Energy 2001, 71, 199–211. [Google Scholar] [CrossRef]
- Ramírez-Minguela, J.; Alfaro-Ayala, J.; Rangel-Hernandez, V.H.; Uribe-Ramírez, A.; Mendoza-Miranda, J.; Pérez-García, V.; Belman, J. Comparison of the thermo-hydraulic performance and the entropy generation rate for two types of low temperature solar collectors using CFD. Sol. Energy 2018, 166, 123–137. [Google Scholar] [CrossRef]
- Allan, J.; Dehouche, Z.; Stankovice, S.; Harries, A. Computational Fluid Dynamics Simulation and Experimental Study of Key Design Parameters of Solar Thermal Collectors. J. Sol. Energy Eng. 2017, 139, 051001. [Google Scholar] [CrossRef]
- Cerón, J.; Pérez-García, J.; Solano, J.; García, A.; Herrero-Martín, R. A coupled numerical model for tube-on-sheet flat-plate solar liquid collectors. Analysis and validation of the heat transfer mechanisms. Appl. Energy 2015, 140, 275–287. [Google Scholar] [CrossRef]
- Jiandong, Z.; Hanzhong, T.; Susu, C. Numerical simulation for structural parameters of flat-plate solar collector. Sol. Energy 2015, 117, 192–202. [Google Scholar] [CrossRef]
- Dović, D.; Andrassy, M. Numerically assisted analysis of flat and corrugated plate solar collectors thermal performances. Sol. Energy 2012, 86, 2416–2431. [Google Scholar] [CrossRef]
- Fan, J.; Shah, L.J.; Furbo, S. Flow distribution in a solar collector panel with horizontally inclined absorber strips. Sol. Energy 2007, 81, 1501–1511. [Google Scholar] [CrossRef]
- Martinopoulos, G.; Missirlis, D.; Tsilingiridis, G.; Yakinthos, K.; Kyriakis, N. CFD modeling of a polymer solar collector. Renew. Energy 2010, 35, 1499–1508. [Google Scholar] [CrossRef]
- Selmi, M.; Al-Khawaja, M.J.; Marafia, A. Validation of CFD simulation for flat plate solar energy collector. Renew. Energy 2008, 33, 383–387. [Google Scholar] [CrossRef]
- Sahin, M.; Owens, R.G. A novel fully implicit finite volume method applied to the lid-driven cavity problem? Part I: High Reynolds number flow calculations. Int. J. Numer. Methods Fluids 2003, 42, 57–77. [Google Scholar] [CrossRef]
- Balam, N.B.; Gupta, A. A fourth-order accurate finite difference method to evaluate the true tran-sient behaviour of natural convection flow in enclosures. Int. J. Numer. Methods Heat Fluid Flow 2020, 33, 1233–1290. [Google Scholar]
- Davis, G.D.V. Natural convection of air in a square cavity: A bench mark numerical solution. Int. J. Numer. Methods Fluids 1983, 3, 249–264. [Google Scholar] [CrossRef]
- Le Quéré, P. Accurate solutions to the square thermally driven cavity at high Rayleigh number. Comput. Fluids 1991, 20, 29–41. [Google Scholar] [CrossRef]
- Syrjälä, S. Higher order penalty-galerkin finite element approach to laminar natural convection in a square cavity. Numer. Heat Transf. Part A Appl. 1996, 29, 197–210. [Google Scholar] [CrossRef]
- Tian, Z.; Ge, Y. A fourth-order compact finite difference scheme for the steady stream function-vorticity formulation of the Navier-Stokes/Boussinesq equations. Int. J. Numer. Methods Fluids 2003, 41, 495–518. [Google Scholar] [CrossRef]
- Kalita, J.C.; Dalal, D.C.; Dass, A.K. Fully compact higher-order computation of steady-state natural convection in a square cavity. Phys. Rev. E 2001, 64, 066703. [Google Scholar] [CrossRef]
- Kondo, N. Numerical simulation of unsteady natural convection in a square cavity by the third-order upwind finite element method. Int. J. Comput. Fluid Dyn. 1994, 3, 281–302. [Google Scholar] [CrossRef]
- Mayne, D.A.; Usmani, A.; Crapper, M. h-adaptive finite element solution of high Rayleigh number thermally driven cavity problem. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 598–615. [Google Scholar] [CrossRef] [Green Version]
- Yapici, K.; Obut, S. Benchmark results for natural and mixed convection heat transfer in a cavity. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 998–1029. [Google Scholar] [CrossRef]
- Wan, D.C.; Patnaik, B.S.V.; Wei, G.W. A new benchmark quality solution for the buoyancy-driven cavity by discrete singular convolution. Numer. Heat Transf. Part B Fundam. 2001, 40, 199–228. [Google Scholar] [CrossRef]
- Christon, M.A.; Gresho, P.M.; Sutton, S.B. Computational predictability of time-dependent natural convection flows in enclosures (including a benchmark solution). Int. J. Numer. Methods Fluids 2002, 40, 953–980. [Google Scholar] [CrossRef]
- Mullick, S.C.; Samdarshi, S.K. An Improved Technique for Computing the Top Heat Loss Factor of a Flat-Plate Collector With a Single Glazing. J. Sol. Energy Eng. 1988, 110, 262–267. [Google Scholar] [CrossRef]
- Subiantoro, A.; Ooi, K.T. Analytical models for the computation and optimization of single and double glazing flat plate solar collectors with normal and small air gap spacing. Appl. Energy 2013, 104, 392–399. [Google Scholar] [CrossRef]
- Holtzman, G.A.; Hill, R.W.; Ball, K.S. Laminar Natural Convection in Isosceles Triangular Enclosures Heated From Below and Symmetrically Cooled From Above. J. Heat Transf. 2000, 122, 485–491. [Google Scholar] [CrossRef]




| Reference | |||||||
|---|---|---|---|---|---|---|---|
| Present Study | 29.3558 | 29.945 | 144.3603 (0.8875) | 691.8772 (0.0188) | 16.6505 | 39.5199 (0.0179) | 1.3374 (1.000) |
| Le Quéré [20] | 29.361 | 30.165 | 148.59 (0.879) | 699.17 (0.021) | 16.523 | 39.39 (0.018) | 1.366 (1) |
| Syrjälä [21] | 29.3616 | ---- | 148.593 (0.8794) | 699.506 (0.0213) | 16.5299 | ---- | ---- |
| Tian and Ge [22] | 29.3562 | 30.155 | 148.5695 (0.8794) | 699.2991 (0.0213) | 16.5106 | 39.2540 (0.0179) | 1.3655 (1) |
| Kalita et al. [23] | 29.382 | ---- | 155.82 (0.863) | 696.238 (0.025) | 16.075 | 34.925 (0.025) | 1.509 (1) |
| Kondo [24] | ---- | ---- | 149.7153 (0.8763) | 702.6753 (0.0187) | 16.5123 | 38.8717 (0.0187) | 1.3767 (1) |
| Mayne et al. [25] | ---- | ---- | 145.2666 (0.8845) | 703.2526 (0.0215) | 16.3869 | 41.0247 (0.0390) | 1.3799 (1) |
| Yapici and Obut [26] | 29.3631 | 30.168 | 148.6179 (0.8801) | 699.4755 (0.0213) | 16.5479 | 39.4796 (0.0174) | 1.3661 (0.9995) |
| Reference | |||||||
|---|---|---|---|---|---|---|---|
| Present Study | 52.2217 | 53.718 | 316.3440 (0.9250) | 2218.115 (0.0125) | 30.1348 | 103.6505 (0.000) | 1.9072 (1.000) |
| Le Quéré [20] | 52.32 | 53.85 | 321.9 (0.928) | 2222 (0.012) | 30.225 | 87.24 (0.008) | 1.919 (1) |
| Kondo [24] | ---- | ---- | 315.2603 (0.9389) | 2241.1841 (0.0136) | 30.1901 | 84.3960 (0.0100) | 2.0798 (1) |
| Mayne et al. [25] | ---- | ---- | 283.0689 (0.9455) | 2223.4424 (0.0130) | 29.6526 | 91.2095 (0.0670) | 2.0440 (1) |
| Wan et al. [27] | ---- | ---- | 296.71 (0.93) | 2259.08 (0.012) | 31.486 | 91.16 (0.010) | 1.766 (1) |
| Yapici and Obut [26] | 52.3577 | 53.883 | 323.1085 (0.9279) | 2220.4766 (0.0125) | 30.3056 | 88.1516 (0.0079) | 1.9172 (0.9995) |
| Point | x-Coordinate | y-Coordinate |
|---|---|---|
| 1 | 0.1810 | 7.3700 |
| 2 | 0.8190 | 0.6300 |
| 3 | 0.1810 | 0.6300 |
| 4 | 0.8190 | 7.3700 |
| 5 | 0.1810 | 4.0000 |
| Contributor | ||||||||
|---|---|---|---|---|---|---|---|---|
| Present Study | 0.057013 | 0.056342 | 0.265781 | 0.043944 | −0.073503 | 0.007189 | −2.351614 | 1.108430 |
| Le Quere | 0.056356 | 0.054828 | 0.265480 | 0.042740 | ---- | ---- | ---- | ---- |
| Christon | 0.058670 | 0.055120 | 0.264140 | 0.042420 | −0.07394 | 0.007106 | −2.1213 | 0.9710 |
| Jhonston | 0.056160 | 0.054520 | 0.264700 | 0.042680 | −0.07348 | 0.006856 | −2.3620 | 0.9940 |
| Davis | 0.056300 | 0.054200 | 0.265500 | 0.042200 | ---- | ---- | ---- | ---- |
| Gresho | 0.056493 | 0.055414 | 0.265722 | 0.043144 | −0.07439 | 0.007100 | −2.4455 | 1.0810 |
| Rayleigh No. | 1 | 100 | 1000 | 2500 |
|---|---|---|---|---|
| Mullick & Samdarshi [29] | 13 | 6.5 | 5.5 | 5.4 |
| Present study | 11.5 | 6.0 | 5.3 | 5.2 |
| |%| Difference | 13 | 8.3 | 3.8 | 3.85 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balam, N.B.; Alam, T.; Gupta, A.; Blecich, P. Higher Order Accurate Transient Numerical Model to Evaluate the Natural Convection Heat Transfer in Flat Plate Solar Collector. Processes 2021, 9, 1508. https://doi.org/10.3390/pr9091508
Balam NB, Alam T, Gupta A, Blecich P. Higher Order Accurate Transient Numerical Model to Evaluate the Natural Convection Heat Transfer in Flat Plate Solar Collector. Processes. 2021; 9(9):1508. https://doi.org/10.3390/pr9091508
Chicago/Turabian StyleBalam, Nagesh Babu, Tabish Alam, Akhilesh Gupta, and Paolo Blecich. 2021. "Higher Order Accurate Transient Numerical Model to Evaluate the Natural Convection Heat Transfer in Flat Plate Solar Collector" Processes 9, no. 9: 1508. https://doi.org/10.3390/pr9091508








