Multidimensional Fractionation of Particles
Abstract
:1. Introduction
2. Particle Property Distributions
3. Methodology
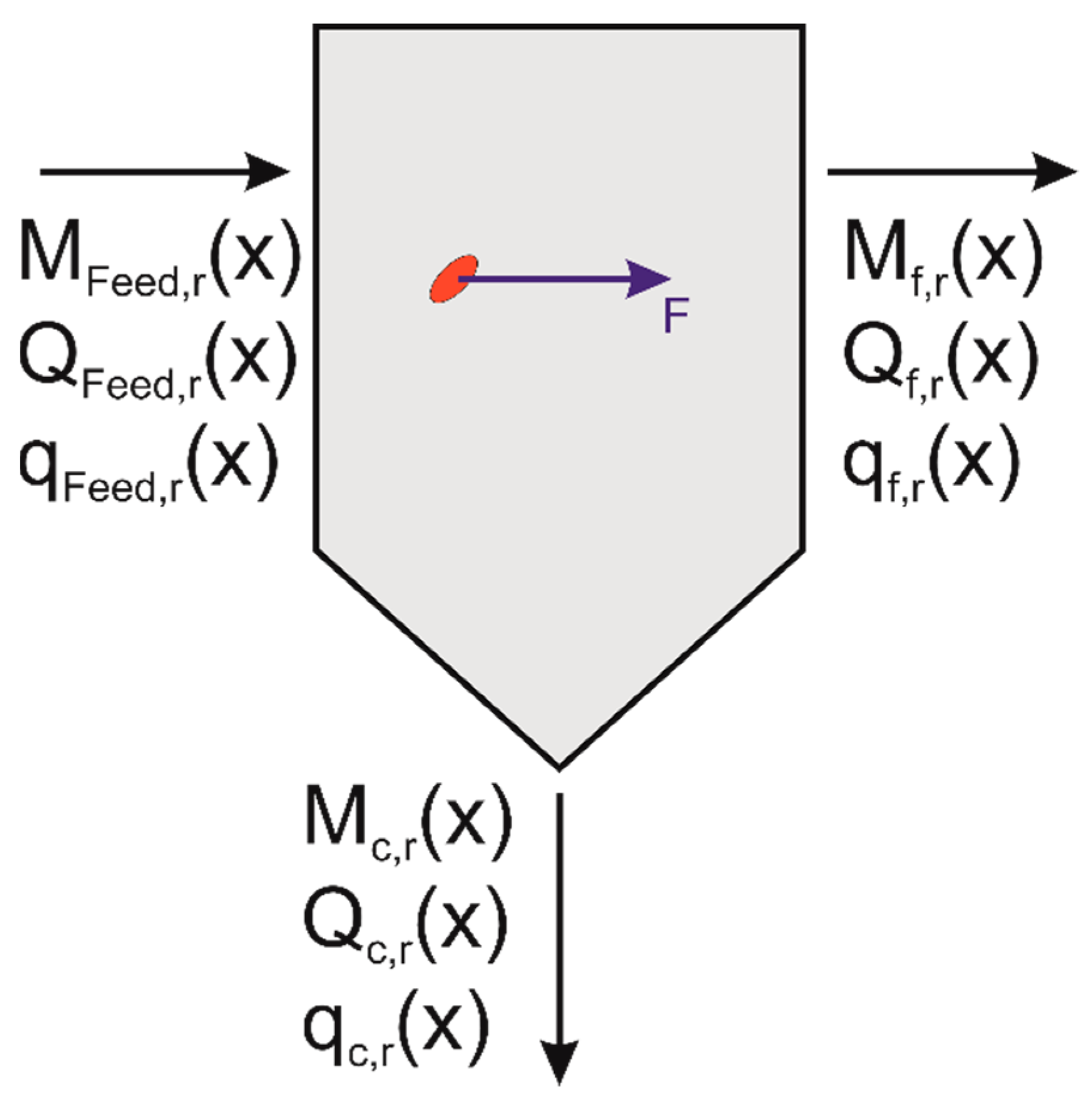
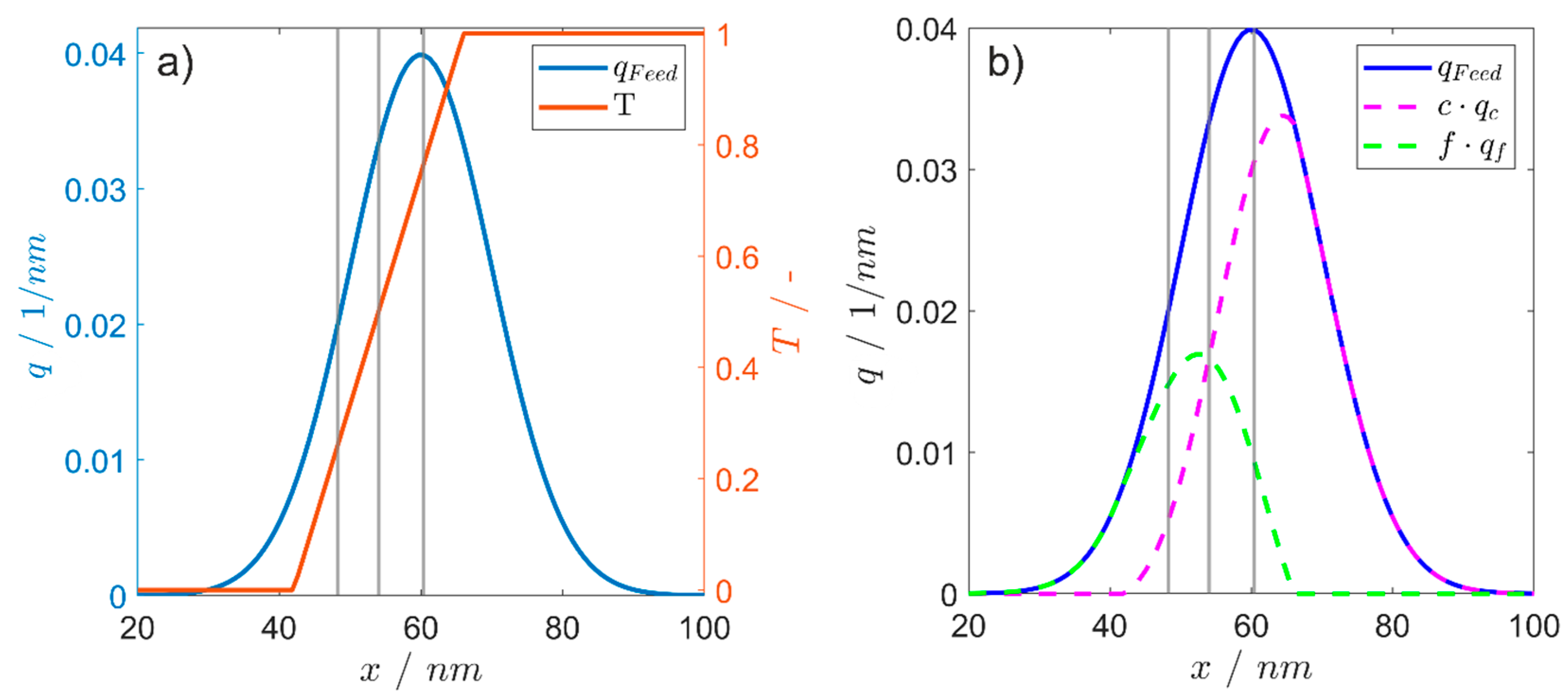
- integral mass balance
- differential mass balance
- separation curves
- yields
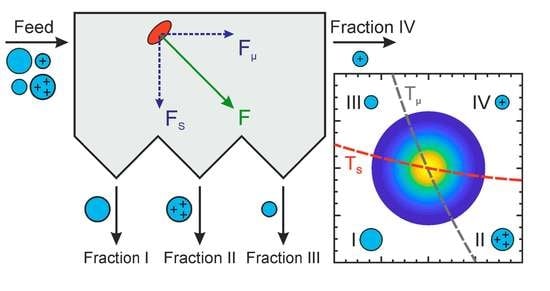
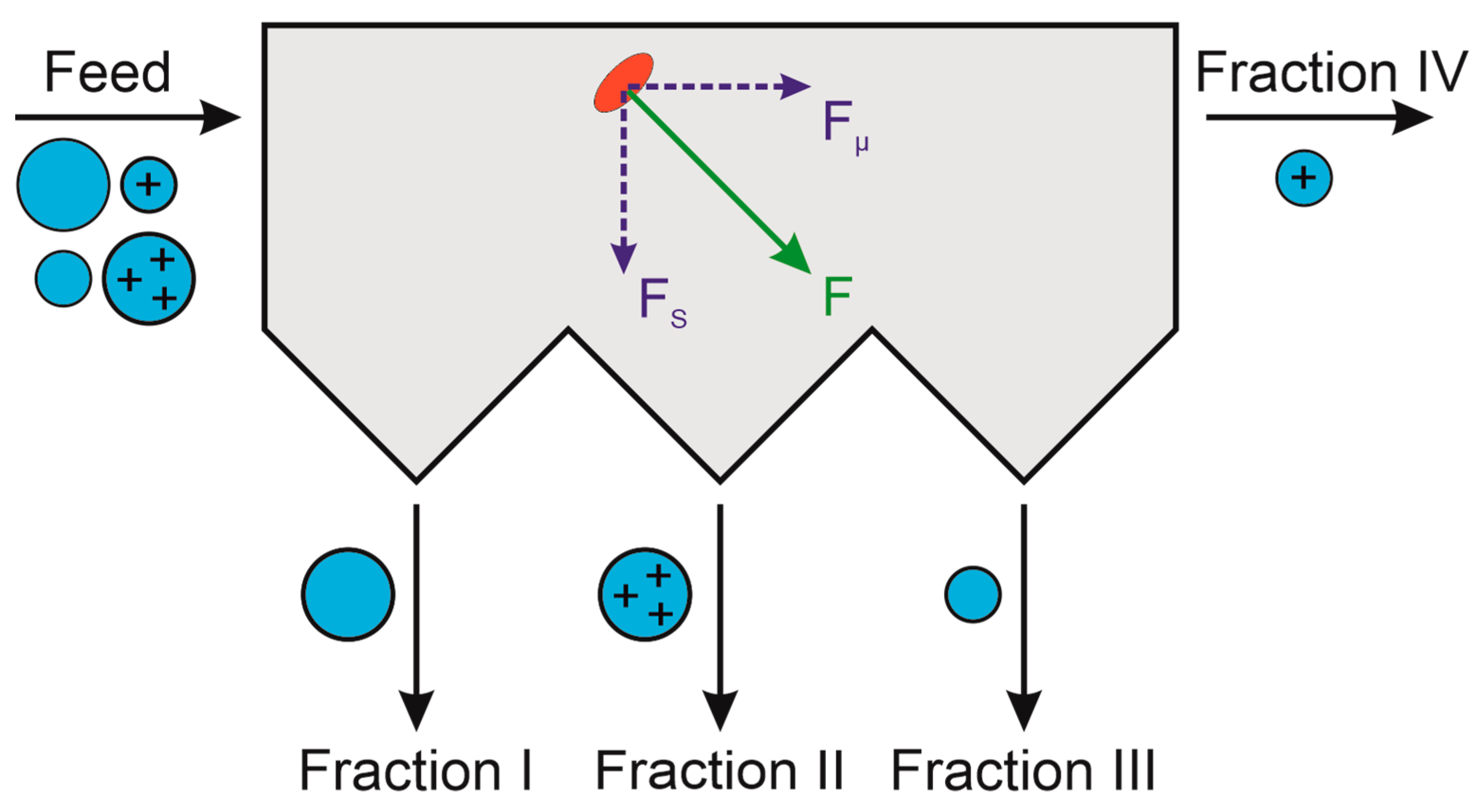
4. Separation Processes Acting on Two-Dimensional Distributions
4.1. One-Dimensional Separation Acting on a Two-Dimensional PSD
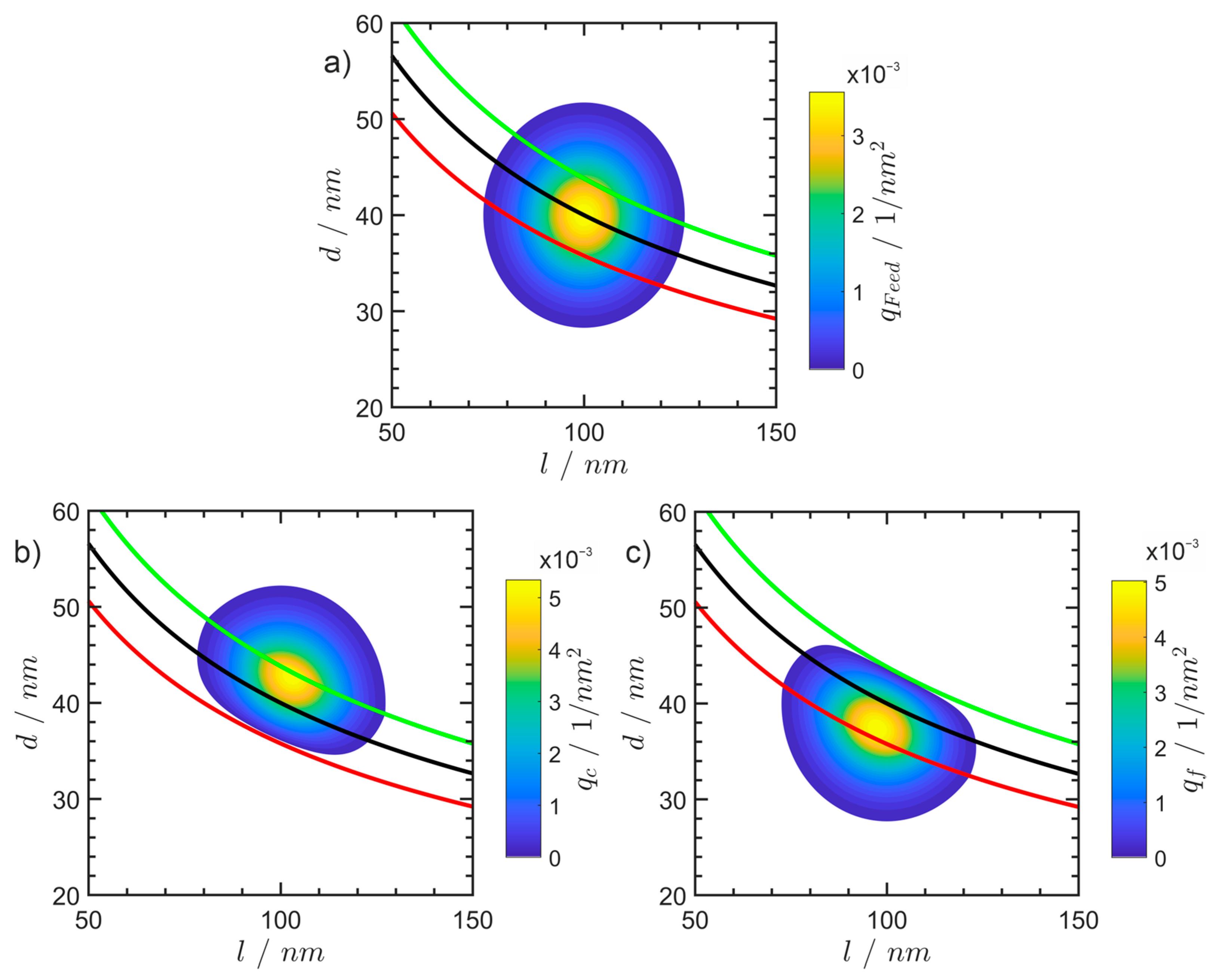
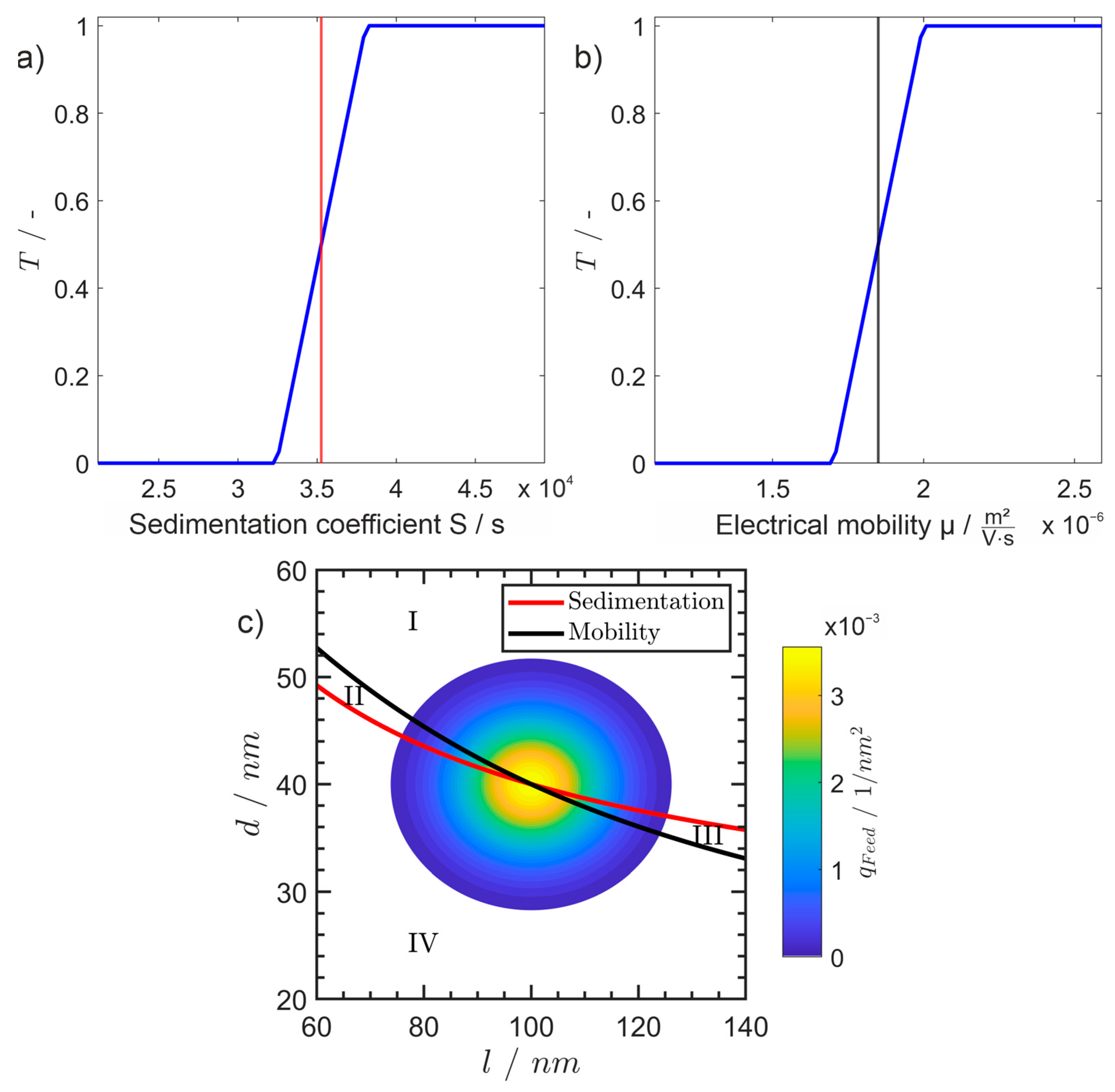
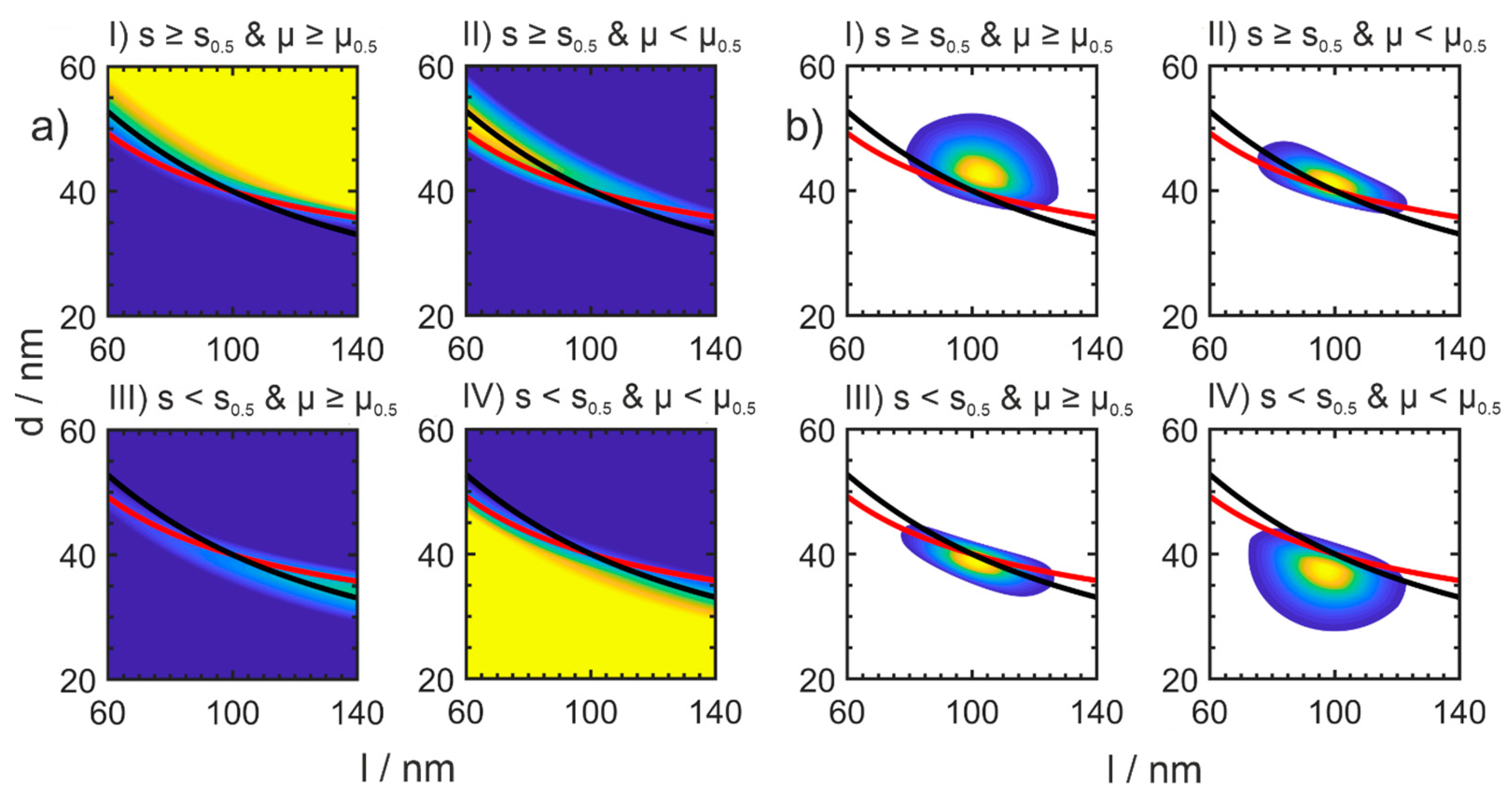
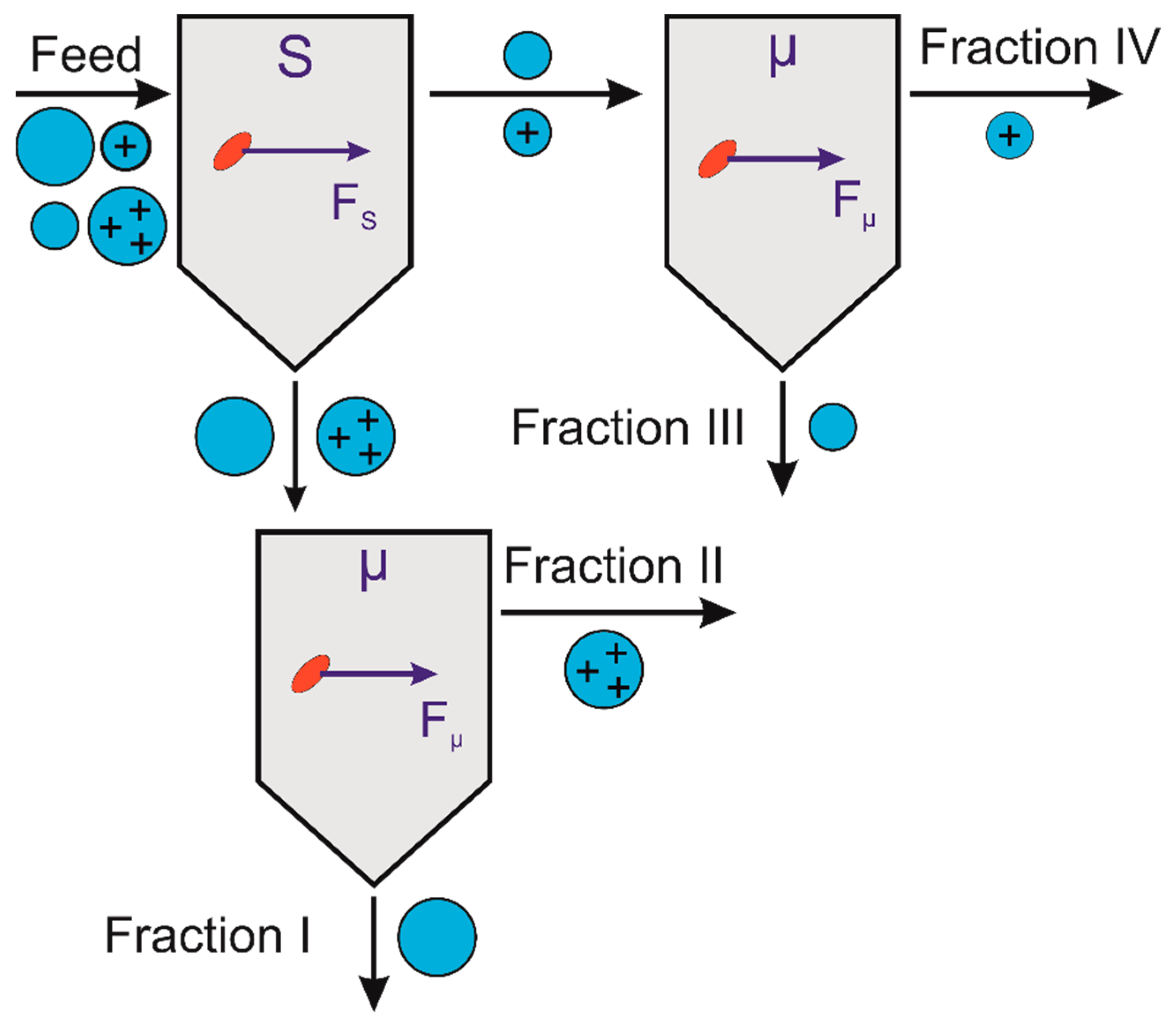
4.2. Two Orthogonal Separations
- Determine the individual separation functions as functions of the acting physical principles, e.g., T1(s), T2(µ);
- Translate the parameter-dependent functions to the set of the investigated parameters, e.g., length and diameter (l d)T;
- Determine the number of fractions;
- Determine if each fraction belongs to the coarse or fine fraction with respect to the individual separations;
- Calculate the effective separation functions for each basin;
- Calculate the PSD for each basin via the effective separation function and the prefactors γi.
4.3. Consecutive Separations
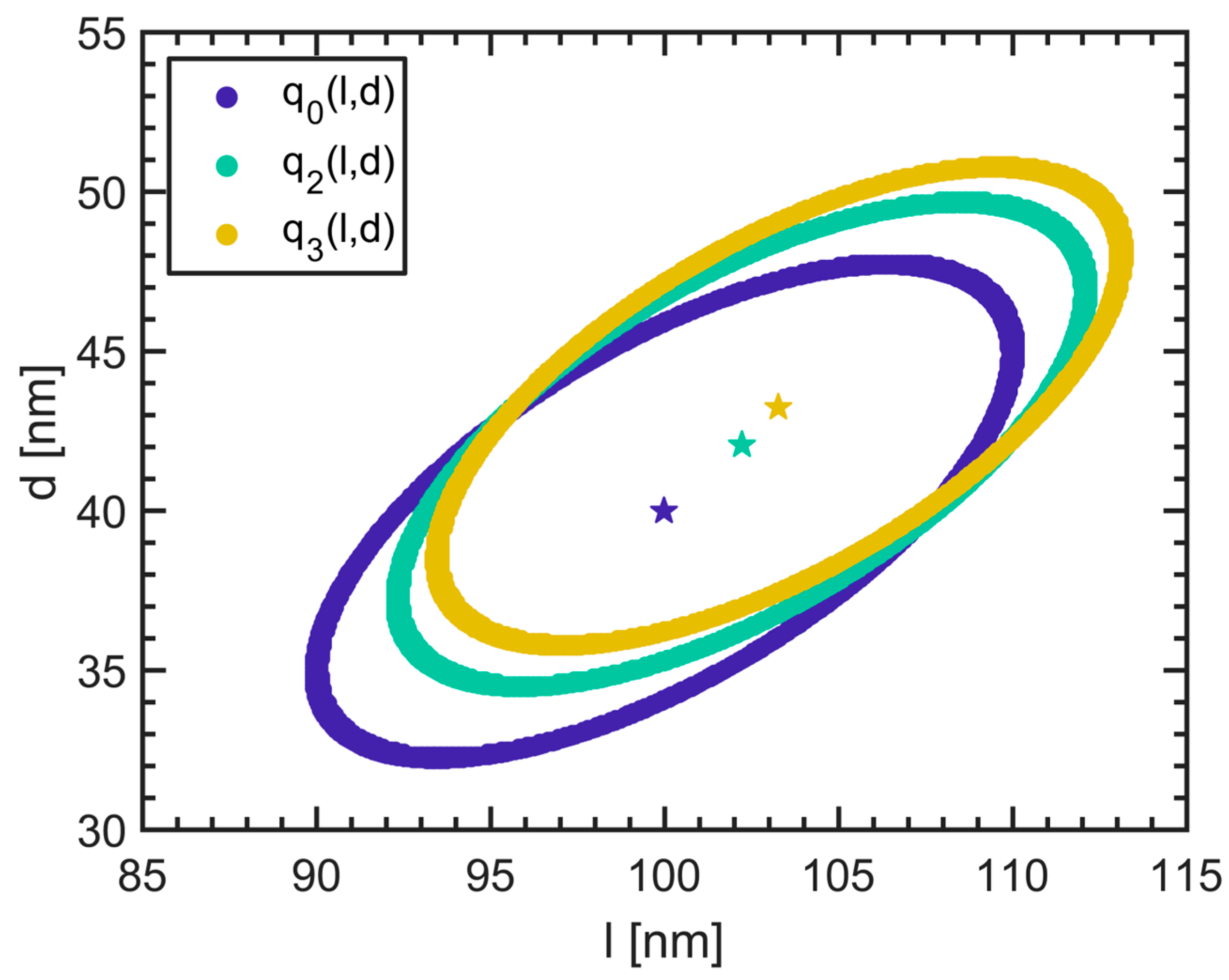
5. Generalization to M-Fold Orthogonal Separations Acting on Multidimensional PSDs
6. Examples of Technical Realizations
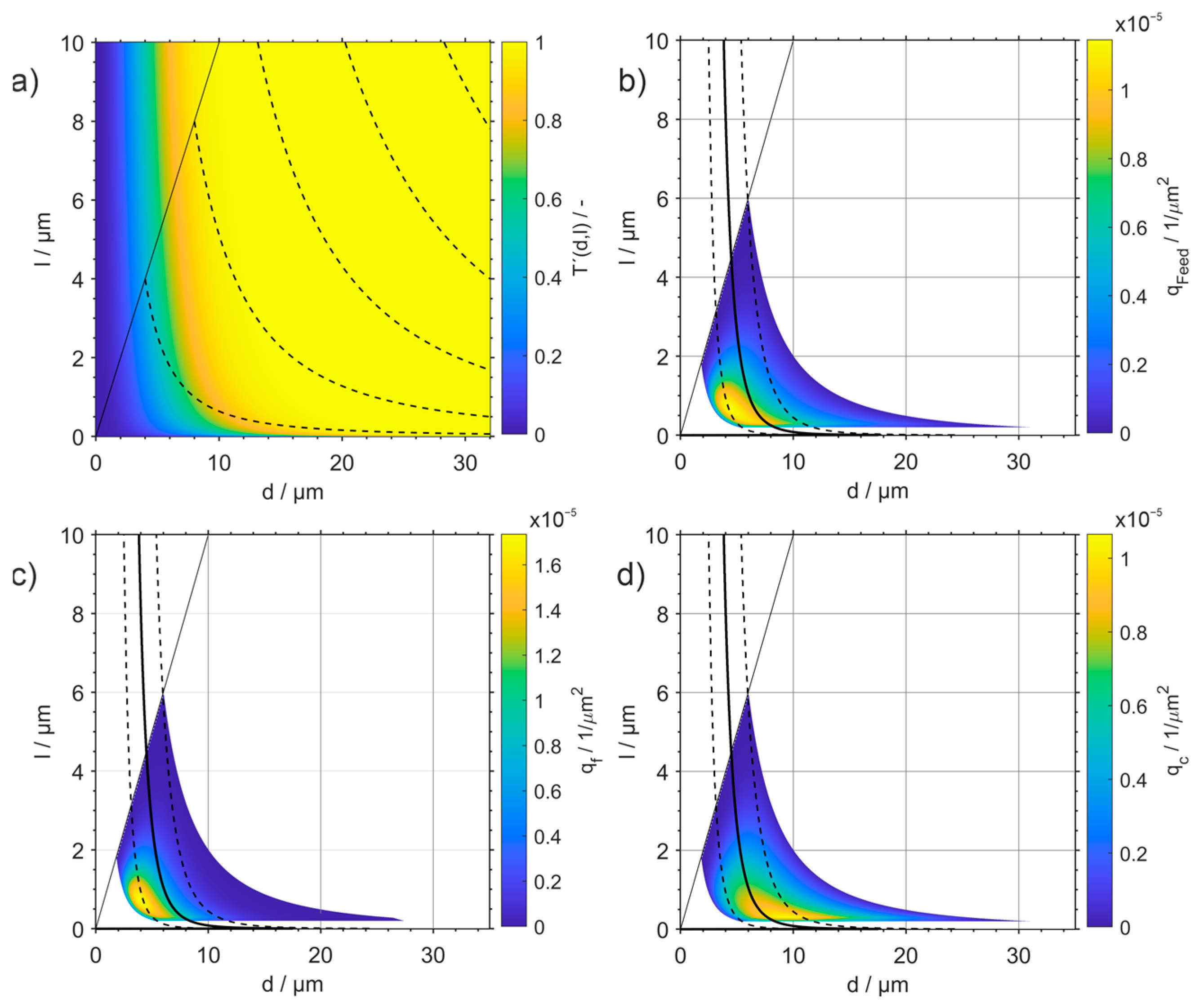
6.1. Hydrocyclone: Fractionation with Respect to Size and Shape
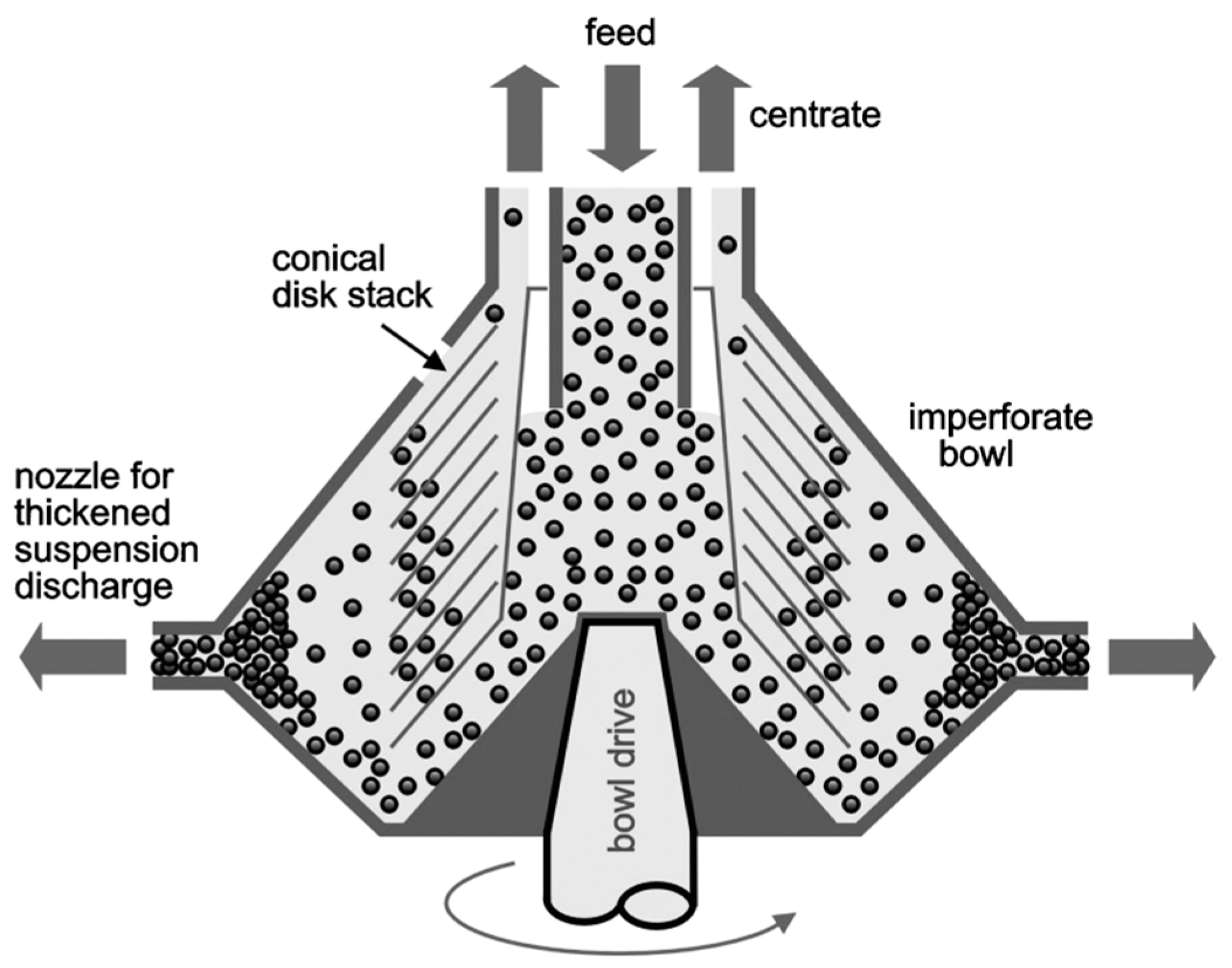
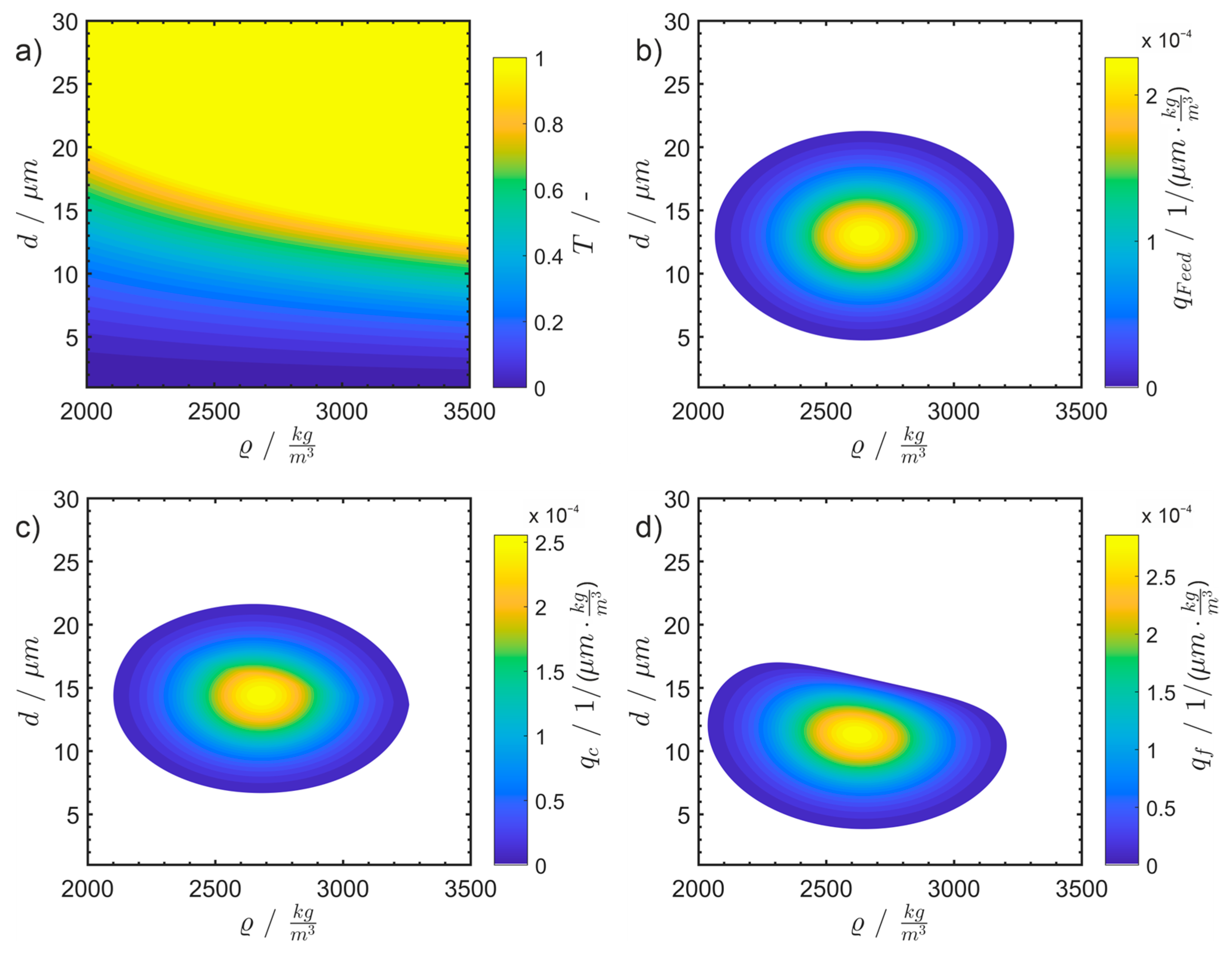
6.2. Disc Separator: Fractionation with Respect to Size and Density Separation
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| µ | electrical mobility |
| aZ | centrifugal acceleration |
| B | number of basins |
| b | measure for the sharpness of separation |
| c | coarse fraction |
| cV | volume concentration |
| d | diameter of a cylinder |
| DC | hydrocyclone diameter |
| Eu | Euler number |
| f | fine fraction |
| f/f0 | frictional ratio |
| FD | drag force |
| FZ | centrifugal force |
| l | length |
| M | mass |
| Mc,r | r weighted amounts of particle |
| Mr,k | moment |
| N | number of disc gaps |
| nD | n-dimensional |
| PSD | particle size distribution |
| qr(x) | r weighted property density distribution |
| Qr(x) | r weighted property sum distribution |
| qr(x) | charge |
| RW | water flow ratio |
| Re | Reynolds number |
| s | sedimentation coefficient |
| T(x) | separation efficiency |
| T(x)′ | corrected separation efficiency |
| V | volume |
| flow rate | |
| x | particle diameter |
| xcut | cut size |
| α | angle |
| γi | normalized mass fractions |
| ΔP | pressure drop |
| η | solvent density |
| κ(x) | a weighting function |
| Λi | yield |
| density | |
| ϕ | form factor |
| ω | angular velocity |
References
- Frank, U.; Wawra, S.E.; Pflug, L.; Peukert, W. Multidimensional Particle Size Distributions and Their Application to Nonspherical Particle Systems in Two Dimensions. Part. Part. Syst. Charact. 2019, 36, 1800554. [Google Scholar] [CrossRef]
- Backes, C.; Higgins, T.M.; Kelly, A.; Boland, C.; Harvey, A.; Hanlon, D.; Coleman, J.N. Guidelines for Exfoliation, Characterization and Processing of Layered Materials Produced by Liquid Exfoliation. Chem. Mater. 2017, 29, 243–255. [Google Scholar] [CrossRef]
- Knieke, C.; Berger, A.; Voigt, M.; Taylor, R.N.K.; Röhrl, J.; Peukert, W. Scalable production of graphene sheets by mechanical delamination. Carbon 2010, 48, 3196–3204. [Google Scholar] [CrossRef]
- Völkl, A.; Klupp Taylor, R.N. Investigation and mitigation of reagent ageing during the continuous flow synthesis of patchy particles. Chem. Eng. Res. Des. 2022, 181, 133–143. [Google Scholar] [CrossRef]
- Akdas, T.; Walter, J.; Segets, D.; Distaso, M.; Winter, B.; Birajdar, B.; Spiecker, E.; Peukert, W. Investigation of the size-property relationship in CuInS2 quantum dots. Nanoscale 2015, 7, 18105–18118. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, R.; Brandl, M.; Distaso, M.; Herre, P.; Spiecker, E.; Hock, R.; Peukert, W. A comprehensive study on the mechanism behind formation and depletion of Cu2 ZnSnS4 (CZTS) phases. CrystEngComm 2015, 17, 6972–6984. [Google Scholar] [CrossRef] [Green Version]
- Nitta, N.; Wu, F.; Lee, J.T.; Yushin, G. Li-ion battery materials: Present and future. Mater. Today 2015, 18, 252–264. [Google Scholar] [CrossRef]
- Winkler, M.; Rhein, F.; Nirschl, H.; Gleiss, M. Real-Time Modeling of Volume and Form Dependent Nanoparticle Fractionation in Tubular Centrifuges. Nanomaterials 2022, 12, 3161. [Google Scholar] [CrossRef]
- Plüisch, C.S.; Bössenecker, B.; Dobler, L.; Wittemann, A. Zonal rotor centrifugation revisited: New horizons in sorting nanoparticles. RSC Adv. 2019, 9, 27549–27559. [Google Scholar] [CrossRef] [Green Version]
- Leschonski, K. The feasibility of producing small cut sizes in an electrostatic classifier. Powder Technol. 1987, 51, 49–59. [Google Scholar] [CrossRef]
- Thajudeen, T.; Walter, J.; Srikantharajah, R.; Lübbert, C.; Peukert, W. Determination of the length and diameter of nanorods by a combination of analytical ultracentrifugation and scanning mobility particle sizer. Nanoscale Horiz. 2017, 2, 253–260. [Google Scholar] [CrossRef] [PubMed]
- Barasinski, M.; Hilbig, J.; Neumann, S.; Rafaja, D.; Garnweitner, G. Simple model of the electrophoretic migration of spherical and rod-shaped Au nanoparticles in gels with varied mesh sizes. Colloids Surf. A Physicochem. Eng. Asp. 2022, 651, 129716. [Google Scholar] [CrossRef]
- Segets, D.; Komada, S.; Butz, B.; Spiecker, E.; Mori, Y.; Peukert, W. Quantitative evaluation of size selective precipitation of Mn-doped ZnS quantum dots by size distributions calculated from UV/Vis absorbance spectra. J. Nanopart. Res. 2013, 15, 1486. [Google Scholar] [CrossRef]
- Michaud, V.; Pracht, J.; Schilfarth, F.; Damm, C.; Platzer, B.; Haines, P.; Harreiß, C.; Guldi, D.M.; Spiecker, E.; Peukert, W. Well-separated water-soluble carbon dots via gradient chromatography. Nanoscale 2021, 13, 13116–13128. [Google Scholar] [CrossRef]
- Hersam, M.C. Progress towards monodisperse single-walled carbon nanotubes. Nat. Nanotechnol. 2008, 3, 387–394. [Google Scholar] [CrossRef]
- Gromotka, L.; Uttinger, M.J.; Schlumberger, C.; Thommes, M.; Peukert, W. Classification and characterization of multimodal nanoparticle size distributions by size-exclusion chromatography. Nanoscale 2022, 14, 17354–17364. [Google Scholar] [CrossRef]
- Süβ, S.; Bartsch, K.; Wasmus, C.; Damm, C.; Segets, D.; Peukert, W. Chromatographic property classification of narrowly distributed ZnS quantum dots. Nanoscale 2020, 12, 12114–12125. [Google Scholar] [CrossRef]
- Backes, C.; Szydłowska, B.M.; Harvey, A.; Yuan, S.; Vega-Mayoral, V.; Davies, B.R.; Zhao, P.-L.; Hanlon, D.; Santos, E.J.G.; Katsnelson, M.I.; et al. Production of Highly Monolayer Enriched Dispersions of Liquid-Exfoliated Nanosheets by Liquid Cascade Centrifugation. ACS Nano 2016, 10, 1589–1601. [Google Scholar] [CrossRef]
- Buchwald, T.; Ditscherlein, R.; Peuker, U.A. Beschreibung von Trennoperationen mit mehrdimensionalen Partikeleigenschaftsverteilungen. Chem. Ing. Tech. 2023, 95, 199–209. [Google Scholar] [CrossRef]
- Frank, U.; Uttinger, M.J.; Wawra, S.E.; Lübbert, C.; Peukert, W. Progress in Multidimensional Particle Characterization. KONA Powder Part. J. 2022, 39, 3–28. [Google Scholar] [CrossRef]
- Wawra, S.E.; Pflug, L.; Thajudeen, T.; Kryschi, C.; Stingl, M.; Peukert, W. Determination of the two-dimensional distributions of gold nanorods by multiwavelength analytical ultracentrifugation. Nat. Commun. 2018, 9, 4898. [Google Scholar] [CrossRef] [PubMed]
- Walter, J.; Gorbet, G.; Akdas, T.; Segets, D.; Demeler, B.; Peukert, W. 2D analysis of polydisperse core-shell nanoparticles using analytical ultracentrifugation. Analyst 2016, 142, 206–217. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Frank, U.; Drobek, D.; Sanchez-Iglesias, A.; Wawra, S.; Nees, N.; Walter, J.; Pflug, L.; Apeleo Zubiri, B.; Spiecker, E.; Liz-Marzan, L.; et al. Determination of 2D particle size distributions in plasmonic nanoparticle colloids via analytical ultracentrifugation - Application to gold bipyramids. ACS Nano 2023, 17, 5785–5798. [Google Scholar] [CrossRef] [PubMed]
- Furat, O.; Leißner, T.; Ditscherlein, R.; Šedivý, O.; Weber, M.; Bachmann, K.; Gutzmer, J.; Peuker, U.; Schmidt, V. Description of Ore Particles from X-Ray Microtomography (XMT) Images, Supported by Scanning Electron Microscope (SEM)-Based Image Analysis. Microsc. Microanal. 2018, 24, 461–470. [Google Scholar] [CrossRef]
- Buchmann, M.; Schach, E.; Tolosana-Delgado, R.; Leißner, T.; Astoveza, J.; Kern, M.; Möckel, R.; Ebert, D.; Rudolph, M.; van den Boogaart, K.; et al. Evaluation of Magnetic Separation Efficiency on a Cassiterite-Bearing Skarn Ore by Means of Integrative SEM-Based Image and XRF–XRD Data Analysis. Minerals 2018, 8, 390. [Google Scholar] [CrossRef] [Green Version]
- Segets, D.; Lutz, C.; Yamamoto, K.; Komada, S.; Süß, S.; Mori, Y.; Peukert, W. Classification of Zinc Sulfide Quantum Dots by Size: Insights into the Particle Surface–Solvent Interaction of Colloids. J. Phys. Chem. C 2015, 119, 4009–4022. [Google Scholar] [CrossRef]
- Leschonski, K.; Alex, W.; Koglin, B. Teilchengrößenanalyse. 1. Darstellung und Auswertung von Teilchengrößenverteilungen. Chem. Ing. Tech. 1974, 46, 23–26. [Google Scholar] [CrossRef]
- Leschonski, K.; Alex, W.; Koglin, B. Teilchengrößenanalyse. 1. Darstellung und Auswertung von Teilchengrößenverteilungen (Fortsetzung). Chem. Ing. Tech. 1974, 46, 101–106. [Google Scholar] [CrossRef]
- Stiess, M. Mechanische Verfahrenstechnik—Partikeltechnologie 1, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-540-32551-2. [Google Scholar]
- Modena, M.M.; Rühle, B.; Burg, T.P.; Wuttke, S. Nanoparticle Characterization: What to Measure? Adv. Mater. 2019, 31, e1901556. [Google Scholar] [CrossRef]
- Coulson, J.M.; Richardson, J.F. Coulson and Richardson’s Chemical Engineering, 6th ed.; Butterworth-Heinemann: Amsterdam, The Netherlands, 2018; ISBN 9780081010976. [Google Scholar]
- Liang, S. Numerical Study of Classification of Ultrafine Particles in a Gas-Solid Field of Elbow-Jet Classifier. Chem. Eng. Commun. 2010, 197, 1016–1032. [Google Scholar] [CrossRef]
- Giddings, J.C. Field-flow fractionation: Analysis of macromolecular, colloidal, and particulate materials. Science 1993, 260, 1456–1465. [Google Scholar] [CrossRef] [PubMed]
- Schach, E.; Buchmann, M.; Tolosana-Delgado, R.; Leißner, T.; Kern, M.; van den Gerald Boogaart, K.; Rudolph, M.; Peuker, U.A. Multidimensional characterization of separation processes—Part 1: Introducing kernel methods and entropy in the context of mineral processing using SEM-based image analysis. Miner. Eng. 2019, 137, 78–86. [Google Scholar] [CrossRef]
- Buchmann, M.; Schach, E.; Leißner, T.; Kern, M.; Mütze, T.; Rudolph, M.; Peuker, U.A.; Tolosana-Delgado, R. Multidimensional characterization of separation processes—Part 2: Comparability of separation efficiency. Miner. Eng. 2020, 150, 106284. [Google Scholar] [CrossRef]
- Cardenas Lopez, P.; Uttinger, M.J.; Traoré, N.E.; Khan, H.A.; Drobek, D.; Apeleo Zubiri, B.; Spiecker, E.; Pflug, L.; Peukert, W.; Walter, J. Multidimensional characterization of noble metal alloy nanoparticles by multiwavelength analytical ultracentrifugation. Nanoscale 2022, 14, 12928–12939. [Google Scholar] [CrossRef] [PubMed]
- Esper, J.D.; Liu, L.; Willnauer, J.; Strobel, A.; Schwenger, J.; Romeis, S.; Peukert, W. Scalable production of glass flakes via compression in the liquid phase. Adv. Powder Technol. 2020, 31, 4145–4156. [Google Scholar] [CrossRef]
- Hansen, S. Translational friction coefficients for cylinders of arbitrary axial ratios estimated by Monte Carlo simulation. J. Chem. Phys. 2004, 121, 9111–9115. [Google Scholar] [CrossRef] [PubMed]
- Esper, J.D.; Maußner, F.; Romeis, S.; Zhuo, Y.; Barr, M.K.S.; Yokosawa, T.; Spiecker, E.; Bachmann, J.; Peukert, W. SiO2–GeO2 Glass–Ceramic Flakes as an Anode Material for High-Performance Lithium-Ion Batteries. Energy Tech. 2022, 10, 2200072. [Google Scholar] [CrossRef]
- Coelho, M.; Medronho, R. A model for performance prediction of hydrocyclones. Chem. Eng. J. 2001, 84, 7–14. [Google Scholar] [CrossRef]
- Castilho, L.R.; Medronho, R.A. A simple procedure for design and performance prediction of Bradley and Rietema hydrocyclones. Miner. Eng. 2000, 13, 183–191. [Google Scholar] [CrossRef]
- Neesse, T.; Dueck, J.; Schwemmer, H.; Farghaly, M. Using a high pressure hydrocyclone for solids classification in the submicron range. Miner. Eng. 2015, 71, 85–88. [Google Scholar] [CrossRef]
- Niazi, S.; Habibian, M.; Rahimi, M. A Comparative Study on the Separation of Different-Shape Particles Using a Mini-Hydrocyclone. Chem. Eng. Technol. 2017, 40, 699–708. [Google Scholar] [CrossRef]
- Tarleton, E.S.; Wakeman, R.J. Solid/Liquid Separation Equipment. Solid/Liquid Separation; Elsevier: Amsterdam, The Netherlands, 2007; pp. 1–77. ISBN 9781856174213. [Google Scholar]
- Mannweiler, K.; Hoare, M. The scale-down of an industrial disc stack centrifuge. Bioprocess Eng. 1992, 8, 19–25. [Google Scholar] [CrossRef]
- Maybury, J.P.; Mannweiler, K.; Titchener-Hooker, N.J.; Hoare, M.; Dunnill, P. The performance of a scaled down industrial disc stack centrifuge with a reduced feed material requirement. Bioprocess Eng. 1998, 18, 191. [Google Scholar] [CrossRef]
- Piesche, M.; Zink, A.; Schütz, S. Strömungs- und Trennverhalten von Tellerseparatoren zur Abscheidung von Ölnebelaerosolen, Untersuchungen zum Rotor/Rotor-Konzept. Chem. Ing. Tech. 2008, 80, 1487–1500. [Google Scholar] [CrossRef]
- Furat, O.; Frank, U.; Weber, M.; Wawra, S.; Peukert, W.; Schmidt, V. Estimation of bivariate probability distributions of nanoparticle characteristics, based on univariate measurements. Inverse Probl. Sci. Eng. 2021, 29, 1343–1368. [Google Scholar] [CrossRef]
- Rietema, K. Performance and design of hydrocyclones—III: Separating power of the hydrocyclone. Chem. Eng. Sci. 1961, 15, 310–319. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Frank, U.; Dienstbier, J.; Tischer, F.; Wawra, S.E.; Gromotka, L.; Walter, J.; Liers, F.; Peukert, W. Multidimensional Fractionation of Particles. Separations 2023, 10, 252. https://doi.org/10.3390/separations10040252
Frank U, Dienstbier J, Tischer F, Wawra SE, Gromotka L, Walter J, Liers F, Peukert W. Multidimensional Fractionation of Particles. Separations. 2023; 10(4):252. https://doi.org/10.3390/separations10040252
Chicago/Turabian StyleFrank, Uwe, Jana Dienstbier, Florentin Tischer, Simon E. Wawra, Lukas Gromotka, Johannes Walter, Frauke Liers, and Wolfgang Peukert. 2023. "Multidimensional Fractionation of Particles" Separations 10, no. 4: 252. https://doi.org/10.3390/separations10040252