Mass Transfer and Droplet Behaviors in Liquid-Liquid Extraction Process Based on Multi-Scale Perspective: A Review
Abstract
1. Introduction
2. Equipment Scale
3. Droplet Scale
3.1. Droplet Breakage
| Authors | Experimental Setup | Conditions | Subject | Objectives |
|---|---|---|---|---|
| Maaβ et al. [70] | Stirred tank | No mass transfer | Single droplet | Breakage probability |
| Zhang et al. [71] | Reciprocating plate column | No mass transfer | Single droplet | Breakage probability |
| Korb et al. [73] | Kühni column | Mass transfer Chemical reaction | Single droplet | Breakage probability; Daughter droplet size distribution |
| Zhou et al. [74,75] | Pulsed disc-and-doughnut column | No mass transfer | Droplet swarm | Breakage frequency; Daughter droplet size distribution |
| Zhou [76] | Stirred tank | No mass transfer | Droplet swarm | Breakage frequency; Daughter droplet size distribution |
| Wang et al. [78,79] | Pulsed disc-and-doughnut column | Mass transfer | Droplet swarm | Effect of mass transfer |
3.2. Droplet Coalescence
4. Interface Scale
4.1. Dynamic Interfacial Tension
4.2. Force between Interfaces
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Glossary
| Nomenclature | |
| Bb | Birth source term of breakage, m−4·s−1 |
| Bc | Birth source term of coalescence, m−4·s−1 |
| B | Breakage frequency, s−1 |
| C1 | Adjustable parameter |
| C2 | Adjustable parameter |
| C3 | Adjustable parameter |
| C4 | Adjustable parameter |
| D | Diffusion coefficient, m2·s−1 |
| Db | Death source term of breakage, m−4·s−1 |
| Dc | Death source term of coalescence, m−4·s−1 |
| d | Diameter, m |
| d32 | Sauter mean diameter, m |
| Ec | Axial diffusion coefficient, m2·s−1 |
| Ecollision | Kinetic collision energy, kg·m2·s−2 |
| Einterfacial | Interfacial energy, kg·m2·s−2 |
| Fβi | Daughter droplet size distribution function (intermediate tensile breakage), 1·m−1 |
| Fβo | Daughter droplet size distribution function (original tensile breakage), 1·m−1 |
| Fβr | Daughter droplet size distribution function (revolving breakage), 1·m−1 |
| fv | Volume ratio of daughter droplet to mother droplet |
| g | Gravitational acceleration, m·s−2 |
| H | Film thickness, m |
| h | Coalescence frequency, m3·s−1 |
| K | Mass transfer coefficient, m·s−1 |
| kc | Mass transfer coefficient of continuous phase, m·s−1 |
| kd | Mass transfer coefficient of dispersed phase, m·s−1 |
| M | Distribution coefficient |
| n | Number density, m−4 |
| p | Pressure, Pa |
| pco | Droplet cohesive force, Pa |
| pv,c | Viscous stress of continuous phase, Pa |
| r | Spatial coordinate, m |
| r | Radial distance, m |
| S | Source term, m−4·s−1 |
| Sb | Breakage source term, m−4·s−1 |
| Sc | Coalescence source term, m−4·s−1 |
| Shc | Continuous phase Sherwood number |
| Shd | Dispersed phase Sherwood number |
| tdrainage | Film drainage time, s |
| tcontact | Droplet contact time, s |
| ucrit | Critical velocity, m·s−1 |
| ucha | Characteristic velocity (collision), m·s−1 |
| U | Bulk velocity, m·s−1 |
| uf | Flooding velocity, m·s−1 |
| Vd | Velocity of dispersed phase, m·s−1 |
| Vc | Velocity of continuous phase, m·s−1 |
| Vslip | Slip velocity, m·s−1 |
| V0 | Characteristic velocity, m·s−1 |
| Wed | Droplet Weber number |
| WeL | Dimensionless Weber number |
| z | Height, m |
| β | Daughter droplet size distribution function, 1·m−1 |
| Γ | The effect the column geometrical characteristics |
| Γ(·) | Upper incomplete gamma function |
| γ | Interfacial tension, N/m |
| ε | Turbulence dissipation rate, m2·s−3 |
| λ | Coalescence efficiency |
| μc | Viscosity of continuous phase, Pa·s |
| μd | Viscosity of dispersed phase, Pa·s |
| Π | The effect of the power input per unit mass |
| ρc | Density of continuous phase, kg·m−3 |
| ρd | Density of dispersed phase, kg·m−3 |
| Φ | The effect of the phase flow rates |
| φ | Hold-up |
| Ω | The effect of physical properties |
| ω | Collision frequency, s−1 |
| Abbreviations | |
| AFM | Atomic force microscopy |
| CFD | Computational fluid dynamics |
| CMC | Critical micelle concentration |
| DBFF | Droplet breakup frequency function |
| LIF | Laser-induced fluorescence |
| MD | Molecular dynamics |
| PBM | Population balance model |
| PBE | Population balance equation |
| PLIF | Planner laser-induced fluorescence |
| RSD | Rainbow schlieren deflectometry |
| SFA | Surface force apparatus |
| TIRM | Total internal reflection microscopy |
| VOF | Volume of fluid method |
References
- Herbst, R.S.; Baron, P.; Nilsson, M. Standard and advanced separation: PUREX processes for nuclear fuel reprocessing. In Advanced Separation Techniques for Nuclear Fuel Reprocessing and Radioactive Waste Treatment; Nash, K.L., Lumetta, G.J., Eds.; Woodhead Publishing: Cambridge, UK, 2011; pp. 141–175. [Google Scholar]
- Guan, Y.X.; Zhu, Z.Q.; Mei, L.H. Technical aspects of extractive purification of penicillin fermentation broth by aqueous two-phase partitioning. Sep. Sci. Technol. 1996, 31, 2589–2597. [Google Scholar] [CrossRef]
- Flett, D.S. Solvent extraction in hydrometallurgy: The role of organophosphorus extractants. J. Organomet. Chem. 2005, 690, 2426–2438. [Google Scholar] [CrossRef]
- Kim, S.J.; Kim, S.C.; Kawasaki, J. Separation and recovery of bicyclic aromatic components in the light cycle oil. Sep. Sci. Technol. 2003, 38, 179–199. [Google Scholar] [CrossRef]
- Long, J.; Shen, B.X.; Ling, H.; Zhao, J.G.; Lu, J.C. Novel solvent deasphalting process by vacuum residue blending with coal tar. Ind. Eng. Chem. Res. 2011, 50, 11259–11269. [Google Scholar] [CrossRef]
- Chagnes, A.; Pospiech, B. A brief review on hydrometallurgical technologies for recycling spent lithium-ion batteries. J. Chem. Technol. Biotechnol. 2013, 88, 1191–1199. [Google Scholar] [CrossRef]
- Smink, D.; Kersten, S.R.A.; Schuur, B. Recovery of lignin from deep eutectic solvents by liquid-liquid extraction. Sep. Purif. Technol. 2020, 235, 116127. [Google Scholar] [CrossRef]
- Sampaio, C.I.; Sousa, L.F.; Dias, A.M. Separation of anthocyaninic and nonanthocyaninic flavonoids by liquid-liquid extraction based on their acid-base properties: A green chemistry approach. J. Chem. Educ. 2020, 97, 4533–4539. [Google Scholar] [CrossRef]
- Molino, A.; Mehariya, S.; Di Sanzo, G.; Larocca, V.; Martino, M.; Leone, G.P.; Marino, T.; Chianese, S.; Balducchi, R.; Musmarra, D. Recent developments in supercritical fluid extraction of bioactive compounds from microalgae: Role of key parameters, technological achievements and challenges. J. CO2 Util. 2020, 36, 196–209. [Google Scholar] [CrossRef]
- Pena-Pereira, F.; Namiesnik, J. Ionic liquids and deep eutectic mixtures: Sustainable solvents for extraction processes. ChemSusChem 2014, 7, 1784–1800. [Google Scholar] [CrossRef]
- TeGrotenhuis, W.E.; Cameron, R.J.; Viswanathan, V.V.; Wegeng, R.S. Solvent extraction and gas absorption using microchannel contactors. In Proceedings of the 3rd International Conference on Microreaction Technology, New Orleans, LA, USA, 18–21 April 1999; pp. 541–549. [Google Scholar]
- Song, J.F.; Niu, X.H.; Li, X.M.; He, T. Selective separation of copper and nickel by membrane extraction using hydrophilic nanoporous ion-exchange barrier membranes. Process Saf. Environ. Prot. 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Takahashi, K.; Abdel-Tawab, A.A.S.; Nii, S.; Yajima, T.; Kawaizumi, F. Extraction of rare earth metals with a multistage mixer-settler extraction column. Chem. Eng. Sci. 2002, 57, 469–478. [Google Scholar] [CrossRef]
- Ferreira, A.E.; Agarwal, S.; Machado, R.M.; Gameiro, M.L.F.; Santos, S.M.C.; Reis, M.T.A.; Ismael, M.R.C.; Correia, M.J.N.; Carvalho, J.M.R. Extraction of copper from acidic leach solution with Acorga M5640 using a pulsed sieve plate column. Hydrometallurgy 2010, 104, 66–75. [Google Scholar] [CrossRef]
- Hamamah, Z.A.; Grutzner, T. Liquid-liquid centrifugal extractors: Types and recent applications—A review. ChemBioEng Rev. 2022, 9, 286–318. [Google Scholar] [CrossRef]
- Wang, K.; Luo, G.S. Microflow extraction: A review of recent development. Chem. Eng. Sci. 2017, 169, 18–33. [Google Scholar] [CrossRef]
- Aoki, N.; Tanigawa, S.; Mae, K. A new index for precise design and advanced operation of mass transfer in slug flow. Chem. Eng. J. 2011, 167, 651–656. [Google Scholar] [CrossRef]
- Roumpea, E.; Chinaud, M.; Angeli, P. Experimental investigations of non-Newtonian/Newtonian liquid-liquid flows in microchannels. AIchE J. 2017, 63, 3599–3609. [Google Scholar] [CrossRef]
- Ghaini, A.; Mescher, A.; Agar, D.W. Hydrodynamic studies of liquid-liquid slug flows in circular microchannels. Chem. Eng. Sci. 2011, 66, 1168–1178. [Google Scholar] [CrossRef]
- Kowalczuk, P.B. Determination of critical coalescence concentration and bubble size for surfactants used as flotation frothers. Ind. Eng. Chem. Res. 2013, 52, 11752–11757. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Tabrizi, H.B.; Ahmadi, G. Geometry effect on deposition and residence time of polydisperse fine drops in mini-risers under developing flow condition. Part. Sci. Technol. 2014, 32, 560–575. [Google Scholar] [CrossRef]
- Loth, E.; O’Brien, T.; Syamlal, M.; Cantero, M. Effective diameter for group motion of polydisperse particle mixtures. Powder Technol. 2004, 142, 209–218. [Google Scholar] [CrossRef]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIchE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Calabrese, R.V.; Chang, T.P.K.; Dang, P.T. Drop breakup in turbulent stirred-tank contactors.1. Effect of dispersed-phase viscosity. AIchE J. 1986, 32, 657–666. [Google Scholar] [CrossRef]
- Fischer, E.A. Drop sizes in agitated liquid-liquid extraction columns. Effect of physical properties, column geometry, agitator type and agitation speed. Verfahrenstechnik 1971, 5, 360–365. [Google Scholar]
- Rincón Rubio, L.M. On the Hydrodynamics of a Wirz-II Extraction Column. Ph.D. Thesis, Swiss Federal Institute of Technology, Zurich, Swiss, 1992. [Google Scholar]
- Kumar, A.; Hartland, S. Unified correlations for the prediction of drop size in liquid-liquid extraction columns. Ind. Eng. Chem. Res. 1996, 35, 2682–2695. [Google Scholar] [CrossRef]
- Jahya, A.B.; Stevens, G.W.; Pratt, H.R.C. Pulsed disc-and-doughnut column performance. Solvent Extr. Ion Exch. 2009, 27, 63–82. [Google Scholar] [CrossRef]
- Rohlfing, E.; Hartmann, H. Effect of mass-transfer on droplet size in a pulsed packed extraction column. Chem. Ing. Tech. 1992, 64, 470–471. [Google Scholar] [CrossRef]
- Kumar, A.; Hartland, S. A unified correlation for the prediction of dispersed-phase hold-up in liquid-liquid extraction columns. Ind. Eng. Chem. Res. 1995, 34, 3925–3940. [Google Scholar] [CrossRef]
- Gayler, R.; Pratt, H. Holdup and pressure drop in packed columns. Trans. Inst. Chem. Eng. 1951, 29, 110–125. [Google Scholar]
- Tsouris, C.; Tavlarides, L.L. Mass-transfer effects on droplet phenomena and extraction column hydrodynamics revisited. Chem. Eng. Sci 1993, 48, 1503–1515. [Google Scholar] [CrossRef]
- Kumar, A.; Hartland, S. Prediction of drop size, dispersed-phase holdup, slip velocity, and limiting throughputs in packed extraction columns. Chem. Eng. Res. Des. 1994, 72, 89–104. [Google Scholar]
- Yu, J.; Fei, W.Y. Hydrodynamics and mass transfer in a pulsed packed column. Can. J. Chem. Eng. 2000, 78, 1040–1045. [Google Scholar]
- Charton, S.; Duhamet, J.; Borda, G.; Ode, D. Axial dispersion in pulsed disk and doughnut columns: A unified law. Chem. Eng. Sci. 2012, 75, 468–477. [Google Scholar] [CrossRef]
- Panahinia, F.; Safdari, J.; Ghannadi-Maragheh, M.; Amani, P.; Mallah, M.H. Modeling and simulation of a horizontal pulsed sieve-plate extraction column using axial dispersion model. Sep. Sci. Technol. 2017, 52, 1537–1552. [Google Scholar] [CrossRef]
- Whitman, W.G. The two-film theory of gas absorption. Chem. Metall. Eng. 1923, 29, 146–148. [Google Scholar] [CrossRef]
- Higbie, R. The rate of absorption of a pure gas into a still liquid during short periods of exposure. Trans. Am. Inst. Chem. Eng. 1935, 31, 365–389. [Google Scholar]
- Danckwerts, P.V. Significance of liquid-film coefficients in gas absorption. Ind. Eng. Chem. 1951, 43, 1460–1467. [Google Scholar] [CrossRef]
- Kumar, A.; Hartland, S. Correlations for prediction of mass transfer coefficients in single drop systems and liquid-liquid extraction columns. Chem. Eng. Res. Des. 1999, 77, 372–384. [Google Scholar] [CrossRef]
- Torab-Mostaedi, M.; Safdari, J. Mass transfer coefficients in a pulsed packed extraction column. Chem. Eng. Process. 2009, 48, 1321–1326. [Google Scholar] [CrossRef]
- Asadollahzadeh, M.; Ghaemi, A.; Torab-Mostaedi, M.; Shahhosseini, S. Experimental mass transfer coefficients in a pilot plant multistage column extractor. Chin. J. Chem. Eng. 2016, 24, 989–999. [Google Scholar] [CrossRef]
- Li, S.W.; Jing, S.; Zhang, Q.; Wu, Q.L. Advances in simulation of liquid-liquid two-phase flow in extraction columns with CFD-PBM. Chin. J. Process Eng. 2012, 12, 702–711. [Google Scholar]
- Yu, X. Population Balance Modeling of Liquid–Liquid Two-Phase Flows in Pulsed Disc and Doughnut Columns and the Application. Ph.D. Thesis, Tsinghua University, Beijing, China, 2021. [Google Scholar]
- Fang, Q.; Jing, D.; Zhou, H.; Li, S.W. Population balance of droplets in a pulsed disc and doughnut column with wettable internals. Chem. Eng. Sci. 2017, 161, 274–287. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, H.; Jing, S.; Lan, W.J.; Li, S.W. Augmented CFD-PBM simulation of liquid-liquid two-phase flows in liquid extraction columns with wettable internal plates. Ind. Eng. Chem. Res. 2020, 59, 8436–8446. [Google Scholar] [CrossRef]
- Drumm, C.; Attarakih, M.M.; Bart, H.J. Coupling of CFD with DPBM for an RDC extractor. Chem. Eng. Sci. 2009, 64, 721–732. [Google Scholar] [CrossRef]
- Mirzaie, M.; Sarrafi, A.; Pour, H.H.; Baghaie, A.; Molaeinasab, M. Experimental investigation and CFD modeling of hydrodynamic parameters in a pulsed packed column. Solvent Extr. Ion Exch. 2016, 34, 643–660. [Google Scholar] [CrossRef]
- Amokrane, A.; Charton, S.; Sheibat-Othman, N.; Becker, J.; Klein, J.P.; Puel, F. Development of a CFD-PBE coupled model for the simulation of the drops behaviour in a pulsed column. Can. J. Chem. Eng. 2014, 92, 220–233. [Google Scholar] [CrossRef]
- Yu, X.; Zhou, H.; Jing, S.; Lan, W.J.; Li, S.W. CFD-PBM simulation of two-phase flow in a pulsed disc and doughnut column with directly measured breakup kernel functions. Chem. Eng. Sci. 2019, 201, 349–361. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, X.; Wang, B.; Jing, S.; Lan, W.J.; Li, S.W. CFD-PBM simulation of liquid-liquid dispersions in a pump-mixer. Ind. Eng. Chem. Res. 2021, 60, 1926–1938. [Google Scholar] [CrossRef]
- Bahmanyar, H.; Slater, M.J. Studies of drop break-up in liquid-liquid systems in a rotating disc contactor. Part I: Conditions of no mass transfer. Chem. Eng. Technol. 1991, 14, 79–89. [Google Scholar] [CrossRef]
- Bahmanyar, H.; Roy Rean, D.; Dowling, I.C.; Ramlochan, K.M.; Slater, M.J.; Yu, W. Studies of drop break-up in liquid-liquid systems in a rotating disc contactor. Part II: Effects of mass transfer and scale-up. Chem. Eng. Technol. 1991, 14, 178–185. [Google Scholar] [CrossRef]
- Cauwenberg, V.; Degreve, J.; Slater, M.J. The interaction of solute transfer, contaminants and drop break-up in rotating disc contactors: Part I. Correlation of drop breakage probabilities. Can. J. Chem. Eng. 1997, 75, 1046–1055. [Google Scholar] [CrossRef]
- Cauwenberg, V.; Degreve, J.; Slater, M.J. The interaction of solute transfer, contaminants and drop break-up in rotating disc contactors: Part II. The coupling of the mass transfer and breakage processes via interfacial tension. Can. J. Chem. Eng. 1997, 75, 1056–1066. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, S.W.; Tan, J.; Wang, Y.J.; Luo, G.S. Preparation of highly monodisperse droplet in a T-junction microfluidic device. AIchE J. 2006, 52, 3005–3010. [Google Scholar] [CrossRef]
- Steegmans, M.L.J.; De Ruiter, J.; Schroen, K.G.P.H.; Boom, R.M. A descriptive force-balance model for droplet formation at microfluidic Y-junctions. AIchE J. 2010, 56, 2641–2649. [Google Scholar] [CrossRef]
- Xu, J.H.; Luo, G.S.; Chen, G.G.; Wang, J.D. Experimental and theoretical approaches on droplet formation from a micrometer screen hole. J. Membr. Sci. 2005, 266, 121–131. [Google Scholar] [CrossRef]
- Xu, J.H.; Li, S.W.; Lan, W.J.; Luo, G.S. Microfluidic approach for rapid interfacial tension measurement. Langmuir 2008, 24, 11287–11292. [Google Scholar] [CrossRef] [PubMed]
- Zhou, H.B.; Yao, Y.; Chen, Q.; Li, G.; Yao, S.H. A facile microfluidic strategy for measuring interfacial tension. Appl. Phys. Lett. 2013, 103, 234102. [Google Scholar] [CrossRef]
- Wang, K.; Lu, Y.C.; Xu, J.H.; Luo, G.S. Determination of dynamic interfacial tension and its effect on droplet formation in the T-shaped microdispersion process. Langmuir 2009, 25, 2153–2158. [Google Scholar] [CrossRef]
- Wang, X.Y.; Riaud, A.; Wang, K.; Luo, G.S. Pressure drop-based determination of dynamic interfacial tension of droplet generation process in T-junction microchannel. Microfluid. Nanofluidics 2015, 18, 503–512. [Google Scholar] [CrossRef]
- Brosseau, Q.; Vrignon, J.; Baret, J.C. Microfluidic dynamic interfacial tensiometry (μDIT). Soft Matter 2014, 10, 3066–3076. [Google Scholar] [CrossRef] [PubMed]
- Moire, M.; Peysson, Y.; Herzhaft, B.; Pannacci, N.; Gallaire, F.; Augello, L.; Dalmazzone, C.; Colin, A. Ultralow interfacial tension measurement through jetting/dripping transition. Langmuir 2017, 33, 2531–2540. [Google Scholar] [CrossRef]
- Li, S.W.; Xu, J.H.; Wang, Y.J.; Luo, G.S. Controllable preparation of nanoparticles by drops and plugs flow in a microchannel device. Langmuir 2008, 24, 4194–4199. [Google Scholar] [CrossRef] [PubMed]
- Lan, W.J.; Wang, C.; Guo, X.Q.; Li, S.W.; Luo, G.S. Study on the transient interfacial tension in a microfluidic droplet formation coupling interphase mass transfer process. AIchE J. 2016, 62, 2542–2549. [Google Scholar] [CrossRef]
- Lan, W.J.; Wang, Z.H.; Wang, M.; Liu, D.; Guo, X.Q.; Sun, Q.; Li, X.X.; Li, S.W. Determination of transient interfacial tension in a microfluidic device using a Laplace sensor. Chem. Eng. Sci. 2019, 209, 115207. [Google Scholar] [CrossRef]
- Liao, Y.X.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Singh, K.K.; Mahajani, S.M.; Shenoy, K.T.; Ghosh, S.K. Population balance modeling of liquid-liquid dispersions in homogeneous continuous-flow stirred tank. Ind. Eng. Chem. Res. 2009, 48, 8121–8133. [Google Scholar] [CrossRef]
- Maaß, S.; Kraume, M. Determination of breakage rates using single drop experiments. Chem. Eng. Sci. 2012, 70, 146–164. [Google Scholar] [CrossRef]
- Zhang, J.Y.Z.; Berry, J.D.; Mumford, K.A.; Harvie, D.J.E.; Fei, W.Y.; Stevens, G.W.; Wang, Y.D. Single drop breakage in a reciprocating plate column. Chem. Eng. J. 2021, 415, 129049. [Google Scholar] [CrossRef]
- Zhang, J.Y.Z.; Li, W.; Mumford, K.; Fei, W.Y.; Stevens, G.; Wang, Y.D. Drop sizes and population balance model for a Karr column. AIchE J. 2022, 68, e17413. [Google Scholar] [CrossRef]
- Korb, C.; Bart, H.J. Solvent extraction in columns in a droplet breakage domain. Hydrometallurgy 2017, 173, 71–79. [Google Scholar] [CrossRef]
- Zhou, H.; Jing, S.; Yu, X.; Zhou, H.; Lan, W.J.; Li, S.W. Study of droplet breakage in a pulsed disc and doughnut column-Part I: Experiments and correlations. Chem. Eng. Sci. 2019, 197, 172–183. [Google Scholar] [CrossRef]
- Zhou, H.; Jing, S.; Fang, Q.; Li, S.W.; Lan, W.J. Direct measurement of droplet breakage in a pulsed disc and doughnut column. AIchE J. 2017, 63, 4188–4200. [Google Scholar] [CrossRef]
- Zhou, H. Studies on the Breakup Behavior of Drop Swarms in Turbulent Flow. Ph.D. Thesis, Tsinghua University, Beijing, China, 2021. [Google Scholar]
- Yu, X.; Zhou, H.; Jing, S.; Lan, W.J.; Li, S.W. Experimental and numerical study of liquid-liquid interphase mass transfer in a pilot-scale extraction column. Chem. Eng. Sci. 2021, 230, 116184. [Google Scholar] [CrossRef]
- Wang, B.; Zhou, H.; Yu, X.; Jing, S.; Zheng, Q.; Lan, W.J.; Li, S.W. Determination of dynamic interfacial tension in a pulsed column under mass transfer condition. AIchE J. 2020, 66, e16257. [Google Scholar] [CrossRef]
- Wang, B. Studies on the Effect of Mass Transfer on Interfacial Tension and Droplet Breakage in a Pulsed Extraction Column. Ph.D. Thesis, Tsinghua University, Beijing, China, 2022. [Google Scholar]
- Krakau, F.; Kraume, M. 3D single bubble breakup tracking in a stirred tank. Chem. Ing. Tech. 2019, 91, 980–990. [Google Scholar] [CrossRef]
- Kamp, J.; Villwock, J.; Kraume, M. Drop coalescence in technical liquid/liquid applications: A review on experimental techniques and modeling approaches. Rev. Chem. Eng. 2017, 33, 1–47. [Google Scholar] [CrossRef]
- Simon, M. Koaleszenz von Tropfen und Tropfenschwärmen. Ph.D. Thesis, Technischen Universität Kaiserslautern, Kaiserslautern, Germany, 2004. [Google Scholar]
- Kovalchuk, N.M.; Reichow, M.; Frommweiler, T.; Vigolo, D.; Simmons, M.J.H. Mass transfer accompanying coalescence of surfactant-laden and surfactant-free drop in a microfluidic channel. Langmuir 2019, 35, 9184–9193. [Google Scholar] [CrossRef]
- Yi, H.Z.; Zhu, C.Y.; Fu, T.T.; Ma, Y.G. Efficient coalescence of microdroplet in the cross-focused microchannel with symmetrical chamber. J. Taiwan Inst. Chem. Eng. 2020, 112, 52–59. [Google Scholar] [CrossRef]
- Deng, Y.J.; Guo, W.X.; Zhu, C.Y.; Fu, T.T.; Ma, Y.G. Coalescence dynamics of two droplets in T-junction microchannel with a lantern-shaped expansion chamber. J. Taiwan Inst. Chem. Eng. 2022, 131, 104193. [Google Scholar] [CrossRef]
- Gao, C.H.; Ling, S.D.; Chen, Z.; Wang, Y.D.; Xu, J.H. Coalescence law of microdroplet swarms in microchannels. Chem. Eng. Sci. 2022, 262, 118055. [Google Scholar] [CrossRef]
- Narayan, S.; Makhnenko, I.; Moravec, D.B.; Hauser, B.G.; Dallas, A.J.; Dutcher, C.S. Insights into the microscale coalescence behavior of surfactant-stabilized droplets using a microfluidic hydrodynamic trap. Langmuir 2020, 36, 9827–9842. [Google Scholar] [CrossRef]
- Eiswirth, R.T.; Bart, H.J.; Ganguli, A.A.; Kenig, E.Y. Experimental and numerical investigation of binary coalescence: Liquid bridge building and internal flow fields. Phys. Fluids 2012, 24, 062108. [Google Scholar] [CrossRef]
- Kamp, J.; Kraume, M. Influence of drop size and superimposed mass transfer on coalescence in liquid/liquid dispersions—Test cell design for single drop investigations. Chem. Eng. Res. Des. 2014, 92, 635–643. [Google Scholar] [CrossRef]
- Coulaloglou, C.A.; Tavlarides, L.L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Liao, Y.X.; Lucas, D. A literature review on mechanisms and models for the coalescence process of fluid particles. Chem. Eng. Sci. 2010, 65, 2851–2864. [Google Scholar] [CrossRef]
- Howarth, W.J. Coalescence of drops in a turbulent flow field. Chem. Eng. Sci. 1964, 19, 33–38. [Google Scholar] [CrossRef]
- Howarth, W.J. Measurement of coalescence frequency in an agitated tank. AIchE J. 1967, 13, 1007–1013. [Google Scholar] [CrossRef]
- Lehr, F.; Millies, M.; Mewes, D. Bubble-size distributions and flow fields in bubble columns. AIchE J. 2002, 48, 2426–2443. [Google Scholar] [CrossRef]
- Lehr, F.; Mewes, D. A transport equation for the interfacial area density applied to bubble columns. Chem. Eng. Sci. 2001, 56, 1159–1166. [Google Scholar] [CrossRef]
- Kamp, J.; Kraume, M. From single drop coalescence to droplet swarms - Scale-up considering the influence of collision velocity and drop size on coalescence probability. Chem. Eng. Sci. 2016, 156, 162–177. [Google Scholar] [CrossRef]
- Vinogradova, O.I.; Yakubov, G.E. Dynamic effects on force measurements. 2. Lubrication and the atomic force microscope. Langmuir 2003, 19, 1227–1234. [Google Scholar] [CrossRef]
- Bhakta, A.; Ruckenstein, E. Decay of standing foams: Drainage, coalescence and collapse. Adv. Colloid Interface Sci. 1997, 70, 1–124. [Google Scholar] [CrossRef]
- Shi, C.; Cui, X.; Xie, L.; Liu, Q.X.; Chan, D.Y.C.; Israelachvili, J.N.; Zeng, H.B. Measuring forces and spatiotemporal evolution of thin water films between an air bubble and solid surfaces of different hydrophobicity. ACS Nano 2015, 9, 95–104. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Singapore, 2011; pp. 1–674. [Google Scholar]
- Sattari-Najafabadi, M.; Esfahany, M.N.N. Intensification of liquid-liquid mass transfer in a circular microchannel in the presence of sodium dodecyl sulfate. Chem. Eng. Process. 2017, 117, 9–17. [Google Scholar] [CrossRef]
- Eiswirth, R.T. Binary Droplet Coalescence of Free Rising Droplets. Ph.D. Thesis, Technischen Universität Kaiserslautern, Kaiserslautern, Germany, 2014. [Google Scholar]
- Klaseboer, E.; Chevaillier, J.P.; Gourdon, C.; Masbernat, O. Film drainage between colliding drops at constant approach velocity: Experiments and modeling. J. Colloid Interface Sci. 2000, 229, 274–285. [Google Scholar] [CrossRef]
- Yeo, L.Y.; Matar, O.K.; de Ortiz, E.S.P.; Hewitt, G.E. Film drainage between two surfactant-coated drops colliding at constant approach velocity. J. Colloid Interface Sci. 2003, 257, 93–107. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.H.; Lu, P.; Wang, Y.; Yang, C.; Mao, Z.S. Experimental investigation and numerical simulation of marangoni effect induced by mass transfer during drop formation. AIchE J. 2013, 59, 4424–4439. [Google Scholar] [CrossRef]
- Sawistowski, V.H.; James, B.R. Einfluß von oberflächenerscheinungen auf die stoffdurchgangszahlen bei der flüssig-flüssig-extraktion. Chem. Ing. Tech. 1963, 35, 175–179. [Google Scholar] [CrossRef]
- Heine, J.S.; Bart, H.J. Mass transfer during droplet formation—A measuring technique study. Chem. Ing. Tech. 2017, 89, 1635–1641. [Google Scholar] [CrossRef]
- Lan, W.J.; Cai, P.X.; Jing, S.; Li, S.W. Study on the dynamic interfacial tension with micro interface sensor. Chem. Eng. Sci. 2023, 268, 118439. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Chen, J.; Feng, X.; Mao, Z.S.; Yang, C. Visual dynamical measurement of the solute-induced Marangoni effect of a growing drop with a PLIF method. Chem. Eng. Sci. 2021, 233, 116401. [Google Scholar] [CrossRef]
- Heine, J.S.; Bart, H.J. Visualization of Mass Transfer during Droplet Formation. Chem. Eng. Technol. 2019, 42, 1388–1394. [Google Scholar] [CrossRef]
- Heine, J.S.; Schulz, J.M.; Junne, H.; Bohm, L.; Kraume, M.; Bart, H.J. Real-time visualization of internal and external concentration fields in multiphase systems via laser-induced fluorescence and rainbow schlieren deflectometry during and after droplet production. Chem. Ing. Tech. 2021, 93, 180–190. [Google Scholar] [CrossRef]
- Wegener, M.; Paschedag, A.R.; Kraume, M. Experimental examinations as well as 2D-and 3D simulations of mass transport in single drops with Marangoni convection. Chem. Ing. Tech. 2007, 79, 73–81. [Google Scholar] [CrossRef]
- Engberg, R.E.; Wegener, M.; Kenig, E.Y. The impact of Marangoni convection on fluid dynamics and mass transfer at deformable single rising droplets - A numerical study. Chem. Eng. Sci. 2014, 116, 208–222. [Google Scholar] [CrossRef]
- Yang, Q.J.; Mao, Q.; Cao, W. Numerical simulation of the Marangoni flow on mass transfer from single droplet with different Reynolds numbers. Colloid Surf. A 2022, 639, 128385. [Google Scholar] [CrossRef]
- Johansson, P.; Galliero, G.; Legendre, D. How molecular effects affect solutal Marangoni flows. Phys. Rev. Fluid 2022, 7, 064202. [Google Scholar] [CrossRef]
- Imai, Y.; Yamamoto, T.; Sekimoto, A.; Okano, Y.; Sato, R.; Shigeta, Y. Numerical investigation of the nano-scale solutal Marangoni convections. J. Taiwan Inst. Chem. Eng. 2019, 98, 20–26. [Google Scholar] [CrossRef]
- Liu, Y.W.; Ganti, R.; Burton, H.G.A.; Zhang, X.R.; Wang, W.C.; Frenkel, D. Microscopic Marangoni flows cannot be predicted on the basis of pressure gradients. Phys. Rev. Lett. 2017, 119, 224502. [Google Scholar] [CrossRef]
- Kalli, M.; Chagot, L.; Angeli, P. Comparison of surfactant mass transfer with drop formation times from dynamic interfacial tension measurements in microchannels. Colloid Interface Sci. 2022, 605, 204–213. [Google Scholar] [CrossRef]
- Liang, X. Dynamic Interfacial Tension and Adsorption Kinetics of Surfactants during Liquid/liquid Micro-Dispersion Process. Ph.D. Thesis, Tsinghua University, Beijing, China, 2022. [Google Scholar]
- Cui, Y.J.; Li, Y.K.; Wang, K.; Deng, J.; Luo, G.S. Determination of dynamic interfacial tension during the generation of tiny droplets in the liquid-liquid jetting flow regime. Langmuir 2020, 36, 13633–13641. [Google Scholar] [CrossRef]
- Adler, J.J.; Rabinovich, Y.I.; Moudgil, B.M. Origins of the non-DLVO force between glass surfaces in aqueous solution. J. Colloid Interface Sci. 2001, 237, 249–258. [Google Scholar] [CrossRef] [PubMed]
- Fa, K.Q.; Nguyen, A.V.; Miller, J.D. Hydrophobic attraction as revealed by AFM force measurements and molecular dynamics simulation. J. Phys. Chem. B 2005, 109, 13112–13118. [Google Scholar] [CrossRef] [PubMed]
- Ducker, W.A.; Xu, Z.; Clarke, D.R.; Israelachvili, J.N. Forces between alumina surfaces in salt-solutions: Non-DLVO forces and the implications for colloidal processing. J. Am. Ceram. Soc. 1994, 77, 437–443. [Google Scholar] [CrossRef]
- Christenson, H.K. Non-DLVO forces between surfaces-solvation, hydration and capillary effects. J. Dispers. Sci. 1988, 9, 171–206. [Google Scholar] [CrossRef]
- Petkov, J.; Senechal, J.; Guimberteau, F.; Leal-Calderon, F. Indirect evidence for non-DLVO forces in emulsions. Langmuir 1998, 14, 4011–4016. [Google Scholar] [CrossRef]
- Dagastine, R.R.; Chau, T.T.; Chan, D.Y.C.; Stevens, G.W.; Grieser, F. Interaction forces between oil-water particle interfaces—Non-DLVO forces. Faraday Discuss. 2005, 129, 111–124. [Google Scholar] [CrossRef]
- Smith, A.M.; Borkovec, M.; Trefalt, G. Forces between solid surfaces in aqueous electrolyte solutions. Adv. Colloid Interface Sci. 2020, 275, 102078. [Google Scholar] [CrossRef]
- Israelachvili, J.N.; Tabor, D. The measurement of van der Waals dispersion forces in the range 1.5 to 130 nm. Proc. Math. Phys. Eng. Sci. 1972, 331, 19–38. [Google Scholar]
- Helden, L.; Dietrich, K.; Bechinger, C. Interactions of colloidal particles and droplets with water-oil interfaces measured by total internal reflection microscopy. Langmuir 2016, 32, 13752–13758. [Google Scholar] [CrossRef]
- Prieve, D.C. Measurement of colloidal forces with TIRM. Adv. Colloid Interface Sci. 1999, 82, 93–125. [Google Scholar] [CrossRef]
- Dagastine, R.R.; Stevens, G.W.; Chan, D.Y.C.; Grieser, F. Forces between two oil drops in aqueous solution measured by AFM. J. Colloid Interface Sci. 2004, 273, 339–342. [Google Scholar] [CrossRef] [PubMed]
- Dagastine, R.R.; Manica, R.; Carnie, S.L.; Chan, D.Y.C.; Stevens, G.W.; Grieser, F. Dynamic forces between two deformable oil droplets in water. Science 2006, 313, 210–213. [Google Scholar] [CrossRef] [PubMed]
- Webber, G.B.; Edwards, S.A.; Stevens, G.W.; Grieser, F.; Dagastine, R.R.; Chan, D.Y.C. Measurements of dynamic forces between drops with the AFM: Novel considerations in comparisons between experiment and theory. Soft Matter 2008, 4, 1270–1278. [Google Scholar] [CrossRef]
- Lockie, H.; Manica, R.; Tabor, R.F.; Stevens, G.W.; Grieser, F.; Chan, D.Y.C.; Dagastine, R.R. Anomalous pull-off forces between surfactant-free emulsion drops in different aqueous electrolytes. Langmuir 2012, 28, 4259–4266. [Google Scholar] [CrossRef]
- Manor, O.; Chau, T.T.; Stevens, G.W.; Chan, D.Y.C.; Grieser, F.; Dagastine, R.R. Polymeric stabilized emulsions: Steric effects and deformation in soft systems. Langmuir 2012, 28, 4599–4604. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.; Luo, G.S.; Xu, J.H. Research progress on quantitative exploration of the interaction mechanism between droplets. CIESC J. 2021, 72, 5955–5964. [Google Scholar]
- Nilsen-Nygaard, J.; Sletmoen, M.; Draget, K.I. Stability and interaction forces of oil-in-water emulsions as observed by optical tweezers - a proof-of-concept study. RSC Adv. 2014, 4, 52220–52229. [Google Scholar] [CrossRef]
- Chen, A.; Li, S.W.; Sang, F.N.; Zeng, H.B.; Xu, J.H. Interactions between micro-scale oil droplets in aqueous surfactant solution determined using optical tweezers. J. Colloid Interface Sci. 2018, 532, 128–135. [Google Scholar] [CrossRef]
- Chen, A.; Li, S.W.; Xu, J.H. A novel approach to study the interactions between polymeric stabilized micron-sized oil droplets by optical tweezers. Chin. J. Chem. Eng. 2020, 28, 1368–1374. [Google Scholar] [CrossRef]
- Lan, W.J.; Cai, D.Z.; Hu, X.J.; Jing, S.; Li, S.W. Determination of dynamic interactions of droplets in continuous fluids using droplet probe. J. Colloid Interface Sci. 2022, 605, 91–100. [Google Scholar] [CrossRef]
- Wada, S.; Kikura, H.; Aritomi, M. Pattern recognition and signal processing of ultrasonic echo signal on two-phase flow. Flow Meas. Instrum. 2006, 17, 207–224. [Google Scholar] [CrossRef]
- Wolf, A.; Jayanti, S.; Hewitt, G.F. Flow development in vertical annular flow. Chem. Eng. Sci. 2001, 56, 3221–3235. [Google Scholar] [CrossRef]
- Xue, T.; Li, Z.L.; Li, C.Y.; Wu, B. Measurement of thickness of annular liquid films based on distortion correction of laser-induced fluorescence imaging. Rev. Sci. Instrum. 2019, 90, 033103. [Google Scholar] [CrossRef] [PubMed]
- Miklavcic, S.J.; Fung, C. Quantifying the force between mercury and mica across an ionic liquid using white light interferometry. J. Colloid Interface Sci. 2019, 538, 218–227. [Google Scholar] [CrossRef]
- Xie, L.; Shi, C.; Cui, X.; Zeng, H.B. Surface forces and interaction mechanisms of emulsion drops and gas bubbles in complex fluids. Langmuir 2017, 33, 3911–3925. [Google Scholar] [CrossRef]
- Liu, B.; Manica, R.; Liu, Q.X.; Klaseboer, E.; Xu, Z.H.; Xie, G.Y. Coalescence of bubbles with mobile interfaces in water. Phys. Rev. Lett. 2019, 122, 194501. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Manica, R.; Zhang, X.R.; Bussonniere, A.; Xu, Z.H.; Xie, G.Y.; Liu, Q.X. Dynamic interaction between a millimeter-sized bubble and surface microbubbles in water. Langmuir 2018, 34, 11667–11675. [Google Scholar] [CrossRef]

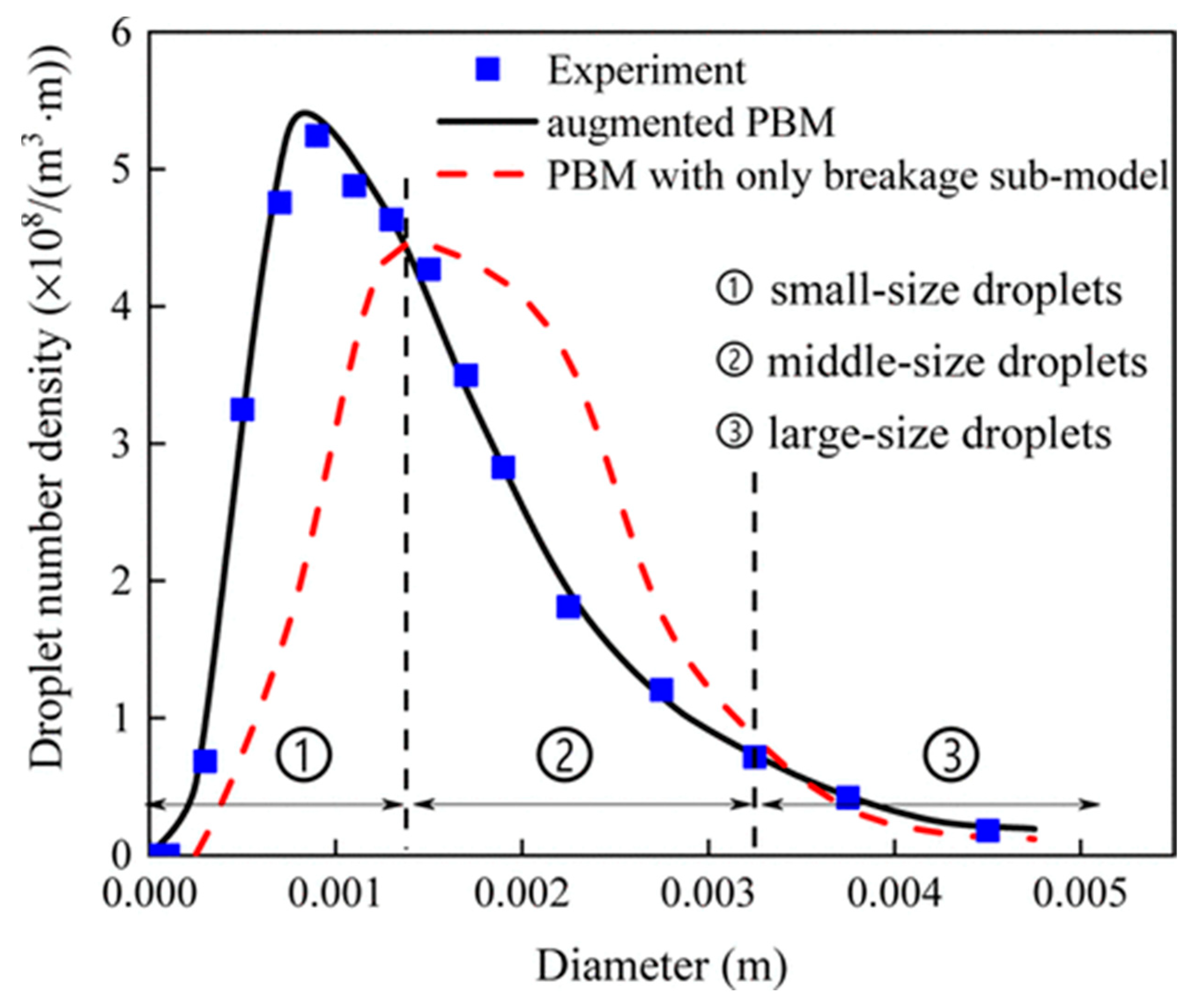

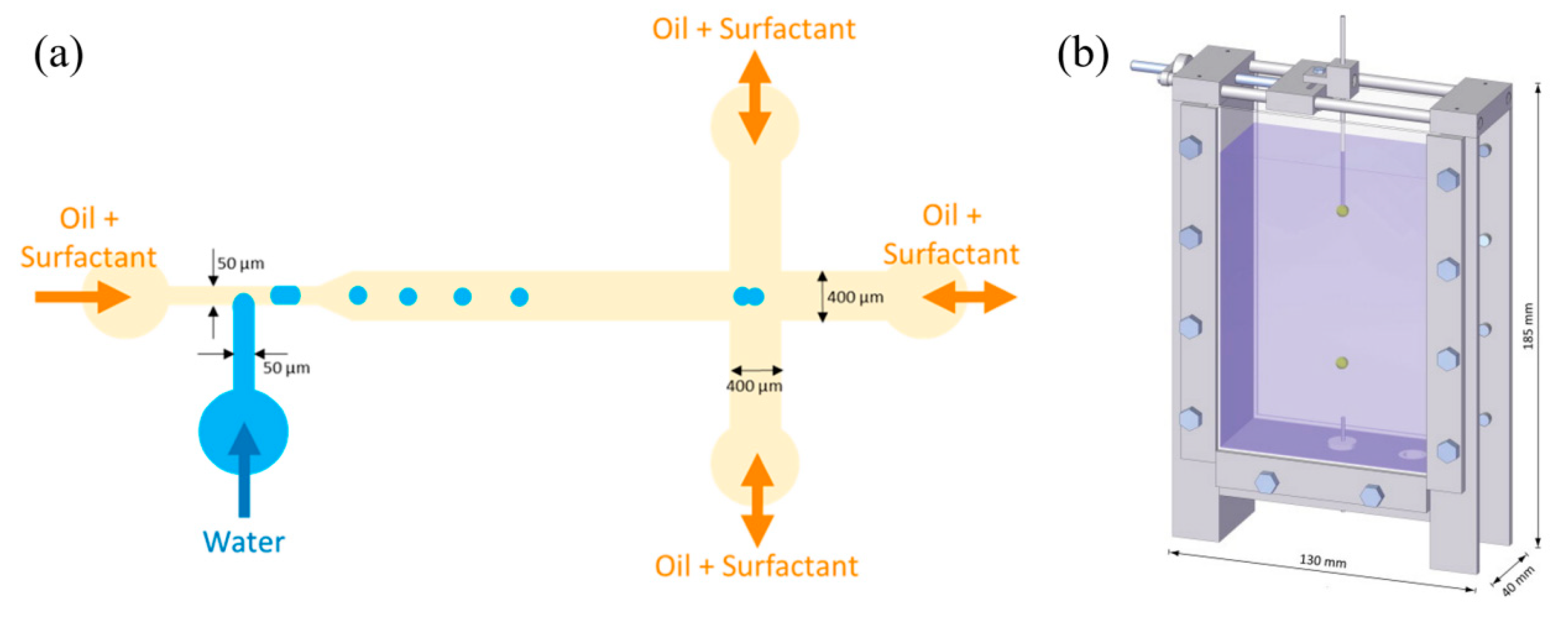
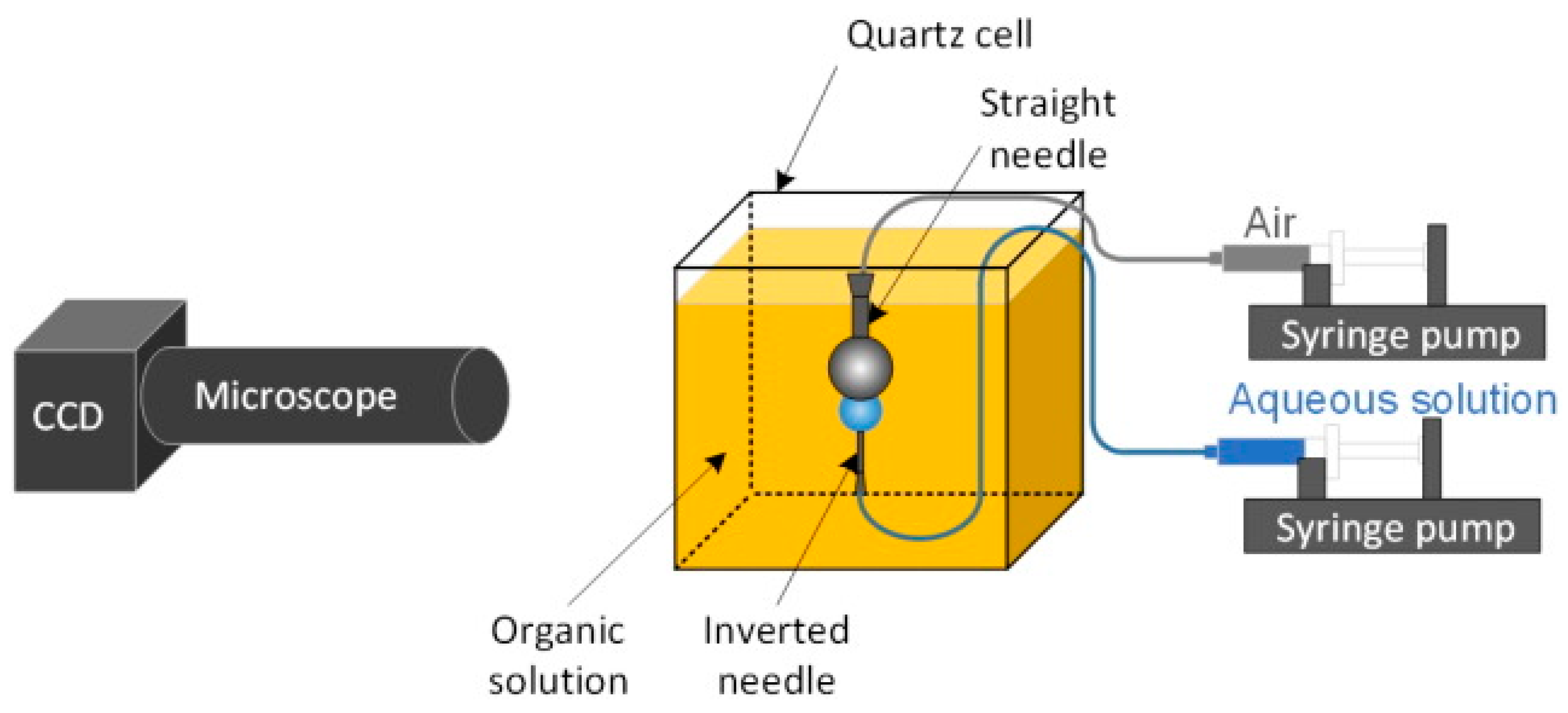


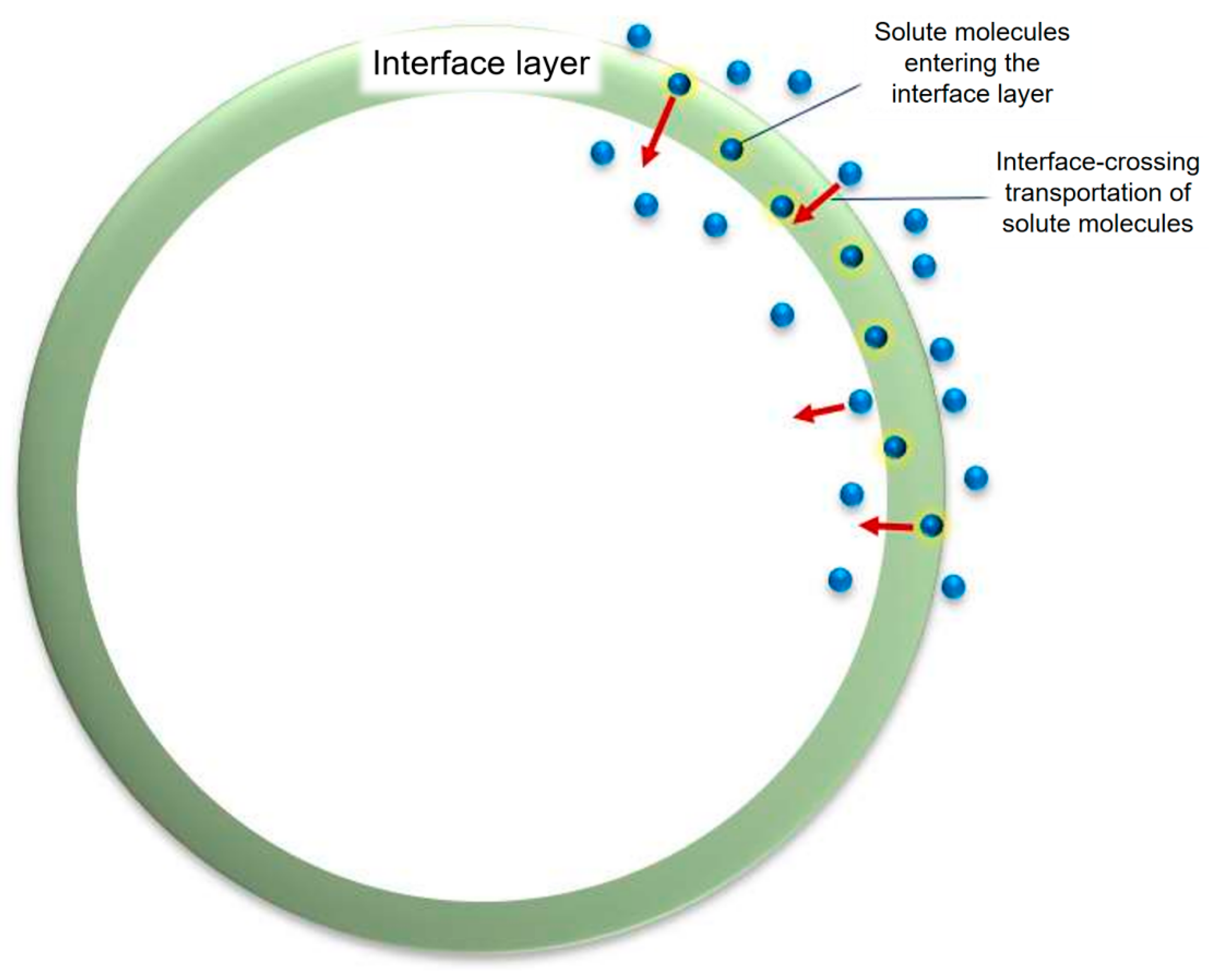

| Parameters | d→c | c→d | Authors |
|---|---|---|---|
| Sauter mean diameter, d32 | Higher | Lower | Rohlfing et al. [29] |
| Hold-up, φ | Lower | Higher | Tsouris et al. [32] |
| Flooding velocity, uf | Higher | Lower | Yu et al. [34] |
| Axial dispersion coefficient, Ec | Lower | Higher | Panahinia et al. [36] |
| Mass transfer coefficient, K | Higher | Lower | Torab-Mostaedi et al. [41] Asadollahzadeh et al. [42] |
| Type of Model | Characteristic Parameters |
|---|---|
| Euler-Euler model (Null-element) | d32 |
| Unary population balanced model | Diameter or volume |
| Binary population balanced model | Diameter or volume, and concentration |
| Authors | Extractors |
|---|---|
| Drumm et al. [47] | Rotating disc column |
| Mirzaie et al. [48] | Pulsed packing column |
| Amokrane et al. [49] | Pulsed disc-and-doughnut column |
| Yu et al. [50] | Pulsed disc-and-doughnut column |
| Zhou et al. [51] | Pump-mixer |
| Authors | Experimental Setup | Conditions | Objectives |
|---|---|---|---|
| Xu et al. [56] | T-junction microchannel | No mass transfer | Effect of μc |
| Steegmans et al. [57] | Y-junction microchannel | No mass transfer | Effect of μd |
| Xu et al. [58] | Micrometer screen hole | No mass transfer | Effect of γ |
| Xu et al. [59] | Coaxial microchannel | No mass transfer | Equilibrium interfacial tension |
| Zhou et al. [60] | Microchannel with tapered sub-channels | No mass transfer | Equilibrium interfacial tension |
| Wang et al. [61] | T-junction microchannel | Surfactant adsorption | Dynamic interfacial tension |
| Wang et al. [62] | T-junction microchannel | Surfactant adsorption | Dynamic interfacial tension |
| Brosseau et al. [63] | Microchannel with a chamber | Surfactant adsorption | Dynamic interfacial tension |
| Moiré et al. [64] | Coaxial microchannel | Surfactant adsorption | Dynamic interfacial tension |
| Li et al. [65] | T-junction microchannel | Mass transfer Chemical reaction | Effect of mass transfer and chemical reaction |
| Lan et al. [66] | Coaxial microchannel | Mass transfer | Dynamic interfacial tension |
| Lan et al. [67] | Coaxial microchannel | Mass transfer | Dynamic interfacial tension |
| Promote Factors | Inhibit Factors | No or Undefined Factors |
|---|---|---|
| Interfacial tension Electrostatic field Temperature Surface wetting Mass transfer d→c | Surface potential, pH Energy input Viscosity Surface active component Mass transfer c→d | Droplet diameter Ionic strength Pressure Density |
| Measurement Tools | Applied Systems | Advantages | Disadvantages |
|---|---|---|---|
| SFA [128] | Force between two planes | Directly measure the absolute separation distance between the two planes | Cannot measure the force between two droplets |
| TIRM [127,129,130] | Force between colloid (6–30 μm) and flat substrate | High distance resolution and high force resolution | Cannot measure the force between two droplets |
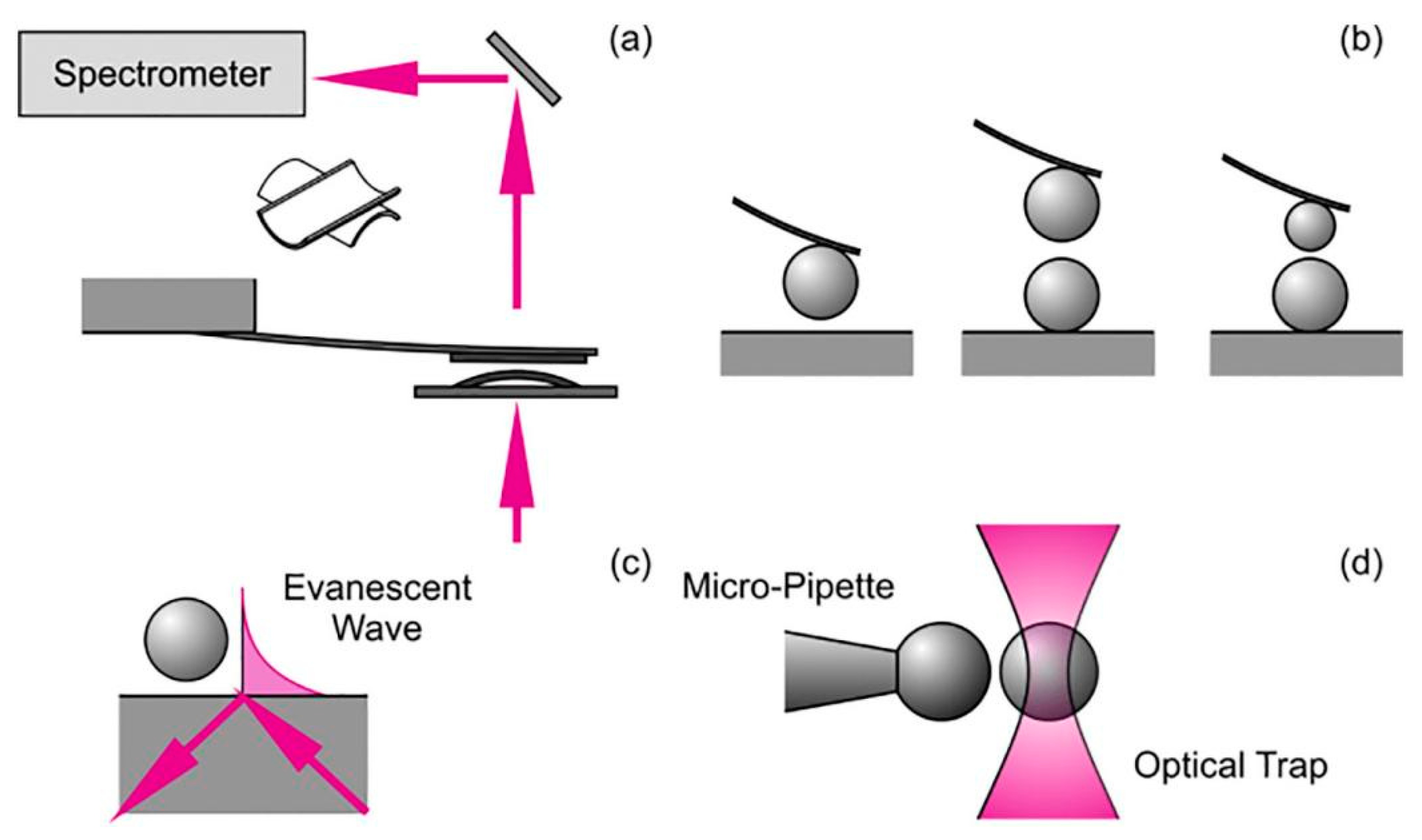
| AFM [131,132,133,134,135] | Force between two particles Force between particle and substrate Particle size (20–200 μm) | Measure the force between droplets directly; Have mature theory support | Cannot measure the front distance between two droplets during the film drainage process |
| Optical tweezers [136,137,138,139] | Force between two particles (0.1–10 μm) | Measure the force between micro-scale droplets directly | Fewer studies; Lack of theoretical model support |
| Droplet probe [140] | Force between two droplets (1–2 mm) | Simplicity Low cost Visual results | Cannot measure the front distance between two droplets during the film drainage process |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, S.; Zhang, J.; Li, S.; Chen, Z.; Wang, Y. Mass Transfer and Droplet Behaviors in Liquid-Liquid Extraction Process Based on Multi-Scale Perspective: A Review. Separations 2023, 10, 264. https://doi.org/10.3390/separations10040264
Yu S, Zhang J, Li S, Chen Z, Wang Y. Mass Transfer and Droplet Behaviors in Liquid-Liquid Extraction Process Based on Multi-Scale Perspective: A Review. Separations. 2023; 10(4):264. https://doi.org/10.3390/separations10040264
Chicago/Turabian StyleYu, Sicen, Jiyizhe Zhang, Shaowei Li, Zhuo Chen, and Yundong Wang. 2023. "Mass Transfer and Droplet Behaviors in Liquid-Liquid Extraction Process Based on Multi-Scale Perspective: A Review" Separations 10, no. 4: 264. https://doi.org/10.3390/separations10040264
APA StyleYu, S., Zhang, J., Li, S., Chen, Z., & Wang, Y. (2023). Mass Transfer and Droplet Behaviors in Liquid-Liquid Extraction Process Based on Multi-Scale Perspective: A Review. Separations, 10(4), 264. https://doi.org/10.3390/separations10040264






