Reliable Network Interdiction Models with Multiple Unit Costs
Abstract
:1. Introduction
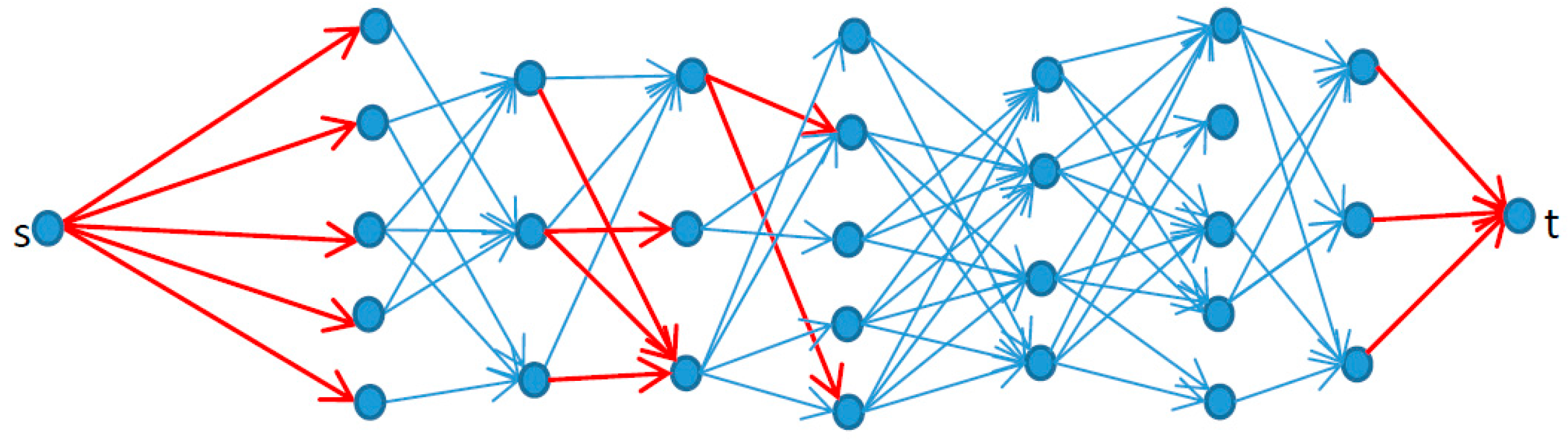
2. Models
3. Computational Complexity
4. Model Solution
5. Numerical Results
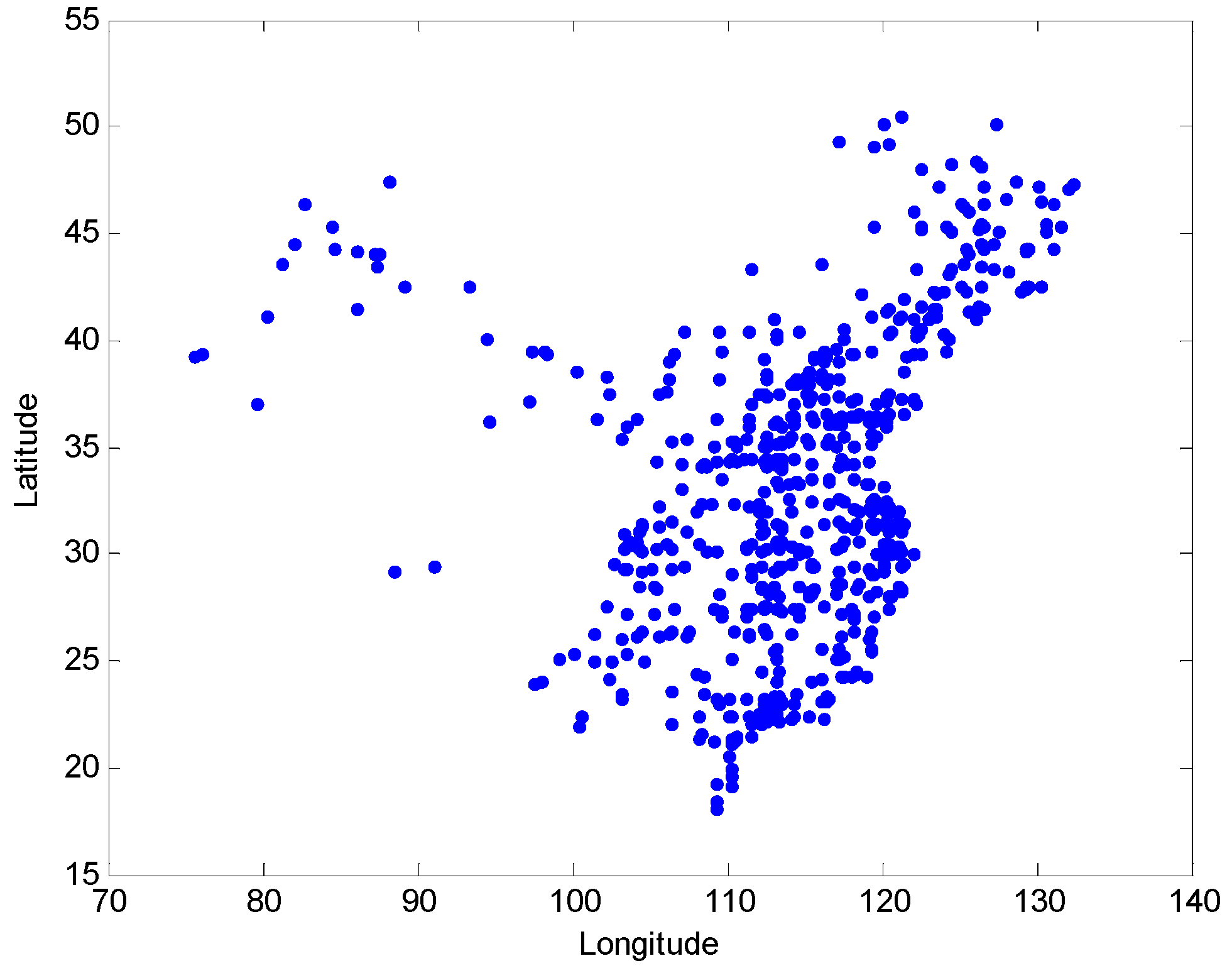
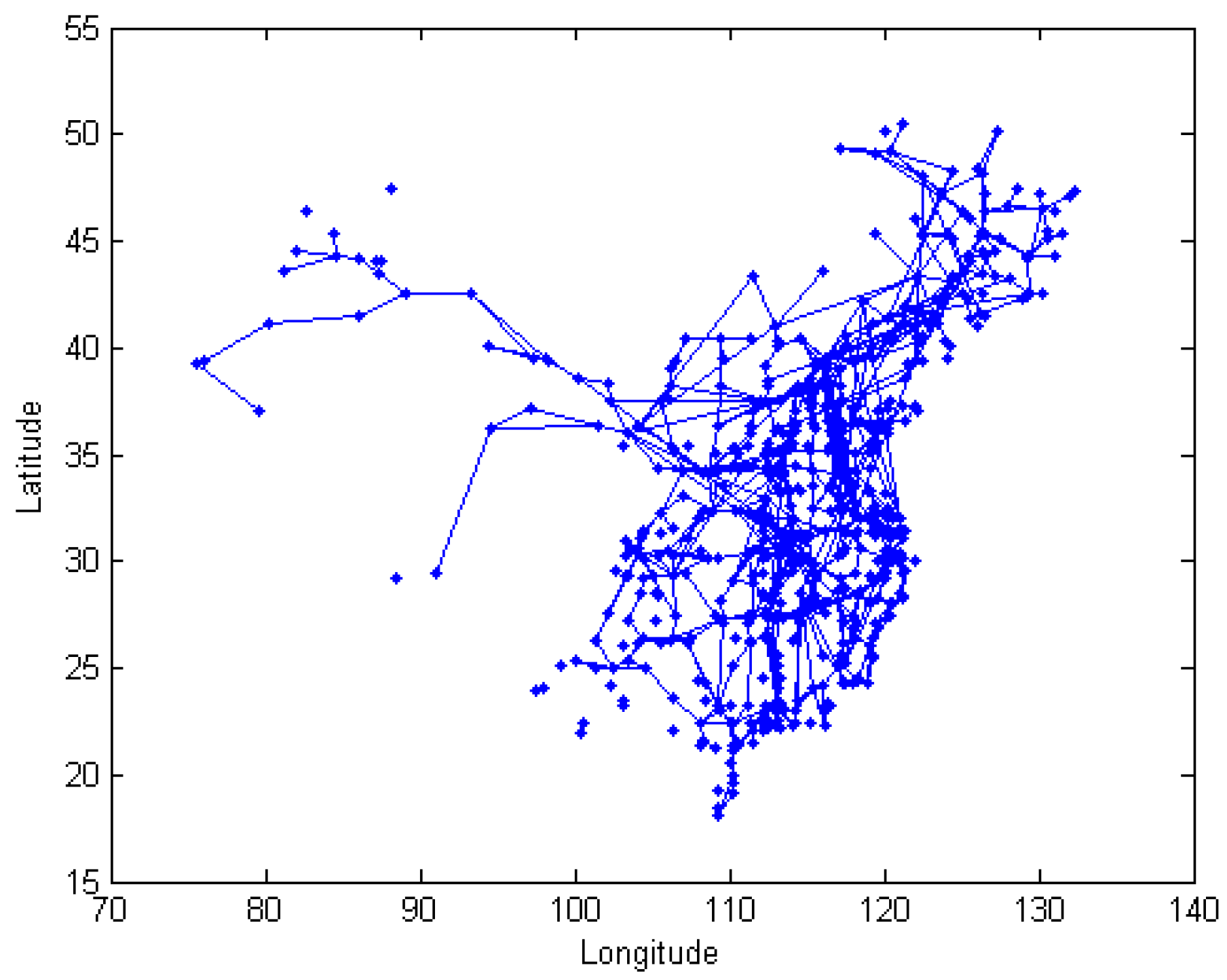
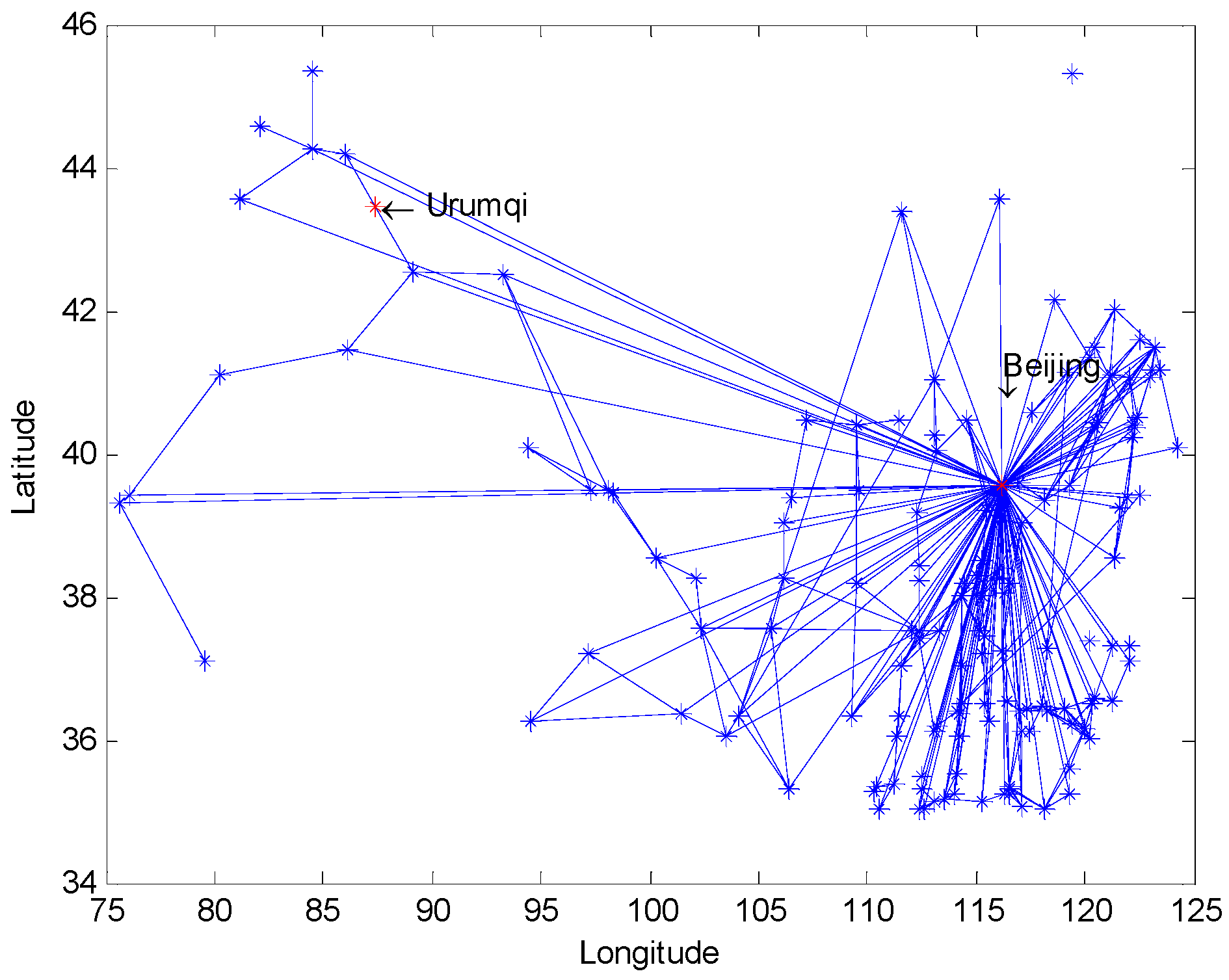
5.1. Data Sources and Pre-Processing
5.2. Software and Parameter Setting
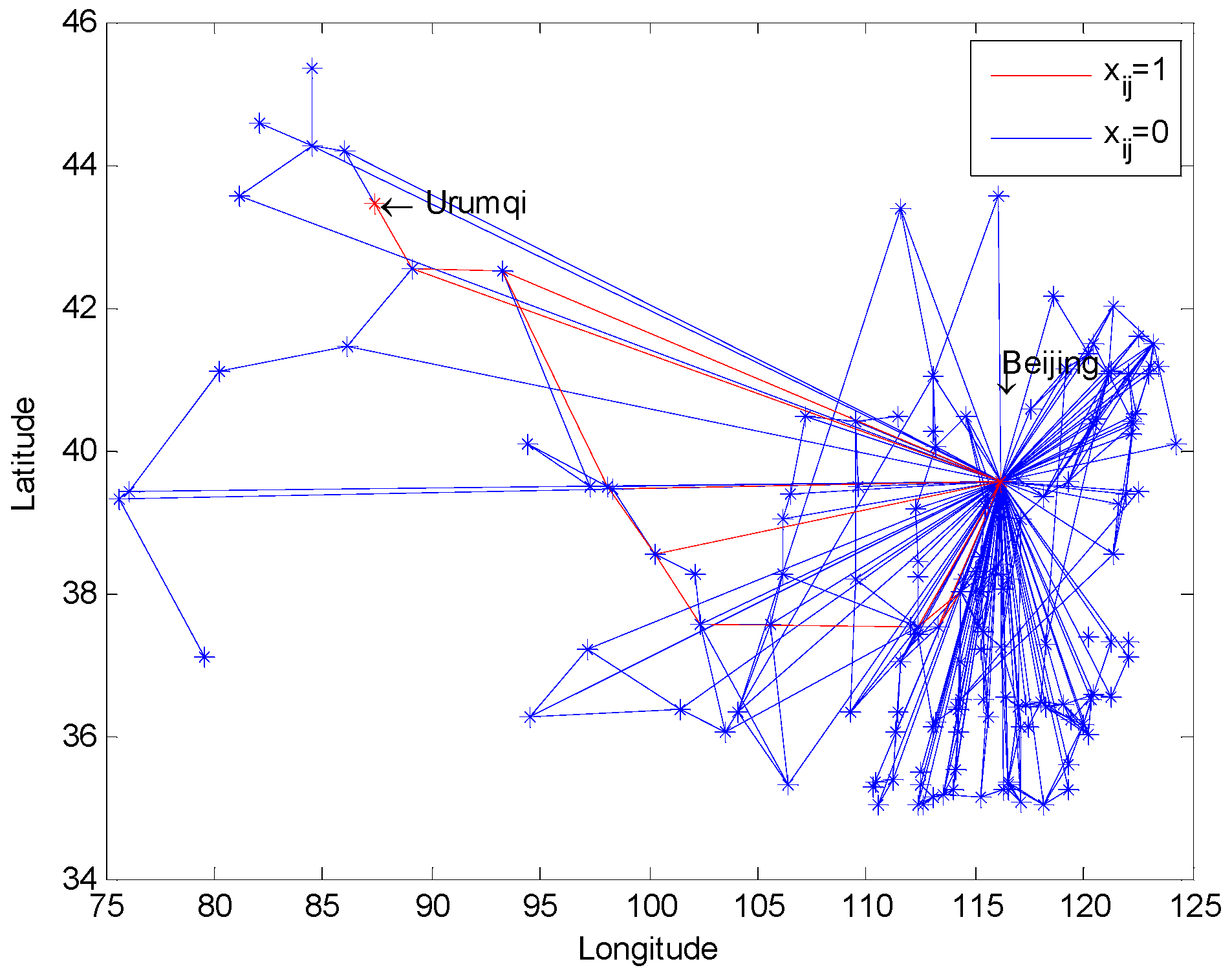
5.3. Solutions
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wollmer, R. Removing arcs from a network. Oper. Res. 1964, 12, 934–940. [Google Scholar] [CrossRef]
- Durbin, E. An Interdiction Model of Highway Transportation; Rand Corporation: Santa Monica, CA, USA, 1966. [Google Scholar]
- Simaan, M.; Cruz, J.B., Jr. On the Stackelberg strategy in nonzero-sum games. J. Optim. Theory Appl. 1973, 11, 533–555. [Google Scholar] [CrossRef]
- Sreekumaran, H.; Liu, A.L.; Uhan, N.A. Multi-agent decentralized network interdiction games. 2015. Available online: https://arxiv.org/abs/1503.01100 (accessed on 2 August 2016).
- Steinrauf, R.L. Network Interdiction Models; Naval Postgraduate School Monterey: Monterey, CA, USA, 1991. [Google Scholar]
- Malaviya, A.; Rainwater, C.; Sharkey, T. Multi-period network interdiction problems with applications to city-level drug enforcement. Iie Trans. 2011, 44, 368–380. [Google Scholar] [CrossRef]
- Wood, R.K. Deterministic network interdiction. Math. Comput. Model. 1993, 17, 1–18. [Google Scholar] [CrossRef]
- Cormican, K.; Morton, D.; Wood, K. Stochastic network interdiction. Oper. Res. 1998, 46, 184–197. [Google Scholar] [CrossRef]
- Watson, J.P.; Phillips, C.A.; Hart, W.E.; Phillips, C.A.; Watson, J.-P. Sensor placement in municipal water networks. J. Water Resour. Plan. Manag. 2003, 131, 237–243. [Google Scholar]
- Glick, S.J. Virtual Checkpoints and Cyber-Terry Stops: Digital Scans to Protect the Nation’s Critical Infrastructure and Key Resources. J. Nat’l Sec. L. & Pol’y. 2011, 6. [Google Scholar]
- Reiter, M.; Rohatgi, P. Homeland Security. Internet Comput. IEEE 2004, 8, 16–17. [Google Scholar] [CrossRef]
- Champion, P.D.; Hofstra, D.E.; Clayton, J.S. Border Control for Potential Aquatic Weeds. Stage 3. Weed Risk Assessment; Science for Conservation 271; Department of Conservation: New Plymouth, New Zealand, 2007; p. 41.
- Alden, E. Immigration and border control. Cato J. 2012, 32, 107–124. [Google Scholar]
- Morton, D.P.; Pan, F.; Saeger, K.J. Models for nuclear smuggling interdiction. IIE Trans. 2007, 39, 3–14. [Google Scholar] [CrossRef]
- Scaparra, M.P.; Church, R.L. A bilevel mixed-integer program for critical infrastructure planning. Comput. Oper. Res. 2008, 35, 1905–1923. [Google Scholar] [CrossRef]
- Royset, J.; Wood, R. Solving the bi-objective maximum-flow network-interdiction problem. INFORMS J. Comput. 2007, 19, 175–184. [Google Scholar] [CrossRef]
- Claudio, M.R.S.; Ramirez-Marquez, J.E. A bi-objective approach for shortest-path network interdiction. Comput. Ind. Eng. 2010, 59, 232–240. [Google Scholar]
- Zenklusen, R. Matching interdiction. Discret. Appl. Math. 2010, 158, 1676–1690. [Google Scholar] [CrossRef]
- Gutin, E.; Kuhn, D.; Wiesemann, W. Interdiction games on Markovian PERT networks. Manag. Sci. 2014, 61, 999–1017. [Google Scholar] [CrossRef]
- Zhu, Y.; Zheng, Z.; Zhang, X.; Cai, X. The r-interdiction median problem with probabilistic protection and its solution algorithm. Comput. Oper. Res. 2013, 40, 451–462. [Google Scholar] [CrossRef]
- Zhao, J.; Wang, J.; Yu, H. A minimum cost k-reliable network interdiction model. In Proceedings of the International Symposium on Operations Research and ITS Applications in Engineering, Technology and Management, Luoyang, China, 21–24 August 2013; pp. 105–109.
- Garey, M.R.; Johnson, D.S. Computers and Intractability: A Guide to the Theory of NP-Completeness; W.H. Freeman & Company: New York, NY, USA, 1979. [Google Scholar]
- List of All Trains in China; 59178.com. Available online: http://www. 59178. com/checi/ (accessed on 10 November 2012).
- Edmonds, J. Matroids and the greedy algorithm. Math Program. 1971, 1, 127–136. [Google Scholar] [CrossRef]
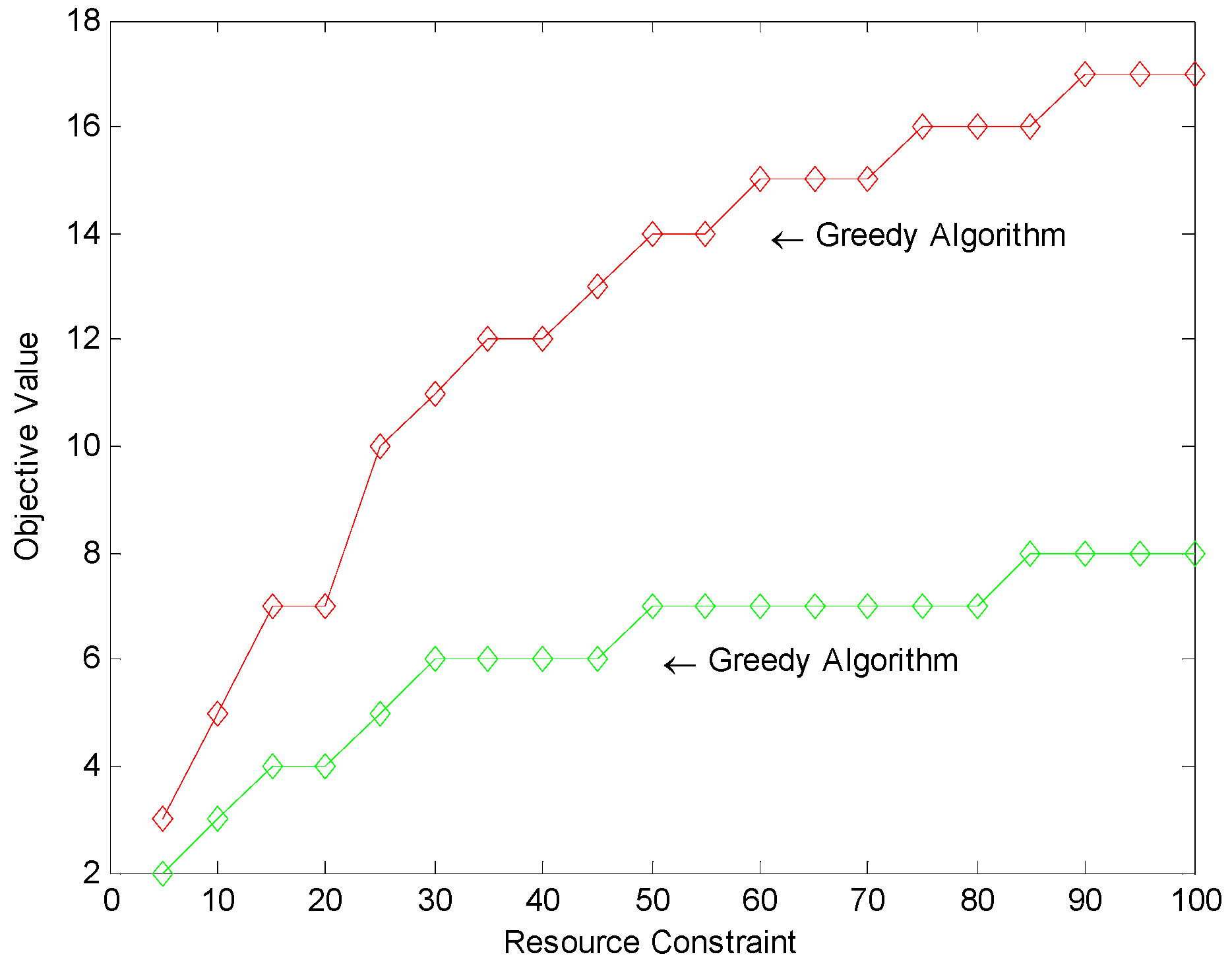
| Algorithm | Objective Value | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| RS | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Greedy Algorithm | 3 | 4 | 6 | 6 | 7 | 7 | 7 | 7 | 8 | 8 |
| MIP | 5 | 7 | 11 | 12 | 14 | 15 | 15 | 16 | 17 | 17 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Sun, G. Reliable Network Interdiction Models with Multiple Unit Costs. Math. Comput. Appl. 2016, 21, 50. https://doi.org/10.3390/mca21040050
Zhao J, Sun G. Reliable Network Interdiction Models with Multiple Unit Costs. Mathematical and Computational Applications. 2016; 21(4):50. https://doi.org/10.3390/mca21040050
Chicago/Turabian StyleZhao, Jia, and Gang Sun. 2016. "Reliable Network Interdiction Models with Multiple Unit Costs" Mathematical and Computational Applications 21, no. 4: 50. https://doi.org/10.3390/mca21040050
APA StyleZhao, J., & Sun, G. (2016). Reliable Network Interdiction Models with Multiple Unit Costs. Mathematical and Computational Applications, 21(4), 50. https://doi.org/10.3390/mca21040050





