Event Triggered Multi-Agent Consensus of DC Motors to Regulate Speed by LQR Scheme

Abstract

In the presented paper, the leader-following consensus algorithm of a multi-agent system (MAS) is used along with the centralized event-triggering scheme to make the speed of the network-coupled multiple-motors synchronizable. In the proposed method, the updates for the controller are event-driven based on local information. Moreover, the basic consensus protocol is also revised such that the speed information of the motors is used in order to reach identical speed. The main benefit of the planned event-triggered methodology is the energy saving by avoiding the continuous control of the system. As far as stability analysis of the system is concerned, a common Lyapunov function is incorporated to validate stability. The acquired results endorse the success of the proposed methodology.

1. Introduction

In the last decade, the multi-agent system (MAS) has received foremost attention from the research community due to its wide area of application in engineering and technology, particularly with there being a requirement for coordinated activities among different entities such as robots, vehicles, or sensors. Furthermore, within the MAS, the area of most concern is the consensus problem. There are plenty of authors who address the aforesaid problem under various scenarios, such as with a leader, without a leader, with delays, with noises, with fixed and switching communication topologies, etc., as given in previous studies [1,2,3,4,5,6,7,8,9].

Traditionally, the control system is analyzed by the assumption of continuous system dynamics, such that the system is supposed to be receiving control command and information continuously from the controller and the neighbors. This type of communication consumes extra energy of the system. To overcome this difficulty, an event-triggered scheme is coined such that communication or control action is performed only when an event condition is violated.

Additionally, it is evident that the network control system (NCS) provides the basis for the multi-agent systems. The use of the network in the control system adds robustness and flexibility to the system by making the system adaptable to unknown disturbance and able to retain stability under any malfunctioning of the sub-system. In [10], the detailed concept of NCS is given and it is shown that the NCS based system uses the network to transfer feedback and control signals to various system components, i.e., sensor, actuator, etc. Moreover, the author encircles different application areas of the NCS with complete analysis, in addition to discussing recent advancement in the NCS. Furthermore, in [11], the sampled-data event-triggered control is presented for the NCS. It is shown that the sampled-data control can provide a better energy saving design of feedback controller and event threshold condition as compared to the existing design methods.

Now, under the event-triggered scheme, there are two different approaches used to model the event-triggered systems, i.e., centralized and decentralized. There is a sufficient amount of work already being performed in the MAS with the event-triggered controllers, either centralized or decentralized. In [12], the issue of a decentralized event-triggered consensus for the second-order MAS is addressed. An event condition is defined as a ratio of error and state norm. The controller updates using information of the agent’s present state and corresponding neighbor’s state. Likewise, in [13], a new decentralized scheme is proposed for the event-triggered control such that the requirement of monitoring the neighbor’s information does not remain necessary. Similarly, in [14], the problem of the even-triggered consensus for the linear MAS is addressed under two different event conditions, i.e., with and without the necessity of continuous communication among neighbors. It is shown that the update scheme for the controller depends on an error, the state of neighbor and a threshold. Moreover, in [15], the event-triggered consensus problem in the leader-following MAS is presented by assuming an input delay. It is shown that controller updates are event-driven and a consensus is reached such that the proposed conditions are satisfied. Furthermore, in [16], a leader-following event-triggered consensus problem is presented for switching network topology. Controller updates are event-driven, depending on neighbor state and network topology. Once again, the consensus is reached such that the proposed sufficiency conditions are satisfied. In [17], the state dependent condition is presented to address the event-triggered consensus problem with jointly connected communication topology with and without the leader. The presented event condition depends on the present, past and neighbor information of an agent. The system stability is proved by using the Lyapunov theorem and it is shown that the event-triggered consensus is reached with and without the leader. Additionally, in [18], an event-triggered controller is proposed to address the formation control problem in the MAS. The event-driven controller updates with respect to the error to the state norm ratio. It is shown that the formation is reached by every agent with any initial condition. In [19], an event-triggered controller is presented to address the consensus problem in the leader-following MAS under fixed topology with linear dynamics, and it is proven that the consensus is reached asymptotically.

Moreover, as far as the Linear Quadratic Regulator (LQR) is concerned, it deals with the optimal control of the system by minimizing the quadratic cost function and involving the determination of the performance index. In the LQR control problem, the optimal gain is obtained by solving the associated algebraic Riccati inequality such that the parameters $Q$ and $R$ need to be known in order to determine the gain $K$ and to minimize the performance index. The LQR control found application in satellite launching methods such that it become easier to determine the least possible fuel consumption or lowest time to reach the target for a satellite or any space rocket. Additionally, the LQR control is also applicable in different control problems, as given in [20,21,22,23].

So, the above-mentioned work encouraged us to further expand the methodology of the leader-following MAS with the centralized event-triggering controller to regulate the speed of the networked multi-motor system such that they regain the synchronous speed if the event condition is violated.

Thus, in this paper, the proposed objective is achieved by (1) designing a unique event-triggered control law aimed at addressing the synchronous control of the motor speed; (2) designing an event condition to monitor the error signal, generated if synchronous speed is disturbed; and (3) designing a common Lyapunov function to ensure the stability of the proposed system. The block diagram presentation of the proposed work for a single motor is shown in Figure 1, which is further extended and simulated for the multi-motor system.

Remark 1.

The presented paper contributes significantly to the advancement of the current speed synchronization methods adopted for the multi-motor system, which is mostly based on traditional schemes of using a wire connected system vulnerable to system cost, efficiency, malfunctioning, and extra consumption of energy.

The rest of the work is organized as follows: Section 2 presents preliminaries related to the MAS while Section 3 presents the system model. Section 4 discusses the consensus protocol for speed regulation and the stability analysis of the proposed system model. Afterwards, Section 5 presents the acquired results. Finally, Section 6 concludes the presented work.

2. Preliminaries

In this paper, Euclidean space is represented by ${ℝ}^n$ with $n$-dimensions $\mathbb{N}\left(1,n\right)=\left\{1,2,\dots .,n\right\}$. The network topology between communicating multi-agents is presented by using the algebraic graph theory such that the graph $G=\left(\rho ,\delta \right)$ is constituted by a set of vertex $\rho =\left\{{\rho }_i\right\}, i\in \mathbb{N}\left(1,n\right)$, and a set of edge $\delta \subseteq \rho \times \rho$. Furthermore, the vertices (agents), ${\rho }_i$ and ${\rho }_j$ are referred to be neighbors if $\left({\rho }_i,{\rho }_j\right)\in \delta ,i,j\in \mathbb{N}\left(1,n\right)$, whereas $N_i=\left\{j:\left({\rho }_i,{\rho }_j\right)\in \delta ,j\ne i\right\}$ is the neighbor set of vertex ${\rho }_i$. Moreover, ${\mathcal{N}}_i$ is the degree of vertex describing its total number of neighbors. Now, for a graph $G$, a $n\times n$ degree matrix $D\left(G\right),$ described the degree of vertex ${\rho }_i$ along its diagonal entries. Additionally, the Laplacian matrix $L\left(G\right),$ of the graph is given as $L\left(G\right)=D\left(G\right)-A\left(G\right).$ Here, $A\left(G\right)$ represents graph adjacency, which is $1$ if $\left({\rho }_i,{\rho }_j\right)\in \delta$ else $0.$ Additionally, for undirected graphs, $L\left(G\right)$ always holds $L\left(G\right)=L{\left(G\right)}^{\mathrm{T}}\ge 0$, therefore, $L\left(G\right)$ has real eigenvalues and is organized as ${\lambda }_1\le {\lambda }_2\le \dots \le {\lambda }_n$.

Lemma 1.

In [24], if $G$ is connected, then $\mathit{L}\left(\mathit{G}\right)$ has ${\lambda }_2$ as the smallest positive eigenvalue while $0$ is the smallest eigenvalue respectively.

Lemma 2.

In [25], ${\lambda }_2\left(G\right)>0$ if $G$ is connected and holds the property $\underset{𝓍\ne 0, 1^T𝓍=0}{\min }\frac{{𝓍}^{T}L𝓍}{{𝓍}^T𝓍}$.

Remark 2.

In undirected graphs, the Laplacian matrix holds $\mathit{L}\left(\mathit{G}\right)\ge 0 i.e., x^{T}Lx\ge 0, \forall x\in {ℝ}^N$, satisfying the property of the sum of the square, i.e., $x^T\mathit{L}x=\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_{ij}{\left(x_i-x_j\right)}^2$.

Definition: 

An event-triggered leader-following consensus is reached for the system given by Equation (5), under the proposed event transmission approach and control protocol $u_i\left(t\right)$ such that $\underset{t\to \infty }{lim}\parallel {\omega }_i\left(t\right)-{\omega }_j\left(t\right)\parallel =0$ for $i,j\in \mathbb{N}\left(1,n\right)$.

Lemma 3.

In [26], a symmetric positive definite matrix $\mathit{H}$ exists for the connected graph $G$ and subgraph $\widehat{G}$ holding property $\mathit{H}\left(\mathit{G}\right)=\mathit{L}\left(\mathit{G}\right)+\mathit{d}$.

Remark 3.

In the case of the leader-following MAS, the matrix $\mathit{H}\left(\mathit{G}\right)=\mathit{L}\left(\mathit{G}\right)+\mathit{d}$ plays an important role such that the matrix $\mathit{H}\left(\mathit{G}\right)$ is symmetric positive definite if and only if the node $0$ is reachable in $\widehat{G}$, whereas node $0$ is allocated for the leader, and $\mathit{d}$ defines the adjacency of the node $0$ as $\mathit{d}=diag\left\{d_1,\dots .,d_n\right\}$ such that $\mathit{d}>0$ if there is a neighbor to the leader, otherwise $\mathit{d}=0$.

Lemma 4.

In [27], $\mathit{H}\left(\mathit{G}\right)$ have real eigenvalues $\left(\eta \right)$ in addition to the property of having an orthogonal matrix $\mathit{W}\mathit{H}{\mathit{W}}^{\mathit{T}}=\mathit{\Pi }=diag \left\{{\eta }_1,\dots ,{\eta }_N\right\}$.

Remark 4.

Since $\mathit{H}$ is the symmetric positive definite matrix, $\mathit{H}={\mathit{H}}^T$ holds. Now, a symmetric matrix $\mathit{H}$ can also be defined as $\mathit{W}\mathit{H}{\mathit{W}}^{\mathit{T}}$ where $\mathit{W}$ is the orthogonal matrix, then the matrix $\mathit{\Pi }=\mathit{W}\mathit{H}{\mathit{W}}^{\mathit{T}}$ is written as

$$\mathit{\Pi }=\mathit{W}\mathit{H}{\mathit{W}}^{\mathit{T}}=\left[\begin{array}{cccc}{w}_1& w_2& \cdots & w_n\end{array}\right]\left[\begin{array}{cccc}{\eta }_1& & & \\ & {\eta }_2& & \\ & & \ddots & \\ & & & {\eta }_n\end{array}\right]\left[\begin{array}{c}{w_1}^T\\ {w_1}^T\\ ⋮\\ {w_n}^T\end{array}\right]$$

(1)

3. System Modeling

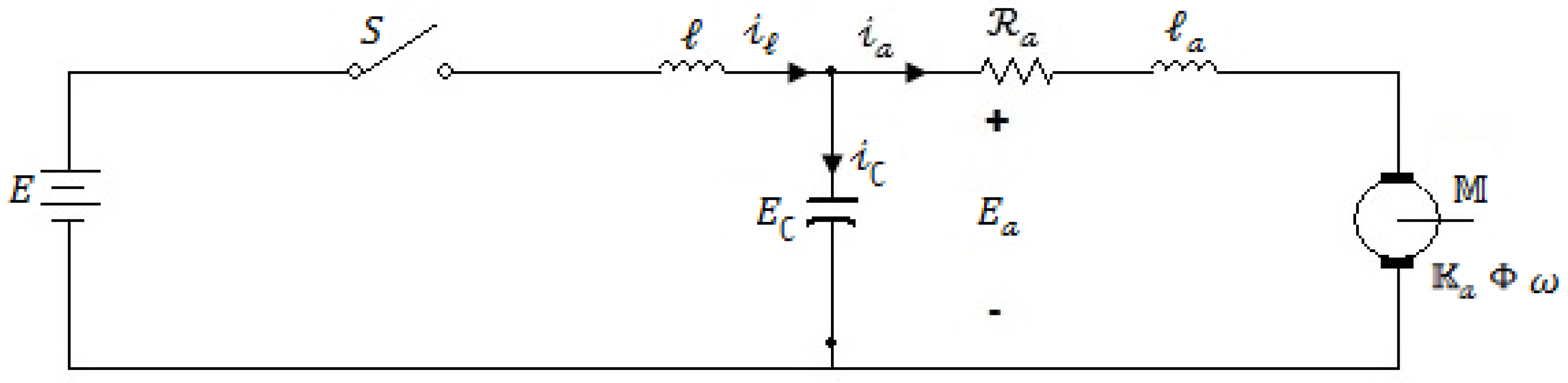
The electric motor system proposed in this paper consists of a Buck converter driving a DC motor. The state space model of the buck converter is given in [28].

$$\left[\begin{array}{c}{𝒾}_{\ell }\\ {\dot{E}}_c\end{array}\right]= \left[\begin{array}{cc}0& -\frac{1}{\ell }\\ \frac{1}{\complement }& -\frac{1}{ℛ\complement }\end{array}\right]\left[\begin{array}{c}{𝒾}_{\ell }\\ E_{\complement }\end{array}\right]+\left[\begin{array}{c}\frac{1}{\ell }\\ 0\end{array}\right]E$$

(2)

Where $\complement$ is the capacitance, $\ell$ is the inductance, $E_{\complement }$ is the capacitor voltage, ${𝒾}_{\ell }$ is the inductor current, $E$ is the voltage supply. While the DC motor model is presented as given in [28].

$$\left[\begin{array}{c}{𝒾}_{𝒶}\\ \dot{\omega }\end{array}\right]= \left[\begin{array}{cc}-\frac{{ℛ}_{𝒶}}{{\ell }_{𝒶}}& -\frac{{\mathbb{K}}_{𝒶} {\Phi }}{{\ell }_{𝒶}}\\ \frac{{\mathbb{K}}_{ℯ}}{𝒿}& 0\end{array}\right] \left[\begin{array}{c}{𝒾}_{𝒶}\\ \omega \end{array}\right]+\left[\begin{array}{c}\frac{1}{{\ell }_{𝒶}}\\ 0\end{array}\right]E_{𝒶}$$

(3)

Where ${ℛ}_{𝒶}$ is the armature resistance, ${\ell }_{𝒶}$ is the armature inductance, ${𝒾}_{𝒶}$ is the armature current, $\omega$ is the speed, $E_{𝒶}$ is the armature voltage, $𝒿$ is the motor inertia, and ${\mathbb{K}}_{ℯ}$ is the motor back electromotive force (emf) constant, ${\mathbb{K}}_{𝒶}$ is the motor design constant and ${\Phi }$ is the motor field flux. When a DC motor is joined with the buck converter, the transformation in the inductor current and capacitor voltage is presented as

$${𝒾}_{\ell }= {𝒾}_{\complement }+ {𝒾}_{𝒶}\Rightarrow {𝒾}_{\ell }=\complement \frac{d{E}_{\complement }}{dt}+{𝒾}_{𝒶}$$

(4)

$$\frac{d{E}_{\complement }}{dt}= \frac{{𝒾}_{\ell }}{\complement }- \frac{ {𝒾}_{𝒶}}{\complement }$$

(5)

Thus, the dynamics of the single ($i_{th}$) agent are presented as

$$\dot{x}={ \mathrm{A}}_{\mathsf{\sigma }} x_i+{\mathrm{B}}_{\mathsf{\sigma }} u_i$$

(6)

$$y=\mathrm{C}{x}_i$$

(7)

where $x\in R^n, \sigma =\left[0,\infty \right)$ is the switching signal with $\left(1,\dots , n\right)$ arrangements and ${𝓊}_{𝒾}$ is the proposed controller.

$$\left[\begin{array}{c}{𝒾}_{\ell }\\ {\dot{E}}_{\complement }\\ {𝒾}_{𝒶}\\ \dot{\omega }\end{array}\right]= \left[\begin{array}{cccc}0& -\frac{1}{\ell }& 0& 0\\ \frac{1}{\complement }& 0& -\frac{1}{\complement }& 0\\ 0& \frac{1}{{\ell }_{𝒶}}& -\frac{{ℛ}_{𝒶}}{{\ell }_{𝒶}}& \frac{{\mathbb{K}}_{𝒶} \Phi }{{\ell }_{𝒶}}\\ 0& 0& \frac{{\mathbb{K}}_{ℯ}}{𝒿}& 0\end{array}\right] \left[\begin{array}{c}{𝒾}_{\ell }\\ E_{\complement }\\ {𝒾}_{𝒶}\\ \omega \end{array}\right]+ \left[\begin{array}{c}\frac{S}{\ell }\\ 0\\ 0\\ 0\end{array}\right]u_i$$

(8)

$$\mathsf{\omega }= \left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right] \left[\begin{array}{c}{𝒾}_{\ell }\\ E_{\complement }\\ {𝒾}_{𝒶}\\ \omega \end{array}\right]$$

(9)

where $S\in \left\{0,1\right\}$ is the switch position. Suppose that $\sigma =1$ and $S=0$, then

$$A_{\mathbf{1}}= \left[\begin{array}{cccc}0& -\frac{1}{\ell }& 0& 0\\ \frac{1}{\complement }& 0& -\frac{1}{\complement }& 0\\ 0& \frac{1}{{\ell }_{𝒶}}& -\frac{{ℛ}_{𝒶}}{{\ell }_{𝒶}}& \frac{{\mathbb{K}}_{𝒶} {\Phi } }{{\ell }_{𝒶}}\\ 0& 0& \frac{{\mathbb{K}}_{ℯ}}{𝒿}& 0\end{array}\right] \mathrm{and} B_{\mathbf{1}}=\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right]$$

(10)

Similarly, if $\sigma =2$ and $S=1$, then

$$A_{\mathbf{2}}= \left[\begin{array}{cccc}0& -\frac{1}{\ell }& 0& 0\\ \frac{1}{\complement }& 0& -\frac{1}{\complement }& 0\\ 0& \frac{1}{{\ell }_{𝒶}}& -\frac{{ℛ}_{𝒶}}{{\ell }_{𝒶}}& \frac{{\mathbb{K}}_{𝒶} {\Phi } }{{\ell }_{𝒶}}\\ 0& 0& \frac{{\mathbb{K}}_{ℯ}}{𝒿}& 0\end{array}\right] \mathrm{and} B_{\mathbf{2}}=\left[\begin{array}{c}\frac{1}{\ell }\\ 0\\ 0\\ 0\end{array}\right]$$

(11)

So, the dynamics of the $i_{th}$ agent are written as

$$A_T= \left[\begin{array}{cccc}0& -\frac{1}{\ell }& 0& 0\\ \frac{1}{\complement }& 0& -\frac{1}{\complement }& 0\\ 0& \frac{1}{{\ell }_{𝒶}}& -\frac{{ℛ}_{𝒶}}{{\ell }_{𝒶}}& \frac{{\mathbb{K}}_{𝒶} {\Phi } }{{\ell }_{𝒶}}\\ 0& 0& \frac{{\mathbb{K}}_{ℯ}}{𝒿}& 0\end{array}\right] \mathrm{and} B_T=\left[\begin{array}{c}\frac{\mu }{\ell }\\ 0\\ 0\\ 0\end{array}\right]$$

(12)

If ${\mathcal{T}}_{\ell }$(loaded torque) is included in the system analysis, then

$$A_T= \left[\begin{array}{cccc}0& -\frac{1}{\ell }& 0& 0\\ \frac{1}{\complement }& 0& -\frac{1}{\complement }& 0\\ 0& \frac{1}{{\ell }_{𝒶}}& -\frac{{ℛ}_{𝒶}}{{\ell }_{𝒶}}& \frac{{\mathbb{K}}_{𝒶} {\Phi } }{{\ell }_{𝒶}}\\ 0& 0& \frac{{\mathbb{K}}_{ℯ}}{𝒿}& 0\end{array}\right] \mathrm{and} B_T=\left[\begin{array}{c}\frac{\mu }{\ell }\\ 0\\ 0\\ -\frac{{\mathcal{T}}_{\ell }}{𝒿}\end{array}\right]$$

(13)

where $\mu \in \left\{0,1\right\}.$ The proposed motor specifications are given in

Table 1. System Specifications of the proposed motor model.

Variable (units)	Value
Capacitance $\complement$ (μF)	$400$
Inductance $\ell$ (mH)	$1.5$
Power Supply $E$ (V)	$160$
Motor Inertia $𝒿$ (Kg.m²)	$7\times {10}^{-6}$
Armature Inductance ${\ell }_{𝒶}$ (mH)	$7$
Armature Resistance ${ℛ}_{𝒶}$ $\left(\mathsf{\Omega }\right)$	$5$
Motor back emf constant ${\mathbb{K}}_{ℯ}$ (V/rad/s)	$0.04$
Motor Constant ${\mathbb{K}}_a$ (Nm/A)	$1.1$
Motor Torque ${\mathcal{T}}_{\ell }$ (Nm)	$65$
Motor Speed $\omega$ (rpm)	$920$

, whereas the motor model along with the chopper circuit is given by Figure 2.

Assumption 1.

Suppose that the system matrices ${\mathit{A}}_{\mathit{\sigma }}$ and ${\mathit{B}}_{\mathit{\sigma }}$ are stable.

Assumption 2.

Assume that the system matrices ${\mathit{A}}_{\mathit{\sigma }}$ and ${\mathit{B}}_{\mathit{\sigma }}$ are controllable.

It is apparent that, if the $i_{th}$ agent is not only controllable but also observable, then all of the network agents are able to follow the leader’s trajectory and reach the consensus, i.e., synchronize with the leader speed.

4. Consensus Design and Stability Analysis

The system theory proposed in the earlier section is verified in this part of the paper using the concept of graph theory and the closed loop system behavior of the event-triggered leader-following MAS. First, error dynamics (commonly called measurement error), of the $i_{th}$ agent are given as

$${\epsilon }_i\left(t\right)={\omega }_i\left(t_k\right)-{\omega }_i\left(t\right), t\in \left[t_{ik},t_{ik+1}\right)$$

(14)

where $t_k$ is the $k_{th}$ event at which the $i_{th}$ agent is triggered. Moreover, the error dynamics of the complete system are given as $\epsilon \left(t\right)={\left[{\epsilon }_1\left(t\right),\dots ,{\epsilon }_N\left(t\right)\right]}^T$. It is obvious that ${\epsilon }_i\left(t\right)$ exists because of $u_i\left(t\right),$ therefore, when the leader is reachable by a follower, an error will decrease. It is already understood that in the leader-following MAS, the leader’s trajectory is unaffected by a follower, thus ${\epsilon }_0\left(t\right)=0$ always. Now, the centralized event-triggering condition is given as

$$t_{k+1}=\parallel \left(I_N\otimes K\right)\epsilon \left(t\right){\parallel }^2>\gamma \parallel \left(H\otimes K\right)\omega \left(t\right)-\left(D\otimes K\right)\left(I_N\otimes {\mathsf{\omega }}_0\left(t\right)\right){\parallel }^2$$

(15)

Thus, it is obvious that an event will be triggered whenever the norm of ${\epsilon }_i\left(t\right)$ surpasses the threshold, thereby resetting ${\epsilon }_i\left(t\right)$ to zero and $i_{th}$ agent state is communicated. Now, the centralized control protocol for the $i_{th}$ following agent is given as

$$u_i\left(t\right)=K{\displaystyle \sum }_{j=1}^N{\mathbf{𝒶}}_{i,j}\left({\widehat{\omega }}_j\left(t\right)-{\widehat{\omega }}_i\left(t\right)\right)+d_i\left({\widehat{\omega }}_0\left(\mathrm{t}\right)-{\widehat{\omega }}_i\left(\mathrm{t}\right)\right)$$

(16)

Observing Equation (16), it is clear that $u_i\left(t\right)$ depends on local information. At this point, it is worth mentioning that the term centralized denotes the synchronization of the event-triggering time sequence for all the agents, i.e., information update for all the following agents is synchronized.

The error dynamics between the leader and $i_{th}$ follower are given as $e_i\left(t\right)={\omega }_i\left(t\right)-{\omega }_0\left(t\right)$ and $\widehat{e_i}\left(t\right)={\widehat{\omega }}_i\left(t\right)-{\widehat{\omega }}_0\left(t\right)$ then

$$\dot{e_i\left(t\right)}=A{e}_i+B{u}_i$$

(17)

$$\dot{e_i\left(t\right)}= A{e}_i+B\left(K{\displaystyle \sum }_{j=1}^N{\mathbf{𝒶}}_{i,j}\left({\widehat{\omega }}_j\left(\mathrm{t}\right)-{\widehat{\omega }}_i\left(\mathrm{t}\right)\right)+d_i\left({\widehat{\omega }}_0\left(\mathrm{t}\right)-{\widehat{\omega }}_i\left(\mathrm{t}\right)\right)\right)$$

(18)

$$\dot{e_i\left(t\right)}= A{e}_i+B\left(K{\displaystyle \sum }_{j=1}^N{\mathbf{𝒶}}_{i,j}\left({\widehat{e}}_j\left(\mathrm{t}\right)-{\widehat{e}}_i\left(\mathrm{t}\right)\right)+d_i\left({\widehat{e}}_0\left(\mathrm{t}\right)-{\widehat{e}}_i\left(\mathrm{t}\right)\right)\right)$$

(19)

$$\dot{e_i\left(t\right)}= A{e}_i+\mathrm{B}\left(K{\displaystyle \sum }_{j=1}^N{\mathbf{𝒶}}_{i,j}\left({\widehat{e}}_j\left(\mathrm{t}\right)-{\widehat{e}}_i\left(\mathrm{t}\right)\right) -BK{d}_i{\widehat{e}}_i\left(\mathrm{t}\right)\right)$$

(20)

Now, considering $\dot{e_i\left(t\right)}$ w.r.t. the closed loop dynamics of the MAS yield

$$\dot{e\left(t\right)}=\left(I_N\otimes A\right) e\left(t\right)-\left[\left(I_M\otimes L\right)\left(I_N\otimes B\right)\left(I_N\otimes K\right)-\left(I_M\otimes d\right)\left(I_N\otimes B\right)\left(I_N\otimes K\right)\right]\left(\epsilon \left(t\right)+e\left(t\right)\right)$$

(21)

Using the property of the Kronecker product of the matrix gives

$$\dot{e\left(t\right)}=\left(I_N\otimes A\right) e\left(t\right)-\left[BK\otimes \left(I_M\otimes L\right)-\mathrm{B}K\otimes \left(I_M\otimes d\right)\right]\left(\epsilon \left(t\right)+e\left(t\right)\right)$$

(22)

$$\dot{e\left(t\right)}=\left(I_N\otimes A\right) e\left(t\right)-BK\otimes \left[\left(I_M\otimes L\right)+\left(I_M\otimes d\right)\right]\left(\epsilon \left(t\right)+e\left(t\right)\right)$$

(23)

$$\dot{e\left(t\right)}=\left(I_N\otimes A\right) e\left(t\right)-BK\otimes \left[L+d\right]\left(\epsilon \left(t\right)+e\left(t\right)\right)$$

(24)

And finally,

$$\dot{e\left(t\right)}=\left(I_N\otimes A\right) e\left(t\right)-\left[BK\otimes H\right]\left(\epsilon \left(t\right)+e\left(t\right)\right)$$

(25)

Now, at this stage, it is necessary to introduce the cost function of the LQR which is given as

$$\mathcal{J}= {{\displaystyle \int }}_0^{\infty }\left(e^T\left(I_{N }\otimes Q\right) e + u^{T}Ru\right)dt$$

(26)

Such that the matrices $Q$ and $R$ are positive definite. Now, to minimize $\mathcal{J}$, if assumptions 1 and 2 hold, then a symmetric (and positive definite) matrix $P$ and a feedback matrix $K$ exist to the given Riccati inequality and $\gamma <\frac{1}{{{\lambda }_N}^2}$

$$A^{T}P+PA-2\alpha R^{-\mathbf{1}}{B}^{T}PBP<-\alpha Q$$

(27)

whereas $K= R^{-\mathbf{1}}{B}^{T}P$.

In order to ensure the stability of the proposed switched system, a common Lyapunov stability criteria is adopted such that the Lyapunov function candidate is given as

$$\mathcal{V}(t)=e{(t)}^T(I_N\otimes P)e(t)$$

(28)

$$\dot{\mathcal{V}(t)}= \dot{e{(t)}^T}(I_N\otimes P)e(t)+e{(t)}^T(I_N\otimes P)\dot{e}(t)$$

(29)

$$\dot{\mathcal{V}(t)}=[(I_N\otimes A^T)e{(t)}^T-(B^T{K}^T\otimes H^T){(\epsilon (t)+e(t))}^T](I_N\otimes P)e(t)+e{(t)}^T(I_N\otimes P)\left[(I_N\otimes A)e(t)-(BK\otimes H)(\epsilon (t)+e(t))\right]$$

(30)

$$\dot{\mathcal{V}(t)}=[(I_N\otimes A^T)(I_N\otimes P)e{(t)}^T-(I_N\otimes P)(B^T{K}^T\otimes H^T){(\epsilon (t)+e(t))}^T]e(t)+e{(t)}^T\left[(I_N\otimes A)(I_N\otimes P)e(t)-(I_N\otimes P)(BK\otimes H)(\epsilon (t)+e(t))\right]$$

(31)

Again, using the properties of Kronecker products and rearranging the above equation gives

$$\dot{\mathcal{V}(t)}=[(I_N\otimes A^{T}P)e{(t)}^T-(H\otimes B^T{K}^{T}P){(\epsilon (t)+e(t))}^T]e(t)+e{(t)}^T\left[(I_N\otimes AP)e(t)-(H\otimes BKP)(\epsilon (t)+e(t))\right]$$

(32)

$$\dot{\mathcal{V}(t)}=[(I_N\otimes A^{T}P)e{(t)}^T-H\otimes B^T{K}^{T}P(\epsilon (t))-H\otimes B^T{K}^{T}P{(e(t))}^T]e(t)+e{(t)}^T\left[(I_N\otimes AP)e(t)-H\otimes BKP (\epsilon (t))-H\otimes BKP (e(t))\right]$$

(33)

$$\dot{\mathcal{V}(t)}=e{(t)}^T[I_N\otimes A^{T}P-H\otimes B^T{K}^{T}P]e(t)-\epsilon (t)[H\otimes B^T{K}^{T}P]e(t)+ e{(t)}^T[I_N\otimes AP-H\otimes BKP]e(t)-\epsilon (t)[H\otimes BKP]e{(t)}^T$$

(34)

$$\dot{\mathcal{V}(t)}=e{(t)}^T[I_N\otimes (A^{T}P+AP)-H\otimes (B^T{K}^{T}P+BKP)]e(t)-\epsilon (t)[H\otimes (B^T{K}^{T}P+BKP)]e{(t)}^T$$

(35)

Now, putting the value of $K= R^{-\mathbf{1}}{B}^{T}P$ and rearranging the above equation gives

$$\dot{\mathcal{V}(t)}=e{(t)}^T[I_N\otimes (A^{T}P+AP)-H\otimes (B^T{(R^{-\mathbf{1}}BP)}^{T}P+B{R}^{-\mathbf{1}}{B}^{T}PP]e(t)-\epsilon (t)[H\otimes (B^T{(R^{-\mathbf{1}}{B}^{T}P)}^{T}P+B(R^{-\mathbf{1}}{B}^{T}P)P)]e{(t)}^T$$

(36)

Thus

$$\dot{\mathcal{V}(t)}=e{(t)}^T[I_N\otimes (A^{T}P+AP)-H\otimes \mathbf{2}{R}^{-\mathbf{1}}{B}^{T}PBP]e(t)- \epsilon (t)[H\otimes \mathbf{2}{R}^{-\mathbf{1}}{B}^{T}PBP]e{(t)}^T$$

(37)

Finally, using the triggering condition in equation (15) and equation (25), we have

$$\dot{\mathcal{V}(t)}<e{(t)}^T[{\mathit{I}}_{\mathit{N}}\otimes (A^{T}P+AP)- H\otimes R^{-\mathbf{1}}{B}^{T}PBP]e(t)+\epsilon {(t)}^T[H\otimes R^{-\mathbf{1}}{B}^{T}PBP]\epsilon (t)$$

(38)

Or

$$\dot{\mathcal{V}(t)}<e{(t)}^T[{\mathit{I}}_{\mathit{N}}\otimes (A^{T}P+AP)-H\otimes R^{-\mathbf{1}}{B}^{T}PBP]e(t)+e{(t)}^T[{({\lambda }_N)}^2\gamma H\otimes R^{-\mathbf{1}}{B}^{T}PBP]e(t)$$

(39)

$$\dot{\mathcal{V}(t)}<e{(t)}^T[{\mathit{I}}_{\mathit{N}}\otimes (A^{T}P+AP)-H\otimes R^{-\mathbf{1}}{B}^{T}PBP(1-{({\lambda }_N)}^2\gamma )] e(t)$$

(40)

5. Results

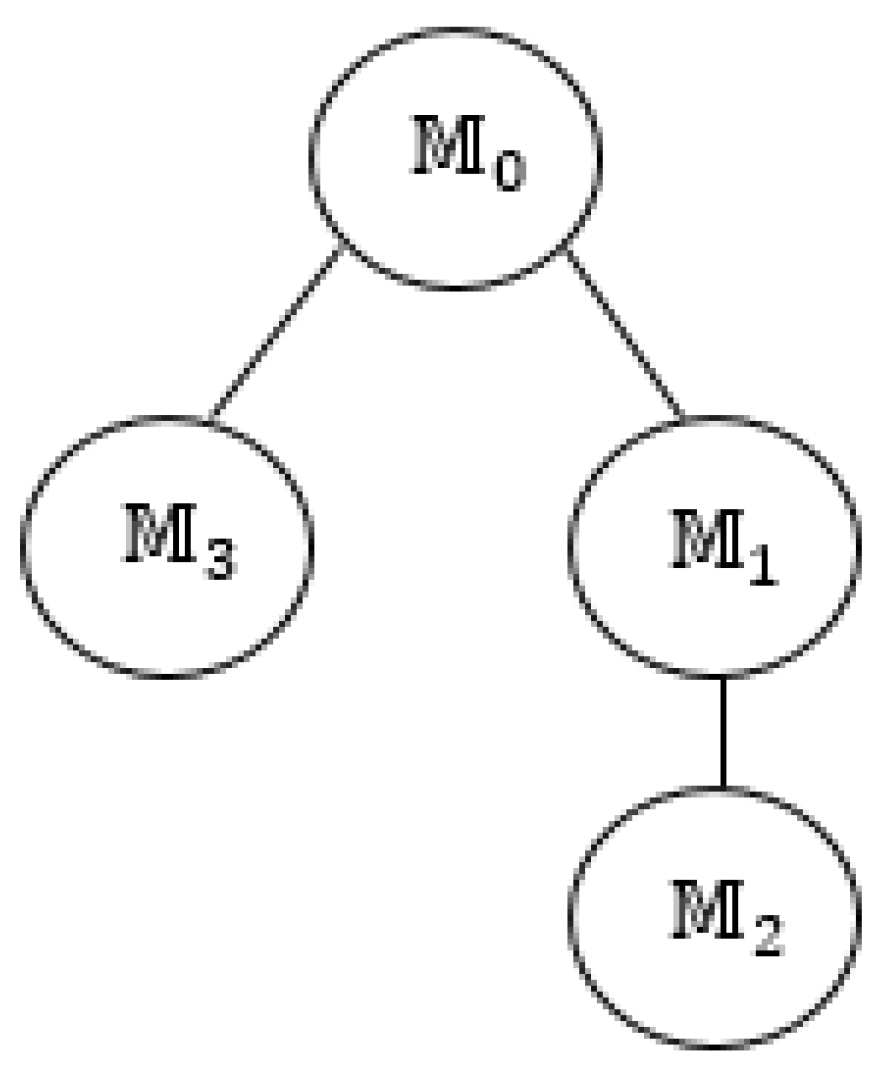
In this part of the paper, the complete analysis of the event-triggered MAS is presented using the methodology proposed in the above-mentioned sections. For the purpose of simulation, the multi-motor system is supposed to be connected in the manner given in Figure 3, with one leader ${\mathbb{M}}_0$ and three following agents, i.e. ${\mathbb{M}}_1-{\mathbb{M}}_3$. Moreover, it is also assumed that no load is applied to the motors and communication is delay-free.

To begin with the system analysis, the system matrices are obtained to be

$$A= \left[\begin{array}{cccc}0& -0.0067& 0& 0\\ 2.500& 0& -2.500& 0\\ 0& 0.0014& -0.0071& -0.0001\\ 0& 0& 0.0571& 0\end{array}\right] \mathrm{and} B=\left[\begin{array}{c}666.66\\ 0\\ 0\\ 0\end{array}\right]$$

Now, with respect to the communication pattern of Figure 3, the matrices $L\left(G\right)$ and $d\left(G\right)$, certifying lemma 1 and 2, are given as

$$L\left(G\right)=\left[\begin{array}{ccc}1& -1& 0\\ -1& 1& 0\\ 0& 0& 0\end{array}\right], d\left(G\right)=\left[\begin{array}{ccc}1& 0& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right]$$

The minimum eigenvalue of $H$ is 0.3820 while the highest value is 2.6180, certifying lemma 3 and 4, thus $\mathsf{\gamma }$ is taken to be 0.72. Now, if $R$ is supposed to be 1, then the feedback matrix $K$ and matrix $P$ are given as

$$\begin{gathered} P=\left[\begin{array}{cccc}0.0437& 0.0002& -0.0263& 0.0020\\ 0.0002& 0.0001& -0.0002& 0\\ -0.0263& -0.0002& 0.1075& 0.0098\\ 0.0020& 0& 0.0098& 0.0017\end{array}\right], \\ K=\left[\begin{array}{cccc}11.1178& 0.0628& -6.6957& 0.5201\end{array}\right] \end{gathered}$$

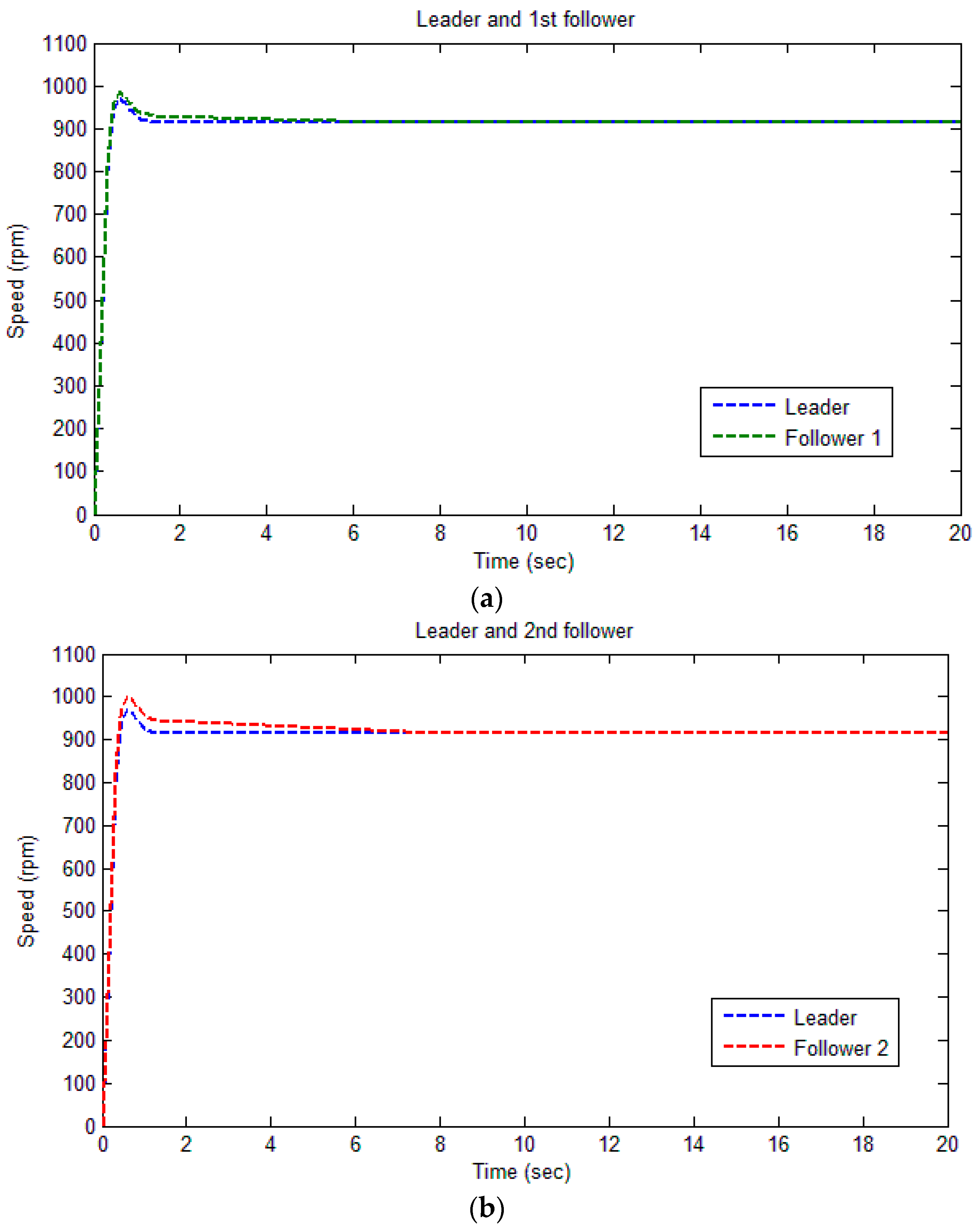
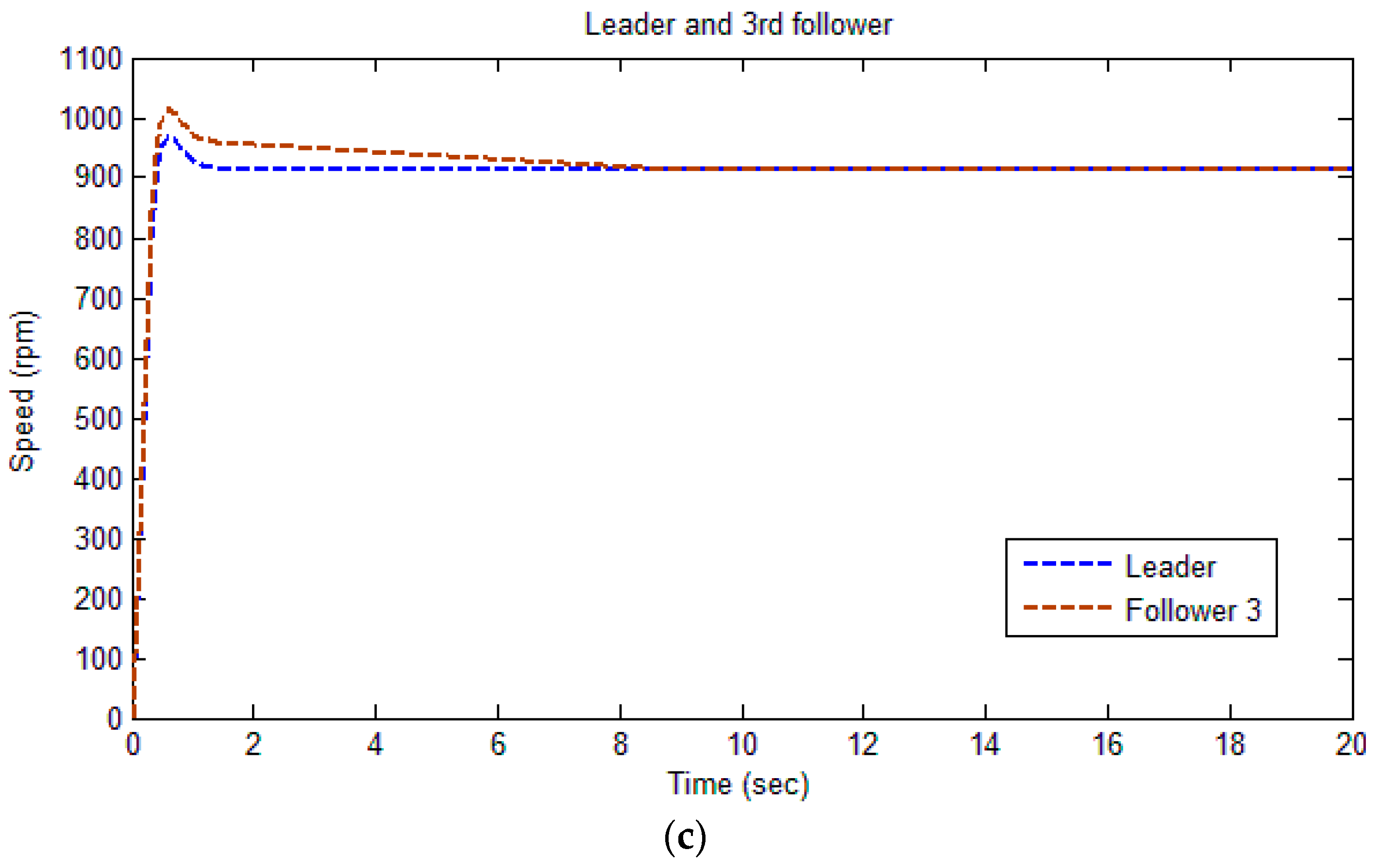
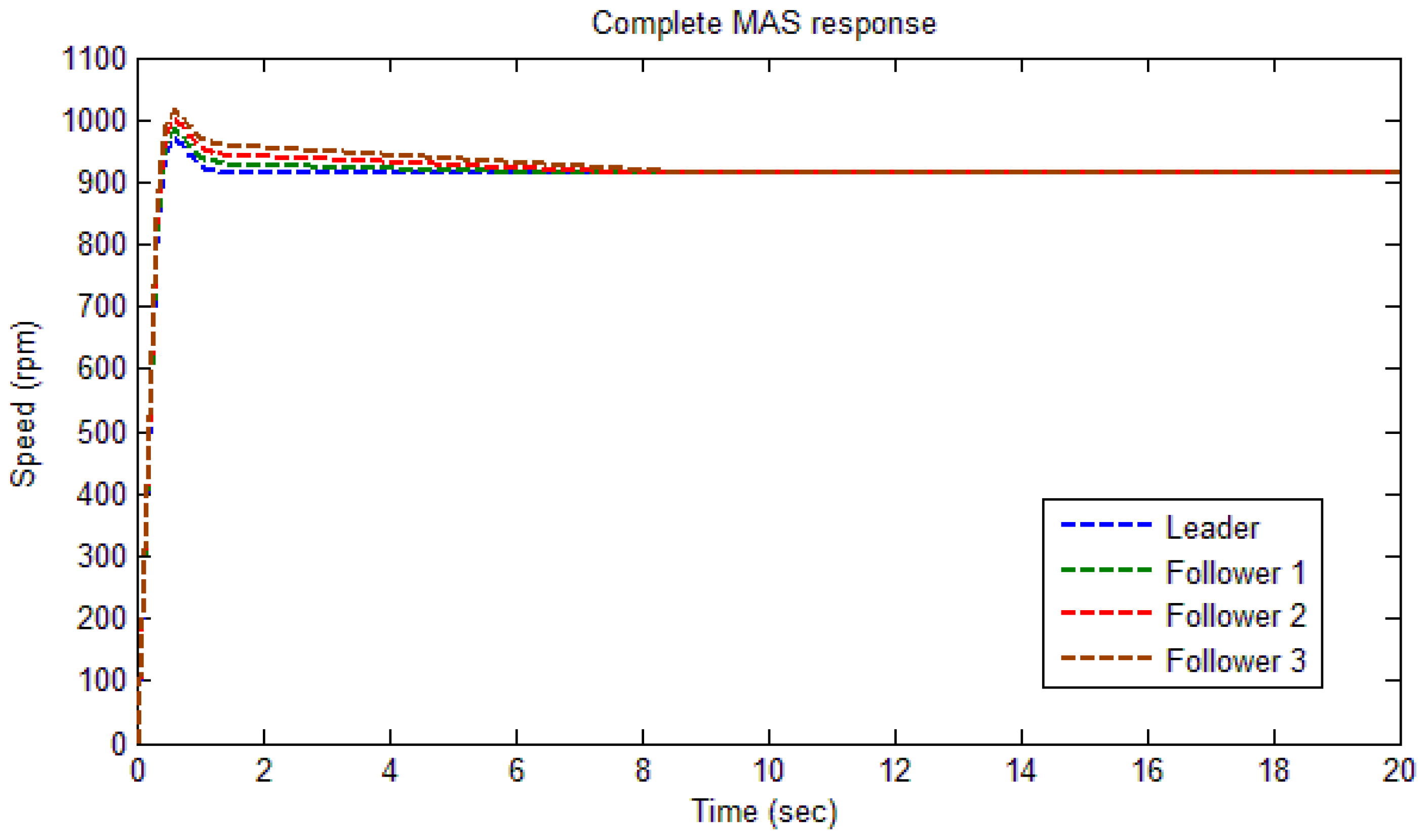
Thus, it is shown in Figure 4a–c and Figure 5 that the consensus is reached among the leader and followers, such that all the following agents regulate the speed in synchronization with the leader. Figure 6 provides the time at which events are triggered between intervals [0, 20 s]. Figure 6 also validates the energy saving strategy as compared to the system without event-triggering schemes.

6. Conclusions

The presented work is motivated by the enormous industrial application of the multi-motor system with there being a requirement for synchronous speed with minimum energy consumption. Therefore, it is worth finding out the energy saving scheme for the aforesaid application. Thus, the paper presents the event-triggered leader-following MAS consensus scheme along with the LQR control to address the synchronous speed problem. The stability of the system is proven by using a common Lyapunov theorem. The obtained results proved the success of the proposed methodology and the graphical results clearly show that the system is running at synchrony with the speed of the leader. Moreover, for future work, it is advised to consider the system with the load, with the network delays, or with noises.