A Time-Domain Artificial Boundary for Near-Field Wave Problem of Fluid Saturated Porous Media
Abstract
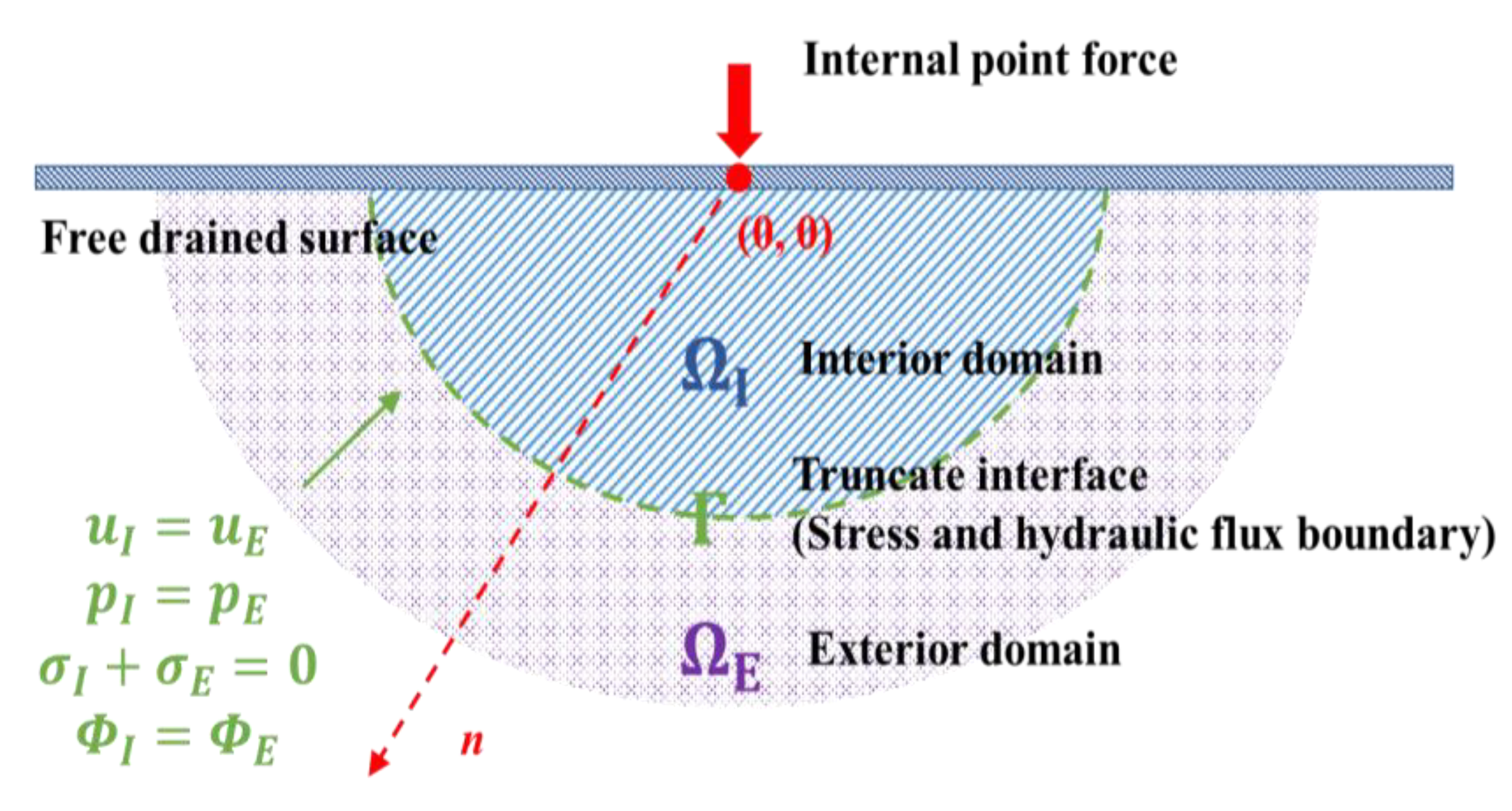
:1. Introduction
2. Wave Velocity
3. Viscous-Spring Artificial Boundary
3.1. Flow Velocity Boundary Condition
3.2. Stress Boundary Condition
3.3. Finite Element Discretization of Artificial Boundary
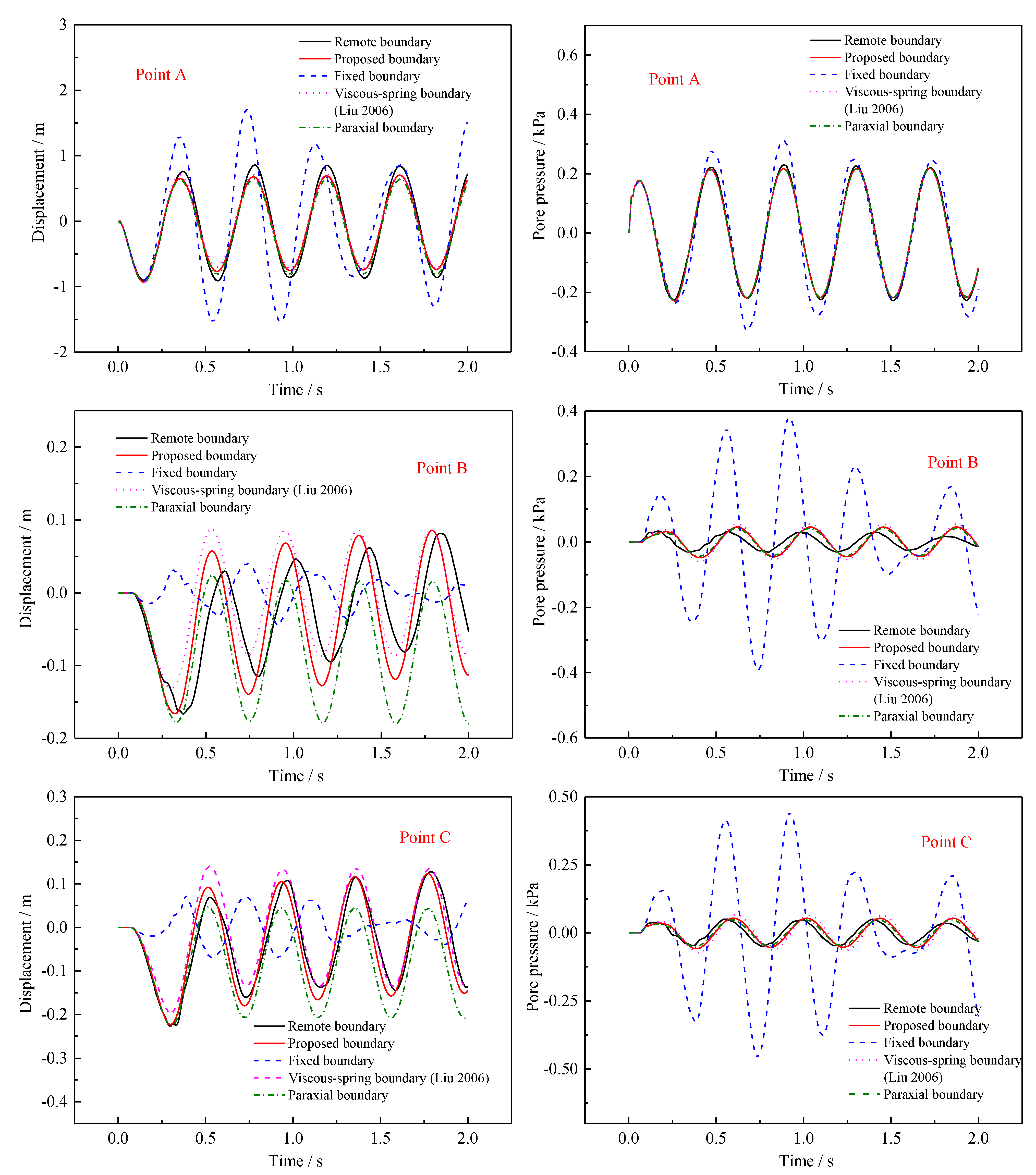
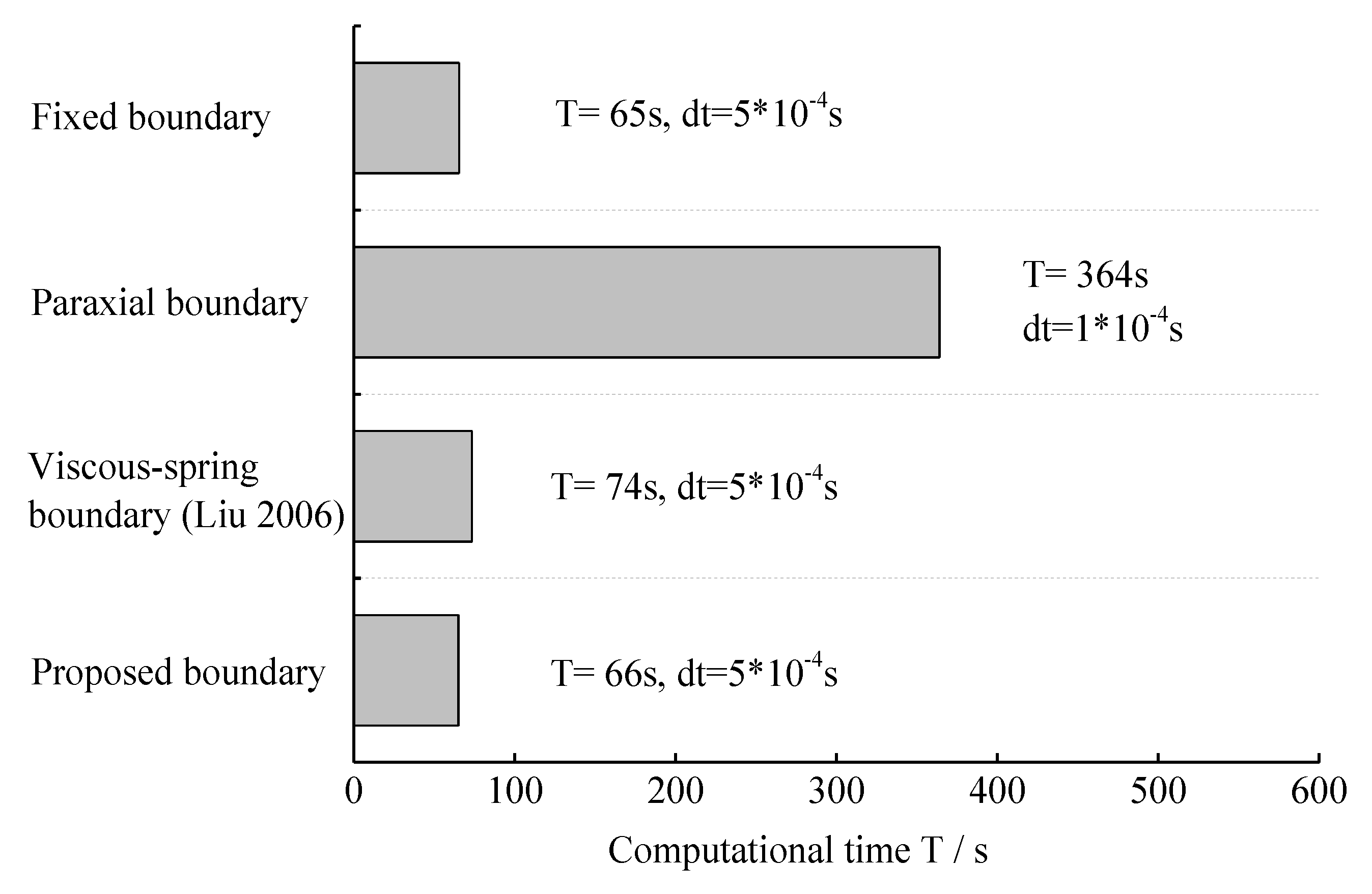
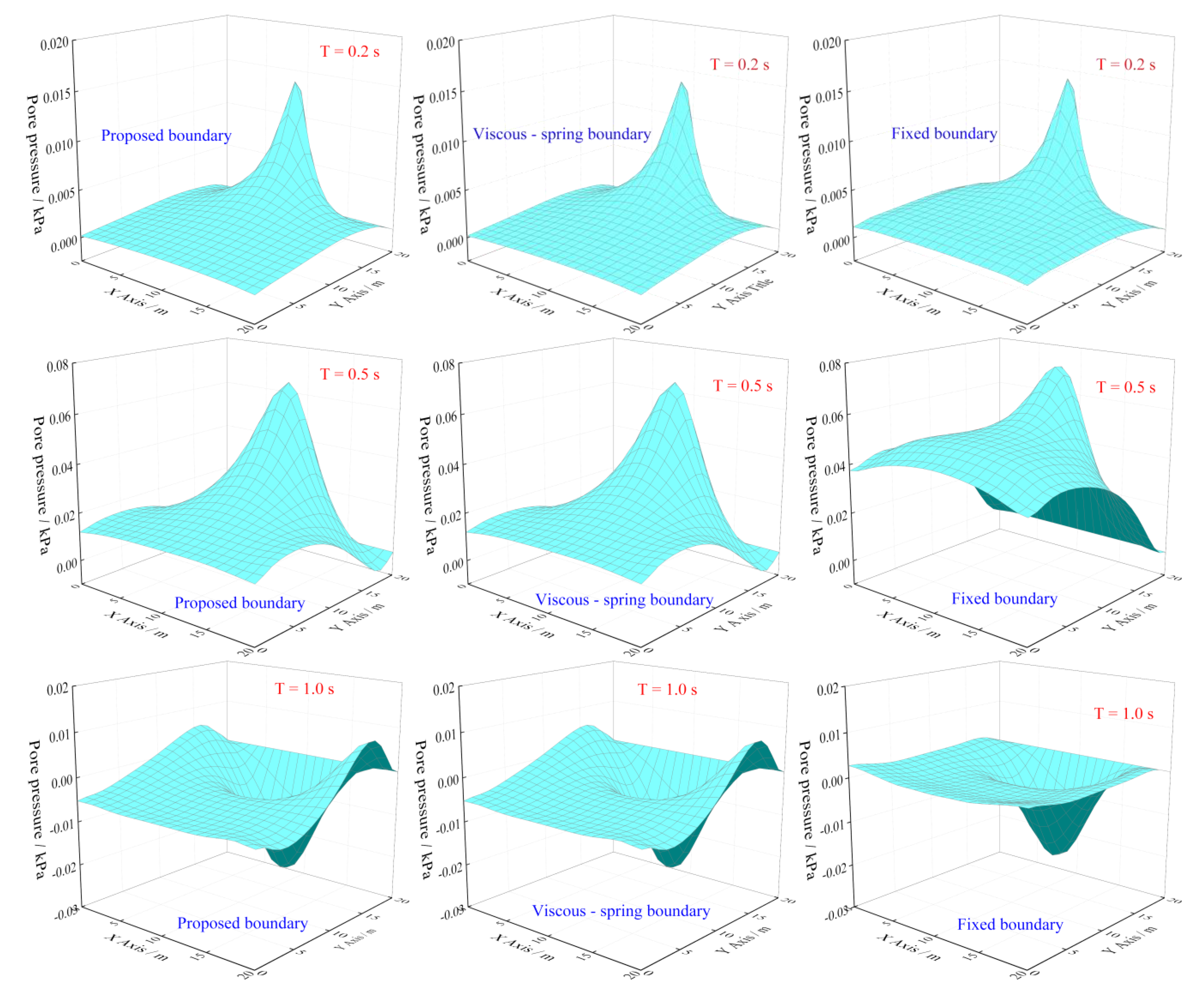
4. Numerical Studies
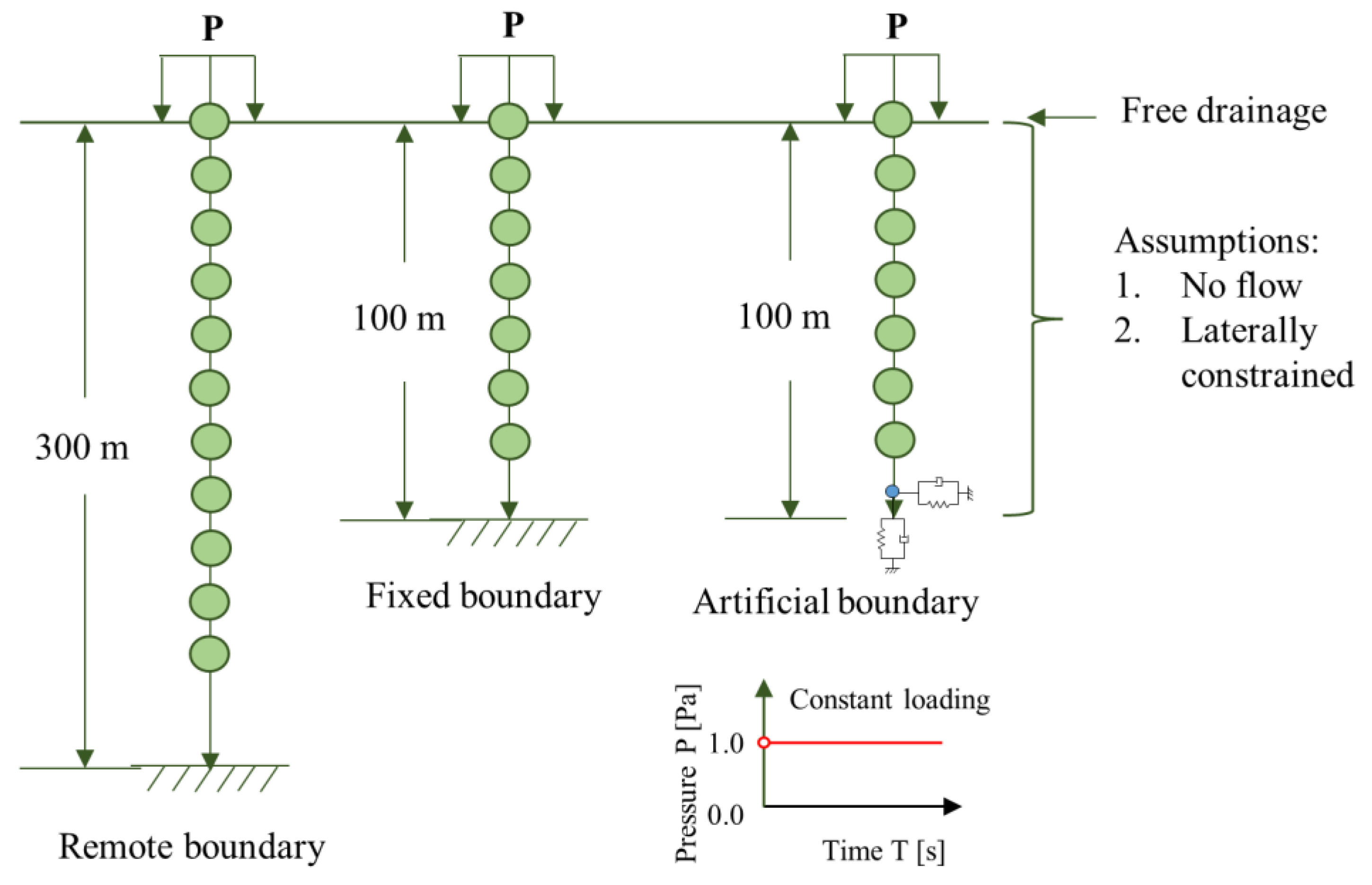
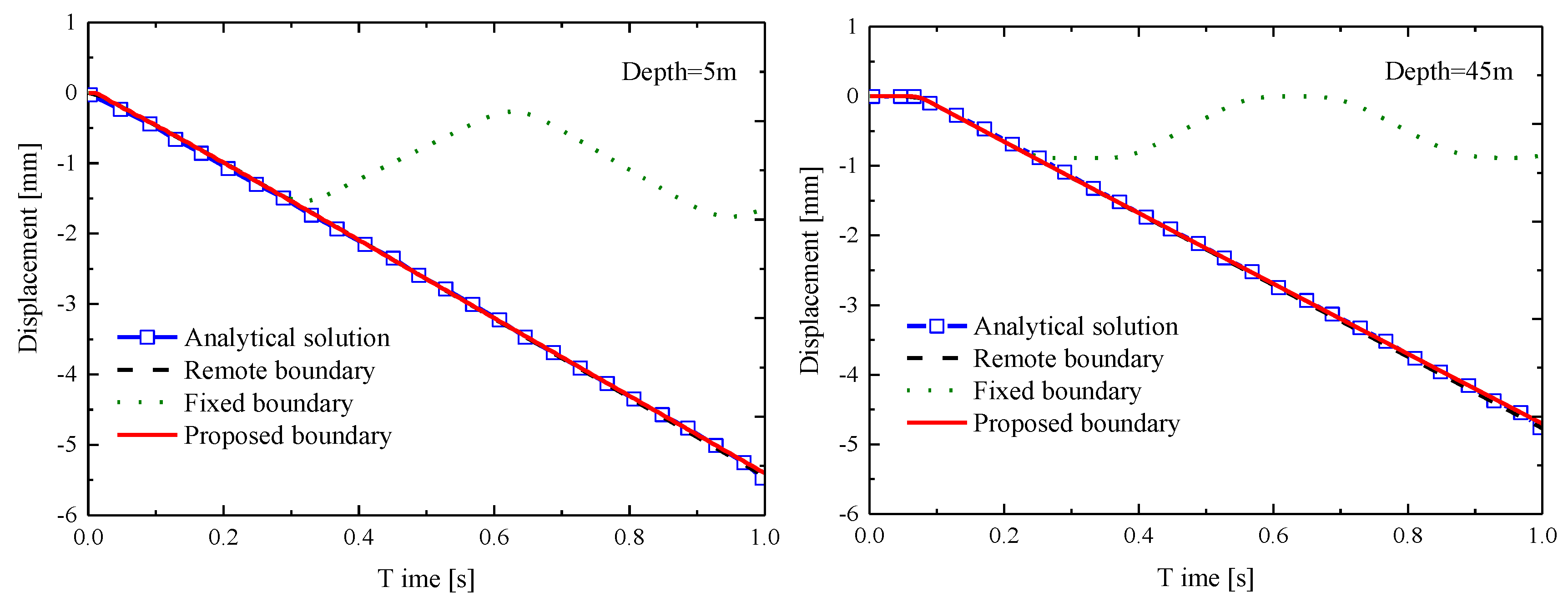
4.1. Example 1
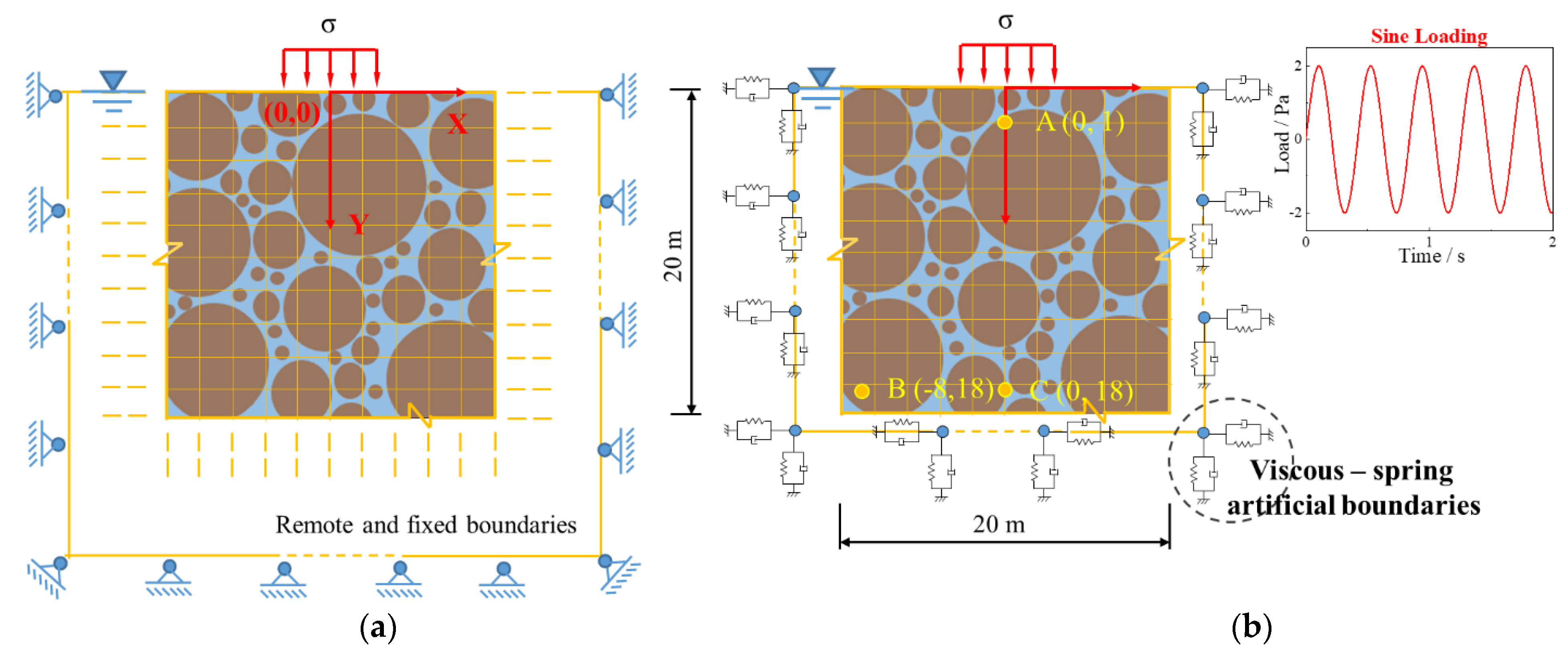
4.2. Example 2
4.3. Example 3
5. Conclusions
- The viscous spring boundary is composed of the stress and flow velocity boundary conditions, which are constructed by the reasonable outgoing wave assumption and Green’s function. The boundary has a simple form and clear physical meaning. Since the overall system equations considering artificial boundaries only need to change the values of the corresponding boundary nodes on the diagonal of the coefficient matrices, the boundary can be easily applied to the finite element method.
- Without the assumption of permeability and using the real wave velocity, the proposed boundary has higher accuracy than the existing boundaries with the assumption of impermeability.
- After considering the viscous spring boundary, the computational system is expressed as lumped mass equations with damping. A complete explicit integration algorithm with second-order accuracy is constructed to solve the equations.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
Explicit Integration Algorithm
- (a)
- The whole of the loading time is divided into several time intervals with a time step , and any time can be expressed as , (k = 1, 2, 3, …). Equation (A1) is solved using the explicit algorithm method [64] to obtain the step-by-step recurrence formula of the solid phase displacement at the time :
- (b)
- To express the acceleration at the time , convert Equation (A1) into the following form:
- (c)
- Apply the Newmark method to get the velocity at the time . The parameters ,where , , , and are known items.
- (d)
- Equation (A2) is solved using the Euler predictor-corrector method [65]. The formulas are shown as follows:
References
- Biot, M.A. General theory of three-dimensional consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. I. Low-frequency range. J. Acoust. Soc. Am. 1956, 28, 168–178. [Google Scholar] [CrossRef]
- Biot, M.A. Theory of propagation of elastic waves in a fluid-saturated porous solid. II. Higher frequency range. J. Acoust. Soc. Am. 1956, 28, 179–191. [Google Scholar] [CrossRef]
- Lévy, T. Propagation of waves in a fluid-saturated porous elastic solid. Int. J. Eng. Sci. 1979, 17, 1005–1014. [Google Scholar] [CrossRef]
- Auriault, J.L. Dynamic behaviour of a porous medium saturated by a Newtonian fluid. Int. J. Eng. Sci. 1980, 18, 775–785. [Google Scholar] [CrossRef]
- Prevost, J.H. Nonlinear transient phenomena in saturated porous media. Comput. Methods Appl. Mech. Eng. 1982, 30, 3–18. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Shiomi, T. Dynamic behaviour of saturated porous media; the generalized Biot formulation and its numerical solution. Int. J. Numer. Anal. Methods Geomech. 1984, 8, 71–96. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Chan, A.H.C.; Pastor, M.; Schrefler, B.A.; Shiomi, T. Computational Geomechanics with Special Reference to Earthquake Enineering; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Men, F.L. Wave propagation in fluid-saturated porous media. Acta Geophys. 1981, 24, 65–75. (In Chinese) [Google Scholar]
- Chen, L.Z.; Wu, S.M.; Zeng, G.X. Propagation of elastic waves in saturated soil. Acta Mech. 1987, 19, 276–283. (In Chinese) [Google Scholar]
- Wu, S.M. Waves in Soil; Science Press: Beijing, China, 1997. (In Chinese) [Google Scholar]
- Zhao, C.G.; Du, X.L.; Cui, J. Advances in wave theory and numerical simulation in solid and fluid multiphase porous media. Adv. Mech. 1998, 28, 83–91. (In Chinese) [Google Scholar]
- Morency, C.; Tromp, J. Spectral-element simulations of wave propagation in porous media. Geophys. J. Int. 2008, 175, 301–345. [Google Scholar] [CrossRef]
- De la Puente, J.; Dumbser, M.; Käser, M.; Igel, H. Discontinuous Galerkin methods for wave propagation in poroelastic media. Geophysics 2008, 73, T77–T97. [Google Scholar] [CrossRef]
- Wang, Y.F.; Liang, J.W.; Chen, A.L.; Wang, Y.S.; Laude, V. Evanescent waves in two-dimensional fluid-saturated porous metamaterials with a transversely isotropic matrix. Phys. Rev. B 2020, 101, 184301. [Google Scholar] [CrossRef]
- Zhao, M. A Comparative Study of Viscoelastic Artificial Boundaries and Their Transmission Artificial Boundaries; Beijing University of Technology: Beijing, China, 2004. (In Chinese) [Google Scholar]
- Zhao, M.; Du, X.L.; Liu, J.B.; Liu, H. Explicit finite element artificial boundary scheme for transient scalar waves in two-dimensional unbounded waveguide. Int. J. Numer. Methods Eng. 2011, 87, 1074–1104. (In Chinese) [Google Scholar] [CrossRef]
- Teng, Z.H. Exact boundary condition for time-dependent wave equation based on boundary integral. J. Comput. Phys. 2003, 190, 398–418. (In Chinese) [Google Scholar] [CrossRef]
- Givoli, D.; Cohen, D. Nonreflecting Boundary Conditions Based on Kirchhoff-Type Formulae. J. Comput. Phys. 1995, 117, 102–113. [Google Scholar] [CrossRef]
- Givoli, D. Exact Representations on Artificial Interfaces and Applications in Mechanics. Appl. Mech. Rev. 1999, 52, 333–349. [Google Scholar] [CrossRef]
- Lysmer, J.; Kuhlemeyer, R.L. Finite dynamic model for infinite media. J. Eng. Mech. Div. 1969, 95, 859–878. [Google Scholar] [CrossRef]
- Deeks, A.J.; Randolph, M.F. Axisymmetric time-domain transmitting boundaries. J. Eng. Mech. 1994, 120, 25–42. [Google Scholar] [CrossRef]
- Kellezi, L. Local transmitting boundaries for transient elastic analysis. Soil Dyn. Earthq. Eng. 2000, 19, 533–547. [Google Scholar] [CrossRef]
- Liu, J.B.; Du, Y.; Du, X.L.; Wang, Z.; Wu, J. 3D viscous-spring artificial boundary in time domain. Earthq. Eng. Eng. Vib. 2006, 5, 93–102. (In Chinese) [Google Scholar] [CrossRef]
- Smith, W.D. A nonreflecting plane boundary for wave propagation problems. J. Comput. Phys. 1974, 15, 492–503. [Google Scholar] [CrossRef]
- Liao, Z.P.; Wong, H.L. A transmitting boundary for the numerical simulation of elastic wave propagation. Int. J. Soil Dyn. Earthq. Eng. 1984, 3, 174–183. (In Chinese) [Google Scholar] [CrossRef]
- Higdon, R.L. Radiation boundary conditions for elastic wave propagation. SIAM J. Numer. Anal. 1990, 27, 831–869. [Google Scholar] [CrossRef]
- Hall, W.S.; Oliveto, G. Boundary Element Methods for Soil-Structure Interaction; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Kausel, E. Thin-layer method: Formulation in the time domain. Int. J. Numer. Methods Eng. 1994, 37, 927–941. [Google Scholar] [CrossRef]
- Givoli, D. Recent advances in the DtN FE method. Arch. Comput. Methods Eng. 1999, 6, 71–116. [Google Scholar] [CrossRef]
- Kuhlemeyer, R.L.; Lysmer, J. Finite element method accuracy for wave propagation problems. J. Soil Mech. Found. Div. 1973, 99, 421–427. [Google Scholar] [CrossRef]
- Du, X.L. Locally decoupled time domain wave analysis method. World Earthq. Eng. 2000, 16, 22–26. (In Chinese) [Google Scholar]
- Du, X.L.; Zhao, M.; Wang, J.T. Artificial stress boundary strips for near-field wave simulation. Acta Mech. 2006, 38, 49–56. (In Chinese) [Google Scholar]
- Li, P.; Song, E.X. A high-order time-domain transmitting boundary for cylindrical wave propagation problems in unbounded saturated poroelastic media. Soil Dyn. Earthq. Eng. 2013, 48, 48–62. (In Chinese) [Google Scholar] [CrossRef]
- Liu, J.B.; Lu, Y. A direct method for analysis of dynamic soil-structure interaction based on interface idea. Dev. Geotech. Eng. 1998, 83, 261–276. (In Chinese) [Google Scholar]
- Kunar, R.R.; Marti, J. Computational methods for infinite domain media-structure interaction. J. Appl. Mech. Div. 1981, 46, 183–204. [Google Scholar]
- Liao, Z.P. Extrapolation non-reflecting boundary conditions. Wave Motion 1996, 24, 117–138. (In Chinese) [Google Scholar] [CrossRef]
- Clayton, R.; Engquist, B. Absorbing boundary conditions for acoustic and elastic wave equations. Bull. Seism. Soc. Am. 1977, 67, 1529–1540. [Google Scholar] [CrossRef]
- Engquist, B.; Majda, A. Radiation boundary conditions for acoustic and elastic wave calculations. Commun. Pure Appl. Math. 1979, 32, 313–357. [Google Scholar] [CrossRef]
- Higdon, R.L. Numerical absorbing boundary conditions for the wave equation. Math. Comput. 1987, 49, 65–90. [Google Scholar] [CrossRef]
- Komatitsch, D.; Martin, R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation. Geophysics 2007, 72, SM155–SM167. [Google Scholar] [CrossRef]
- Zeng, Y.Q.; He, J.Q.; Liu, Q.H. The application of the perfectly matched layer in numerical modeling of wave propagation in poroelastic media. Geophysics 2001, 66, 1258–1266. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, C.; Valliappan, S. A dynamic infinite element for three-dimensional infinite-domain wave problems. Int. J. Numer. Methods Eng. 1993, 36, 2567–2580. [Google Scholar] [CrossRef]
- Zhao, C. Dynamic and Transient Infinite Elements: Theory and Geophysical, Geotechnical and Geoenvironmental Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Zhao, C. Coupled method of finite and dynamic infinite elements for simulating wave propagation in elastic solids involving infinite domains. Sci. China Technol. Sci. 2010, 53, 1678–1687. [Google Scholar] [CrossRef]
- Modaressi, H.; Benzenati, I. An absorbing boundary element for dynamic analysis of two-phase media. In Proceedings of the 10th World Conference on Earthquake Engineering, Madrid, Spain, 19–24 July 1992; pp. 1157–1163. [Google Scholar]
- Modaressi, H.; Benzenati, I. Paraxial approximation for poroelastic media. Soil Dyn. Earthq. Eng. 1994, 13, 117–129. [Google Scholar] [CrossRef]
- Akiyoshi, T.; Fuchida, K.; Fang, H. Absorbing boundary conditions for dynamic analysis of fluid-saturated porous media. Soil Dyn. Earthq. Eng. 1994, 13, 387–397. [Google Scholar] [CrossRef]
- Akiyoshi, T.; Fang, H.L.; Fuchida, K.; Matsumoto, H. A non-linear seismic response analysis method for saturated soil-structure system with absorbing boundary. Int. J. Numer. Anal. Methods Géoméch. 1996, 20, 307–329. [Google Scholar] [CrossRef]
- Akiyoshi, T.; Sun, X.; Fuchida, K. General absorbing boundary conditions for dynamic analysis of fluid-saturated porous media. Soil Dyn. Earthq. Eng. 1998, 17, 397–406. [Google Scholar] [CrossRef]
- Liu, G.L.; Song, E.X. Viscoelastic transport boundary of numerical simulation of saturated infinite foundation. Chin. J. Geotech. Eng. 2006, 28, 2128–2133. (In Chinese) [Google Scholar]
- Du, X.L.; Li, L.Y. A Viscoelastic Artificial Boundary for Near-Field Fluctuation Analysis of Saturated Porous Media. Chin. J. Geophys. 2008, 51, 575–581. (In Chinese) [Google Scholar]
- Wang, Z.H.; Zhao, C.G.; Dong, L. An approximate spring dashpot artificial boundary for transient wave analysis of fluid-saturated porous media. Comput. Geotech. 2009, 36, 199–210. (In Chinese) [Google Scholar] [CrossRef]
- Wang, G.J.; Zhao, C.G. Artificial boundary of viscoelastic dynamics of fluid saturated porous media. World Seismol. Eng. 2007, 23, 54–59. (In Chinese) [Google Scholar]
- Li, P.; Song, E.X. A viscous-spring transmitting boundary for cylindrical wave propagation in saturated poroelastic media. Soil Dyn. Earthq. Eng. 2014, 65, 269–283. (In Chinese) [Google Scholar] [CrossRef]
- Degrande, G.; De Roeck, G. An absorbing boundary condition for wave propagation in saturated poroelastic media—Part I: Formulation and efficiency evaluation. Soil Dyn. Earthq. Eng. 1993, 12, 411–421. [Google Scholar] [CrossRef]
- Degrande, G.; De Roeck, G. An absorbing boundary condition for wave propagation in saturated poroelastic media—Part II: Finite element formulation. Soil Dyn. Earthq. Eng. 1993, 12, 423–432. [Google Scholar] [CrossRef]
- Gajo, A.; Saetta, A.; Vitaliani, R. Silent boundary conditions for wave propagation in saturated porous media. Int. J. Numer. Anal. Methods Geomech. 1996, 20, 253–273. [Google Scholar] [CrossRef]
- Zerfa, Z.; Loret, B. A viscous boundary for transient analyses of saturated porous media. Earthq. Eng. Struct. Dyn. 2003, 33, 89–110. [Google Scholar] [CrossRef]
- Song, J. Wave Numerical Method of Saturated Soil Site and Its Engineering Application; Beijing University of Technology: Beijing, China, 2012. (In Chinese) [Google Scholar]
- Philippacopoulos, A.J. Lamb’s problem for fluid-saturated, porous media. Bull. Seismol. Soc. Am. 1988, 78, 908–923. [Google Scholar]
- Passty, G.B.; Haberman, R. Elementary Applied Partial Differential Equations with Fourier Series and Boundary Value Problems. Am. Math. Mon. 1985, 92, 441. [Google Scholar] [CrossRef]
- Simon, B.R.; Zienkiewicz, O.C.; Paul, D.K. An analytical solution for the transient response of saturated porous elastic solids. Int. J. Numer. Anal. Methods Géoméch. 1984, 8, 381–398. [Google Scholar] [CrossRef]
- Du, X.L.; Wang, J.T. An explicit difference formulation of dynamic response calculation of elastic structure with damping. Eng. Mech. 2000, 17, 37–43. [Google Scholar]
- Xue, Y. Numerical Analysis and Scientific Computing; Science Press: Beijing, China, 2011; pp. 355–363. (In Chinese) [Google Scholar]



| Parameter | Value | ||
| ES | 3000 Pa | Young’s modulus | |
| R | 0.306 kg/m3 | Density of two-phase media | |
| ρf | 0.2977 kg/m3 | Density of pore fluid | |
| np | 0.333 | Porosity | |
| C | 0.2 | Poisson’s ratio | |
| kf | 0.004883 m3s/kg | Dynamic permeability coefficient | |
| L | 833.3 Pa | Lame constant | |
| G | 1250 Pa | Modulus of shear | |
| Material Number | Value 1 | Value 2 | |
| Kf | 0.3999 × 105 Pa | 0.6106 × 105 Pa | Pore fluid volume modulus |
| Ks | ∞ | 0.5005 × 104 Pa | Solid-phase soil skeleton volume modulus |
| Qb | 0.1201 × 106 Pa | 0.1385 × 105 Pa | Pore fluid compressibility coefficient |
| Wave Velocity | |||
| Actual Wave Velocity | Material No. | ||
| 1 | 2 | ||
| Cp | 635.12 m/s | 176.15 m/s | P wave velocity |
| Cs | 63.92 m/s | 63.92 m/s | S wave velocity |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, J.; Wang, F.; Jia, K.; Shen, H. A Time-Domain Artificial Boundary for Near-Field Wave Problem of Fluid Saturated Porous Media. Math. Comput. Appl. 2022, 27, 71. https://doi.org/10.3390/mca27040071
Song J, Wang F, Jia K, Shen H. A Time-Domain Artificial Boundary for Near-Field Wave Problem of Fluid Saturated Porous Media. Mathematical and Computational Applications. 2022; 27(4):71. https://doi.org/10.3390/mca27040071
Chicago/Turabian StyleSong, Jia, Fujie Wang, Kemin Jia, and Haohao Shen. 2022. "A Time-Domain Artificial Boundary for Near-Field Wave Problem of Fluid Saturated Porous Media" Mathematical and Computational Applications 27, no. 4: 71. https://doi.org/10.3390/mca27040071






