A Four-Variable Shear Deformation Theory for the Static Analysis of FG Sandwich Plates with Different Porosity Models
Abstract
:1. Introduction
2. Theoretical Model and Formulas
2.1. Material Properties and Porosity Models
2.1.1. FG with Even Porosities (Model A)
2.1.2. FG with Uneven Porosities (Model B)
2.1.3. FG with Linear-Uneven Porosities (Model C)
2.2. Displacement Field and Constitutive Equations
3. Governing Equations
4. Solution Method
5. Results and Discussion
5.1. Material Properties
5.2. Nondimensional Parameters
5.3. Comparison and Validation
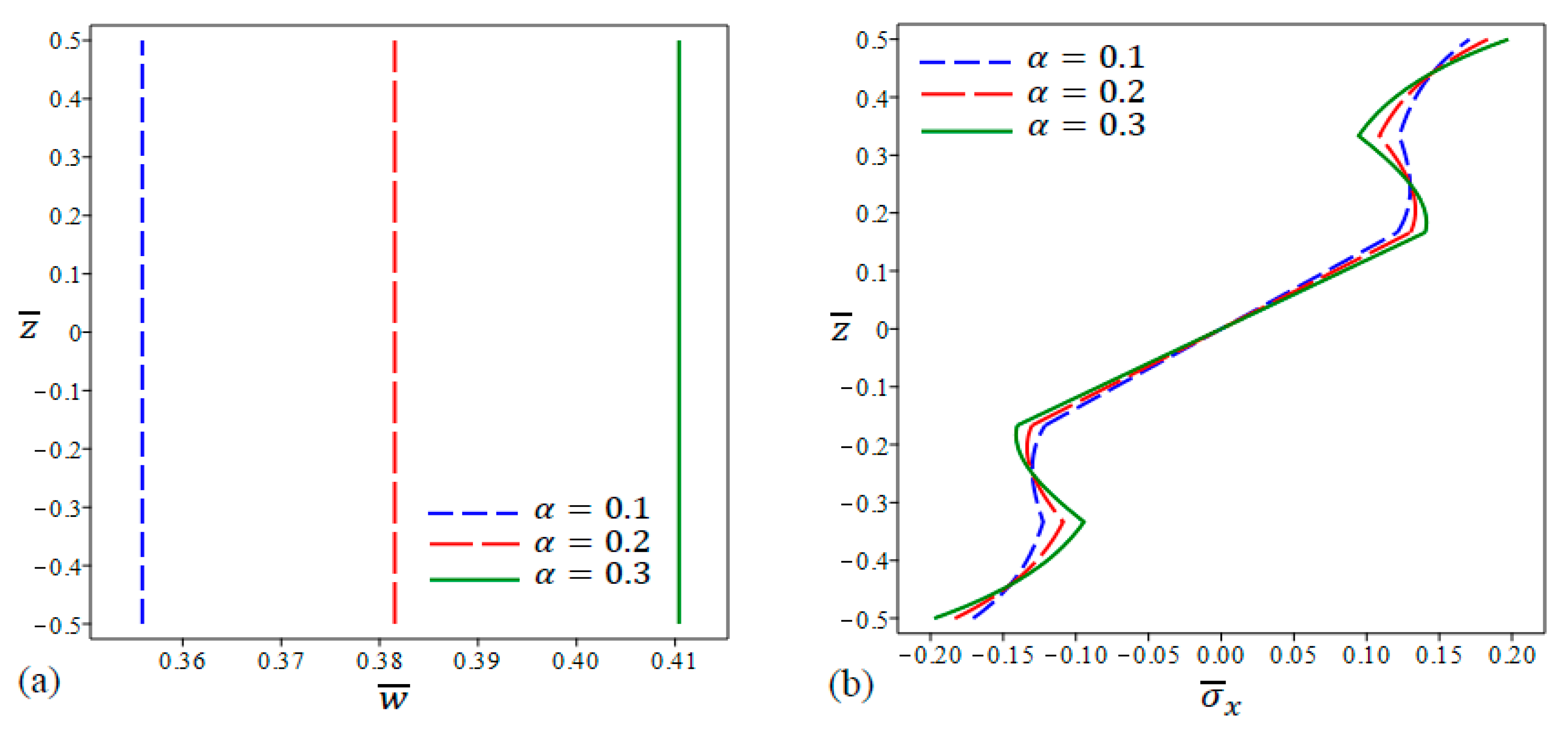
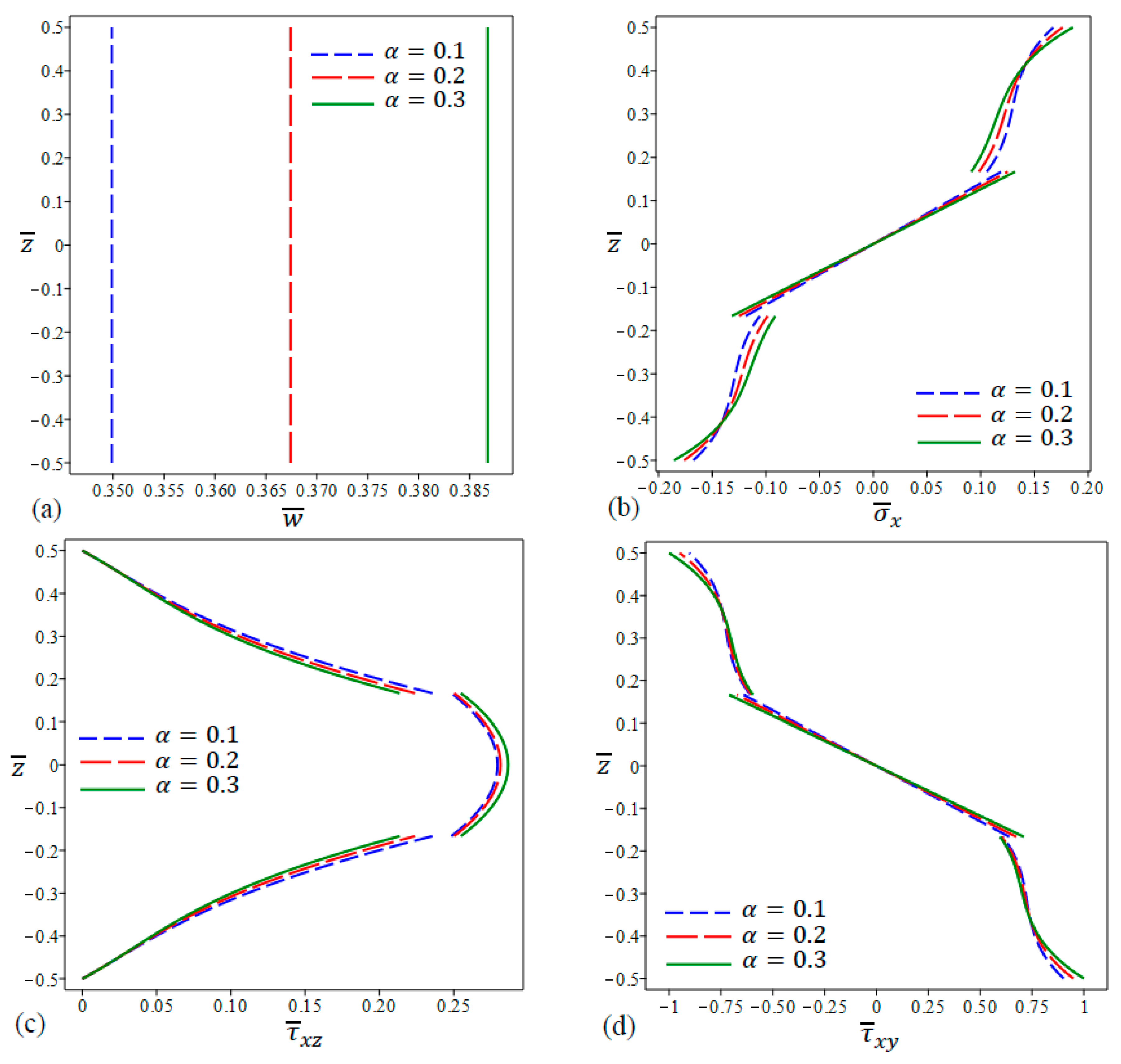
5.4. Bending Analysis of the FG Porous Sandwich Plates
5.4.1. Sandwich Plates with Ceramic Core
5.4.2. Sandwich Plates with Metal Core
6. Conclusions
- Employing the four-variable shear deformation theory proved its soundness since it yielded similar results to those found in the literature.
- The current findings exhibit a strong similarity to the outcomes obtained through the Third Shear Deformation Theory (TSDT).
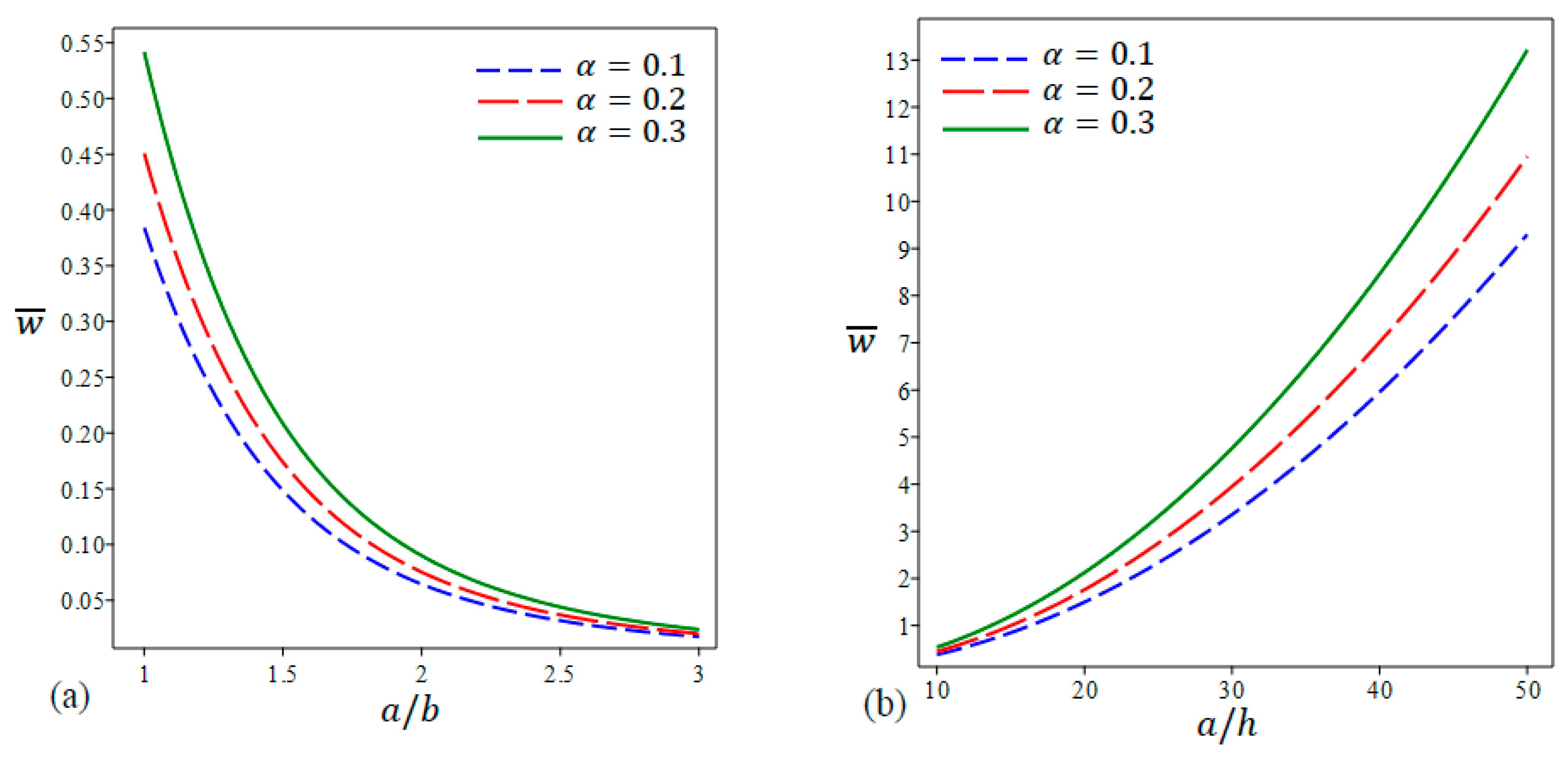
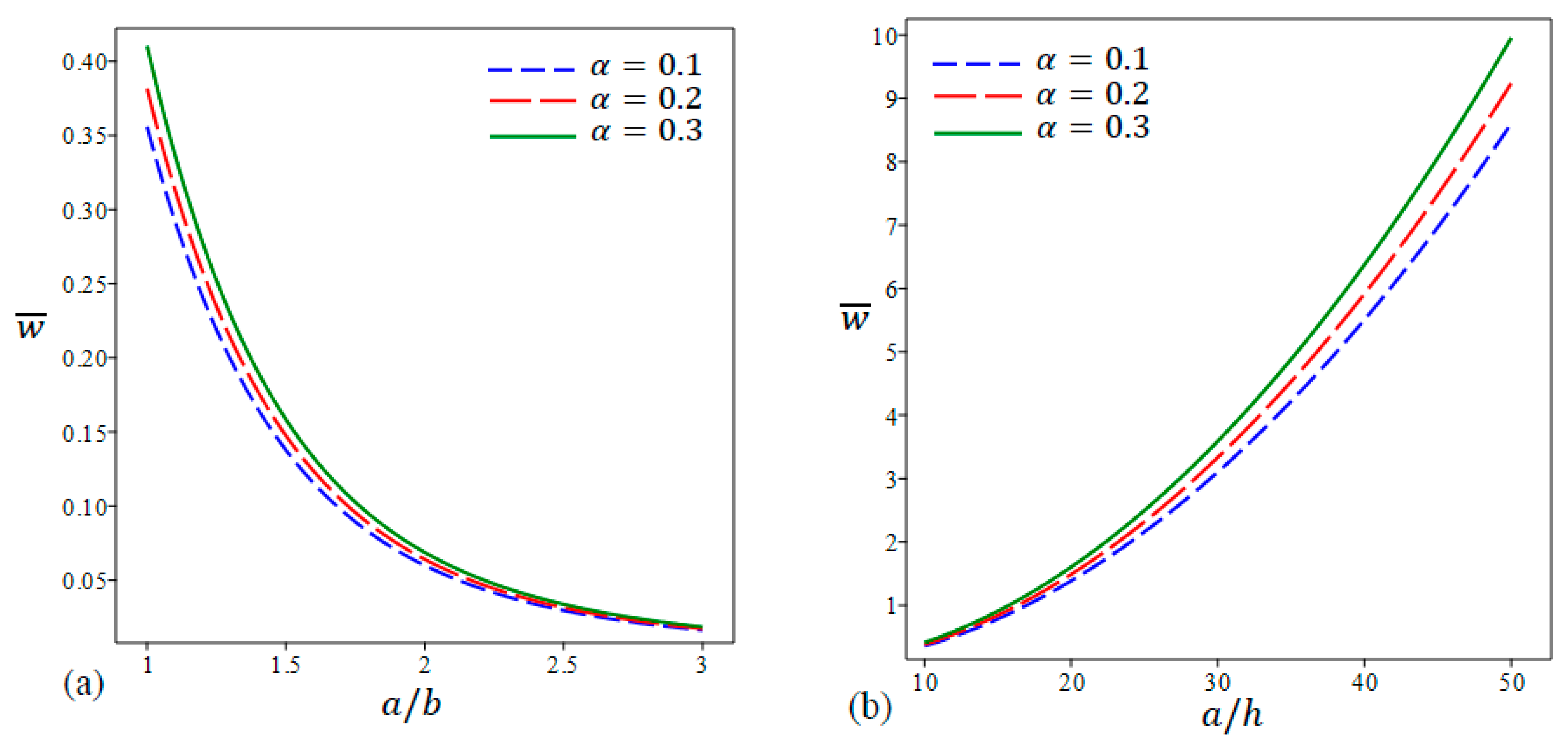
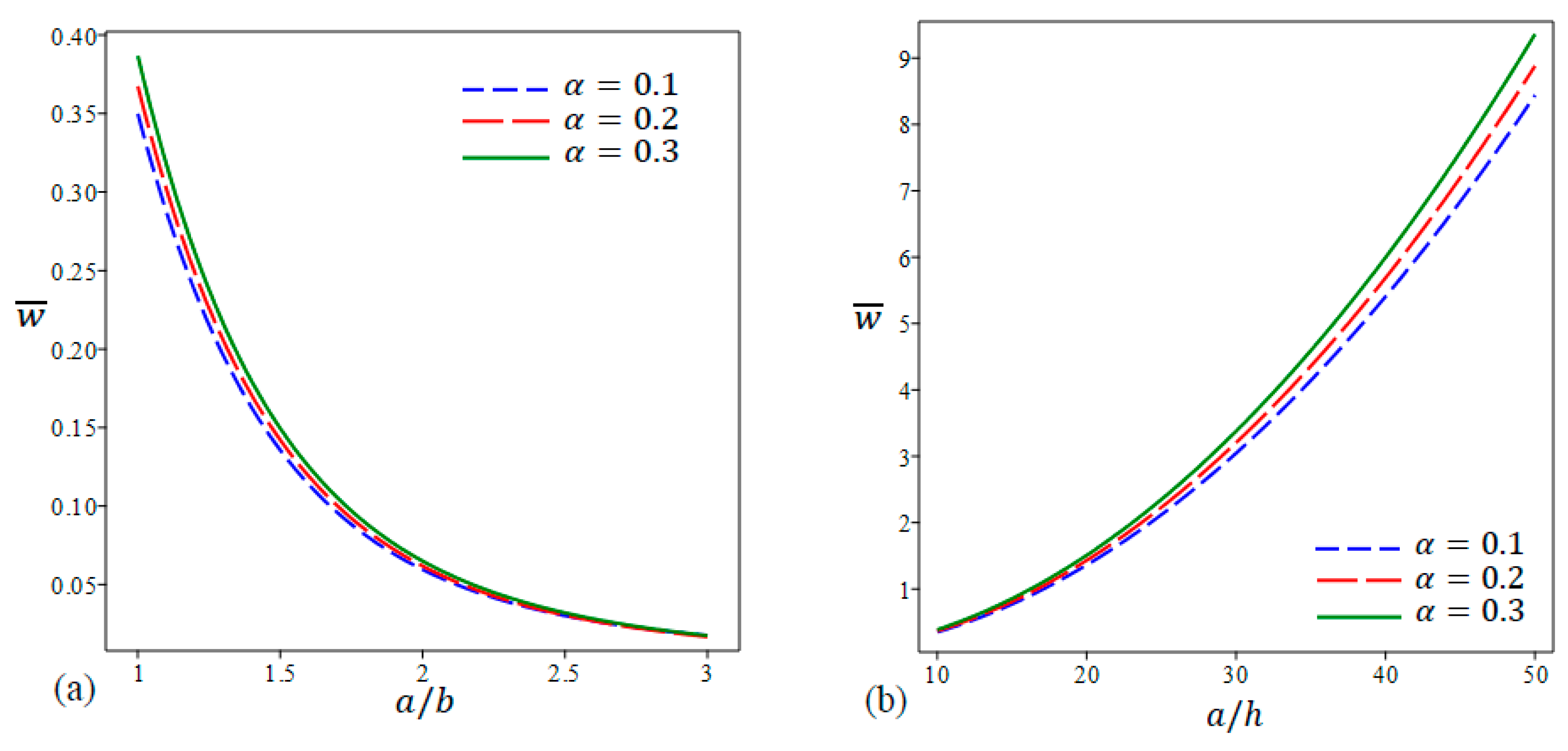
- Higher porosity leads to larger deflections. This can be referred to as the degradation in the modulus of elasticity as a consequence of high porosities, which leads to a reduction in the bending stiffness of the plate. The central deflection is further magnified at lower aspect ratios and at higher side-to-thickness ratios due to the reduction in the plate bending stiffness in these cases.
- At the same porosity coefficient (α), the central deflection is highest in the case of Model A, lower in Model B, and lowest in Model C. This is due to the gradual reduction in the modulus of elasticity in the porosity models from Model C down to Model A. In addition, Higher values of (defined in the volume fraction functions) result in higher central defections.
- When the core layer in Model B is made of metal instead of ceramic, the nondimensional central deflection increases linearly with the porosity coefficient α. The increase in the deflection is due to the reduction in the modulus of elasticity of as a consequence of increasing the porosity.
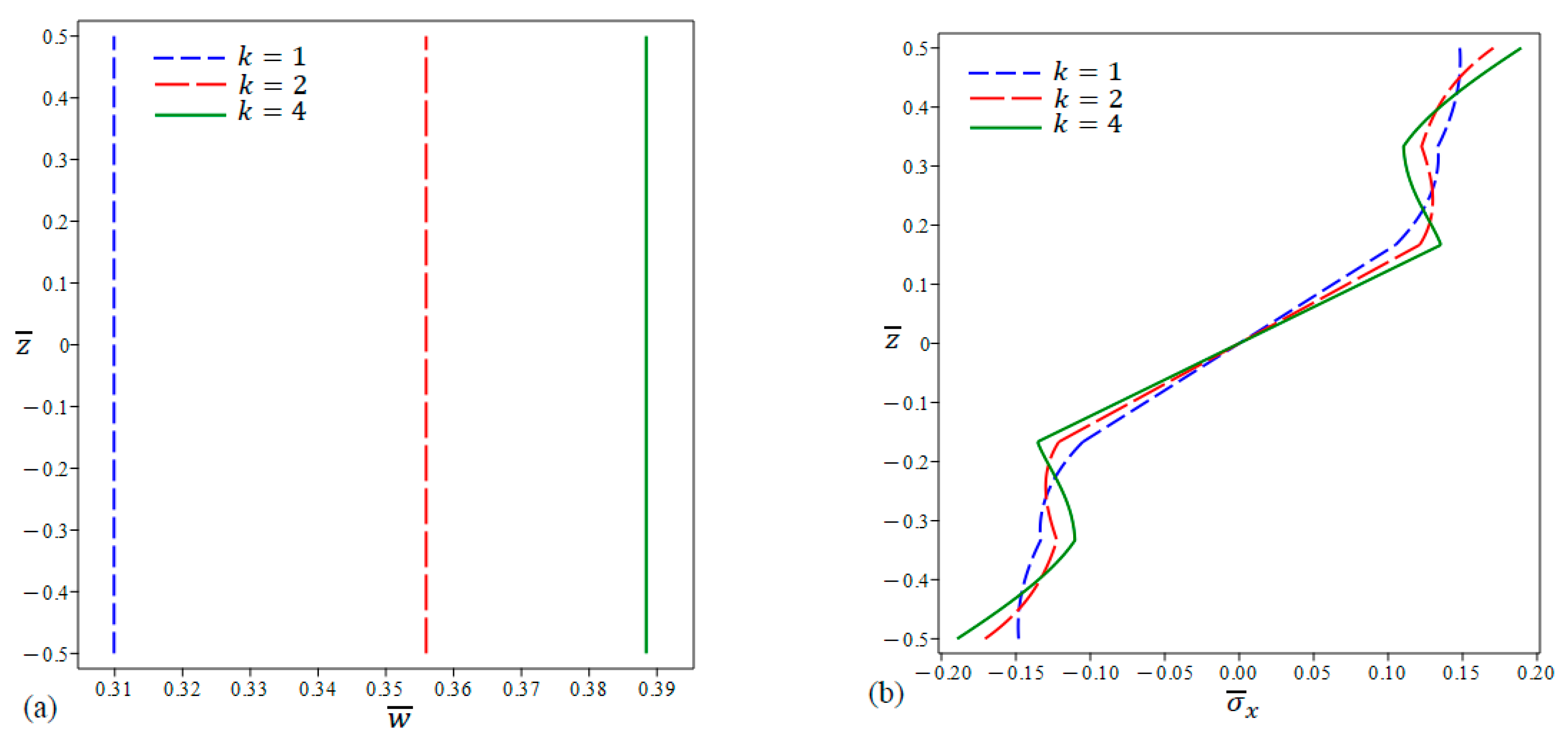
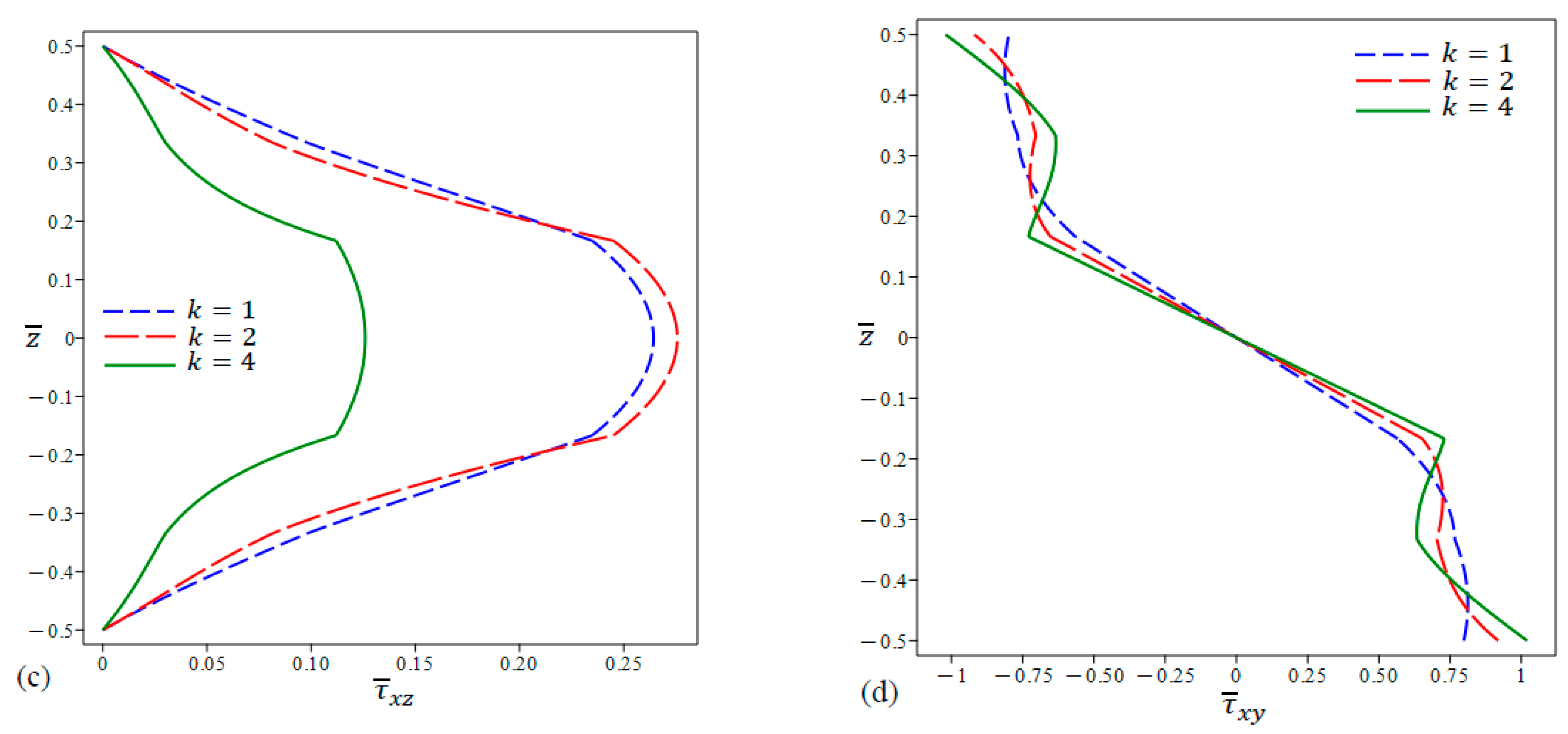
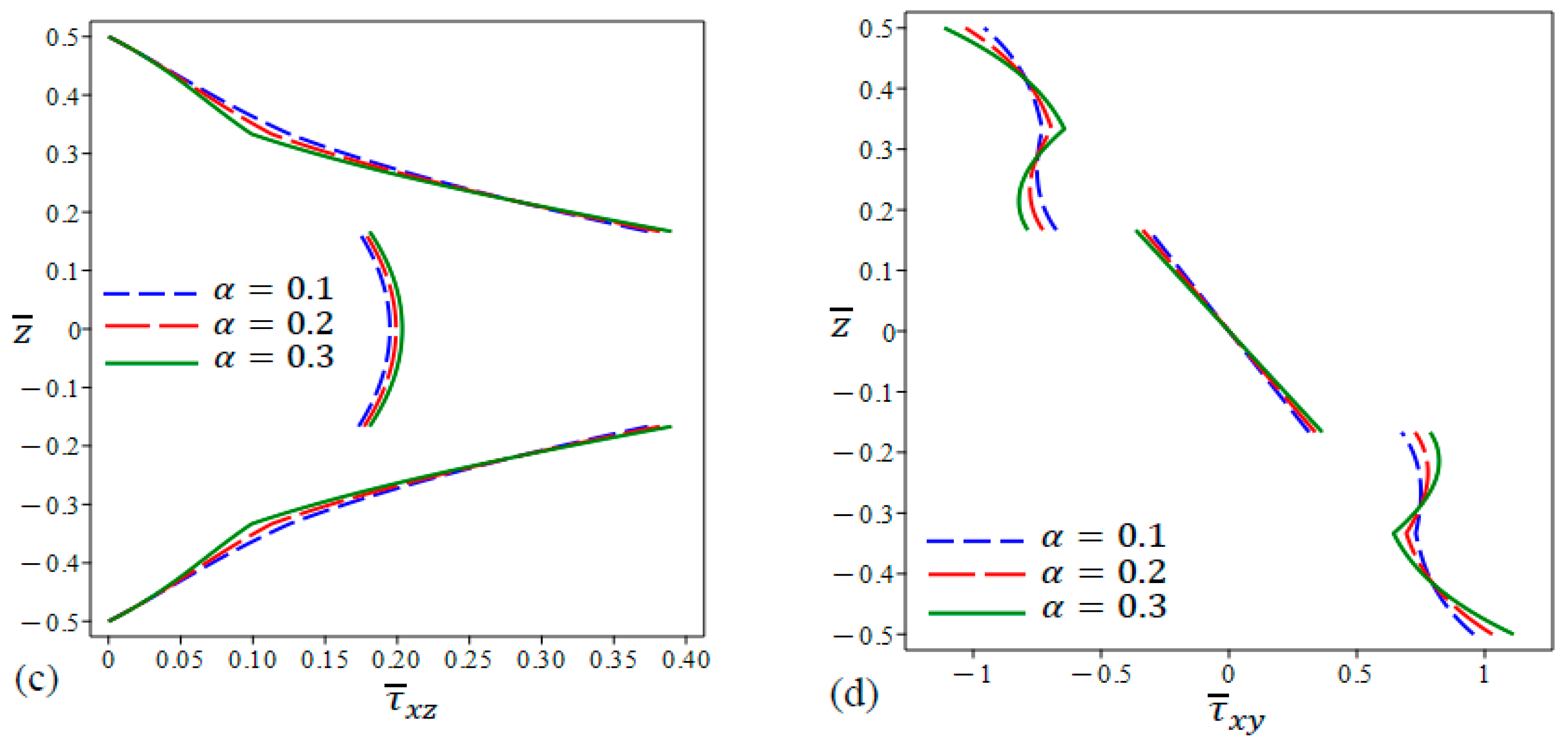
- The stress distributions differ according to the porosity models as well as the value of the porosity coefficient. In addition, the trend exhibited in the middle homogenous layer can be maintained or reversed once or twice in the external FG layers.
- The distributions of all stress types experience a jump at the interfaces between different layers in the case of sandwich plates with a metal core.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Miyamoto, Y.; Kaysser, W.A.; Rabin, B.H.; Kawasaki, A.; Ford, R.G. Functionally Graded Materials: Design, Processing and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 5. [Google Scholar] [CrossRef]
- Udupa, G.; Rao, S.S.; Gangadharan, K.V. Functionally Graded Composite Materials: An Overview. Procedia Mater. Sci. 2014, 5, 1291–1299. [Google Scholar] [CrossRef]
- Reddy, J.N. A General Non-linear Third Order Theory of Plates with Moderate Thickness. Int. J. Non-Linear Mech. 1990, 25, 677–686. [Google Scholar] [CrossRef]
- Reddy, J.N. Analysis of functionally graded plates. Int. J. Numer. Methods Eng. 2000, 47, 663–684. [Google Scholar] [CrossRef]
- Mantari, J.L.; Guedes Soares, C. Bending analysis of thick exponentially graded plates using a new trigonometric higher order shear deformation theory. Compos. Struct. 2012, 94, 1991–2000. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Alghanmi, R.A. Bending of functionally graded plates via a refined quasi-3D shear and normal deformation theory. Curved Layer. Struct. 2018, 5, 190–200. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, Q.; Ma, J. Thermo-mechanical dynamics of two-dimensional FG microbeam subjected to a moving harmonic load. Acta Astronaut. 2021, 178, 681–692. [Google Scholar] [CrossRef]
- Thinh, T.I.; Tu, T.M.; Quoc, T.H.; Long, N.V. Vibration and buckling analysis of functionally graded plates using new eight-unknown higher order shear deformation theory. Lat. Am. J. Solids Struct. 2016, 13, 456–477. [Google Scholar] [CrossRef]
- Van, T.D.; Van, V.P.; Hoang, N.N. On the development of refined plate theory for static bending behavior of functionally graded plates. Math. Probl. Eng. 2020, 2020, 2836763. [Google Scholar] [CrossRef]
- Madan, R.; Bhowmick, S. Modeling of functionally graded materials to estimate effective thermomechanical properties. World J. Eng. 2021, 19, 291–301. [Google Scholar] [CrossRef]
- Abdalla, H.; Casagrande, D. An intrinsic material tailoring approach for functionally graded ax-isymmetric hollow bodies under plane elasticity. J. Elast. 2021, 144, 15–32. [Google Scholar] [CrossRef]
- Eldeeb, A.; Shabana, Y.; Elsawaf, A. Influences of angular deceleration on the thermoelastoplastic behaviors of nonuniform thickness multilayer FGM discs. Compos. Struct. 2021, 258, 113092. [Google Scholar] [CrossRef]
- Eldeeb, A.; Shabana, Y.; Elsawaf, A. Thermo-elastoplastic behavior of a rotating sandwich disc made of temperature-dependent functionally graded materials. J. Sandw. Struct. Mater. 2021, 23, 1761–1783. [Google Scholar] [CrossRef]
- Zenkour, A.M. A comprehensive analysis of functionally graded sandwich plates: Part 1—Deflection and stresses. Int. J. Solids Struct. 2005, 42, 5224–5242. [Google Scholar] [CrossRef]
- Zenkour, A.M. A comprehensive analysis of functionally graded sandwich plates: Part 2—Buckling and free vibration. Int. J. Solids Struct. 2005, 42, 5243–5258. [Google Scholar] [CrossRef]
- Thai, H.T.; Nguyen, T.K.; Vo, T.P.; Lee, J. Analysis of functionally graded sandwich plates using a new first-order shear deformation theory. Eur. J. Mech.-A/Solids 2014, 45, 211–225. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Nguyen, V.H.; Chau-Dinh, T.; Vo, T.P.; Nguyen-Xuan, H. Static and vibration analysis of isotropic and functionally graded sandwich plates using an edge-based MITC3 finite elements. Compos. Part B-Eng. 2016, 107, 162–173. [Google Scholar] [CrossRef]
- Mantari, J.; Granados, E. A Refined FSDT for the Static Analysis of Functionally Graded Sandwich Plates. Thin-Walled Struct. 2015, 90, 150–158. [Google Scholar] [CrossRef]
- Naghavi, M.; Sarrami-Foroushani, S.; Azhari, F. Bending Analysis of Functionally Graded Sandwich Plates Using the Refined Finite Strip Method. J. Sandw. Struct. Mater. 2022, 24, 448–483. [Google Scholar] [CrossRef]
- Hirane, H.; Belarbi, M.O.; Houari, M.S.A.; Tounsi, A. On the Layerwise Finite Element Formulation for Static and Free Vibration Analysis of Functionally Graded Sandwich Plates. Eng. Comput. 2021, 38, 3871–3899. [Google Scholar] [CrossRef]
- Cho, J.R. Free Vibration Analysis of Functionally Graded Sandwich Plates with a Homogeneous Core. Appl. Sci. 2022, 12, 6054. [Google Scholar] [CrossRef]
- Monajati, L.; Farid, N.; Farid, M.; Parandvar, H. Vibration and buckling analyses of functionally graded plates based on refined plate theory using airy stress function. Proc. Inst. Mech. Eng. Part C 2022, 236, 8231–8244. [Google Scholar] [CrossRef]
- Zhu, J.; Lai, Z.; Yin, Z.; Jeon, J.; Lee, S. Fabrication of ZrO2–NiCr Functionally Graded Material by Powder Metallurgy. Mater. Chem. Phys. 2001, 68, 130–135. [Google Scholar] [CrossRef]
- Jabbari, M.; Mojahedin, A.; Haghi, M. Buckling Analysis of Thin Circular FG Plates Made of Saturated Porous-Soft Ferromagnetic Materials in Transverse Magnetic Field. Thin-Walled Struct. 2014, 85, 50–56. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Jafari, A. Buckling Behavior of Smart MEE-FG Porous Plate with Various Boundary Conditions Based on Refined Theory. Adv. Mater. Res. 2016, 5, 279–298. [Google Scholar] [CrossRef]
- Feyzi, M.R.; Khorshidvand, A.R. Axisymmetric Post-Buckling Behavior of Saturated Porous Circular Plates. Thin-Walled Struct. 2017, 112, 149–158. [Google Scholar] [CrossRef]
- Rezaei, A.S.; Saidi, A.R. Buckling Response of Moderately Thick Fluid-Infiltrated Porous Annular Sector Plates. Acta Mech. 2017, 228, 3929–3945. [Google Scholar] [CrossRef]
- Liu, Y.; Suab, S.; Huang, H.; Liang, Y. Thermal-Mechanical Coupling Buckling Analysis of Porous Functionally Graded Sandwich Beams Based on Physical Neutral Plane. Part B-Eng. 2019, 168, 236–242. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Prusty, B.G.; Kelly, D.; Hoffman, M. Free Vibration Analysis of Layered Functionally Graded Beams with Experimental Validation. Mater. Des. (1980–2015) 2012, 36, 182–190. [Google Scholar] [CrossRef]
- Chen, D.; Yang, J.; Kitipornchai, S. Free and Forced Vibrations of Shear Deformable Functionally Graded Porous Beams. Int. J. Mech. Sci. 2016, 108–109, 14–22. [Google Scholar] [CrossRef]
- Ghadiri, M.; SafarPour, H. Free Vibration Analysis of Size-dependent Functionally Graded Porous Cylindrical Microshells in Thermal Environment. J. Therm. Stress. 2016, 40, 55–71. [Google Scholar] [CrossRef]
- Shafiei, N.; Mirjavadi, S.S.; MohaselAfshari, B.; Rabby, S.; Kazemi, M. Vibration of Two-dimensional Imperfect Functionally Graded (2D-FG) Porous Nano-/Micro-Beams. Methods Appl. Mech. Eng. 2017, 322, 615–632. [Google Scholar] [CrossRef]
- Arshid, E.; Khorshidvand, A.R. Free Vibration Analysis of Saturated Porous FG Circular Plates Integrated with Piezoelectric Actuators via Differential Quadrature Method. Thin-Walled Struct. 2018, 125, 220–233. [Google Scholar] [CrossRef]
- Akbas, S. Forced Vibration Analysis of Functionally Graded Porous Deep Beams. Compos. Struct. 2018, 186, 293–302. [Google Scholar] [CrossRef]
- Wu, D.; Liu, A.; Huang, Y.; Pi, Y.; Gao, W. Dynamic Analysis of Functionally Graded Porous Structures through Finite Element Analysis. Eng. Struct. 2018, 165, 287–301. [Google Scholar] [CrossRef]
- Gao, K.; Li, R.; Yang, J. Dynamic Characteristics of Functionally Graded Porous Beams with Interval Material Properties. Eng. Struct. 2019, 197, 109441. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Radwan, A.F. Bending Response of FG Plates Resting on Elastic Foundations in Hygrothermal Environment with Porosities. Compos. Struct. 2019, 213, 133–143. [Google Scholar] [CrossRef]
- Alghanmi, R.A.; Zenkour, A.M. An Electromechanical Model for Functionally Graded Porous Plates Attached to Piezoelectric Layer Based on Hyperbolic Shear and Normal Deformation Theory. Compos. Struct. 2021, 274, 114352. [Google Scholar] [CrossRef]
- Alghanmi, R.A.; Zenkour, A.M. Effect of Porosity on the Bending of Functionally Graded Plates Integrated with PFRC Layer. Eur. Phys. J. Plus 2021, 136, 142. [Google Scholar] [CrossRef]
- Benferhat, R.; Daouadji, T.H.; Abderezak, R. Effect of Porosity on Fundamental Frequencies of FGM Sandwich Plates. Materials 2021, 13, 25. [Google Scholar]
- Vinh, P.V.; Huy, L.Q. Finite Element Analysis of Functionally Graded Sandwich Plates with Porosity via a New Hyperbolic Shear Deformation Theory. Def. Technol. 2022, 18, 490–508. [Google Scholar] [CrossRef]
- Dastjerdi, S.; Malikan, M.; Dimitri, R.; Tornabene, F. Nonlocal Elasticity Analysis of Moderately Thick Porous Functionally Graded Plates in a Hygro-Thermal Environment. Compos. Struct. 2021, 255, 112925. [Google Scholar] [CrossRef]
- Alghanmi, R.A. Nonlocal Strain Gradient Theory for the Bending of Functionally Graded Porous Nanoplates. Materials 2022, 15, 8601. [Google Scholar] [CrossRef] [PubMed]
- Zenkour, A.M.; Alghanmi, R.A. Hygro-Thermo-Electro-Mechanical Bending Analysis of Sandwich Plates with FG Core and Piezoelectric Faces. Mech. Adv. Mater. Struct. 2021, 28, 282–294. [Google Scholar] [CrossRef]
- Mota, A.F.; Loja, M.A.R.; Barbosa, J.I.; Rodrigues, J.A. Porous Functionally Graded Plates: An Assessment of the Influence of Shear Correction Factor on Static Behavior. Math. Comput. Appl. 2020, 25, 25. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Aljadani, M.H. Buckling Response of Functionally Graded Porous Plates Due to a Quasi-3D Refined Theory. Mathematics 2022, 10, 565. [Google Scholar] [CrossRef]
- Dhuria, M.; Grover, N.; Goyal, K. Influence of Porosity Distribution on Static and Buckling Responses of Porous Functionally Graded Plates. Structures 2021, 34, 1458–1474. [Google Scholar] [CrossRef]
- Alghanmi, R. Hygrothermal Bending Analysis of Sandwich Nanoplates with FG Porous Core and Piezomagnetic Faces via Nonlocal Strain Gradient Theory. Nanotechnol. Rev. 2023, 12, 20230123. [Google Scholar] [CrossRef]
- Quan, T.Q.; Ha, D.T.T.; Duc, N.D. Analytical Solutions for Nonlinear Vibration of Porous Functionally Graded Sandwich Plate Subjected to Blast Loading. Thin-Walled Struct. 2022, 170, 108606. [Google Scholar] [CrossRef]
- Shimpi, R.P.; Patel, H.G. A Two Variable Refined Plate Theory for Orthotropic Plate Analysis. Int. J. Solids Struct. 2006, 43, 6783–6799. [Google Scholar] [CrossRef]
- Thai, H.T.; Kim, S.E. Analytical Solution of a Two Variable Refined Plate Theory for Bending Analysis of Orthotropic Levy-Type Plates. Int. J. Mech. Sci. 2012, 54, 269–276. [Google Scholar] [CrossRef]








| Scheme | Method | |||||
|---|---|---|---|---|---|---|
| 1-0-1 | CPT [14] | 1.16247 | 0.91865 | 0.35885 | 0.13590 | 0.05742 |
| FSDT [14] | 1.19200 | 0.94473 | 0.37514 | 0.14592 | 0.06393 | |
| SSDT [14] | 1.18808 | 0.94124 | 0.37297 | 0.14458 | 0.06305 | |
| TSDT [14] | 1.18877 | 0.94186 | 0.37335 | 0.14481 | 0.06321 | |
| Present | 1.18877 | 0.94186 | 0.37335 | 0.14481 | 0.06321 | |
| 2-1-2 | CPT [14] | 1.09971 | 0.86891 | 0.33942 | 0.12854 | 0.05431 |
| FSDT [14] | 1.12611 | 0.89237 | 0.35408 | 0.13756 | 0.06017 | |
| SSDT [14] | 1.12204 | 0.88876 | 0.35183 | 0.13617 | 0.05926 | |
| TSDT [14] | 1.12293 | 0.88955 | 0.35231 | 0.13647 | 0.05946 | |
| Present | 1.12293 | 0.88945 | 0.35231 | 0.13647 | 0.05946 | |
| 1-1-1 | CPT [14] | 1.03895 | 0.82090 | 0.32067 | 0.12144 | 0.05131 |
| FSDT [14] | 1.06369 | 0.84289 | 0.33411 | 0.12989 | 0.05680 | |
| SSDT [14] | 1.05989 | 0.83952 | 0.33230 | 0.12895 | 0.05619 | |
| TSDT [14] | 1.06096 | 0.84046 | 0.33289 | 0.12895 | 0.05619 | |
| Present | 1.06096 | 0.84046 | 0.33289 | 0.12895 | 0.05619 | |
| 2-2-1 | CPT [14] | 0.98512 | 0.77837 | 0.30405 | 0.11514 | 0.04085 |
| FSDT [14] | 1.00911 | 0.79969 | 0.31738 | 0.12334 | 0.05398 | |
| SSDT [14] | 1.00585 | 0.79679 | 0.34557 | 0.12222 | 0.05325 | |
| TSDT [14] | 1.00694 | 0.79776 | 0.31617 | 0.12260 | 0.05325 | |
| Present | 1.00694 | 0.79776 | 0.31617 | 0.12260 | 0.05349 | |
| 1-2-1 | CPT [14] | 0.94269 | 0.74489 | 0.29095 | 0.11018 | 0.04655 |
| FSDT [14] | 0.96563 | 0.76524 | 0.30370 | 0.10803 | 0.05165 | |
| SSDT [14] | 0.96248 | 0.76243 | 0.30195 | 0.11694 | 0.05094 | |
| TSDT [14] | 0.96371 | 0.76353 | 0.30263 | 0.11737 | 0.05122 | |
| Present | 0.96371 | 0.76353 | 0.30263 | 0.11737 | 0.05122 | |
| Perfect | Model A | Model B | Model C | ||
|---|---|---|---|---|---|
| 10 | 0 | 0.33289 | -- | -- | -- |
| 0.1 | -- | 0.38414 | 0.35595 | 0.34794 | |
| 0.2 | -- | 0.45086 | 0.38155 | 0.36742 | |
| 0.3 | -- | 0.54184 | 0.41039 | 0.38677 | |
| 20 | 0 | 1.29489 | -- | -- | -- |
| 0.1 | -- | 1.49856 | 1.38653 | 1.36044 | |
| 0.2 | -- | 1.76382 | 1.48859 | 1.43190 | |
| 0.3 | -- | 2.12577 | 1.60341 | 1.50869 | |
| 50 | 0 | 8.02885 | -- | -- | -- |
| 0.1 | -- | 9.29942 | 8.60067 | 8.44051 | |
| 0.2 | -- | 10.95449 | 9.23779 | 8.88325 | |
| 0.3 | -- | 13.21322 | 9.95453 | 9.36211 |
| Perfect | Model A | Model B | Model C | ||
|---|---|---|---|---|---|
| 10 | 0 | 1.59370 | -- | -- | -- |
| 0.1 | -- | 0.14810 | 0.17069 | 0.16741 | |
| 0.2 | -- | 0.13692 | 0.18325 | 0.17624 | |
| 0.3 | -- | 0.12218 | 0.19741 | 0.18569 | |
| 20 | 0 | 1.58524 | -- | -- | -- |
| 0.1 | -- | 0.14827 | 0.16982 | 0.16666 | |
| 0.2 | -- | 0.13632 | 0.18239 | 0.17538 | |
| 0.3 | -- | 0.12169 | 0.19654 | 0.18483 | |
| 50 | 0 | 1.58287 | -- | -- | -- |
| 0.1 | -- | 0.14807 | 0.16957 | 0.16641 | |
| 0.2 | -- | 0.13615 | 0.18215 | 0.17515 | |
| 0.3 | -- | 0.12156 | 0.19629 | 0.18459 |
| Perfect | Model A | Model B | Model C | ||
|---|---|---|---|---|---|
| 10 | 0 | 0.27188 | -- | -- | -- |
| 0.1 | -- | 0.28065 | 0.27541 | 0.23777 | |
| 0.2 | -- | 0.29074 | 0.27915 | 0.28146 | |
| 0.3 | -- | 0.30260 | 0.28313 | 0.28661 | |
| 20 | 0 | 0.27197 | -- | -- | -- |
| 0.1 | -- | 0.28074 | 0.27507 | 0.26221 | |
| 0.2 | -- | 0.29083 | 0.27925 | 0.28155 | |
| 0.3 | -- | 0.30267 | 0.28323 | 0.28671 | |
| 50 | 0 | 0.27200 | -- | -- | -- |
| 0.1 | -- | 0.28077 | 0.27498 | 0.26998 | |
| 0.2 | -- | 0.29085 | 0.27928 | 0.28158 | |
| 0.3 | -- | 0.30270 | 0.28326 | 0.28674 |
| Perfect | Model A | Model B | Model C | ||
|---|---|---|---|---|---|
| 10 | 0 | 0.73130 | -- | -- | -- |
| 0.1 | -- | 0.76124 | 0.70389 | 0.73064 | |
| 0.2 | -- | 0.79066 | 0.66632 | 0.72685 | |
| 0.3 | -- | 0.81927 | 0.61660 | 0.72113 | |
| 20 | 0 | 1.46421 | -- | -- | -- |
| 0.1 | -- | 1.52380 | 1.40915 | 1.46221 | |
| 0.2 | -- | 1.58231 | 1.33397 | 1.45539 | |
| 0.3 | -- | 1.63915 | 1.23438 | 1.44396 | |
| 50 | 0 | 3.66166 | -- | -- | -- |
| 0.1 | -- | 3.81042 | 3.52382 | 3.65625 | |
| 0.2 | -- | 3.95646 | 3.33586 | 3.63964 | |
| 0.3 | -- | 4.09830 | 3.08676 | 3.61108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alghanmi, R.A.; Aljaghthami, R.H. A Four-Variable Shear Deformation Theory for the Static Analysis of FG Sandwich Plates with Different Porosity Models. Math. Comput. Appl. 2024, 29, 20. https://doi.org/10.3390/mca29020020
Alghanmi RA, Aljaghthami RH. A Four-Variable Shear Deformation Theory for the Static Analysis of FG Sandwich Plates with Different Porosity Models. Mathematical and Computational Applications. 2024; 29(2):20. https://doi.org/10.3390/mca29020020
Chicago/Turabian StyleAlghanmi, Rabab A., and Rawan H. Aljaghthami. 2024. "A Four-Variable Shear Deformation Theory for the Static Analysis of FG Sandwich Plates with Different Porosity Models" Mathematical and Computational Applications 29, no. 2: 20. https://doi.org/10.3390/mca29020020
APA StyleAlghanmi, R. A., & Aljaghthami, R. H. (2024). A Four-Variable Shear Deformation Theory for the Static Analysis of FG Sandwich Plates with Different Porosity Models. Mathematical and Computational Applications, 29(2), 20. https://doi.org/10.3390/mca29020020





