Variability on Functionally Graded Plates’ Deflection Due to Uncertainty on Carbon Nanotubes’ Properties
Abstract
:1. Introduction
2. Materials and Methods
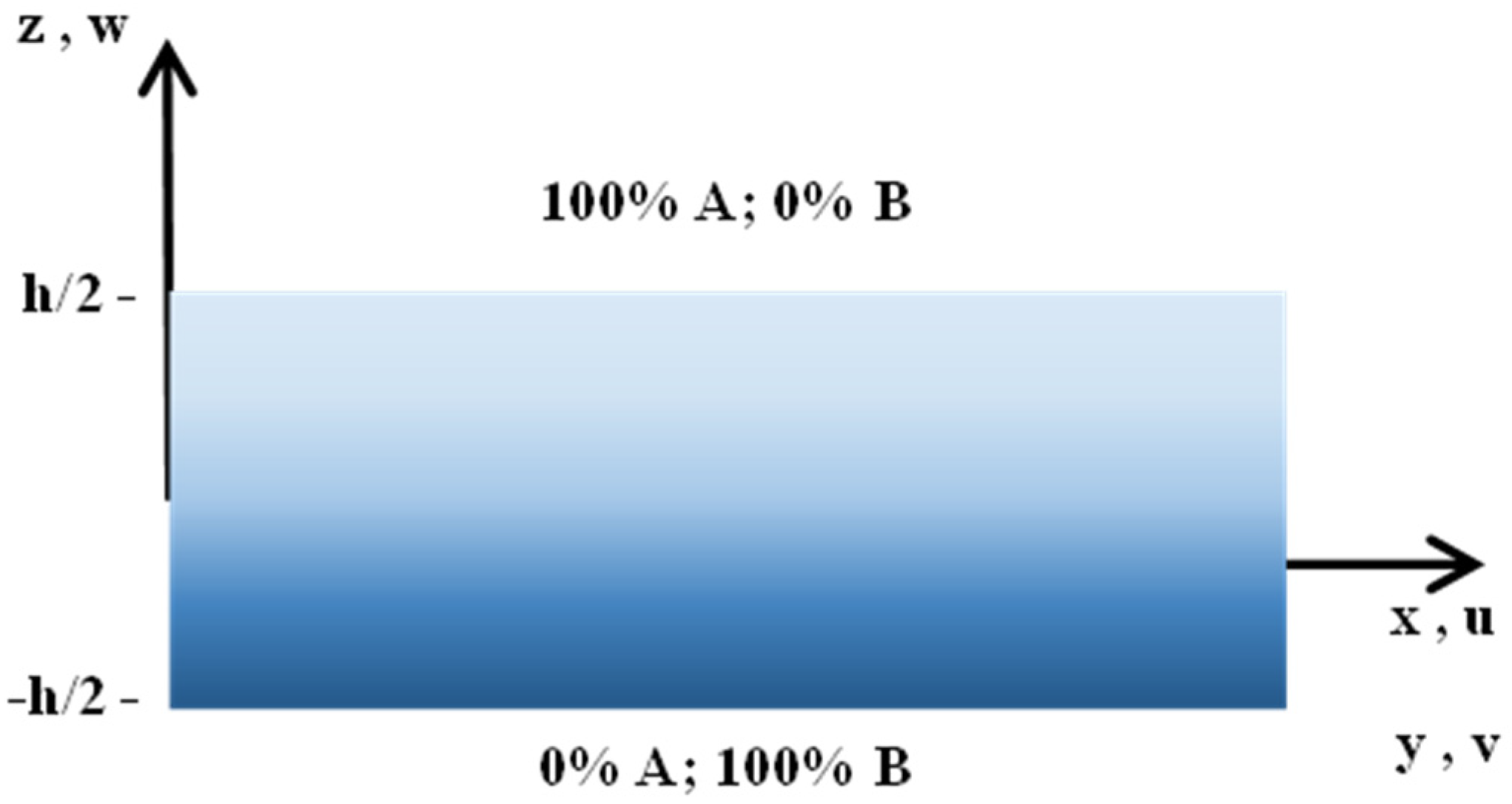
2.1. Functionally Graded Materials
2.2. Displacement Field and Constitutive Relations
2.3. Finite Element Model
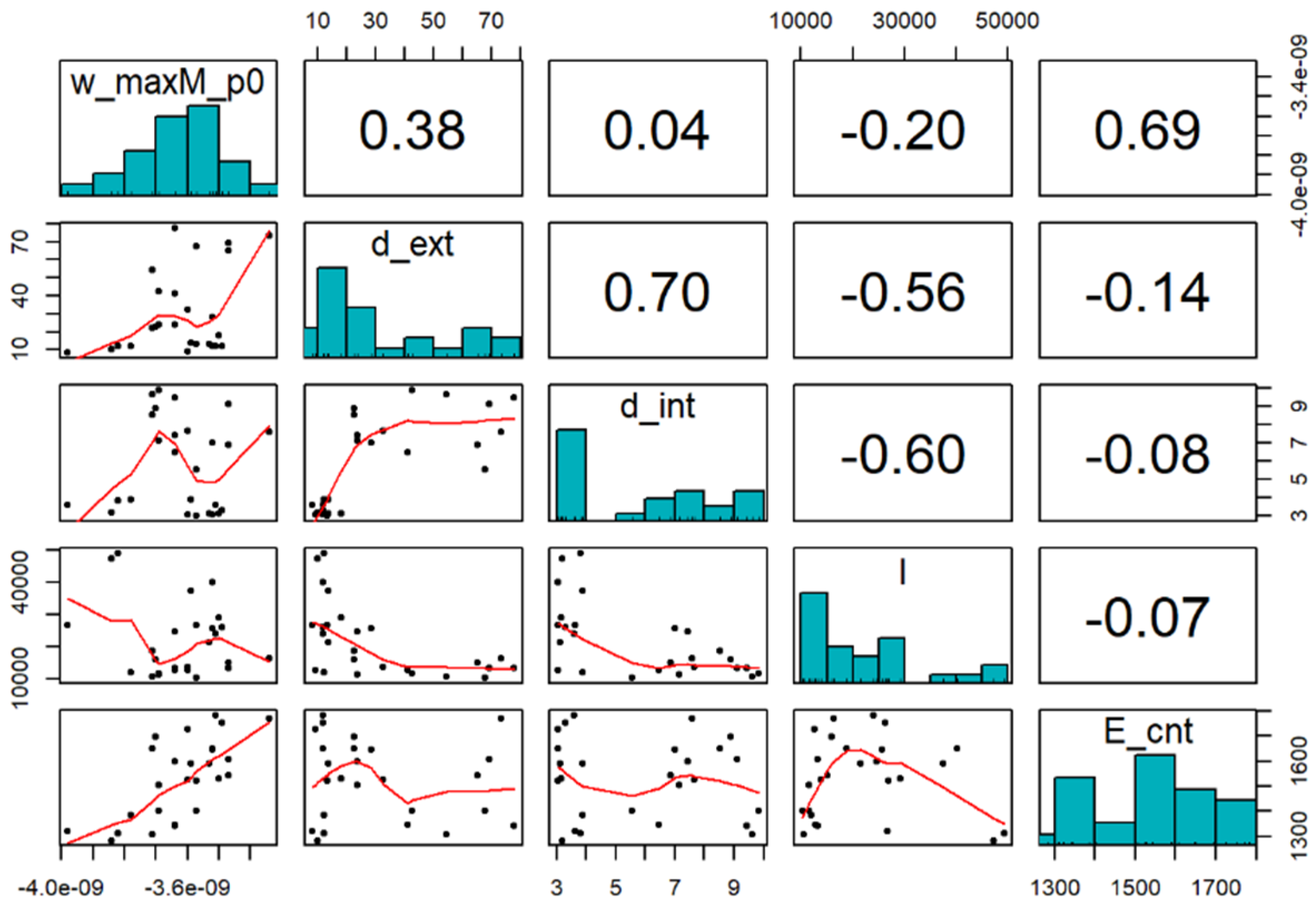
2.4. Statistical Methods
The Friedman Test
3. Maximum Static Deflection: Verification Study
4. Case Study
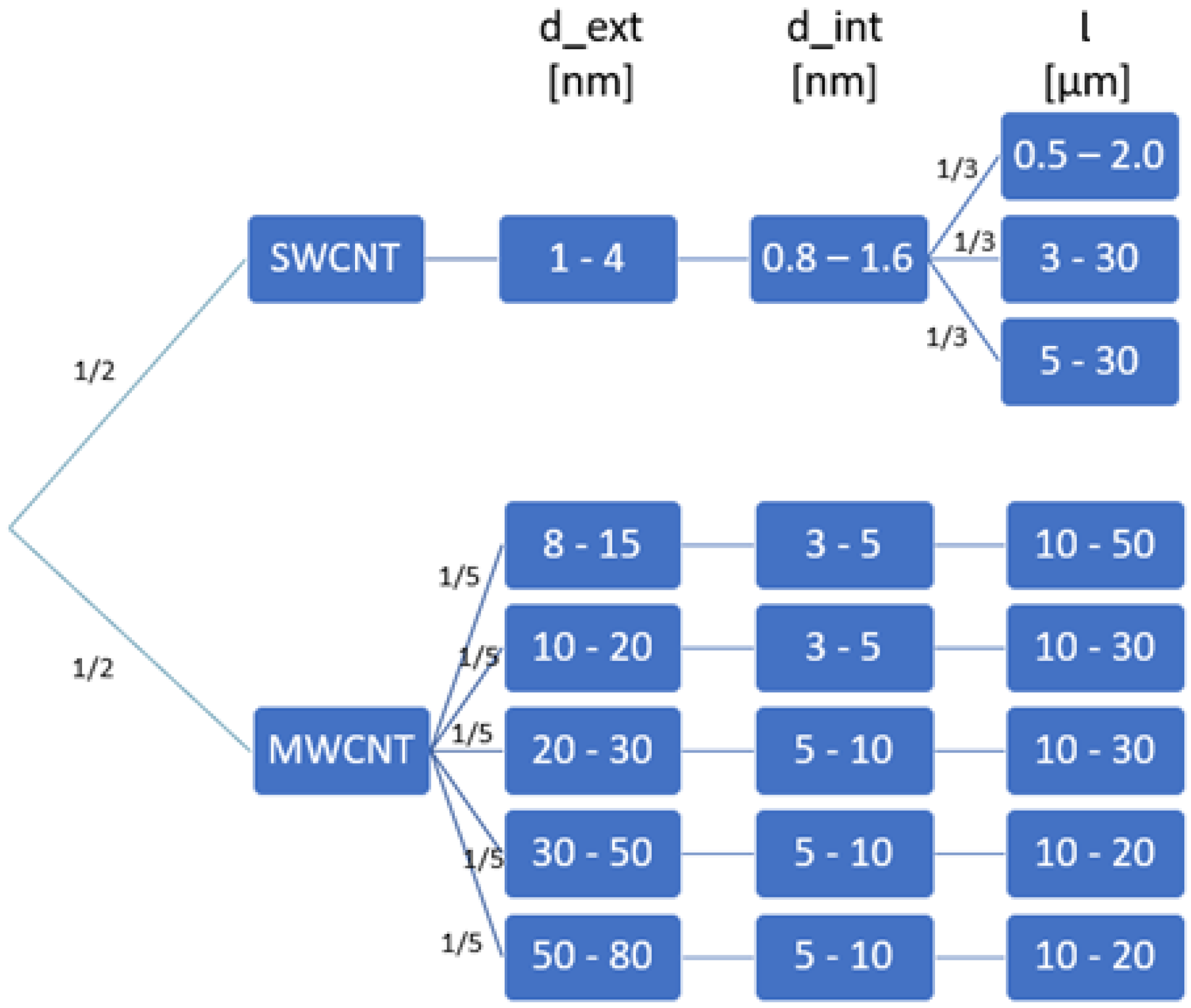
4.1. Data Simulation for Carbon Nanotubes
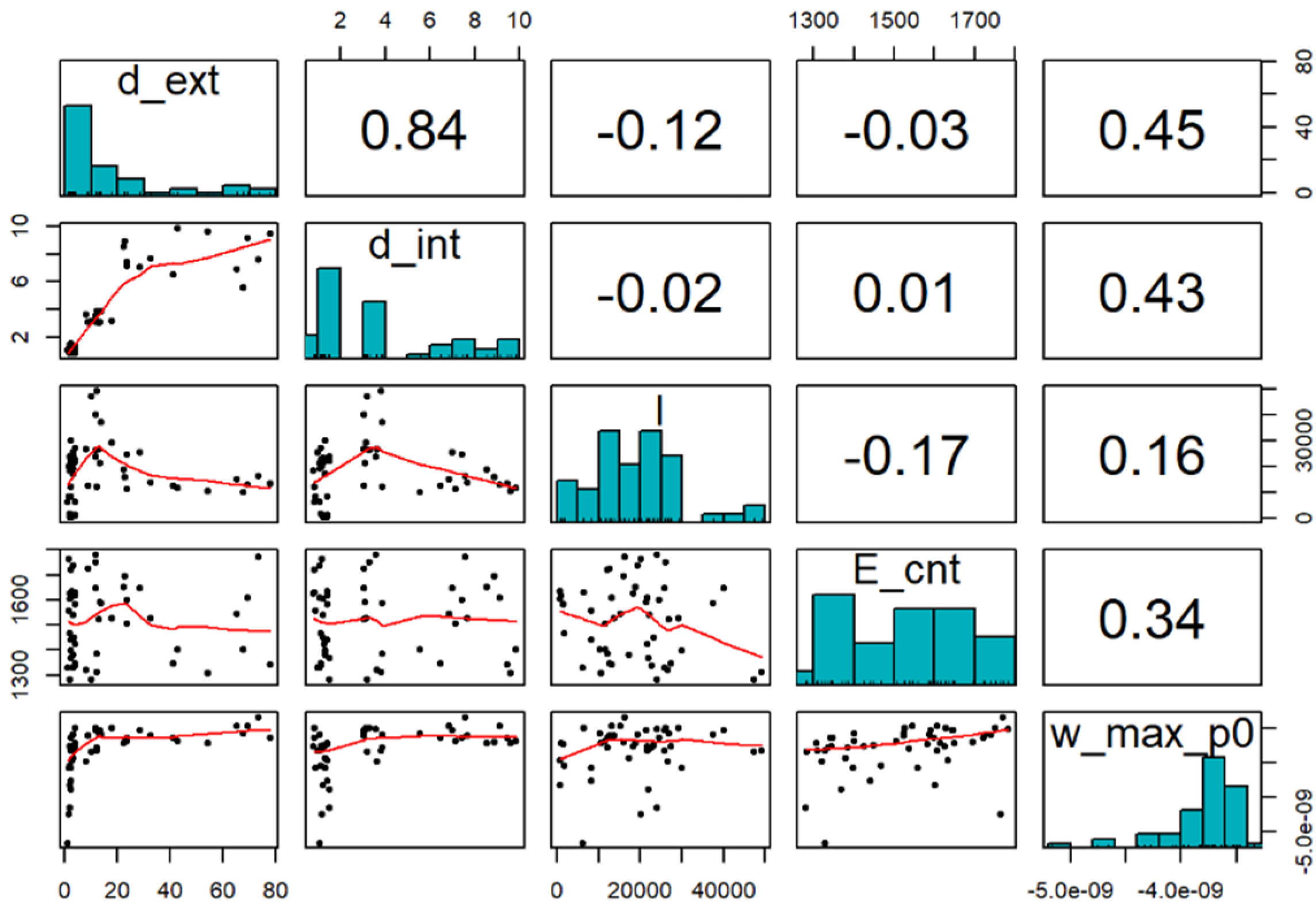
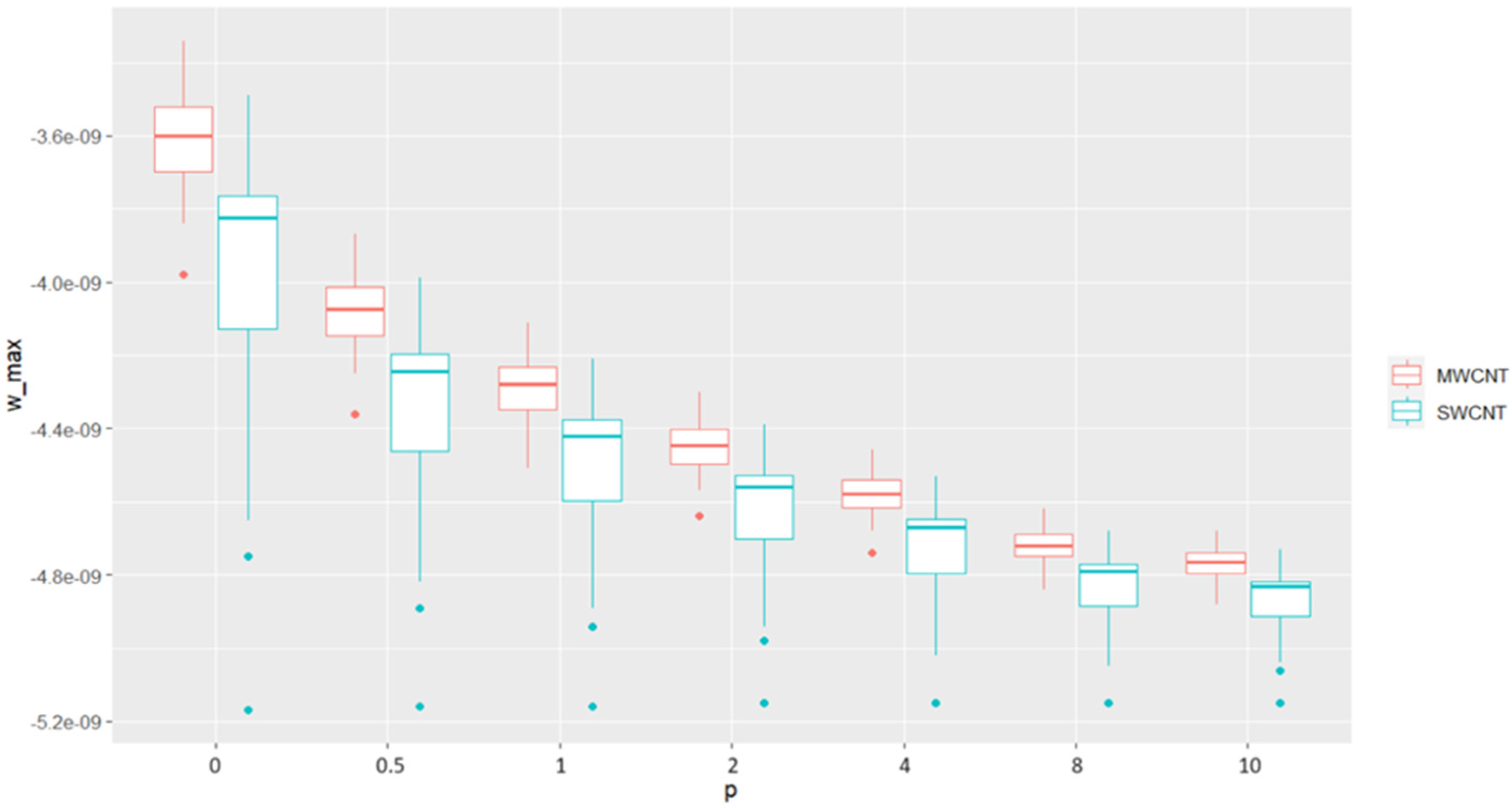
4.2. Plates’ Maximum Transverse Displacement Distributions
4.3. Model for Plates’ Maximum Transverse Displacement—p = 0
4.3.1. Model I—Plates with SWCNT
4.3.2. Model II—Plates with MWCNT
4.4. Model for Plates’ Maximum Transverse Displacement—Other Values of
- Significant overall model (F-test) and all model variables are significant (t-tests) at α = 1%;
- No multicollinearity issues (VIF less than 5 for all independent variables);
- Homoscedastic residuals (Breusch-Pagan test), uncorrelated residuals (Durbin–Watson test), and normal distribution of residuals (Shapiro-Wilk test) considering α = 1%.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Birman, V.; Byrd, L.W. Modeling and analysis of functionally graded materials and structures. Appl. Mech. Rev. 2007, 60, 195–216. [Google Scholar] [CrossRef]
- Gupta, N.; Gupta, S.M.; Sharma, S.K. Carbon nanotubes: Synthesis, properties and engineering applications. Carbon Lett. 2019, 29, 419–447. [Google Scholar] [CrossRef]
- Rathinavel, S.; Priyadharshini, K.; Panda, D. A review on carbon nanotube: An overview of synthesis, properties, functionalization, characterization, and the application. Mater. Sci. Eng. 2021, 268, 11509. [Google Scholar] [CrossRef]
- Liew, K.M.; Lei, Z.X.; Zhang, L.W. Mechanical analysis of functionally graded carbon nanotube reinforced composites: A review. Compos. Struct. 2015, 120, 90–97. [Google Scholar] [CrossRef]
- Radhamani, A.V.; Chung Lau, H.; Ramakrishna, S. CNT-reinforced Metal and Steel Nanocomposites: A Comprehensive Assessment of Progress and Future Directions. Compos. Part A Appl. Sci. Manuf. 2018, 114, 170–187. [Google Scholar] [CrossRef]
- Vinyas, M.; Atul, J.; Nguyen Thoi, T.; Loja, M.A.R. A Comprehensive Review on Analysis of Nanocomposites: From Manufacturing to Properties Characterization. Mater. Res. Express 2019, 6, 092002. [Google Scholar] [CrossRef]
- Zhao, S.; Zhao, Z.; Yang, Z.; Ke, L.; Kitipornchai, S.; Yang, J. Functionally graded graphene reinforced composite structures: A review. Eng. Struct. 2020, 210, 110339. [Google Scholar] [CrossRef]
- Shoukat, R.; Khan, M.I. Carbon nanotubes: A review on properties. synthesis methods and applications in micro and nanotechnology. Microsyst. Technol. 2021, 27, 4183–4192. [Google Scholar] [CrossRef]
- Soni, S.K.; Thomas, B.; Swain, A.; Roy, T. Functionally graded carbon nanotubes reinforced composite structures: An extensive review. Compos. Struct. 2022, 299, 116075. [Google Scholar] [CrossRef]
- Valencia Murillo, C.E.; Gutierrez Rivera, M.E.; Celaya Garcia, L.D. Thermal–Structural Linear Static Analysis of Functionally Graded Beams Using Reddy Beam Theory. Math. Comput. Appl. 2023, 28, 84. [Google Scholar] [CrossRef]
- Kurpa, L.; Pellicano, F.; Shmatko, T.; Zippo, A. Free Vibration Analysis of Porous Functionally Graded Material Plates with Variable Thickness on an Elastic Foundation Using the R-Functions Method. Math. Comput. Appl. 2024, 29, 10. [Google Scholar] [CrossRef]
- Alghanmi, R.A.; Aljaghthami, R.H. A Four-Variable Shear Deformation Theory for the Static Analysis of FG Sandwich Plates with Different Porosity Models. Math. Comput. Appl. 2024, 29, 20. [Google Scholar] [CrossRef]
- Ruoff, R.S.; Lorents, D.C. Mechanical and Thermal Properties of Carbon Nanotubes. In Carbon Nanotubes; Elsevier: Amsterdam, The Netherlands, 1996; pp. 143–148. [Google Scholar]
- Xie, S.; Li, W.; Pan, Z.; Chang, B.; Sun, L. Mechanical and physical properties on carbon nanotube. J. Phys. Chem. Solids 2000, 61, 1153–1158. [Google Scholar] [CrossRef]
- Fidelusa, J.D.; Wiesela, E.; Gojnyb, F.H.; Schulteb, K.; Wagner, H.D. Thermo-mechanical properties of randomly oriented carbon/epoxy nanocomposites. Compos. Part A 2005, 36, 1555–1561. [Google Scholar] [CrossRef]
- Martone, A.; Faiella, G.; Antonucci, V.; Giordano, M.; Zarrelli, M. The effect of the aspect ratio of carbon nanotubes on their effective reinforcement modulus in an epoxy matrix. Compos. Sci. Technol. 2011, 71, 1117–1123. [Google Scholar] [CrossRef]
- Qiu, H.; Yang, J. Structure and Properties of Carbon Nanotubes. In Industrial Applications of Carbon Nanotubes. Micro and Nano Technologies; Peng, H., Li, Q., Chen, T., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 47–69. [Google Scholar]
- Loja, M.A.R. Dynamic Response of Soft Core Sandwich Beams with Metal-Graphene Nanocomposite Skins. Shock Vib. 2017, 2017, 7842413. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Garg, A.; Chalak, H.D.; Zenkour, A.M.; Belarbi, M.-O.; Houari, M.-S.-A. A Review of Available Theories and Methodologies for the Analysis of Nano Isotropic, Nano Functionally Graded, and CNT Reinforced Nanocomposite Structures. Arch. Comput. Methods Eng. 2022, 29, 2237–2270. [Google Scholar] [CrossRef]
- Reddy, J.N.; Pang, S.D. Nonlocal continuum theories of beams for the analysis of carbon nanotubes. J. Appl. Phys. 2008, 103, 23511. [Google Scholar] [CrossRef]
- Kong, L.; Zhang, B.; Li, C. Thermal Buckling and Postbuckling Behaviors of Couple Stress and Surface Energy-Enriched FG-CNTR Nanobeams. Symmetry 2022, 14, 2228. [Google Scholar] [CrossRef]
- Reddy, J.N.; Kim, J. A nonlinear modified couple stress-based third-order theory of functionally graded plates. Compos. Struct. 2012, 94, 1128–1143. [Google Scholar] [CrossRef]
- Liu, S.; Yu, T.; Bui, T.Q.; Xia, S. Size-dependent analysis of homogeneous and functionally graded microplates using IGA and a non-classical Kirchhoff plate theory. Compos. Struct. 2017, 172, 34–44. [Google Scholar] [CrossRef]
- Thanh, C.-L.; Vu-Huu, T.; Phung-Van, P.; Nguyen-Xuan, H.; Abdel Wahab, M. Size-Dependent Analysis for FG-CNTRC Nanoplates Based on Refined Plate Theory and Modified Couple Stress. In Proceedings of the 1st International Conference on Numerical Modelling in Engineering, NME 2018, Ghent, Belgium, 28–29 August 2018; Lecture Notes in Civil Engineering, 20. Springer: Singapore, 2019; pp. 225–237. [Google Scholar]
- Zhang, B.; Li, C.; Zhang, L.; Xie, F. Size-Dependent Free Vibration of Non-Rectangular Gradient Elastic Thick Microplates. Symmetry 2022, 14, 2592. [Google Scholar] [CrossRef]
- Sotiropoulos, D.G.; Tserpes, K. Interval-Based Computation of the Uncertainty in the Mechanical Properties and the Failure Analysis of Unidirectional Composite Materials. Math. Comput. Appl. 2022, 27, 38. [Google Scholar] [CrossRef]
- Yin, S.; Qin, H.; Gao, Q. An Efficient Orthogonal Polynomial Method for Auxetic Structure Analysis with Epistemic Uncertainties. Math. Comput. Appl. 2022, 27, 49. [Google Scholar] [CrossRef]
- Bouwer, J.M.; Wilke, D.N.; Kok, S. Spatio-Temporal Gradient Enhanced Surrogate Modeling Strategies. Math. Comput. Appl. 2023, 28, 57. [Google Scholar] [CrossRef]
- Takakura, A.; Beppu, K.; Nishihara, T.; Fukui, A.; Kozeki, T.; Namazu, T.; Miyauchi, Y.; Itami, K. Strength of carbon nanotubes depends on their chemical structures. Nat. Commun. 2019, 10, 3040. [Google Scholar] [CrossRef]
- García-Macías, E.; Castro-Triguero, R.; Friswell, M.I.; Adhikari, S.; Sáez, A. Metamodel-based approach for stochastic free vibration analysis of functionally graded carbon nanotube reinforced plates. Compos. Struct. 2016, 152, 183–198. [Google Scholar] [CrossRef]
- Pouresmaeeli, S.; Fazelzadeh, S.A. Uncertain Buckling and Sensitivity Analysis of Functionally Graded Carbon Nanotube-Reinforced Composite Beam. Int. J. Appl. Mech. 2017, 9, 1750071. [Google Scholar] [CrossRef]
- Carvalho, A.; Silva, T.A.N.; Loja, M.A.R.; Damásio, F.R. Assessing the influence of material and geometrical uncertainty on the mechanical behavior of FGM plates. Mech. Adv. Mater. Struct. 2017, 24, 417–426. [Google Scholar] [CrossRef]
- Rosa, R.S.B.; Loja, M.A.R.; Carvalho, A.C.J.V.N. Toward variability characterization and statistic models constitution for the prediction of exponentially graded plates’ static response. J. Compos. Sci. 2018, 2, 59. [Google Scholar] [CrossRef]
- Karsh, P.K.; Mukhopadhyay, T.; Dey, S. Stochastic dynamic analysis of twisted functionally graded plates. Compos. Part B Eng. 2018, 147, 259–278. [Google Scholar] [CrossRef]
- Wang, Q.; Wu, D.; Tin-Loi, F.; Gao, W. Machine learning aided stochastic structural free vibration analysis for functionally graded bar-type structures. Thin-Walled Struct. 2019, 144, 106315. [Google Scholar] [CrossRef]
- Gao, K.; Do, D.M.; Li, R.; Kitipornchai, S.; Yang, J. Probabilistic stability analysis of functionally graded graphene reinforced porous beams. Aerosp. Sci. Technol. 2020, 98, 105738. [Google Scholar] [CrossRef]
- Baghlani, A.; Najafgholipour, M.A.; Khayat, M. The influence of mechanical uncertainties on the free vibration of functionally graded graphene-reinforced porous nanocomposite shells of revolution. Eng. Struct. 2021, 228, 111356. [Google Scholar] [CrossRef]
- Halpin, J.C.; Kardos, J.L. The Halpin-Tsai Equations: A Review. Polym. Eng. Sci. 1976, 16, 344–352. [Google Scholar]
- Costa, D.M.S.; Loja, M.A.R. Assessing the static behavior of hybrid CNT-metal-ceramic composite plates. AIMS Mater. Sci. 2016, 3, 808–831. [Google Scholar] [CrossRef]
- Reddy, J.N. An evaluation of equivalent-single-layer and layerwise theories of composite laminates. Compos. Struct. 1993, 25, 21–35. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Singha, M.K.; Prakash, T.; Ganapathi, M. Finite element analysis of functionally graded plates under transverse load. Finite Elem. Anal. Des. 2011, 47, 453–460. [Google Scholar] [CrossRef]
- Mota, A.F.; Loja, M.A.R.; Barbosa, J.I.; Rodrigues, J.A. Porous Functionally Graded Plates: An Assessment of the Influence of Shear Correction Factor on Static Behavior. Math. Comput. Appl. 2020, 25, 25. [Google Scholar] [CrossRef]
- Zienkiewicz, O.C.; Taylor, R.L. The Finite Element Method, 5th ed.; Butterworth-Heinemann: Oxford, UK, 2000; Volume 1. [Google Scholar]
- Durbin, J.; Watson, G.S. Testing for Serial Correlation in Least Squares Regression. Biometrika 1951, 38, 159–179. [Google Scholar] [CrossRef] [PubMed]
- Breusch, T.S.; Pagan, A.R. A Simple Test for Heteroskedasticity and Random Coefficient Variation. Econometrica 1979, 47, 1287–1294. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar]
- Siegel, S.; Castellan, N.J., Jr. Nonparametric Statistics for the Behavioral Sciences, 2nd ed.; Mcgraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Hollander, M.; Wolfe, D.A. Nonparametric Statistical Methods; John Wiley & Sons: New York, NY, USA, 2013; pp. 139–146. [Google Scholar]
- Demirhan, P.A.; Taskin, V. Levy solution for bending analysis of functionally graded sandwich plates based on four variable plate theory. Compos. Struct. 2017, 177, 80–95. [Google Scholar] [CrossRef]

| a/h | ||||||
|---|---|---|---|---|---|---|
| 10 | 20 | |||||
| p | [51] | [51] | ||||
| 0 | 0.4666 | 0.4655 | −0.23 | 0.4494 | 0.4480 | −0.31 |
| 0.5 | 0.6590 | 0.6574 | −0.25 | 0.6401 | 0.6381 | −0.31 |
| 2 | 1.0153 | 1.0129 | −0.23 | 0.9945 | 0.9912 | −0.33 |
| 10 | 1.4296 | 1.4194 | −0.72 | 1.3997 | 1.3944 | −0.38 |
| 1.80 × 10−9 | ||||||
| 1.20 × 10−11 | 1.10 × 10−5 | |||||
| 4.30 × 10−13 | 8.50 × 10−10 | 1.70 × 10−5 | ||||
| 1.50 × 10−13 | 1.10 × 10−11 | 1.30 × 10−9 | 3.00 × 10−5 | |||
| 1.10 × 10−14 | 2.90 × 10−13 | 3.60 × 10−12 | 1.90 × 10−10 | 3.20 × 10−7 | ||
| 4.90 × 10−15 | 1.60 × 10−13 | 6.20 × 10−13 | 2.20 × 10−11 | 3.40 × 10−9 | 0.064 |
| Estimate | Std. Error | t | p-Value 1 | |
|---|---|---|---|---|
| Intercept | −5.252 × 10−9 | 5.886 × 10−10 | −8.924 | 2.07 × 10−8 *** |
| −6.226 × 10−10 | 2.081 × 10−10 | −2.992 | 0.00721 ** | |
| 3.686 × 10−10 | 4.546 × 10−11 | 8.109 | 9.44 × 10−8 *** | |
| 6.603 × 10−10 | 2.989 × 10−13 | 2.209 | 0.03901 * |
| Estimate | Std. Error | t | p-Value 1 | |
|---|---|---|---|---|
| Intercept | −11.732 × 10−9 | 2.234 × 10−9 | −5.250 | 3.88 × 10−5 *** |
| −0.7828 × 10−9 | 1.591 × 10−10 | −4.919 | 8.27 × 10−5 *** | |
| 0.9688 × 10−9 | 7.490 × 10−11 | 12.935 | 3.57 × 10−11 *** | |
| 0.9498 × 10−9 | 3.043 × 10−10 | 3.121 | 0.00538 ** |
| Estimate | Std. Error | t | p-Value 1 | |
|---|---|---|---|---|
| Intercept | −4.635 × 10−9 | 1.331 × 10−10 | −34.815 | <2 × 10−16 *** |
| −2.558 × 10−11 | 7.277 × 10−12 | −3.515 | 0.00195 ** | |
| 4.849 × 10−12 | 7.947 × 10−13 | 6.101 | 3.85 × 10−6 *** | |
| 6.647 × 10−13 | 8.304 × 10−14 | 8.004 | 5.85 × 10−8 *** |
| Estimate | Std. Error | t | p-Value 1 | |
|---|---|---|---|---|
| Intercept | −1.151 × 10−8 | 6.169 × 10−10 | −18.656 | 1.50 × 10−14 *** |
| −2.489 × 10−10 | 3.138 × 10−11 | −7.933 | 9.41 × 10−8 *** | |
| 2.227 × 10−10 | 1.948 × 10−11 | 11.432 | 1.77 × 10−10 *** | |
| 1.001 × 10−11 | 7.626 × 10−11 | 13.129 | 1.36 × 10−11 *** | |
| 2.708 × 10−11 | 2.210 × 10−11 | 1.226 | 0.234 |
| Estimate | Std. Error | t | p-Value 1 | |
|---|---|---|---|---|
| Intercept | 1.120 × 10−8 | 5.697 × 10−10 | −19.659 | 1.91 × 10−15 *** |
| −2.576 × 10−10 | 3.092 × 10−11 | −8.331 | 2.99 × 10−8 *** | |
| 2.158 × 10−10 | 1.886 × 10−11 | 11.441 | 9.88 × 10−11 *** | |
| 1.001 × 10−9 | 7.712 × 10−11 | 12.974 | 8.76 × 10−12 *** |
| Intercept | |||||
|---|---|---|---|---|---|
| 0.894 | −11.732 × 10−9 (2.234 × 10−9) *** | −7.828 × 10−10 (1.591 × 10−10) *** | 9.688 × 10−10 (7.490 × 10−11) *** | 9.498 × 10−10 (3.043 × 10−10) ** | |
| 0.909 | −9.775 × 10−9 (1.453 × 10−9) *** | −5.684 × 10−10 (1.035 × 10−10) *** | 6.834 × 10−10 (4.873 × 10−11) *** | 6.647 × 10−10 (1.980 × 10−10) ** | |
| 0.912 | −8.923 × 10−9 (1.161 × 10−9) *** | −4.694 × 10−10 (8.273 × 10−11) *** | 5.552 × 10−10 (3.894 × 10−11) *** | 5.415 × 10−10 (1.582 × 10−10) ** | |
| 0.913 | −8.220 × 10−9 (9.283 × 10−10) *** | −3.783 × 10−10 (6.613 × 10−11) *** | 4.465 × 10−10 (3.113 × 10−11) *** | 4.410 × 10−10 (1.265 × 10−10) ** | |
| 0.917 | −7.592 × 10−9 (7.434 × 10−10) *** | −3.099 × 10−10 (5.295 × 10−11) *** | 3.675 × 10−10 (2.492 × 10−11) *** | 3.502 × 10−10 (1.013 × 10−10) ** | |
| 0.925 | −7.090 × 10−9 (5.367 × 10−10) *** | −2.438 × 10−10 (3.823 × 10−11) *** | 2.778 × 10−10 (1.799 × 10−11) *** | 2.774 × 10−10 (7.311 × 10−11) ** |
| Intercept | |||||
|---|---|---|---|---|---|
| 0.917 | −11.201 × 10−9 (5.697 × 10−10) *** | −2.576 × 10−10 (3.092 × 10−11) *** | 2.158 × 10−10 (1.886 × 10−11) *** | 10.01 × 10−10 (7.712 × 10−11) *** | |
| 0.914 | −9.799 × 10−9 (4.421 × 10−10) *** | −1.977 × 10−10 (2.399 × 10−11) *** | 1.659 × 10−10 (1.464 × 10−11) *** | 7.532 × 10−10 (5.985 × 10−11) *** | |
| 0.919 | −9.017 × 10−9 (3.554 × 10−10) *** | −1.681 × 10−10 (1.928 × 10−11) *** | 1.383 × 10−10 (1.177 × 10−11) *** | 6.238 × 10−10 (4.811 × 10−11) *** | |
| 0.910 | −8.329 × 10−9 (3.074 × 10−10) *** | −1.311 × 10−10 (1.668 × 10−11) *** | 1.125 × 10−10 (1.018 × 10−11) *** | 5.103 × 10−10 (4.161 × 10−11) *** | |
| 0.910 | −7.806 × 10−9 (2.563 × 10−10) *** | −1.114 × 10−10 (1.391 × 10−11) *** | 0.942 × 10−10 (8.485 × 10−12) *** | 4.247 × 10−10 (3.469 × 10−11) *** | |
| 0.923 | −7.306 × 10−9 (1.873 × 10−10) *** | −0.869 × 10−10 (1.016 × 10−11) *** | 0.743 × 10−10 (6.200 × 10−12) *** | 3.403 × 10−10 (2.535 × 10−11) *** |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Carvalho, A.; Martins, A.; Mota, A.F.; Loja, M.A.R. Variability on Functionally Graded Plates’ Deflection Due to Uncertainty on Carbon Nanotubes’ Properties. Math. Comput. Appl. 2024, 29, 22. https://doi.org/10.3390/mca29020022
Carvalho A, Martins A, Mota AF, Loja MAR. Variability on Functionally Graded Plates’ Deflection Due to Uncertainty on Carbon Nanotubes’ Properties. Mathematical and Computational Applications. 2024; 29(2):22. https://doi.org/10.3390/mca29020022
Chicago/Turabian StyleCarvalho, Alda, Ana Martins, Ana F. Mota, and Maria A. R. Loja. 2024. "Variability on Functionally Graded Plates’ Deflection Due to Uncertainty on Carbon Nanotubes’ Properties" Mathematical and Computational Applications 29, no. 2: 22. https://doi.org/10.3390/mca29020022







