On Phase and Amplitude Extraction in Bichromatic Ionization: A Proposal
Abstract
:1. Introduction
2. Theoretical Model
3. Discussion of the Geometry Setup
4. Spectroscopy
5. Results and Discussion
6. Complementary
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goeppert-Mayer, M. Uber Elementarakte mit zwei Quantensprungen (Elementary processes with two quantum transitions). Ann. Phys. 1951, 9, 273. (In German) [Google Scholar]
- Kohler, M.; Pfeifer, T.; Hatsagortsyan, K.; Keitel, C. Chapter 4—Frontiers of Atomic High-Harmonic Generation. In Advances in Atomic, Molecular, and Optical Physics; Berman, P., Arimondo, E., Lin, C., Eds.; Academic Press: Cambridge, MA, USA, 2012; Volume 61, pp. 159–208. [Google Scholar] [CrossRef]
- Krausz, F.; Ivanov, M. Attosecond physics. Rev. Mod. Phys. 2009, 81, 163–234. [Google Scholar] [CrossRef]
- Strelkov, V.V.; Platonenko, V.T.; Sterzhantov, A.F.; Ryabikin, M.Y. Attosecond electromagnetic pulses: Generation, measurement, and application. Generation of high-order harmonics of intense laser field for attosecond pulse production. Phys. Usp. 2016, 59, 425. [Google Scholar] [CrossRef]
- Allaria, E.; Appio, R.; Badano, L.; Barletta, W.A.; Bassanese, S.; Biedron, S.G.; Borga, A.; Busetto, E.; Castronovo, D.; Cinquegrana, P.; et al. Highly Coherent Stable Pulses FERMI Seeded Free-Electron Laser Extrem Ultraviolet. Nat. Photonics 2012, 6, 699. [Google Scholar] [CrossRef]
- Callegari, C.; Grum-Grzhimailo, A.N.; Ishikawa, K.L.; Prince, K.C.; Sansone, G.; Ueda, K. Atomic, molecular and optical physics applications of longitudinally coherent and narrow bandwidth Free-Electron Lasers. Phys. Rep. 2021, 904, 1–59. [Google Scholar] [CrossRef]
- Prince, K.C.; Allaria, E.; Callegari, C.; Cucini, R.; Ninno, G.D.; Mitri, S.D.; Diviacco, B.; Ferrari, E.; Finetti, P.; Gauthier, D.; et al. Coherent control with a short-wavelength free-electron laser. Nat. Photonics 2016, 10, 176–179. [Google Scholar] [CrossRef]
- Paul, P.M.; Toma, E.S.; Breger, P.; Mullot, G.; Augé, F.; Balcou, P.; Muller, H.G.; Agostini, P. Observation of a Train of Attosecond Pulses from High Harmonic Generation. Science 2001, 292, 1689–1692. [Google Scholar] [CrossRef] [PubMed]
- Tzallas, P.; Charalambidis, D.; Papadogiannis, N.A.; Witte, K.; Tsakiris, G.D. Direct observation of attosecond light bunching. Nature 2003, 426, 267–271. [Google Scholar] [CrossRef]
- Maroju, P.K.; Grazioli, C.; Di Fraia, M.; Moioli, M.; Ertel, D.; Ahmadi, H.; Plekan, O.; Finetti, P.; Allaria, E.; Giannessi, L. Attosecond pulse shaping using a seeded free-electron laser. Nature 2020, 578, 386–391. [Google Scholar] [CrossRef]
- You, D.; Ueda, K.; Gryzlova, E.V.; Grum-Grzhimailo, A.N.; Popova, M.M.; Staroselskaya, E.I.; Tugs, O.; Orimo, Y.; Sato, T.; Ishikawa, K.L.; et al. New Method for Measuring Angle-Resolved Phases in Photoemission. Phys. Rev. X 2020, 10, 031070. [Google Scholar] [CrossRef]
- Di Fraia, M.; Plekan, O.; Callegari, C.; Prince, K.C.; Giannessi, L.; Allaria, E.; Badano, L.; De Ninno, G.; Trovò, M.; Diviacco, B.; et al. Complete Characterization of Phase and Amplitude of Bichromatic Extreme Ultraviolet Light. Phys. Rev. Lett. 2019, 123, 213904. [Google Scholar] [CrossRef] [PubMed]
- Armstrong, G.S.J.; Clarke, D.D.A.; Benda, J.; Wragg, J.; Brown, A.C.; van der Hart, H.W. Modeling tomographic measurements of photoelectron vortices in counter-rotating circularly polarized laser pulses. Phys. Rev. A 2019, 100, 063416. [Google Scholar] [CrossRef]
- Niikura, H.; Dudovich, N.; Villeneuve, D.M.; Corkum, P.B. Mapping Molecular Orbital Symmetry on High-Order Harmonic Generation Spectrum Using Two-Color Laser Fields. Phys. Rev. Lett. 2010, 105, 053003. [Google Scholar] [CrossRef] [PubMed]
- Sarantseva, T.S.; Frolov, M.V.; Manakov, N.L.; Ivanov, M.Y.; Starace, A.F. Harmonic generation spectroscopy with a two-colour laser field having orthogonal linear polarizations. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 231001. [Google Scholar] [CrossRef]
- Milošević, D.B.; Becker, W.; Kopold, R. Generation of circularly polarized high-order harmonics by two-color coplanar field mixing. Phys. Rev. A 2000, 61, 063403. [Google Scholar] [CrossRef]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photonics 2014, 8, 543–549. [Google Scholar] [CrossRef]
- Chen, C.; Tao, Z.; Hernández-García, C.; Matyba, P.; Carr, A.; Knut, R.; Kfir, O.; Zusin, D.; Gentry, C.; Grychtol, P.; et al. Tomographic reconstruction of circularly polarized high-harmonic fields: 3D attosecond metrology. Sci. Adv. 2016, 2, e1501333. [Google Scholar] [CrossRef]
- Khairulin, I.; Antonov, V.; Ryabikin, M.; Berrill, M.A.; Shlyaptsev, V.N.; Rocca, J.J.; Kocharovskaya, O. Amplification of elliptically polarized sub-femtosecond pulses in neon-like X-ray laser modulated by an IR field. Sci. Rep. 2022, 12, 6204. [Google Scholar] [CrossRef]
- Demekhin, P.V.; Artemyev, A.N.; Kastner, A.; Baumert, T. Photoelectron Circular Dichroism with Two Overlapping Laser Pulses of Carrier Frequencies ω and 2ω Linearly Polarized in Two Mutually Orthogonal Directions. Phys. Rev. Lett. 2018, 121, 253201. [Google Scholar] [CrossRef]
- Mayer, N.; Patchkovskii, S.; Morales, F.; Ivanov, M.; Smirnova, O. Imprinting Chirality on Atoms Using Synthetic Chiral Light Fields. Phys. Rev. Lett. 2022, 129, 243201. [Google Scholar] [CrossRef]
- De Silva, A.H.N.C.; Atri-Schuller, D.; Dubey, S.; Acharya, B.P.; Romans, K.L.; Foster, K.; Russ, O.; Compton, K.; Rischbieter, C.; Douguet, N.; et al. Using Circular Dichroism to Control Energy Transfer in Multiphoton Ionization. Phys. Rev. Lett. 2021, 126, 023201. [Google Scholar] [CrossRef]
- Zipp, L.J.; Natan, A.; Bucksbaum, P.H. Probing electron delays in above-threshold ionization. Optica 2014, 1, 361–364. [Google Scholar] [CrossRef]
- Cao, C.; Li, M.; Liang, J.; Yan, J.; Guo, K.; Li, Z.; Liu, Y.; Zhou, Y.; Lu, P. Angular distribution of near-threshold photoelectrons from resonance-enhanced multiphoton ionization of argon. Phys. Rev. A 2022, 106, 033112. [Google Scholar] [CrossRef]
- López, S.D.; Donsa, S.; Nagele, S.; Arbó, D.G.; Burgdörfer, J. Phase delays in ω − 2ω above-threshold ionization. Phys. Rev. A 2021, 104, 043113. [Google Scholar] [CrossRef]
- Ayuso, D.; Jiménez-Galán, A.; Morales, F.; Ivanov, M.; Smirnova, O. Attosecond control of spin polarization in electron–ion recollision driven by intense tailored fields. New J. Phys. 2017, 19, 073007. [Google Scholar] [CrossRef]
- Milošević, D.B. Atomic and Molecular Processes in a Strong Bicircular Laser Field. Atoms 2018, 6, 61. [Google Scholar] [CrossRef]
- Schafer, K.J.; Kulander, K.C. Phase-dependent effects in multiphoton ionization induced by a laser field and its second harmonic. Phys. Rev. A 1992, 45, 8026–8033. [Google Scholar] [CrossRef] [PubMed]
- Douguet, N.; Bartschat, K. Photoelectron momentum distributions in the strong-field ionization of atomic hydrogen by few-cycle elliptically polarized optical pulses. Phys. Rev. A 2022, 106, 053112. [Google Scholar] [CrossRef]
- Grum-Grzhimailo, A.N.; Gryzlova, E.V.; Staroselskaya, E.I.; Venzke, J.; Bartschat, K. Interfering one-photon and two-photon ionization by femtosecond VUV pulses in the region of an intermediate resonance. Phys. Rev. A 2015, 91, 063418. [Google Scholar] [CrossRef]
- Gryzlova, E.V.; Grum-Grzhimailo, A.N.; Staroselskaya, E.I.; Douguet, N.; Bartschat, K. Quantum coherent control of the photoelectron angular distribution in bichromatic-field ionization of atomic neon. Phys. Rev. A 2018, 97, 013420. [Google Scholar] [CrossRef]
- Baranova, N.B.; Beterov, I.M.; Zel’dovich, B.Y.; Ryabtsev, I.I.; Chudinov, A.N.; Shul’ginov, A.A. Observation of an interference of one- and two-photon ionization of the sodium 4s state. Pis’ma Zh. Eksp. Teor. Fiz. 1992, 55, 431, (JETP Lett. 1992, 55, 439). [Google Scholar]
- Anderson, D.Z.; Baranova, N.B.; Green, K.; Zel’dovich, B.Y. Interference of one- and two-photon processes in the ionization of atoms and molecules. Zh. Eksp. Teor. Fiz. 1992, 75, 210, (JETP Lett. 1992, 102, 397). [Google Scholar]
- Yin, Y.Y.; Chen, C.; Elliott, D.S.; Smith, A.V. Asymmetric photoelectron angular distributions from interfering photoionization processes. Phys. Rev. Lett. 1992, 69, 2353–2356. [Google Scholar] [CrossRef] [PubMed]
- Ehlotzky, F. Atomic phenomena in bichromatic laser fields. Phys. Rep. 2001, 345, 175–264. [Google Scholar] [CrossRef]
- Shapiro, M.; Brumer, P. Coherent Control of Atomic, Molecular, and Electronic Processes. In Advances in Atomic, Molecular, and Optical Physics; Academic Press: Cambridge, MA, USA, 2000; Volume 42, pp. 287–345. [Google Scholar] [CrossRef]
- Ohmura, H.; Nakanaga, T.; Tachiya, M. Coherent Control of Photofragment Separation in the Dissociative Ionization of IBr. Phys. Rev. Lett. 2004, 92, 113002. [Google Scholar] [CrossRef]
- Goetz, R.E.; Koch, C.P.; Greenman, L. Quantum Control of Photoelectron Circular Dichroism. Phys. Rev. Lett. 2019, 122, 013204. [Google Scholar] [CrossRef]
- Stevens, M.J.; Smirl, A.L.; Bhat, R.D.R.; Najmaie, A.; Sipe, J.E.; van Driel, H.M. Quantum Interference Control of Ballistic Pure Spin Currents in Semiconductors. Phys. Rev. Lett. 2003, 90, 136603. [Google Scholar] [CrossRef]
- Fortier, T.M.; Roos, P.A.; Jones, D.J.; Cundiff, S.T.; Bhat, R.D.R.; Sipe, J.E. Carrier-Envelope Phase-Controlled Quantum Interference of Injected Photocurrents in Semiconductors. Phys. Rev. Lett. 2004, 92, 147403. [Google Scholar] [CrossRef]
- Popova, M.M.; Gryzlova, E.V.; Kiselev, M.D.; Grum-Grzhimailo, A.N. Symmetry Violation in Bichromatic Ionization by a Free-Electron Laser: Photoelectron Angular Distribution and Spin Polarization. Symmetry 2021, 13, 1015. [Google Scholar] [CrossRef]
- Manakov, N.L.; Ovsiannikov, V.D.; Starace, A.F. dc Field-Induced, Phase and Polarization Control of Interference between One- and Two-Photon Ionization Amplitudes. Phys. Rev. Lett. 1999, 82, 4791–4794. [Google Scholar] [CrossRef]
- Bolovinos, A.; Cohen, S.; Liontos, I. One- and two-photon phase-sensitive coherent control of total ionization yields in the presence of static electric fields. Phys. Rev. A 2008, 77, 023413. [Google Scholar] [CrossRef]
- Yamazaki, R.; Elliott, D.S. Strong variation of the phase lag in the vicinity of autoionizing resonances. Phys. Rev. A 2007, 76, 053401. [Google Scholar] [CrossRef]
- Bello, R.Y.; Borràs, V.J.; González-Vázquez, J.; Martín, F. Electronic coherences in argon through interfering one- and two-photon ionization processes in the vicinity of Feshbach resonances. Phys. Rev. Res. 2022, 4, 043028. [Google Scholar] [CrossRef]
- Wang, Y.; Greene, C.H. Coherent-control phase lag across doubly excited atomic strontium resonances in an ω ࢤ 2ω interference scheme. Phys. Rev. A 2023, 107, 032804. [Google Scholar] [CrossRef]
- Gryzlova, E.V.; Carpeggiani, P.; Popova, M.M.; Kiselev, M.D.; Douguet, N.; Reduzzi, M.; Negro, M.; Comby, A.; Ahmadi, H.; Wanie, V.; et al. Influence of an atomic resonance on the coherent control of the photoionization process. Phys. Rev. Res. 2022, 4, 033231. [Google Scholar] [CrossRef]
- Hofbrucker, J.; Böning, B.; Volotka, A.V.; Fritzsche, S. Elliptical dichroism in biharmonic ionization of atoms. Phys. Rev. A 2021, 104, 013102. [Google Scholar] [CrossRef]
- Fritzsche, S.; Hofbrucker, J. Biharmonic (ω, 2ω) ionization of atoms by elliptically-polarized light. Carving the photoelectron angular distributions. New J. Phys. 2022, 24, 103031. [Google Scholar] [CrossRef]
- Popova, M.M.; Gryzlova, E.V.; Kiseleva, M.D.; Grum-Grzhimailo, A.N. Ionization of Atoms by a Bichromatic Fields of ω+2ω Multiple Frequencies with Arbitrary Polarization. J. Exp. Theor. Phys. 2022, 135, 58–72. [Google Scholar] [CrossRef]
- Balashov, V.V.; Grum-Grzhimailo, A.N.; Kabachnik, .M. Polarization and Correlation Phenomena in Atomic Collisions. A Practical Theory Course; Kluwer Plenum: New York, NY, USA, 2000. [Google Scholar] [CrossRef]
- Cormier, E.; Lambropoulos, P. Extrapolation method for the evaluation of above threshold ionization cross sections for one- and two-electron systems. J. Phys. B At. Mol. Opt. Phys. 1995, 28, 5043. [Google Scholar] [CrossRef]
- Sobelman, I.I. Atomic Spectra and Radiative Transitions; Springer: Berlin/Heidelberg, Germany, 1992. [Google Scholar] [CrossRef]
- Gao, B.; Starace, A.F. Variational Calculation of Multiphoton Ionization Processes for the H Atom. Phys. Rev. Lett. 1988, 61, 404–407. [Google Scholar] [CrossRef]
- Orel, A.; Rescigno, T. An algebraic variational approach to the calculation of total cross sections for one- and two-photon ionization. Chem. Phys. Lett. 1988, 146, 434–438. [Google Scholar] [CrossRef]
- Staroselskaya, E.; Grum-Grzhimailo, A. A variationally stable method in the problem of two-photon atomic ionization. Mosc. Univ. Phys. Bull. 2015, 70, 374–381. [Google Scholar] [CrossRef]
- Salvat, F.; Fernández-Varea, J.M. Radial: A Fortran subroutine package for the solution of the radial Schrödinger and Dirac wave equations. Comput. Phys. Commun. 2019, 240, 165–177. [Google Scholar] [CrossRef]
- Froese Fischer, C.; Brage, T.; Jönsson, P. Computational Atomic Structure. An MCHF Approach; Institute of Physics Publishing: Bristol, UK, 1997. [Google Scholar] [CrossRef]
- Haber, L.H.; Doughty, B.; Leone, S.R. Continuum phase shifts and partial cross sections for photoionization from excited states of atomic helium measured by high-order harmonic optical pump-probe velocity map imaging. Phys. Rev. A 2009, 79, 031401. [Google Scholar] [CrossRef]
- Marr, G.; West, J. Absolute photoionization cross-section tables for helium, neon, argon, and krypton in the VUV spectral regions. At. Data Nucl. Data Tables 1976, 18, 497–508. [Google Scholar] [CrossRef]
- Saenz, A.; Lambropoulos, P. Theoretical two-, three- and four-photon ionization cross sections of helium in the XUV range. J. Phys. B At. Mol. Opt. Phys. 1999, 32, 5629. [Google Scholar] [CrossRef]
- Nikolopoulos, L.A.A.; Lambropoulos, P. Multichannel theory of two-photon single and double ionization of helium. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 545. [Google Scholar] [CrossRef]
- Hofbrucker, J.; Volotka, A.V.; Fritzsche, S. Maximum Elliptical Dichroism in Atomic Two-Photon Ionization. Phys. Rev. Lett. 2018, 121, 053401. [Google Scholar] [CrossRef]
- Boll, D.I.R.; Fojón, O.A.; McCurdy, C.W.; Palacios, A. Angularly resolved two-photon above-threshold ionization of helium. Phys. Rev. A 2019, 99, 023416. [Google Scholar] [CrossRef]
- Kramida, A.; Ralchenko, Y.; Reader, J.; NIST ASD Team. NIST Atomic Spectra Database (Ver. 5.10); National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022. Available online: https://physics.nist.gov/asd (accessed on 24 July 2023).
- Hofbrucker, J.; Ramakrishna, S.; Volotka, A.V.; Fritzsche, S. Polarization effects in the total rate of biharmonic ω+3ω ionization of atoms. Phys. Rev. A 2022, 106, 013118. [Google Scholar] [CrossRef]



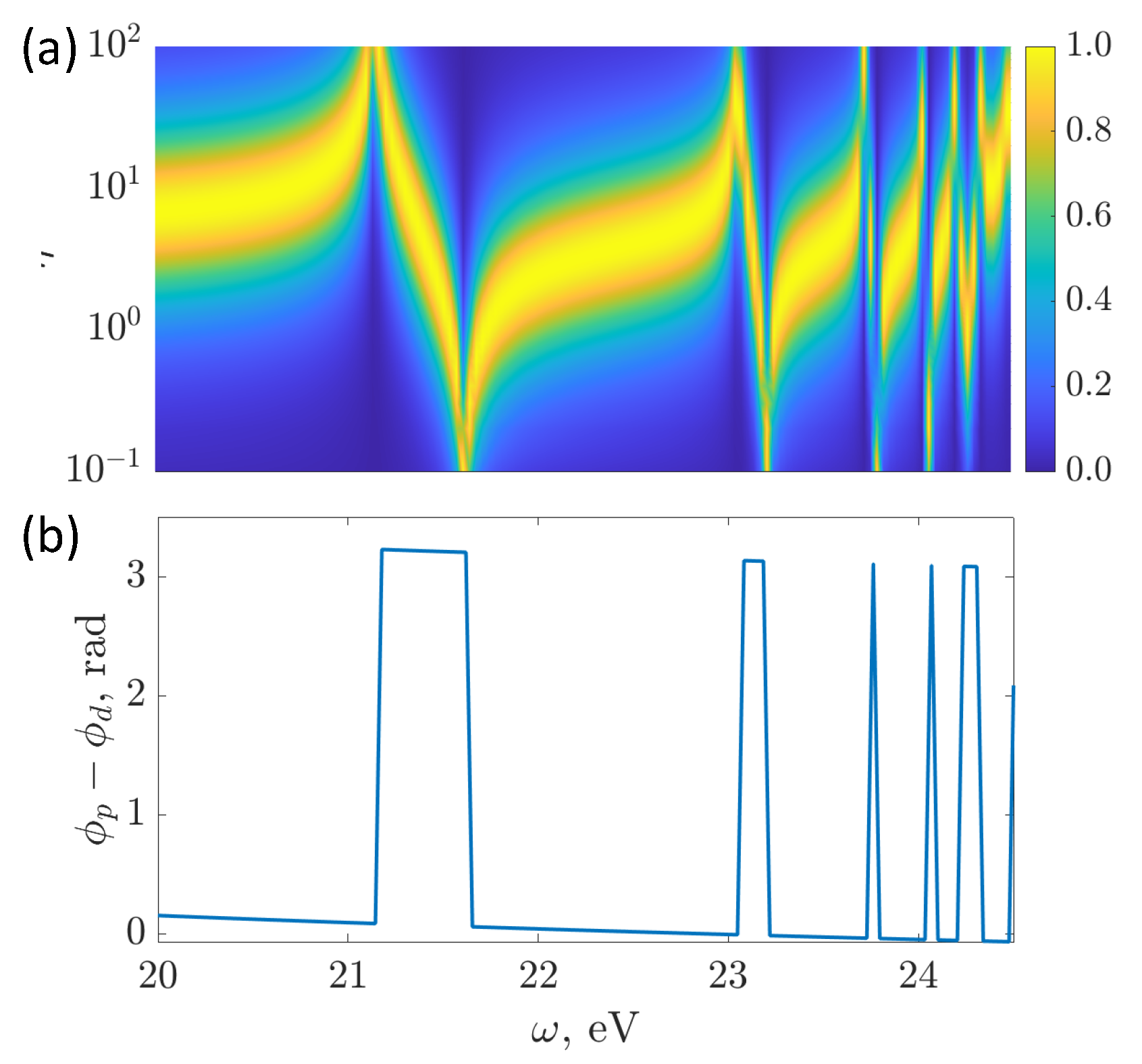
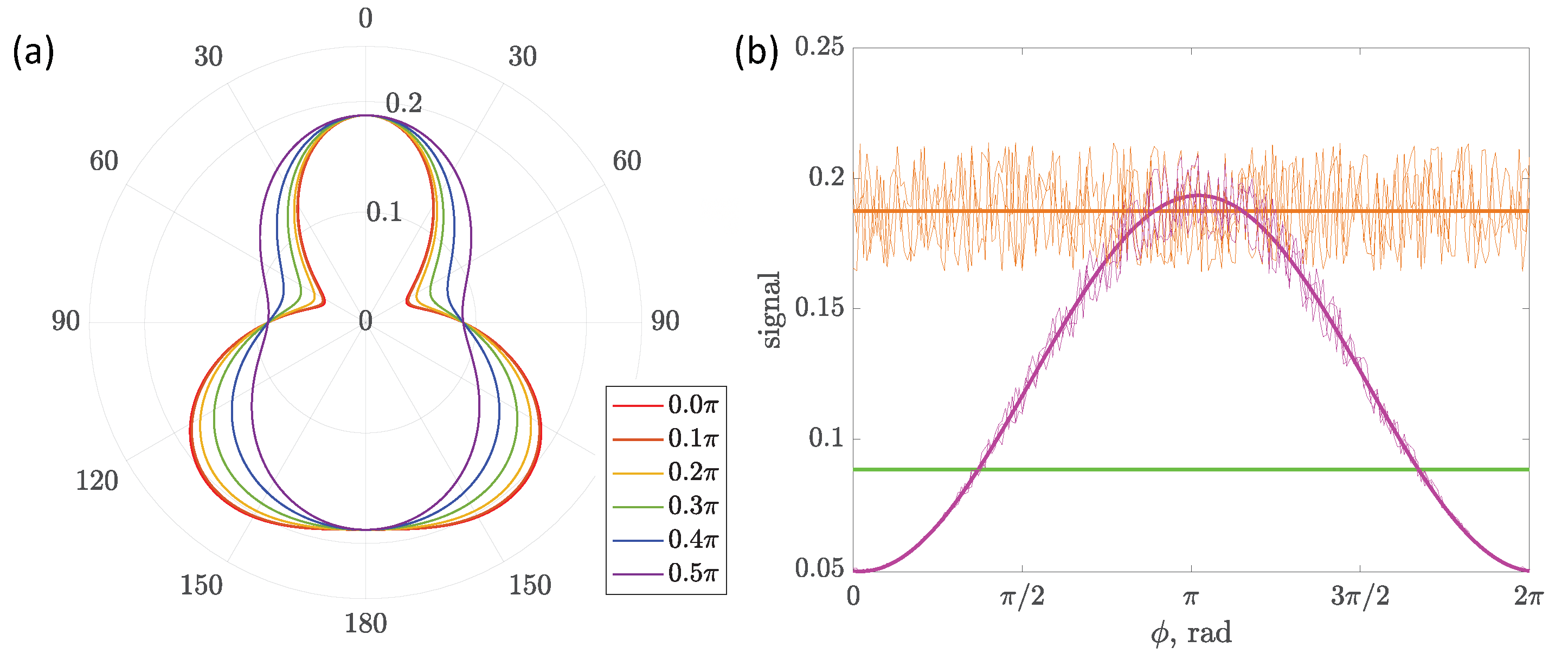
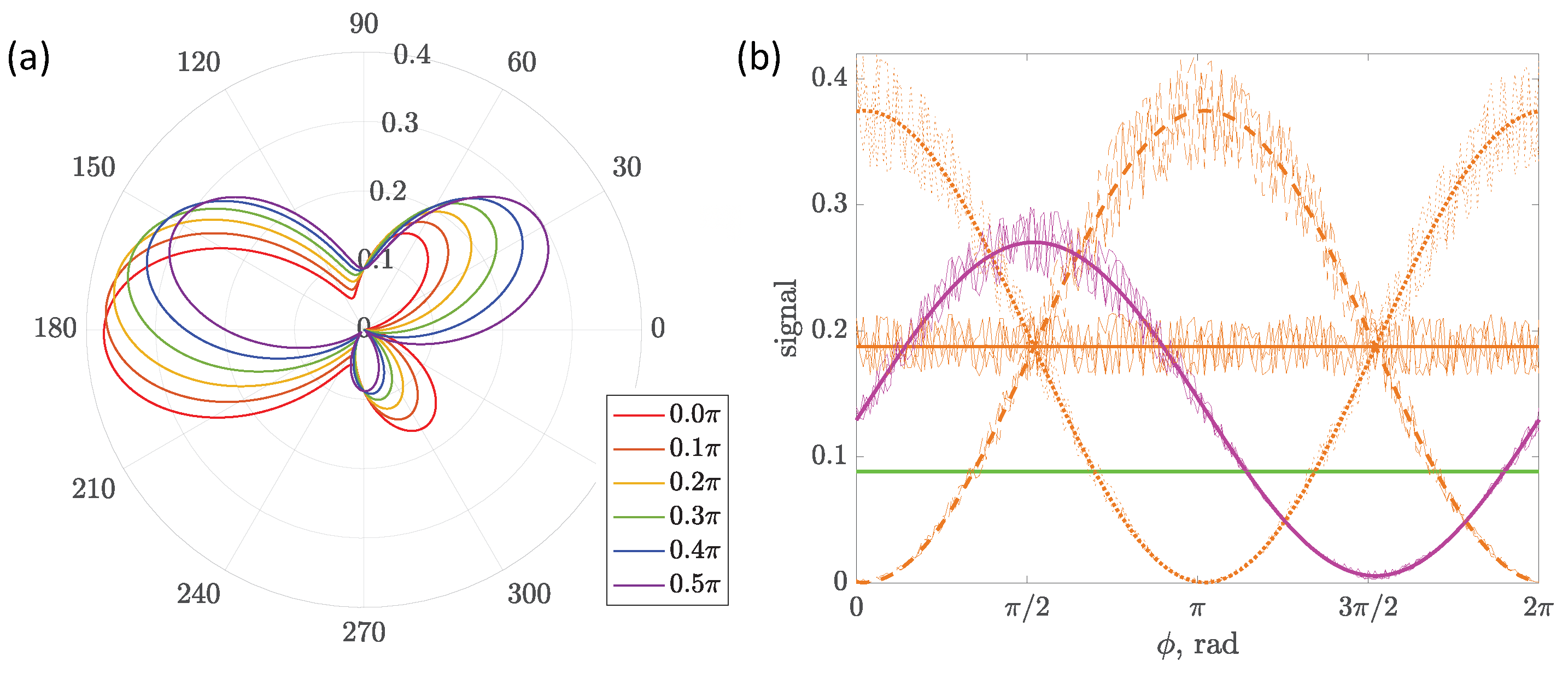
| Resonance | Theory | Experiment [65] |
|---|---|---|
| 21.14 | 21.22 | |
| 23.06 | 23.09 | |
| 23.73 | 23.74 | |
| 24.04 | 24.05 | |
| 24.21 | 24.21 | |
| 24.34 | 24.31 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popova, M.M.; Grum-Grzhimailo, A.N.; Gryzlova, E.V. On Phase and Amplitude Extraction in Bichromatic Ionization: A Proposal. Photonics 2023, 10, 1069. https://doi.org/10.3390/photonics10101069
Popova MM, Grum-Grzhimailo AN, Gryzlova EV. On Phase and Amplitude Extraction in Bichromatic Ionization: A Proposal. Photonics. 2023; 10(10):1069. https://doi.org/10.3390/photonics10101069
Chicago/Turabian StylePopova, Maria M., Alexei N. Grum-Grzhimailo, and Elena V. Gryzlova. 2023. "On Phase and Amplitude Extraction in Bichromatic Ionization: A Proposal" Photonics 10, no. 10: 1069. https://doi.org/10.3390/photonics10101069





