Controlling Plasmon Resonance of Gold and Silver Nanoparticle Arrays with Help of Liquid Crystal
Abstract
:1. Introduction
2. Structure Description
3. Materials and Methods
4. Results
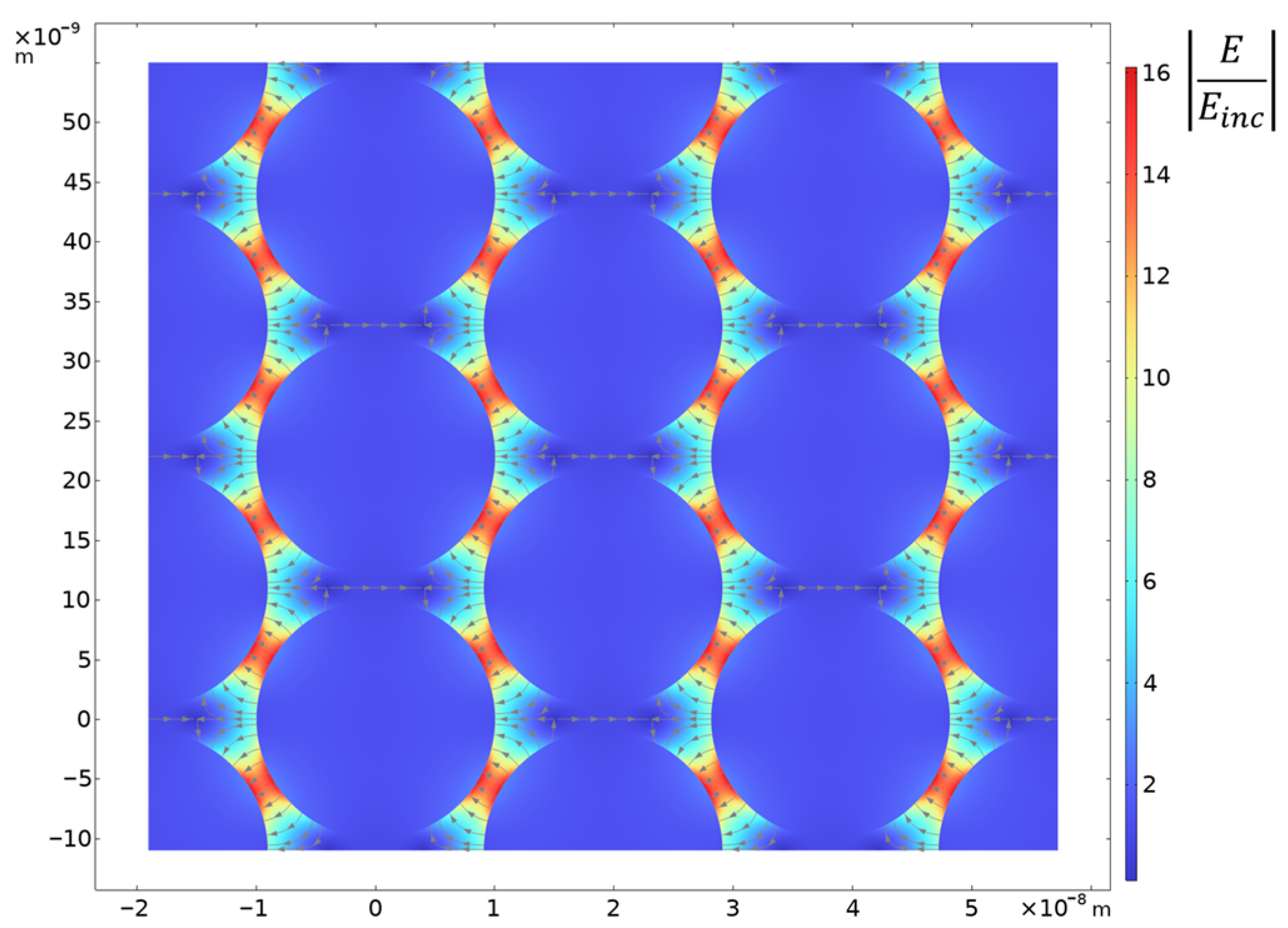
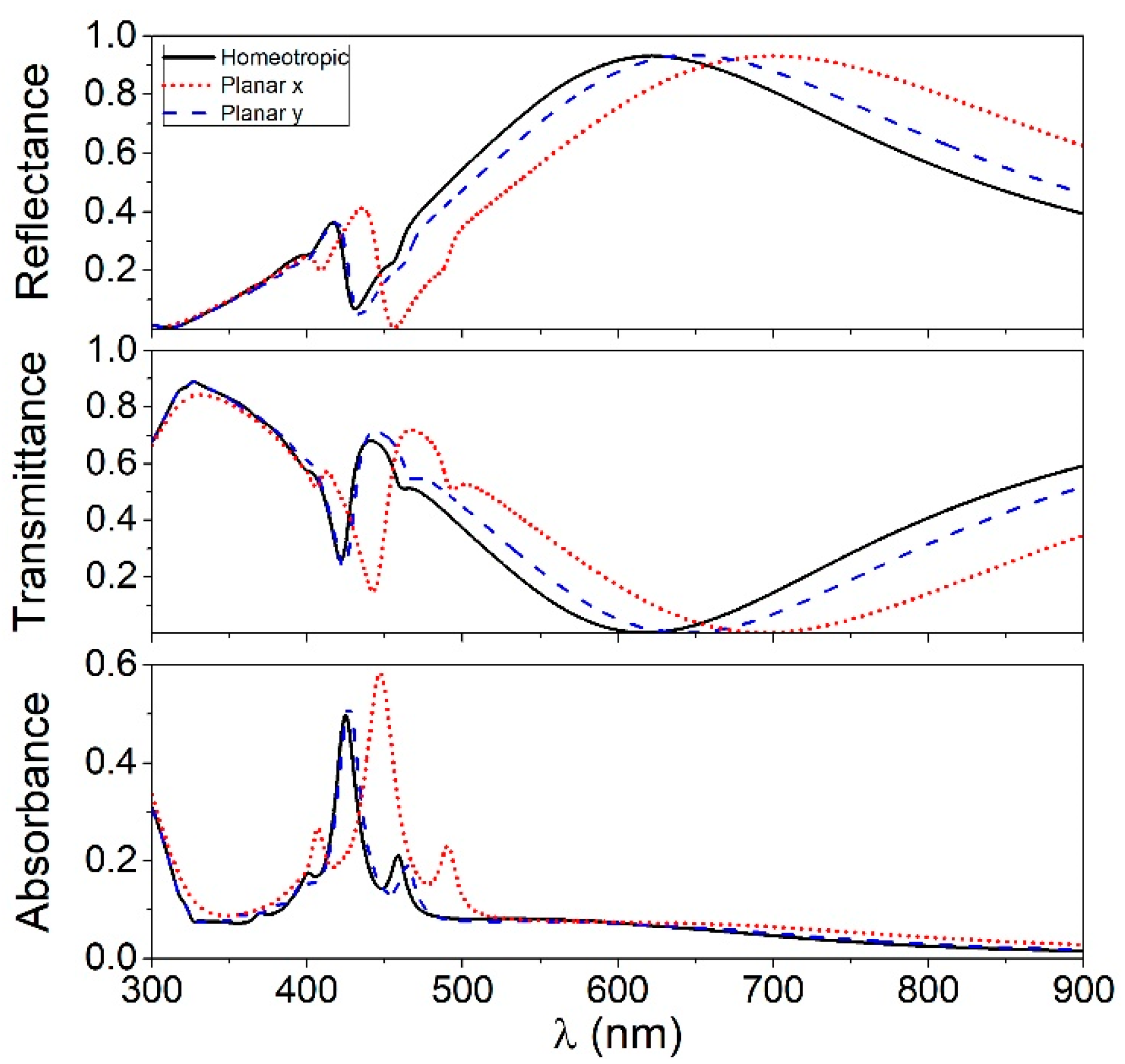
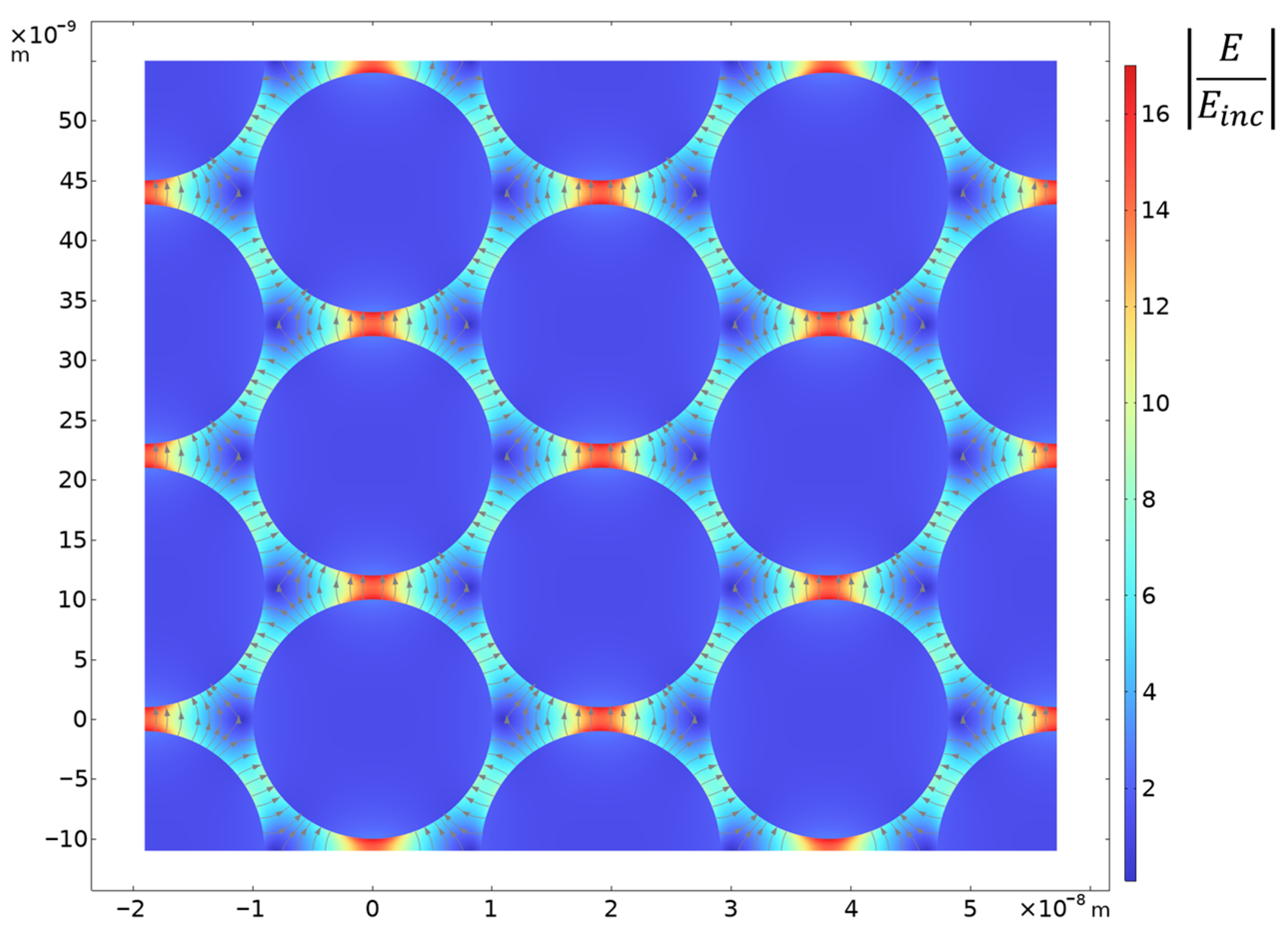
4.1. Optical Spectra for the Gold Nanoparticle Array
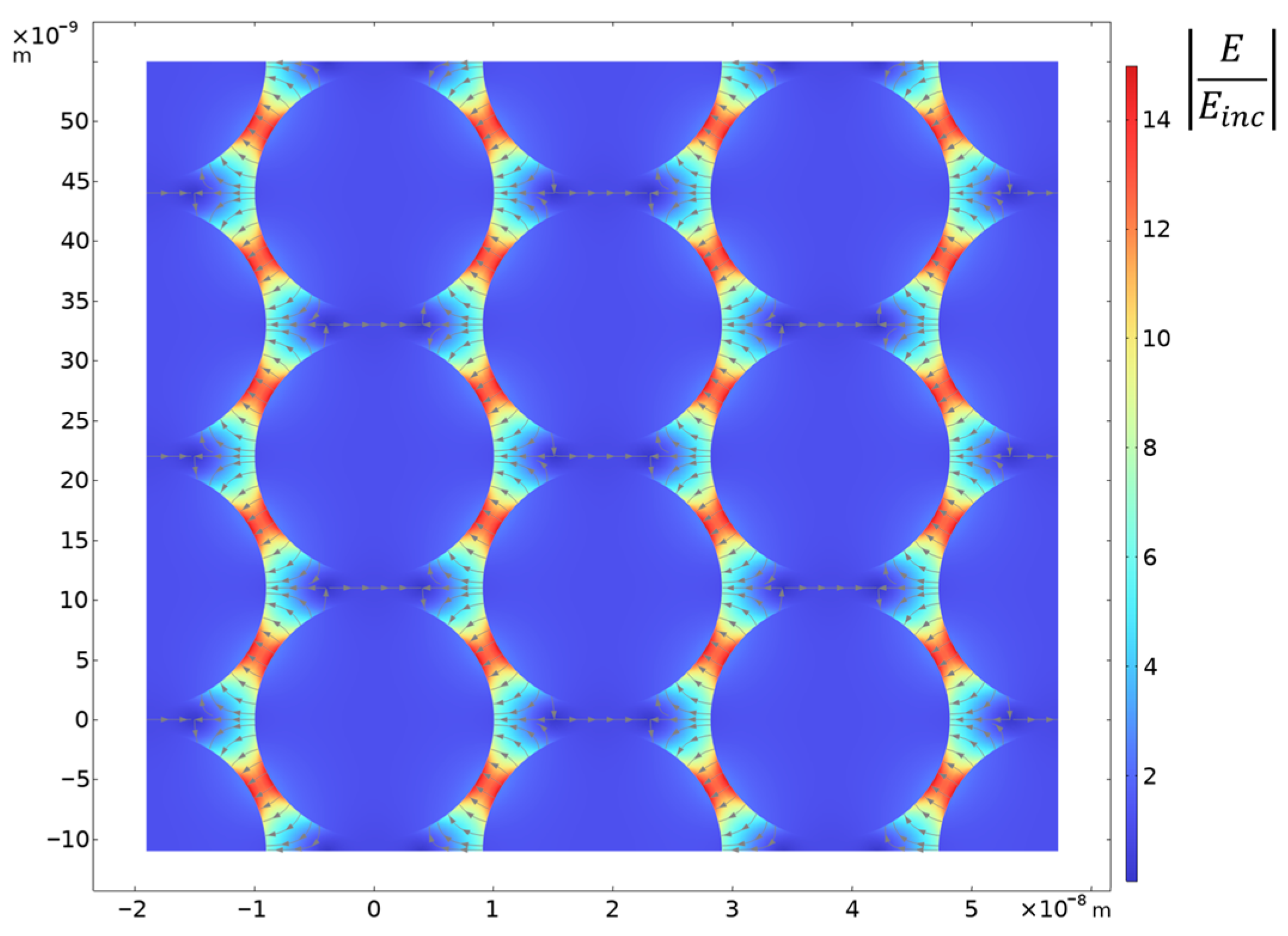
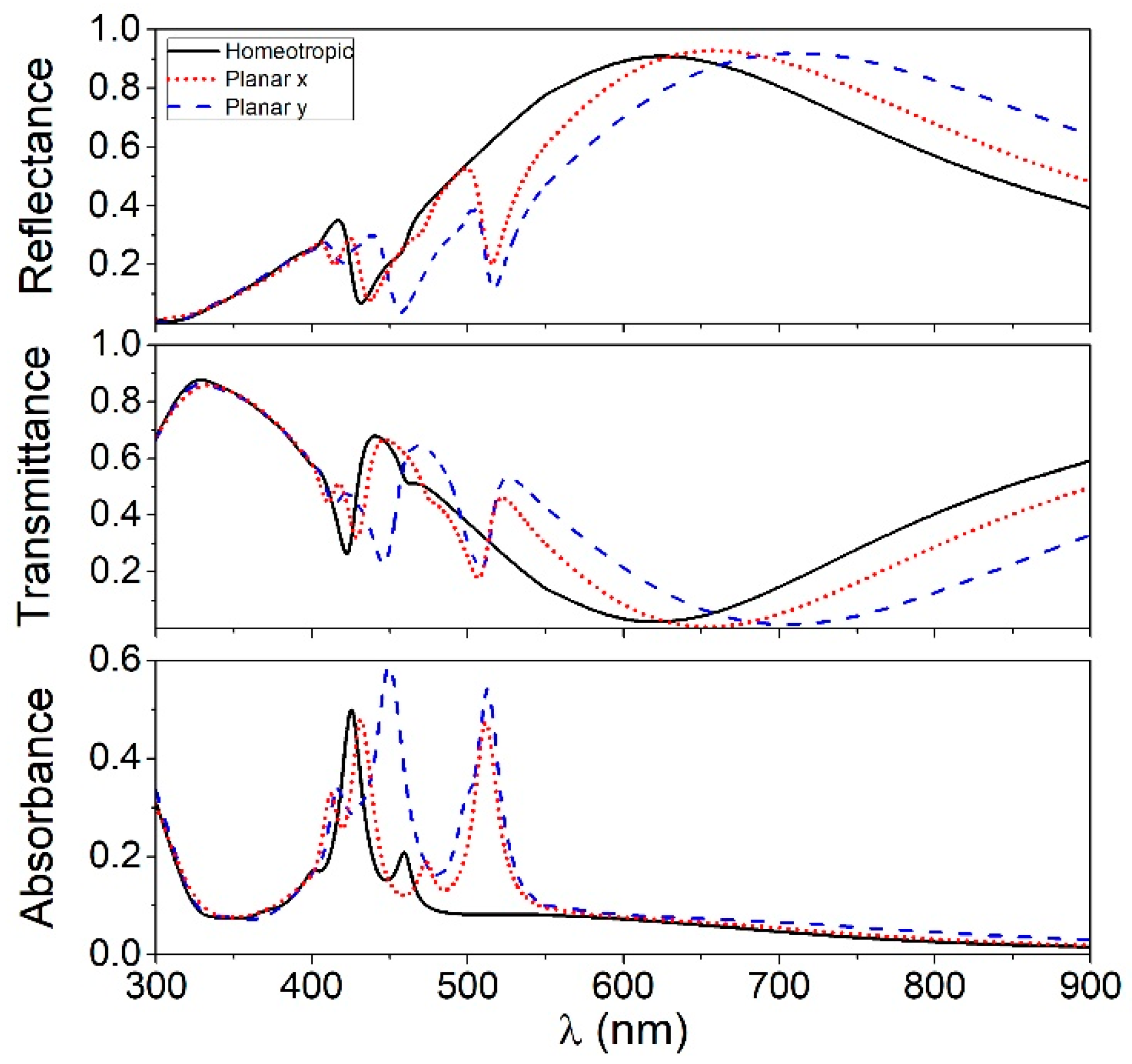
4.2. Optical Spectra for the Silver Nanoparticle Array
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kravets, V.G.; Kabashin, A.V.; Barnes, W.L.; Grigorenko, A.N. Plasmonic surface lattice resonances: A review of properties and applications. Chem. Rev. 2018, 118, 5912–5951. [Google Scholar] [CrossRef] [PubMed]
- Borah, R.; Verbruggen, S.W. Coupled plasmon modes in 2d gold nanoparticle clusters and their effect on local temperature control. J. Phys. Chem. C 2019, 123, 30594–30603. [Google Scholar] [CrossRef]
- Bi, Y.-G.; Feng, J.; Ji, J.-H.; Yi, F.-S.; Li, Y.-F.; Liu, Y.-F.; Zhang, X.-L.; Sun, H.-B. Nanostructures induced light harvesting enhancement in organic photovoltaics. Nanophotonics 2017, 7, 371–391. [Google Scholar] [CrossRef]
- Stratakis, E.; Kymakis, E. Nanoparticle-based plasmonic organic photovoltaic devices. Mater. Today 2013, 16, 133–146. [Google Scholar] [CrossRef]
- Ou, Q.-D.; Xie, H.-J.; Chen, J.-D.; Zhou, L.; Li, Y.-Q.; Tang, J.-X. Enhanced light harvesting in flexible polymer solar cells: Synergistic simulation of a plasmonic meta-mirror and a transparent silver mesowire electrode. J. Mater. Chem. A 2016, 4, 18952–18962. [Google Scholar] [CrossRef]
- Lim, S.Y.; Law, C.S.; Bertó-Roselló, F.; Liu, L.; Markovic, M.; Ferré-Borrull, J.; Abell, A.D.; Voelcker, N.H.; Marsal, L.F.; Santos, A. Tailor-engineered plasmonic single-lattices: Harnessing localized surface plasmon resonances for visible-NIR light-enhanced photocatalysis. Catal. Sci. Technol. 2020, 10, 3195–3211. [Google Scholar] [CrossRef]
- Li, S.; Miao, P.; Zhang, Y.; Wu, J.; Zhang, B.; Du, Y.; Han, X.; Sun, J.; Xu, P. Recent advances in plasmonic nanostructures for enhanced photocatalysis and electrocatalysis. Adv. Mater. 2021, 33, e2000086. [Google Scholar] [CrossRef]
- Song, L.; Qiu, N.; Huang, Y.; Cheng, Q.; Yang, Y.; Lin, H.; Su, F.; Chen, T. Macroscopic orientational gold nanorods monolayer film with excellent photothermal anticounterfeiting performance. Adv. Opt. Mater. 2020, 8, 1902082. [Google Scholar] [CrossRef]
- Lin, K.-T.; Lin, H.; Jia, B. Plasmonic nanostructures in photodetection, energy conversion and beyond. Nanophotonics 2020, 9, 3135–3163. [Google Scholar] [CrossRef]
- Wang, H.; Yao, L.; Mao, X.; Wang, K.; Zhu, L.; Zhu, J. Gold nanoparticle superlattice monolayer with tunable in-terparticle gap for surface-enhanced Raman spectroscopy. Nanoscale 2019, 11, 13917–13923. [Google Scholar] [CrossRef]
- Bai, S.; Hu, A.; Hu, Y.; Ma, Y.; Obata, K.; Sugioka, K. Plasmonic superstructure arrays fabricated by laser near-field reduction for wide-range sers analysis of fluorescent materials. Nanomaterials 2022, 12, 970. [Google Scholar] [CrossRef]
- Su, D.; Yang, S.; Xiong, Y.; Yang, X.; Yu, X.; Zeng, P.; Wu, Y.; Cheng, Y.; Zhang, T.; Shen, H.; et al. Ordered Gold Nanocluster-Based Plasmonic Hotspot Arrays for SERS Detection of Single Molecules. ACS Appl. Nano Mater. 2022, 5, 17067–17077. [Google Scholar] [CrossRef]
- Pang, J.S.; Theodorou, I.G.; Centeno, A.; Petrov, P.K.; Alford, N.M.; Ryan, M.P.; Xie, F. Tunable Three-Dimensional Plasmonic Arrays for Large Near-Infrared Fluorescence Enhancement. ACS Appl. Mater. Interfaces 2019, 11, 23083–23092. [Google Scholar] [CrossRef]
- Saito, T.; Takahashi, S.; Obara, T.; Itabashi, N.; Imai, K. Platinum plasmonic nanostructure arrays for massively parallel single-molecule detection based on enhanced fluorescence measurements. Nanotechnology 2011, 22, 445708. [Google Scholar] [CrossRef]
- Mayerhöfer, T.G.; Popp, J. Periodic array-based substrates for surface-enhanced infrared spectrosco-py. Nanophotonics 2018, 7, 39–79. [Google Scholar] [CrossRef]
- Yang, X.; Sun, Z.; Low, T.; Hu, H.; Guo, X.; García de Abajo, F.J.; Avouris, P.; Dai, Q. Nanomaterial-based plasmon-enhanced infrared spectroscopy. Adv. Mater. 2018, 30, 1704896. [Google Scholar] [CrossRef]
- Piltan, S.; Sievenpiper, D. Plasmonic nano-arrays for enhanced photoemission and photodetection. J. Opt. Soc. Am. B 2018, 35, 208–213. [Google Scholar] [CrossRef]
- Fleischer, K.; Ualibek, O.; Verre, R.; Shvets, I.V. Formation of plasmonic nanoparticle arrays -rules and recipes for an ordered growth. Phys. Status Solidi (B) 2016, 253, 198–205. [Google Scholar] [CrossRef]
- Gao, B.; Arya, G.; Tao, A.R. Self-orienting nanocubes for the assembly of plasmonic nanojunctions. Nat. Nanotechnol. 2012, 7, 433–437. [Google Scholar] [CrossRef]
- Angioletti-Uberti, S. Theory, simulations and the design of functionalized nanoparticles for biomedical applications: A Soft Matter Perspective. npj Comput. Mater. 2017, 3, 48. [Google Scholar] [CrossRef]
- Lin, J.X.; Hu, H.W.; Luo, J.; Miao, L.; Yang, Z.H.; Chen, M.; Zhang, M.; Ou, J.Z. Micro/nanoarrays and their ap-plications in flexible sensors: A review. Mater. Today Nano 2022, 19, 100224. [Google Scholar] [CrossRef]
- Mühlig, S.; Cunningham, A.; Dintinger, J.; Scharf, T.; Bürgi, T.; Lederer, F.; Rockstuhl, C. Self-assembled plasmonic metamaterials. Nanophotonics 2013, 2, 211–240. [Google Scholar] [CrossRef]
- Conti, Y.; Passarelli, N.; Mendoza-Carreño, J.; Scarabelli, L.; Mihi, A. Colloidal Silver Nanoparticle Plasmonic Arrays for Versatile Lasing Architectures via Template-Assisted Self-Assembly. Adv. Opt. Mater. 2023, 2300983. [Google Scholar] [CrossRef]
- Rastogi, R.; Beggiato, M.; Adam, P.M.; Juodkazis, S.; Krishnamoorthy, S. Nanoplasmonic Arrays with High Spatial Resolutions, Quality, and Throughput for Quantitative Detection of Molecular Analytes. In Nanoplasmonics; IntechOpen: London, UK, 2019. [Google Scholar]
- Hwang, Y.; Ferhan, A.R.; Yoon, B.K.; Sut, T.N.; Jeon, W.-Y.; Koo, D.J.; Jackman, J.A.; Cho, N.-J. Surface engineering of plasmonic gold nanoisland platforms for high-sensitivity refractometric biosensing applications. Appl. Mater. Today 2022, 26, 101280. [Google Scholar] [CrossRef]
- Tay, L.-L.; Hulse, J. Self-Assembled Plasmonic Array Sensors for Cannabinoids. In Optical Sensors; Optica Publishing Group: Washington, DC, USA, 2022; p. SM4E-6. [Google Scholar]
- Ghosh, S.K.; Nath, S.; Kundu, S.; Esumi, K.; Pal, T. Solvent and Ligand Effects on the Localized Surface Plasmon Resonance (LSPR) of Gold Colloids. J. Phys. Chem. B 2004, 108, 13963–13971. [Google Scholar] [CrossRef]
- Templeton, A.C.; Pietron, J.J.; Murray, R.W.; Mulvaney, P. Solvent refractive index and core charge influences on the surface plasmon absorbance of alkanethiolate monolayer-protected gold clusters. J. Phys. Chem. B 2000, 104, 564–570. [Google Scholar] [CrossRef]
- Underwood, S.; Mulvaney, P. Effect of the Solution Refractive Index on the Color of Gold Colloids. Langmuir 1994, 10, 3427–3430. [Google Scholar] [CrossRef]
- Chu, K.C.; Chao, C.Y.; Chen, Y.F.; Wu, Y.C.; Chen, C.C. Electrically controlled surface plasmon resonance frequency of gold nanorods. Appl. Phys. Lett. 2006, 89, 2335812. [Google Scholar] [CrossRef]
- Evans, P.R.; Wurtz, G.A.; Hendren, W.R.; Atkinson, R.; Dickson, W.; Zayats, A.V.; Pollard, R.J. Electrically switchable nonreciprocal transmission of plasmonic nanorods with liquid crystal. Appl. Phys. Lett. 2007, 91, 043101. [Google Scholar] [CrossRef]
- Müller, J.; Sönnichsen, C.; von Poschinger, H.; von Plessen, G.; Klar, T.A.; Feldmann, J. Electrically controlled light scattering with single metal nanoparticles. Appl. Phys. Lett. 2002, 81, 171–173. [Google Scholar] [CrossRef]
- Khatua, S.; Chang, W.-S.; Swanglap, P.; Olson, J.; Link, S. Active Modulation of Nanorod Plasmons. Nano Lett. 2011, 11, 3797–3802. [Google Scholar] [CrossRef]
- Wang, Y. Voltage-induced color-selective absorption with surface plasmons. Appl. Phys. Lett. 1995, 67, 2759–2761. [Google Scholar] [CrossRef]
- Wang, Y.; Russell, S.D.; Shimabukuro, R.L. Voltage-induced broad-spectrum reflectivity change with sur-face-plasmon waves. Journal of applied physics 2005, 97, 023708. [Google Scholar] [CrossRef]
- Li, H.; Xu, S.; Gu, Y.; Wang, K.; Xu, W. Active modulation of wavelength and radiation direction of fluorescence via liquid crystal-tuned surface plasmons. Appl. Phys. Lett. 2013, 102, 051107. [Google Scholar] [CrossRef]
- Cetin, A.E.; Mertiri, A.; Huang, M.; Erramilli, S.; Altug, H. Thermal Tuning of Surface Plasmon Polaritons Using Liquid Crystals. Adv. Opt. Mater. 2013, 1, 915–920. [Google Scholar] [CrossRef]
- Dickson, W.; Wurtz, G.A.; Evans, P.R.; Pollard, R.J.; Zayats, A.V. Electronically controlled surface plasmon disper-sion and optical transmission through metallic hole arrays using liquid crystal. Nano Lett. 2008, 8, 281–286. [Google Scholar] [CrossRef]
- Dolan, J.A.; Cai, H.; Delalande, L.; Li, X.; Martinson, A.B.F.; de Pablo, J.J.; López, D.; Nealey, P.F. Broadband Liquid Crystal Tunable Metasurfaces in the Visible: Liquid Crystal Inhomogeneities Across the Metasurface Parameter Space. ACS Photonics 2021, 8, 567–575. [Google Scholar] [CrossRef]
- Decker, M.; Kremers, C.; Minovich, A.; Staude, I.; Miroshnichenko, A.E.; Chigrin, D.; Neshev, D.N.; Jagadish, C.; Kivshar, Y.S. Electro-optical switching by liquid-crystal controlled metasurfaces. Opt. Express 2013, 21, 8879–8885. [Google Scholar] [CrossRef]
- Zou, C.; Amaya, C.; Fasold, S.; Muravsky, A.A.; Murauski, A.A.; Pertsch, T.; Staude, I. Multiresponsive Dielectric Metasurfaces. ACS Photonics 2021, 8, 1775–1783. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Wróbel, J.; Kula, P. Ultrafast electrical switching of nanostructured metadevice with dual-frequency liquid crystal. Sci. Rep. 2019, 9, 20367. [Google Scholar] [CrossRef]
- Xiao, S.; Chettiar, U.K.; Kildishev, A.V.; Drachev, V.; Khoo, I.C.; Shalaev, V.M. Tunable magnetic response of metamaterials. Appl. Phys. Lett. 2009, 95, 033115. [Google Scholar] [CrossRef]
- Komar, A.; Fang, Z.; Bohn, J.; Sautter, J.; Decker, M.; Miroshnichenko, A.; Pertsch, T.; Brener, I.; Kivshar, Y.S.; Staude, I.; et al. Electrically tunable all-dielectric optical metasurfaces based on liquid crystals. Appl. Phys. Lett. 2017, 110, 071109. [Google Scholar] [CrossRef]
- Zou, C.; Komar, A.; Fasold, S.; Bohn, J.; Muravsky, A.A.; Murauski, A.A.; Pertsch, T.; Neshev, D.N.; Staude, I. Electrically Tunable Transparent Displays for Visible Light Based on Dielectric Metasurfaces. ACS Photonics 2019, 6, 1533–1540. [Google Scholar] [CrossRef]
- Sautter, J.; Staude, I.; Decker, M.; Rusak, E.; Neshev, D.N.; Brener, I.; Kivshar, Y.S. Active Tuning of All-Dielectric Metasurfaces. ACS Nano 2015, 9, 4308–4315. [Google Scholar] [CrossRef]
- Bohn, J.; Bucher, T.; Chong, K.E.; Komar, A.; Choi, D.-Y.; Neshev, D.N.; Kivshar, Y.S.; Pertsch, T.; Staude, I. Active Tuning of Spontaneous Emission by Mie-Resonant Dielectric Metasurfaces. Nano Lett. 2018, 18, 3461–3465. [Google Scholar] [CrossRef]
- Kossyrev, P.A.; Yin, A.; Cloutier, S.G.; Cardimona, D.A.; Huang, D.; Alsing, P.M.; Xu, J.M. Electric Field Tuning of Plasmonic Response of Nanodot Array in Liquid Crystal Matrix. Nano Lett. 2005, 5, 1978–1981. [Google Scholar] [CrossRef]
- Li, J.; Ma, Y.; Gu, Y.; Khoo, I.-C.; Gong, Q. Large spectral tunability of narrow geometric resonances of periodic arrays of metallic nanoparticles in a nematic liquid crystal. Appl. Phys. Lett. 2011, 98, 3592756. [Google Scholar] [CrossRef]
- Abass, A.; Rodriguez, S.R.-K.; Ako, T.; Aubert, T.; Verschuuren, M.; Van Thourhout, D.; Beeckman, J.; Hens, Z.; Rivas, J.G.; Maes, B. Active Liquid Crystal Tuning of Metallic Nanoantenna Enhanced Light Emission from Colloidal Quantum Dots. Nano Lett. 2014, 14, 5555–5560. [Google Scholar] [CrossRef]
- van Heijst, E.A.P.; ter Huurne, S.E.T.; Sol, J.A.H.P.; Castellanos, G.W.; Ramezani, M.; Murai, S.; Debije, M.G.; Rivas, J.G. Electric tuning and switching of the resonant response of nanoparticle arrays with liquid crystals. J. Appl. Phys. 2022, 131, 083101. [Google Scholar] [CrossRef]
- Dridi, M.; Vial, A. Modeling of metallic nanostructures embedded in liquid crystals: Application to the tuning of their plasmon resonance. Opt. Lett. 2009, 34, 2652–2654. [Google Scholar] [CrossRef]
- Ee, H.-S.; Agarwal, R. Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate. Nano Lett. 2016, 16, 2818–2823. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, Y.; Zheng, H.; Linares, A.E.; Ugwu, F.C.; Li, D.; Sun, H.-B.; Bai, B.; Valentine, J.G. Reconfigurable Metasurface for Image Processing. Nano Lett. 2021, 21, 8715–8722. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Yang, Y.; Bozhevolnyi, S.I. Dynamic Metasurfaces Using Phase-Change Chalcogenides. Adv. Opt. Mater. 2019, 7, 1801709. [Google Scholar] [CrossRef]
- Yao, Y.; Shankar, R.; Kats, M.A.; Song, Y.; Kong, J.; Loncar, M.; Capasso, F. Electrically Tunable Metasurface Perfect Absorbers for Ultrathin Mid-Infrared Optical Modulators. Nano Lett. 2014, 14, 6526–6532. [Google Scholar] [CrossRef]
- Huang, Y.-W.; Lee, H.W.H.; Sokhoyan, R.; Pala, R.A.; Thyagarajan, K.; Han, S.; Tsai, D.P.; Atwater, H.A. Gate-Tunable Conducting Oxide Metasurfaces. Nano Lett. 2016, 16, 5319–5325. [Google Scholar] [CrossRef]
- Borah, R.; Ninakanti, R.; Bals, S.; Verbruggen, S.W. Plasmon resonance of gold and silver nanoparticle arrays in the Kretschmann (attenuated total reflectance) vs. direct incidence configuration. Sci. Rep. 2022, 12, 15738. [Google Scholar] [CrossRef]
- Borah, R.; Smets, J.; Ninakanti, R.; Tietze, M.L.; Ameloot, R.; Chigrin, D.N.; Bals, S.; Lenaerts, S.; Verbruggen, S.W. Self-Assembled Ligand-Capped Plasmonic Au Nanoparticle Films in the Kretschmann Configuration for Sensing of Volatile Organic Compounds. ACS Appl. Nano Mater. 2022, 5, 11494–11505. [Google Scholar] [CrossRef]
- Johnson, P.B.; Christy, R.W. Optical Constants of the Noble Metals. Phys. Rev. B 1972, 6, 4370. [Google Scholar] [CrossRef]
- Arakawa, Y.; Kang, S.; Tsuji, H.; Watanabe, J.; Konishi, G.-I. The design of liquid crystalline bistolane-based materials with extremely high birefringence. RSC Adv. 2016, 6, 92845–92851. [Google Scholar] [CrossRef]
- Dąbrowski, R.; Kula, P.; Herman, J. High Birefringence Liquid Crystals. Crystals 2013, 3, 443–482. [Google Scholar] [CrossRef]
- Palermo, G.; Cataldi, U.; De Sio, L.; Bürgi, T.; Tabiryan, N.; Umeton, C. Optical control of plasmonic heating effects using reversible photo-alignment of nematic liquid crystals. Appl. Phys. Lett. 2016, 109, 191906. [Google Scholar] [CrossRef]
- Yaroshchuk, O.; Reznikov, Y. Photoalignment of liquid crystals: Basics and current trends. J. Mater. Chem. 2012, 22, 286–300. [Google Scholar] [CrossRef]
- Hirankittiwong, P.; Chattham, N.; Limtrakul, J.; Haba, O.; Yonetake, K.; Eremin, A.; Stannarius, R.; Takezoe, H. Optical manipulation of the nematic director field around microspheres covered with an azo-dendrimer monolayer. Opt. Express 2014, 22, 20087–20093. [Google Scholar] [CrossRef] [PubMed]
- Kolwas, K.; Derkachova, A. Impact of the Interband Transitions in Gold and Silver on the Dynamics of Propagating and Localized Surface Plasmons. Nanomaterials 2020, 10, 1411. [Google Scholar] [CrossRef] [PubMed]
- Abdulhalim, I. Liquid crystal active nanophotonics and plasmonics: From science to devices. J. Nanophotonics 2012, 6, 061001. [Google Scholar] [CrossRef]
- Alabastri, A.; Tuccio, S.; Giugni, A.; Toma, A.; Liberale, C.; Das, G.; De Angelis, F.; Di Fabrizio, E.; Zaccaria, R.P. Molding of Plasmonic Resonances in Metallic Nanostructures: Dependence of the Non-Linear Electric Permittivity on System Size and Temperature. Materials 2013, 6, 4879–4910. [Google Scholar] [CrossRef]
- Yang, H.U.; D’Archangel, J.; Sundheimer, M.L.; Tucker, E.; Boreman, G.D.; Raschke, M.B. Optical dielectric function of silver. Phys. Rev. B 2015, 91, 235137. [Google Scholar] [CrossRef]
- Abdulhalim, I. Surface plasmon TE and TM waves at the anisotropic film–metal interface. J. Opt. A: Pure Appl. Opt. 2008, 11, 015002. [Google Scholar] [CrossRef]
- Abdulhalim, I. Coupling configurations between extended surface electromagnetic waves and localized surface plas-mons for ultrahigh field enhancement. Nanophotonics 2018, 7, 1891–1916. [Google Scholar] [CrossRef]
- Li, A.; Isaacs, S.; Abdulhalim, I.; Li, S. Ultrahigh Enhancement of Electromagnetic Fields by Exciting Localized with Extended Surface Plasmons. J. Phys. Chem. C 2015, 119, 19382–19389. [Google Scholar] [CrossRef]
- Li, A.; Srivastava, S.K.; Abdulhalim, I.; Li, S. Engineering the hot spots in squared arrays of gold nanoparticles on a silver film. Nanoscale 2016, 8, 15658–15664. [Google Scholar] [CrossRef] [PubMed]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yakovkin, I.; Reshetnyak, V. Controlling Plasmon Resonance of Gold and Silver Nanoparticle Arrays with Help of Liquid Crystal. Photonics 2023, 10, 1088. https://doi.org/10.3390/photonics10101088
Yakovkin I, Reshetnyak V. Controlling Plasmon Resonance of Gold and Silver Nanoparticle Arrays with Help of Liquid Crystal. Photonics. 2023; 10(10):1088. https://doi.org/10.3390/photonics10101088
Chicago/Turabian StyleYakovkin, Ivan, and Victor Reshetnyak. 2023. "Controlling Plasmon Resonance of Gold and Silver Nanoparticle Arrays with Help of Liquid Crystal" Photonics 10, no. 10: 1088. https://doi.org/10.3390/photonics10101088




