Simulation Analysis of an Atmospheric Turbulence Wavefront Measurement System
Abstract
:1. Introduction
2. Methodology
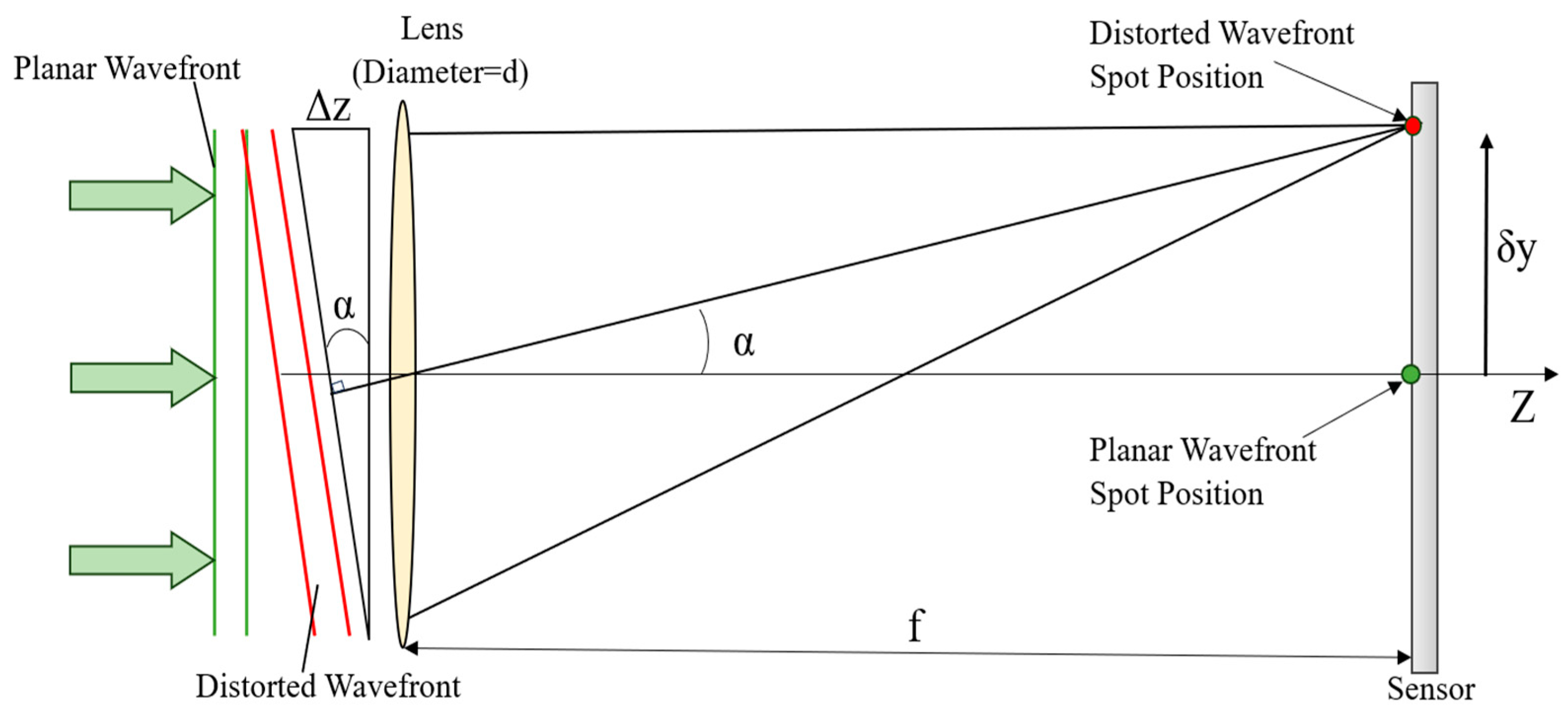
2.1. Wavefront Generation
2.2. Wavefront Reconstruction Algorithm
2.3. Evaluation Method of Wavefront Reconstruction Accuracy
3. Numerical Simulation Conditions
3.1. Simulation System Parameters
3.2. Lens Array Arrangement
4. Results and Discussion
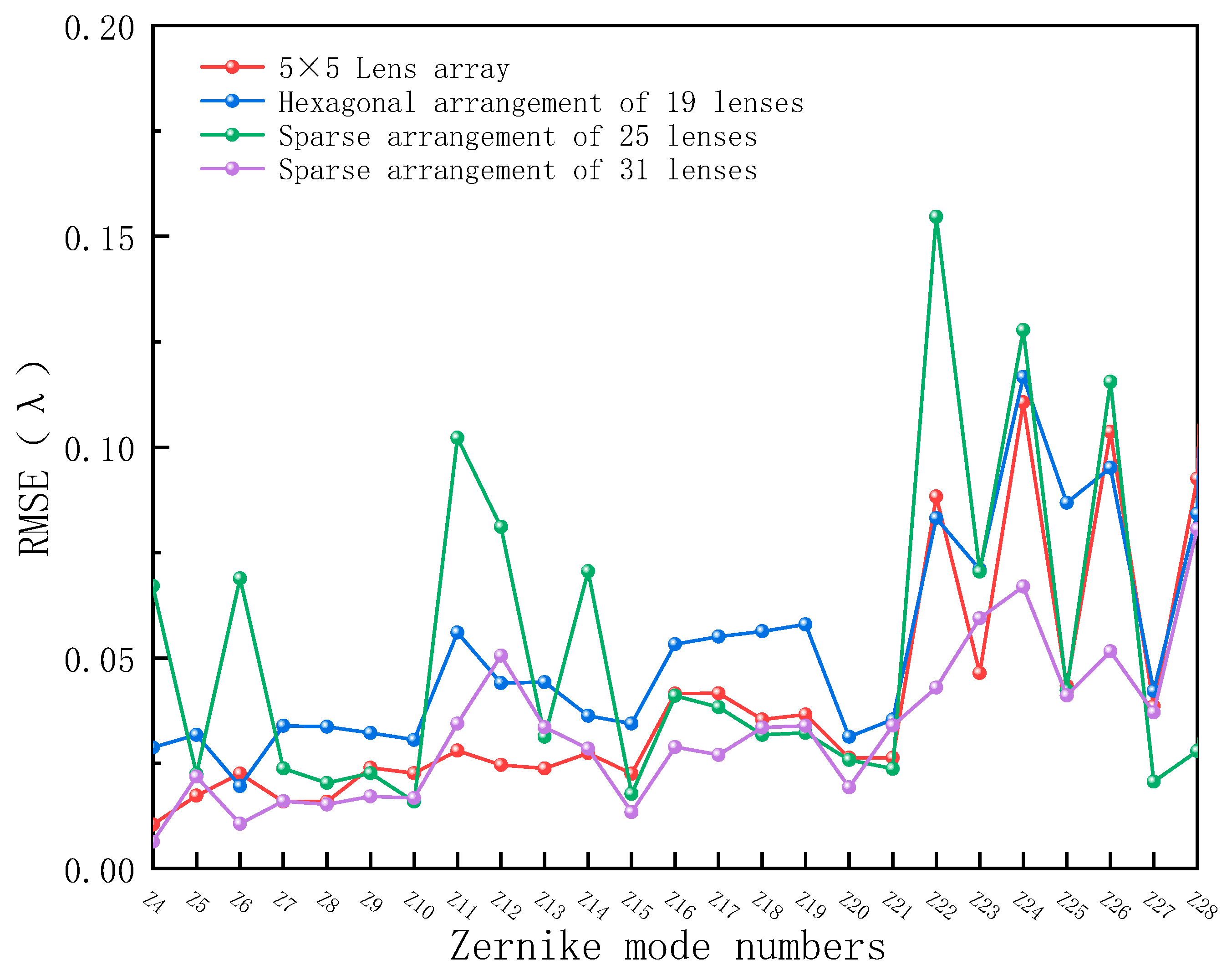
4.1. Single Aberration Analysis
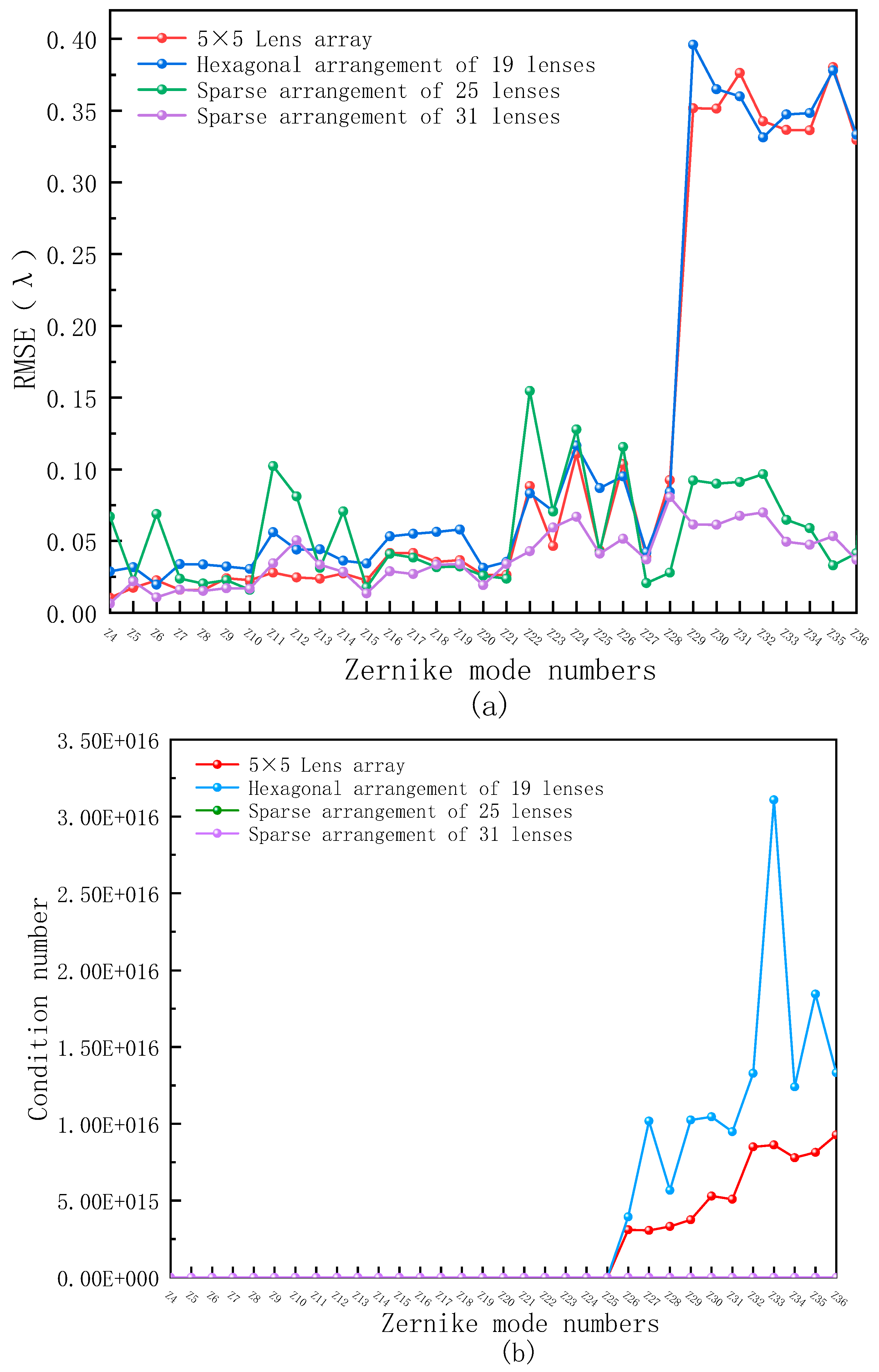
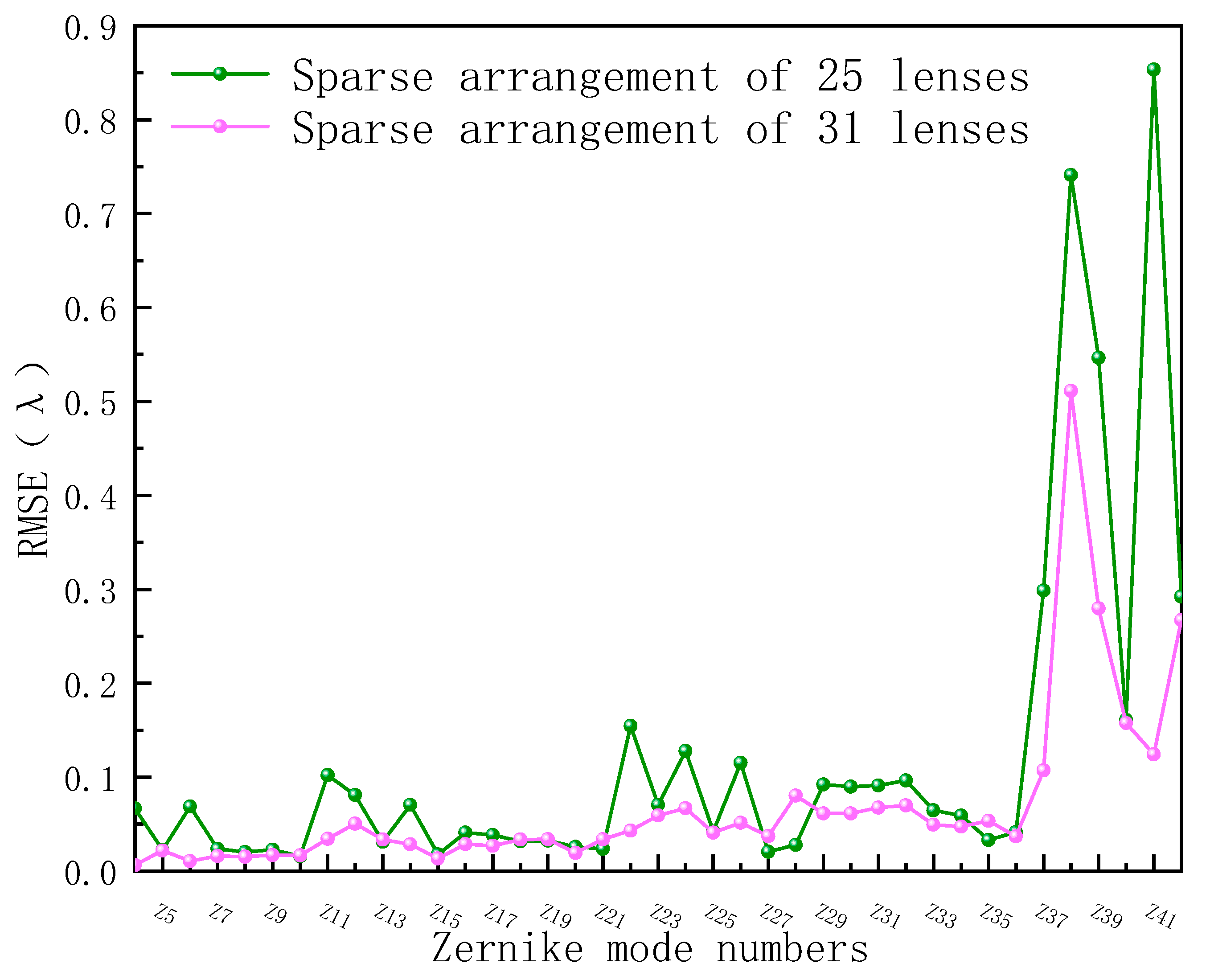
4.2. Maximum Recognizable Mode Order of the System
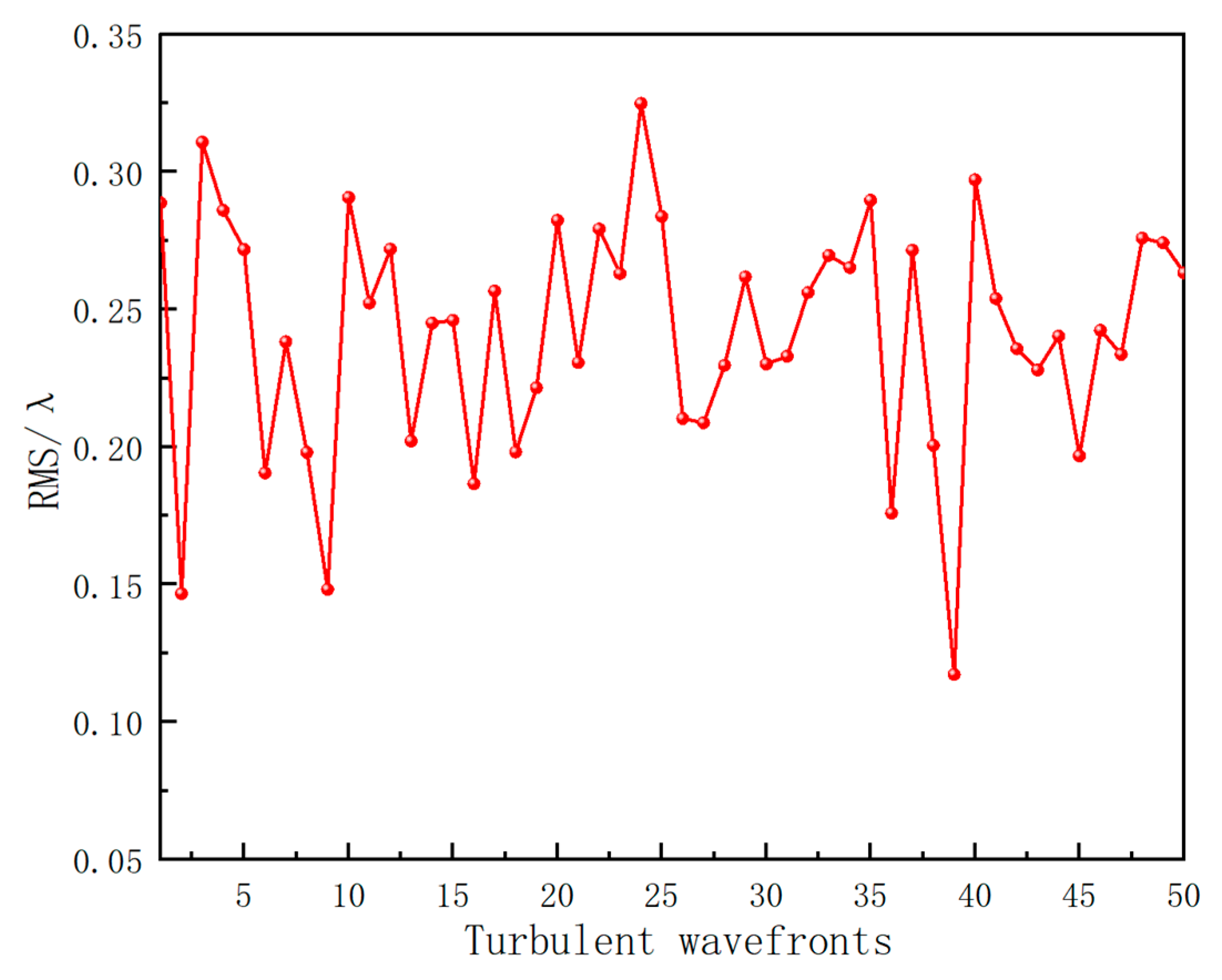
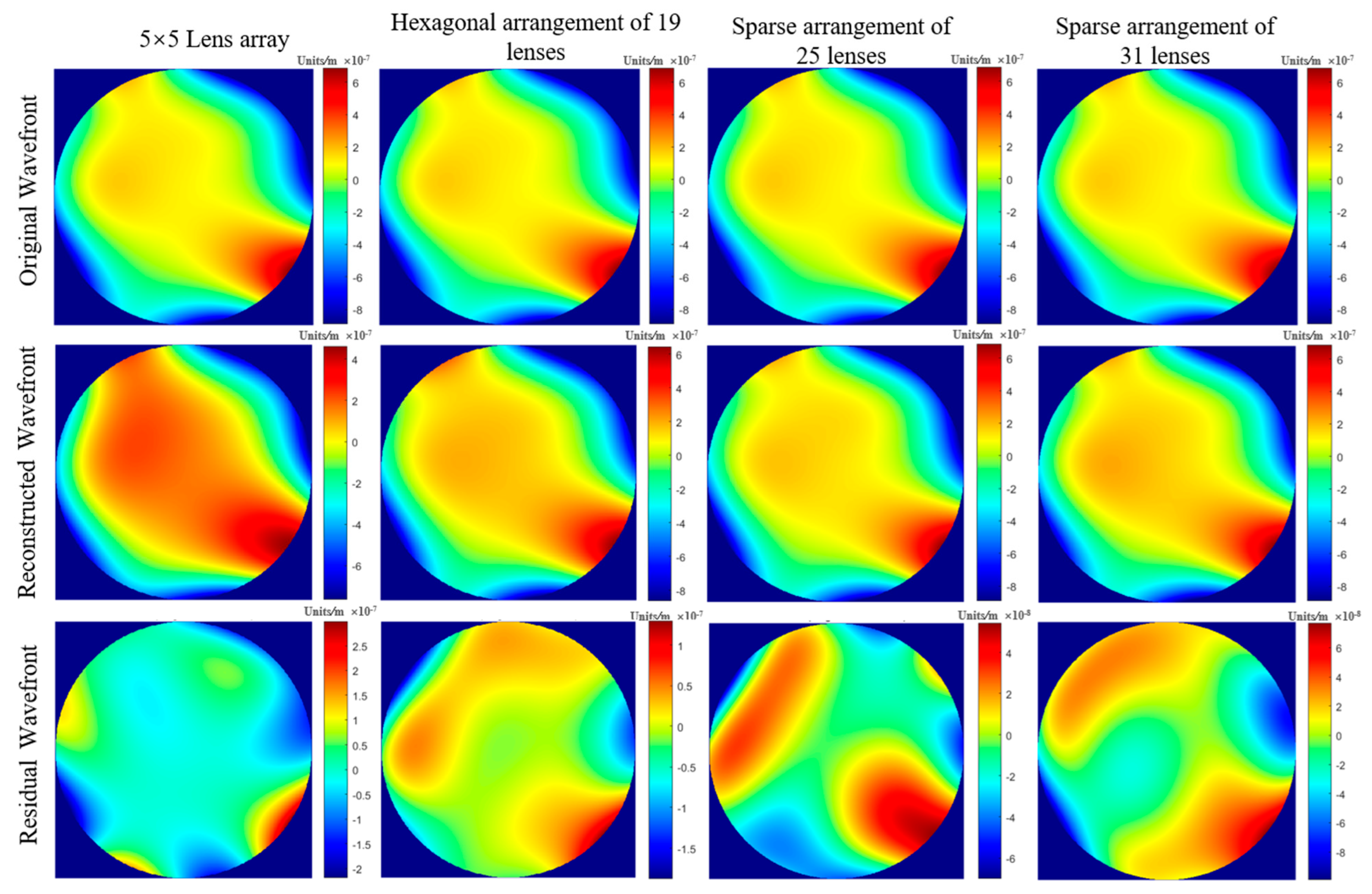
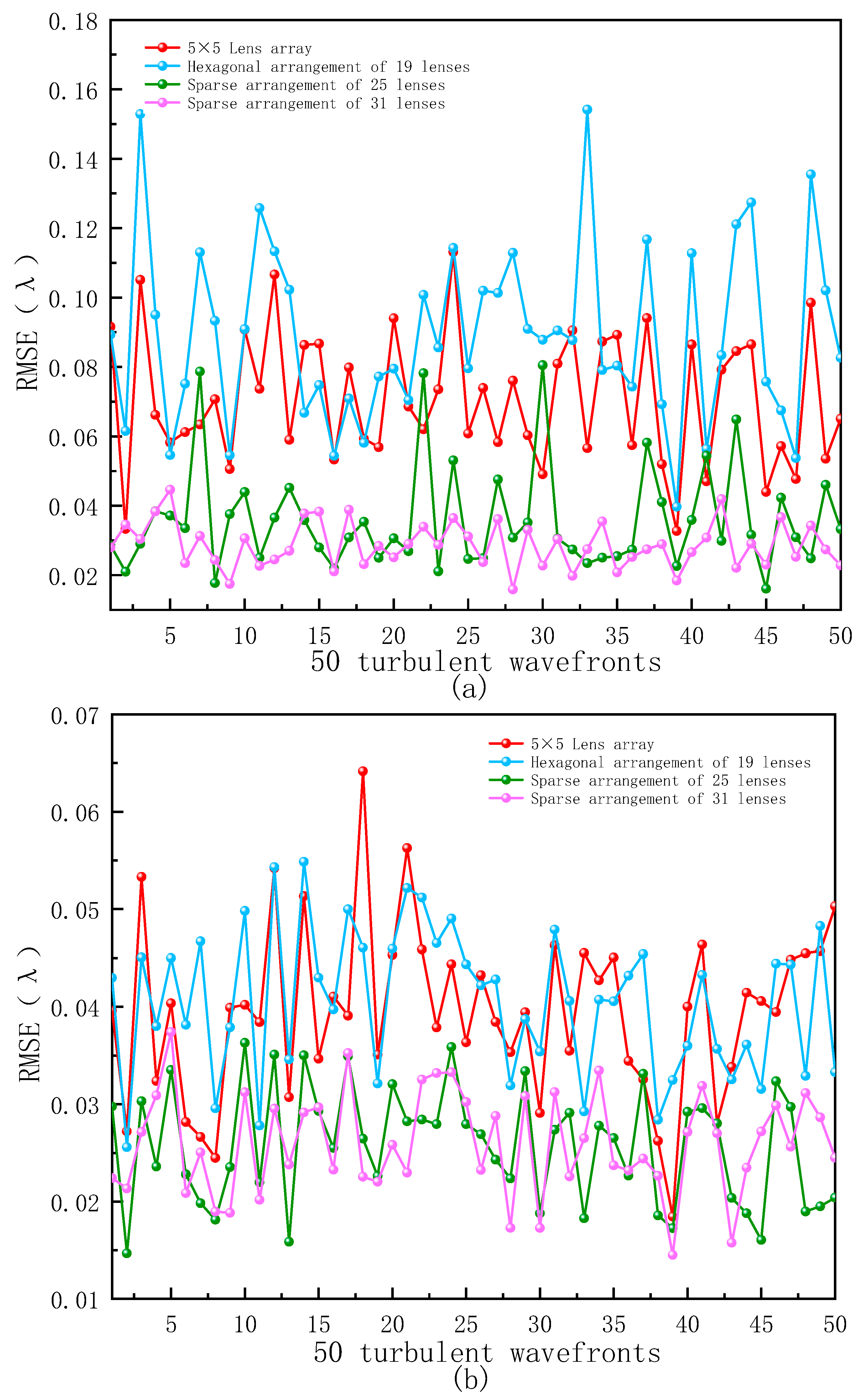
4.3. Turbulent Wavefront Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lukin, V.P.; Bol’basova, L.A.; Nosov, V.V. Comparison of Kolmogorov’s and coherent turbulence. Appl. Opt. 2014, 53, B231–B236. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.; Guo, H.; Yu, S.; Luo, B. Spreading and direction of Gaussian–Schell model beam through a non-Kolmogorov turbulence. Opt. Lett. 2010, 35, 715–717. [Google Scholar] [CrossRef]
- Cheng, Z.; He, L.; Zhang, X.; Mu, C.; Tan, M. Autocorrected preconditioning regularization inversion algorithm for an atmospheric turbulence profile. Appl. Opt. 2020, 59, 8773–8788. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Liu, X.; Cai, Y.; Ponomarenko, S.A.; Liang, C. Structurally stable beams in the turbulent atmosphere: Dark and antidark beams on incoherent background [Invited]. J. Opt. Soc. Am. A 2022, 39, C51–C57. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.D.; Xue, C.; Liu, X.Y.; Wang, J.L.; Wei, P.F. Current status and research development of wavefront correctors for adaptive optics. Chin. Opt. 2012, 5, 337–351. [Google Scholar]
- Davis, J.I. Consideration of Atmospheric Turbulence in Laser Systems Design. Appl. Opt. 1966, 5, 139–147. [Google Scholar] [CrossRef] [PubMed]
- Liou, K.N.; Ou, S.-C.; Takano, Y.; Cetola, J. Remote sensing of three-dimensional cirrus clouds from satellites: Application to continuous-wave laser atmospheric transmission and backscattering. Appl. Opt. 2006, 45, 6849–6859. [Google Scholar] [CrossRef] [PubMed]
- Liang, X.; Zhong, M.; Xu, T.; Xiao, J.; Jiao, K.; Wang, X.; Bin, Y.; Liu, J.; Wang, X.; Zhao, Z.; et al. Mid-Infrared Single-Mode Ge-As-S Fiber for High Power Laser Delivery. J. Lightwave Technol. 2022, 40, 2151–2156. [Google Scholar] [CrossRef]
- Bolbasova, L.A.; Gritsuta, A.N.; Kopylov, E.A.; Lavrinov, V.V.; Lukin, V.P.; Selin, A.A.; Soin, E.L. Atmospheric turbulence meter based on a Shack–Hartmann wavefront sensor. J. Opt. Technol. 2019, 86, 426–430. [Google Scholar] [CrossRef]
- McCrae, J.E.; Bose-Pillai, S.; Current, M.; Lee, K.; Fiorino, S. Analysis of Turbulence Anisotropy with a Hartmann Sensor. In Proceeding of the Imaging and Applied Optics 2017, Beijing, China, 4–6 June 2017. [Google Scholar]
- Anzuola, E.; Zepp, A.; Marin, P.; Gladysz, S.; Stein, K. Holographic Wavefront Sensing for Atmospheric Turbulence using Karhunen-Loève Decomposition. In Proceeding of the Imaging and Applied Optics 2016, Heidelberg, Germany, 25–28 July 2016. [Google Scholar]
- Conan, R. Random generation of the turbulence slopes of a Shack–Hartmann wavefront sensor. Opt. Lett. 2014, 39, 1390–1393. [Google Scholar] [CrossRef] [PubMed]
- Griffiths, R.; Osborn, J.; Farley, O.; Butterley, T.; Townson, M.J.; Wilson, R. Demonstrating 24-h continuous vertical monitoring of atmospheric optical turbulence. Opt. Express 2023, 31, 6730–6740. [Google Scholar] [CrossRef]
- Silbaugh, E.E.; Welsh, B.M.; Roggemann, M.C. Characterization of atmospheric turbulence phase statistics using wave-front slope measurements. J. Opt. Soc. Am. A 1996, 13, 2453–2460. [Google Scholar] [CrossRef]
- Joo, J.Y.; Han, S.G.; Lee, J.H.; Rhee, H.-G.; Huh, J.; Lee, K.; Park, S.Y. Development and Characterization of an Atmospheric Turbulence Simulator Using Two Rotating Phase Plates. Curr. Opt. Photon. 2022, 6, 445–452. [Google Scholar]
- Nelson, D.H.; Walters, D.L.; MacKerrow, E.P.; Schmitt, M.J.; Quick, C.R.; Porch, W.M.; Petrin, R.R. Wave optics simulation of atmospheric turbulence and reflective speckle effects in CO2 lidar. Appl. Opt. 2000, 39, 1857–1871. [Google Scholar] [CrossRef] [PubMed]
- Lukin, V.P. Models and measurements of atmospheric turbulence characteristics and their impact on AO design. In Proceeding of the Adaptive Optics 1996, Maui, HI, USA, 8–12 July 1996. [Google Scholar]
- Caldwell, E.D.; Swann, W.C.; Ellis, J.L.; Bodine, M.I.; Mak, C.; Kuczun, N.; Newbury, N.R.; Sinclair, L.C.; Muschinski, A.; Rieker, G.B. Optical timing jitter due to atmospheric turbulence: Comparison of frequency comb measurements to predictions from micrometeorological sensors. Opt. Express 2020, 28, 26661–26675. [Google Scholar] [CrossRef] [PubMed]
- Bol’basova, L.A.; Lukin, V.P. Issues of wavefront tilt measurement. J. Opt. Technol. 2021, 88, 625–629. [Google Scholar] [CrossRef]
- Van Zandt, N.R.; Spencer, M.F.; Fiorino, S.T. Speckle mitigation for wavefront sensing in the presence of weak turbulence. Appl. Opt. 2019, 58, 2300–2310. [Google Scholar] [CrossRef]
- Wei, P.; Li, X.Y.; Luo, X.; Li, J.F. Design and Verification of Digital Simulation Platform for Shack-Hartmann Wavefront Sensors. Chin. J. Lasers 2021, 48, 141–150. [Google Scholar]
- Dai, G.M. Modal compensation of atmospheric turbulence with the use of Zernike polynomials and Karhunen–Loève functions. J. Opt. Soc. Am. A 1995, 12, 2182–2193. [Google Scholar] [CrossRef]
- Zepp, A.; Gladysz, S.; Stein, K.; Osten, W. Optimization of the holographic wavefront sensor for open-loop adaptive optics under realistic turbulence. Part I: Simulations. Appl. Opt. 2021, 60, F88–F98. [Google Scholar] [CrossRef] [PubMed]
- Dai, G.M. Modal wave-front reconstruction with Zernike polynomials and Karhunen–Loève functions. J. Opt. Soc. Am. A 1996, 13, 1218–1225. [Google Scholar] [CrossRef]
- Noll, R.J. Zernike polynomials and atmospheric turbulence. J. Opt. Soc. Am. 1976, 66, 207–211. [Google Scholar] [CrossRef]
- Roddier, N. Atmospheric wavefront simulation using zernike polynomials. Opt. Eng. 1990, 29, 1174–1180. [Google Scholar] [CrossRef]
- Lukin, V.P.; Nosov, E.V.; Nosov, V.V.; Torgaev, A.V. Causes of non-Kolmogorov turbulence in the atmosphere. Appl. Opt. 2016, 55, B163–B168. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.Y.; Hou, Z.H.; Qin, L.A.; Jing, X.; Wu, Y. Simulation Analysis of a Wavefront Reconstruction of a Large Aperture Laser Beam. Sensors 2023, 23, 623. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Jiang, W.H.; Xu, B. Reconstruction of Turbulent Optical Wavefront Realized by Zernike Polynomial. Opto-Electron. Eng. 1998, 25, 15–19. [Google Scholar]
- Li, J.; Liu, J.; Liu, D.; Tian, W.; Jin, S.; Hu, S.; Guo, J.; Jin, Y. Ultrafast Random Number Generation Based on Random Laser. J. Lightwave Technol. 2023, 41, 5233–5243. [Google Scholar] [CrossRef]
- Twietmeyer, K.; Chipman, R. Condition Number as a Metric for the Effectiveness of Polarimetric Algorithms. In Proceeding of the Frontiers in Optics 2005, San Jose, CA, USA, 18–22 October 2015. [Google Scholar]
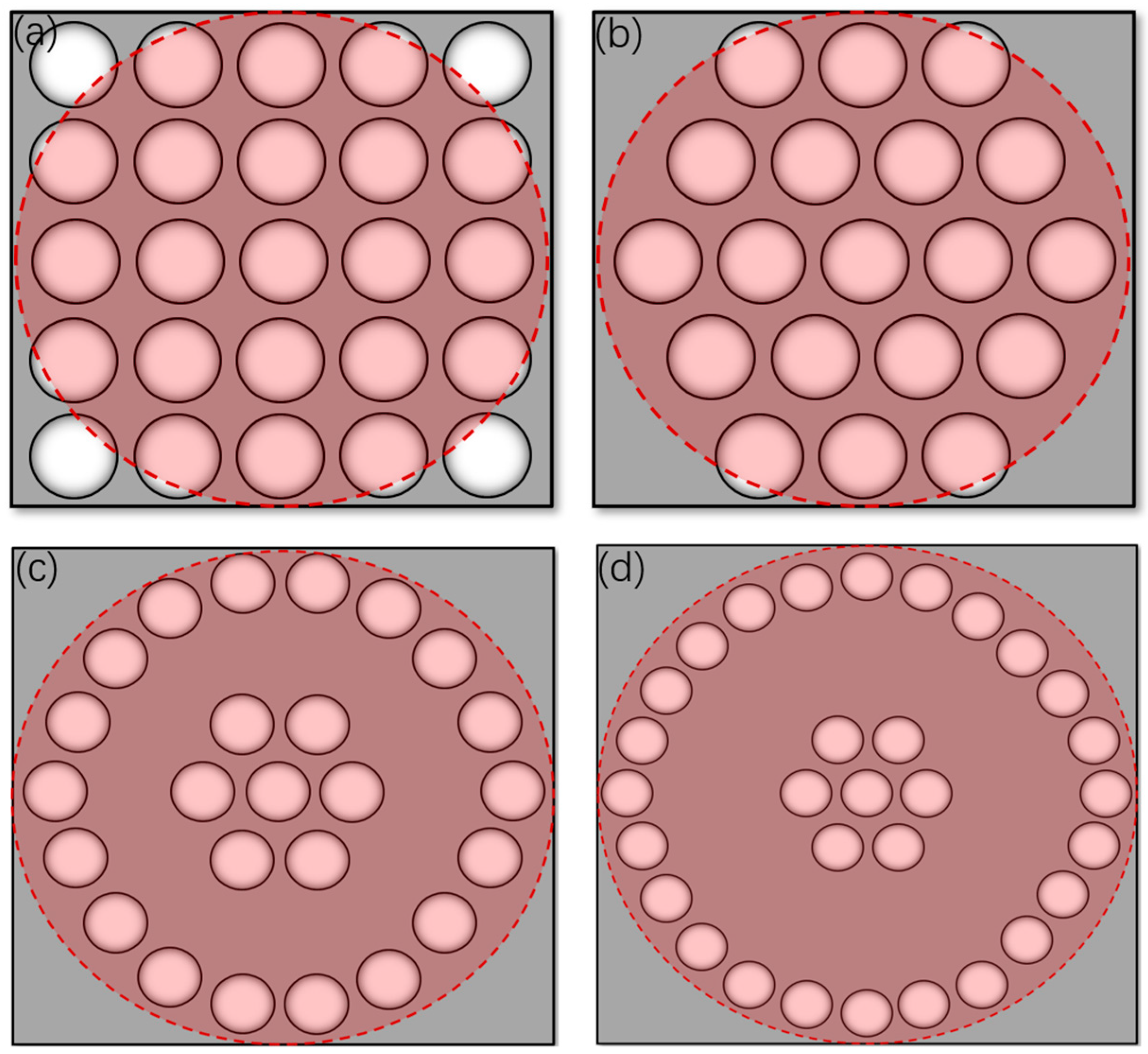

| Parameter | Description |
|---|---|
| Pixel size/μm | 4.5 |
| Beam wavelength/nm | 1064 |
| Lens size/mm | 25.4 |
| Lens spacing/mm | 6.35 |
| Duty factor | 0.8 |
| Lens focal length/mm | 1200 |
| Quantity | Mean | Standard Deviation | Variance | |
|---|---|---|---|---|
| 5 × 5 Lens array | 25 | 0.03944 | 0.02821 | 7.96036 × 10−4 |
| Hexagonal arrangement of 19 lenses | 25 | 0.05175 | 0.02475 | 6.12562 × 10−4 |
| 25 Units sparsely arranged | 25 | 0.05184 | 0.03849 | 0.00148 |
| 31 Units sparsely arranged | 25 | 0.03282 | 0.01831 | 3.35307 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Qin, L.; Li, Y.; Cheng, Y.; Jing, X.; Chen, G.; Hou, Z. Simulation Analysis of an Atmospheric Turbulence Wavefront Measurement System. Photonics 2024, 11, 383. https://doi.org/10.3390/photonics11040383
Wang G, Qin L, Li Y, Cheng Y, Jing X, Chen G, Hou Z. Simulation Analysis of an Atmospheric Turbulence Wavefront Measurement System. Photonics. 2024; 11(4):383. https://doi.org/10.3390/photonics11040383
Chicago/Turabian StyleWang, Gangyu, Laian Qin, Yang Li, Yilun Cheng, Xu Jing, Gongye Chen, and Zaihong Hou. 2024. "Simulation Analysis of an Atmospheric Turbulence Wavefront Measurement System" Photonics 11, no. 4: 383. https://doi.org/10.3390/photonics11040383





