Abstract
The structural, electronic, and magnetochemical properties of the star-shaped polyoxopalladate [Pd15O10(SeO3)10]10− (POPd) and its lanthanide-functionalized derivatives have been investigated on the basis of density functional theory, followed by a ligand field analysis using the Radial Effective Charge (REC) model. Our study predicts that heteroPOPd is a robust cryptand that enforces D5h symmetry around the encapsulated Ln3+ centers. This rigid coordination environment favors an interesting potential magnetic behavior in the Er and Ho derivatives, and the presence of a cavity in the structure suggests an effective insulation of the electronic system from the lattice phonons, which may be of interest for molecular spintronics and quantum computing applications.
1. Introduction
Quantum computing is an emerging area of research based on the explicit use of quantum-mechanical phenomena to implement logic operations for the purposes of highly efficient information and communication technologies. In contrast to conventional computers which store information in one of the two definite states ‘0’ or ‘1’, the basic units of a quantum computer are quantum bits (qubits), which can be a superposition of the basis states. Within this new paradigm, magnetic molecules are quantum two-level systems that have been proposed as promising candidates to build up quantum computers [1,2,3,4,5,6]. In this regard, magnetic molecules exhibit remarkable structural and chemical versatility, tunable physicochemical properties, and inherent scalability, considering the enormous opportunities of (self-)organization [7]. Although the current prospects for their technological implementation remain elusive due to challenges such as loss of quantum coherence [8], a series of recent breakthroughs in the field have been encouraging [9,10,11,12,13,14].
In this context, polyoxometalate (POM) chemistry has shown some advantageous chemical, structural, and electronic features such as robustness, highly symmetrical encapsulating environments, and absence of nuclear spins around the magnetic ion [15]. Indeed, lanthanide-based polyoxometalates (POMs) are among the first examples of single-ion magnets (SIMs) [16] and have also contributed significantly to the field of molecular spin qubits [17,18]. Some relevant examples in molecular magnetism include two families of lanthanide-containing polyoxomolybdates [19] and the cube-shaped polyoxopalladates (POPds) [20].
In this work, we focus on a different series of lanthanide-containing POPds as model systems with the aim to rationally design new molecular nanomagnets. The theoretical investigation we present herein is based on the polynuclear star-shaped heteoropoly-15-palladate(II) polyanion [Pd15Se10O40]10− (1) (Figure 1a) [21,22]. This negatively charged nanocluster is the selenite analogue of the star-shaped polyanion of general formula [Pd15O10(PO4)10]20− reported in 2009 [23] and belongs to the family of non-classical late transition metal-based POMs (Ni, Cu, Pd, Pt, and Au) [24,25,26,27,28]. The chemical structure of 1 presents an internal cavity defined by oxo ligands positioned at the vertices of a virtual pentagonal prism that is suitable for encapsulation of metal cations and water molecules (Figure 1b) [21,22,23,29,30]. Among the other available phosphate- or phenyl arsenate-capped polyanions [23,29,30], we decided to study 1 because it contains the lowest number of atoms and a relatively low negative charge, while retaining the high overall D5h symmetry. Using density functional theory (DFT), we initially explore the diamagnetic [NaPd15Se10O40]9− (1-Na) POPd system and we find a suitable level of theory that can accurately estimate the geometry of the inner cavity. As a second step, we calculate and discuss the structural and electronic properties of three lanthanide-encapsulating model systems with general formula [LnPd15Se10O40]7−, where Ln = La(1-La), Gd(1-Gd) and Lu(1-Lu). Finally, we use the optimized molecular geometry of the Gd3+ derivative to explore the spin energy levels and ground doublet composition of the Tb3+(1-Tb), Dy3+(1-Dy), Ho3+(1-Ho), and Er3+(1-Er) derivatives. Our approach provides a general protocol based on the former two steps, i.e., DFT calculations followed by a ligand field analysis, for the inexpensive estimation of the potential of coordination complexes as molecular nanomagnets and spin qubits prior to beginning the experimental work.
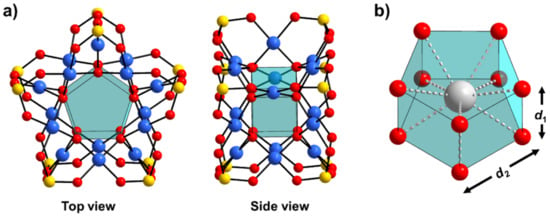
Figure 1.
Combined polyhedral and ball-and-stick representation polyanion 1 (a) with detail of the inner cavity suitable for encapsulation of metal cations (b). The assigned d1 and d2 refer to interatomic O∙∙∙O distances that define the size of the inner cavity (vide infra). Color code: Se = yellow, Pd = blue, O = red, and Na/Ln = grey spheres. {O10}/{MO10} = cyan transparent polyhedra.
2. Results and Discussion
2.1. Structural and Electronic Properties
The structural and electronic properties of 1, 1-Na, 1-La, 1-Gd, and 1-Lu were investigated by means of relativistic density functional theory (DFT) as implemented in the ADF code (ADF 2017, SCM, Theoretical Chemistry, Vrije Univesity, Amsterdam, The Netherlands) [31]. The geometry of 1-Na in water was followed at different theoretical levels (Table S1) that have been successfully used previously for an accurate estimation of the structure of noble metal-based POMs [32,33,34,35]. Considering that for the ligand field analysis it is more essential to have geometries that primarily provide an accurate estimation of positions of the oxo ligands that coordinate to the encapsulated lanthanide centers, we have found that geometry optimization calculations of the model system 1-Na at BP86/TZ2P/ZSC/COSMO-water level provide the most accurate approximation of the coordination environment around the Na+ center, while the Pd–O and Se–O bonds are also well approximated (see Table S1). Subsequently, polyanions 1, 1-La, 1-Gd, and 1-Lu were optimized at this level as well. To confirm energy minima, vibrational analysis was performed at the same theoretical level (Figure S4). All insights on the electronic structure and bonding energies are discussed based on single-point calculation performed at (U)B3LYP/TZ2P/ZSC/COSMO-water level (see Supplementary Materials).
Our calculations show that polyanions 1, 1-Na, 1-La, 1-Gd, and 1-Lu exhibit very narrow Se–O, Pd–O(Pd), Pd–O(Se) bond lengths in the ranges of 1.731–1.733 Å, 1.994–2.008 Å, and 2.058–2.092 Å, respectively (Table S2). The interatomic distances d1(O∙∙∙O) and d2(O∙∙∙O) that define the internal pentagonal cavity (Figure 1b) are found in the range of 2.646–2.701 Å and 2574–2672 Å, respectively. The changes induced by encapsulation of the different cations are in the range of <0.1 Å, which implies that the internal cavities are generally unaffected by the encapsulation. The calculated Ln–O bonds/distances are in the range of 2.559–2.644 Å, which are characteristic for lanthanide-containing POM systems [16,17,18,19,20].
The optimized systems 1-La, 1-Gd, and 1-Lu exhibit a gap energy of ca 3.5–3.6 eV between the highest occupied and the lowest unoccupied molecular orbital (i.e., HOMO and LUMO). The high gap energy is comparable to that of the reported polyanions 1 (3.4 eV) and 1-Na (3.5 eV), which substantiates that the proposed lanthanide-encapsulating systems exhibit significant intrinsic stability making them promising candidates for future preparation (see Table S4). The HOMO in systems 1-La, 1-Gd, and 1-Lu is doubly degenerate and is composed of Pd-centered - and -type orbitals and O-centered p-type orbitals (Figure 2a). The LUMO in 1-La, 1-Gd, and 1-Lu is also doubly degenerate and populates mainly O and Pd centers but also minorly Se4+ and Ln3+ centers (Figure 2a). The antibonding LUMO exhibits nodes between the Pd-centered -type orbitals and O-centered p-type orbitals, suggesting that population of this molecular orbital (e.g., via electrochemical reduction) can destabilize these bonds. The transition between the HOMO to LUMO corresponds predominantly to d–d transitions accompanied by metal-to-ligand charge transfer (Pd → O) (Table S5).
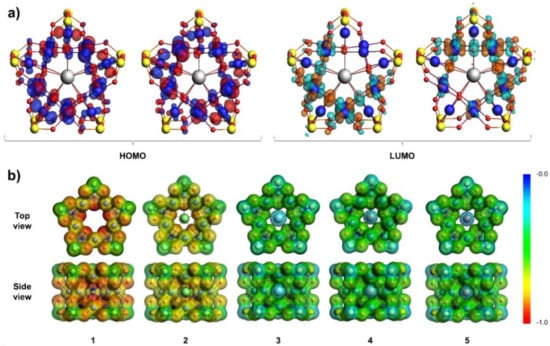
Figure 2.
(a) The doubly degenerate highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of 1-La which is also representative for 1-Gd and 1-Lu; (b) molecular electrostatic potential plotted over the density isosurface of polyanions 1–5. The most negative potentials are colored in red. All calculations are performed at (U)B3LYP/TZ2P/ZSC/COSMO-water level. Color code: Se = yellow, Pd = blue, O = red, and Ln = grey spheres.
In our view, polyanions 3–9 can be potentially prepared in a two-step approach, where polyanions 1 or 2 serve as precursors and are reacted with the lanthanide trications to yield [LnPd15Se10O40]7−, either by direct encapsulation or by Na+ cation exchange. Some aspects of the DFT calculations substantiate this opportunity. First, polyanions 1 and 1-Na exhibit pentagonal entrance defined by five oxo ligands that is comparable in size to that of the Preyssler-type polyoxoanions, (Figure S1) which is well-known to permeate lanthanide cations [16]. The inscribed virtual radius of the pentagonal entrance in 1 is ca. 1.79 Å, which is significantly larger than the effective ionic radius of the bare lanthanide trications [36]. Second, Mulliken charge analysis (Table S3) and molecular electrostatic potential (Figure 2b) of 1 show that the inner oxygen atoms defining the inner cavity are highly negatively charged and thus very nucleophilic. The high nucleophilicity of the inner cavity is the driving force for encapsulation of Na+, showing favorable binding energies of −201.2 kcal/mol, which is in line with the experimental evidence [21]. In contrast, the lanthanide trications show more negative binding energies which increase along the lanthanide series (La3+ = −983.9 kcal/mol, Gd3+ = −1031.1 kcal/mol, and Lu3+ = −1060.6 kcal/mol).
2.2. Ligand Field Analysis
Starting from the DFT-relaxed structure of the 1-Gd, we have applied the Radial Effective Charge (REC) model [37] using the SIMPRE computational package [38] to the 1-Tb, 1-Dy, 1-Ho, and 1-Er derivatives. This parametric model introduces covalency effects by placing an effective charge at an effective distance determined by a radial displacement Dr (see Section Five of Supplementary Materials for details). One of its main advantages is that, for similar families of homoleptic coordination complexes, such parameters are reusable, allowing an inexpensive determination of the spectroscopic and magnetic properties [39]. Thus, we have taken advantage of the semi-empirical information of the recently reported [LnPd12(AsPh)8O32]5− series [20] to provide an estimation of the ligand field splitting of the ground-J multiple as well as the ground state composition of each derivative. As the coordination number in these two families of POPds is different, 8 in the case of [LnPd12(AsPh)8O32]5− and 10 in [LnPd15Se10O40]7− and we do not have access to the X-ray structures, we have explored different possibilities for the REC parameters, always keeping constant the total f = Dr·Zi product [40]. The scanning of the REC parameters at different levels of covalency allows us to evaluate the robustness of the composition of the ground state with the aim of identifying which candidates are more suitable to exhibit single-molecule magnet (SMM) behavior. The resulting energy level pattern as a function of the value of the radial displacement for 1-Tb, 1-Dy, 1-Ho, and 1-Er is reported in Figure 3.
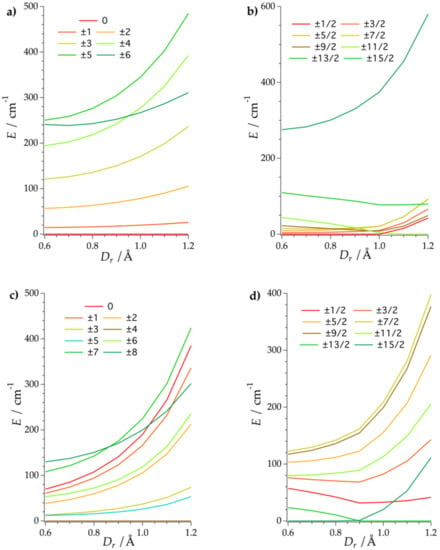
Figure 3.
Energy level scheme of the (a) 1-Tb; (b) 1-Dy; (c) 1-Ho, and (d) 1-Er as a function of Dr using the Radial Effective Charge (REC) model. The different colors indicate the main MJ contribution to the wave function.
A general trend that one can observe in the evolution of the energy levels versus Dr is that the larger the covalent correction, the larger the total ligand field splitting. This is related to the 1/(RiK+1) dependence of the k = 2, 4, 6 ligand field parameters in the model, where Ri is the effective distance between the point charge and the Ln3+ ion (see Section Five of Supplementary Materials, Equations (2a)–(2c)). Because of the almost perfect D5h geometry around the lanthanide, the extra-diagonal ligand field Bkq parameters, which are responsible of the mixing between MJ microstates, are practically negligible. This results in almost pure wave functions (~100% |MJ>) (Table S7). Regarding the ground state compositions, one can notice that for the non-Kramers ions (1-Tb and 1-Ho), the same MJ is the most stable along our exploration. In the case of 1-Tb, the equatorial geometry of {Pd15Se10O40} yields to a diamagnetic state MJ = 0, whereas for 1-Ho, the ground state is composed by two ±4 microstates. This indicates that we can practically discard the 1-Tb as a molecular nanomagnet, whereas the 1-Ho derivative is a potential candidate as a quantum two-level system, as long as small distortions in the real structure of the complex create a sufficiently large tunneling splitting between these two states [17]. On the other hand, the ground states of the 1-Dy and 1-Er derivatives present two different possibilities based on our magnetostructural investigation. Thus, we cannot state accurately the main MJ contribution to the ground doublet of these systems, as it will be very sensitive to the real coordinates of the compounds. However, whereas the 1-Dy analogue can be either ±1/2 or ±11/2, the 1-Er analogue is clearly the most promising of the series, as the model consistently predicts a ground state determined by a pure high MJ microstate (either ±15/2 or ±13/2). This preference of the polyoxoanion for stabilizing larger spin microstates in 1-Er is a direct consequence of the equatorial distribution of the electrostatic charge around the magnetic center [5,41]. Thus, according to our calculations, we can conclude that compound 1-Ho presents an interesting composition of the ground state to design a molecular spin qubit with possible operating points, whereas 1-Er has a very favorable coordination environment to exhibit slow relaxation of the magnetization. In comparison with the [LnPd12(AsPh)8O32]5− family [20], where the lack of anisotropy prevented SMM behavior in all the analogues of the series, the [LnPd15Se10O40]7− derivatives offer a promising pathway to develop POPd-based nanomagnets. Finally, the internal rigid cavity of the POM is expected to reduce the loss of quantum information by shielding the electronic structure from lattice vibrations, which means larger coherence times.
3. Conclusions
In summary, we have theoretically investigated the structural, electronic, and magnetic properties of a high-symmetry molecular structure based on POPds, providing a general protocol for the inexpensive screening of potential molecular nanomagnets and quantum two-level systems. Our calculations based on density functional theory and a ligand field approach indicate that the rigid near-perfect D5h coordination environment practically cancels all the extra-diagonal contributions to the ligand field Hamiltonian, leading to almost pure spin states in all the systems of the series. The equatorially expanded charge distribution around the lanthanide favors the stabilization of a high-spin ground doublet in the 1-Er derivative, which can be considered as a potential single-ion magnet. On the other hand, the ground state of the 1-Ho derivative offers an interesting playground to break ±4 degeneracy through ligand field-induced tunneling splitting which can be of interest for quantum computing applications. Our efforts to shed more experimental light on these systems are currently underway.
Supplementary Materials
The following are available online at http://www.mdpi.com/2304-6740/6/4/101/s1. Figure S1: Combined ball-and-stick and polyhedral representation of the [P5W30O110]15− polyanion, Figure S2: Ball-and-stick representation depicting segment of the 1, 1-Na, 1-La, 1-Gd, and 1-Lu polyanions, Figure S3: Spin density isosurface of 1-Gd indicating accumulation of α spins at the GdIII center as calculated at UB3LYP/TZ2P/ZSC/COSMO level. Color code: Pd = blue, O = red, and Se = yellow spheres, Table S1: Characteristic bond lengths of polyanion 1-Na system as calculated at different theoretical levels, Table S2: Characteristic bond lengths and interatomic distances in polyanions 1, 1-Na, 1-La, 1-Gd, and 1-Lu as calculated at BP/TZ2P/ZSC/COSMO-water levels, Table S3: Mulliken charge populations of 1, 1-Na, 1-La, 1-Gd, and 1-Lu obtained at (U)B3LYP/TZ2P/ZSC/ COSMO for different O atoms, following the labeling in Figure S2, Table S4: HOMO, LUMO, and HOMO–LUMO gap (∆LUMO–HOMO) energies in eV of 1, 1-Na, 1-La, 1-Gd, and 1-Lu, calculated at (U)B3LYP/TZ2P/ZSC/COSMO, Table S5: Contributions (in %) of the Kohn–Sham orbitals centered on palladium, oxygen, selenium, and the incorporated cations to the HOMO and the LUMO orbitals of 1, 1-Na, 1-La, 1-Gd, and 1-Lu, Table S6: Crystal field parameters ( Stevens notation) in cm−1 calculated for 1-Tb, 1-Dy, 1-Ho, and 1-Er, Table S7: Ground multiplet energy level scheme (cm−1) and main |MJ> contributions to the wave function calculated for 1-Tb, 1-Dy, 1-Ho, and 1-Er, Figure S4: Calculated spectrum of bare 1-La on BP/TZ2P/ZSC/COSMO-water levels. Main absorptions at 747 cm−1 and 671 cm−1 correspond to Se–O stretch, while a combination of stretch and bending modes corresponds to the absorption at 535 cm−1. References [16,20,21,24,31,32,33,34,37,38,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61] are cited in the supplementary materials.
Author Contributions
J.J.B. conceived the original idea on this project. J.J.B. and A.K. conceptualized the project, generated, analyzed, and discussed the results and contributed in writing the manuscript.
Funding
J.J.B. thanks the EU for a Marie Curie Fellowship (H2020-MSCA-IF-2016-751047). A.K. thanks Research Foundation Flanders (FWO) for the postdoctoral research grant (166497/12Y9218N LV 5457). This publication was also made possible through funding support of the KU Leuven Fund for Fair Open Access.
Acknowledgments
Max Planck Institute for the Structure and Dynamics of Matter (MPSD) and KU Leuven are thanked for research support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hill, S.; Edwards, R.S.; Aliaga-Alcalde, N.; Christou, G. Quantum Coherence in an Exchange-Coupled Dimer of Single-Molecule Magnets. Science 2003, 302, 1015–1018. [Google Scholar] [CrossRef] [PubMed]
- Cerletti, V.; Coish, W.A.; Gywat, O.; Loss, D. Recipes for spin-based quantum computing. Nanotechnology 2005, 16, R27. [Google Scholar] [CrossRef]
- Bertaina, S.; Gambarelli, S.; Mitra, T.; Tsukerblat, B.; Müller, A.; Barbara, B. Quantum oscillations in a molecular magnet. Nature 2008, 453, 203–206. [Google Scholar] [CrossRef] [PubMed]
- Stamp, P.C.E.; Gaita-Ariño, A. Spin-based quantum computers made by chemistry: Hows and whys. J. Mater. Chem. 2009, 19, 1718–1730. [Google Scholar] [CrossRef]
- Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Palii, A. Rational Design of Single-Ion Magnets and Spin Qubits Based on Mononuclear Lanthanoid Complexes. Inorg. Chem. 2012, 51, 12565–12574. [Google Scholar] [CrossRef] [PubMed]
- Atzori, M.; Morra, E.; Tesi, L.; Albino, A.; Chiesa, M.; Sorace, L.; Sessoli, R. Quantum Coherence Times Enhancement in Vanadium(IV)-based Potential Molecular Qubits: The Key Role of the Vanadyl Moiety. J. Am. Chem. Soc. 2016, 138, 11234–11244. [Google Scholar] [CrossRef] [PubMed]
- Gaita-Ariño, A.; Prima-García, H.; Cardona-Serra, S.; Escalera-Moreno, L.; Rosaleny, L.E.; Baldoví, J.J. Coherence and organisation in lanthanoid complexes: From single ion magnets to spin qubits. Inorg. Chem. Front. 2016, 3, 568–577. [Google Scholar] [CrossRef]
- Schleich, W.P. Quantum physics: Engineering decoherence. Nature 2000, 403, 256–257. [Google Scholar] [CrossRef] [PubMed]
- Goodwin, C.A.P.; Ortu, F.; Reta, D.; Chilton, N.F.; Mills, D.P. Molecular magnetic hysteresis at 60 kelvin in dysprosocenium. Nature 2017, 548, 439–442. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.-S.; Day, B.M.; Chen, Y.-C.; Tong, M.-L.; Mansikkamäki, A.; Layfield, R.A. A Dysprosium Metallocene Single-Molecule Magnet Functioning at the Axial Limit. Angew. Chem. Int. Ed. 2017, 56, 11445–11449. [Google Scholar] [CrossRef] [PubMed]
- Zadrozny, J.M.; Niklas, J.; Poluektov, O.G.; Freedman, D.E. Millisecond Coherence Time in a Tunable Molecular Electronic Spin Qubit. ACS Cent. Sci. 2015, 1, 488–492. [Google Scholar] [CrossRef] [PubMed]
- Bader, K.; Dengler, D.; Lenz, S.; Endeward, B.; Jiang, S.-D.; Neugebauer, P.; van Slageren, J. Room temperature quantum coherence in a potential molecular qubit. Nat. Commun. 2014, 5, 5304. [Google Scholar] [CrossRef] [PubMed]
- Donati, F.; Rusponi, S.; Stepanow, S.; Wäckerlin, C.; Singha, A.; Persichetti, L.; Baltic, R.; Diller, K.; Patthey, F.; Fernandes, E.; et al. Magnetic remanence in single atoms. Science 2016, 352, 318–321. [Google Scholar] [CrossRef] [PubMed]
- Escalera-Moreno, L.; Baldoví, J.J.; Gaita-Ariño, A.; Coronado, E. Spin states, vibrations and spin relaxation in molecular nanomagnets and spin qubits: A critical perspective. Chem. Sci. 2018, 9, 3265–3275. [Google Scholar] [CrossRef] [PubMed]
- Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariñoa, A. Magnetic polyoxometalates: From molecular magnetism to molecular spintronics and quantum computing. Chem. Soc. Rev. 2012, 41, 7464–7478. [Google Scholar] [CrossRef] [PubMed]
- Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Camón, A.; Evangelisti, M.; Luis, F.; Martínez-Pérez, M.J.; Sesé, J. Lanthanoid Single-Ion Magnets Based on Polyoxometalates with a 5-fold Symmetry: The Series [LnP5W30O110]12− (Ln3+ = Tb, Dy, Ho, Er, Tm, and Yb). J. Am. Chem. Soc. 2012, 134, 14982–14990. [Google Scholar] [CrossRef] [PubMed]
- Shiddiq, M.; Komijani, D.; Duan, Y.; Gaita-Ariño, A.; Coronado, E.; Hill, S. Enhancing coherence in molecular spin qubits via atomic clock transitions. Nature 2016, 531, 348–351. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Prima-García, H. Coherent manipulation of spin qubits based on polyoxometalates: The case of the single ion magnet [GdW30P5O110]14−. Chem. Commun. 2013, 49, 8922–8924. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Duan, Y.; Bustos, C.; Cardona-Serra, S.; Gouzerh, P.; Villanneau, R.; Gontard, G.; Clemente-Juan, J.M.; Gaita-Ariño, A.; Giménez-Saiz, C.; et al. Single ion magnets based on lanthanoid polyoxomolybdate complexes. Dalton Trans. 2016, 45, 16653–16660. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Rosaleny, L.E.; Ramachandran, V.; Christian, J.; Dalal, N.S.; Clemente-Juan, J.M.; Yang, P.; Kortz, U.; Gaita-Ariño, A.; Coronado, E. Molecular spin qubits based on lanthanide ions encapsulated in cubic polyoxopalladates: Design criteria to enhance quantum coherence. Inorg. Chem. Front. 2015, 2, 893–897. [Google Scholar] [CrossRef]
- Delferro, M.; Graiff, C.; Elviri, L.; Predieri, G. Self-assembly of polyoxoselenitopalladate nanostars [Pd15(μ3-SeO3)10(μ3-O)10Na]9− and their supramolecular pairing in the solid state. Dalton Trans. 2010, 39, 4479–4481. [Google Scholar] [CrossRef] [PubMed]
- Lin, Z.-G.; Wang, B.; Cao, J.; Chen, B.-K.; Gao, Y.-Z.; Chi, Y.-N.; Xu, C.; Huang, X.-Q.; Han, R.-D.; Su, S.-Y.; et al. Cation-Induced Synthesis of New Polyoxopalladates. Inorg. Chem. 2012, 51, 4435–4437. [Google Scholar] [CrossRef] [PubMed]
- Izarova, N.V.; Biboum, R.N.; Keita, B.; Mifsud, M.; Arends, I.W.C.E.; Jameson, G.B.; Kortz, U. Self-assembly of star-shaped heteropoly-15-palladate(II). Dalton Trans. 2009, 9385–9387. [Google Scholar] [CrossRef] [PubMed]
- Izarova, N.V.; Pope, M.T.; Kortz, U. Noble metals in polyoxometalates. Angew. Chem. Int. Ed. 2012, 51, 9492–9510. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Parac-Vogt, T.P. Keggin Structure, Quō Vādis? Front. Chem. 2018, 6, 346. [Google Scholar] [CrossRef] [PubMed]
- Yang, P.; Kortz, U. Discovery and Evolution of Polyoxopalladates. Acc. Chem. Res. 2018, 51, 1599–1608. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Monakhov, K.Y. Breaking the Gordian Knot in the Structural Chemistry of Polyoxometalates: Copper(II)–Oxo/Hydroxo Clusters. Chem. Eur. J. 2017, 23, 7841–7852. [Google Scholar] [CrossRef] [PubMed]
- Büchner, O. Münzmetalle mit und in komplexen Anionen: Synthese, Struktur und Eigenschaften. Ph.D. Thesis, Carl von Ossietzky Universität Oldenburg, Oldenburg, Germany, 2005. Available online: https://oops.uni-oldenburg.de/id/eprint/63 (accessed on 1 April 2018).
- Yang, P.; Xiang, Y.; Lin, Z.; Lang, Z.; Jiménez-Lozano, P.; Carbó, J.J.; Poblet, J.M.; Fan, L.; Hu, C.; Kortz, U. Discrete Silver(I)-Palladium(II)-Oxo Nanoclusters, {Ag4Pd13} and {Ag5Pd15}, and the Role of Metal-Metal Bonding Induced by Cation Confinement. Angew. Chem. Int. Ed. 2016, 55, 15766–15770. [Google Scholar] [CrossRef] [PubMed]
- Xu, F.; Scullion, R.A.; Yan, J.; Miras, H.N.; Busche, C.; Scandurra, A.; Pignataro, B.; Long, D.; Cronin, L. A Supramolecular Heteropolyoxopalladate {Pd15} Cluster Host Encapsulating a {Pd2} Dinuclear Guest: [PdII2⊂{H7PdII15O10(PO4)10}]9−. J. Am. Chem. Soc. 2011, 133, 4684–4686. [Google Scholar] [CrossRef] [PubMed]
- Te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Guerra, C.F.; Van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T.J. Chemistry with ADF. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Izarova, N.; Lin, Z.; Yang, P.; Kondinski, A.; Vankova, N.; Heine, T.; Kortz, U. The polyoxo-22-palladate(II), [Na2PdII22O12(AsVO4)15(AsVO3OH)]25−. Dalton Trans. 2016, 45, 2394–2398. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Vankova, N.; Schinle, F.; Jäger, P.; Hampe, O.; Kortz, U.; Heine, T. How Counterions Affect the Solution Structure of Polyoxoaurates: Insights from UV–Vis Spectral Simulations and Electrospray Mass Spectrometry. Eur. J. Inorg. Chem. 2014, 3771–3778. [Google Scholar] [CrossRef]
- Izarova, N.; Kondinski, A.; Vankova, N.; Heine, T.; Jäger, P.; Schinle, F.; Hampe, O.; Kortz, U. The mixed gold-palladium polyoxo-noble-metalate, [NaAuIII4PdII8O8(AsO4)8]11−. Chem. Eur. J. 2014, 20, 8556–8560. [Google Scholar] [CrossRef] [PubMed]
- Barsukova-Stuckart, M.; Izarova, N.V.; Barrett, R.; Wang, Z.; van Tol, J.; Kroto, H.W.; Dalal, N.S.; Keita, B.; Heller, D.; Kortz, U. 3d Metal Ions in Highly Unusual Eight-Coordination: The Phosphate-Capped Dodecapalladate(II) Nanocube. Chem. Eur. J. 2012, 18, 6167–6171. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.D. Revised Effective Ionic Radii and Systematic Studies of Interatomic Distances in Halides and Chalcogenides. Acta Cryst. 1976, A32, 751–767. [Google Scholar] [CrossRef]
- Baldoví, J.J.; Borrás-Almenar, J.J.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A. Modeling the properties of lanthanoid single-ion magnets using an effective point-charge approach. Dalton Trans. 2012, 41, 13705–13710. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Cardona-Serra, S.; Clemente-Juan, J.M.; Coronado, E.; Gaita-Ariño, A.; Palii, A. SIMPRE: A software package to calculate crystal field parameters, energy levels, and magnetic properties on mononuclear lanthanoid complexes based on charge distributions. J. Comput. Chem. 2013, 34, 1961–1967. [Google Scholar] [CrossRef]
- Baldoví, J.J.; Duan, Y.; Morales, R.; Gaita-Ariño, A.; Ruiz, E.; Coronado, E. Rational Design of Lanthanoid Single-Ion Magnets: Predictive Power of the Theoretical Models. Chem. Eur. J. 2016, 22, 13532–13539. [Google Scholar] [CrossRef] [PubMed]
- Baldoví, J.J.; Gaita-Ariño, A.; Coronado, E. Modeling the magnetic properties of lanthanide complexes: Relationship of the REC parameters with Pauling electronegativity and coordination number. Dalton Trans. 2015, 44, 12535–12538. [Google Scholar] [CrossRef] [PubMed]
- Rinehart, J.D.; Long, J.R. Exploiting single-ion anisotropy in the design of f-element single-molecule magnets. Chem. Sci. 2011, 2, 2078–2085. [Google Scholar] [CrossRef]
- Becke, A.D. A multicenter numerical integration scheme for polyatomic molecules. J. Chem. Phys. 1988, 88, 2547–2553. [Google Scholar] [CrossRef]
- Franchini, M.; Philipsen, P.H.T.; Visscher, L. The Becke Fuzzy Cells Integration Scheme in the Amsterdam Density Functional Program Suite. J. Comput. Chem. 2013, 34, 1819–1827. [Google Scholar] [CrossRef] [PubMed]
- Vosko, S.H.; Wilk, L.; Nusair, M. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: A critical analysis. Can. J. Phys. 1980, 58, 1200–1211. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B Condens. Matter Mater. Phys. 1986, 33, 8822–8824. [Google Scholar] [CrossRef]
- Van Lenthe, E.; Baerends, E.J. Optimized Slater-type basis sets for the elements 1–118. J. Comput. Chem. 2003, 24, 1142–1156. [Google Scholar] [CrossRef] [PubMed]
- Lenthe, E.V.; Baerends, E.J.; Snijders, J.G. Relativistic regular two-component Hamiltonians. J. Chem. Phys. 1993, 99, 4597–4610. [Google Scholar] [CrossRef]
- Pye, C.C.; Ziegler, T. An implementation of the conductor-like screening model of solvation within the Amsterdam density functional package. Theor. Chem. Acc. 1999, 101, 396–408. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M. Ab Initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Poblet, J.M.; López, X. Computational Methods: Heteropolyoxoanions. In Encyclopedia of Inorganic and Bioinorganic Chemistry; Scott, R.A., Ed.; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Barsukova-Stuckart, M.; Izarova, N.V.; Barrett, R.A.; Wang, Z.; van Tol, J.; Kroto, H.W.; Dalal, N.S.; Jiménez-Lozano, P.; Carbó, J.J.; Poblet, J.M.; et al. Polyoxopalladates Encapsulating 8-Coordinated Metal Ions, [MO8PdII12L8]n− (M = Sc3+, Mn2+, Fe3+, Co2+, Ni2+, Cu2+, Zn2+, Lu3+; L = PhAsO32−, PhPO32−, SeO32−). Inorg. Chem. 2012, 51, 13214–13228. [Google Scholar] [CrossRef] [PubMed]
- Lang, Z.; Yang, P.; Lin, Z.; Yan, L.; Li, M.-X.; Carbó, J.J.; Kortz, U.; Poblet, J.M. Size and charge effect of guest cations in the formation of polyoxopalladates: A theoretical and experimental study. Chem. Sci. 2017, 8, 7862–7872. [Google Scholar] [CrossRef] [PubMed]
- Kondinski, A.; Heine, T.; Monakhov, K.Yu. Rotational Isomerism, Electronic Structures, and Basicity Properties of “Fully-Reduced” V14-type Heteropolyoxovanadates. Inorg. Chem. 2016, 55, 3777–3788. [Google Scholar] [CrossRef] [PubMed]
- Fernández, J.A.; López, X.; Bo, C.; de Graaf, C.; Baerends, E.J.; Poblet, J.M. Polyoxometalates with Internal Cavities: Redox Activity, Basicity, and Cation Encapsulation in [Xn+P5W30O110](15−n)− Preyssler Complexes, with X = Na+, Ca2+, Y3+, La3+, Ce3+, and Th4+. J. Am. Chem. Soc. 2007, 129, 12244–12253. [Google Scholar] [CrossRef] [PubMed]
- Rudowicz, C.; Chung, C.Y. The generalization of the extended Stevens operators to higher ranks and spins, and a systematic review of the tables of the tensor operators and their matrix elements. J. Phys. Condens. Matter 2004, 16, 5825–5847. [Google Scholar] [CrossRef]
- Rudowicz, C. Transformation relations for the conventional Okq and normalised O’kq Stevens operator equivalents with k = 1 to 6 and −k ≤ q ≤ k. J. Phys. C Solid State Phys. 1985, 18, 1415–1430. [Google Scholar] [CrossRef]
- Rudowicz, C. Transformation relations for the conventional Okq and normalised O’kq Stevens operator equivalents with k = 1 to 6 and −k ≤ q ≤ k. J. Phys. C Solid State Phys. 1985, 18, 3837. [Google Scholar] [CrossRef]
- Ryabov, I.D. On the Generation of Operator Equivalents and the Calculation of Their Matrix Elements. J. Magn. Reson. 1999, 140, 141–145. [Google Scholar] [CrossRef] [PubMed]
- Stevens, K.W.H. Matrix Elements and Operator Equivalents Connected with the Magnetic Properties of Rare Earth Ions. Proc. Phys. Soc. 1952, 65, 209. [Google Scholar] [CrossRef]
- Edvardsson, S.; Klinterberg, M. Role of the electrostatic model in calculating rare-earth crystal-field parameters. J. Alloy. Comp. 1998, 275–277, 230–233. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).