Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood
Abstract
:1. Introduction
2. Geometry-Based Identification of Halogen Bonding
2.1. Early Recognition
2.2. The Birth of Halogen Bonding and the σ-Hole Concept
2.3. Classification of Halogen Bonding
2.4. The Many-fold Controversy
2.4.1. Is an Atom–Atom Contact a Bond (or an Interaction)?
2.4.2. How to Define a Bond?
2.4.3. Is the Concept of Atomic Charge Meaningful?
2.4.4. Is the Directionality Feature in Halogen-Centered Noncovalent Interactions Understood?
2.4.5. Polarization Induced σ-Hole: Is It Real or a Provocation?
2.4.6. Is the σ-Hole Model a Unified Model?
2.5. The Topology of Fluorine Centered Bonding
2.6. The X3 Synthon in Crystals
3. Charge Density Models for Visualizing Noncovalent Interactions
4. Prototypical Examples of Halogen-Centered Noncovalent Interactions
4.1. The Tetrafluoromethane (CF4) System
4.2. The Tetrachloromethane (CCl4) System
4.3. The Tetrabromomethane (CBr4) System
4.4. The Tetraiodomethane (CI4) System
4.5. The Chlorine Monofluoride (ClF) Crystal System
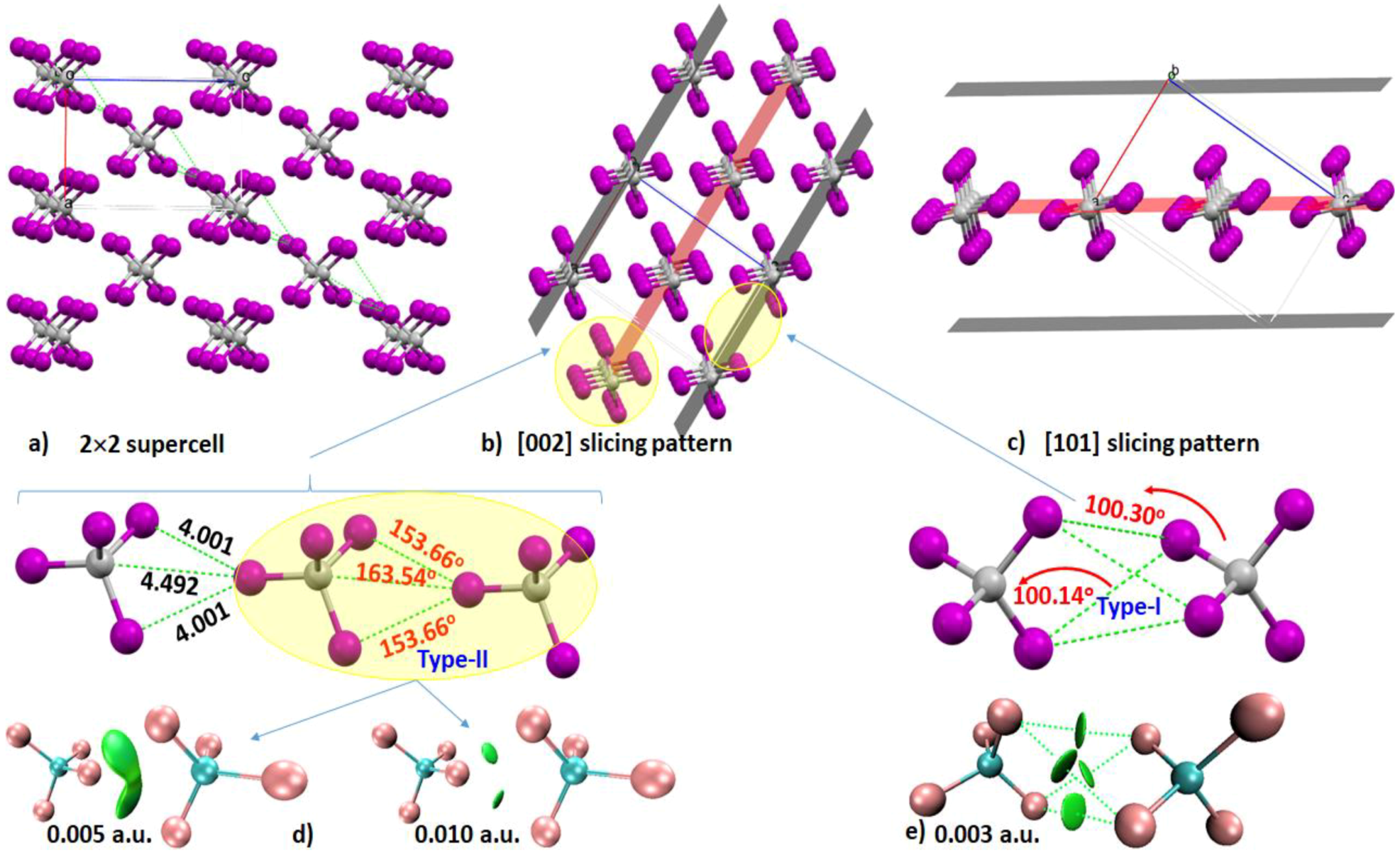
4.6. Examples of Some Crystal Systems Stabilized by Type-I and -II Contacts
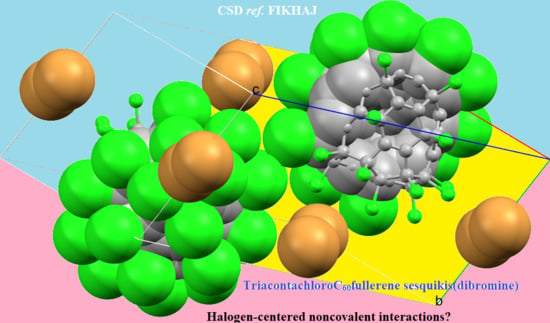
4.6.1. Some Halogen-Substituted Fullerene Systems
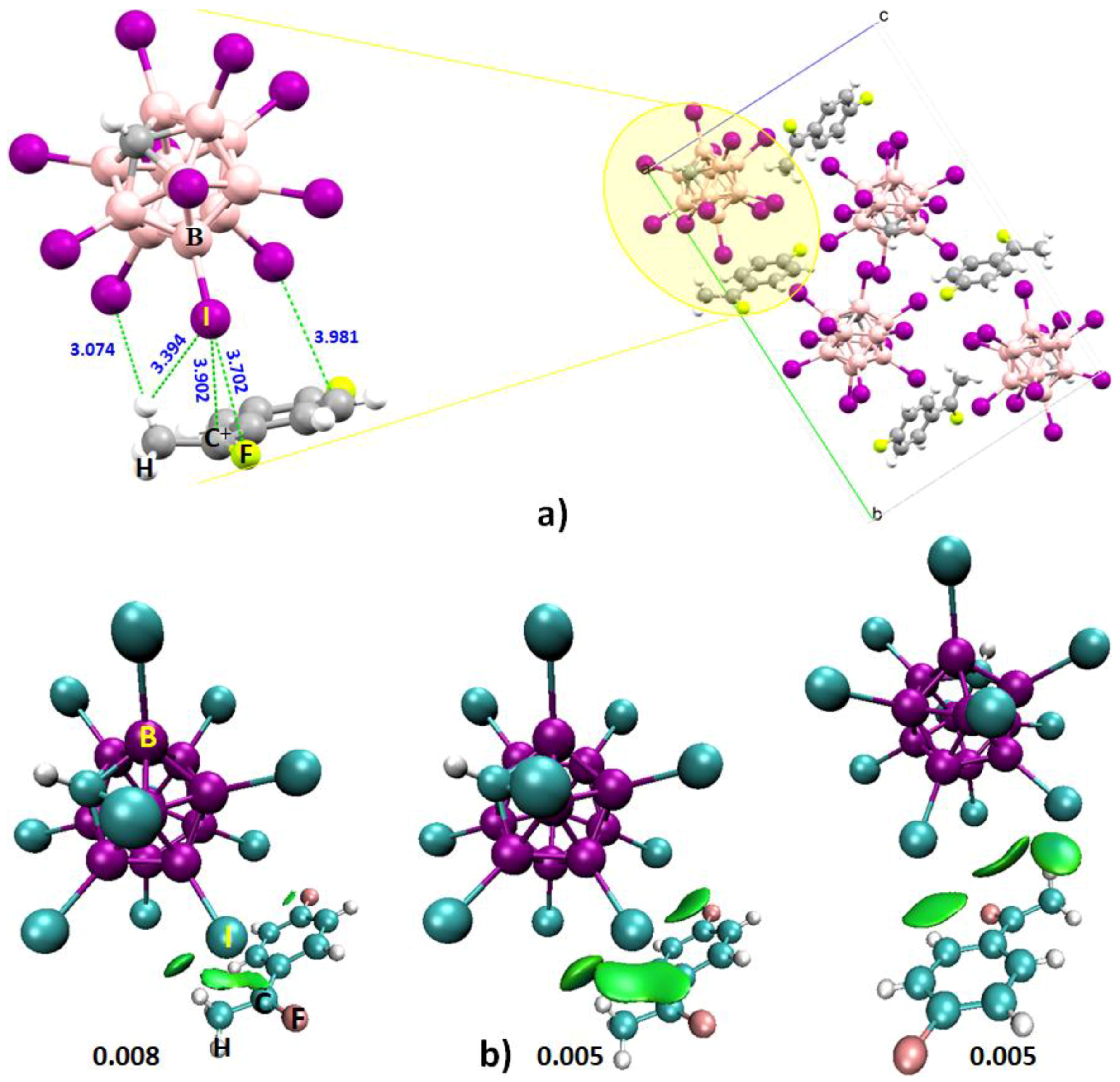
4.6.2. Some Halogen-Substituted Borane Systems
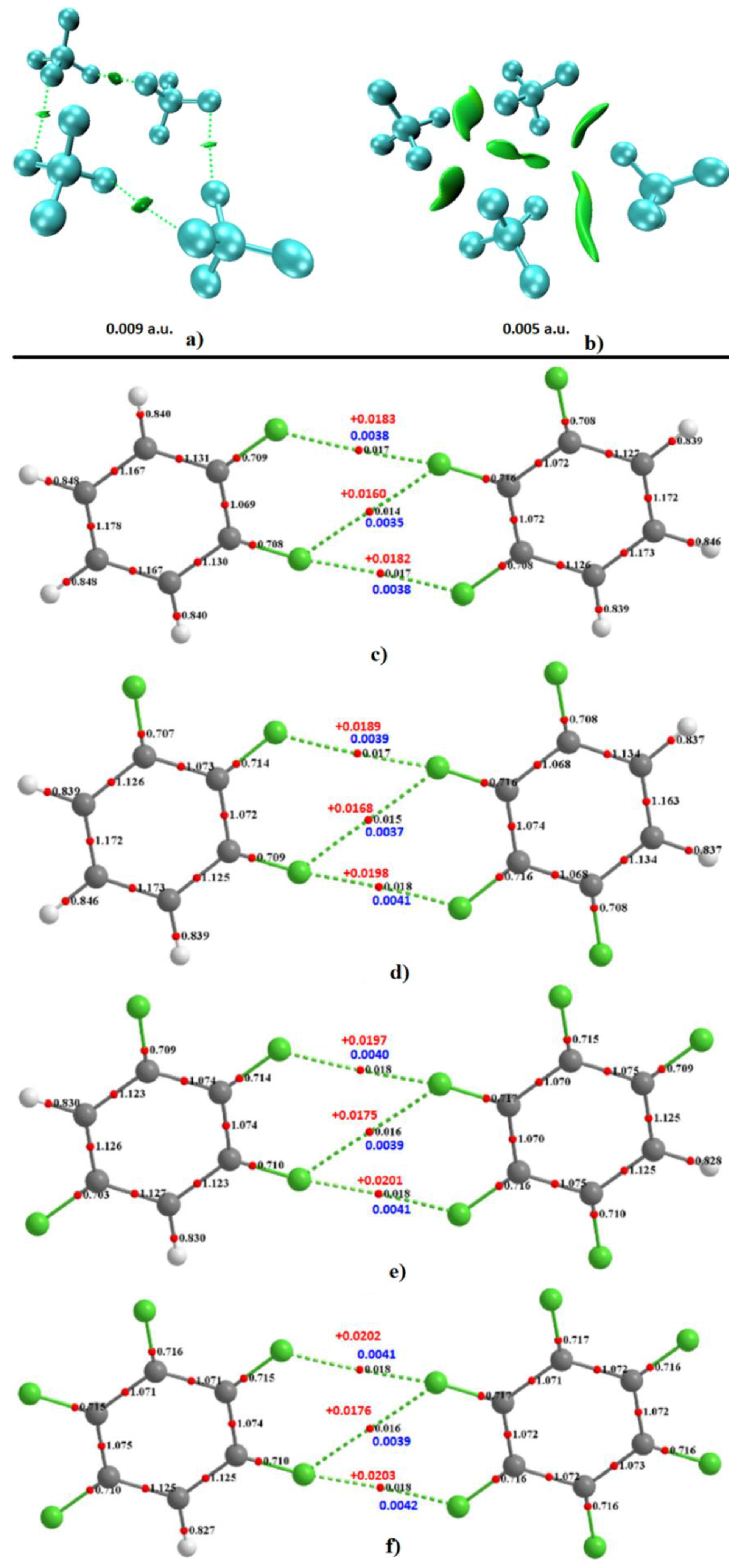
4.6.3. Some Halogen-Substituted Aromatic and Nonaromatic Systems
5. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chan, Y.-C.; Yeung, Y.-Y. Halogen Bond Catalyzed Bromocarbocyclization. Angew. Chem. Int. Ed. 2018, 57, 3483–3487. [Google Scholar] [CrossRef] [PubMed]
- Robertson, C.C.; Wright, J.S.; Carrington, E.J.; Perutz, R.N.; Hunter, C.A.; Brammer, L. Hydrogen bonding vs. halogen bonding: The solvent decides. Chem. Sci. 2017, 8, 5392–5398. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wang, J.; Li, G.-X.; He, G.; Chen, G. Halogen-Bond-Promoted Photoactivation of Perfluoroalkyl Iodides: A Photochemical Protocol for Perfluoroalkylation Reactions. Org. Lett. 2017, 19, 1442–1445. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, W.; Jin, W.J. σ-Hole Bond vs. π-Hole Bond: A Comparison Based on Halogen Bond. Chem. Rev. 2016, 116, 5072–5104. [Google Scholar] [CrossRef] [PubMed]
- Brammer, L. Halogen bonding, chalcogen bonding, pnictogen bonding, tetrel bonding: Origins, current status and discussion. Faraday Discuss. 2017, 203, 485–507. [Google Scholar] [CrossRef] [PubMed]
- Wolters, L.P.; Schyman, P.; Pavan, M.J.; Jorgensen, W.L.; Bickelhaupt, F.M.; Kozuch, S. The many faces of halogen bonding: A review of theoretical models and methods. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 523–540. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. Molecular electrostatic potentials and noncovalent interactions. WIREs Comput. Mol. Sci. 2017, 7, e1326. [Google Scholar] [CrossRef]
- Riley, K.E.; Hobza, P. Strength and Character of Halogen Bonds in Protein–Ligand Complexes. Cryst. Growth Des. 2011, 11, 4272–4278. [Google Scholar] [CrossRef]
- Auffinger, P.; Hays, F.A.; Westhof, E.; Ho, P.S. Halogen bonds in biological molecules. Proc. Natl. Acad. Sci. USA 2004, 101, 16789–16794. [Google Scholar] [CrossRef]
- Cavallo, G.; Metrangolo, P.; Milani, R.; Pilati, T.; Priimagi, A.; Resnati, G.; Terraneo, G. The halogen bond. Chem. Rev. 2016, 116, 2478–2601. [Google Scholar] [CrossRef]
- Saha, A.; Rather, S.A.; Sharada, D.; Saha, B.K. C–X⋯X–C vs. C–H⋯X–C, Which One Is the More Dominant Interaction in Crystal Packing (X = Halogen)? Cryst. Growth Des. 2018, 18, 6084–6090. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. Revealing Factors Influencing the Fluorine-Centered Non-Covalent Interactions in Some Fluorine-Substituted Molecular Complexes: Insights from First-Principles Studies. ChemPhysChem 2018, 19, 1486–1499. [Google Scholar] [CrossRef]
- Stone, A.J. Are Halogen Bonded Structures Electrostatically Driven? J. Am. Chem. Soc. 2013, 135, 7005–7009. [Google Scholar] [CrossRef]
- Bayse, C.A. Halogen bonding from the bonding perspective with considerations for mechanisms of thyroid hormone activation and inhibition. New J. Chem. 2018, 42, 10623–10632. [Google Scholar] [CrossRef]
- Ding, X.; Tuikka, M.; Haukka, M. Halogen Bonding in Crystal Engineering. In Recent Advances in Crystallography; Benedict, J.B., Ed.; IntechOpen: London, UK, 2012. [Google Scholar] [Green Version]
- Kawai, S.; Sadeghi, A.; Xu, F.; Peng, L.; Orita, A.; Otera, J.; Goedecker, S.; Meyer, E. Extended halogen bonding between fully fluorinated aromatic molecules. ACS Nano 2015, 9, 2574–2583. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. CondMat Public Archive. Comment on “Extended Halogen Bonding between Fully Fluorinated Aromatic Molecules; Kawai et al., ACS Nano, 2015, 9, 2574–2583”. Available online: https://arxiv.org/ftp/arxiv/papers/1802/1802.09995.pdf (accessed on 7 February 2019).
- Lu, Y.; Liu, Y.; Xu, Z.; Li, H.; Liu, H.; Zhu, W. Halogen bonding for rational drug design and new drug discovery. Expert Opin. Drug Discov. 2012, 7, 375–383. [Google Scholar] [CrossRef]
- Mukherjee, A.; Tothadi, S.; Desiraju, G.R. Halogen Bonds in Crystal Engineering: Like Hydrogen Bonds yet Different. Acc. Chem. Res. 2014, 47, 2514–2524. [Google Scholar] [CrossRef]
- Gilday, L.C.; Robinson, S.W.; Barendt, T.A.; Langton, M.J.; Mullaney, B.R.; Beer, P.D. Halogen Bonding in Supramolecular Chemistry. Chem. Rev. 2015, 115, 7118–7195. [Google Scholar] [CrossRef]
- Jungbauer, S.H.; Bulfield, D.; Kniep, F.; Lehmann, C.W.; Herdtweck, E.; Huber, S.M. Toward Molecular Recognition: Three-Point Halogen Bonding in the Solid State and in Solution. J. Am. Chem. Soc. 2014, 136, 16740–16743. [Google Scholar] [CrossRef]
- Hostaš, J.; Řezáč, J. Accurate DFT-D3 Calculations in a Small Basis Set. J. Chem. Theory Comput. 2017, 13, 3575–3585. [Google Scholar] [CrossRef]
- Otero-de-la-Roza, A.; Johnson, E.R.; DiLabio, G.A. Halogen Bonding from Dispersion-Corrected Density-Functional Theory: The Role of Delocalization Error. J. Chem. Theory Comput. 2014, 10, 5436–5447. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kozuch, S.; Martin, J.M.L. Halogen Bonds: Benchmarks and Theoretical Analysis. J. Chem. Theory Comput. 2013, 9, 1918–1931. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The σ-hole revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Resnati, G.; Politzer, P. Close contacts and noncovalent interactions in crystals. Faraday Discuss. 2017, 203, 113–130. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Mathematical modeling and physical reality in noncovalent interactions. J. Mol. Model. 2015, 21, 52. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Walker, M.; Harvey, A.J.A.; Sen, A.; Dessent, C.E.H. Performance of M06, M06-2X, and M06-HF Density Functionals for Conformationally Flexible Anionic Clusters: M06 Functionals Perform Better than B3LYP for a Model System with Dispersion and Ionic Hydrogen-Bonding Interactions. J. Phys. Chem. A 2013, 117, 12590–12600. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. A DFT assessment of some physical properties of iodine-centered halogen bonding and other non-covalent interactions in some experimentally reported crystal geometries. Phys. Chem. Chem. Phys. 2018, 20, 15316–15329. [Google Scholar] [CrossRef]
- Angarov, V.; Kozuch, S. On the σ, π and δ hole interactions: A molecular orbital overview. New J. Chem. 2018, 42, 1413–1422. [Google Scholar] [CrossRef]
- Koohi, A.M.; Mahdavifar, Z.; Noorizadeh, S. Can Fluorine form Halogen Bond? Investigation of Halogen Bonds through Steric Charge. ChemistrySelect 2017, 2, 2713–2717. [Google Scholar] [CrossRef]
- Roy, D.; Marianski, M.; Maitra, N.T.; Dannenberg, J.J. Comparison of some dispersion-corrected and traditional functionals with CCSD(T) and MP2 ab initio methods: Dispersion, induction, and basis set superposition error. J. Chem. Phys. 2012, 137, 134109. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Jin, X.; Yu, H.S.; Truhlar, D.G.; He, X. Revised M06-L functional for improved accuracy on chemical reaction barrier heights, noncovalent interactions, and solid-state physics. Proc. Natl. Acad. Sci. USA 2017, 114, 8487–8492. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Paranthaman, S. Assessment of DFT Functionals in Predicting Bond Length and Atomization Energy of Catalytically Important Metal Dimer. Croat. Chem. Acta 2017, 90, 17–26. [Google Scholar] [CrossRef]
- Vydrov, O.A.; Van Voorhis, T. Benchmark Assessment of the Accuracy of Several van der Waals Density Functionals. J. Chem. Theory Comput. 2012, 8, 1929–1934. [Google Scholar] [CrossRef]
- Kovács, A.; Dobrowolski, J.C.; Ostrowski, S.; Rode, J.E. Benchmarking density functionals in conjunction with Grimme’s dispersion correction for noble gas dimers (Ne2, Ar2, Kr2, Xe2, Rn2). Int. J. Quantum Chem. 2017, 117, e25358. [Google Scholar] [CrossRef]
- Ayers, P.W.; Parr, R.G. Is it impossible to find the universal density functional? Or is it just well-hidden? Ind. J. Chem. 2014, 53A, 929–931. [Google Scholar]
- Desiraju, G.R.; Shing Ho, P.; Kloo, L.; Legon, A.C.; Marquardt, R.; Metrangolo, P.; Politzer, P.; Resnati, G.; Rissanen, K. Definition of the halogen bond (IUPAC Recommendations 2013). Pure Appl. Chem. 2013, 85, 1711–1713. [Google Scholar] [CrossRef] [Green Version]
- Thirman, J.; Engelage, E.; Huber, S.M.; Head-Gordon, M. Characterizing the interplay of Pauli repulsion, electrostatics, dispersion and charge transfer in halogen bonding with energy decomposition analysis. Phys. Chem. Chem. Phys. 2018, 20, 905–915. [Google Scholar] [CrossRef]
- Huber, S.M.; Jimenez-Izal, E.; Ugalde, J.M.; Infante, I. Unexpected Trends in Halogen-Bond Based Noncovalent Adducts. Chem. Commun. 2012, 48, 7708–7710. [Google Scholar] [CrossRef]
- Tawfik, M.; Donald, K.J. Halogen Bonding: Unifying Perspectives on Organic and Inorganic Cases. J. Phys. Chem. A 2014, 118, 10090–10100. [Google Scholar] [CrossRef]
- Scheiner, S. Systematic Elucidation of Factors That Influence the Strength of Tetrel Bonds. J. Phys. Chem. A 2017, 121, 5561–5568. [Google Scholar] [CrossRef] [Green Version]
- Dong, W.; Li, Q.; Scheiner, S. Comparative Strengths of Tetrel, Pnicogen, Chalcogen, and Halogen Bonds and Contributing Factors. Molecules 2018, 23, 1681. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Unusual bonding modes of perfluorobenzene in its polymeric (dimeric, trimeric and tetrameric) forms: Entirely negative fluorine interacting cooperatively with entirely negative fluorine. Phys. Chem. Chem. Phys. 2015, 17, 31624–31645. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Varadwaj, P.R.; Jin, B.-Y. Can an entirely negative fluorine in a molecule, viz. perfluorobenzene, interact attractively with the entirely negative site(s) on another molecule(s)? Like liking like! RSC Adv. 2016, 6, 19098–19110. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Do surfaces of positive electrostatic potential on different halogen derivatives in molecules attract? Like attracting like! J. Comput. Chem. 2018, 39, 343–350. [Google Scholar] [CrossRef] [PubMed]
- Schneider, H.-J. Hydrogen bonds with fluorine. Studies in solution, in gas phase and by computations, conflicting conclusions from crystallographic analyses. Chem. Sci. 2012, 3, 1381–1394. [Google Scholar] [CrossRef]
- Varadwaj, P.; Varadwaj, A.; Marques, H.; Yamashita, K. Can Combined Electrostatic and Polarization Effects Alone Explain the F⋯F Negative-Negative Bonding in Simple Fluoro-Substituted Benzene Derivatives? A First-Principles Perspective. Computation 2018, 6, 51. [Google Scholar] [CrossRef]
- Tantardini, C. When does a hydrogen bond become a van der Waals interaction? A topological answer. J. Comput. Chem. 2019, 40, 937–943. [Google Scholar] [CrossRef]
- Wang, C.; Danovich, D.; Shaik, S.; Wu, W.; Mo, Y. Attraction between electrophilic caps: A counterintuitive case of noncovalent interactions. J. Comput. Chem 2019, 40, 1015–1022. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.-Y. Halogen bonding interaction of chloromethane withseveral nitrogen donating molecules: Addressing thenature of the chlorine surface σ-hole. Phys. Chem. Chem. Phys. 2014, 16, 19573–19589. [Google Scholar] [CrossRef]
- Riley, K.E.; Vazquez, M.; Umemura, C.; Miller, C.; Tran, K.-A. Exploring the (Very Flat) Potential Energy Landscape of R–Br⋯π Interactions with Accurate CCSD(T) and SAPT Techniques. Chem. Eur. J. 2016, 22, 17690–17695. [Google Scholar] [CrossRef]
- Arunan, E.; Desiraju, G.R.; Klein, R.A.; Sadlej, J.; Scheiner, S.; Alkorta, I.; Clary, D.C.; Crabtree, R.H.; Dannenberg, J.J.; Hobza, P.; et al. Definition of the hydrogen bond (IUPAC Recommendations 2011). Pure Appl. Chem. 2011, 83, 1637–1641. [Google Scholar] [CrossRef] [Green Version]
- Clark, T. Halogen bonds and σ-holes. Faraday Discuss. 2017, 203, 9–27. [Google Scholar] [CrossRef] [PubMed]
- Arunan, E. Hydrogen bond seen, halogen bond defined and carbon bond proposed: Intermolecular bonding, a field that is maturing! Curr. Sci. 2013, 105, 892–894. [Google Scholar]
- Zhang, J.; Chen, P.; Yuan, B.; Ji, W.; Cheng, Z.; Qiu, X. Real-Space Identification of Intermolecular Bonding with Atomic Force Microscopy. Science 2013, 342, 611–614. [Google Scholar] [CrossRef]
- Ritter, S.K. The Cheimcal Bond. C E News Arch. 2007, 85, 37–40. [Google Scholar] [CrossRef]
- Bader, R.W.F. Bond paths are not chemical bonds. J. Phys. Chem. A 2009, 113, 10391–10396. [Google Scholar] [CrossRef] [PubMed]
- De Oteyza, D.G.; Gorman, P.; Chen, Y.-C.; Wickenburg, S.; Riss, A.; Mowbray, D.J.; Etkin, G.; Pedramrazi, Z.; Tsai, H.-Z.; Rubio, A.; et al. Direct Imaging of Covalent Bond Structure in Single-Molecule Chemical Reactions. Science 2013. [Google Scholar] [CrossRef]
- Itatani, J.; Levesque, J.; Zeidler, D.; Spanner, M.; Corkum, P.B.; Villeneuve, D.M. Tomographic imaging of molecular orbitals with high harmonic generation. In Proceedings of the 14th International Conference on Ultrafast Phenomena, Niigata, Japan, 25–30 July 2004; p. M3. [Google Scholar]
- Itatani, J.; Levesque, J.; Zeidler, D.; Niikura, H.; Pépin, H.; Kieffer, J.C.; Corkum, P.B.; Villeneuve, D.M. Tomographic imaging of molecular orbitals. Nature 2004, 432, 867. [Google Scholar] [CrossRef] [PubMed]
- Mulder, P. Are Orbitals Observable? HYLE Int. J. Philos. Chem. 2011, 17, 24–35. [Google Scholar]
- Schwarz, W.H.E. Measuring Orbitals: Provocation or Reality? Angew Chem. Int. Ed. 2006, 45, 1508–1517. [Google Scholar] [CrossRef]
- Scerri, E.R. Have Orbitals Really Been Observed? J. Chem. Ed. 2000, 77, 1492. [Google Scholar] [CrossRef] [Green Version]
- Ivanov, M.V.; Reid, S.A.; Rathore, R. Game of Frontier Orbitals: A View on the Rational Design of Novel Charge-Transfer Materials. J. Phys. Chem. Lett. 2018, 9, 3978–3986. [Google Scholar] [CrossRef] [PubMed]
- Ito, O.; D’Souza, F. Recent Advances in Photoinduced Electron Transfer Processes of Fullerene-Based Molecular Assemblies and Nanocomposites. Molecules 2012, 17, 5816. [Google Scholar] [CrossRef] [PubMed]
- Torrente, I.F.; Franke, K.J.; Pascual, J.I. Spectroscopy of C60 single molecules: The role of screening on energy level alignment. J. Phys. Condens. Matter 2008, 20, 184001. [Google Scholar] [CrossRef]
- Wu, Q.; Zhao, D.; Goldey, M.B.; Filatov, A.S.; Sharapov, V.; Colón, Y.J.; Cai, Z.; Chen, W.; de Pablo, J.; Galli, G.; et al. Intra-molecular Charge Transfer and Electron Delocalization in Non-fullerene Organic Solar Cells. ACS Appl. Mater. Interfaces 2018, 10, 10043–10052. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.J.; Woo, J.H.; Xiao, Y.; Kim, E.; Mazur, L.M.; Kreher, D.; Attias, A.-J.; Matczyszyn, K.; Samoc, M.; Heinrich, B.; et al. Structure–charge transfer property relationship in self-assembled discotic liquid-crystalline donor–acceptor dyad and triad thin films. RSC Adv. 2016, 6, 57811–57819. [Google Scholar] [CrossRef] [Green Version]
- Tishchenko, O.; Truhlar, D.G. Atom-Cage Charge Transfer in Endohedral Metallofullerenes: Trapping Atoms within a Sphere-Like Ridge of Avoided Crossings. J. Chem. Phys. Lett. 2013, 4, 422–425. [Google Scholar] [CrossRef]
- Campanera, J.M.; Bo, C.; Olmstead, M.M.; Balch, A.L.; Poblet, J.M. Bonding within the Endohedral Fullerenes Sc3N@C78 and Sc3N@C80 as Determined by Density Functional Calculations and Reexamination of the Crystal Structure of {Sc3N@C78}·Co(OEP)}·1.5(C6H6)·0.3(CHCl3). J. Phys Chem. A 2002, 106, 12356–12364. [Google Scholar] [CrossRef]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef]
- Wang, B.; Zheng, S.; Saha, A.; Bao, L.; Lu, X.; Guldi, D.M. Understanding Charge-Transfer Characteristics in Crystalline Nanosheets of Fullerene/(Metallo)porphyrin Cocrystals. J. Am. Chem. Soc. 2017, 139, 10578–10584. [Google Scholar] [CrossRef] [PubMed]
- Alhameedi, K.; Karton, A.; Jayatilaka, D.; Thomas, S.P. Bond orders for intermolecular interactions in crystals: Charge transfer, ionicity and the effect on intramolecular bonds. IUCrJ 2018, 5, 635–646. [Google Scholar] [CrossRef] [PubMed]
- Davey, J.B.; Legon, A.C.; Waclawik, E.R. Inter- and intramolecular electron transfer in the complex OC⋯ICl determined from iodine and chlorine nuclear quadrupole hyperfine structure in its rotational spectrum. Phys. Chem. Chem. Phys. 1999, 1, 3097–3101. [Google Scholar] [CrossRef]
- Legon, A.C. Angular and radial geometries, charge transfer and binding strength in isolated complexes B⋯ICl: Some generalisations. Chem. Phys. Lett. 1999, 314, 472–480. [Google Scholar] [CrossRef]
- Legon, A.C. Tetrel, pnictogen and chalcogen bonds identified in the gas phase before they had names: A systematic look at non-covalent interactions. Phys. Chem. Chem. Phys. 2017, 19, 14884–14896. [Google Scholar] [CrossRef] [PubMed]
- Davey, J.B.; Legon, A.C.; Waclawik, E.R. Measurement of inter- and intramolecular charge transfer in the complex N2⋯ICl from analysis of halogen nuclear quadrupole hyperfine structure in the rotational spectrum. J. Mol. Struct. THEOCHEM 2000, 500, 403–411. [Google Scholar] [CrossRef]
- Legon, A.C.; Thumwood, J.M.A.; Waclawik, E.R. Rotational spectroscopy of H3P⋯BrCl and the systematics of intermolecular electron transfer in the series B⋯BrCl, where B=CO, HCN, H2O, C2H2, C2H4, H2S, NH3, and PH3. J. Chem. Phys. 2000, 113, 5278. [Google Scholar] [CrossRef]
- Davey, J.B.; Legon, A.C. A gas phase complex of acetylene and bromine: Geometry, binding strength and charge transfer from rotational spectroscopy. Chem. Phys. Lett. 2001, 350, 39–50. [Google Scholar] [CrossRef]
- Legon, A.C.; Waclawik, E.R. Angular geometry, binding strength and charge transfer for the complex H2S⋯ICl determined by rotational spectroscopy. Chem. Phys. Lett. 1999, 312, 385–393. [Google Scholar] [CrossRef]
- Legon, A.C. Prereactive Complexes of Dihalogens XY with Lewis Bases B in the Gas Phase: A Systematic Case for the Halogen Analogue B⋯XY of the Hydrogen Bond B⋯HX. Angew. Chem. Int. Ed. 1999, 38, 2686–2714. [Google Scholar] [CrossRef]
- Herrebout, W.A.; Legon, A.C.; Waclawik, E.R. Is there significant intermolecular charge transfer in the ground state of the HCN⋯ICI complex? An answer from rotational spectroscopy. Phys. Chem. Chem. Phys. 1999, 1, 4961–4966. [Google Scholar] [CrossRef]
- Legon, A.C.; Millen, D.J.; Rogers, S.C. Microwave spectrum of a gas-phase charge-transfer complex. J. Chem. Soc. Chem. Commun. 1975, 580–581. [Google Scholar] [CrossRef]
- Bloemink, H.I.; Legon, A.C.; Thorn, J.C. ‘Charge-transfer’ complexes of ammonia with halogens. Nature of the binding in H3N⋯BrCl from its rotational spectrum. J. Chem. Soc. Faraday Trans. 1995, 91, 781–787. [Google Scholar] [CrossRef]
- Campbell, E.J.; Keenan, M.R.; Buxton, L.W.; Balle, T.J.; Soper, P.O.; Legon, A.C.; Flygare, W.H. 83Kr Nuclear quadrupole coupling in KrHF: Evidence for charge transfer. Chem. Phys. Lett. 1980, 70, 420–424. [Google Scholar] [CrossRef]
- Legon, A.C. π-Electron “Donor–Acceptor” Complexes B⋯ClF and the Existence of the “Chlorine Bond”. Chem. Eur. J. 1998, 4, 1890–1897. [Google Scholar] [CrossRef]
- Clark, T.; Politzer, P.; Murray, J.S. Correct electrostatic treatment of noncovalent interactions: The importance of polarization. WIRES Comput. Mol. Sci. 2015, 5, 169–177. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E.; Cremer, D. Quantitative Assessment of Halogen Bonding Utilizing Vibrational Spectroscopy. Inorg. Chem. 2017, 56, 488–502. [Google Scholar] [CrossRef]
- Sexton, T.; Kraka, E.; Cremer, D. Extraordinary Mechanism of the Diels–Alder Reaction: Investigation of Stereochemistry, Charge Transfer, Charge Polarization, and Biradicaloid Formation. J. Phys Chem. A 2016, 120, 1097–1111. [Google Scholar] [CrossRef]
- Zhao, Z.; Rogers, D.M.; Beck, T.L. Polarization and charge transfer in the hydration of chloride ions. J. Chem. Phys. 2010, 132, 014502. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, V.; Kraka, E.; Cremer, D. The intrinsic strength of the halogen bond: Electrostatic and covalent contributions described by coupled cluster theory. Phys. Chem. Chem. Phys. 2016, 18, 33031–33046. [Google Scholar] [CrossRef]
- Oliveira, V.; Kraka, E. Systematic Coupled Cluster Study of Noncovalent Interactions Involving Halogens, Chalcogens, and Pnicogens. J. Phys. Chem. A 2017, 121, 9544–9556. [Google Scholar] [CrossRef] [PubMed]
- Řezáč, J.; de la Lande, A. On the role of charge transfer in halogen bonding. Phys. Chem. Chem. Phys. 2017, 19, 791–803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.Y. Ligand(s)-to-metal charge transfer as a factor controlling the equilibrium constants of late first-row transition metal complexes: Revealing the Irving-Williams thermodynamical series. Phys. Chem. Chem. Phys. 2015, 17, 805–811. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R. Methylammonium Lead Trihalide Perovskite Solar Cell Semiconductors Are Not Organometallic: A Perspective. Helv. Chim. Acta 2017, 100, e1700090. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Revealing the Cooperative Chemistry of the Organic Cation in the Methylammonium Lead Triiodide Perovskite Semiconductor System. ChemistrySelect 2018, 3, 7269–7282. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Yamashita, K. Hybrid organic–inorganic CH3NH3PbI3 perovskite building blocks: Revealing ultra-strong hydrogen bonding and mulliken inner complexes and their implications in materials design. J. Comput. Chem. 2017, 38, 2802–2818. [Google Scholar] [CrossRef]
- Zieleniewska, A.; Lodermeyer, F.; Roth, A.; Guldi, D.M. Fullerenes—How 25 years of charge transfer chemistry have shaped our understanding of (interfacial) interactions. Chem. Soc. Rev. 2018, 47, 702–714. [Google Scholar] [CrossRef] [PubMed]
- Mollahosseini, M.; Karunaratne, E.; Gibson, G.N.; Gascón, J.A.; Papadimitrakopoulos, F. Fullerene-Assisted Photoinduced Charge Transfer of Single-Walled Carbon Nanotubes through a Flavin Helix. J. Am. Chem. Soc. 2016, 138, 5904–5915. [Google Scholar] [CrossRef] [PubMed]
- Meng, Y.-S.; Sato, O.; Liu, T. Manipulating Metal-to-Metal Charge Transfer for Materials with Switchable Functionality. Angew Chem. Int. Ed. 2018, 57, 12216–12226. [Google Scholar] [CrossRef]
- Dunsch, L.; Yang, S. The Recent State of Endohedral Fullerene Research. The Electrochemical Society: Interface. 2006, pp. 34–39. Available online: https://www.electrochem.org/dl/interface/sum/sum06/sum06_p34.pdf (accessed on 7 February 2019).
- Stasyuk, A.J.; Solà, M.; Voityuk, A.A. Reliable charge assessment on encapsulated fragment for endohedral systems. Sci. Rep. 2018, 8, 2882. [Google Scholar] [CrossRef]
- Robinson, S.W.; Mustoe, C.L.; White, N.G.; Brown, A.; Thompson, A.L.; Kennepohl, P.; Beer, P.D. Evidence for Halogen Bond Covalency in Acyclic and Interlocked Halogen-Bonding Receptor Anion Recognition. J. Am. Chem. Soc. 2015, 137, 499–507. [Google Scholar] [CrossRef] [PubMed]
- Mustoe, C.L.; Gunabalasingam, M.; Yu, D.; Patrick, B.O.; Kennepohl, P. Probing covalency in halogen bonds through donor K-edge X-ray absorption spectroscopy: Polyhalides as coordination complexes. Faraday Discuss. 2017, 203, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Puttreddy, R.; Topić, F.; Valkonen, A.; Rissanen, K. Halogen-Bonded Co-Crystals of Aromatic N-oxides: Polydentate Acceptors for Halogen and Hydrogen Bonds. Crystals 2017, 7, 214. [Google Scholar] [CrossRef]
- Ruedenberg, K. The Physical Nature of the Chemical Bond. Rev. Mod. Phys. 1962, 34, 326–376. [Google Scholar] [CrossRef]
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W. Molecular fragments or chemical bonds. Acc. Chem. Res. 1975, 8, 34–40. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Nguyen-Dang, T.T. Quantum Theory of Atoms in Molecules–Dalton Revisited. In Advances in Quantum Chemistry; Löwdin, P.-O., Ed.; Academic Press: New York, NY, USA, 1981; Volume 14, pp. 63–124. [Google Scholar]
- Bader, R.F.W.; Nguyen-Dang, T.T.; Tai, Y. A topological theory of molecular structure. Rep. Prog. Phys. 1981, 44, 893–947. [Google Scholar] [CrossRef]
- Bader, R.F.W. Atoms in molecules. Acc. Chem. Res. 1985, 18, 9–15. [Google Scholar] [CrossRef]
- Grabowski, S.J. What is the covalency of hydrogen bonding? Chem. Rev. 2011, 111, 2597–2625. [Google Scholar] [CrossRef]
- Quiñonero, D.; Alkorta, I.; Elguero, J. Cation–cation and anion–anion complexes stabilized by halogen bonds. Phys. Chem. Chem. Phys. 2016, 18, 27939–27950. [Google Scholar] [CrossRef] [Green Version]
- Politzer, P.; Huheey, J.E.; Murray, J.S.; Grodzicki, M. Electronegativity and the concept of charge capacity. J. Mol. Struct. THEOCHEM 1992, 259, 99–120. [Google Scholar] [CrossRef]
- Clark, T.; Murray, J.S.; Politzer, P. The σ-Hole Coulombic Interpretation of Trihalide Anion Formation. ChemPhysChem 2018, 19, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Riley, K.E.; Bulat, F.A.; Murray, J.S. Perspectives on Halogen Bonding and Other σ-Hole Interactions: Lex Parsimoniae (Occam’s Razor). Comput. Theor. Chem. 2012, 998, 2–8. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. σ-Hole Bonding: A Physical Interpretation. In Halogen Bonding I: Impact on Materials Chemistry and Life Science; Metrangolo, P., Resnati, G., Eds.; Springer International Publishing: Cham, Switzerland, 2015. [Google Scholar]
- Clark, T. σ-Holes. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2013, 3, 13–20. [Google Scholar] [CrossRef]
- Cremer, D.; Wu, A.; Larsson, A.; Kraka, E. Some Thoughts about Bond Energies, Bond Lengths, and Force Constants. J. Mol. Model. 2000, 6, 396–412. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. From Molecular Vibrations to Bonding, Chemical Reactions, and Reaction Mechanism. Curr. Org. Chem. 2010, 14, 1524–1560. [Google Scholar] [CrossRef]
- Zhu, T.; de Silva, P.; Van Voorhis, T. Self-Attractive Hartree Decomposition: Partitioning Electron Density into Smooth Localized Fragments. J. Chem. Theory Comput. 2018, 14, 92–103. [Google Scholar] [CrossRef]
- Wick, C.R.; Clark, T. On bond-critical points in QTAIM and weak interactions. J. Mol. Model. 2018, 24, 142. [Google Scholar] [CrossRef]
- Jansen, G. Symmetry-adapted perturbation theory based on density functional theory for noncovalent interactions. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 127–144. [Google Scholar] [CrossRef]
- Esterhuysen, C.; Heßelmann, A.; Clark, T. Trifluoromethyl: An Amphiphilic Noncovalent Bonding Partner. ChemPhysChem 2017, 18, 772–784. [Google Scholar] [CrossRef]
- Sharapa, D.I.; Margraf, J.T.; Hesselmann, A.; Clark, T. Accurate Intermolecular Potential for the C60 Dimer: The Performance of Different Levels of Quantum Theory. J. Chem. Theory Comput. 2017, 13, 274–285. [Google Scholar] [CrossRef] [PubMed]
- Vandenbrande, S.; Waroquier, M.; Speybroeck, V.V.; Verstraelen, T. The Monomer Electron Density Force Field (MEDFF): A Physically Inspired Model for Noncovalent Interactions. J. Chem. Theory Comput. 2017, 13, 161–179. [Google Scholar] [CrossRef] [PubMed]
- Heidar-Zadeh, F.; Ayers, P.W.; Verstraelen, T.; Vinogradov, I.; Vöhringer-Martinez, E.; Bultinck, P. Information-Theoretic Approaches to Atoms-in-Molecules: Hirshfeld Family of Partitioning Schemes. J. Phys. Chem. A 2018, 122, 4219–4245. [Google Scholar] [CrossRef] [PubMed]
- Verstraelen, T.; Ayers, P.W.; Van Speybroeck, V.; Waroquier, M. Hirshfeld-E Partitioning: AIM Charges with an Improved Trade-off between Robustness and Accurate Electrostatics. J. Chem. Theory Comput. 2013, 9, 2221–2225. [Google Scholar] [CrossRef] [PubMed]
- Szalewicz, K. Symmetry-adapted perturbation theory of intermolecular forces. WIREs Comput. Mol. Sci. 2012, 2, 254–272. [Google Scholar] [CrossRef]
- Fanfrlík, J.; Pecina, A.; Řezáč, J.; Sedlak, R.; Hnyk, D.; Lepšík, M.; Hobza, P. B–H⋯π: A nonclassical hydrogen bond or dispersion contact? Phys. Chem. Chem. Phys. 2017, 19, 18194–18200. [Google Scholar] [CrossRef]
- Zou, W.; Zhang, X.; Dai, H.; Yan, H.; Cremer, D.; Kraka, E. Description of an unusual hydrogen bond between carborane and a phenyl group. J. Organomet. Chem. 2018, 865, 114–127. [Google Scholar] [CrossRef]
- Zhang, X.; Dai, H.; Yan, H.; Zou, W.; Cremer, D. B–H⋯π Interaction: A New Type of Nonclassical Hydrogen Bonding. J. Am. Chem. Soc. 2016, 138, 4334–4337. [Google Scholar] [CrossRef]
- CSD 5.38; Cambridge Crystallographic Data Centre (CCDC): Cambridge, UK, 2016.
- Mackenzie, C.F.; Spackman, P.R.; Jayatilaka, D.; Spackman, M.A. CrystalExplorer model energies and energy frameworks: Extension to metal coordination compounds, organic salts, solvates and open-shell systems. IUCrJ 2017, 4, 575–587. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Varadwaj, A.; Jin, B.Y. Significant evidence of C⋯O and C⋯C long-range contacts in several heterodimeric complexes of CO with CH3–X, should one refer to them as carbon and dicarbon bonds! Phys. Chem. Chem. Phys. 2014, 16, 17238–17252. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A. Aerogen Bonding Interaction: A New Supramolecular Force? Angew Chem. Int. Ed. 2015, 54, 7340–7343. [Google Scholar] [CrossRef] [PubMed]
- Mitra, M.; Manna, P.; Bauzá, A.; Ballester, P.; Seth, S.K.; Ray Choudhury, S.; Frontera, A.; Mukhopadhyay, S. 3-Picoline Mediated Self-Assembly of M(II)–Malonate Complexes (M = Ni/Co/Mn/Mg/Zn/Cu) Assisted by Various Weak Forces Involving Lone Pair–π, π–π, and Anion⋯π–Hole Interactions. J. Phys. Chem. B 2014, 118, 14713–14726. [Google Scholar] [CrossRef] [PubMed]
- Shahi, A.; Arunan, E. Hydrogen bonding, halogen bonding and lithium bonding: An atoms in molecules and natural bond orbital perspective towards conservation of total bond order, inter- and intra-molecular bonding. Phys. Chem. Chem. Phys. 2014, 16, 22935–22952. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Marques, H.M.; Varadwaj, P.R. Is the Fluorine in Molecules Dispersive? Is Molecular Electrostatic Potential a Valid Property to Explore Fluorine-Centered Non-Covalent Interactions? Molecules 2019, 24, 379. [Google Scholar] [CrossRef]
- Eskandari, K.; Lesani, M. Does fluorine participate in halogen bonding? Chem. Eur. J. 2015, 21, 4739–4746. [Google Scholar] [CrossRef]
- Huggins, M.L. 50 Years of Hydrogen Bond Theory. Angew. Chem. Int. Ed. Engl. 1971, 10, 147–152. [Google Scholar] [CrossRef]
- Huggins, M.L. Hydrogen bridges in organic compounds. J. Org. Chem. 1936, 01, 407–456. [Google Scholar] [CrossRef]
- Pauling, L. The Structure and Entropy of Ice and of Other Crystals with Some Randomness of Atomic Arrangement. J. Am. Chem. Soc. 1935, 57, 2680–2684. [Google Scholar] [CrossRef]
- Colin, M.M.; Gaultier de Claubry, H. Sur Le Combinaisons de L’iode Avec Les Substances Végétales et Animales. Ann. Chim. 1814, 90, 87–100. [Google Scholar]
- Colin, M. Note Sur Quelques Combinaisons de L’iode. Ann. Chim. 1814, 91, 252–272. [Google Scholar]
- Guthrie, F. On the Iodide of Diammonium J. Chem. Soc. 1863, 16, 239–244. [Google Scholar] [CrossRef]
- Hassel, O. Structural Aspects on Interatomic Charge-Transfer Bonding. Science 1970, 170, 497–502. [Google Scholar] [CrossRef] [PubMed]
- Strømme, K.O. An X-Ray Analysis of the 1:1 Compound Trimethylamine-Iodine. Acta Chem. Scand. 1959, 13, 268–274. [Google Scholar] [CrossRef]
- Hassel, O.; Strømme, K.O. Crystal Structure of the Addition Compound 1,4-Dioxan-Chlorine. Acta Chem. Scand. 1959, 13, 1775–1780. [Google Scholar] [CrossRef]
- Hassel, O.; Strømme, K.O. Crystal Structure of the 1:1 Addition Compound Formed by Acetone and Bromine. Acta Chem. Scand. 1959, 13, 275–280. [Google Scholar] [CrossRef]
- Hassel, O. Structural Aspects of Interatomic Charge-Transfer Bonding. In Nobel Lectures, Chemistry 1963–1970; Elsevier Publishing Company: Amsterdam, The Netherlands, 1972; pp. 314–329. [Google Scholar]
- Dumas, J.-M.; Peurichard, H.; Gomel, M. CX4⋯Base Interactions as Models of Weak Charge-transfer Interactions: Comparison with Strong Charge-transfer and Hydrogen-bond Interactions. J. Chem. Res. S 1978, 2, 54–57. [Google Scholar]
- Jones, R.H.; Knight, K.S.; Marshall, W.G.; Coles, S.J.; Horton, P.N.; Pitak, M.B. The competition between halogen bonds (Br⋯O) and C–H⋯O hydrogen bonds: The structure of the acetone–bromine complex revisited. CrystEngComm 2013, 15, 8572–8577. [Google Scholar] [CrossRef]
- Marshall, W.G.; Jones, R.H.; Knight, K.S. Negative 2D thermal expansion in the halogen bonded acetone bromine complex. CrystEngComm 2018, 20, 3246–3250. [Google Scholar] [CrossRef]
- Bauzá, A.; Frontera, A. On the Importance of Halogen–Halogen Interactions in the Solid State of Fullerene Halides: A Combined Theoretical and Crystallographic Study. Crystals 2017, 7, 191. [Google Scholar] [CrossRef]
- Varadwaj, A.; Varadwaj, P.R.; Jin, B.-Y. Fluorines in tetrafluoromethane as halogen bond donors: Revisiting address the nature of the fluorine’s σ-hole. Int. J. Quantum Chem. 2015, 115, 453–470. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Lange, A.; Heidrich, J.; Zimmermann, M.O.; Exner, T.E.; Boeckler, F.M. Scaffold Effects on Halogen Bonding Strength. J. Chem. Inf. Model. 2019. [Google Scholar] [CrossRef] [PubMed]
- Brinck, T.; Murray, J.S.; Politzer, P. Surface electrostatic potentials of halogenated methanes as indicators of directional intermolecular interactions. Int. J. Quantum Chem. 1992, 44, 57–64. [Google Scholar] [CrossRef]
- Groenewald, F.; Esterhuysen, C.; Dillen, J. Extensive theoretical investigation: Influence of the electrostatic environment on the I3−⋯I3− anion–anion interaction. Theor. Chem. Acc. 2012, 131, 1281. [Google Scholar] [CrossRef]
- Pedireddi, V.R.; Reddy, D.S.; Goud, B.S.; Craig, D.C.; Rae, A.D.; Desiraju, G.R. The nature of halogen⋯halogen interactions and the crystal structure of 1,3,5,7-tetraiodoadamantane. J. Chem. Soc. Perkin Trans. 2 1994, 2353–2360. [Google Scholar] [CrossRef]
- Saha, B.K.; Nangia, A.; Nicoud, J.-F. Using Halogen⋯Halogen Interactions to Direct Noncentrosymmetric Crystal Packing in Dipolar Organic Molecules. Cryst. Growth Des. 2006, 6, 1278–1281. [Google Scholar] [CrossRef]
- Saha, B.K.; Saha, A.; Rather, S.A. Shape and Geometry Corrected Statistical Analysis on Halogen⋯Halogen Interactions. Cryst. Growth Des. 2017, 17, 2314–2318. [Google Scholar] [CrossRef]
- Saha, B.K.; Rather, S.A.; Saha, A. Interhalogen Interactions in the Light of Geometrical Correction. Cryst. Growth Des. 2016, 16, 3059–3062. [Google Scholar] [CrossRef]
- Bosch, E.; Barnes, C.L. Triangular Halogen-Halogen-Halogen Interactions as a Cohesive Force in the Structures of Trihalomesitylenes. Cryst. Growth Des. 2002, 2, 299–302. [Google Scholar] [CrossRef]
- Foi, A.; Corrêa, R.S.; Ellena, J.; Doctorovich, F.; Di Salvo, F. Halogen⋯halogen contacts for the stabilization of a new polymorph of 9,10-dichloroanthracene. J. Mol. Struct. 2014, 1059, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Metrangolo, P.; Resnati, G. Type II halogen⋯halogen contacts are halogen bonds. IUCrJ 2014, 1, 5–7. [Google Scholar] [CrossRef]
- Dunitz, J.D. Intermolecular atom–atom bonds in crystals? IUCrJ 2015, 2, 157–158. [Google Scholar] [CrossRef]
- Lecomte, C.; Espinosa, E.; Matta, C.F. On atom-atom "short contact" bonding interactions in crystals. IUCrJ 2015, 2, 161–163. [Google Scholar] [CrossRef]
- Tejender, S.; Thakur, T.S.; Dubeyb, R.; Desirajub, G.R. Intermolecular atom–atom bonds in crystals—A chemical perspective. IUCrJ 2015, 2, 159–160. [Google Scholar]
- Desiraju, G.R. Crystal engineering and IUCrJ. IUCrJ 2016, 3, 1–2. [Google Scholar] [CrossRef] [Green Version]
- Ayers, P.L.; Boyd, R.J.; Bultinck, P.; Caffarel, M.; Carbó-Dorca, R.; Causá, M.; Cioslowski, J.; Contreras-Garcia, J.; Cooper, D.L.; Coppens, P.; et al. Six questions on topology in theoretical chemistry. Comput. Theor. Chem. 2015, 1051, 2–16. [Google Scholar] [CrossRef]
- Huber, S.M.; Scanlon, J.D.; Jimenez-Izal, E.; Ugalde, J.M.; Infante, I. On the directionality of halogen bonding. Phys. Chem. Chem. Phys. 2013, 15, 10350–10357. [Google Scholar] [CrossRef]
- Grant Hill, J.; Legon, A.C. On the directionality and non-linearity of halogen and hydrogen bonds. Phys. Chem. Chem. Phys. 2015, 17, 858–867. [Google Scholar] [CrossRef] [Green Version]
- Desiraju, G.R. A bond by any other name. Angew. Chem. Int. Ed. 2011, 50, 52–59. [Google Scholar] [CrossRef]
- McAllister, L. Experimental and Theoretical Studies of the Halogen Bond and the Electrophilic Bromination Reaction. Ph.D. Thesis, The University of York, York, UK, 2014. [Google Scholar]
- Bader, R.F.W. Definition of Molecular Structure: By Choice or by Appeal to Observation? J. Phys. Chem. A 2010, 114, 7431–7444. [Google Scholar] [CrossRef]
- Meister, J.; Schwarz, W.H.E. Principal Components of Ionicity. J. Phys. Chem. 1994, 98, 8245–8252. [Google Scholar] [CrossRef]
- Matczak, P. A Test of Various Partial Atomic Charge Models for Computations on Diheteroaryl Ketones and Thioketones. Computation 2016, 4, 3. [Google Scholar] [CrossRef]
- Volkov, A.; Gatti, C.; Abramov, Y.; Coppens, P. Evaluation of net atomic charges and atomic and molecular electrostatic moments through topo-logical analysis of the experimental charge density. Acta Cryst. A 2000, 56, 252–258. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Matta, C.F. Atomic charges are measurable quantum expectation values: A rebuttal of criticisms of QTAIM charges. J. Phys. Chem. A 2004, 108, 8385–8394. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Concha, M.C. σ-hole bonding between like atoms; a fallacy of atomic charges. J. Mol. Model. 2008, 14, 659–665. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. The electrostatic potential: An overview. WIREs Comput. Mol. Sci. 2011, 1, 153–163. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Zadeh, D.H.; Lane, P.; Politzer, P. The role of “excluded” electronic charge in noncovalent interactions. Mol. Phys. 2018. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. The Hellmann-Feynman theorem: A perspective. J. Mol. Model. 2018, 24, 266. [Google Scholar] [CrossRef] [PubMed]
- Bultinck, P.; Cardenas, C.; Fuentealba, P.; Johnson, P.A.; Ayers, P.W. Atomic Charges and the Electrostatic Potential Are Ill-Defined in Degenerate Ground States. J. Chem. Theory Comput. 2013, 9, 4779–4788. [Google Scholar] [CrossRef]
- Ionescu, C.-M.; Sehnal, D.; Falginella, F.L.; Pant, P.; Pravda, L.; Boucha, T.; Vařeková, R.S.; Geidl, S.; Koča, J. Atomic Charge Calculator: Interactive web-based calculation of atomic charges in large biomolecular complexes and drug-like molecules. J. Cheminform. 2015, 7, 50. [Google Scholar] [CrossRef] [PubMed]
- Hamad, S.; Balestra, S.R.G.; Bueno-Perez, R.; Calero, S.; Ruiz-Salvador, A.R. Atomic charges for modeling metal–organic frameworks: Why and how. J. Solid State Chem. 2015, 223, 144–151. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Zhong, C. A General Approach for Estimating Framework Charges in Metal-Organic Frameworks. J. Phys. Chem. C 2010, 114, 5035–5042. [Google Scholar] [CrossRef]
- Mobley, D.L.; Dumont, E.; Chodera, J.D.; Dill, K.A. Comparison of Charge Models for Fixed-Charge Force Fields: Small-Molecule Hydration Free Energies in Explicit Solvent. J. Phys. Chem. B 2007, 111, 2242–2254. [Google Scholar] [CrossRef]
- Riniker, S. Fixed-Charge Atomistic Force Fields for Molecular Dynamics Simulations in the Condensed Phase: An Overview. J. Chem. Inf. Model. 2018, 58, 565–578. [Google Scholar] [CrossRef] [PubMed]
- Martin-Noble, G.C.; Reilley, D.; Rivas, L.M.; Smith, M.D.; Schrier, J. EQeq+C: An Empirical Bond-Order Corrected Extended Charge Equilibration Method. J. Chem. Theory Comput. 2015, 11, 3364–3374. [Google Scholar] [CrossRef] [PubMed]
- Lynden-Bell, R.M.; Stone, A.J. A model with charges and polarizability for CS2 in an ionic liquid. J. Chem. Sci. 2017, 129, 883–890. [Google Scholar] [CrossRef]
- Scholfield, M.R.; Ford, M.C.; Carlsson, A.-C.C.; Butta, H.; Mehl, R.A.; Ho, P.S. Structure–Energy Relationships of Halogen Bonds in Proteins. Biochemistry 2017, 56, 2794–2802. [Google Scholar] [CrossRef]
- Scholfield, M.R.; Zanden, C.M.V.; Carter, M.; Shing Ho, P. Halogen bonding (X-bonding): A biological perspective. Protein Sci. 2013, 22, 139–152. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Lane, P.; Concha, M.C. Electrostatically driven complexes of SiF4 with amines. Int. J. Quant. Chem. 2009, 109, 3773–3780. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding: An electrostatically-driven highly directional noncovalent interaction. Phys. Chem. Chem. Phys. 2010, 12, 7748–7757. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Lane, P.; Concha, M.C.; Ma, Y.; Murray, J.S. An Overview of Halogen Bonding. J. Mol. Model. 2007, 13, 305–311. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Riley, R.E.; Politzer, P.; Clark, T. Directional weak intermolecular interactions: σ-hole bonding. Aust. J. Chem. 2010, 63, 1598–1607. [Google Scholar] [CrossRef]
- Riley, K.E.; Tran, K.-A. Strength, character, and directionality of halogen bonds involving cationic halogen bond donors. Faraday Discuss. 2017, 203, 47–60. [Google Scholar] [CrossRef] [PubMed]
- Yahia-Ouahmed, M.; Tognetti, V.; Joubert, L. Intramolecular halogen bonding: An interacting quantum atoms study. Theor. Chem. Acc. 2016, 135, 45. [Google Scholar] [CrossRef]
- Lin, F.-Y.; MacKerell, A.D. Do Halogen–Hydrogen Bond Donor Interactions Dominate the Favorable Contribution of Halogens to Ligand–Protein Binding? J. Phys. Chem. B 2017, 121, 6813–6821. [Google Scholar] [CrossRef]
- Neaton, J.B. A direct look at halogen bonds. Science 2017, 358, 167–168. [Google Scholar] [CrossRef]
- Riley, K.E.; Hobza, P. Investigations into the Nature of Halogen Bonding Including Symmetry Adapted Perturbation Theory Analyses. J. Chem. Theory Comput. 2008, 4, 232–242. [Google Scholar] [CrossRef]
- Mu, X.; Wang, Q.; Wang, L.-P.; Fried, S.D.; Piquemal, J.-P.; Dalby, K.N.; Ren, P. Modeling Organochlorine Compounds and the σ-Hole Effect Using a Polarizable Multipole Force Field. J. Phys. Chem. B 2014, 118, 6456–6465. [Google Scholar] [CrossRef]
- Kolář, M.H.; Hobza, P. Computer Modeling of Halogen Bonds and Other σ-Hole Interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [Green Version]
- Johansson, M.P.; Swart, M. Intramolecular halogen–halogen bonds? Phys. Chem. Chem. Phys. 2013, 15, 11543–11553. [Google Scholar] [CrossRef] [PubMed]
- Mo, Y.; Bao, P.; Gao, J. Energy decomposition analysis based on a block-localized wavefunction and multistate density functional theory. Phys. Chem. Chem. Phys. 2011, 13, 6760–6775. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. Electrostatically enhanced F⋯F interactions through hydrogen bonding, halogen bonding and metal coordination: An ab initio study. Phys. Chem. Chem. Phys. 2016, 18, 20381–20388. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Frontera, A. Theoretical study on σ- and π-hole carbon⋯carbon bonding interactions: Implications in CFC chemistry. Phys. Chem. Chem. Phys. 2016, 18, 32155–32159. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Murray, J.S.; Pilati, T.; Politzer, P.; Resnati, G.; Terraneo, G. The fluorine atom as a halogen bond donor, viz. a positive site. Cryst. Eng. Commun. 2011, 13, 6593–6596. [Google Scholar] [CrossRef] [Green Version]
- Metrangolo, P.; Murray, J.S.; Pilati, T.; Politzer, P.; Resnati, G.; Terraneo, G. Fluorine-centered halogen bonding: A factor in recognition phenomena and reactivity. Cryst. Growth Des. 2011, 11, 4238–4246. [Google Scholar] [CrossRef]
- Panini, P.; Chopra, D. Understanding of Noncovalent Interactions Involving Organic Fluorine. In Hydrogen Bonded Supramolecular Structures. Lecture Notes in Chemistry; Li, Z.T., Wu, L.Z., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; Volume 87. [Google Scholar]
- Chaplot, S.L.; McIntyre, G.J.; Mierzejewski, A.; Pawley, G.S. Structure of 1,3,5-trichloro-2,4,6-trifluorobenzene. Acta Crystallogr. B 1981, 37, 1896–1900. [Google Scholar] [CrossRef] [Green Version]
- Desiraju, G.R. Supramolecular Synthons in Crystal Engineering—A New Organic Synthesis. Angew. Chem. Int. Ed. 1995, 34, 2311–2327. [Google Scholar] [CrossRef]
- Legon, A.C.; Walker, N.R. What’s in a name? “Coinage-metal” non-covalent bonds and their definition. Phys. Chem. Chem. Phys. 2018, 20, 19332–19338. [Google Scholar] [CrossRef]
- Ghosh, S.; Reddy, C.M.; Desiraju, G.R. Hexaiodobenzene: A redetermination at 100 K. Acta Crystallogr. E 2007, 63, o910–o911. [Google Scholar] [CrossRef]
- Khotsyanova, T.L.; Smirnova, V.I. Crystal and Molecular Structure of hexaiodobenzene. Kristallografiya 1968, 13, 787–790. [Google Scholar]
- Steer, R.J.; Watkins, S.F.; Woodward, P. Crystal and molecular structure of hexaiodobenzene. J. Chem. Soc. C 1970, 403–408. [Google Scholar] [CrossRef]
- Han, Z.; Czap, G.; Chiang, C.; Xu, C.; Wagner, P.J.; Wei, X.; Zhang, Y.; Wu, R.; Ho, W. Imaging the halogen bond in self-assembled halogenbenzenes on silver. Science 2017, 358, 206–210. [Google Scholar] [CrossRef]
- Liu, M.; Zeng, Y.; Sun, Z.; Meng, L. Predicting the halogen-n (n = 3–6) synthons to form the “windmill” pattern bonding based on the halogen-bonded interactions. J. Comput. Chem. 2019. [Google Scholar] [CrossRef]
- Bader, R.F. Atoms in Molecules: A Quantum Theory; Oxford University Press: Oxford, UK, 1990. [Google Scholar]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef] [Green Version]
- De Silva, P.; Corminboeuf, C. Simultaneous Visualization of Covalent and Noncovalent Interactions Using Regions of Density Overlap. J. Chem. Theory Comput. 2014, 10, 3745–3756. [Google Scholar] [CrossRef]
- Becke, A.D.; Edgecombe, K.E. A simple measure of electron localization in atomic and molecular systems. J. Chem. Phys. 1990, 92, 5397–5403. [Google Scholar] [CrossRef]
- Silvi, B.; Savin, A. Classification of chemical bonds based on topological analysis of electron localization functions. Nature 1994, 371, 683. [Google Scholar] [CrossRef]
- Yu, M.; Trinkle, D.R. Accurate and efficient algorithm for Bader charge integration. J. Chem. Phys. 2011, 134, 064111. [Google Scholar] [CrossRef]
- Parr, R.G.; Weitao, Y. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Keith, T.A. AIMAll, version 17.01.25; TK Gristmill Software: Overland Park, KS, USA, 2016; Available online: http://aim.tkgristmill.com (accessed on 7 February 2019).
- Bader, R.F.W. A Bond Path: A Universal Indicator of Bonded Interactions. J. Phys. Chem. A 1998, 102, 7314–7323. [Google Scholar] [CrossRef]
- Panini, P.; Gonnade, R.G.; Chopra, D. Experimental and computational analysis of supramolecular motifs involving Csp2(aromatic)–F and CF3 groups in organic solids. New J. Chem. 2016, 40, 4981–5001. [Google Scholar] [CrossRef]
- Bankiewicz, B.; Matczak, P.; Palusiak, M. Electron Density Characteristics in Bond Critical Point (QTAIM) versus Interaction Energy Components (SAPT): The Case of Charge-Assisted Hydrogen Bonding. J. Phys. Chem. A 2012, 116, 452–459. [Google Scholar] [CrossRef] [PubMed]
- Checinska, L.; Grabowsky, S.; Malecka, M.; Rybarczyk-Pirek, A.J.; Józwiak, A.; Paulmann, C.; Luger, P. Experimental and theoretical electron-density study of three isoindole derivatives: Topological and Hirshfeld surface analysis of weak intermolecular interactions. Acta Crystallogr. B 2011, 67, 569–581. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, A.; Varadwaj, P.R.; Marques, H.M.; Yamashita, K. Halogen in materials design: Revealing the nature of hydrogen bonding and other non-covalent interactions in the polymorphic transformations of methylammonium lead tribromide perovskite. Mater. Today Chem. 2018, 9, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Varadwaj, P.R.; Varadwaj, A.; Marques, H.M.; Yamashita, K. Significance of hydrogen bonding and other noncovalent interactions in determining octahedral tilting in the CH3NH3PbI3 hybrid organic–inorganic halide perovskite solar cell semiconductor. Sci. Rep. 2019, 9, 50. [Google Scholar] [CrossRef] [PubMed]
- Escudero-Adán, E.C.; Bauzá, A.; Lecomte, C.; Frontera, A.; Ballester, P. Boron triel bonding: A weak electrostatic interaction lacking electron-density descriptors. Phys. Chem. Chem. Phys. 2018, 20, 24192–24200. [Google Scholar] [CrossRef] [PubMed]
- Lane, J.R.; Schrøder, S.D.; Saunders, G.C.; Kjaergaard, H.G. Intramolecular Hydrogen Bonding in Substituted Aminoalcohols. J. Phys. Chem. A 2016, 120, 6371–6378. [Google Scholar] [CrossRef] [PubMed]
- Lane, J.R.; Contreras-García, J.; Piquemal, J.-P.; Miller, B.J.; Kjaergaard, H.G. Are Bond Critical Points Really Critical for Hydrogen Bonding? J. Chem. Theory Comput. 2013, 9, 3263–3266. [Google Scholar] [CrossRef]
- Outeiral, C.; Vincent, M.A.; Martín Pendás, Á.; Popelier, P.L.A. Revitalizing the concept of bond order through delocalization measures in real space. Chem. Sci. 2018, 9, 5517–5529. [Google Scholar] [CrossRef]
- Poater, J.; Duran, M.; Solà, M.; Silvi, B. Theoretical Evaluation of Electron Delocalization in Aromatic Molecules by Means of Atoms in Molecules (AIM) and Electron Localization Function (ELF) Topological Approaches. Chem. Rev. 2005, 105, 3911–3947. [Google Scholar] [CrossRef]
- Poater, J.; Fradera, X.; Duran, M.; Solá, M. The delocalization index as an electronic aromaticity criterion: Application to a series of planar polycyclic aromatic hydrocarbons. Chem. Eur. J. 2003, 9, 400–406. [Google Scholar] [CrossRef] [PubMed]
- Firme, C.L.; Antunes, O.A.C.; Esteves, P.M. Relation between bond order and delocalization index of QTAIM. Chem. Phys. Lett. 2009, 468, 129–133. [Google Scholar] [CrossRef]
- Farrugia, L.J.; Evans, C.; Lentz, D.; Roemer, M. The QTAIM Approach to Chemical Bonding Between Transition Metals and Carbocyclic Rings: A Combined Experimental and Theoretical Study of (η5-C5H5)Mn(CO)3, (η6-C6H6)Cr(CO)3, and (E)-((η5-C5H4)CF=CF(η5-C5H4))(η5-C5H5)2Fe2. J. Am. Chem. Soc. 2009, 131, 1251–1268. [Google Scholar] [CrossRef] [PubMed]
- Monza, E.; Gatti, C.; Lo Presti, L.; Ortoleva, E. Revealing Electron Delocalization through the Source Function. J. Phys. Chem. A 2011, 115, 12864–12878. [Google Scholar] [CrossRef] [PubMed]
- Bader, R.F.W.; MacDougall, P.J. Toward a theory of chemical reactivity based on the charge density. J. Am. Chem. Soc. 1985, 107, 6788–6795. [Google Scholar] [CrossRef]
- Cremer, D.; Kraka, E. A Description of the Chemical Bond in Terms of Local Properties of Electron Density and Energy. Croat. Chem. Acta 1984, 57, 1259–1281. [Google Scholar]
- Cremer, D.; Kraka, E. Chemical Bonds without Bonding Electron Density—Does the Difference Electron-Density Analysis Suffice for a Description of the Chemical Bond? Angew. Chem. Int. Ed. Engl. 1984, 23, 627–628. [Google Scholar] [CrossRef]
- Kraka, E.; Cremer, D. Chemical Implications of Local Features of the Electron Density Distribution; Springer-Verlag: Heidelberg, Germany, 1990; Volume 2. [Google Scholar]
- Lane, J.R.; Hansen, A.S.; Mackeprang, K.; Kjaergaard, H.G. Kinetic Energy Density as a Predictor of Hydrogen-Bonded OH-Stretching Frequencies. J. Phys. Chem. A 2017, 121, 3452–3460. [Google Scholar] [CrossRef] [PubMed]
- Varadwaj, P.R.; Marques, H.M. The physical chemistry of coordinated aqua-, ammine-, and mixed-ligand Co2+ complexes: DFT studies on the structure, energetics, and topological properties of the electron density. Phys. Chem. Chem. Phys. 2010, 12, 2126–2138. [Google Scholar] [CrossRef]
- Varadwaj, P.R.; Marques, H.M. The physical chemistry of [M(H2O)4(NO3)2] (M = Mn2+, Co2+, Ni2+, Cu2+, Zn2+) complexes: Computational studies of their structure, energetics and the topological properties of the electron density. Theor. Chem. Acc. 2010, 127, 711–725. [Google Scholar] [CrossRef]
- Lefebvre, C.; Rubez, G.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Hénon, E. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density. Phys. Chem. Chem. Phys. 2017, 19, 17928–17936. [Google Scholar] [CrossRef] [PubMed]
- Lefebvre, C.; Khartabil, H.; Boisson, J.-C.; Contreras-García, J.; Piquemal, J.-P.; Hénon, E. The Independent Gradient Model: A New Approach for Probing Strong and Weak Interactions in Molecules from Wave Function Calculations. ChemPhysChem 2018, 19, 724–735. [Google Scholar] [CrossRef] [PubMed]
- An, X.; Kang, Y.; Li, G. The interaction between chitosan and tannic acid calculated based on the density functional theory. Chem. Phys. 2019, 520, 100–107. [Google Scholar] [CrossRef]
- Kyzyma, O.; Bashmakova, N.; Gorshkova, Y.; Ivankov, O.; Mikheev, I.; Kuzmenko, M.; Kutovyy, S.; Nikolaienko, T. Interaction between the plant alkaloid berberine and fullerene C70: Experimental and quantum-chemical study. J. Mol. Liquids 2019, 278, 452–459. [Google Scholar] [CrossRef]
- Venkataramanan, N.S.; Suvitha, A. Nature of bonding and cooperativity in linear DMSO clusters: A DFT, AIM and NCI analysis. J. Mol. Graph. Model. 2018, 81, 50–59. [Google Scholar] [CrossRef]
- Zhao, X.; Huang, S.; Liu, Y.; Li, J.; Zhu, W. Effects of Noncovalent Interactions on the Impact Sensitivity of HNS-Based Cocrystals: A DFT Study. Cryst. Growth Des. 2019, 19, 756–767. [Google Scholar] [CrossRef]
- Lu, T.; Chen, F. A multifunctional wavefunction analyzer. J. Comput. Chem. 2012, 33, 580–592. [Google Scholar] [CrossRef]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Greer, S.C.; Meyer, L. CF4: Crystal Structure and Solid Phase Diagram with Ar. J. Chem. Phys. 1969, 51, 4583–4586. [Google Scholar] [CrossRef]
- Bol’shutkin, D.N.; Gasan, V.M.; Prokhvatilov, A.I.; Erenburg, A.I. The crystal structure of α-CF4. Acta Cryst. B 1972, 28, 3542–3547. [Google Scholar] [CrossRef]
- Pepè, G.; Gay, J.-M. Structure of α-CF4 at low temperature. J. Chem. Phys. 1989, 90, 5735–5737. [Google Scholar] [CrossRef]
- Fitch, A.N. The structure of solid carbon tetrafluoride. Z. Krist. Cryst. Mater. 1993, 203, 29–40. [Google Scholar]
- Metrangolo, P.; Resnati, G. Halogen Versus Hydrogen. Science 2008, 321, 918–919. [Google Scholar] [CrossRef] [PubMed]
- Donald, K.J.; Tawfik, M. The Weak Helps the Strong: σ-Holes and the Stability of MF4·Base Complexes. J. Phys. Chem. A 2013, 117, 14176–14183. [Google Scholar] [CrossRef]
- Osuna, R.M.; Hernández, V.; Navarrete, J.T.L.; D’Oria, E.; Novoa, J.J. Theoretical evaluation of the nature and strength of the F⋯F intermolecular interactions present in fluorinated hydrocarbons. Theor. Chem. Acc. 2011, 128, 541–553. [Google Scholar] [CrossRef]
- Wheeler, S.E.; Bloom, J.W.G. Toward a More Complete Understanding of Noncovalent Interactions Involving Aromatic Rings. J. Phys. Chem. A 2014, 118, 6133–6147. [Google Scholar] [CrossRef]
- Grabowski, S. Lewis Acid Properties of Tetrel Tetrafluorides—The Coincidence of the σ-Hole Concept with the QTAIM Approach. Crystals 2017, 7, 43. [Google Scholar] [CrossRef]
- Alabugin, I.V.; Gilmore, K.M.; Peterson, P.W. Hyperconjugation. WIREs Comput. Mol. Sci. 2011, 1, 109–141. [Google Scholar] [CrossRef]
- Piermarini, G.J.; Braun, A.B. Crystal and molecular structure of CCl4 III: A high pressure polymorph at 10 kbar. J. Chem. Phys. 1973, 58, 1974–1982. [Google Scholar] [CrossRef]
- Cohen, S.; Powers, R.; Rudman, R. Polymorphism of the crystalline methylchloromethane compounds. VI. The crystal and molecular structure of ordered carbon tetrachloride. Acta Cryst. B 1979, 35, 1670–1674. [Google Scholar] [CrossRef] [Green Version]
- More, M.; Baert, F.; Lefebvre, J. Solid-state phase transition in carbon tetrabromide CBr4. I. The crystal structure of phase II at room temperature. Acta Cryst. B 1977, 33, 3681–3684. [Google Scholar] [CrossRef]
- Lindeman, S.V.; Hecht, J.; Kochi, J.K. The Charge-Transfer Motif in Crystal Engineering. Self-Assembly of Acentric (Diamondoid) Networks from Halide Salts and Carbon Tetrabromide as Electron-Donor/Acceptor Synthons. J. Am. Chem. Soc. 2003, 125, 11597–11606. [Google Scholar] [CrossRef]
- Eucken, A. Rotation von Molekeln und Iongruppen in Kristallen. Z. Elektrochem. Angew. Phys. Chem. 1939, 45, 126–150. [Google Scholar]
- Pohl, S. Die Kristallstruktur von CI4. Z. Krisattlogr. 1982, 159, 211. [Google Scholar] [CrossRef]
- Troyanov, S.I.; Shustova, N.B.; Popov, A.A.; Sidorov, L.N.; Kemnitz, E. Preparation and Structural Characterization of Two Kinetically Stable Chlorofullerenes, C60Cl28 and C60Cl30. Angew. Chem. 2005, 117, 436–439. [Google Scholar] [CrossRef]
- Troshin, P.A.; Kemnitz, E.; Troyanov, S.I. CCDC 230207: Experimental Crystal Structure Determination; Cambridge Crystallographic Data Centre: Cambridge, UK, 2004; p. 2675. [Google Scholar]
- Singh, G.; Verma, R.; Gadre, S.R. Understanding Packing Patterns in Crystals by Analysis of Small Aggregates: A Case Study of CS2. J. Phys. Chem. A 2015, 119, 13055–13063. [Google Scholar] [CrossRef] [PubMed]
- Douvris, C.; Stoyanov, E.S.; Tham, F.S.; Reed, C.A. Isolating fluorinated carbocations. Chem. Commun. 2007, 1145–1147. [Google Scholar] [CrossRef] [PubMed]
- Metrangolo, P.; Pilati, T.; Resnati, G.; Stevenazzi, A. Metric engineering of perfluorocarbon–hydrocarbon layered solids driven by the halogen bonding. Chem. Commun. 2004, 1492–1493. [Google Scholar] [CrossRef]
- Metrangolo, P.; Präsang, C.; Resnati, G.; Liantonio, R.; Whitwood, A.C.; Bruce, D.W. Fluorinated liquid crystals formed by halogen bonding. Chem. Commun. 2006, 3290–3292. [Google Scholar] [CrossRef]
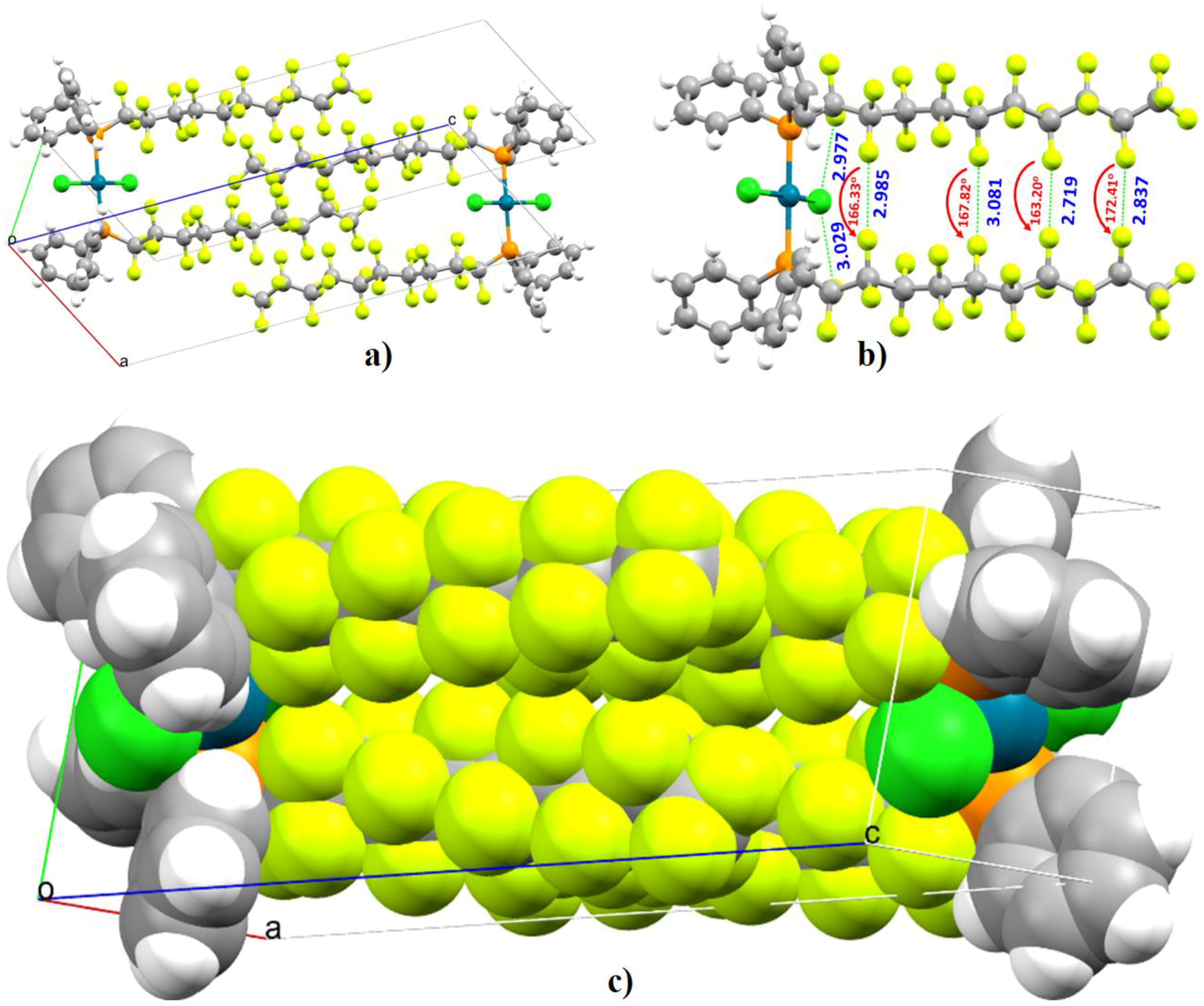
- Brisdon, A.K.; Muneer, A.M.T.; Pritchard, R.G. Halogen bonding in a series of Br(CF2)nBr–DABCO adducts (n = 4, 6, 8). Acta Crystallogr. C 2017, 73, 874–879. [Google Scholar] [CrossRef]
- Liu, X.; McMillen, C.D.; Thrasher, J.S. Cooperative intermolecular S–Cl⋯O and F⋯F associations in the crystal packing of α,ω-di(sulfonyl chloride) perfluoroalkanes, ClSO2(CF2)nSO2Cl, where n = 4, 6. New J. Chem. 2018, 42, 10484–10488. [Google Scholar] [CrossRef]
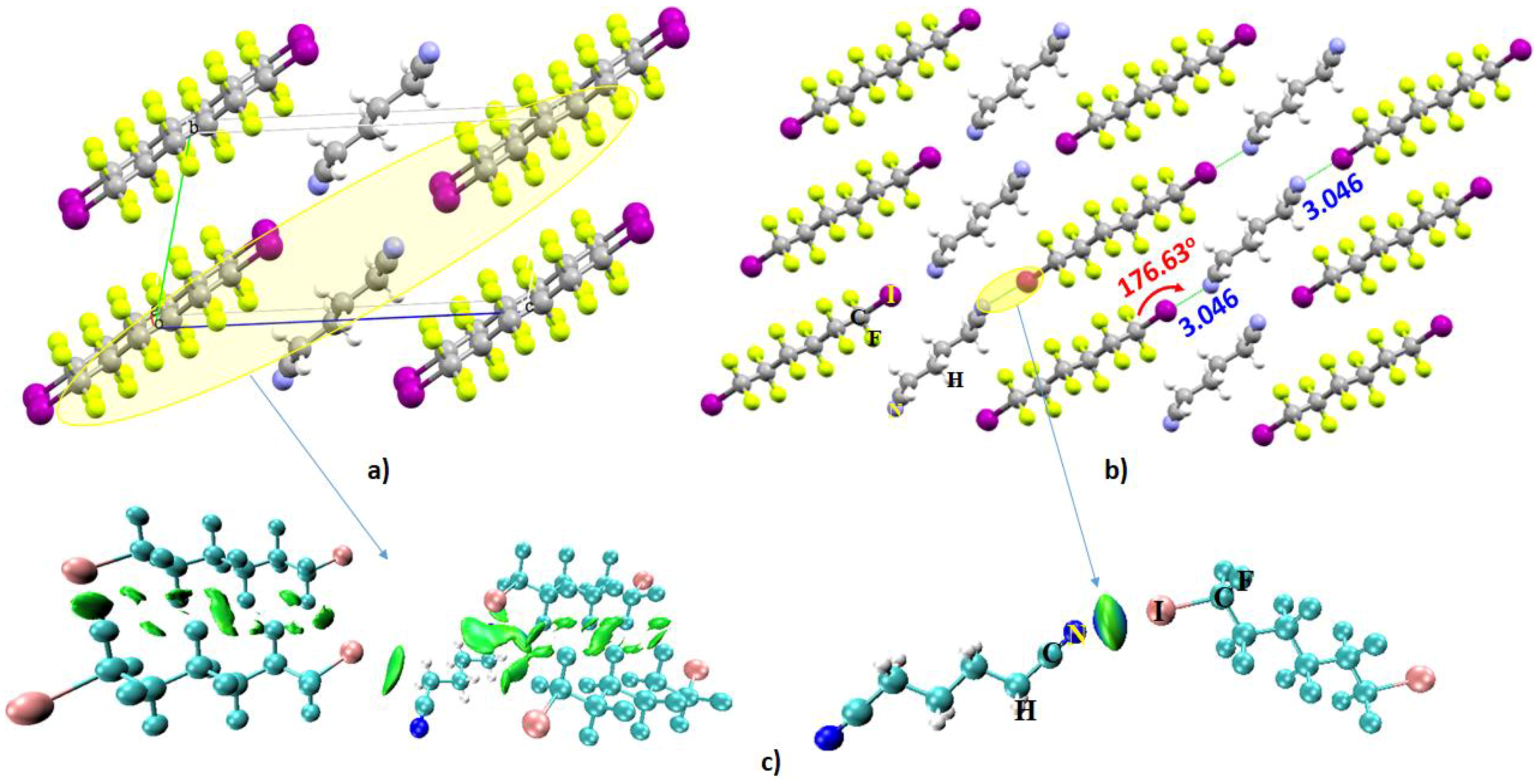
- Kawaguchi, S.-I.; Minamida, Y.; Ohe, T.; Nomoto, A.; Sonoda, M.; Ogawa, A. Synthesis and Properties of Perfluoroalkyl Phosphine Ligands: Photoinduced Reaction of Diphosphines with Perfluoroalkyl Iodides. Angew. Chem. Int. Ed. 2013, 52, 1748–1752. [Google Scholar] [CrossRef] [PubMed]






















| 0.0010 | 0.0015 | 0.00165 | 0.0017 | 0.0018 | 0.0020 | 0.0025 | 0.0030 | 0.0035 | 0.0040 | 0.0050 | 0.0055 |
| - a | - a | −3.72 | −3.70 | −3.64 | −3.50 | −3.10 | −2.60 | −2.10 | −1.52 | −0.25 | +0.41 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varadwaj, P.R.; Varadwaj, A.; Marques, H.M. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics 2019, 7, 40. https://doi.org/10.3390/inorganics7030040
Varadwaj PR, Varadwaj A, Marques HM. Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood. Inorganics. 2019; 7(3):40. https://doi.org/10.3390/inorganics7030040
Chicago/Turabian StyleVaradwaj, Pradeep R., Arpita Varadwaj, and Helder M. Marques. 2019. "Halogen Bonding: A Halogen-Centered Noncovalent Interaction Yet to Be Understood" Inorganics 7, no. 3: 40. https://doi.org/10.3390/inorganics7030040