FEDformer-Based Paddy Quality Assessment Model Affected by Toxin Change in Different Storage Environments
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Data
2.1.2. Experimental Environment
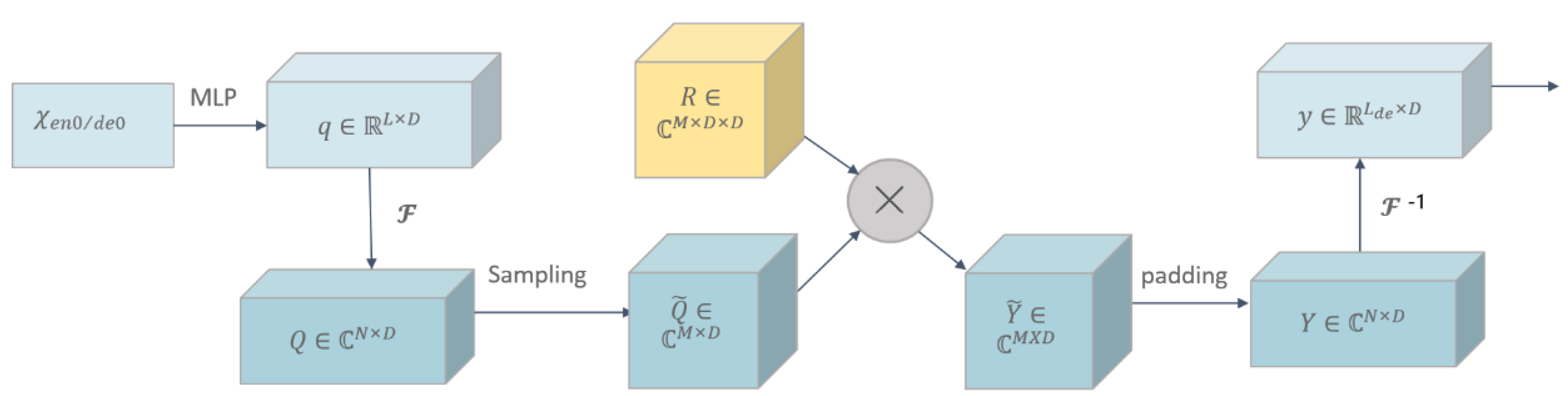
2.2. FEDformer-Based Paddy Quality Prediction Model
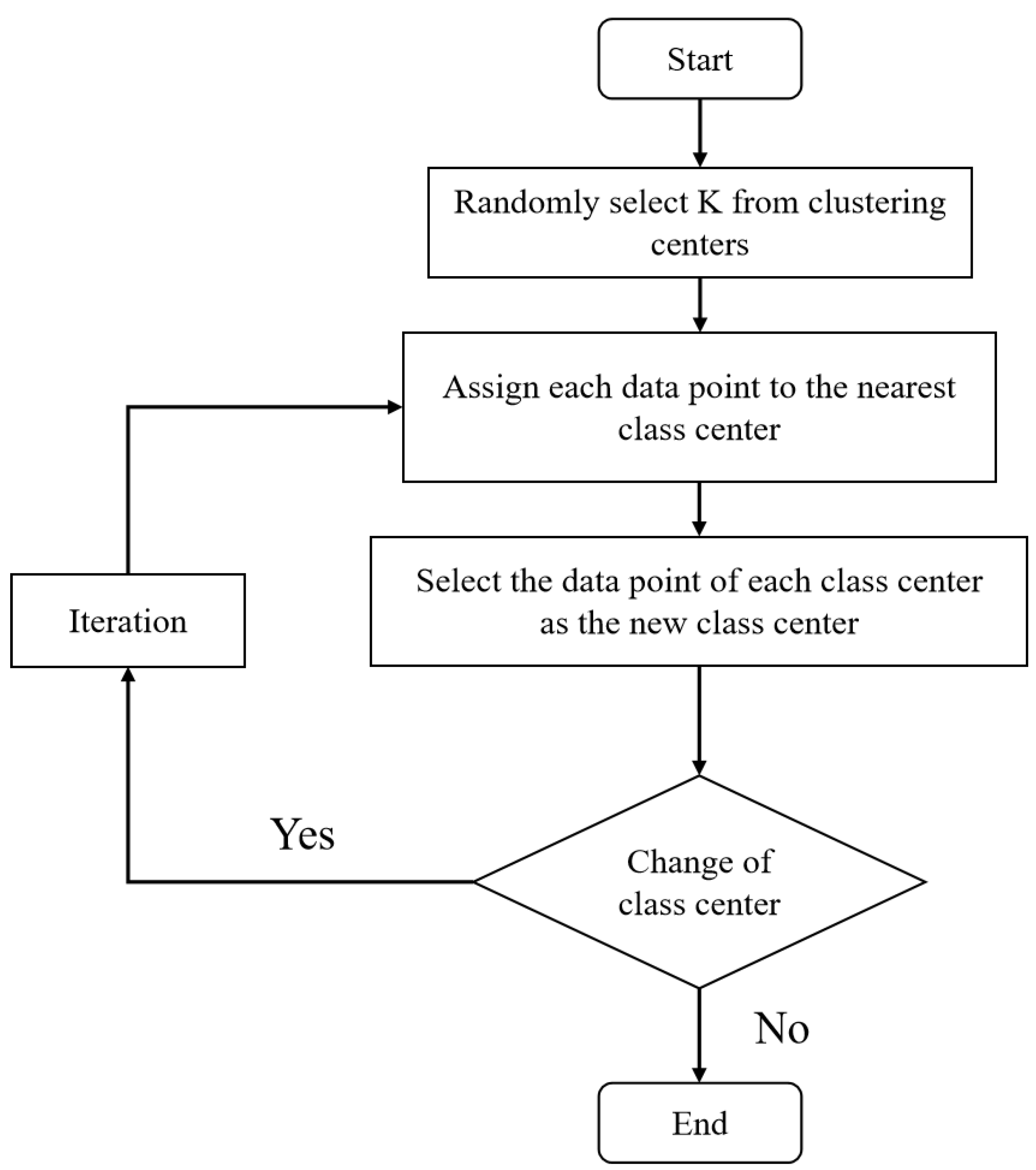
2.3. K-Medoids-Based Model for Paddy Quality Assessment
2.4. Model Evaluation Metrics
2.4.1. Evaluation Metrics for Predictive Models
2.4.2. Evaluation Metrics for Clustering Models
3. Results and Discussion
3.1. Comparison of Predictive Paddy Quality Assessment Models
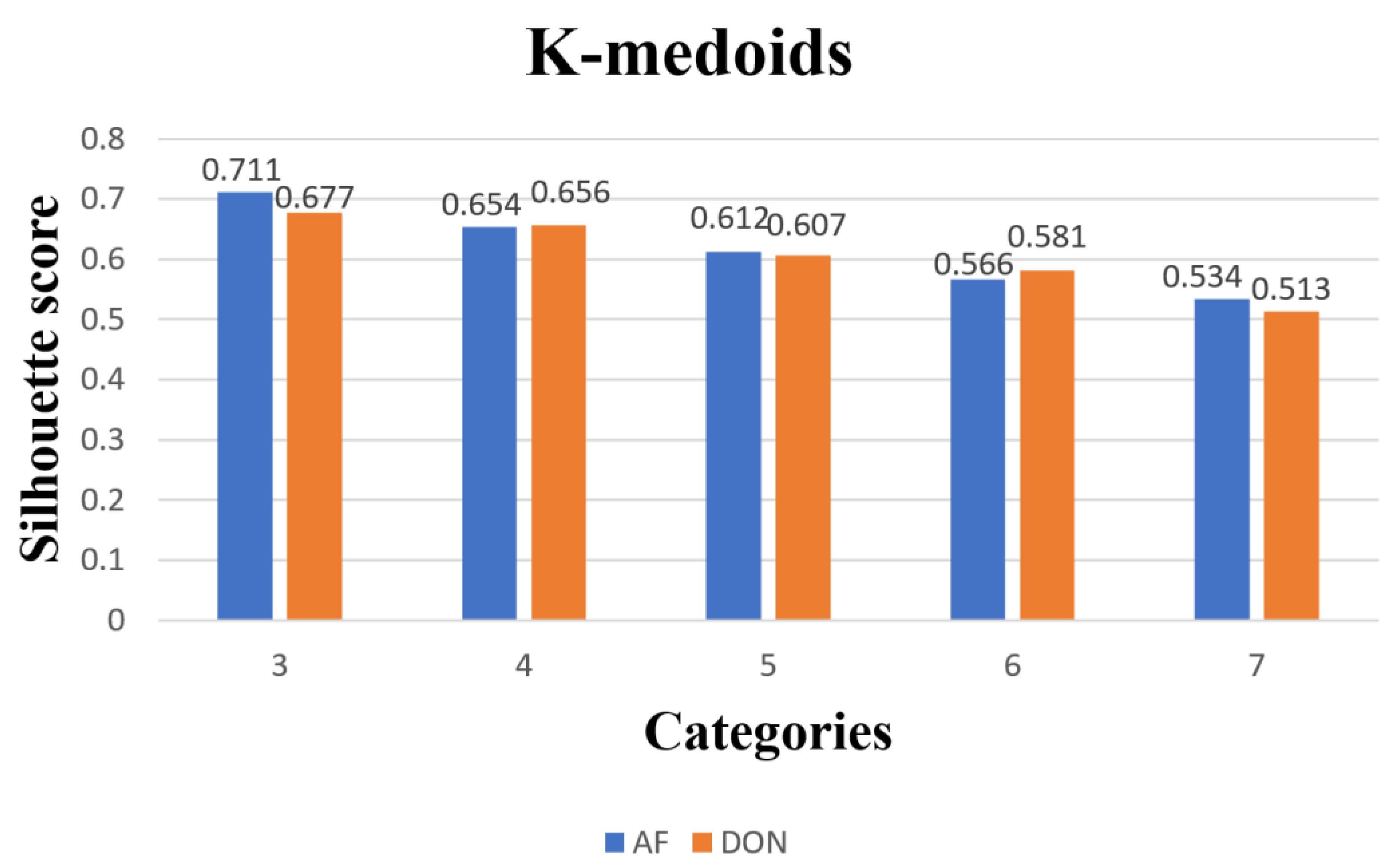
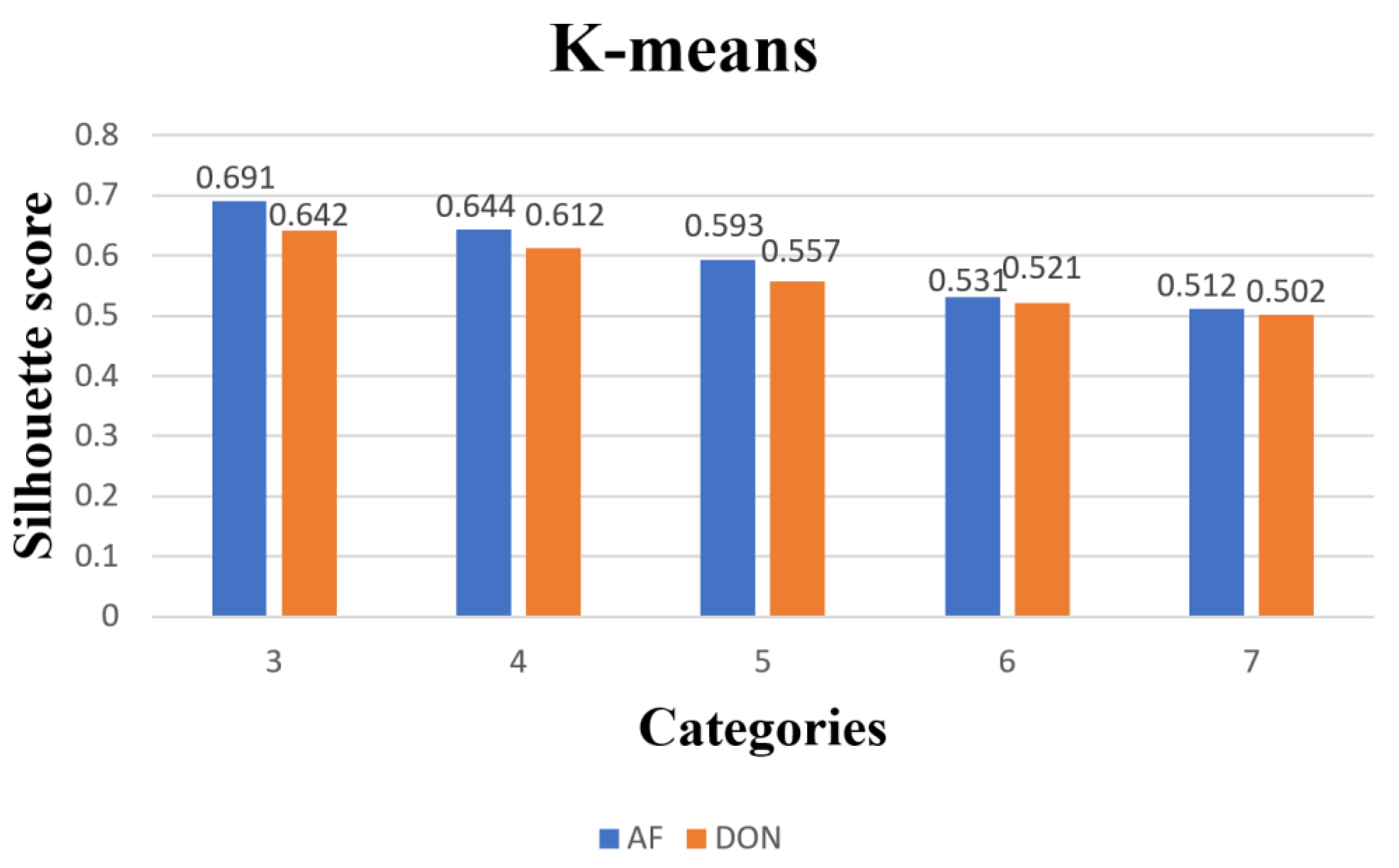
3.2. Comparison of Clustering Models for Paddy Quality Variation
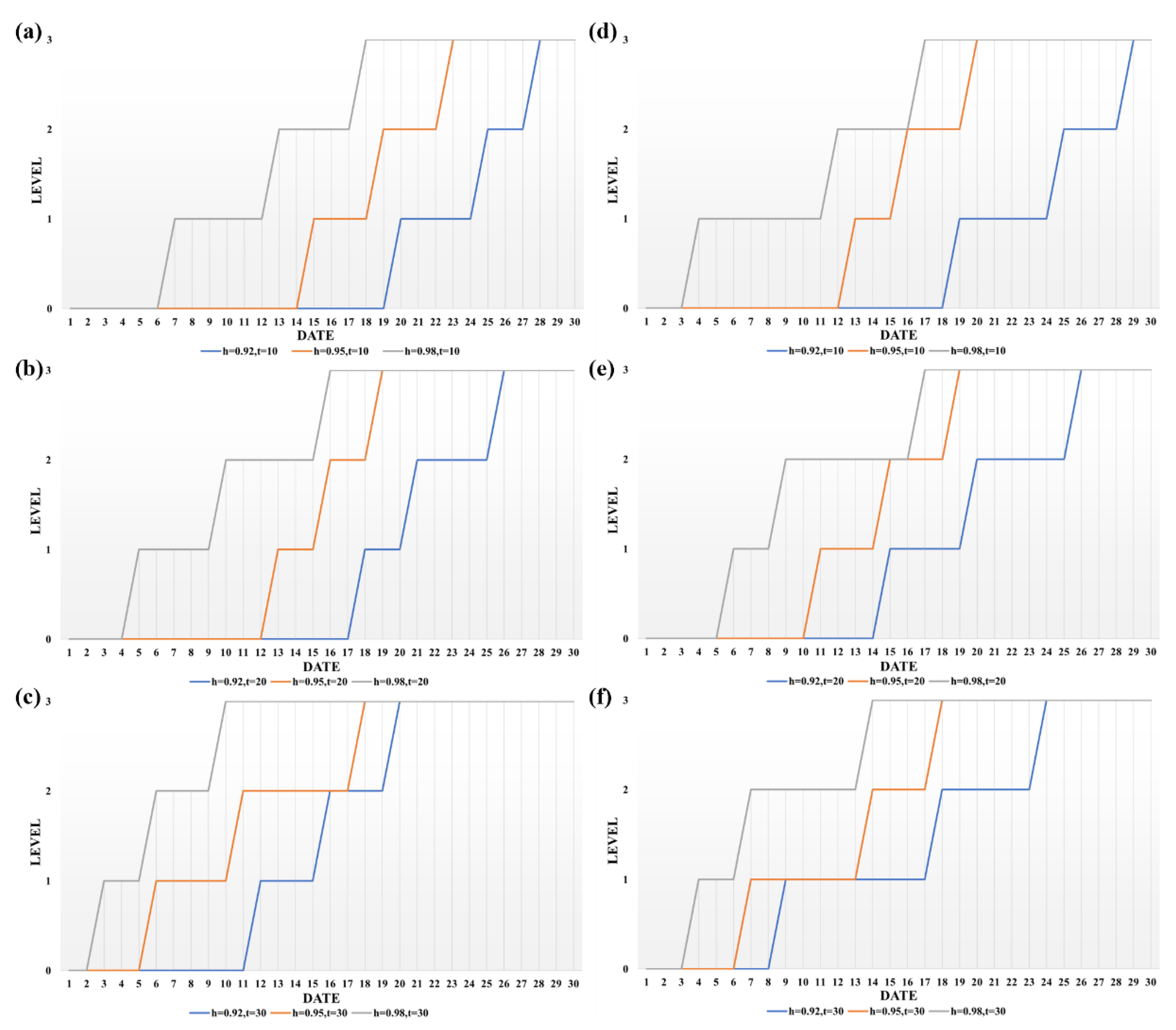
3.3. Analysis of Paddy Quality Change Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Iqbal, S.Z.; Asi, M.R.; Hanif, U.; Zuber, M.; Jinap, S. The Presence of Aflatoxins and Ochratoxin A in Rice and Rice Products; and Evaluation of Dietary Intake. Food Chem. 2016, 210, 135–140. [Google Scholar] [CrossRef] [PubMed]
- Carbas, B.; Simões, D.; Soares, A.; Freitas, A.; Ferreira, B.; Carvalho, A.R.F.; Silva, A.S.; Pinto, T.; Diogo, E.; Andrade, E.; et al. Occurrence of Fusarium spp. in Maize Grain Harvested in Portugal and Accumulation of Related Mycotoxins during Storage. Foods 2021, 10, 375. [Google Scholar] [CrossRef] [PubMed]
- Bacala, R.; Fu, B.X.; Cordova, K.; Hatcher, D.W. Wheat Fusarium Protease Specificity and Effect on Dough Properties. Foods 2021, 10, 1585. [Google Scholar] [CrossRef] [PubMed]
- Balendres, M.; Karlovsky, P.; Cumagun, C. Mycotoxigenic Fungi and Mycotoxins in Agricultural Crop Commodities in the Philippines: A Review. Foods 2019, 8, 249. [Google Scholar] [CrossRef] [PubMed]
- Faree, A.; Wang, Y.; Li, G. Modeling Grain Storage Quality with Linear Regression. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 2904–2909. [Google Scholar]
- Coradi, P.C.; Lutz, É.; dos Santos Bilhalva, N.; Jaques, L.B.A.; Leal, M.M.; Teodoro, L.P.R. Prototype Wireless Sensor Network and Internet of Things Platform for Real-Time Monitoring of Intergranular Equilibrium Moisture Content and Predict the Quality Corn Stored in Silos Bags. Expert Syst. Appl. 2022, 208, 118242. [Google Scholar] [CrossRef]
- Squire, R.A. Ranking Animal Carcinogens: A Proposed Regulatory Approach. Science 1981, 214, 877–880. [Google Scholar] [CrossRef]
- Raghavender, C.; Reddy, B. Human and Animal Disease Outbreaks in India Due to Mycotoxins Other Than Aflatoxins. World Mycotoxin J. 2009, 2, 23–30. [Google Scholar] [CrossRef]
- Lv, C.; Jin, J.; Wang, P.; Dai, X.; Liu, Y.; Zheng, M.; Xing, F. Interaction of Water Activity and Temperature on the Growth, Gene Expression and Aflatoxin Production by Aspergillus Flavus on Paddy and Polished Rice. Food Chem. 2019, 293, 472–478. [Google Scholar] [CrossRef]
- Lutz, É.; Coradi, P.C.; Jaques, L.B.A.; de Oliveira Carneiro, L.; Teodoro, L.P.R.; Teodoro, P.E.; Meneghetti, V.L.; de Souza, G.A.C. Real-Time Equilibrium Moisture Content Monitoring to Predict Grain Quality of Corn Stored in Silo and Raffia Bags. J. Food Process Eng. 2022, 45, e14076. [Google Scholar] [CrossRef]
- Kumar, D.; Kalita, P. Reducing Postharvest Losses during Storage of Grain Crops to Strengthen Food Security in Developing Countries. Foods 2017, 6, 8. [Google Scholar] [CrossRef]
- Coradi, P.C.; Padia, C.L.; Jaques, L.B.A.; de Souza, G.A.C.; Lima, R.E.; Müller, A.; Teodoro, P.E.; Steinhaus, J.I.; de Oliveira Carneiro, L. Adaptation of Technological Packaging for Conservation of Soybean Seeds in Storage Units as an Alternative to Modified Atmospheres. PLoS ONE 2020, 15, e0241787. [Google Scholar] [CrossRef] [PubMed]
- Sun, S.; Li, B.; Yang, T.; Luo, F.; Zhao, J.; Cao, J.; Lin, Q. Preservation Mechanism of High Concentration Carbon Dioxide Controlled Atmosphere for Paddy Rice Storage Based on Quality Analyses and Molecular Modeling Tools. J. Cereal Sci. 2019, 85, 279–285. [Google Scholar] [CrossRef]
- Shu, Z.; Jia, W.; Zhang, W.; Wang, P. Selected Quality Attributes of Paddy Rice as Affected by Storage Temperature History. Int. J. Food Prop. 2021, 24, 316–324. [Google Scholar] [CrossRef]
- Li, X.; Han, X.; Gao, G.; Wu, J. Rice Freshness Determination during Paddy Storage Based on Solvent Retention Capacity. Cereal Chem. 2022, 99, 593–602. [Google Scholar] [CrossRef]
- Lu, X.; Wang, L.; Xiao, Y.; Wang, F.; Zhang, G.; Tang, W.; Deng, H. Grain Quality Characterization of Hybrid Rice Restorer Lines with Resilience to Suboptimal Temperatures during Filling Stage. Foods 2022, 11, 3513. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Zhang, D.; Zhao, L.; Liu, J.; Shang, B.; Yang, W.; Duan, X.; Sun, H. Metabolomic Analysis Reveals Insights into Deterioration of Rice Quality during Storage. Foods 2022, 11, 1729. [Google Scholar] [CrossRef] [PubMed]
- Jaques, L.B.A.; Coradi, P.C.; Muller, A.; Rodrigues, H.E.; Teodoro, L.P.R.; Teodoro, P.E.; Teixeira, A.L.; Steinhaus, J.I. Portable-Mechanical-Sampler System for Real-Time Monitoring and Predicting Soybean Quality in the Bulk Transport. IEEE Trans. Instrum. Meas. 2022, 71, 1–12. [Google Scholar] [CrossRef]
- Youness, J.; Driss, M. An ARIMA Model for Modeling and Forecasting the Dynamic of Univariate Time Series: The Case of Moroccan Inflation Rate. In Proceedings of the 2022 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 18–20 May 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- Liu, D.; Chen, H.; Tang, Y.; Liu, C.; Cao, M.; Gong, C.; Jiang, S. Slope Micrometeorological Analysis and Prediction Based on an ARIMA Model and Data-Fitting System. Sensors 2022, 22, 1214. [Google Scholar] [CrossRef] [PubMed]
- Drucker, H.; Burges, C.J.C.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support Vector Regression Machines. In Advances in Neural Information Processing Systems 9 (NIPS 1996); The MIT Press: Cambridge, MA, USA, 1997; pp. 779–784. [Google Scholar]
- Jie, Y. A Bayesian Inference Based Two-Stage Support Vector Regression Framework for Soft Sensor Development in Batch Bioprocesses. Comput. Chem. Eng. 2012, 41, 134–144. [Google Scholar] [CrossRef]
- Asadollahfardi, G.; Zangooi, H.; Asadi, M.; Tayebi Jebeli, M.; Meshkat-Dini, M.; Roohani, N. Comparison of Box-Jenkins Time Series and ANN in Predicting Total Dissolved Solid at the Zāyandé-Rūd River, Iran. J. Water Supply: Res. Technol.-Aqua 2018, 67, 673–684. [Google Scholar] [CrossRef]
- Shi, H.; Xu, M.; Li, R. Deep Learning for Household Load Forecasting—A Novel Pooling Deep RNN. IEEE Trans. Smart Grid 2018, 9, 5271–5280. [Google Scholar] [CrossRef]
- Che, Z.; Purushotham, S.; Cho, K.; Sontag, D.; Liu, Y. Recurrent Neural Networks for Multivariate Time Series with Missing Values. Sci. Rep. 2018, 8, 6085. [Google Scholar] [CrossRef]
- Gensler, A.; Henze, J.; Sick, B.; Raabe, N. Deep Learning for Solar Power Forecasting—An Approach Using AutoEncoder and LSTM Neural Networks. In Proceedings of the 2016 IEEE International Conference on Systems, Man, and Cybernetics (SMC), Budapest, Hungary, 9–12 October 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2858–2865. [Google Scholar]
- Zheng, H.; Lin, F.; Feng, X.; Chen, Y. A Hybrid Deep Learning Model with Attention-Based Conv-LSTM Networks for Short-Term Traffic Flow Prediction. IEEE Trans. Intell. Transport. Syst. 2021, 22, 6910–6920. [Google Scholar] [CrossRef]
- Zheng, J.; Xu, C.; Zhang, Z.; Li, X. Electric Load Forecasting in Smart Grid Using Long-Short-Term-Memory Based Recurrent Neural Network. In Proceedings of the 2017 51st Annual Conference on Information Sciences and Systems (CISS), Baltimore, MD, USA, 22–24 March 2017. [Google Scholar]
- Kang, H.; Yang, S.; Huang, J.; Oh, J. Time Series Prediction of Wastewater Flow Rate by Bidirectional LSTM Deep Learning. Int. J. Control Autom. Syst. 2020, 18, 3023–3030. [Google Scholar] [CrossRef]
- Vo, A.H.; Nguyen, T.; Le, T. Brent Oil Price Prediction Using Bi-LSTM Network. Intell. Autom. Soft Comput. 2020, 26, 1307–1317. [Google Scholar] [CrossRef]
- Lu, K.; Zhao, Y.; Wang, X.; Cheng, Y.; Pang, X.; Sun, W.; Jiang, Z.; Zhang, Y.; Xu, N.; Zhao, X. Short-Term Electricity Load Forecasting Method Based on Multilayered Self-Normalizing GRU Network. In Proceedings of the 2017 IEEE Conference on Energy Internet and Energy System Integration (EI2), Beijing, China, 26–28 November 2017. [Google Scholar]
- Ji, S.P.; Meng, Y.L.; Yan, L.; Dong, G.S.; Liu, D. GRU-Corr Neural Network Optimized by Improved PSO Algorithm for Time Series Prediction. Int. J. Artif. Intell. Tools 2020, 27, 07n08. [Google Scholar] [CrossRef]
- Yang, H.; Wu, S. Prediction of Remaining Time of Tram Charging Based on Bi-GRU. In Proceedings of the 2022 3rd Asia-Pacific Conference on Image Processing, Electronics and Computers, Dalian, China, 14–16 April 2022; ACM: New York, NY, USA, 2022; pp. 521–524. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention Is All You Need. In Proceedings of the 31st Annual Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Zhang, J.; Zhang, H.; Ding, S.; Zhang, X. Power Consumption Predicting and Anomaly Detection Based on Transformer and K-Means. Front. Energy Res. 2021, 9, 779587. [Google Scholar] [CrossRef]
- Zhou, H.; Zhang, S.; Peng, J.; Zhang, S.; Li, J.; Xiong, H.; Zhang, W. Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. AAAI 2021, 35, 11106–11115. [Google Scholar] [CrossRef]
- da Silva André, G.; Coradi, P.C.; Teodoro, L.P.R.; Teodoro, P.E. Predicting the Quality of Soybean Seeds Stored in Different Environments and Packaging Using Machine Learning. Sci. Rep. 2022, 12, 8793. [Google Scholar] [CrossRef]
- Kumar, R.; Baloch, G.; Pankaj; Baseer, A.; Bhatti, J. Fungal Blast Disease Detection in Rice Seed Using Machine Learning. IJACSA 2021, 12, 248–258. [Google Scholar] [CrossRef]
- Sampaio, P.S.; Almeida, A.S.; Brites, C.M. Use of Artificial Neural Network Model for Rice Quality Prediction Based on Grain Physical Parameters. Foods 2021, 10, 3016. [Google Scholar] [CrossRef] [PubMed]
- Daniya, T.; Vigneshwari, S. Deep Neural Network for Disease Detection in Rice Plant Using the Texture and Deep Features. Comput. J. 2022, 65, 1812–1825. [Google Scholar] [CrossRef]
- Ge, L.; Chen, E. Research on Grain Storage Temperature Prediction Model Based on Improved Long Short-Term Memory. J. Clin. Med. 2021, 21, 1145–1154. [Google Scholar] [CrossRef]
- Sabanci, K.; Aslan, M.F.; Ropelewska, E.; Unlersen, M.F.; Durdu, A. A Novel Convolutional-Recurrent Hybrid Network for Sunn Pest–Damaged Wheat Grain Detection. Food Anal. Methods 2022, 15, 1748–1760. [Google Scholar] [CrossRef]
- Zhou, Q.; Huang, Z.; Zheng, S.; Jiao, L.; Wang, L.; Wang, R. A Wheat Spike Detection Method Based on Transformer. Front. Plant Sci. 2022, 13, 1023924. [Google Scholar] [CrossRef]
- PyTorch. Available online: https://pytorch.org/ (accessed on 2 November 2022).
- Zhou, T.; Ma, Z.; Wen, Q.; Wang, X.; Sun, L.; Jin, R. FEDformer: Frequency Enhanced Decomposed Transformer for Long-Term Series Forecasting. arXiv 2022, arXiv:2201.12740. [Google Scholar]
- Wen, Q.; Gao, J.; Song, X.; Sun, L.; Xu, H.; Zhu, S. RobustSTL: A Robust Seasonal-Trend Decomposition Algorithm for Long Time Series. AAAI 2019, 33, 5409–5416. [Google Scholar] [CrossRef]


| Dataset | Training Set | Test Set | Validation Set |
|---|---|---|---|
| 2970 | 2079 | 594 | 297 |
| Interpreter | Programming Languages | Dependency Packages |
|---|---|---|
| Toolkit | Python (3.7, PSF, FDK, MD, United States) | Numpy 1.21.5 |
| Scikit_Learn 1.0.2 | ||
| Pandas 0.25.1 | ||
| Torch 1.12.0 | ||
| Matplotlib 3.5.2 |
| Model | Learn Rate | Encoder Layers | Decoder Layers | MAPE |
|---|---|---|---|---|
| FEDformer | 0.001 | 3 | 3 | 0.12 |
| 0.001 | 3 | 2 | 0.10 | |
| 0.0001 | 2 | 2 | 0.07 | |
| 0.0001 | 2 | 1 | 0.04 |
| Model | MAE | MSE | RMSE | MAPE | MSPE |
|---|---|---|---|---|---|
| RNN | 0.25 | 0.04 | 0.21 | 0.85 | 7.32 |
| GRU | 0.24 | 0.04 | 0.20 | 0.85 | 7.30 |
| LSTM | 0.21 | 0.03 | 0.17 | 0.83 | 6.40 |
| Transformer | 0.027 | 0.0012 | 0.03 | 0.55 | 2.30 |
| FEDformer | 0.008 | 0.0002 | 0.01 | 0.08 | 0.04 |
| Categories | Sample Size | Quality Level | |||
|---|---|---|---|---|---|
| AFB1 1 | 2.6036 | 4.1476 | 5.9409 | 695 | Level 1 |
| AFB1 2 | 4.4638 | 6.2585 | 8.7218 | 693 | Level 2 |
| AFB1 3 | 6.0306 | 9.4696 | 12.6445 | 196 | Level 3 |
| DON 1 | 262.8922 | 321.1738 | 405.2554 | 495 | Level 1 |
| DON 2 | 482.1590 | 584.5295 | 685.5420 | 905 | Level 2 |
| DON 3 | 787.0462 | 992.1297 | 1143.4456 | 184 | Level 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Z.; Zhang, Q.; Dong, W.; Liu, Y.; Wei, S.; Zuo, M. FEDformer-Based Paddy Quality Assessment Model Affected by Toxin Change in Different Storage Environments. Foods 2023, 12, 1681. https://doi.org/10.3390/foods12081681
Li Z, Zhang Q, Dong W, Liu Y, Wei S, Zuo M. FEDformer-Based Paddy Quality Assessment Model Affected by Toxin Change in Different Storage Environments. Foods. 2023; 12(8):1681. https://doi.org/10.3390/foods12081681
Chicago/Turabian StyleLi, Zihan, Qingchuan Zhang, Wei Dong, Yingjie Liu, Siwei Wei, and Min Zuo. 2023. "FEDformer-Based Paddy Quality Assessment Model Affected by Toxin Change in Different Storage Environments" Foods 12, no. 8: 1681. https://doi.org/10.3390/foods12081681
APA StyleLi, Z., Zhang, Q., Dong, W., Liu, Y., Wei, S., & Zuo, M. (2023). FEDformer-Based Paddy Quality Assessment Model Affected by Toxin Change in Different Storage Environments. Foods, 12(8), 1681. https://doi.org/10.3390/foods12081681






