Abstract
Streamflow prediction plays a vital role in water resources planning in order to understand the dramatic change of climatic and hydrologic variables over different time scales. In this study, we used machine learning (ML)-based prediction models, including Random Forest Regression (RFR), Long Short-Term Memory (LSTM), Seasonal Auto- Regressive Integrated Moving Average (SARIMA), and Facebook Prophet (PROPHET) to predict 24 months ahead of natural streamflow at the Lees Ferry site located at the bottom part of the Upper Colorado River Basin (UCRB) of the US. Firstly, we used only historic streamflow data to predict 24 months ahead. Secondly, we considered meteorological components such as temperature and precipitation as additional features. We tested the models on a monthly test dataset spanning 6 years, where 24-month predictions were repeated 50 times to ensure the consistency of the results. Moreover, we performed a sensitivity analysis to identify our best-performing model. Later, we analyzed the effects of considering different span window sizes on the quality of predictions made by our best model. Finally, we applied our best-performing model, RFR, on two more rivers in different states in the UCRB to test the model’s generalizability. We evaluated the performance of the predictive models using multiple evaluation measures. The predictions in multivariate time-series models were found to be more accurate, with RMSE less than 0.84 mm per month, R-squared more than 0.8, and MAPE less than 0.25. Therefore, we conclude that the temperature and precipitation of the UCRB increases the accuracy of the predictions. Ultimately, we found that multivariate RFR performs the best among four models and is generalizable to other rivers in the UCRB.
1. Introduction
Streamflow is a spatially and temporally integrated response of a watershed to precipitation input, storage, and runoff processes. It is a very useful indicator of water availability and hydro-climatic changes [1,2,3,4]. From a water resources management perspective, streamflow forecasting plays a vital role in water resources planning for understanding the dramatic change of climatic and hydrologic variables over different time scales, especially under extreme weather events such as floods and droughts [5]. Therefore, accurately predicting streamflow is needed by hydrologists, watershed managers, planners and stakeholders in planning for flood control and designing engineering structures, industrial operations, irrigated agricultural production, municipal water supplies, and recreations [6]. Streamflow prediction lies under the subject of hydrologic modeling as an application to enhance our understanding of hydrologic phenomena and watershed behavior. Forecasting the streamflow is a difficult task since the atmosphere is nonlinear and chaotic, which affects groundwater and streamflow on the Earth [7].
One of the biggest challenges of streamflow forecasting is to define a reasonable long-time lead (aka horizon/prediction window) streamflow predicting approach that could provide accurate information to help water resources managers and decision makers to understand the system and plan for future management scenarios. Streamflow prediction at different time scales, such as hourly, daily, monthly, and yearly, is very important for optimizing the water use in different applications. For example, prediction on a yearly scale provides water managers with a long overview of the watershed [8], while a monthly scale allows more detailed insights in the following months [9,10]. According to previous studies, a lead-time length greater than 24 months is considered as large lead-time streamflow prediction when working with monthly data [11,12]. As a result, an effective model is the one that can precisely predict streamflow values after the lead-time of greater than 24 months, providing water managers with adequate time to decide and prepare for future disasters.
At present, there are two prevalent approaches used for streamflow forecasting [13]. The first approach is the model-driven, which is a physical model that represents different hydrological processes and variables, such as rainfall-runoff, infiltration, groundwater process, and evapotranspiration [14]. Although this approach is widely used in hydrologic simulation and forecasting, and can help in understanding the underlying physical processes [15], there are various weaknesses identified in previous studies in terms of performance or uncertainty analysis. Physically-based models usually require a large amount of data input, such as forcing (meteorological) data and domain static data (e.g., land cover maps, soil maps, or digital elevation models) along with model parameters that require complex calculation to calibrate to match the watershed characteristics [16]. Another disadvantage of using this approach is that sometimes the collected data are inconsistent or not available at data sources for some regions, making this process very time-consuming and work-intensive [17,18]. Another possible issue in developing rainfall-runoff models is the close dependency on precipitation. However, precipitation in some cases is not the driving force of downstream flood occurrence and could be due to the flow regulation of large numbers of dams or reservoirs, especially for large scale river basins [19]. While there is a growing tendency for improving the performance of process-based hydrologic modeling by incorporating more detailed characteristics, there are still parametric and structural uncertainties in the model formation that may not lead to more accurate prediction [20].
In addition to process-based models, the data-driven approach is based on statistical modeling of both linear and non-linear relationships between input and output [21,22]. This is usually achieved by optimizing the model parameters by closing the gap between the model’s predictions and true measurements [23]. This method recently demonstrated advantages and attracted significant interests due to their accuracy in streamflow forecasting with low information requirements. According to recent studies [24], data-driven models usually outperform physically-based models. Traditional statistics and machine learning (ML) models have been used very frequently in time series forecasting [25,26]. Lately, deep learning models have demonstrated significant improvements and shown better results in time series forecasting compared with physics-based models [27]. In this work, we aim to analyze several ML-based models, including traditional statistical methods along with machine learning and deep learning methods.
Among the statistical forecasting models, autoregressive integrated moving average (ARIMA) [28] is widely used for forecasting time series data without considering the seasonality. ARIMA leverages series differentiation in the earlier autoregressive moving average (ARMA) model for improving prediction accuracy. Several research efforts have been conducted to evaluate the accuracy of the ARIMA model compared to the previous forecasting models. One study on the prediction of the inflow of a dam reservoir in the past 12 months demonstrates that the ARIMA model has less error rate than the ARMA model [29]. Therefore, ARIMA is considered as one of the viable solutions for river streamflow forecasting [30]. An improvement to the ARIMA model is the Seasonal ARIMA (SARIMA), where seasonality is considered. In comparison to ARIMA and ARMA, SARIMA has shown better accuracy and R-squared metric in long-term runoff prediction [31].
Another successful statistical model for time-series forecasting is Facebook’s Prophet model, which is based on an additive model to forecast the future [32]. The Prophet model has been recently used in drought forecasting [33], evapotranspiration estimation [34], and runoff simulation [35]. A comparison between Prophet model and Support Vector Regression (SVR) shows that the Prophet model outperforms SVR variants with similar data input and target tasks [34].
Random Forest Regression (RFR) is another model used for streamflow prediction, in which the ensemble learning method is used to forecast the future data [36]. A comparative analysis of different regression methods for predicting runoff signatures has been done by Ref. [37], where the result shows that the regression tree ensemble is superior to the multiple linear regression approaches, particularly in predicting dynamic flow signatures. Random Forest models result in better predictions with higher accuracy compared to other machine learning models such as Support Vector Machine (SVM) and Linear Regression [38,39,40].
One of the most recent models is the Long Short-Term Memory (LSTM) network, which is a widely used deep learning model for learning sequence data (e.g., text, speech, time series). The LSTM is an artificial neural network that is an improvement of the Recurrent Neural Network (RNN) and is thoroughly capable of addressing the challenge of long-range dependencies of the sequence data [41,42]. LSTM and GRU models are specific types of RNN, where GRU is computationally faster than LSTM, and LSTM has more learnable parameters and takes more training time. For the ability to handle long sequences, LSTM has been preferably used in hydrology applications [43]. LSTM models have been shown to predict the rainfall-runoff with outstanding performance compared to the baseline hydrological models including vanilla RNN-based models [44,45]. Furthermore, attention-based LSTM models significantly improve the accuracy of streamflow prediction models in daily-data cases [46]. Several other LSTM-based models have been proposed in recent years to forecast the streamflow in varying time scales [47,48]. In addition to the deep sequence learning models, spatial dependency capturing models based on Convolutional Neural Network (CNN) have been used to predict streamflow from image data. LSTM and CNN have also been used together to make more accurate predictions [49]. However, a recent study reveals that even a simple LSTM-based model outperforms the CNN model in river streamflow prediction [50].
In addition, regardless of the forecasting approaches, most analyses contain only historic streamflow data in order to forecast the future values. However, we may observe improvements by considering meteorological features such as temperature and precipitation since these features are the most influential factors in water flow changes on Earth. Refs. [51,52] indicate that the streamflow is sensitive to climate changes, and it shows a strong dependency to temperature and precipitation. Figure 1 shows the impact of temperature and precipitation on the river’s streamflow. These meteorological components cause snow and rain near the surface, resulting in melt and runoff on the ground. Eventually, the groundwater ends in the streamflow on rivers.
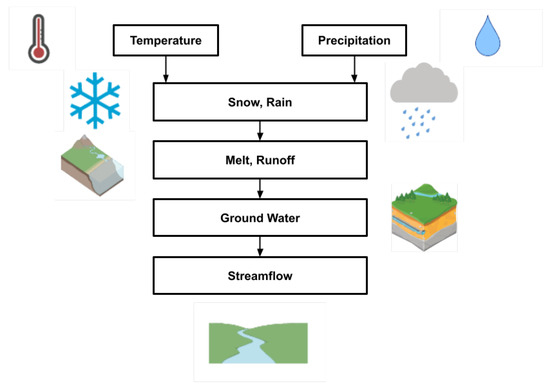
Figure 1.
Impact of meteorological components on a river’s streamflow.
Considering previous works of streamflow prediction, we select a set of statistical, machine learning, and deep learning models for comparing their performances, and to choose the best model that can help hydrologists in effective streamflow forecasting. Therefore, our analyses cover four different ML models: Seasonal Auto-Regressive Integrated Moving Average (SARIMA), Prophet (PROPHET), Random Forest Regression (RFR), and Long Short-Term Memory (LSTM). Later, we consider meteorological components such as temperature and precipitation as new features to find potential improvements to the models mentioned earlier, since the studies indicate that temperature and precipitation are among the most fundamental indicators that can influence the climatic changes of the water bodies. In this regard, we aim to understand the impact of those factors on the streamflow prediction. Therefore, we analyze multiple approaches for streamflow forecasting. Our first approach consists of analyzing univariate data. For this, we only consider historic streamflow data to forecast the future streamflow data. Our second approach consists of employing more features rather than using solely historic streamflow data. This approach is an instance of multivariate time-series analysis, in which the model contains multiple time-dependent variables. An example of related multivariate analysis is the snow flow prediction that used hybrid models trained by meteorological data [53]. Moreover, Ref. [54] shows that streamflow predictions using SVMs were improved when considering atmospheric circulations. In addition, Ref. [55] concludes that the Pacific sea surface temperature provides us with better streamflow predictions in the Upper Colorado River Basin. Eventually, we pick the best model to perform further analysis, and evaluate in more detail using sequence analysis. We also performed a sensitivity analysis to explore the robustness of the model. The former is done to find the impacts of lead-time, which can result in different accuracies, and the latter is performed since there is a need to evaluate the robustness of the models with the presence of noise in data.
While many catchment areas are enthralling to observe, we focus on the Colorado catchment in our study. We aim to forecast future discharges for this area using historic streamflow data and additional climate data. The river basin is an essential source of water for several states of the United States, including Colorado, Wyoming, Utah, New Mexico, Arizona, Nevada, California, and also the Republic of Mexico [56]. The Colorado river catchment currently faces uncommon stresses. The problem with the Colorado catchment is the shortage of water, which has become an important and controversial issue lately. The dry conditions over the past 20 years, along with the global climate change, affect this catchment, which covers a large area in the United States and may affect many other states in the near future. Studies reveal that the Colorado river basin will be faced with reductions in runoff of approximately 19% by the middle of the 21st century [57]. On the other hand, prolonged rainfalls over several days in some seasons cause flooding in this area [58]. For these reasons, making timely decisions and taking actions in advance have become critical in this area. Therefore, streamflow prediction in this area would assist water resource managers and basin stakeholders in reducing the risks of disasters, help policy-makers assess whether there is adequate water in drought periods, and facilitate the decision-making on efficient water allocation. In particular, we concentrate on the Lees Ferry site, which lies in the very bottom part of the Upper Colorado River Basin. Since the last century, Lees Ferry has been the site of a stream gauge where the hydrologists monitor, test, and measure the water level, streamflow, etc. Studies indicate that the Lees Ferry will be faced with a shortage of water and reductions in streamflow in the near future. Precise streamflow prediction can be valuable to overcome the impact of global climate change in this region, which serves and provides millions of people with water.
In this study we will address the following questions—(1) Which one of the ML approaches is robust for streamflow forecasting? (2) Do climate variables such as precipitation and temperature improve the streamflow prediction? and (3) How do the accuracies of the prediction models vary with the input and output sequences?
2. Study Site
The Colorado River is a vital water supply for the southwestern United States and northwestern Mexico [56]. It provides water for nearly 40 million people and is used to irrigate 2.5 million acres of farmland [59,60]. The river’s watershed covers parts of seven US states, including Wyoming, Colorado, Utah, New Mexico, Nevada, Arizona, and California. Given the large domain extension of the Colorado River Basin, it is divided into two regions; the upper basin lies north of Lees Ferry, Arizona; and the lower basin lies south of Lees Ferry [61].
In this study, we focused only on the Upper Colorado River Basin (UCRB), which spans parts of four US states, including Colorado, New Mexico, Utah, and Wyoming. The drainage area of the basin is approximately 113,347 square miles in area with the outlet at Lees Ferry, Arizona [62]. The elevation of UCRB is ranging from 12,800 feet at its headwaters to 4325 feet near the Colorado- Utah state line [63]. The primary stream in the UCRB is the Upper Colorado River, with major tributaries including Williams Fork, Blue River, Muddy Creek, Eagle River, Roaring Fork River, Rifle Creek, Gunnison River, Plateau Creek, and Fraser River. The major water use in the UCRB is irrigation, with several irrigation ditches diverting from the main-stem Colorado River and its tributaries crossing many mountains within the basin [64]. Other water uses include industrial, municipal, and power generation [65].
A critical feature of the natural streamflow system is the significant variation in hydroclimate conditions of the basin due to land topography and elevation, which play a critical role in driving the sharp gradients in precipitation and temperature [66]. In the UCRB, most mountain ranges are oriented north-south, creating a physical barrier and enhancing orographic lift (air is forced to rise and subsequently cool). As a result, the condensation increases, leading to increased precipitation rates in a given storm event on the windward mountainside [67]. The basin has consistently high monthly precipitation in the winter season (November–April), where 50$ of precipitation falls as snow [63,68]. The average monthly precipitation over the UCRB is between 7.11 mm (0.28 inches) and 33.2 mm (1.31 inches) [69,70]. The temperature of the basin has a persistent significant warming trend of about +0.5 per decade due to anthropogenic climate change and natural variability [71]. The mean monthly temperature is between −3.6 C (25.4 F) and 24.3 C (75.8 F) [69,70]. The high water demand is expected to increase due to population growth, which is projected to increase to a million by 2020. Moreover, climate change is another factor expected to further exacerbate the water problem in the UCRB. According to climate models forecasting, UCRB experiences warmer temperature and reduction in precipitation, leading to reduction in the water availability for humans and ecosystems [72].
3. Data
We used two datasets for our studies: (1) historic streamflow data for the univariate time series forecasting, and (2) historic streamflow data associated with spatiotemporal temperature and precipitation features for the multivariate time series forecasting. The discharge data in both our studies is collected from the United States Bureau of Reclamation (USBR) website (https://www.usbr.gov/lc/region/g4000/NaturalFlow/previous.html (accessed on 1 January 2023)). We collected 113 years of monthly discharges, the natural flow at the Lees Ferry site in Acre-feet per month (ac-ft/month). Figure 2 shows the Colorado river basin containing our study area. We show the result in millimeter per month (mm/m) by dividing the streamflow values by the UCRB area and performing a unit conversion. The dataset ranges from December 1905 to January 2019. It is important to mention that the data is divided into train and test sets that contain 107 years and 6 years of monthly data, respectively. The testing period starts in December 2012 and ends in January 2019. The test set is chosen to evaluate the performance of our models on unseen data. The sliding window for the test data is chosen to be equal to one due to the inadequate data. As a result, 6 years of monthly test data is considered to assess the predictions of the models.
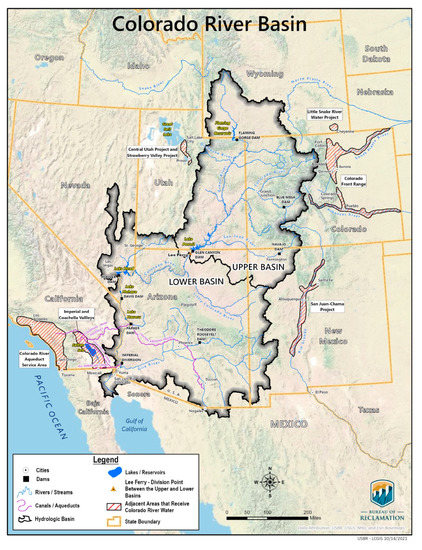
Figure 2.
Colorado River Basin (https://www.usbr.gov/lc/region/programs/PilotSysConsProg/report_to_congressW_appendices2021.pdf (accessed on 1 January 2023)).
The spatiotemporal data for our second task contains the additional features such as temperature, and precipitation of the Upper Colorado River Basin. They are obtained from the PRISM Climate Group (https://prism.oregonstate.edu/ (accessed on 13 December 2022), which provides climate observations such as temperature and precipitation. The PRISM website contains historical past and recent years data that are stabilized after 6 months. We add a single measure of monthly temperature and precipitation by computing the average of those spatial observations for the Upper Colorado River Basin. Figure 3 and Figure 4 illustrate the samples of spatial temperature and precipitation of the UCRB in January 2018, respectively. Each pixel shows the intensity of temperature and precipitation on the corresponding Figure. For example, the average of the temperature in January 2018 is computed by calculating the mean of the values in Figure 3.
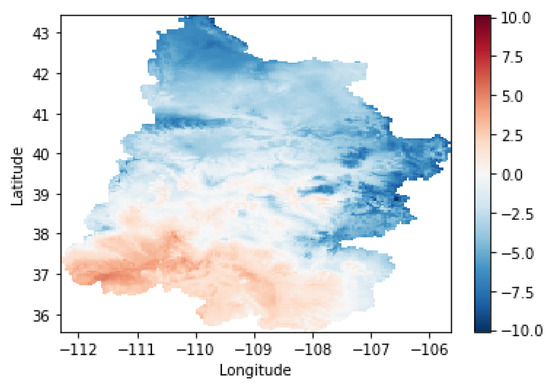
Figure 3.
Temperature mean (C) of the Upper Colorado River Basin in January 2018.
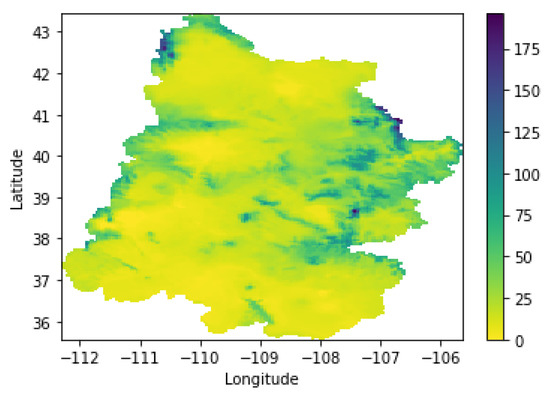
Figure 4.
Precipitation (mm) of the Upper Colorado River Basin in January 2018.
The evaluation of both tasks is done by repeating each model’s prediction 50 times to ensure their consistent performances on unseen data. In addition, we used multiple techniques to test the generalization capability of the models and ensure the robustness of the results. Figure 5 illustrates the past and observed streamflow at Lees Ferry. The red line represents the ground truth (observations) that we aim to compare with our predictions, while the blue one shows the past streamflow at Lees Ferry in millimeter per month from December 1905 to January 2019. As shown in Figure 5, Lees Ferry experienced a severe lack of water in 2013 and 2018. As a result, the actual streamflow values from December 2012 to October 2013 differ from most values in the training dataset; therefore, this may cause a divergence between predictions and actual values and reduce the overall performance of our work. However, ML-based models should handle this issue by training more samples with low discharge values.
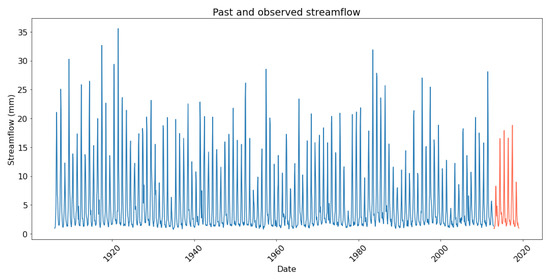
Figure 5.
Past and observed streamflow at Lees Ferry.
4. Methodology
This section introduces the methods that we used to forecast the streamflow. We explain mathematical expressions for the models and evaluation metrics in detail. We divide this section into three subsections: (1) univariate time-series prediction model, (2) multivariate time-series prediction model, and (3) evaluation metrics.
4.1. Univariate Time-Series Prediction Model
In univariate time series prediction model, we considered only past discharges without additional features to predict the natural streamflow at Lees Ferry for the next 24 months. We trained RFR, LSTM, SARIMA, and PROPHET to predict the next months of discharges. A pre-processing technique was applied for RFR and LSTM to convert the data into sequences of past and future values (input-output pairs), where each value represents a discharge for its corresponding month. We considered a couple of input sequences such as 12, 24, 36, 48, 60, and 72 months of streamflow data and for RFR and LSTM, in which the lengths 24 and 72 were found to be optimal for the models, respectively. Therefore, we accumulated sequences of 24 months of input data with their corresponding 24 months output sequence for RFR, and sequences of 72 months of input data with their corresponding 24 months output sequence for LSTM. In this way, we modeled the problem as a supervised learning task, where the sequences are made by crossing through the entire dataset by moving one month at a time. In addition, a standardization technique is performed on the data before we feed input-output sequences to LSTM. More specifically, we performed z-normalization for the train and test sets prior to prediction. Z-normalization is defined by the following equation:
where and are the mean and standard deviation of the data. Z-normalization is preferred over other normalization techniques due to the presence of outliers in the dataset that affects the training phase [73]. On the other hand, statistical models SARIMA and PROPHET were trained for each trial to predict the next 24 months of natural streamflow since they require the entire past data instead of receiving sequences of data. For the sake of fairness, an equal number of training data were considered at each trial.
4.1.1. RFR
As a representative of the tree-based induction model, we use Random Forest Regression (RFR). RFR is a model based on Decision Tree (DT), where predictions of numerous DTs are averaged to calculate the final prediction. Figure 6 illustrates a simplified structure of random forest regression in which the depth of each tree is 2. In general, random forest regression can be defined as the following equation:
where N is the number of decision trees, is the prediction made by the tree i on input x, and is the average prediction.
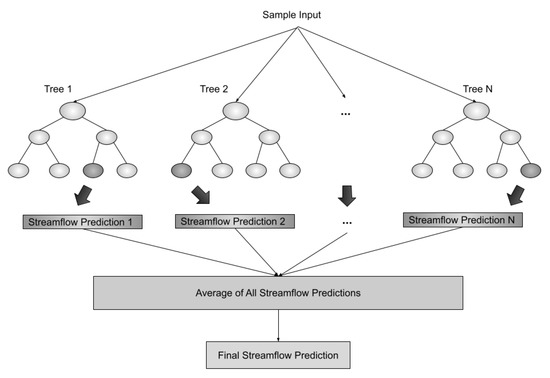
Figure 6.
A simplified structure of Random Forest Regression.
We performed hyperparameter tuning to build the optimal models. RFR was trained with 1000 estimators, minimum samples split of 2, minimum samples leaf of 1, maximum depth of 8, and with bootstrapping. In addition, the random state is fixed to generate the reproducible result. Different lengths of look-back windows were studied to find the best possible one. As a result, it was set to 24 as the best sequence for univariate time-series RFR.
4.1.2. LSTM
Recurrent Neural Network (RNN) is a type of Artificial Neural Network (ANN) that learns sequence representations through recurrent connections of cells made of fully connected neural networks [74]. Long Short-Term Memory (LSTM) network is a RNN variant that handles long-term dependencies and solves the problem of vanishing and exploding gradients using the gates included in its architecture. Figure 7 shows the functions of a memory unit of LSTM. The sigmoid layers transform the input to a probability in the range of 0 and 1. The first sigmoid layer in the LSTM cell decides how much information the cell should throw away, and the second sigmoid layer with tanh nonlinearity helps the network store the information that needs to be kept in the cell state. Finally, the rightmost sigmoid layer decides which portion of the input will be returned as output. The tanh activation function pushes the output to be in the range of −1 and 1. The cell state, the straight horizontal line on top of the network, takes the updates every time and outputs the result.
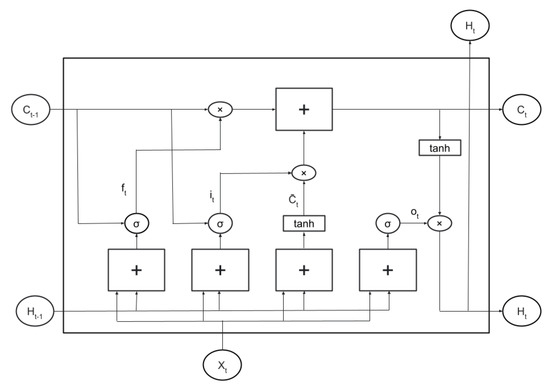
Figure 7.
The structure of LSTM memory unit.
In general, LSTM is defined by the following equations:
where is sigmoid function, is input vector at time t, is cell state and is hidden state. The Equations (3), (4) and (6) are the input, forget, and output gates, respectively. W represents weight and b denotes bias. Eventually, ∗ represents element-wise multiplication.
For LSTM-based streamflow forecasting, we need the full sequence as the output. To produce the output similar to the input sequences, we use the many-to-many structure of LSTM by returning the hidden states’ representations. In this work, Rectified Linear Unit (ReLU) is used as the activation function for hidden layers which is defined as:
LSTM was trained with 3 hidden layers of 100 neuron units each and a dense layer of 24 units with a linear activation function to predict the next two years. We added the dropout regularization factor of 0.2 to avoid overfitting, and added ReLU activation functions to each hidden layer. Twelve epochs with a batch size of 8 and a validation set of 30% of training data were used to train the model. The loss function was set as Root Mean Square Error (RMSE) between the observations and predictions during the training period. A random seed is set to generate reproducible results each time we run the training phase. It is important to mention that the input shape is set to (72, 1) since the look back window size is 72 months. This look back length has been chosen by manually setting the hyperparameter to provide us with the best possible model.
4.1.3. SARIMA
SARIMA, Seasonal Autoregressive Integrated Moving Average model, considers past data in order to predict its future, and it is defined as:
Here, p is the trend autoregression order, d is the trend difference order, and q is the trend moving average order. Other parameters P, D, Q, and m are seasonal autoregressive order, seasonal difference order, seasonal moving average order, and the number of time steps for a single seasonal period respectively. We trained SARIMA with the best possible hyperparameters. The differencing term has been ignored by automatic hyperparameter tuning since there is no observable trend in our data. Therefore, we considered , , , , , and as the best parameter set found by auto ARIMA. The term m was set to 12 since the data is monthly and the seasonality repeats every year.
4.1.4. PROPHET
PROPHET was trained with a change point prior scale of 0.1, number of change points of 150, multiplicative seasonality mode, yearly seasonality, and interval width of 95%. The following expression defines the mathematics behind Facebook’s PROPHET model:
where is the piecewise linear or logistic growth curve for modeling non-periodic changes in time series, is the periodic changes, is effects of holidays (disabled in our work), and is the error term. PROPHET, as a regressor, fits several linear and nonlinear functions to the model [74]. As an example, a nonlinear model for non-periodic changes is defined as follows:
where C, k, and m are carrying capacity, growth rate, and offset parameter.
Finally, the seasonal effect is defined by the following Fourier series:
where P is the period for seasonality effect, that is set to 30 for monthly seasonality.
4.2. Multivariate Time-Series Model Prediction
Meteorological components such as temperature and precipitation of the watershed can affect the streamflow. In this regard, we added these variables to our data as extra features to be considered in addition to the past streamflow. The spatiotemporal data were used to compute the average temperature and precipitation of the Upper Colorado River Basin for each month. Accordingly, the average of those features was calculated and added to our new data.
To do so, we applied the shapefile of the Upper Colorado River Basin to subset the monthly temperature and precipitation of the Upper Colorado River Basin from the PRISM data, which covers the conterminous United States. Figure 3 and Figure 4 show the result of such processes. We use the similar machine learning models as introduced earlier in the univariate model section. However, the input data size was increased since we added two more features. Model-specific changes for the multivariate data are listed below.
- RFR: RFR’s input sequence is tripled in which the first 24 elements represent the discharge values, the second 24 elements represent the temperature values, and the last 24 elements represent the precipitation values.
- LSTM: LSTM’s input is a 2-dimensional matrix of shape (72, 3). The first dimension represents the number of elements, and the latter represents the three features, i.e., discharge, temperature, and precipitation.
- SARIMAX: Since we added extra features to the model, SARIMAX has been used instead of SARIMA. The exogenous factor of SARIMAX allows us to forecast future streamflow using external factors such as temperature and precipitation [75,76]. SARIMAX, as a seasonal auto-regressive integrated moving average model with exogenous factors, is defined as:
- PROPHET: Two additional regressors have been added to consider temperature and precipitation for the PROPHET model.
Hyperparameter tuning was performed to build the best possible models. As discussed in the previous subsection, the random seed was fixed to generate reproducible results each time we run the training phase. RFR was trained with 500 estimators, minimum samples split of 2, minimum samples leaf of 7, maximum depth of 5, and with bootstrapping. LSTM has trained with 3 hidden layers of 400 units each and a dense layer of 24 units with a linear activation function to predict the next two years. We added dropouts of 0.5, and ReLU activation functions to each hidden layer. Twelve epochs with a batch size of 8 and a validation size of 30% were used to train the model. SARIMAX was trained with , and . This parameter set is the best parameter set found by auto Arima. We also added temperature and precipitation to the model as exogenous variables. PROPHET was trained with a change point prior scale of 0.1, number of change points of 100, multiplicative seasonality mode, yearly seasonality, and interval width of 95%.
4.3. Evaluation Metrics
To evaluate the models, we use multiple metrics on the test dataset such as Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE), Symmetric Mean Absolute Percentage Error (SMAPE), R-squared (), Nash–Sutcliff Efficiency (NSE), and Kling–Gupta Efficiency (KGE). The evaluation metrics based on predicted values , observed values , and number of observations n are discussed below.
- Root Mean Square Error (RMSE): RMSE is widely used in regression-based prediction tasks, and it quantifies the closeness between predictions and observations. RMSE is defined as follows:
- R-squared (): R-squared metric, as a coefficient of determination, is used to measure how the prediction is aligned with the observation. is defined as:where RSS is the sum of the squared residuals, and TSS is the total sum of squares. The closer the value of R-squared to 1, the better the model’s predictions compared to the actual values.
- Mean Absolute Percentage Error (MAPE): MAPE is one of the most widely used metrics in the literature, and is defined as:
- Kling–Gupta efficiency (KGE): We use KGE, which is a revised version of NSE [79]. KGE is defined as below:
5. Experimental Results
The experimental result section is presented in four subsections: (1) comparison of ML models, (2) univariate and multivariate time series forecasting, (3) sensitivity analysis, and (4) sequence analysis. Figure 8 shows the flowchart of the experiment design in this paper. In each subsection, we will discuss different models and evaluate their prediction performances.
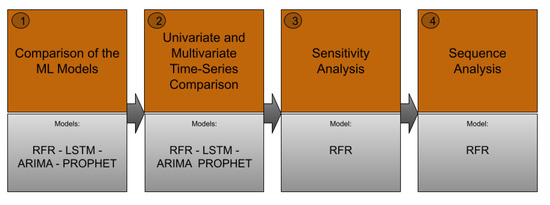
Figure 8.
The flowchart of streamflow prediction using ML-based models.
As discussed earlier in this paper, long-range streamflow prediction helps water managers to decide and act ahead of time. Although choosing an appropriate lead-time is important, forcing a long lead-time may affect the performance, resulting in low accuracy. Various lead-time predictions have been presented by researchers ranging from days to months and years. We conduct our analysis with a lead-time of 24 months, where we compare ML models, and analyzed the effects of temperature and precipitation. Two years of prediction is reasonably long enough for the stakeholders to approximate the future streamflow of the UCRB. Moreover, we perform a sequence analysis for our best model at the end of this section to indicate how choosing a various range of look-back and look-ahead (lead-time) sequences affects the performance of streamflow prediction. We plot prediction values against the observations to demonstrate the results qualitatively. As mentioned earlier, we use multiple metrics on the test dataset such as RMSE, MAPE, SMAPE, NSE, and KGE to quantitatively assess the models.
5.1. Comparison of the ML Models
First, we demonstrate the RMSE of our models as a normal distribution to compare them qualitatively. As shown in Figure 9, RFR has the least RMSE among the four models. Both the median and average RMSE in RFR is less than 1.1 mm/month, which indicates RFR’s superior performance in this experiment. In addition, SARIMA performed well, resulting in low RMSE on average. On the other hand, LSTM and PROPHET performed the worst, where the median and average RMSE are in the range of 1.79 and 1.82 mm/month. Furthermore, the predictions of all models have low variance, which means that there are only a few unsatisfactory predictions out of 50 trials. To be specific, the predictions of the models are well-generated and robust.
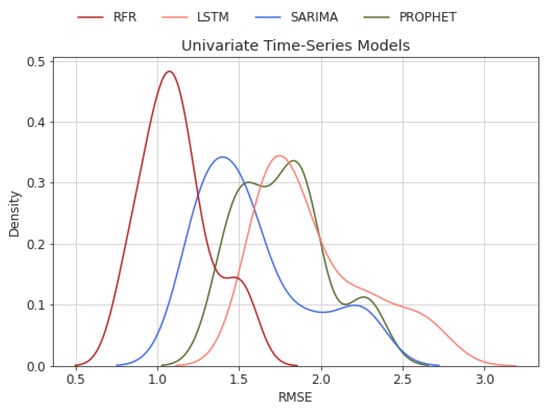
Figure 9.
RMSE distribution of univariate time-series Models.
Figure 10 illustrates all metric values for those models over 50 trials in box plots. Each box plot contains the corresponding metric values of 50 trials of the forecast on the test dataset. RFR and SARIMA show less SMAPE and MAPE since their predictions are very close to the observations. This can be further justified by comparing RMSE values. RFR shows a better RMSE, while SARIMA is superior considering the MAPE. In addition, R-squared allows us to observe the relationship between the independent variable (time) and the dependent variable (discharge). It reveals how well the model predicts against the ground truth. The first observation is that the predictions of SARIMA follow the ground truth more precisely than the other models. The predictions of LSTM result in smaller R-squared values, and come with higher variance in comparison with other models. Nevertheless, a smaller R-squared does not necessarily mean that we have an inapplicable model. Considering other criteria such as RMSE and MAPE along with the R-squared assures a fair evaluation. Eventually, RFR and SARIMA show outstanding result with mean NSE and KGE of 0.85. Therefore, RFR and SARIMA are very competitive in univariate time-series prediction.
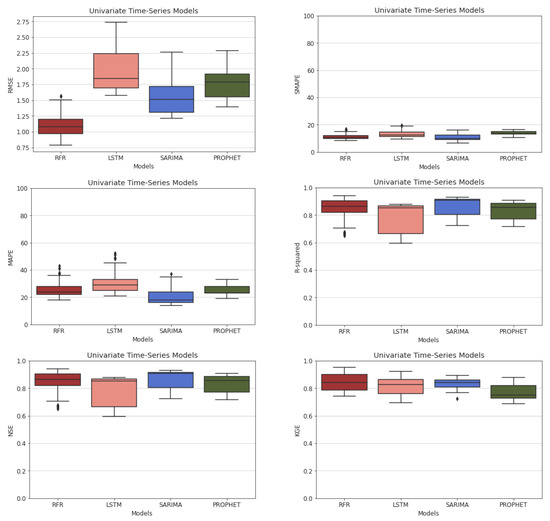
Figure 10.
RMSE, SMAPE, MAPE, R-squared, NSE, and KGE results of univariate time-series ML models.
Next, we demonstrate the distributions of model predictions over 50 trials in the multivariate case, as shown in Figure 11. Similar to the univariate case, RFR has the least RMSE. RFR achieved a better result by reducing the median and average RMSE from 1.1 mm/month to 0.9 mm/month. Similarly, LSTM attained lower RMSE with less than 1.65 mm/month. Correspondingly, SARIMAX showed less RMSE for multivariate cases compared with the univariate ones. On the other hand, PROPHET achieved similar RMSE in the multivariate case.
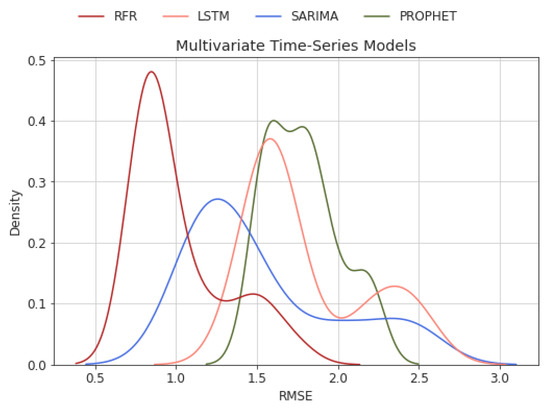
Figure 11.
RMSE distribution of multivariate time-series models.
The box plots of all performance metrics for each ML model in the multivariate case are shown in Figure 12. RFR has a higher median in R-squared, but it has a high variance. We observe that the predictions of RFR follow the ground truth more precisely than the other models. Most of the R-squared values for all models are high enough to approximate the ground truth. According to the definition of R-squared, the result of 0 means that the quality of the predictions is worse than setting a straight horizontal line among the data points. In this regard, the prediction values of our models are satisfactory, since the mean R-squared of 0.92 for RFR represents sufficient accuracy. Additionally, we compared the predictions in terms of SMAPE and MAPE metrics, which show that RFR and LSTM are superior to the other models. NSE and KGE improved to 0.86 in RFR multivariate time-series predictions.
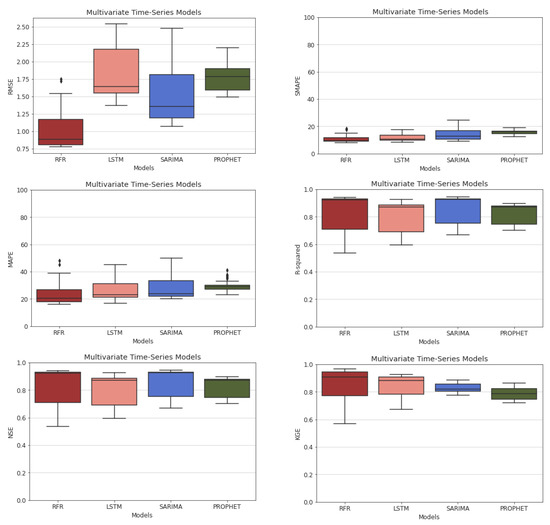
Figure 12.
RMSE, SMAPE, MAPE, R-squared, NSE, and KGE results of the ML models in multivariate time-series forecasting.
Figure 13 demonstrates predictions against the ground truth of 24 months ahead for 2 trials in both univariate and multivariate cases, which include the periods of May 2013 to April 2015, and from May 2015 to April 2017. It is worth mentioning that Figure 13 shows a subset of the testing period that starts from December 2012 and ends in January 2019. Visually, all models are prominent and decent. For the sake of fair evaluation of the performance of models in detail, we employed the previously-mentioned metrics and repeated them over 50 different test datasets to validate our results. As it had been estimated earlier, we observed higher errors in predictions starting from December 2012 to October 2013. However, the rest of the predictions had a lower error margin, as shown in Figure 16.
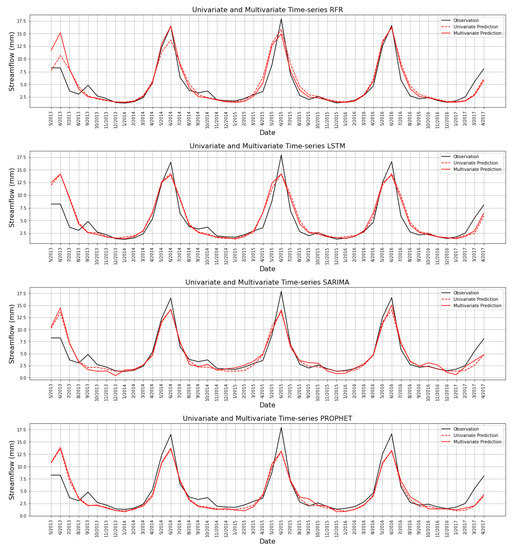
Figure 13.
Prediction against ground truth streamflow of univariate and multivariate time-series models for two trials from May 2013 to April 2015 and from May 2015 to April 2017 over the test set.
It is important to note that these differences have been extracted for each month irrespective of the 24-month average. A qualitative comparison between the plots reveals that adding monthly temperature and precipitation of the Upper Colorado catchment improves the streamflow predictions in the Lees Ferry river over 24 months.
5.2. Univariate and Multivariate Time-Series Comparison
Both univariate and multivariate time-series models demonstrated decent results in predicting streamflow of 24 months lead-time. This subsection aims to compare the performances in univariate and multivariate cases of all ML models. In other words, the purpose of this experiment is to discern potential improvements in predictions while considering meteorological components of the Upper Colorado River Basin along with the past streamflow. We hypothesize that the monthly temperature and precipitation of the Upper Colorado River Basin may affect the streamflow in the Colorado river, in particular the Lees Ferry site. In this subsection, we experimentally validate that hypothesis. Figure 14 shows the RMSE distributions of all 50 trials for both univariate and multivariate time-series models. Multivariate time-series RFR shows improvement in the RMSE plot by reducing the error. Consequently, we conclude that considering the temperature and precipitation of the Upper Colorado River Basin minimizes the error in the prediction of streamflow using RFR. Likewise, LSTM has less RMSE in its multivariate time-series model than its univariate counterpart.
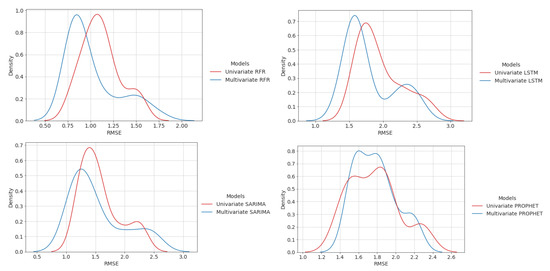
Figure 14.
RMSE distribution of univariate and multivariate time-series for all models.
SARIMAX shows improvement in the multivariate case. However, it shows a high variance in the multivariate model, which implies that there are unacceptable predictions in some of the trials. On the other hand, multivariate PROPHET does not reduce the RMSEs. We also observe that the multivariate time-series PROPHET reduced the variance in predictions compared to the univariate model.
R-squared values of multivariate RFR show significant progress compared with the univariate case, as shown in Figure 15. Analyzing both RMSE and R-squared figures reveals that multivariate RFR precisely predicts and accurately approximates the ground truth in most trials. However, the multivariate predictions have high variance, i.e., the predictions in some trials are not as satisfactory as the univariate case.
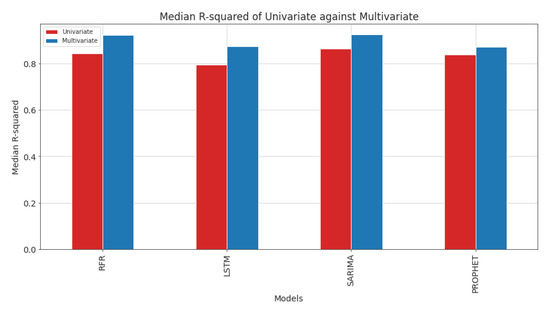
Figure 15.
Median R-squared of univariate against multivariate time-series models.
Multivariate LSTM achieved a higher R-squared since the median of its box plot is higher than the univariate case. Therefore, including temperature and precipitation as extra features increased R-squared in LSTM, i.e., the predictions in most trials follow the observed streamflow more precisely.
Multivariate SARIMA (SARIMAX) outperformed univariate SARIMA in terms of the R-squared metric, as shown in Figure 15. However, SARIMAX shows a higher variance of R-squared. Eventually, multivariate PROPHET shows a slight improvement in R-squared, meaning adding temperature and precipitation did not help achieve significantly higher R-squared. However, the RMSE was greatly reduced in its multivariate case.
The difference between forecasts and actual values can be informative to evaluate the models, and to observe the closeness of the predictions and observations. Figure 16 demonstrates the differences between forecasts and actual values in all test datasets for univariate and multivariate models. RFR shows lower differences (close to the center) for most of the months. As Figure 16 illustrates, RFR and SARIMA achieved the best results since the differences between predictions and observations are prone to zero. The x-axis represents the months that we aimed to predict. We repeated 24-month predictions 50 times over the test dataset. Therefore, the plots illustrate the deviation of 1200 months of predictions from the observations. We set a reasonable threshold of 2.1 mm for observing the differences between forecasts and observations. This threshold is considered based on average streamflow and it provides us with a fair comparison between the points. The shaded area covers the difference of 2.1 mm per month. The points that lie in this area are considered acceptable predictions since the deviation between observation and forecast is less than 2.1 mm per month. Table 1 shows the number of points that lie in-between the range of −2.1 and 2.1 mm per month for each model. Since the difference is computed by subtracting the forecasts from the observations, the points above the blue line represent that the values of forecasts are less than the actual values, and vice versa. As Table 1 shows, multivariate time-series RFR and SARIMA have the highest number of points in the shaded area, which means that most of the predictions are closer to the observations; 1001 and 1054 out of 1200 instances, respectively. Moreover, most models achieved a higher number of points in-between the range in their multivariate phase, which indicates that the multivariate time-series models improve the predictions by reducing the difference between predictions and observations. It is important to mention that these different values are computed for each instance, therefore, the comparison with the RMSE distributions that we have done in the previous sections is not fair since the RMSEs previously were computed by calculating the average RMSE of every 24-month window. As a result, we consider this study as a different assessment of the models, illustrating every single forecast value during the testing period.
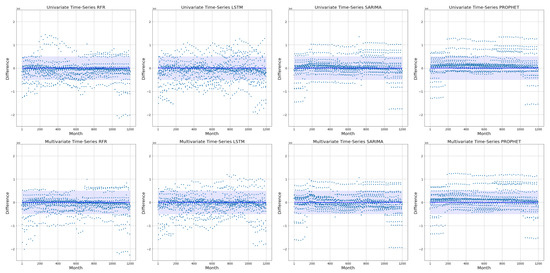
Figure 16.
Difference between predictions and observations for univariate and multivariate time-series models.

Table 1.
Number of points in Figure 16 that lie in-between the shaded area.
5.3. Sensitivity Analysis
In the previous sections, we ran several models to predict the streamflow for 24 months. Finally, we concluded that the multivariate Random Forest Regression (RFR) outperforms the other models, as shown by the evaluation metrics. In this section, by considering RFR as our best model to predict future streamflow at Lees Ferry, we aim to analyze the sensitivity of our best model in predicting future streamflow. Sensitivity Analysis explores the impact exerted on the predictions by manipulating the input data. Sensitivity analysis consists of adding noise to the input data in the testing phase. To do so, we added several Gaussian noises to all input features such as discharge, temperature, and precipitation. Noises A, B, C, and D with Gaussian (Normal) distribution with zero mean and standard deviation of 1, 2, 3, and 4 were added to the input data, respectively (Figure 17). Adding noise was applied meticulously only to the input sequences, leaving the output sequences as they are supposed to be observed. The purpose of this task is to observe how well we can predict future streamflow in the presence of uncertainty and unexpected values, i.e., noise, in the input data.
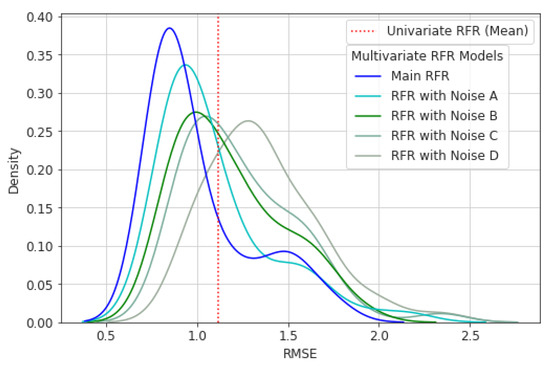
Figure 17.
The effect of adding Gaussian noise to the input data in multivariate time-series RFR.
As the standard deviation of noise increases, the performance of the multivariate time-series RFR model drops. RMSE distribution of the RFR model is the worst when we add noise D, in which the standard deviation is 4. Figure 17 demonstrates the effect of adding Gaussian noises to the multivariate time-series RFR model. Noise D with a standard deviation of 4 has the highest influence on our model. This is the breaking point for our RFR model, since adding noise D makes RFR fail in forecasting the streamflow. The best performance was achieved when there was no noise. We also added the mean of univariate time-series RFR to the plot as shown in Figure 17. The mean of 1.1 mm/month in univariate time-series RFR shows that the univariate model outperforms the multivariate model with the presence of noise D.
5.4. Sequence Analysis
In addition to the previous experiments, we compare different input and output sequence lengths for the best model, RFR, to observe the variations in the results. In other words, we explore the effects of considering different lead-time lengths along with different input sequences for assessing the quality of predictions. Therefore, a number of look back and look ahead span windows as 6, 12, 18, 24, 30, 36, 42, and 48 months are considered in this experiment. We increased the size of the test dataset to report a fair evaluation between different models since we consider four years of monthly data in the look back and look ahead sequences. To do so, the size of the test dataset is doubled, and consequently, the size of the training dataset is reduced. It is important to understand that this may bring about variance in the performance compared to the previous sections. However, our goal in this section is not to achieve the best result by increasing the training dataset, but rather to highlight the importance of selecting appropriate sequence lengths by comparing them together.
Figure 18 shows heat maps of the average RMSE, SMAPE, MAPE, R-squared, NSE, and KGE of all trials for each univariate time-series RFR model that covers four years of streamflow prediction. By considering Figure 18b, it can be clearly observed from the heat map that increasing the length of look back sequence reduces the average SMAPE while increasing the length of look ahead sequence increases the average SMAPE. However, increasing the size of look back and look ahead windows do not reduce the error since RFR may not be able to handle sequences that are too large. Likewise, we conclude the same results for RMSE, MAPE, R-squared, NSE, and KGE. However, a comparison between the R-squared of 6 months ahead and the rest may not be fair because R-squared is sensitive to the number of samples it receives. The same conclusion can be made for NSE and KGE. As a result, predicting the streamflow using RFR can be applicable as far as the look back and look ahead sequences are chosen cautiously. That being the case, a look back window of size equal to 24 was chosen for univariate time-series RFR. It is worth mentioning that the heat maps of R-squared and NSE are very similar since the Nash–Sutcliffe model efficiency coefficient is nearly identical to the coefficient of determination (R-squared) in its nature.
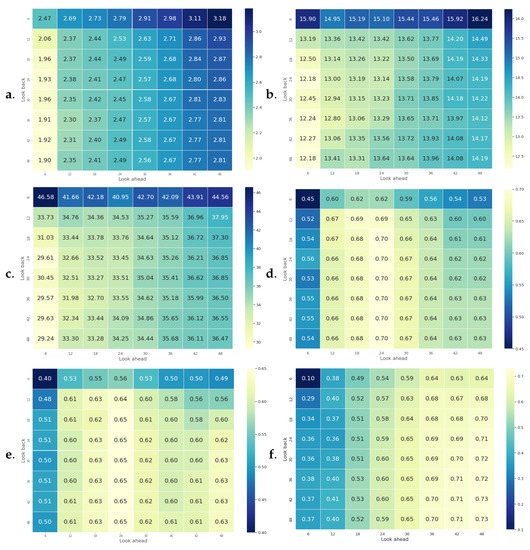
Figure 18.
Analysis of different look-back and look-ahead span windows for univariate time-series RFR in terms of their average RMSE, SMAPE, MAPE, R-squared, NSE, and KGE in sub-figures (a–f) respectively.
Figure 19 illustrates the same result as shown in Figure 18c. In addition, we added 1-month ahead prediction results since it is important to explore how the model predicts the streamflow for the next month. We considered look back windows of sizes 6, 12, 18, 24, 30, 36, 42, and 48, and evaluated them with MAPE, as shown in Figure 19. It can be observed that 1 month ahead prediction model outperforms the other ones. The model can easily learn from the data when the look-ahead window is set to one. In addition, the MAPE improved to 27 when we increased the length of the lookback window. The same trend can be observed from the other models, showing that increasing the look back improves the predictions as long as we reach the length of 24. The plots demonstrate that increasing the size of the look back window will not elevate the performance of models. On the other hand, the error grows by increasing the size of the look-ahead window.
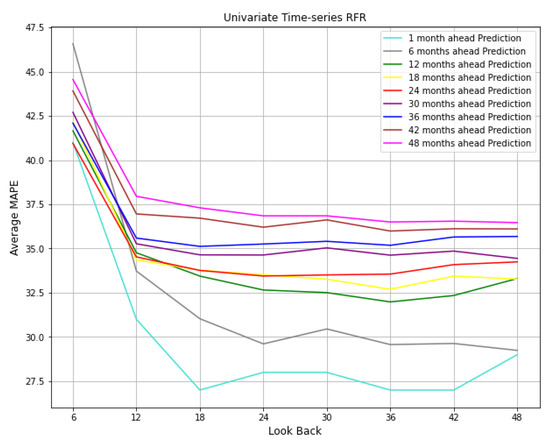
Figure 19.
Comparison between models with different look ahead windows and their corresponding look back windows in univariate time-series RFR.
Lastly, we investigated the predictions of univariate time-series RFR qualitatively in Figure 20, from May 2014 to April 2016, to observe the effects of various sequence lengths under which the RFR model performs very well or poorly. The comparison is reported on 6 months for each of the 4 time periods, since the lowest lead-time was 6 months; therefore, the predictions after the 6th month are not shown for the rest of the models. Figure 20 illustrates the predictions of all 8 RFR models, which are different in terms of their look ahead window sizes ranging from 6 to 48 months against the observations. All models have the same look back window that is equal to 24. It can be seen that they have very similar results in these periods and the predictions are very close to the observations. Additionally, considering smaller look ahead window sizes such as 6 and 12 enhances the predictions on average. However, these plots illustrate a qualitative result of how choosing different lead-time sequences affect the predictions.
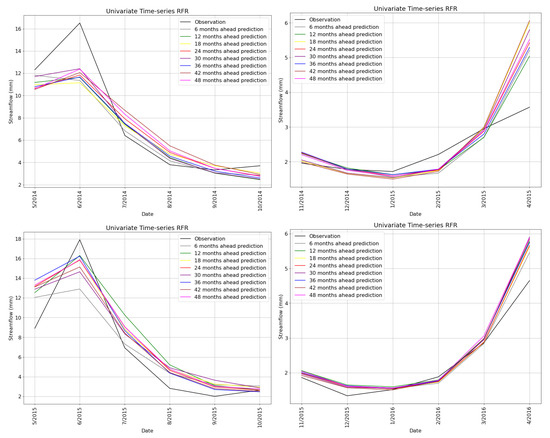
Figure 20.
Predictions of univariate time-series RFR models trained with different look-ahead span windows against the ground truth from May 2014 to April 2016.
Next, we explore the same analysis of Figure 18 for multivariate time-series RFR. Heat maps of RMSE, SMAPE, MAPE, and R-squared in Figure 21 demonstrate similar results as the univariate time-series RFR achieved earlier. The RMSE increases by increasing the look ahead window size and decreasing the look back window size. However, the variation rate in multivariate time-series RFR is slower than the univariate one, as shown in Figure 21. The major reason for this slow improvement may be due to the increased size of input data in the multivariate case, since we have added the temperature and precipitation. In other words, the dimensionality of the input sequences is tripled in multivariate time-series RFR by adding temperature and precipitation as additional features. The high-dimensionality of input may prevent the model to perform the best. Nevertheless, the multivariate forecasting performance is superior to the univariate one. Finally, the heat maps of multivariate RFR for R-squared and NSE are similar for the reason that has been mentioned earlier. The multivariate case shows higher similarity since the variation rate is slower.
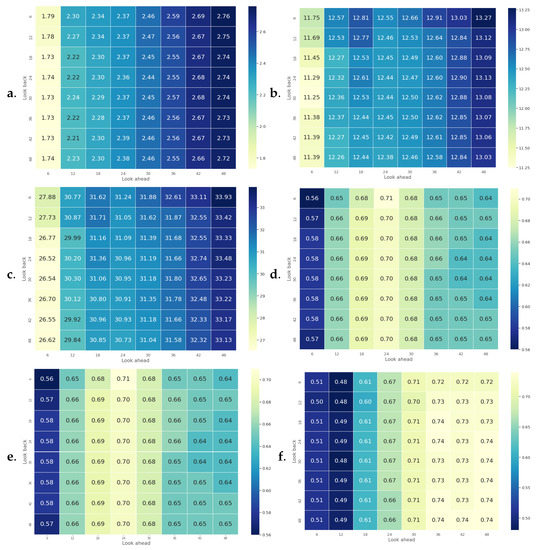
Figure 21.
Analysis of different look-back and look-ahead span windows for multivariate time-series RFR in terms of their average RMSE, SMAPE, MAPE, R-squared, NSE, and KGE in sub-figures (a–f) respectively.
A comparison between models with different look ahead windows and their corresponding look back windows in multivariate time-series RFR is shown in Figure 22. As mentioned earlier, the variation rate is slow. Considering 6 months ahead prediction the model shows that increasing the look back size reduces the error until we reach the size of 24. The error in most of the models becomes steady after increasing the look back window from 24 to 48 except for the 1-month look-ahead prediction model in which increasing the look-back window size does not help us elevate the performance. Furthermore, it can be observed that increasing the look-ahead window size increases the error. The MAPE for 1 month ahead prediction model is 25 while the MAPE for 6 months ahead prediction model is almost 28, and continues in the same way.
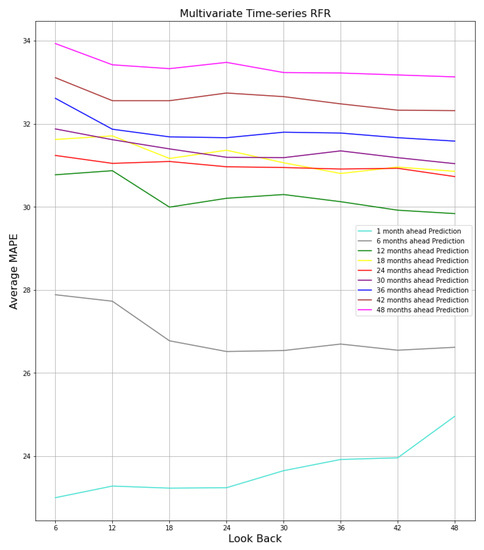
Figure 22.
Comparison between models with different look ahead windows and their corresponding look back windows in multivariate time-series RFR.
Finally, we demonstrate the predictions of multivariate time-series RFR models trained with different look ahead span windows against ground truth from May 2014 to April 2016, to explore their performance qualitatively. The comparison is reported on 6 months for each of the 4 time periods, similar to the univariate case. Figure 23 illustrates the predictions of all 8 multivariate time-series RFR models that are different in terms of their look ahead window sizes ranging from 6 to 48 months against the observations. All models have the same look-back window size of 24. It can be seen that choosing smaller look-ahead window sizes provides us with more accurate predictions. The major difference between Figure 20 and Figure 23 is that the predictions of the multivariate time-series RFR models are closer to the observations. For example, considering May to October 2014 reveals that the multivariate time-series RFR outperforms the univariate one.
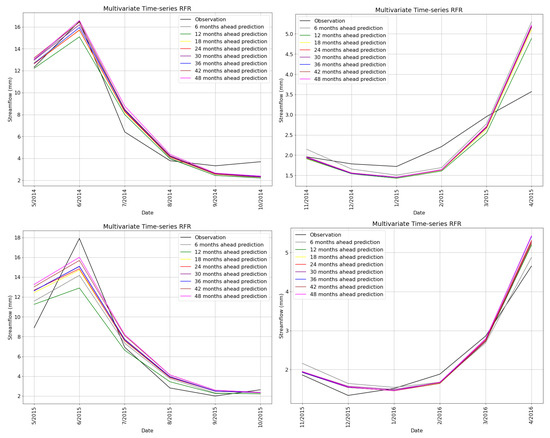
Figure 23.
Predictions of multivariate time-series RFR models trained with different look-ahead span windows against ground truth from May 2014 to April 2016.
6. Discussions
RFR demonstrated satisfactory results among the four ML-based models used in this study. In particular, multivariate RFR performed the best by achieving the highest performance according to the six evaluation metrics presented in the previous sections. The most controversial result might be the superior performance of RFR over LSTM, which is a deep learning and successful model. The reason might be due to the fact that random forest avoids overfitting by increasing the number of trees in the training phase. Moreover, RFR has been found to be more accurate than Artificial Neural Networks (ANNs) in several streamflow prediction tasks [80]. The fluctuations and seasonality in streamflow data might be an essential factor that random forest is able to effectively capture, such as the underlying information and non-linear relationships that are present in data, which it can learn it in a better way. A recent study of suspended sediment prediction in a river shows that random forest outperforms support vector machines and neural networks [81,82].
Furthermore, the predictions of random forest and neural networks are always within the range of the observations since they avoid extrapolation [83]. However, the other features made random forest perform better than LSTM, and neural networks are extremely dependent on the amount of training data.
In general, the performance of PROPHET was worse than other models. However, PROPHET deals with missing values and handles outliers and changes in time series as mentioned in Ref. [84]. On the other hand, SARIMA exceeded PROPHET and univariate LSTM by achieving decent results close to RFR. Ref. [85] indicates that SARIMA outperforms ML-based models in drought conditions.
To our knowledge, this is the first study that explores not only the impact of using multivariate time series models, but also investigates different look back and look ahead window lengths for RFR in the streamflow prediction task. These findings are highly valuable because multivariate RFR achieved excellent results based on the evaluation methods. In our opinion, the performance of RFR could be further improved by adding more predictor variables, such as snowmelt images or other meteorological components. However, failing to provide an interpretable result is the main limitation of the presented ML-based models in this paper. It is difficult to understand and explain why a particular prediction was made by most of the ML models. Ultimately, it is worth mentioning that the streamflow prediction in drought-stricken UCRB is more challenging than in wet areas. In addition, Ref. [86] indicates that the data-driven models on a monthly scale perform better in wet conditions than in dry conditions.
While the purpose of this work was to concentrate on Lees Ferry to explore this vital station in detail, we also applied the RFR model on multiple rivers in different states to test the generalizability of the work that has been done on Lees Ferry in the previous sections. To do so, we picked two more stations that lie in the UCRB. San Juan River Near Bluff is a station that is located in Utah. The other station that we were interested in analyzing its future streamflow was Yampa River Near Maybell, which is located in the upper part of the Colorado state. The average level of water in these two stations is extremely lower than in Lees Ferry. As shown in Figure 24, three candidate stations that are located in three different states belonging to the UCRB have been explored to assess our best performing model. It can be observed that our univariate and multivariate RFR models have low error when performed on Lees Ferry and Yampa stations. On the other hand, univariate RFR has higher SMAPE on data derived from San Juan station. However, multivariate time series RFR remarkably reduced the SMAPE for San Juan, as shown in Figure 24. Therefore, we conclude that the time series RFR model can be generalized to more stations in UCRB to perform real-life streamflow prediction.
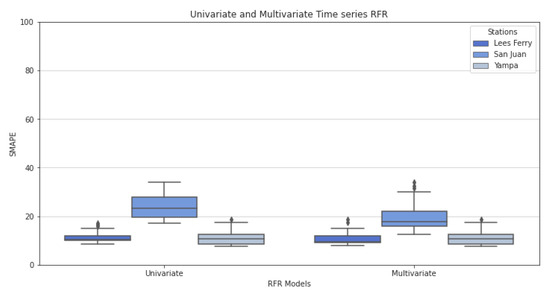
Figure 24.
Generalizability test by applying RFR in multiple rivers. Univariate and multivariate time series RFR are compared for 24 months streamflow prediction at Lees Ferry, San Juan, and Yampa stations.
At the end, the uncertainty of the model should be further investigated in rare conditions since some models are relatively variable when faced with extreme climate conditions such as unexpected and occasional floods or drought. Furthermore, it is still an open question to distinctly understand the impact of temperature and precipitation on streamflow prediction in this area. We anticipate that the temperature plays a major factor and has more influence than precipitation on the streamflow at Lees Ferry because it is located in drought-stricken UCRB. On the other hand, we expect that the precipitation plays a critical role in wet conditions and can be considered an important driving force in those areas.
7. Conclusions
In this paper, we used machine learning models to predict the future streamflow of the Lees Ferry site of the Upper Colorado River Basin, where the river is a source of water for several states in the United States. Over 113 years of monthly data were used for training and testing the ML models. Four ML models such as RFR, LSTM, SARIMA, and PROPHET were compared with each other. In this regard, we first only used past streamflow to predict its future values for 24 months. Various input sequences and hyperparameters were analyzed for each model in order to choose the best possible model and to compare their performances. All models achieved satisfactory performance with low RMSE and obtained high R-squared, and also the MAPEs for all models were less than 25%, which means that the presented models are able to predict future streamflow accurately for at least 24 months. RFR and SARIMA were the two models that outperformed the others with low error.
Subsequently, we improved the earlier models by adding meteorological components such as temperature and precipitation to our dataset, i.e., training multivariate time-series models by considering past streamflow, temperature, and precipitation to predict future streamflow. We used monthly spatiotemporal temperature and precipitation values to compute the mean meteorological feature values of each month. We performed multiple trials, and showed performance gain in multivariate predictions. Multivariate predictions were more precise in approximating the observed streamflow. We conclude that the temperature and precipitation of the Upper Colorado River Basin had positive impact on the streamflow prediction in this area. Adding monthly temperature improved R-squared and reduced the error of our models, especially for RFR and LSTM. The predictions in both univariate and multivaraite tasks were shown to be robust for predicting the streamflow at Lees Ferry for 24 months. However, the variance of some models was higher than the rest. This could be improved by training with more data and also by validating the performance of models in a larger test dataset. Therefore, based on our study at Lees Ferry, the multivariate time-series RFR model achieved more promising performance by producing better predictions.
In the final section, we explored sequence and sensitivity analysis for our best model, multivariate time-series RFR. Our sensitivity analysis suggested that the multivariate time-series RFR is robust to noise. Furthermore, the results of average RMSE, SMAPE, MAPE, and R-squared in sequence analysis indicate that choosing very short look-back window sizes leads to inaccurate predictions. Increasing the look-back window size helps us make better predictions, while there is a threshold that prevents us from choosing a very large window size. Furthermore, increasing the look-ahead window size leads to inaccurate predictions. Choosing the best sequence length lies under the task of hyperparameter tuning, which can help the model work at its best performance.
In the end, we conclude that considering past temperature and precipitation of the Upper Colorado catchment improves the predictions of future streamflow of Lees Ferry, where the site lies in the middle of the Colorado Basin. Nevertheless, several cases need further investigation and extra work. To this end, one may extend this work to observe the influence of meteorological components in various parts of the Colorado basin. In addition, we only considered the boundary of the Upper Colorado Basin. One may consider a variety of boundaries instead of the Upper Colorado River Basin to observe the influences of those boundaries on the streamflow prediction in the Lees Ferry station. Finally, obtaining larger data helps us fairly evaluate the models’ predictions since choosing a small-size test dataset may bring about biased results. Therefore, collecting more data matters highly in our case, mainly when dealing with monthly or yearly data.
Lastly, given the importance of temperature and precipitation in streamflow prediction, further work could be performed on the state-of-the-art models such as CNN-LSTM [87,88] and transformer [89,90] considering the past discharge, temperature, and precipitation of the Upper Colorado River Basin as spatiotemporal data in order to predict the streamflow at Lees Ferry for at least 2 years based on monthly data.
Author Contributions
P.H. implemented, analyzed, and wrote the paper. A.N. and S.F.B. supervised the research, contributed with ideas during the interpretation of results, and reviewed the paper S.M.H. contributed with ideas and reviewed the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data presented in this study are openly available in the United States Bureau of Reclamation (USBR) website at https://www.usbr.gov/lc/region/g4000/NaturalFlow/previous.html (accessed on 13 December 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Bai, J.; Shi, H.; Yu, Q.; Xie, Z.; Li, L.; Luo, G.; Jin, N.; Li, J. Satellite-observed vegetation stability in response to changes in climate and total water storage in Central Asia. Sci. Total Environ. 2019, 659, 862–871. [Google Scholar] [CrossRef]
- Sabzi, H.Z.; Moreno, H.A.; Fovargue, R.; Xue, X.; Hong, Y.; Neeson, T.M. Comparison of projected water availability and demand reveals future hotspots of water stress in the Red River basin, USA. J. Hydrol. Reg. Stud. 2019, 26, 100638. [Google Scholar] [CrossRef]
- Hannaford, J. Climate-driven changes in UK river flows: A review of the evidence. Prog. Phys. Geogr. 2015, 39, 29–48. [Google Scholar] [CrossRef]
- Milly, P.C.; Dunne, K.A.; Vecchia, A.V. Global pattern of trends in streamflow and water availability in a changing climate. Nature 2005, 438, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Xu, Y.P.; Teegavarapu, R.S.; Guo, Y.; Xie, J. Assessing different roles of baseflow and surface runoff for long-term streamflow forecasting in southeastern China. Hydrol. Sci. J. 2021, 66, 2312–2329. [Google Scholar] [CrossRef]
- Golembesky, K.; Sankarasubramanian, A.; Devineni, N. Improved drought management of Falls Lake Reservoir: Role of multimodel streamflow forecasts in setting up restrictions. J. Water Resour. Plan. Manag. 2009, 135, 188–197. [Google Scholar] [CrossRef]
- Lorenz, E.N. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Delgado-Ramos, F.; Hervás-Gámez, C. Simple and low-cost procedure for monthly and yearly streamflow forecasts during the current hydrological year. Water 2018, 10, 1038. [Google Scholar] [CrossRef]
- Donegan, S.; Murphy, C.; Harrigan, S.; Broderick, C.; Foran Quinn, D.; Golian, S.; Knight, J.; Matthews, T.; Prudhomme, C.; Scaife, A.A.; et al. Conditioning ensemble streamflow prediction with the North Atlantic Oscillation improves skill at longer lead times. Hydrol. Earth Syst. Sci. 2021, 25, 4159–4183. [Google Scholar] [CrossRef]
- Arnal, L.; Cloke, H.L.; Stephens, E.; Wetterhall, F.; Prudhomme, C.; Neumann, J.; Krzeminski, B.; Pappenberger, F. Skilful seasonal forecasts of streamflow over Europe? Hydrol. Earth Syst. Sci. 2018, 22, 2057–2072. [Google Scholar] [CrossRef]
- Eldardiry, H.; Hossain, F. The value of long-term streamflow forecasts in adaptive reservoir operation: The case of the High Aswan Dam in the transboundary Nile River basin. J. Hydrometeorol. 2021, 22, 1099–1115. [Google Scholar] [CrossRef]
- Souza Filho, F.A.; Lall, U. Seasonal to interannual ensemble streamflow forecasts for Ceara, Brazil: Applications of a multivariate, semiparametric algorithm. Water Resour. Res. 2003, 39, 1307. [Google Scholar] [CrossRef]
- Liu, P.; Wang, L.; Ranjan, R.; He, G.; Zhao, L. A survey on active deep learning: From model-driven to data-driven. ACM Comput. Surv. 2021, 54, 1–34. [Google Scholar] [CrossRef]
- Brêda, J.P.L.F.; de Paiva, R.C.D.; Collischon, W.; Bravo, J.M.; Siqueira, V.A.; Steinke, E.B. Climate change impacts on South American water balance from a continental-scale hydrological model driven by CMIP5 projections. Clim. Chang. 2020, 159, 503–522. [Google Scholar] [CrossRef]
- Vieux, B.E.; Cui, Z.; Gaur, A. Evaluation of a physics-based distributed hydrologic model for flood forecasting. J. Hydrol. 2004, 298, 155–177. [Google Scholar] [CrossRef]
- Zang, S.; Li, Z.; Zhang, K.; Yao, C.; Liu, Z.; Wang, J.; Huang, Y.; Wang, S. Improving the flood prediction capability of the Xin’anjiang model by formulating a new physics-based routing framework and a key routing parameter estimation method. J. Hydrol. 2021, 603, 126867. [Google Scholar] [CrossRef]
- Lu, D.; Konapala, G.; Painter, S.L.; Kao, S.C.; Gangrade, S. Streamflow simulation in data-scarce basins using bayesian and physics-informed machine learning models. J. Hydrometeorol. 2021, 22, 1421–1438. [Google Scholar] [CrossRef]
- Clark, M.P.; Bierkens, M.F.; Samaniego, L.; Woods, R.A.; Uijlenhoet, R.; Bennett, K.E.; Pauwels, V.; Cai, X.; Wood, A.W.; Peters-Lidard, C.D. The evolution of process-based hydrologic models: Historical challenges and the collective quest for physical realism. Hydrol. Earth Syst. Sci. 2017, 21, 3427–3440. [Google Scholar] [CrossRef]
- Mei, X.; Van Gelder, P.; Dai, Z.; Tang, Z. Impact of dams on flood occurrence of selected rivers in the United States. Front. Earth Sci. 2017, 11, 268–282. [Google Scholar] [CrossRef]
- Riley, M.; Grandhi, R. A method for the quantification of model-form and parametric uncertainties in physics-based simulations. In Proceedings of the 52nd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference 19th AIAA/ASME/AHS Adaptive Structures Conference 13t, Denver, CO, USA, 4–7 April 2011; p. 1765. [Google Scholar]
- Siddiqi, T.A.; Ashraf, S.; Khan, S.A.; Iqbal, M.J. Estimation of data-driven streamflow predicting models using machine learning methods. Arab. J. Geosci. 2021, 14, 1–9. [Google Scholar] [CrossRef]
- Gauch, M.; Mai, J.; Gharari, S.; Lin, J. Data-driven vs. physically-based streamflow prediction models. In Proceedings of the 9th International Workshop on Climate Informatics, Paris, France, 2–4 October 2019. [Google Scholar]
- Mosavi, A.; Ozturk, P.; Chau, K.w. Flood prediction using machine learning models: Literature review. Water 2018, 10, 1536. [Google Scholar] [CrossRef]
- Gauch, M. Machine Learning for Streamflow Prediction. Master’s Thesis, University of Waterloo, Waterloo, ON, Canada, 2020. [Google Scholar]
- Rasouli, K. Short Lead-Time Streamflow Forecasting by Machine Learning Methods, with Climate Variability Incorporated. Ph.D. Thesis, University of British Columbia Vancouver, Vancouver, BC, Canada, 2010. [Google Scholar]
- Yan, J.; Jia, S.; Lv, A.; Zhu, W. Water resources assessment of China’s transboundary river basins using a machine learning approach. Water Resour. Res. 2019, 55, 632–655. [Google Scholar] [CrossRef]
- Gumiere, S.J.; Camporese, M.; Botto, A.; Lafond, J.A.; Paniconi, C.; Gallichand, J.; Rousseau, A.N. Machine learning vs. physics-based modeling for real-time irrigation management. Front. Water 2020, 2, 8. [Google Scholar] [CrossRef]
- Kumar, K.; Jain, V.K. Autoregressive integrated moving averages (ARIMA) modelling of a traffic noise time series. Appl. Acoust. 1999, 58, 283–294. [Google Scholar] [CrossRef]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Comparison of the ARMA, ARIMA, and the autoregressive artificial neural network models in forecasting the monthly inflow of Dez dam reservoir. J. Hydrol. 2013, 476, 433–441. [Google Scholar] [CrossRef]
- Ghimire, B.N. Application of ARIMA model for river discharges analysis. J. Nepal Phys. Soc. 2017, 4, 27–32. [Google Scholar] [CrossRef]
- Valipour, M. Long-term runoff study using SARIMA and ARIMA models in the United States. Meteorol. Appl. 2015, 22, 592–598. [Google Scholar] [CrossRef]
- Taylor, S.J.; Letham, B. Forecasting at scale. Am. Stat. 2018, 72, 37–45. [Google Scholar] [CrossRef]
- Basak, A.; Rahman, A.S.; Das, J.; Hosono, T.; Kisi, O. Drought forecasting using the Prophet model in a semi-arid climate region of western India. Hydrol. Sci. J. 2022, 67, 1397–1417. [Google Scholar] [CrossRef]
- Rahman, A.S.; Hosono, T.; Kisi, O.; Dennis, B.; Imon, A.R. A minimalistic approach for evapotranspiration estimation using the Prophet model. Hydrol. Sci. J. 2020, 65, 1994–2006. [Google Scholar] [CrossRef]
- Xiao, Q.; Zhou, L.; Xiang, X.; Liu, L.; Liu, X.; Li, X.; Ao, T. Integration of Hydrological Model and Time Series Model for Improving the Runoff Simulation: A Case Study on BTOP Model in Zhou River Basin, China. Appl. Sci. 2022, 12, 6883. [Google Scholar] [CrossRef]
- Segal, M.R. Machine Learning Benchmarks and Random Forest Regression; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Zhang, Y.; Chiew, F.H.; Li, M.; Post, D. Predicting runoff signatures using regression and hydrological modeling approaches. Water Resour. Res. 2018, 54, 7859–7878. [Google Scholar] [CrossRef]
- Li, J.; Wang, Z.; Lai, C.; Zhang, Z. Tree-ring-width based streamflow reconstruction based on the random forest algorithm for the source region of the Yangtze River, China. Catena 2019, 183, 104216. [Google Scholar] [CrossRef]
- Kombo, O.H.; Kumaran, S.; Sheikh, Y.H.; Bovim, A.; Jayavel, K. Long-term groundwater level prediction model based on hybrid KNN-RF technique. Hydrology 2020, 7, 59. [Google Scholar] [CrossRef]
- Dastjerdi, S.Z.; Sharifi, E.; Rahbar, R.; Saghafian, B. Downscaling WGHM-Based Groundwater Storage Using Random Forest Method: A Regional Study over Qazvin Plain, Iran. Hydrology 2022, 9, 179. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef]
- Hu, Y.; Yan, L.; Hang, T.; Feng, J. Stream-flow forecasting of small rivers based on LSTM. arXiv 2020, arXiv:2001.05681. [Google Scholar]
- Fu, M.; Fan, T.; Ding, Z.; Salih, S.Q.; Al-Ansari, N.; Yaseen, Z.M. Deep learning data-intelligence model based on adjusted forecasting window scale: Application in daily streamflow simulation. IEEE Access 2020, 8, 32632–32651. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall–runoff modelling using long short-term memory (LSTM) networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef]
- Rahimzad, M.; Moghaddam Nia, A.; Zolfonoon, H.; Soltani, J.; Danandeh Mehr, A.; Kwon, H.H. Performance comparison of an lstm-based deep learning model versus conventional machine learning algorithms for streamflow forecasting. Water Resour. Manag. 2021, 35, 4167–4187. [Google Scholar] [CrossRef]
- Alizadeh, B.; Bafti, A.G.; Kamangir, H.; Zhang, Y.; Wright, D.B.; Franz, K.J. A novel attention-based LSTM cell post-processor coupled with bayesian optimization for streamflow prediction. J. Hydrol. 2021, 601, 126526. [Google Scholar] [CrossRef]
- Feng, D.; Fang, K.; Shen, C. Enhancing streamflow forecast and extracting insights using long-short term memory networks with data integration at continental scales. Water Resour. Res. 2020, 56, e2019WR026793. [Google Scholar] [CrossRef]
- Apaydin, H.; Sattari, M.T.; Falsafian, K.; Prasad, R. Artificial intelligence modelling integrated with Singular Spectral analysis and Seasonal-Trend decomposition using Loess approaches for streamflow predictions. J. Hydrol. 2021, 600, 126506. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow prediction using an integrated methodology based on convolutional neural network and long short-term memory networks. Sci. Rep. 2021, 11, 1–26. [Google Scholar] [CrossRef]
- Le, X.H.; Nguyen, D.H.; Jung, S.; Yeon, M.; Lee, G. Comparison of deep learning techniques for river streamflow forecasting. IEEE Access 2021, 9, 71805–71820. [Google Scholar] [CrossRef]
- Risbey, J.S.; Entekhabi, D. Observed Sacramento Basin streamflow response to precipitation and temperature changes and its relevance to climate impact studies. J. Hydrol. 1996, 184, 209–223. [Google Scholar] [CrossRef]
- Fu, G.; Charles, S.P.; Chiew, F.H. A two-parameter climate elasticity of streamflow index to assess climate change effects on annual streamflow. Water Resour. Res. 2007, 43, W11419. [Google Scholar] [CrossRef]
- Xu, T.; Longyang, Q.; Tyson, C.; Zeng, R.; Neilson, B.T. Hybrid Physically Based and Deep Learning Modeling of a Snow Dominated, Mountainous, Karst Watershed. Water Resour. Res. 2022, 58, e2021WR030993. [Google Scholar] [CrossRef]
- Asefa, T.; Kemblowski, M.; McKee, M.; Khalil, A. Multi-time scale stream flow predictions: The support vector machines approach. J. Hydrol. 2006, 318, 7–16. [Google Scholar] [CrossRef]
- Zhao, S.; Fu, R.; Zhuang, Y.; Wang, G. Long-lead seasonal prediction of streamflow over the Upper Colorado River Basin: The role of the Pacific sea surface temperature and beyond. J. Clim. 2021, 34, 6855–6873. [Google Scholar] [CrossRef]
- Water, G. The Sustainable Use of Water in the Lower Colorado River Basin; Pacific Institute for Studies in Development, Environment, and Security: Oakland, CA, USA, 1996. [Google Scholar]
- Vano, J.A.; Udall, B.; Cayan, D.R.; Overpeck, J.T.; Brekke, L.D.; Das, T.; Hartmann, H.C.; Hidalgo, H.G.; Hoerling, M.; McCabe, G.J.; et al. Understanding uncertainties in future Colorado River streamflow. Bull. Am. Meteorol. Soc. 2014, 95, 59–78. [Google Scholar] [CrossRef]
- Smith, J.A.; Baeck, M.L.; Yang, L.; Signell, J.; Morin, E.; Goodrich, D.C. The paroxysmal precipitation of the desert: Flash floods in the Southwestern United States. Water Resour. Res. 2019, 55, 10218–10247. [Google Scholar] [CrossRef]
- Barnett, T.P.; Pierce, D.W. Sustainable water deliveries from the Colorado River in a changing climate. Proc. Natl. Acad. Sci. USA 2009, 106, 7334–7338. [Google Scholar] [CrossRef] [PubMed]
- Cohen, M.; Christian-Smith, J.; Berggren, J. Water to supply the land. Pac. Inst. 2013. [Google Scholar]
- Xiao, M.; Udall, B.; Lettenmaier, D.P. On the causes of declining Colorado River streamflows. Water Resour. Res. 2018, 54, 6739–6756. [Google Scholar] [CrossRef]
- Board, C.W.C. Flood Hazard Mitigation Plan for Colorado. Integration 2010, 2, 1. [Google Scholar]
- Kopytkovskiy, M.; Geza, M.; McCray, J. Climate-change impacts on water resources and hydropower potential in the Upper Colorado River Basin. J. Hydrol. Reg. Stud. 2015, 3, 473–493. [Google Scholar] [CrossRef]
- Rumsey, C.A.; Miller, M.P.; Schwarz, G.E.; Hirsch, R.M.; Susong, D.D. The role of baseflow in dissolved solids delivery to streams in the Upper Colorado River Basin. Hydrol. Process. 2017, 31, 4705–4718. [Google Scholar] [CrossRef]
- Hadjimichael, A.; Quinn, J.; Wilson, E.; Reed, P.; Basdekas, L.; Yates, D.; Garrison, M. Defining robustness, vulnerabilities, and consequential scenarios for diverse stakeholder interests in institutionally complex river basins. Earth’s Future 2020, 8, e2020EF001503. [Google Scholar] [CrossRef]
- Hwang, J.; Kumar, H.; Ruhi, A.; Sankarasubramanian, A.; Devineni, N. Quantifying Dam-Induced Fluctuations in Streamflow Frequencies Across the Colorado River Basin. Water Resour. Res. 2021, 57, e2021WR029753. [Google Scholar] [CrossRef]
- Kirk, J.P.; Schmidlin, T.W. Moisture transport associated with large precipitation events in the Upper Colorado River Basin. Int. J. Climatol. 2018, 38, 5323–5338. [Google Scholar] [CrossRef]
- Ayers, J.; Ficklin, D.L.; Stewart, I.T.; Strunk, M. Comparison of CMIP3 and CMIP5 projected hydrologic conditions over the Upper Colorado River Basin. Int. J. Climatol. 2016, 36, 3807–3818. [Google Scholar] [CrossRef]
- Salehabadi, H.; Tarboton, D.; Kuhn, E.; Udall, B.; Wheeler, K.; Rosenberg, D.; Goeking, S.; Schmidt, J.C. The future hydrology of the Colorado River Basin. In The Future of the Colorado River Project; White Paper No. 4; Utah State University, Quinney College of Natural Resources Center for Colorado River Studies: Logan, UT, USA, 2020; 71p. [Google Scholar]
- Lukas, J.; Payton, E. Colorado River Basin Climate and Hydrology: State of the Science; Western Water Assessment, University of Colorado Boulder: Boulder, CO, USA, 2020. [Google Scholar]
- McCabe, G.J.; Wolock, D.M.; Pederson, G.T.; Woodhouse, C.A.; McAfee, S. Evidence that recent warming is reducing upper Colorado River flows. Earth Interact. 2017, 21, 1–14. [Google Scholar] [CrossRef]
- McCoy, A.L.; Jacobs, K.L.; Vano, J.A.; Wilson, J.K.; Martin, S.; Pendergrass, A.G.; Cifelli, R. The Press and Pulse of Climate Change: Extreme Events in the Colorado River Basin. JAWRA J. Am. Water Resour. Assoc. 2022, 58, 1076–1097. [Google Scholar] [CrossRef]
- Kappal, S. Data normalization using median median absolute deviation MMAD based Z-score for robust predictions vs. min–max normalization. Lond. J. Res. Sci. Nat. Form. 2019, 19. [Google Scholar]
- Toharudin, T.; Pontoh, R.S.; Caraka, R.E.; Zahroh, S.; Lee, Y.; Chen, R.C. Employing long short-term memory and Facebook prophet model in air temperature forecasting. Commun.-Stat.-Simul. Comput. 2020, 52, 279–290. [Google Scholar] [CrossRef]
- Bercu, S.; Proïa, F. A SARIMAX coupled modelling applied to individual load curves intraday forecasting. J. Appl. Stat. 2013, 40, 1333–1348. [Google Scholar] [CrossRef]
- Sarhadi, A.; Kelly, R.; Modarres, R. Snow water equivalent time-series forecasting in Ontario, Canada, in link to large atmospheric circulations. Hydrol. Process. 2014, 28, 4640–4653. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Gupta, H.V.; Kling, H.; Yilmaz, K.K.; Martinez, G.F. Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. J. Hydrol. 2009, 377, 80–91. [Google Scholar] [CrossRef]
- Shortridge, J.E.; Guikema, S.D.; Zaitchik, B.F. Machine learning methods for empirical streamflow simulation: A comparison of model accuracy, interpretability, and uncertainty in seasonal watersheds. Hydrol. Earth Syst. Sci. 2016, 20, 2611–2628. [Google Scholar] [CrossRef]
- Al-Mukhtar, M. Random forest, support vector machine, and neural networks to modelling suspended sediment in Tigris River-Baghdad. Environ. Monit. Assess. 2019, 191, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Minns, A.; Hall, M. Artificial neural networks as rainfall-runoff models. Hydrol. Sci. J. 1996, 41, 399–417. [Google Scholar] [CrossRef]
- Francke, T.; López-Tarazón, J.; Schröder, B. Estimation of suspended sediment concentration and yield using linear models, random forests and quantile regression forests. Hydrol. Process. Int. J. 2008, 22, 4892–4904. [Google Scholar] [CrossRef]
- Aguilera, H.; Guardiola-Albert, C.; Naranjo-Fernández, N.; Kohfahl, C. Towards flexible groundwater-level prediction for adaptive water management: Using Facebook’s Prophet forecasting approach. Hydrol. Sci. J. 2019, 64, 1504–1518. [Google Scholar] [CrossRef]
- Khodakhah, H.; Aghelpour, P.; Hamedi, Z. Comparing linear and non-linear data-driven approaches in monthly river flow prediction, based on the models SARIMA, LSSVM, ANFIS, and GMDH. Environ. Sci. Pollut. Res. 2022, 29, 21935–21954. [Google Scholar] [CrossRef]
- Yaghoubi, B.; Hosseini, S.A.; Nazif, S. Monthly prediction of streamflow using data-driven models. J. Earth Syst. Sci. 2019, 128, 1–15. [Google Scholar] [CrossRef]
- Livieris, I.E.; Pintelas, E.; Pintelas, P. A CNN–LSTM model for gold price time-series forecasting. Neural Comput. Appl. 2020, 32, 17351–17360. [Google Scholar] [CrossRef]
- Lu, W.; Li, J.; Li, Y.; Sun, A.; Wang, J. A CNN-LSTM-based model to forecast stock prices. Complexity 2020, 2020, 6622927. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30. [Google Scholar]
- Wang, C.; Chen, Y.; Zhang, S.; Zhang, Q. Stock market index prediction using deep Transformer model. Expert Syst. Appl. 2022, 208, 118128. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).