Optimal Signal Quality Index for Photoplethysmogram Signals
Abstract
:1. Introduction
2. Methods
2.1. Data Collection
2.2. Annotation
- Excellent for diagnosis: The “excellent” for diagnosis group (G1) includes only PPG signals where the systolic and diastolic waves are salient.
- Acceptable for diagnosis: The “acceptable” for diagnosis group (G2) includes only PPG signals where the systolic and diastolic waves are salient but where HR can be determined.
- Unfit for diagnosis: The “unfit” for diagnosis group (G3) includes only noisy PPG signals where HR cannot be determined and the systolic and diastolic waves cannot be distinguished.
2.3. Signal Quality Indices
- Perfusion (): As previously mentioned, this is the gold standard for assessing PPG signal quality [14,15,16,17]. The perfusion index is the ratio of the pulsatile blood flow to the nonpulsatile or static blood in peripheral tissue. In other words, it is the difference of the amount of light absorbed through the pulse of when light is transmitted through the finger, which can be defined as follows:where is the perfusion index, is the statistical mean of the x signal (raw PPG signal), and y is the filtered PPG signal.
- Skewness (): This statistic measure was tested, as Krishnan et al. [18] found that skewness is associated with corrupted PPG signals. Skewness is a measure of the symmetry (or the lack of it) of a probability distribution, which is defined as:where and σ are the empirical estimate of the mean and standard deviation of , respectively, and N is the number of samples in the PPG signal.
- Kurtosis (): Recently, Selvaraj et al. [19] found that kurtosis is a good indicator for PPG signal quality. Kurtosis is a statistical measure used to describe the distribution of observed data around the mean. It represents a heavy tail and peakedness or a light tail and flatness of a distribution relative to the normal distribution, which is defined as:where and σ are the empirical estimate of the mean and standard deviation of , respectively; and N is the number of samples in the PPG signal.
- Entropy (): Recently, Selvaraj et al. [19] found that entropy is a good indicator for PPG signal quality. Entropy quantifies how much the probability density function (PDF) of the signal differs from a uniform distribution and thus provides a quantitative measure of the uncertainty present in the signal [24], which is defined [25] as:where x signal is the raw PPG signal and N is the number of data points.
- Zero crossing rate (): This is the rate of sign-changes in the processed signal, that is, the rate at which the signal changes from positive to negative or back [26], which is defined as:where y is the filtered PPG signal of length N, and , the indicator function , is 1 if its argument A is true, and 0 otherwise.
- Signal-to-noise ratio (): This is a measure used in science and engineering that compares the level of a desired signal to the level of background noise. There are many ways to define signal-to-noise ratio [27]; however, here the ratio of signal variance to the noise variance was used, as follows:where is the standard deviation of the absolute value of the filtered PPG signal (y) and is the standard deviation of the y signal.
- Matching of multiple systolic wave detection algorithms (): Because different PPG algorithms are sensitive to different types of noise [28], the comparison of how accurately multiple PPG systolic wave detectors isolate each event (such as a beat or noise artifact) provides one estimate of the level of noise in the PPG. In this study, two well-known systolic wave detection algorithms were used. One is based on first derivative with adaptive thresholds [29], and the other is based on local maxima and minima [30]. These algorithms are referred to as Bing’s and Billauer’s algorithms. The reason for selecting Bing’s and Billauer’s algorithms is that both are easy to implement and each algorithm approaches the PPG signal from different perspectives [22]. We defined the matching of the algorithm outputs as follows:where represents the systolic waves detected by Bing’s algorithm, and represents the systolic waves detected by Billauer’s algorithm.
- Relative power (): The frequency domain was explored to assess the PPG signal quality, a different perspective from the time domain features discussed above. Because most of the energy of the systolic and diastolic waves is concentrated within the 1– Hz [22] frequency band, the ratio of the power spectral density (PSD) in this band compared to the PSD in the overall signal 0–8 Hz [22] provides a measure of the signal quality, which is defined as follows:where PSD was calculated using Welch’s method.
2.4. Statistical Analysis
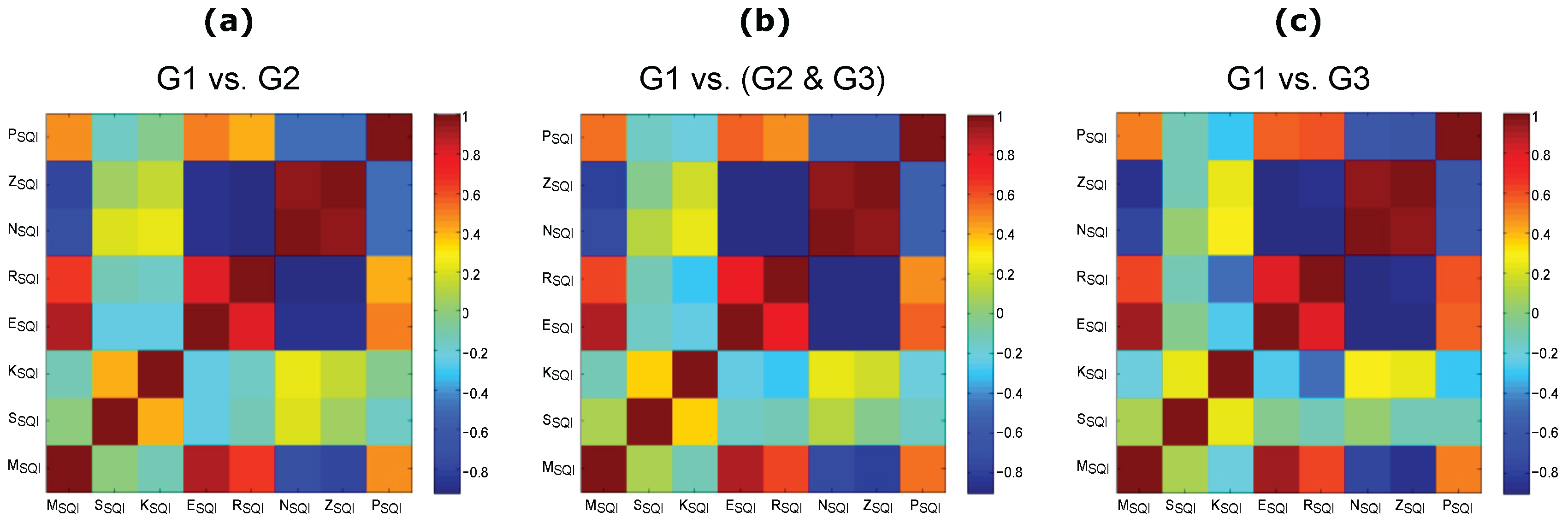
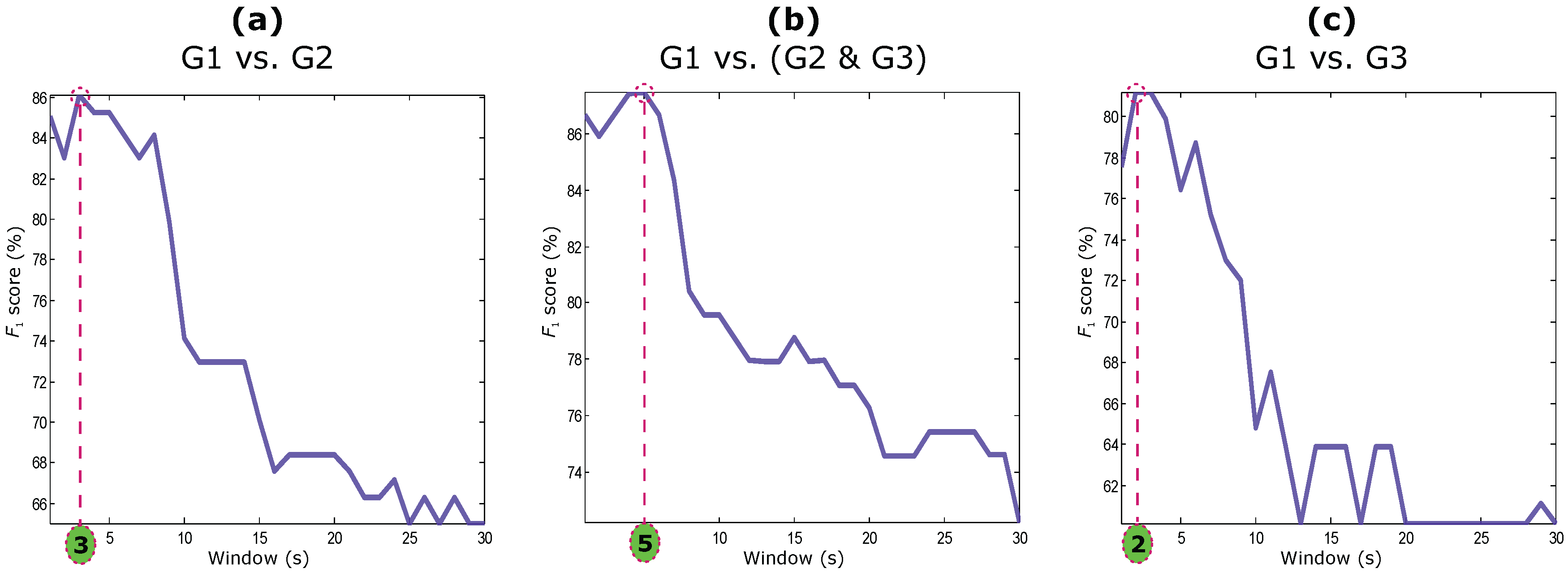
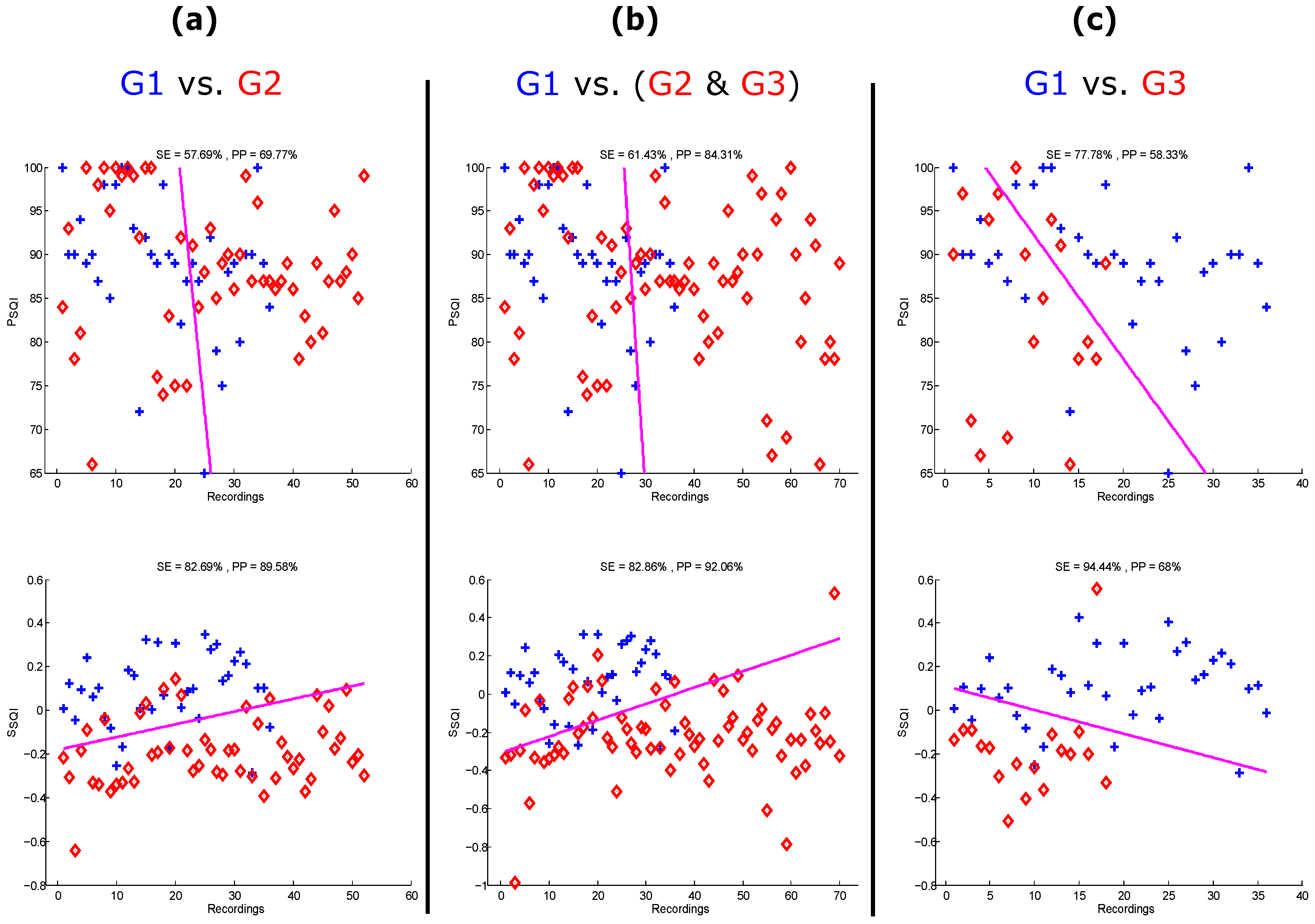
3. Results and Discussion
4. Limitations of the Study and Future Work
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Yoon, G.; Lee, J.Y.; Jeon, K.J.; Park, K.K.; Yeo, H.S.; Hwang, H.T.; Kim, H.S.; Hwang, I.D. Multiple diagnosis based on photoplethysmography: Hematocrit, SpO2, pulse, and respiration. Proc. SPIE 2002, 4916, 185–188. [Google Scholar]
- Lu, S.; Zhao, H.; Ju, K.; Shin, K.; Lee, M.; Shelley, K.; Chon, K. Can photoplethysmography variability serve as an alternative approach to obtain heart rate variability information? J. Clin. Monit. Comput. 2008, 22, 23–29. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. On the analysis of fingertip photoplethysmogram signals. Curr. Cardiol. Rev. 2012, 8, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Shelley, K. Photoplethysmography: Beyond the calculation of arterial oxygen saturation and heart rate. Anesth. Analg. 2007, 105 (Suppl. 6), S31–S36. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. Standard terminologies for photoplethysmogram signals. Curr. Cardiol. Rev. 2012, 8, 215–219. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Norton, I.; Brearley, M.; Abbott, D.; Schuurmans, D. Detection of a and b waves in the acceleration photoplethysmogram. BioMed. Eng. OnLine 2014, 13, 139. [Google Scholar] [CrossRef] [PubMed]
- Petterson, M.T.; Begnoche, V.L.; Graybeal, J.M. The effect of motion on pulse oximetry and its clinical significance. Anesth. Analg. 2007, 105 (Suppl. 6), S78–S84. [Google Scholar] [CrossRef] [PubMed]
- Seki, H. Classification of wave contour by first and second derivative of plethysmogram. Pulse Wave 1977, 7, 42–50. (In Japanese) [Google Scholar]
- Takazawa, K.; Fujita, M.; Kiyoshi, Y.; Sakai, T.; Kobayashi, T.; Maeda, K.; Yamashita, Y.; Hase, M.; Ibukiyama, C. Clinical usefulness of the second derivative of a plethysmogram (acceleration plethysmogram). Cardiology 1993, 23, 207–217. [Google Scholar]
- Takazawa, K.; Tanaka, N.; Fujita, M.; Matsuoka, O.; Saiki, T.; Aikawa, M.; Tamura, S.; Ibukiyama, C. Assessment of vasoactive agents and vascular aging by the second derivative of photoplethysmogram waveform. Hypertension 1998, 32, 365–370. [Google Scholar] [CrossRef] [PubMed]
- Bortolotto, A.; Jacques, B.; Takeshi, K.; Kenji, T.; Michel, S. Assessment of vascular aging and atherosclerosis in hypertensive subjects: Second derivative of photoplethysmogram versus pulse wave velocity. Am. J. Hypertens. 2000, 13, 165–171. [Google Scholar] [CrossRef]
- Elgendi, M.; Fletcher, R.R.; Norton, I.; Brearley, M.; Abbott, D.; Lovell, N.H.; Schuurmans, D. Frequency analysis of photoplethysmogram and its derivatives. Comput. Methods Programs Biomed. 2015, 122, 503–512. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Norton, I.; Brearley, M.; Fletcher, R.R.; Abbott, D.; Lovell, N.H.; Schuurmans, D. Towards investigating global warming impact on human health using derivatives of photoplethysmogram signals. Int. J. Environ. Res. Public Health 2015, 12, 12776. [Google Scholar] [CrossRef] [PubMed]
- Gehring, H.; Hornberger, C.; Matz, H.; Konecny, E.; Schmucker, P. The effects of motion artifact and low perfusion on the performance of a new generation of pulse oximeters in volunteers undergoing hypoxemia. Respir. Care 2002, 47, 48–60. [Google Scholar] [PubMed]
- Cannesson, M.; Delannoy, B.; Morand, A.; Rosamel, P.; Attof, Y.; Bastien, O.; Lehot, J.J. Does the pleth variability index indicate the respiratory-induced variation in the plethysmogram and arterial pressure waveforms? Anesth. Analg. 2008, 106, 1189–1194. [Google Scholar] [CrossRef] [PubMed]
- Colquhoun, D.; Forkin, K.; Durieux, M.; Thiele, R. Ability of the Masimo pulse CO-Oximeter to detect changes in hemoglobin. J. Clin. Monit. Comput. 2012, 26, 69–73. [Google Scholar] [CrossRef] [PubMed]
- Shan, C. Motion Robust Vital Signal Monitoring. U.S. Patent 20150250425 A1, 10 September 2015. [Google Scholar]
- Krishnan, R.; Natarajan, B.; Warren, S. Two-stage approach for detection and reduction of motion artifacts in photoplethysmographic data. IEEE Trans. Biomed. Eng. 2010, 57, 1867–1876. [Google Scholar] [CrossRef] [PubMed]
- Selvaraj, N.; Mendelson, Y.; Shelley, K.; Silverman, D.; Chon, K. Statistical approach for the detection of motion/noise artifacts in Photoplethysmogram. In Proceedings of the 2011 33th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Boston, MA, USA, 30 August–3 September 2011; pp. 4972–4975.
- Clifford, G.; Behar, J.; Li, Q.; Rezek, I. Signal quality indices and data fusion for determining clinical acceptability of electrocardiograms. Physiol. Meas. 2012, 33, 1419. [Google Scholar] [CrossRef] [PubMed]
- Brearley, M.B.; Heaney, M.F.; Norton, I.N. Physiological responses of medical team members to a simulated emergency in tropical field conditions. Prehosp. Dis. Med. 2013, 28, 139–144. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Norton, I.; Brearley, M.; Abbott, D.; Schuurmans, D. Systolic peak detection in acceleration photoplethysmograms measured from emergency responders in tropical conditions. PLoS ONE 2013, 8, e76585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cohen, J. A Coefficient of Agreement for Nominal Scales. Educ. Psychol. Meas. 1960, 20, 37–46. [Google Scholar] [CrossRef]
- Tong, S.; Li, Z.; Zhu, Y.; Thakor, N. Describing the nonstationarity level of neurological signals based on quantifications of time-frequency representation. IEEE Trans. Biomed. Eng. 2007, 54, 1780–1785. [Google Scholar] [CrossRef] [PubMed]
- Coifman, R.; Wickerhauser, M. Entropy-based algorithms for best basis selection. IEEE Trans. Inf. Theory 1992, 38, 713–718. [Google Scholar] [CrossRef]
- Chen, C.H. Signal Processing Handbook; CRC Press: New York, NY, USA, 1988. [Google Scholar]
- Vaseghi, S.V. Advanced Digital Signal Processing and Noise Reduction; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Elgendi, M. Detection of c, d, and e waves in the acceleration photoplethysmogram. Comput. Methods Programs Biomed. 2014, 117, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Li, B.N.; Dong, M.C.; Vai, M.I. On an automatic delineator for arterial blood pressure waveforms. Biomed. Signal Process. Control 2010, 5, 76–81. [Google Scholar] [CrossRef]
- Billauer, E. Peakdet: Peak Detection Using MATLAB, 2012. Available online: http://billauer.co.il/peakdet.html (accessed on 24 August 2016).
- Bonferroni, C. Teoria Statistica Delle Classi e Calcolo Delle Probabilità; Pubblicazioni del R Istituto Superiore di Scienze Economiche e Commerciali di Firenze; Libreria internazionale Seeber: Florence, Italy, 1936; Volume 8, pp. 3–62. [Google Scholar]
- Holm, S. A simple sequentially rejective multiple test procedure. Scand. J. Stat. 1979, 6, 65–70. [Google Scholar]
- Chen, C.; Liaw, A.; Breiman, L. Using Random Forest to Learn Imbalanced Data; University of California: Berkeley, CA, USA, 2004. [Google Scholar]
- Orphanidou, C.; Bonnici, T.; Charlton, P.; Clifton, D.; Vallance, D.; Tarassenko, L. Signal-Quality indices for the electrocardiogram and photoplethysmogram: Derivation and applications to wireless monitoring. IEEE J. Biomed. Health Inform. 2015, 19, 832–838. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Clifford, G. Dynamic time warping and machine learning for signal quality assessment of pulsatile signals. Physiol. Meas. 2012, 33, 1491–1501. [Google Scholar] [CrossRef] [PubMed]
- Behar, J.; Oster, J.; Li, Q.; Clifford, G.D. ECG signal quality during arrhythmia and its application to false alarm reduction. IEEE Trans. Biomed. Eng. 2013, 60, 1660–1666. [Google Scholar] [CrossRef] [PubMed]
- Silva, I.; Moody, G.B.; Celi, L. Improving the quality of ECGs collected using mobile phones: The Physionet/Computing in Cardiology Challenge 2011. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; pp. 273–276.

| Excellent | Acceptable | Unfit | Total | |
|---|---|---|---|---|
| Excellent | 29 | 13 | 2 | 44 |
| Acceptable | 3 | 7 | 11 | 21 |
| Unfit | 1 | 6 | 34 | 41 |
| Total | 33 | 26 | 47 | 106 |
| Annotator 1 | |||||||||||
| G1 versus G2 | G1 versus (G2 & G3) | G1 versus G3 | |||||||||
| Index | G1 () | G2 () | Value | Index | G1 () | G2 & G3 () | Value | Index | G1 () | G3 () | Value |
| 0.07 ± 0.20 | −0.07 ± 0.19 | 3.8 **,† | 0.07 ± 0.20 | −0.14 ± 0.18 | 1.0 **,† | 0.07 ± 0.20 | −0.18 ± 0.17 | 2.78 **,† | |||
| 0.88 ± 0.10 | 0.91 ± 0.07 | * | 95.45 ± 8.99 | 66.69 ± 41.35 | 2.57 **,† | 95.45 ± 8.99 | 57.39 ± 43.19 | 2.90 **,† | |||
| 57.60 ± 3.76 | 57.11 ± 6.42 | 0.072 | 61.13 ± 2.62 | 67.45 ± 11.89 | ** | 61.13 ± 2.62 | 70.15 ± 13.50 | 2.12 **,† | |||
| 4.82 ± 0.56 | 4.96 ± 1.10 | 0.073 | 91.24 ± 6.61 | 86.40 ± 9.05 | *,† | 91.24 ± 6.61 | 84.17 ± 9.17 | 5.96 **,† | |||
| 2.05 ± 0.16 | 2.01 ± 0.16 | 0.147 | 2.05 ± 0.16 | 2.01 ± 0.14 | 0.14 | 2.05 ± 0.16 | 2.01 ± 0.13 | 0.24 | |||
| 95.45 ± 8.99 | 83.50 ± 32.18 | 0.161 | 57.60 ± 3.76 | 61.51 ± 13.90 | 0.34 | 4.82 ± 0.56 | 3.77 ± 2.18 | 0.39 | |||
| 61.13 ± 2.62 | 62.59 ± 5.82 | 0.436 | 0.88 ± 0.10 | 0.82 ± 0.23 | 0.45 | 57.60 ± 3.76 | 63.95 ± 16.22 | 0.84 | |||
| 91.24 ± 6.61 | 90.42 ± 7.43 | 0.485 | 4.82 ± 0.56 | 4.19 ± 1.95 | 0.85 | 0.88 ± 0.10 | 0.78 ± 0.28 | 0.86 | |||
| Annotator 2 | |||||||||||
| G1 versus G2 | G1 versus (G2 & G3) | G1 versus G3 | |||||||||
| Index | G1 () | G2 () | Value | Index | G1 () | G2 & G3 () | Value | Index | G1 () | G3 () | Value |
| 0.07 ± 0.18 | −0.10 ± 0.20 | 1.9 **,† | 0.07 ± 0.18 | −0.17 ± 0.17 | 3.4 **,† | 0.07 ± 0.18 | −0.21 ± 0.14 | 7.4 **,† | |||
| 91.73 ± 21.62 | 65.66 ± 42.88 | *,† | 91.73 ± 21.62 | 64.22 ± 41.48 | 4.9 **,† | 61.82 ± 5.87 | 69.58 ± 12.46 | 9.5 **,† | |||
| 58.23 ± 6.34 | 59.86 ± 12.22 | 0.121 | 61.82 ± 5.87 | 68.09 ± 12.02 | 3.1 **,† | 91.73 ± 21.62 | 63.49 ± 41.26 | 5.2 **,† | |||
| 2.05 ± 0.17 | 1.97 ± 0.10 | 0.123 | 89.93 ± 7.81 | 86.47 ± 8.96 | * | 89.93 ± 7.81 | 85.98 ± 9.70 | * | |||
| 89.93 ± 7.81 | 87.43 ± 7.44 | 0.176 | 58.23 ± 6.34 | 61.76 ± 14.41 | 0.29 | 4.77 ± 0.92 | 4.03 ± 2.04 | 0.56 | |||
| 0.87 ± 0.13 | 0.85 ± 0.22 | 0.182 | 2.05 ± 0.17 | 2.01 ± 0.12 | 0.48 | 58.23 ± 6.34 | 62.73 ± 15.47 | 0.64 | |||
| 61.82 ± 5.87 | 65.18 ± 10.82 | 0.546 | 4.77 ± 0.92 | 4.12 ± 2.00 | 0.70 | 0.87 ± 0.13 | 0.80 ± 0.25 | 0.73 | |||
| 4.77 ± 0.92 | 4.30 ± 1.95 | 0.933 | 0.87 ± 0.13 | 0.82 ± 0.24 | 0.72 | 2.05 ± 0.17 | 2.03 ± 0.13 | 1.00 | |||
| Adjudicator | |||||||||||
| G1 versus G2 | G1 versus (G2 & G3) | G1 versus G3 | |||||||||
| Index | G1 () | G2 () | Value | Index | G1 () | G2 & G3 () | Value | Index | G1 () | G3 () | Value |
| 0.11 ± 0.17 | −0.17 ± 0.14 | 3.3 **,† | 0.11 ± 0.17 | −0.17 ± 0.17 | 6.3 **,† | 0.11 ± 0.17 | −0.16 ± 0.23 | 1.1 **,† | |||
| 60.07 ± 7.69 | 59.40 ± 13.35 | **,† | 84.26 ± 31.62 | 71.21 ± 39.10 | 0.01 * | 63.20 ± 7.95 | 69.97 ± 11.69 | 1.4 **,† | |||
| 2.06 ± 0.16 | 1.97 ± 0.08 | 0.005 *,† | 63.20 ± 7.95 | 66.66 ± 11.30 | 0.01 * | 84.26 ± 31.62 | 64.04 ± 42.07 | 1.3 **,† | |||
| 0.85 ± 0.14 | 0.86 ± 0.23 | 0.016 * | 60.07 ± 7.69 | 60.41 ± 13.54 | 0.01 * | 2.06 ± 0.16 | 2.14 ± 0.17 | 0.05 | |||
| 4.39 ± 1.20 | 4.60 ± 1.82 | 0.021 * | 4.39 ± 1.20 | 4.39 ± 1.87 | 0.13 | 0.85 ± 0.14 | 0.76 ± 0.24 | 0.20 | |||
| 84.26 ± 31.62 | 73.69 ± 38.13 | 0.049 * | 2.06 ± 0.16 | 2.01 ± 0.13 | 0.14 | 88.89 ± 7.81 | 84.22 ± 10.98 | 0.23 | |||
| 63.20 ± 7.95 | 65.52 ± 11.05 | 0.115 | 0.85 ± 0.14 | 0.83 ± 0.23 | 0.16 | 4.39 ± 1.20 | 3.77 ± 1.91 | 0.40 | |||
| 88.89 ± 7.81 | 88.50 ± 8.10 | 0.557 | 88.89 ± 7.81 | 87.40 ± 9.04 | 0.37 | 60.07 ± 7.69 | 63.32 ± 14.05 | 0.88 | |||
| G1 () vs. G2 () | |||||||||||||
| Mahalanobis | LDA | QDA | SVM | Overall | |||||||||
| Index | SE | PP | SE | PP | SE | PP | SE | PP | OF | ||||
| 83.33 | 73.17 | 77.92 | 80.56 | 74.36 | 77.33 | 80.56 | 74.36 | 77.33 | 80.56 | 74.36 | 77.33 | 77.60 | |
| 83.33 | 46.88 | 60.00 | 83.33 | 46.15 | 59.41 | 83.33 | 43.48 | 57.14 | 88.89 | 45.07 | 59.81 | 63.07 | |
| 80.56 | 42.03 | 55.24 | 83.33 | 42.86 | 56.60 | 88.89 | 41.03 | 56.14 | 94.44 | 42.50 | 58.62 | 61.85 | |
| 63.89 | 46.94 | 54.12 | 55.56 | 55.56 | 55.56 | 38.89 | 70.00 | 50.00 | 55.56 | 57.14 | 56.34 | 54.96 | |
| 47.22 | 39.53 | 43.04 | 66.67 | 48.00 | 55.81 | 66.67 | 36.92 | 47.52 | 83.33 | 41.10 | 55.05 | 52.57 | |
| 11.11 | 66.67 | 19.05 | 30.56 | 44.00 | 36.07 | 86.11 | 51.67 | 64.58 | 13.89 | 31.25 | 19.23 | 39.51 | |
| 5.56 | 100.00 | 10.53 | 19.44 | 50.00 | 28.00 | 91.67 | 41.25 | 56.90 | 8.33 | 37.50 | 13.64 | 38.57 | |
| 0.00 | 0.00 | NaN | 27.78 | 47.62 | 35.09 | 86.11 | 41.33 | 55.86 | 11.11 | 40.00 | 17.39 | NaN | |
| G1 () vs. (G2 [] & G3 []) | |||||||||||||
| Mahalanobis | LDA | QDA | SVM | Overall | |||||||||
| Index | SE | PP | SE | PP | SE | PP | SE | PP | OF | ||||
| 80.56 | 69.05 | 74.36 | 80.56 | 69.05 | 74.36 | 80.56 | 69.05 | 74.36 | 80.56 | 69.05 | 74.36 | 74.65 | |
| 83.33 | 40.00 | 54.05 | 83.33 | 39.47 | 53.57 | 83.33 | 37.50 | 51.72 | 88.89 | 38.10 | 53.33 | 58.89 | |
| 83.33 | 37.50 | 51.72 | 86.11 | 37.35 | 52.10 | 88.89 | 35.16 | 50.39 | 94.44 | 35.79 | 51.91 | 58.73 | |
| 47.22 | 33.33 | 39.08 | 66.67 | 41.38 | 51.06 | 83.33 | 37.50 | 51.72 | 80.56 | 36.71 | 50.43 | 51.58 | |
| 5.56 | 100.00 | 10.53 | 72.22 | 30.95 | 43.33 | 86.11 | 34.07 | 48.82 | 94.44 | 33.01 | 48.92 | 50.66 | |
| 11.11 | 33.33 | 16.67 | 75.00 | 32.53 | 45.38 | 88.89 | 34.78 | 50.00 | 94.44 | 35.05 | 51.13 | 47.36 | |
| 44.44 | 37.21 | 40.51 | 47.22 | 41.46 | 44.16 | 22.22 | 40.00 | 28.57 | 36.11 | 44.83 | 40.00 | 38.89 | |
| 2.78 | 100.00 | 5.41 | 25.00 | 12.33 | 16.51 | 88.89 | 42.67 | 57.66 | 27.78 | 12.50 | 17.24 | 34.06 | |
| G1 () vs. G3 () | |||||||||||||
| Mahalanobis | LDA | QDA | SVM | Overall | |||||||||
| Index | SE | PP | SE | PP | SE | PP | SE | PP | OF | ||||
| 77.78 | 93.33 | 84.85 | 80.56 | 90.63 | 85.29 | 83.33 | 90.91 | 86.96 | 77.78 | 93.33 | 84.85 | 85.80 | |
| 86.11 | 73.81 | 79.49 | 88.89 | 72.73 | 80.00 | 88.89 | 71.11 | 79.01 | 88.89 | 72.73 | 80.00 | 80.14 | |
| 83.33 | 73.17 | 77.92 | 83.33 | 73.17 | 77.92 | 83.33 | 71.43 | 76.92 | 88.89 | 71.11 | 79.01 | 78.30 | |
| 72.22 | 76.47 | 74.29 | 80.56 | 74.36 | 77.33 | 88.89 | 71.11 | 79.01 | 88.89 | 71.11 | 79.01 | 77.77 | |
| 75.00 | 69.23 | 72.00 | 77.78 | 68.29 | 72.73 | 88.89 | 71.11 | 79.01 | 91.67 | 71.74 | 80.49 | 76.49 | |
| 66.67 | 72.73 | 69.57 | 77.78 | 75.68 | 76.71 | 83.33 | 75.00 | 78.95 | 83.33 | 75.00 | 78.95 | 76.14 | |
| 47.22 | 77.27 | 58.62 | 86.11 | 72.09 | 78.48 | 86.11 | 67.39 | 75.61 | 94.44 | 68.00 | 79.07 | 74.20 | |
| 72.22 | 74.29 | 73.24 | 72.22 | 76.47 | 74.29 | 75.00 | 71.05 | 72.97 | 72.22 | 76.47 | 74.29 | 73.73 | |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgendi, M. Optimal Signal Quality Index for Photoplethysmogram Signals. Bioengineering 2016, 3, 21. https://doi.org/10.3390/bioengineering3040021
Elgendi M. Optimal Signal Quality Index for Photoplethysmogram Signals. Bioengineering. 2016; 3(4):21. https://doi.org/10.3390/bioengineering3040021
Chicago/Turabian StyleElgendi, Mohamed. 2016. "Optimal Signal Quality Index for Photoplethysmogram Signals" Bioengineering 3, no. 4: 21. https://doi.org/10.3390/bioengineering3040021
APA StyleElgendi, M. (2016). Optimal Signal Quality Index for Photoplethysmogram Signals. Bioengineering, 3(4), 21. https://doi.org/10.3390/bioengineering3040021






