Theoretical Insight into the Biodegradation of Solitary Oil Microdroplets Moving through a Water Column
Abstract
1. Introduction
2. Model Formulation
2.1. Considerations on Modeling the Three Major Biodegradation Modes
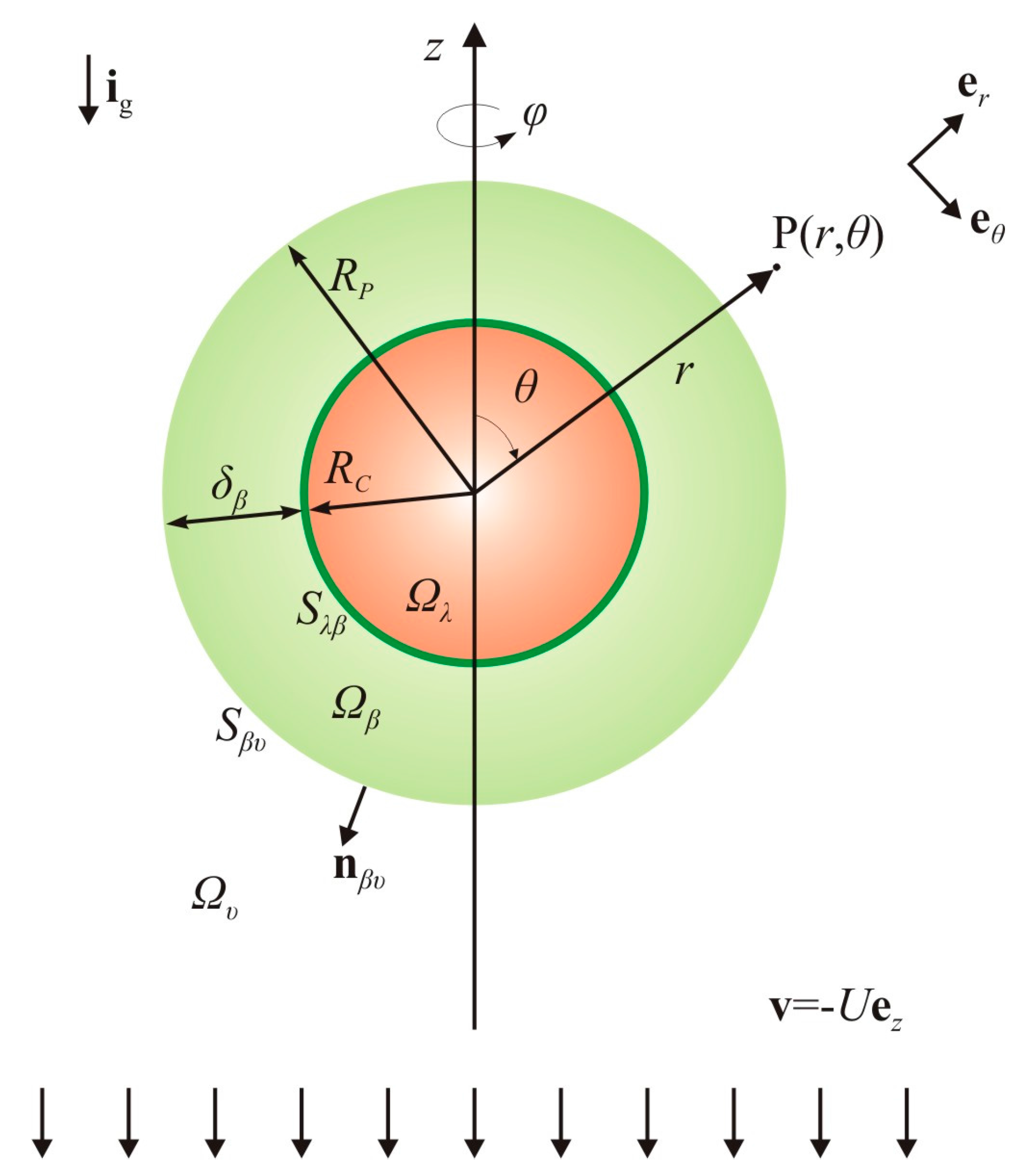
2.2. Basic Hypotheses for the Hydrodynamics and Mass Transport
2.3. Overall Dissolution Rate: Analysis of the Local Mass Balances
2.3.1. Advection-Dominated Transport in the Aqueous Phase without Bioreaction
2.3.2. Advection-Dominated Transport and Homogeneous Bioreaction in the Aqueous Phase
2.3.3. Diffusion and Reaction in the Biofilm Phase
2.4. Evolution of the Particle Size: Analysis of the Overall Mass Balances
2.4.1. Overall Mass Balance for the λ-Phase
2.4.2. Overall Mass Balance for the β-Phase
2.4.3. Compact and Dimless Forms of the Coupled ODEs
3. Results and Discussion
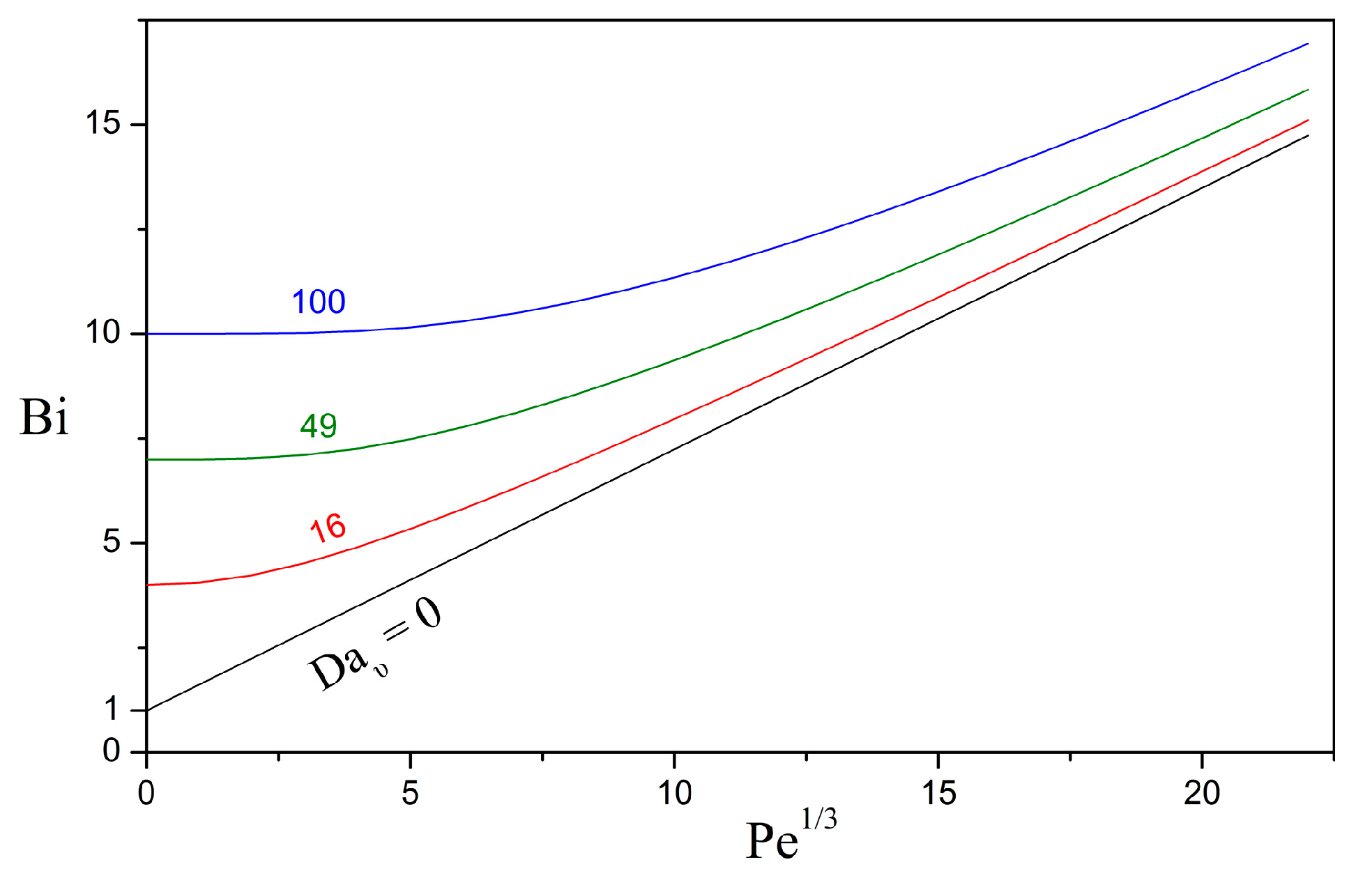
3.1. Overall Sherwood Number
3.2. Relative Importance of the Bioreaction and Dissolution Processes
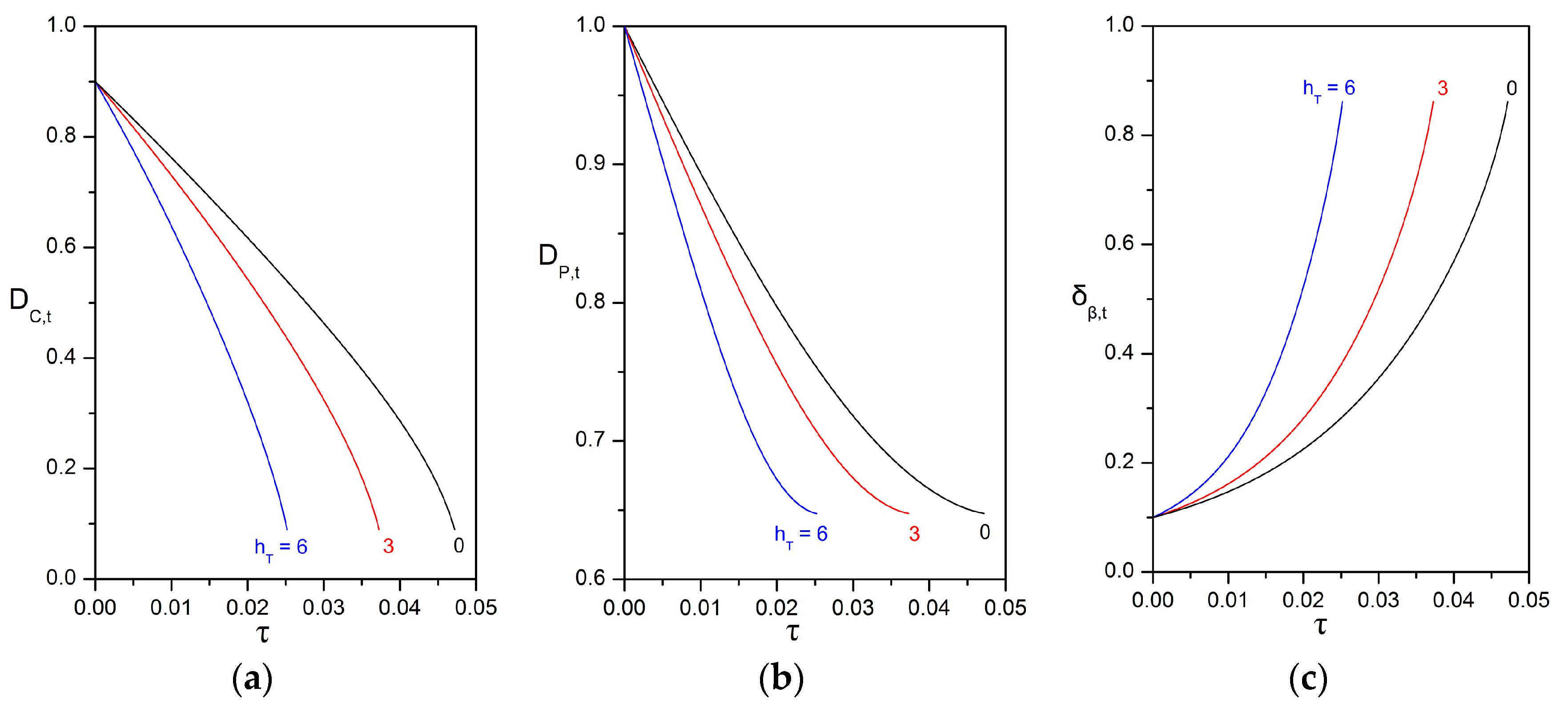
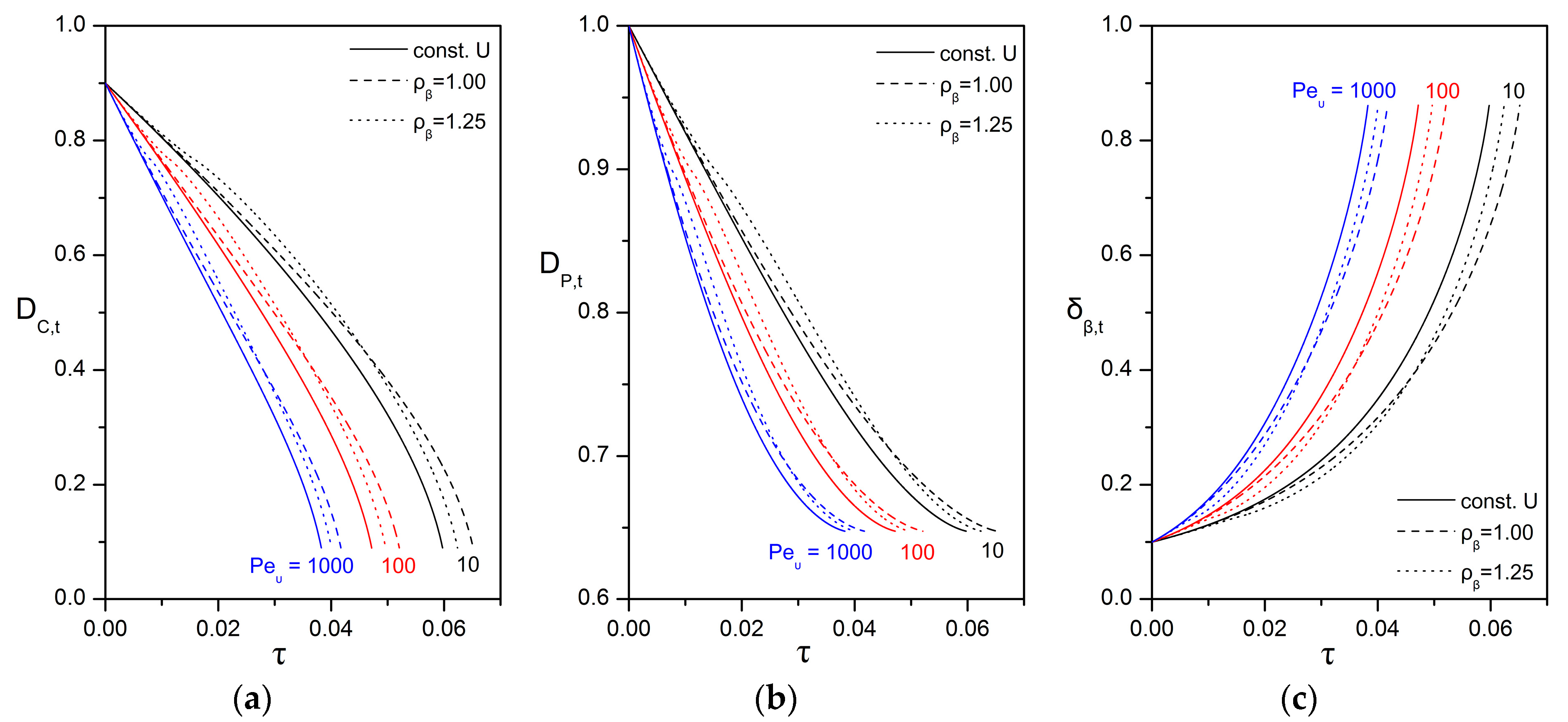
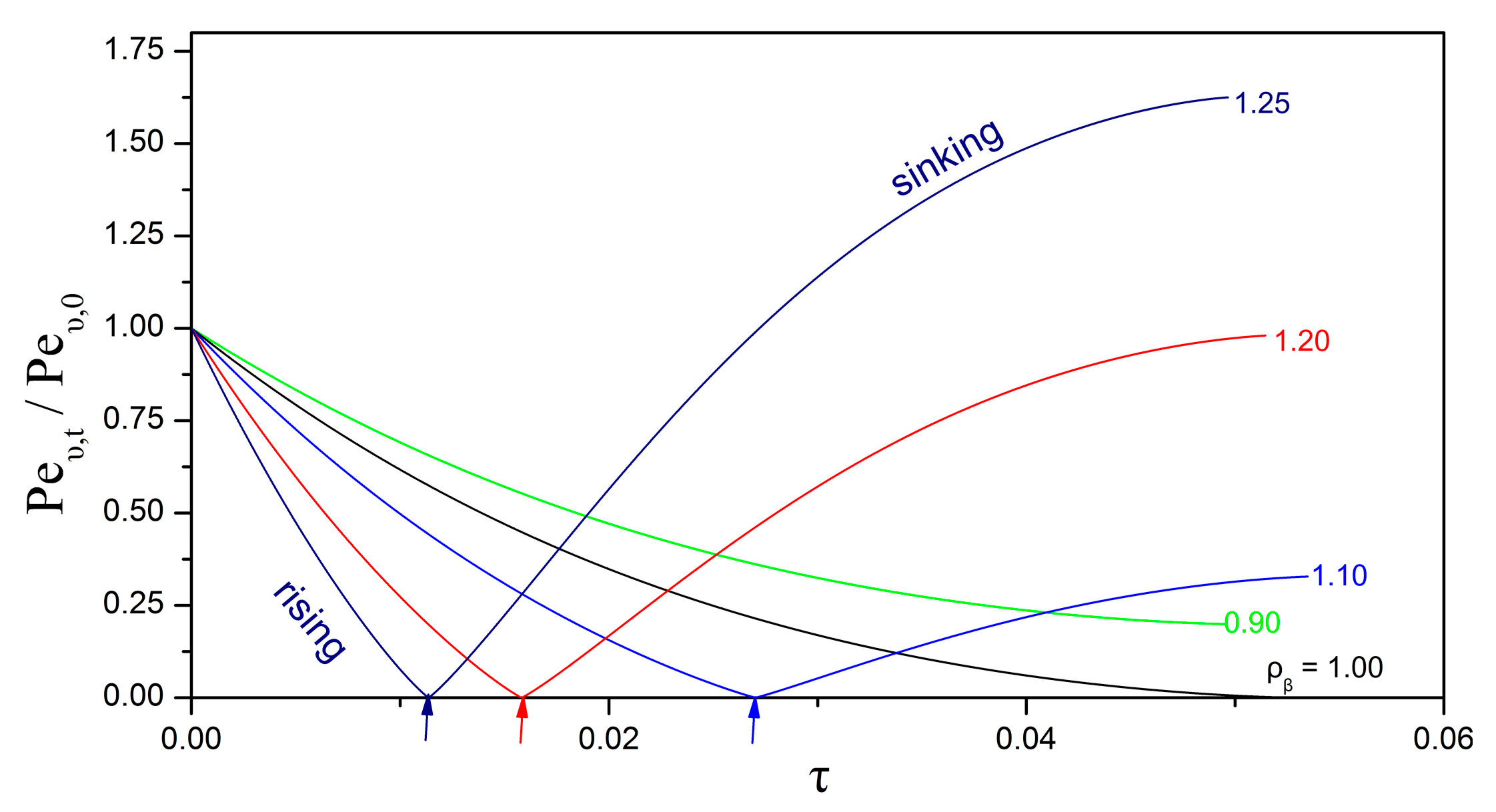
3.3. Impact of the Péclet and Thiele Numbers on the Particle Size Evolution
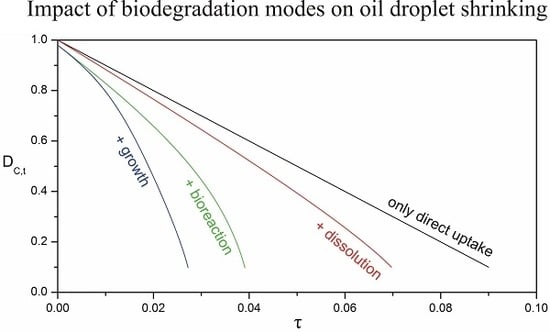
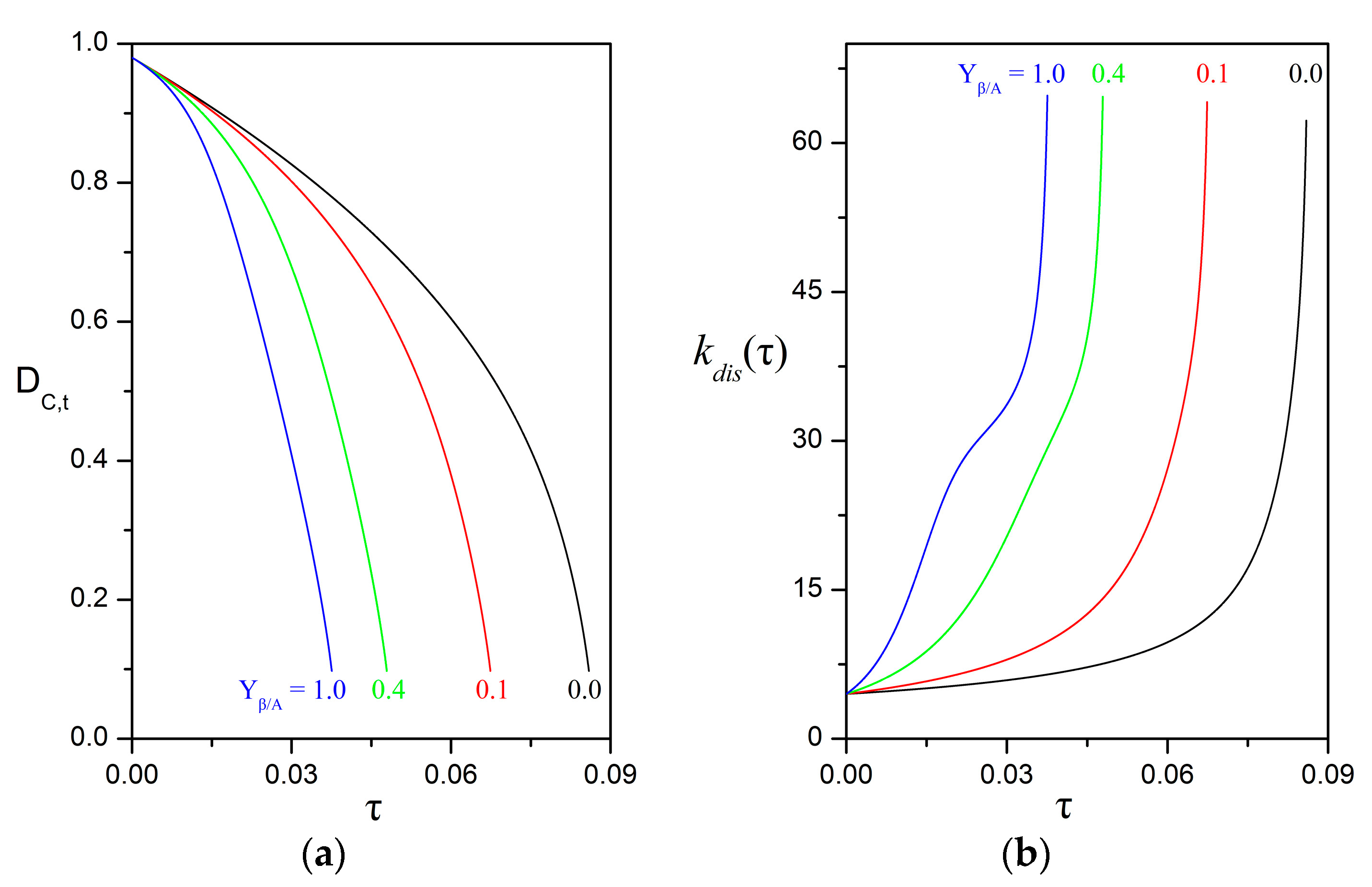
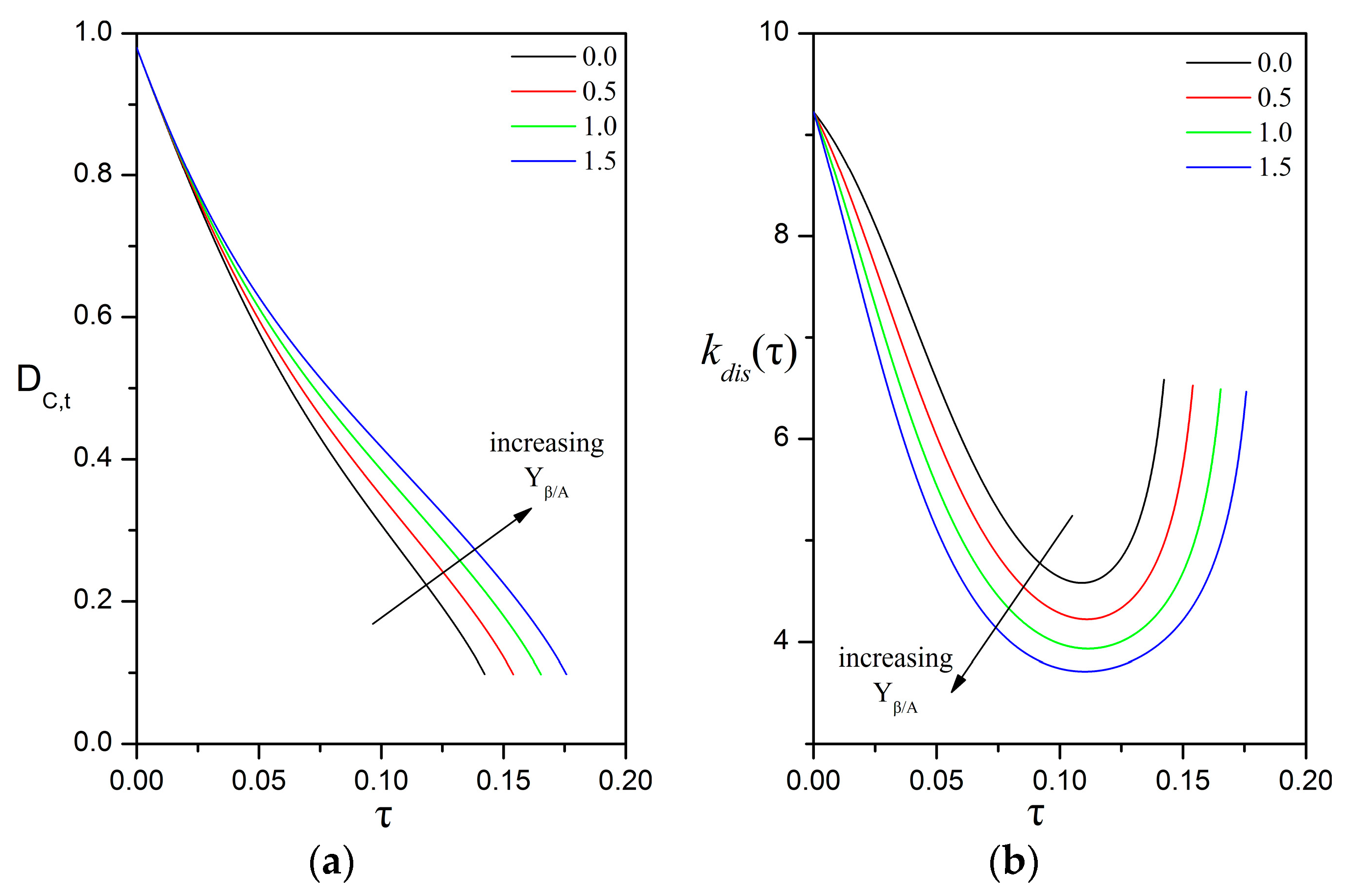
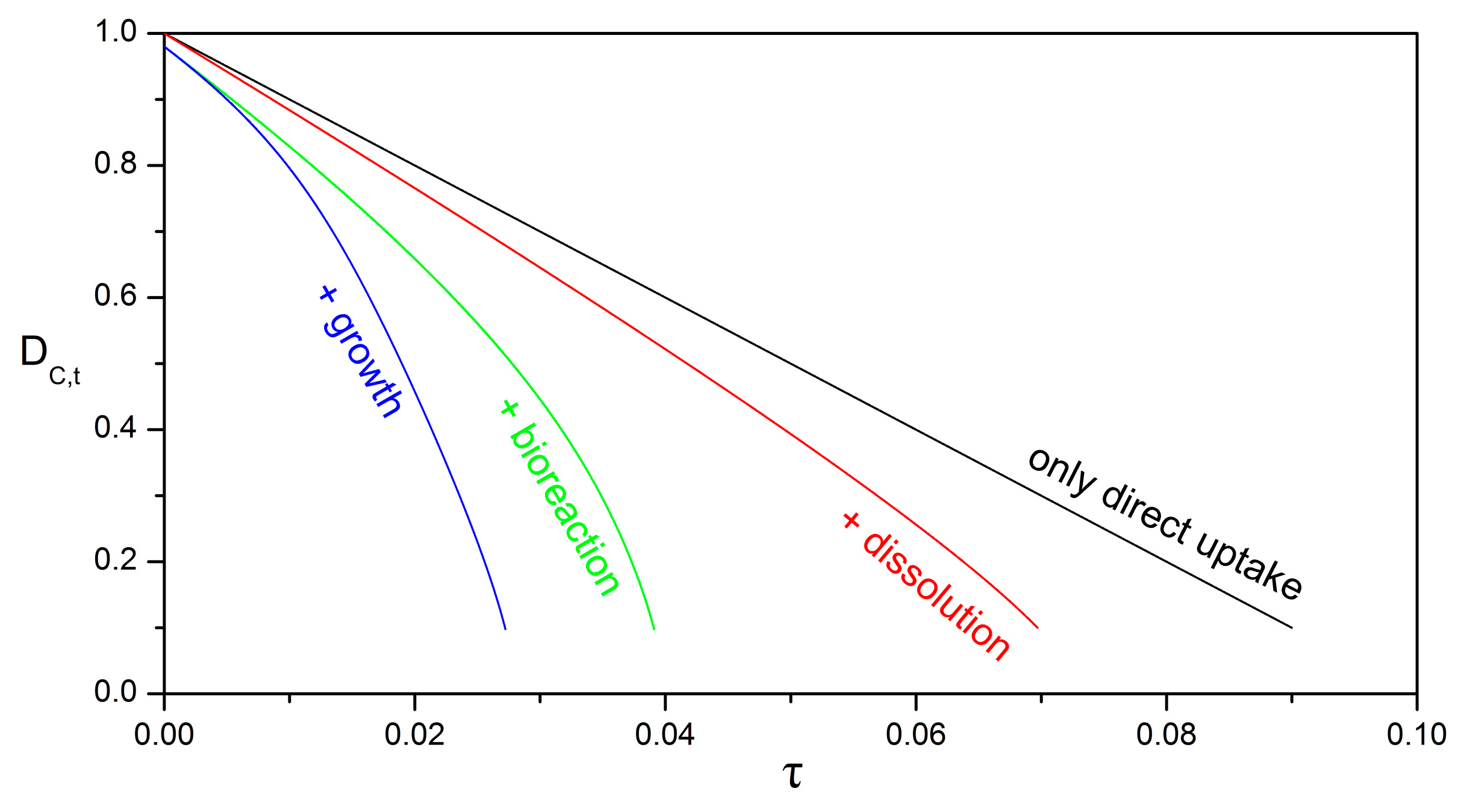
3.4. Impact of Biofilm Growth and Direct Uptake on the Particle Size Evolution
3.5. Implications for the Biodegradation of Crude Oil Microdroplets in the Sea
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| concentration of active cells in the αth phase, ; | |
| interfacial concentration of active cells, ; | |
| Biot number, ; | |
| mass concentration of oil in the αth phase, , dimless ; | |
| solubility of oil in the αth phase, ; | |
| volume averaged concentration of oil in the β-phase, Equation (35), ; | |
| diffusion coefficient of the A solute in the αth phase, ; | |
| Damköhler number in the αth phase, ; | |
| diameter of the oily core, , dimless ; | |
| diameter of the compound particle, , dimless ; | |
| gravitational acceleration, ; | |
| solubility ratio, ; | |
| Hatta modulus, ; | |
| Thiele number in the biofilm shell, ; | |
| mass flux of oil in the αth phase, , dimless ; | |
| first-order reaction rate constant in the αth phase, Equation (4), ; | |
| mass transfer coefficient for external mass transfer with , Equation (21), ; | |
| mass transfer coefficient for external mass transfer, Equation (24), ; | |
| mass transfer coefficient for the dissolution of the oily core, Equation (33), ; | |
| droplet shrinking rate caused by dissolution, Equation (50b), , dimless Equation (54); | |
| biofilm expansion rate due to growth, Equation (50c), , dimless Equation (54); | |
| droplet shrinking rate caused by direct uptake, Equation (50a), , dimless Equation (54); | |
| half-saturation constant for the A solute in the αth phase, ; | |
| unit normal vector on the αω-interface pointing from the α-phase to the ω-phase; | |
| radial coordinate, , dimless ; | |
| oil consumption rate in the αth phase, ; | |
| microbial cell proliferation rate in the αth phase, ; | |
| biofilm production rate, , ; | |
| Péclet number in the αth phase, ; | |
| radius of the oily core, , dimless ; | |
| radius of the compound particle, , dimless ; | |
| area of the compound particle surface, , ; | |
| area of the oily core surface, , ; | |
| Sherwood number for external mass transfer with , Equation (22); | |
| Sherwood number for external mass transfer, Equation (24); | |
| overall Sherwood number for the dissolution of the oily core, Equation (34); | |
| undisturbed velocity of the approaching fluid, ; | |
| volume of the biofilm shell, , ; | |
| velocity of the aqueous fluid, , dimless ; | |
| number of active cells per unit biofilm mass, [cells/mg-biofilm]; | |
| yield coefficient of cells in the αth phase, [cells/mg-oil]; | |
| biofilm yield coefficient, , [mg-biofilm/mg-oil]; | |
| external mass transfer rate: from the particle surface to the υ-phase, Equation (26), ; | |
| overall dissolution rate at the surface of the oily core, Equation (32), ; | |
| Greek letters | |
| thickness of the biofilm shell, , ; | |
| dimless thickness of the biofilm shell, ; | |
| excess density, , ; | |
| maximum specific growth rate of active cells, ; | |
| viscosity of the υ-phase, ; | |
| diffusivity ratio, ; | |
| density of the αth phase, , dimless ; | |
| scaled characteristic diffusion time, Equation (52), ; | |
| dimless time,; | |
| mass fraction of oil biodegraded within the biofilm shell, Equation (63a); | |
| mass fraction of oil released into the aqueous phase, Equation (63b); | |
References
- Li, C.; Miller, J.; Wang, J.; Koley, S.S.; Katz, J. Size distribution and dispersion of droplets generated by impingement of breaking waves on oil slicks. J. Geophys. Res. Oceans 2017, 122, 7938–7957. [Google Scholar] [CrossRef]
- Nissanka, I.D.; Yapa, P.D. Oil slicks on water surface: Breakup, coalescence, and droplet formation under breaking waves. Mar. Pollut. Bull. 2017, 114, 480–493. [Google Scholar] [CrossRef] [PubMed]
- Johansen, Ø.; Rye, H.; Cooper, C. DeepSpill—Field study of a simulated oil and gas blowout in deep water. Spill Sci. Technol. Bull. 2003, 8, 433–443. [Google Scholar] [CrossRef]
- Brandvik, P.J.; Johansen, Ø.; Leirvik, F.; Farooq, U.; Daling, P.S. Droplet breakup in subsurface oil releases—Part 1: Experimental study of droplet breakup and effectiveness of dispersant injection. Mar. Pollut. Bull. 2013, 73, 319–326. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Boufadel, M.C.; King, T.; Robinson, B.; Gao, F.; Socolofsky, S.A.; Lee, K. Droplet and bubble formation of combined oil and gas releases in subsea blowouts. Mar. Pollut. Bull. 2017, 120, 203–216. [Google Scholar] [CrossRef] [PubMed]
- Camilli, R.; Reddy, C.M.; Yoerger, D.R.; Van Mooy, B.A.S.; Jakuba, M.V.; Kinsey, J.C.; McIntyre, C.P.; Sylva, S.P.; Maloney, J.V. Tracking hydrocarbon plume transport and biodegradation at Deepwater Horizon. Science 2010, 330, 201–204. [Google Scholar] [CrossRef] [PubMed]
- Hazen, T.C.; Dubinsky, E.A.; DeSantis, T.Z.; Andersen, G.L.; Piceno, Y.M.; Singh, N.; Jansson, J.K.; Probst, A.; Borglin, S.E.; Fortney, J.L.; et al. Deep-sea oil plume enriches indigenous oil-degrading bacteria. Science 2010, 330, 204–208. [Google Scholar] [CrossRef] [PubMed]
- Atlas, R.M.; Hazen, T.C. Oil biodegradation and bioremediation: A tale of the two worst spills in U.S. history. Environ. Sci. Technol. 2011, 45, 6709–6715. [Google Scholar] [CrossRef] [PubMed]
- McGenity, T.J.; Folwell, B.D.; McKew, B.A.; Sanni, G.O. Marine crude-oil biodegradation: A central role for interspecies interactions. Aquat. Biosyst. 2012, 8, 10. [Google Scholar] [CrossRef] [PubMed]
- Hazen, T.C.; Prince, R.C.; Mahmoudi, N. Marine oil biodegradation. Environ. Sci. Technol. 2016, 50, 2121–2129. [Google Scholar] [CrossRef] [PubMed]
- Almeda, R.; Hyatt, C.; Buskey, E.J. Toxicity of dispersant Corexit 9500A and crude oil to marine microzooplankton. Ecotoxicol. Environ. Saf. 2014, 106, 76–85. [Google Scholar] [CrossRef] [PubMed]
- Carroll, J.; Vikebø, F.; Howell, D.; Broch, O.J.; Nepstad, R.; Augustine, S.; Skeie, G.M.; Bast, R.; Juselius, J. Assessing impacts of simulated oil spills on the Northeast Arctic cod fishery. Mar. Pollut. Bull. 2018, 126, 63–73. [Google Scholar] [CrossRef] [PubMed]
- Van Eenennaam, J.S.; Rahsepar, S.; Radović, J.R.; Oldenburg, T.B.P.; Wonink, J.; Langenhoff, A.A.M.; Murk, A.J.; Foekema, E.M. Marine snow increases the adverse effects of oil on benthic invertebrates. Mar. Pollut. Bull. 2018, 126, 339–348. [Google Scholar] [CrossRef] [PubMed]
- Buskey, E.J.; White, H.K.; Esbaugh, A.J. Impact of oil spills on marine life in the Gulf of Mexico. Oceanography 2016, 29, 174–181. [Google Scholar] [CrossRef]
- Lindo-Atichati, D.; Paris, C.B.; Le Hénaff, M.; Schedler, M.; Valladares Juárez, A.G.; Müller, R. Simulating the effects of droplet size, high-pressure biodegradation, and variable flow rate on the subsea evolution of deep plumes from the Macondo blowout. Deep Sea Res. Part II Top. Stud. Oceanogr. 2016, 129, 301–310. [Google Scholar] [CrossRef]
- Leal, L.G. Advanced Transport Phenomena: Fluid Mechanics and Convective Transport Processes; Cambridge University Press: Cambridge, UK, 2007; ISBN 978-0-521-84910-4. [Google Scholar]
- Daly, K.L.; Passow, U.; Chanton, J.; Hollander, D. Assessing the impacts of oil-associated marine snow formation and sedimentation during and after the Deepwater Horizon oil spill. Anthropocene 2016, 13, 18–33. [Google Scholar] [CrossRef]
- Romero, I.C.; Toro-Farmer, G.; Diercks, A.-R.; Schwing, P.; Muller-Karger, F.; Murawski, S.; Hollander, D.J. Large-scale deposition of weathered oil in the Gulf of Mexico following a deep-water oil spill. Environ. Pollut. 2017, 228, 179–189. [Google Scholar] [CrossRef] [PubMed]
- Law, A.M.J.; Aitken, M.D. Bacterial chemotaxis to naphthalene desorbing from a nonaqueous liquid. Appl. Environ. Microbiol. 2003, 69, 5968–5973. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Lanning, L.M.; Ford, R.M. Enhanced retention of chemotactic bacteria in a pore network with residual NAPL contamination. Environ. Sci. Technol. 2016, 50, 165–172. [Google Scholar] [CrossRef] [PubMed]
- Lambert, R.A.; Variano, E.A. Collision of oil droplets with marine aggregates: Effect of droplet size. J. Geophys. Res. Oceans 2016, 121, 3250–3260. [Google Scholar] [CrossRef]
- Levich, V.G. Physicochemical Hydrodynamics; Prentice-Hall: Englewood Cliffs, NJ, USA, 1962; ISBN 0136744400. [Google Scholar]
- Miller, R.M.; Bartha, R. Evidence from liposome encapsulation for transport-limited microbial metabolism of solid alkanes. Appl. Environ. Microbiol. 1989, 55, 269–274. [Google Scholar] [PubMed]
- Banat, I.M. Biosurfactants production and possible uses in microbial enhanced oil recovery and oil pollution remediation: A review. Bioresour. Technol. 1995, 51, 1–12. [Google Scholar] [CrossRef]
- Brown, D.G. Relationship between micellar and hemi-micellar processes and the bioavailability of surfactant-solubilized hydrophobic organic compounds. Environ. Sci. Technol. 2007, 41, 1194–1199. [Google Scholar] [CrossRef] [PubMed]
- Li, J.-L.; Chen, B.-H. Surfactant-mediated biodegradation of polycyclic aromatic hydrocarbons. Materials 2009, 2, 76–94. [Google Scholar] [CrossRef]
- Antoniou, E.; Fodelianakis, S.; Korkakaki, E.; Kalogerakis, N. Biosurfactant production from marine hydrocarbon-degrading consortia and pure bacterial strains using crude oil as carbon source. Front. Microbiol. 2015, 6, 274. [Google Scholar] [CrossRef] [PubMed]
- Hua, F.; Wang, H.Q. Uptake and transmembrane transport of petroleum hydrocarbons by microorganisms. Biotechnol. Biotechnol. Equip. 2014, 28, 165–175. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.K.; Sherry, A.; Gray, N.D.; Jones, D.M.; Bowler, B.F.J.; Head, I.M. Kinetic parameters for nutrient enhanced crude oil biodegradation in intertidal marine sediments. Front. Microbiol. 2014, 5, 160. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sandoval, K.; Ding, Y.; Stoeckel, D.; Minard-Smith, A.; Andersen, G.; Dubinsky, E.A.; Atlas, R.; Gardinali, P. Biodegradation of dispersed Macondo crude oil by indigenous Gulf of Mexico microbial communities. Sci. Total Environ. 2016, 557–558, 453–468. [Google Scholar] [CrossRef] [PubMed]
- Kapellos, G.E. Microbial strategies for oil biodegradation. In Modeling of Microscale Transport in Biological Processes; Becker, S.M., Ed.; Academic Press: Cambridge, MA, USA, 2017; pp. 19–39. [Google Scholar]
- Vilcáez, J.; Li, L.; Hubbard, S.S. A new model for the biodegradation kinetics of oil droplets: Application to the Deepwater Horizon oil spill in the Gulf of Mexico. Geochem. Trans. 2013, 14, 4. [Google Scholar] [CrossRef] [PubMed]
- Denis, B.; Pérez, O.A.; Lizardi-Jiménez, M.A.; Dutta, A. Numerical evaluation of direct interfacial uptake by a microbial consortium in an airlift bioreactor. Int. Biodeterior. Biodegrad. 2017, 119, 542–551. [Google Scholar] [CrossRef]
- North, E.W.; Adams, E.E.; Thessen, A.E.; Schlag, Z.; He, R.; Socolofsky, S.A.; Masutani, S.M.; Peckham, S.D. The influence of droplet size and biodegradation on the transport of subsurface oil droplets during the Deepwater Horizon spill: A model sensitivity study. Environ. Res. Lett. 2015, 10, 024016. [Google Scholar] [CrossRef]
- MacLeod, C.T.; Daugulis, A.J. Interfacial effects in a two-phase partitioning bioreactor: Degradation of polycyclic aromatic hydrocarbons (PAHs) by a hydrophobic Mycobacterium. Process Biochem. 2005, 40, 1799–1805. [Google Scholar] [CrossRef]
- Stone, H.A. Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid Mech. 1994, 26, 65–102. [Google Scholar] [CrossRef]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978; ISBN 0-12-176950-X. [Google Scholar]
- Michaelides, E.E. Hydrodynamic force and heat/mass transfer from particles, bubbles, and drops—The Freeman Scholar lecture. J. Fluids Eng. 2003, 125, 209–238. [Google Scholar] [CrossRef]
- Deen, W.M. Analysis of Transport Phenomena; Oxford University Press: New York, NY, USA, 1998; ISBN 0195084942. [Google Scholar]
- Johnson, A.I.; Akehata, T. Reaction accompanied mass transfer from fluid and solid spheres at low Reynolds numbers. Can. J. Chem. Eng. 1965, 43, 10–15. [Google Scholar] [CrossRef]
- Goddard, J.D.; Acrivos, A. An analysis of laminar forced-convection mass transfer with homogeneous chemical reaction. Q. J. Mech. Appl. Math. 1967, 20, 471–497. [Google Scholar] [CrossRef]
- Chen, W.C.; Pfeffer, R. Local and overall mass transfer rates around solid spheres with first-order homogeneous chemical reactions. Ind. Eng. Chem. Fundam. 1970, 9, 101–107. [Google Scholar] [CrossRef]
- Ruckenstein, E.; Dang, V.-D.; Gill, W.N. Mass transfer with chemical reaction from spherical one or two component bubbles or drops. Chem. Eng. Sci. 1971, 26, 647–668. [Google Scholar] [CrossRef]
- Hashimoto, H.; Kawano, S. Mass transfer around a moving encapsulated liquid drop. Int. J. Multiph. Flow 1993, 19, 213–228. [Google Scholar] [CrossRef]
- Juncu, G. The influence of the Henry number on the conjugate mass transfer from a sphere: II—Mass transfer accompanied by a first-order chemical reaction. Heat Mass Transf. 2002, 38, 523–534. [Google Scholar] [CrossRef]
- Stewart, P.S. A review of experimental measurements of effective diffusive permeabilities and effective diffusion coefficients in biofilms. Biotechnol. Bioeng. 1998, 59, 261–272. [Google Scholar] [CrossRef]
- Kapellos, G.E.; Alexiou, T.S.; Payatakes, A.C. A multiscale theoretical model for diffusive mass transfer in cellular biological media. Math. Biosci. 2007, 210, 177–237. [Google Scholar] [CrossRef] [PubMed]
- Arnaouteli, S.; MacPhee, C.E.; Stanley-Wall, N.R. Just in case it rains: Building a hydrophobic biofilm the Bacillus subtilis way. Curr. Opin. Microbiol. 2016, 34, 7–12. [Google Scholar] [CrossRef] [PubMed]
- Passow, U.; Ziervogel, K.; Asper, V.; Diercks, A. Marine snow formation in the aftermath of the Deepwater Horizon oil spill in the Gulf of Mexico. Environ. Res. Lett. 2012, 7, 035301. [Google Scholar] [CrossRef]
- Rivas, D.; Badan, A.; Sheinbaum, J.; Ochoa, J.; Candela, J. Vertical velocity and vertical heat flux observed within loop current eddies in the central Gulf of Mexico. J. Phys. Oceanogr. 2008, 38, 2461–2481. [Google Scholar] [CrossRef]
- Chiswell, S.M. Mean velocity decomposition and vertical eddy diffusivity of the Pacific ocean from surface GDP drifters and 1000-m Argo floats. J. Phys. Oceanogr. 2016, 46, 1751–1768. [Google Scholar] [CrossRef]
- North, E.W.; Adams, E.E.; Schlag, Z.; Sherwood, C.R.; He, R.; Hyun, K.H.; Socolofsky, S.A. Simulating oil droplet dispersal from the Deepwater Horizon spill with a Lagrangian approach. In Monitoring and Modeling the Deepwater Horizon Oil Spill: A Record-Breaking Enterprise (Geophysical Monograph Series 195); Liu, Y., Macfadyen, A., Ji, Z.-G., Weisberg, R.H., Eds.; American Geophysical Union: Washington, DC, USA, 2011; pp. 217–226. [Google Scholar] [CrossRef]
- Buckley, J.S.; Fan, T. Crude oil/brine interfacial tensions. Petrophysics 2007, 48, A1. [Google Scholar]
- Moeini, F.; Hemmati-Sarapardeh, A.; Ghazanfari, M.-H.; Masihi, M.; Ayatollahi, S. Toward mechanistic understanding of heavy crude oil/brine interfacial tension: The roles of salinity, temperature and pressure. Fluid Phase Equilibria 2014, 375, 191–200. [Google Scholar] [CrossRef]
- Epstein, A.K.; Pokroy, B.; Seminara, A.; Aizenberg, J. Bacterial biofilm shows persistent resistance to liquid wetting and gas penetration. Proc. Natl. Acad. Sci. USA 2011, 108, 995–1000. [Google Scholar] [CrossRef] [PubMed]
- Stocker, R. Marine microbes see a sea of gradients. Science 2012, 338, 628–633. [Google Scholar] [CrossRef] [PubMed]
- Meile, C.; Tuncay, K. Scale dependence of reaction rates in porous media. Adv. Water Resour. 2006, 29, 62–71. [Google Scholar] [CrossRef]
- Medina-Moreno, S.A.; Jiménez-González, A.; Gutiérrez-Rojas, M.; Lizardi-Jiménez, M.A. Hexadecane aqueous emulsion characterization and uptake by an oil-degrading microbial consortium. Int. Biodeterior. Biodegrad. 2013, 84, 1–7. [Google Scholar] [CrossRef]
- Nikolopoulou, M.; Pasadakis, N.; Kalogerakis, N. Evaluation of autochthonous bioaugmentation and biostimulation during microcosm-simulated oil spills. Mar. Pollut. Bull. 2013, 72, 165–173. [Google Scholar] [CrossRef] [PubMed]
- Torlapati, J.; Boufadel, M.C. Evaluation of the biodegradation of Alaska North Slope oil in microcosms using the biodegradation model BIOB. Front. Microbiol. 2014, 5, 212. [Google Scholar] [CrossRef] [PubMed]
- Brakstad, O.G.; Nordtug, T.; Throne-Holst, M. Biodegradation of dispersed Macondo oil in seawater at low temperature and different oil droplet sizes. Mar. Pollut. Bull. 2015, 93, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Prince, R.C.; Butler, J.D.; Redman, A.D. The rate of crude oil biodegradation in the sea. Environ. Sci. Technol. 2017, 51, 1278–1284. [Google Scholar] [CrossRef] [PubMed]
- Thessen, A.E.; North, E.W. Calculating in situ degradation rates of hydrocarbon compounds in deep waters of the Gulf of Mexico. Mar. Pollut. Bull. 2017, 122, 77–84. [Google Scholar] [CrossRef] [PubMed]
- Rahsepar, S.; Langenhoff, A.A.M.; Smit, M.P.J.; van Eenennaam, J.S.; Murk, A.J.; Rijnaarts, H.H.M. Oil biodegradation: Interactions of artificial marine snow, clay particles, oil and Corexit. Mar. Pollut. Bull. 2017, 125, 186–191. [Google Scholar] [CrossRef] [PubMed]
- Kapellos, G.E.; Alexiou, T.S. Modeling momentum and mass transport in cellular biological media: From the molecular to the tissue scale. In Transport in Biological Media; Becker, S.M., Kuznetsov, A.V., Eds.; Academic Press: Waltham, MA, USA, 2013; pp. 1–40. [Google Scholar] [CrossRef]
- Billings, N.; Birjiniuk, A.; Samad, T.S.; Doyle, P.S.; Ribbeck, K. Material properties of biofilms—A review of methods for understanding permeability and mechanics. Rep. Prog. Phys. 2015, 78, 036601. [Google Scholar] [CrossRef] [PubMed]
- Sudarsan, R.; Ghosh, S.; Stockie, J.; Eberl, H.J. Simulating biofilm deformation and detachment with the immersed boundary method. Commun. Comput. Phys. 2016, 19, 682–732. [Google Scholar] [CrossRef]
- Hollenbeck, E.C.; Douarche, C.; Allain, J.-M.; Roger, P.; Regeard, C.; Cegelski, L.; Fuller, G.G.; Raspaud, E. Mechanical Behavior of a Bacillus subtilis Pellicle. J. Phys. Chem. B 2016, 120, 6080–6088. [Google Scholar] [CrossRef] [PubMed]


| oil | ||||||
|---|---|---|---|---|---|---|
| ALK | 0.600 | 0.086 | 0.056 | 55.8 | 0.00314 | |
| BTEX | 0.320 | 0.129 | 0.020 | 19.8 | 0.00168 | |
| PAH | 0.053 | 0.028 | 0.015 | 15.1 | 0.00028 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kapellos, G.E.; Paraskeva, C.A.; Kalogerakis, N.; Doyle, P.S. Theoretical Insight into the Biodegradation of Solitary Oil Microdroplets Moving through a Water Column. Bioengineering 2018, 5, 15. https://doi.org/10.3390/bioengineering5010015
Kapellos GE, Paraskeva CA, Kalogerakis N, Doyle PS. Theoretical Insight into the Biodegradation of Solitary Oil Microdroplets Moving through a Water Column. Bioengineering. 2018; 5(1):15. https://doi.org/10.3390/bioengineering5010015
Chicago/Turabian StyleKapellos, George E., Christakis A. Paraskeva, Nicolas Kalogerakis, and Patrick S. Doyle. 2018. "Theoretical Insight into the Biodegradation of Solitary Oil Microdroplets Moving through a Water Column" Bioengineering 5, no. 1: 15. https://doi.org/10.3390/bioengineering5010015
APA StyleKapellos, G. E., Paraskeva, C. A., Kalogerakis, N., & Doyle, P. S. (2018). Theoretical Insight into the Biodegradation of Solitary Oil Microdroplets Moving through a Water Column. Bioengineering, 5(1), 15. https://doi.org/10.3390/bioengineering5010015