2. The Mathematical Model and Numerical Code
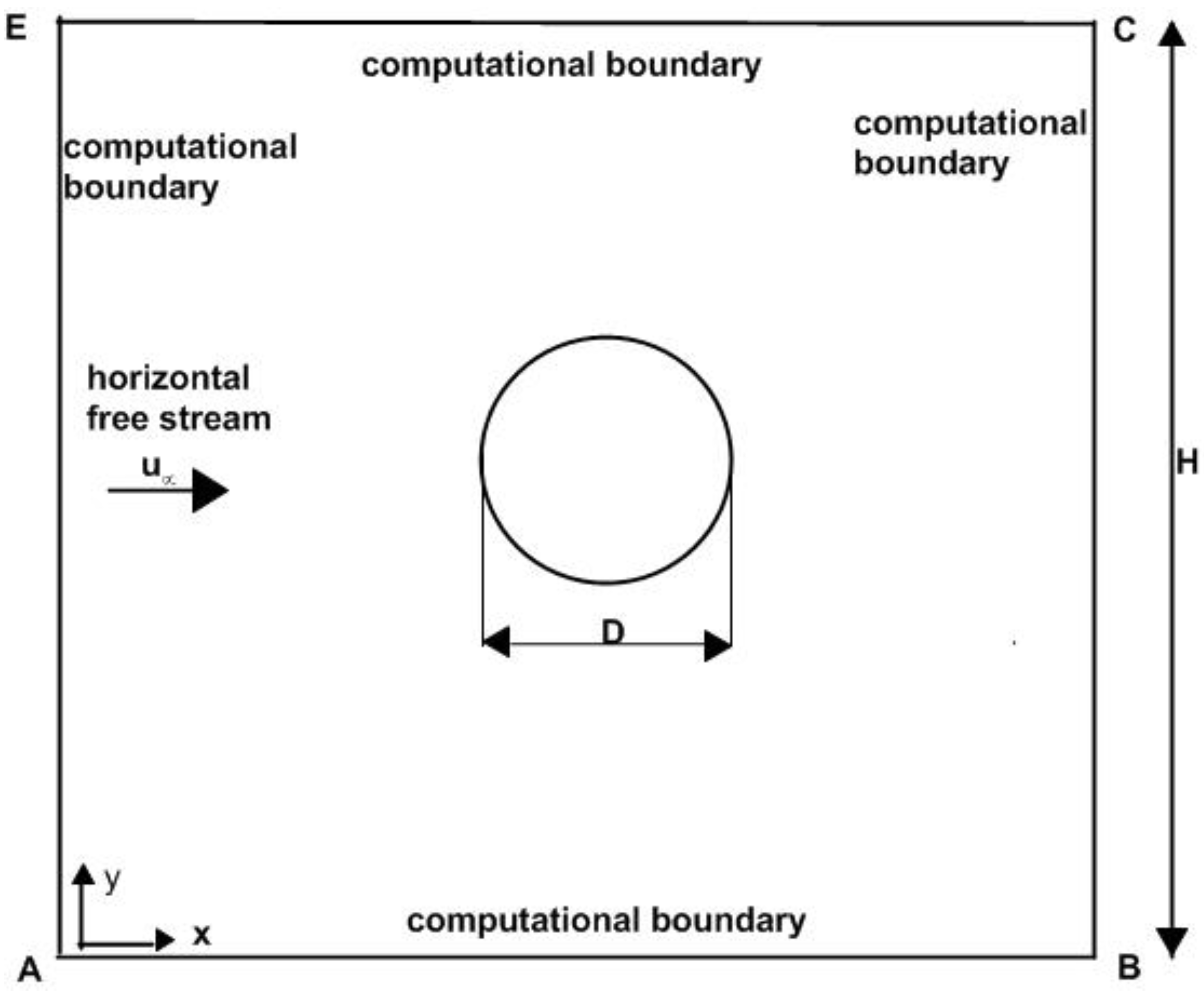
Consider the flow of a non-Newtonian power-law fluid across a horizontal circular cylinder as it is shown in
Figure 1. The full equations of this flow are [
2] the continuity equation:
the
x-momentum equation:
and the
y-momentum equation:
The relation between the stress tensor
and the rate-of-strain tensor
is the following:
where
is the apparent viscosity and the strain tensor is
Taking into account Equations (4) and (5), the momentum equations take the form of the
x-momentum equation:
and the
y-momentum equation:
where
is the horizontal coordinate,
is the vertical coordinate,
is the horizontal velocity,
is the vertical velocity,
is the pressure and
ρ is the fluid density. The apparent viscosity is:
where
n is the power-law index and
is the consistency coefficient which reduces to dynamic viscosity in the case of Newtonian fluids. The fluid is characterized as shear-thinning for
, shear-thickening for
n > 1 and Newtonian for
n = 1. In the shear-thinning regime with a low power-law index (
) there are polymer melts, rubber, styling gel and some paints, whereas aggregates with particles and pastes belong to shear-thickening fluids. During the last years the US Army has shown great interest in shear-thickening fluids (STF). They came to the conclusion that impregnating STF into Kevlar fabrics improved its performance. It seems that the most suitable STF for such application is the suspension of silica particles in ethylene glycol. Ethylene glycol is an organic compound widely used as automotive antifreeze. It was chosen as a solvent due to its volatility and thermal stability. The silica particles were, for better dispersibility, predispersed in methanol and then blended with ethylene glycol. Experimental research suggests that the best way to include STF in body armor vests is to impregnate it into Kevlar fabrics. A great advantage of STF impregnated over neat Kevlar is the protection against stabbing [
3].
The flow is governed by the Reynolds number which is given by the following relationship,
where
is the cylinder diameter and
is the free stream velocity. The drag coefficient is defined as
where
is the force acting on the body, S is the surface area and
is the horizontal component of the unit vector normal to the surface of the cylinder. The first surface integral represents the pressure force and the second the stress force.
The present numerical study has been carried out using ANSYS FLUENT (version 12.0). The two-dimensional, steady, laminar solver was used with the third-order scheme for the convective terms in the momentum equation. The coupled scheme was used for pressure-velocity coupling and the non-Newtonian power-law model was used for viscosity. A double precision accuracy was used and a convergence criterion of 10−10 was used for the x- and y-velocity components as well as for the residuals of continuity.
The applied boundary conditions (
Figure 1) are the following according to the ANSYS FLUENT code. The boundary AE was defined as the “velocity inlet” where the horizontal velocity is constant and the vertical velocity is zero, while the boundary BC was defined as the “outflow”. The boundaries AB and EC were defined as a “moving wall” with velocity equal to the free stream velocity. The cylinder surface was defined as a “stationary wall” (no slip condition). In order to achieve grid-independent results, all computational boundaries were placed far away from the cylinder (at distance of 25,000 D). Although this computational field is very large, all calculations were carried out within this large field. The cylinder diameter was 10 mm and the perimeter length was 31.4 mm. On the cylinder surface 314 grid points were located and each step on the cylinder surface was 0.1 mm long. The first grid point normal to the cylinder surface was located at a distance of 0.05 mm (0.005 D). The grid step at the boundaries was 800 mm. However, this was only the initial mesh. In ANSYS FLUENT there is a grid-adaptation function which adds more grid points at places where the solution is not satisfactory. Therefore, this initial mesh changed and was made much denser using the grid adaptation function.
3. Results and Discussion
The validation of the present model has been done extensively in two previous works by the present author [
4,
5] and no further information will be given here.
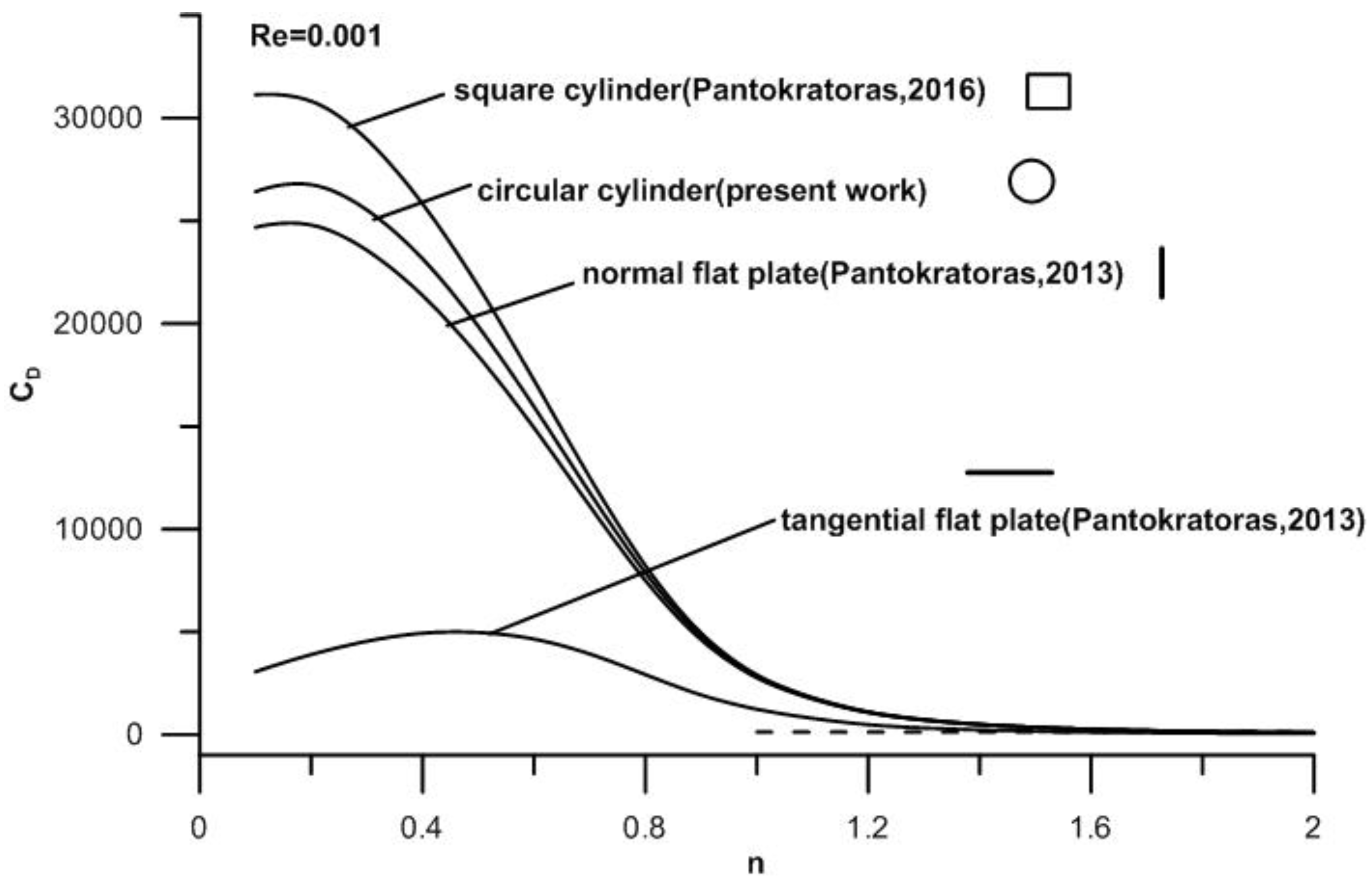
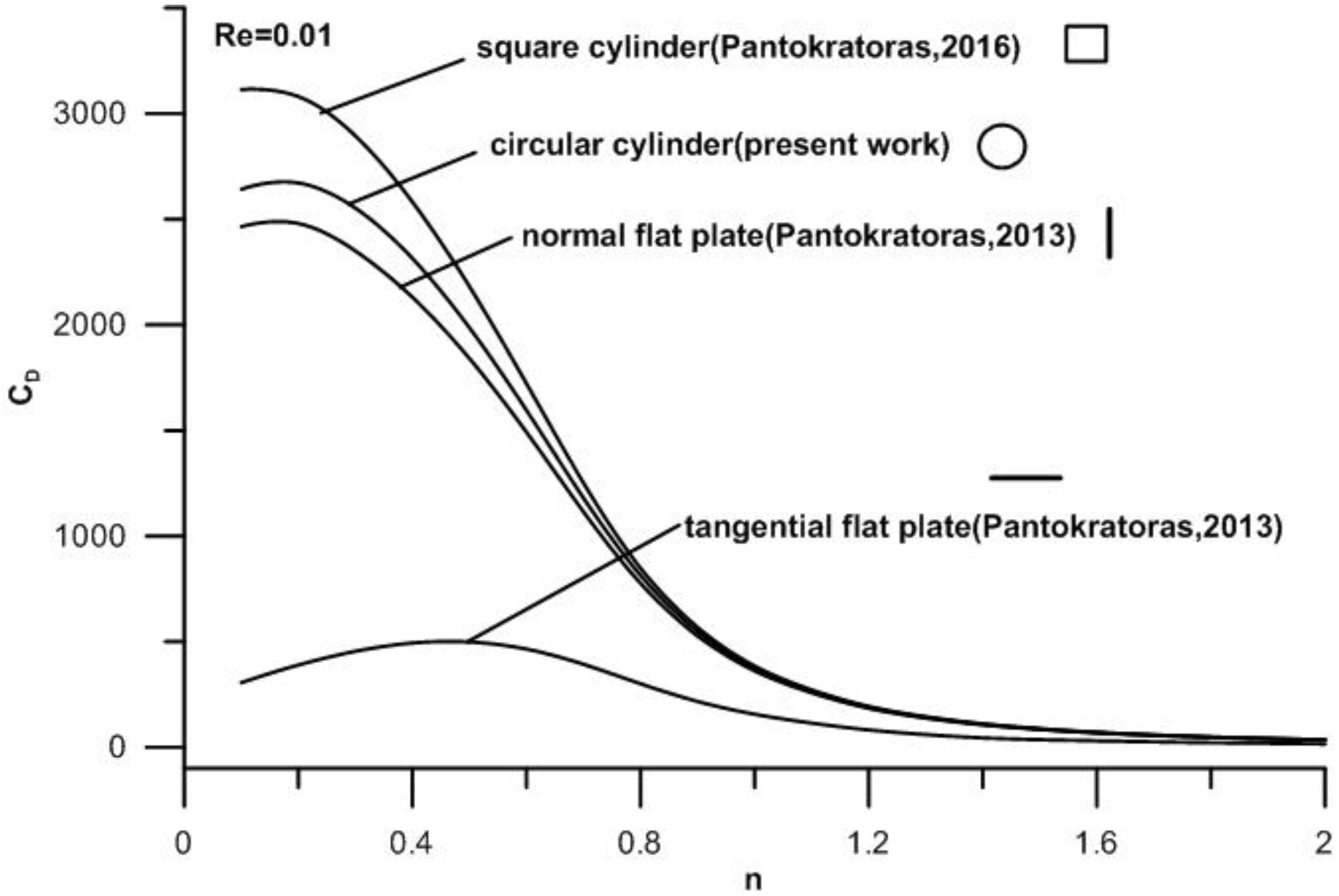
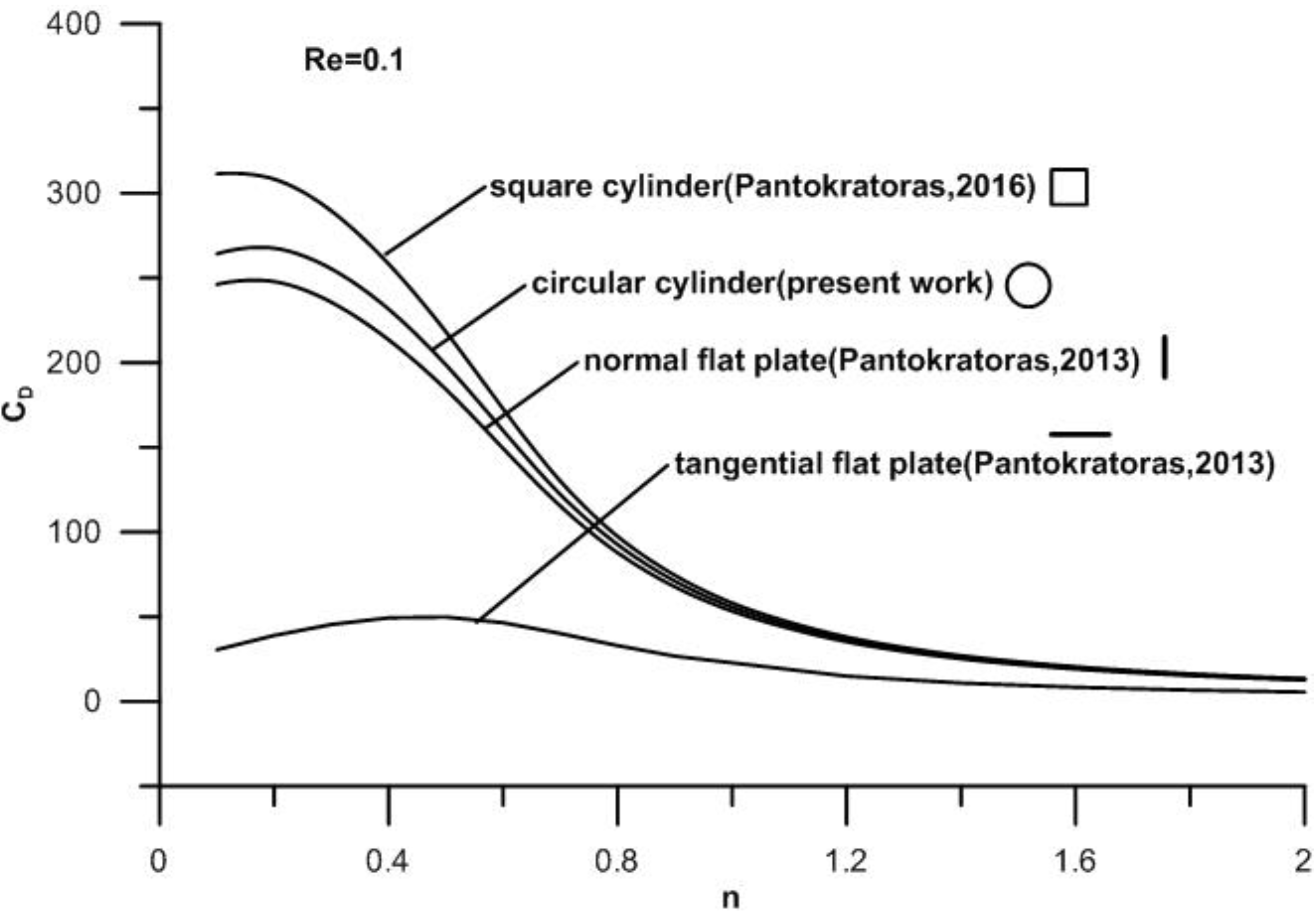
In
Table 1 we present the values of the drag coefficient for very low Reynolds numbers for three two-dimensional cylindrical bodies (a circular cylinder, a square cylinder and a normal flat plate). The results for the square cylinder and normal flat plate were taken from Pantokratoras [
4,
5] whereas the results for the circular cylinder were calculated in the present work. In addition, for a Newtonian fluid (
) and the circular cylinder, the results based on the Oseen [
6] formula
are included for comparison. It is seen that the results of the present work compare well with those of Oseen [
6] at low Reynolds numbers, but as the Re number increases, the divergence increases. This is rational because the Oseen formula is valid for very low Re numbers. From this table it is seen that in the range of low Reynolds numbers (
) and a low power-law index (
), the drag coefficient obeys the law
for all cases. Values of the constant A for the circular cylinder are given in
Table 2.
Although the relation
is clear from
Table 1, a theoretical proof will be given here. Tanner ([
7] Equation (34)), using dimensional analysis, produced the following equation for the force acting on a circular cylinder by a non-Newtonian power-law fluid with (
)
where R is the radius of the circular cylinder and a and b are constants. The above relation is valid when a small amount of inertia is present. In our case the Reynolds number is very small and Equation (11) takes the form
In Equation (12) we used the diameter of the cylinder instead of the radius. Combining Equations (10) and (12), the drag coefficient takes the form
. It is seen that this simple form of the drag coefficient, which is obvious from the numerical results included in
Table 1, is also based on the dimensional analysis of the shear-thinning fluids and is apparently correct.
Another conclusion drawn from
Table 1 is the fact that, as the power-law index increases, approaching 2, the drag coefficients of all bodies tend to coincide. For example, the drag coefficients of the circular and square cylinders at Re = 0.001 and
n = 0.1 differ 15% and the difference becomes 1% at
n = 2. The drag coefficients of the square cylinder and flat plate at Re = 0.001 and
n = 0.1 differ 21% and the difference becomes 2% at
n = 2. This trend is clearly shown in
Figure 2,
Figure 3 and
Figure 4.
The physical explanation for the above behavior of drag coefficients at high values of the power-law index will be given here and is based on the work of Whitney and Rodin [
8]. These authors investigated the problem of rigid bodies translating through unbounded shear-thinning power-law fluids and found the relationship between the velocity and the force acting on the rigid body. Referring to shear-thinning fluids, the authors say, “
The velocity gradient decay is much stronger for highly non-linear fluids than for Newtonian fluids. This implies that in highly non-linear fluids one should expect strong flow localization near the body whereas in Newtonian fluids the localization is weak and the flow intensity decays gradually with distance. Consequently, one should expect that the strong flow localization makes problems that involve highly non-linear fluids very sensitive to the geometrical details of the body.” The meaning of the above excerpt is that for highly non-linear fluids, such as shear-thinning fluids, the drag coefficient depends strongly on the body cross-section. In contrast to shear-thinning fluids which are highly non-linear, the shear-thickening fluids with a high n tend to become linear with very small viscosity [
9]. Extending the above argument of Whitney and Rodin [
8], we expect that at shear-thickening fluids the drag coefficient will not be sensitive to the geometrical details of the body and this argument is supported by the present results.