Experimental and Numerical Study of Windage Losses in the Narrow Gap Region of a High-Speed Electric Motor
Abstract
:1. Introduction
2. Materials and Methods
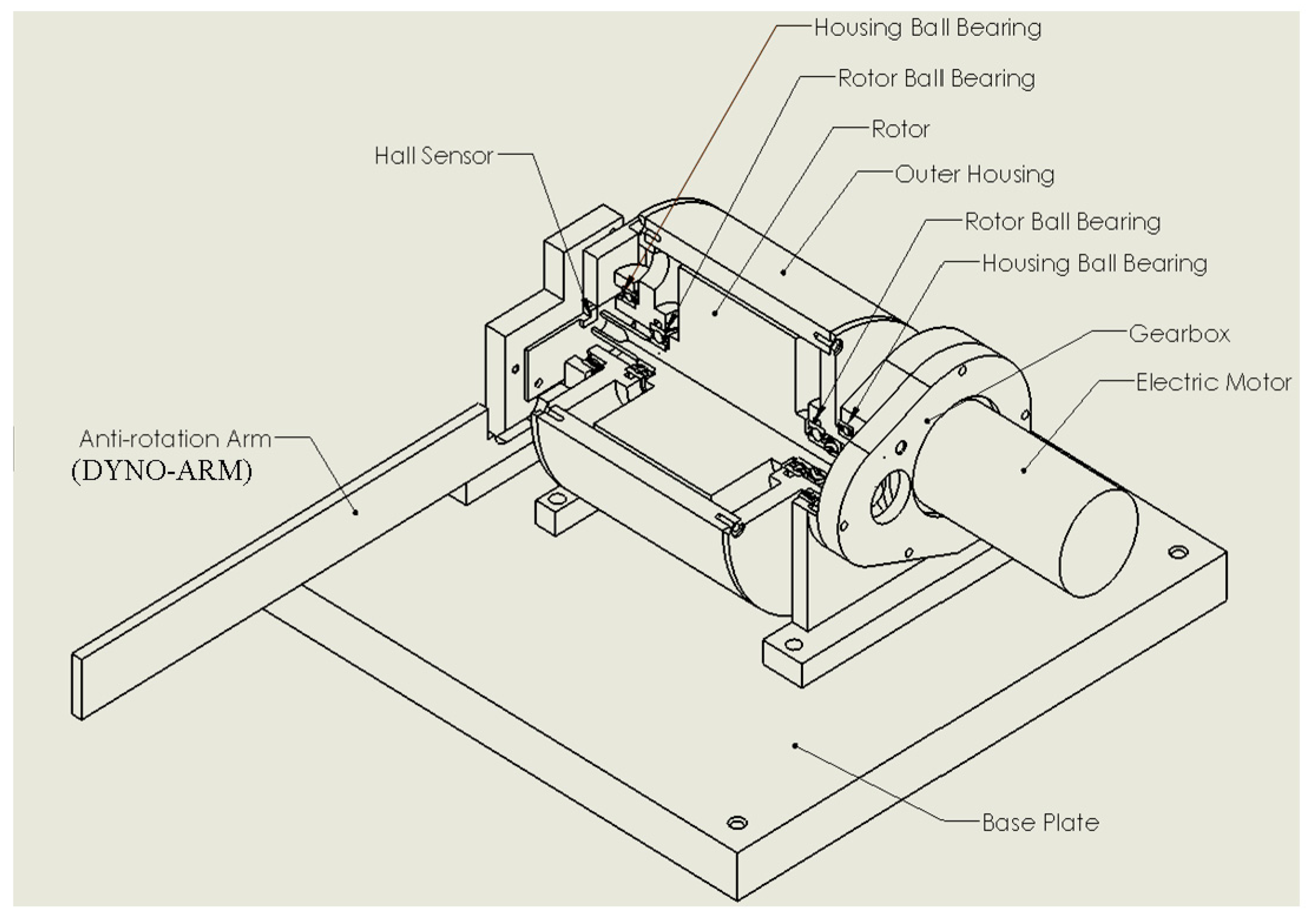
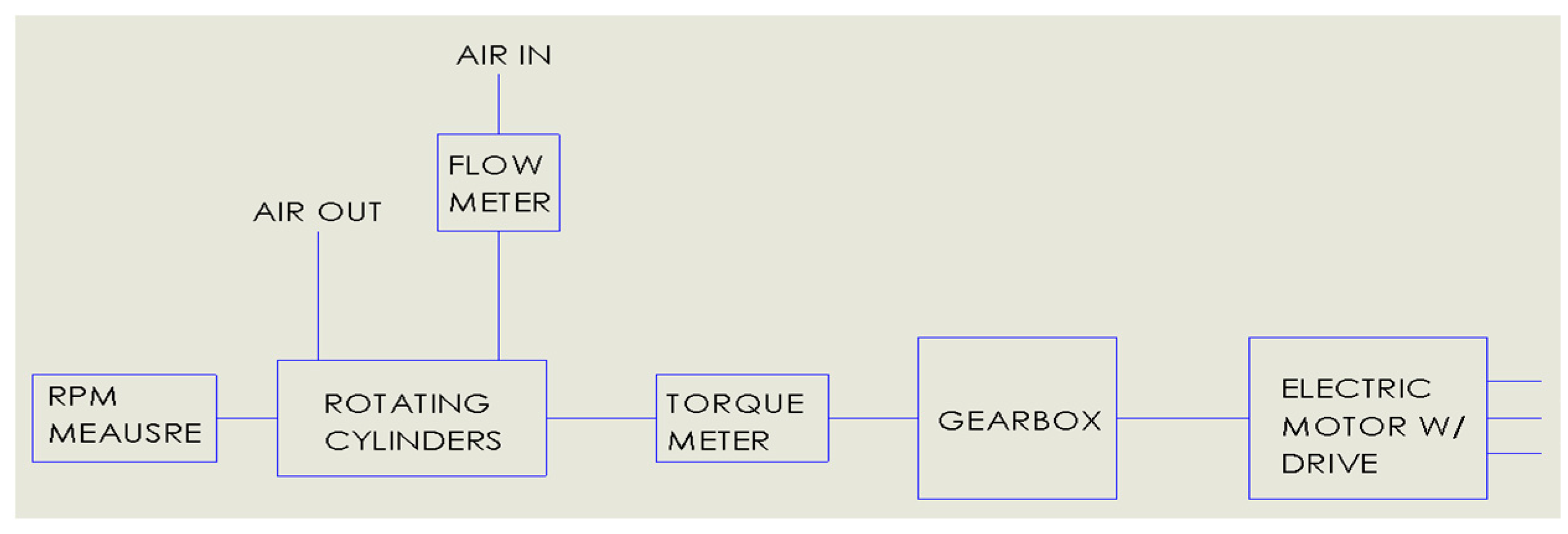
2.1. Experimental Apparatus
2.2. Uncertainty Analysis
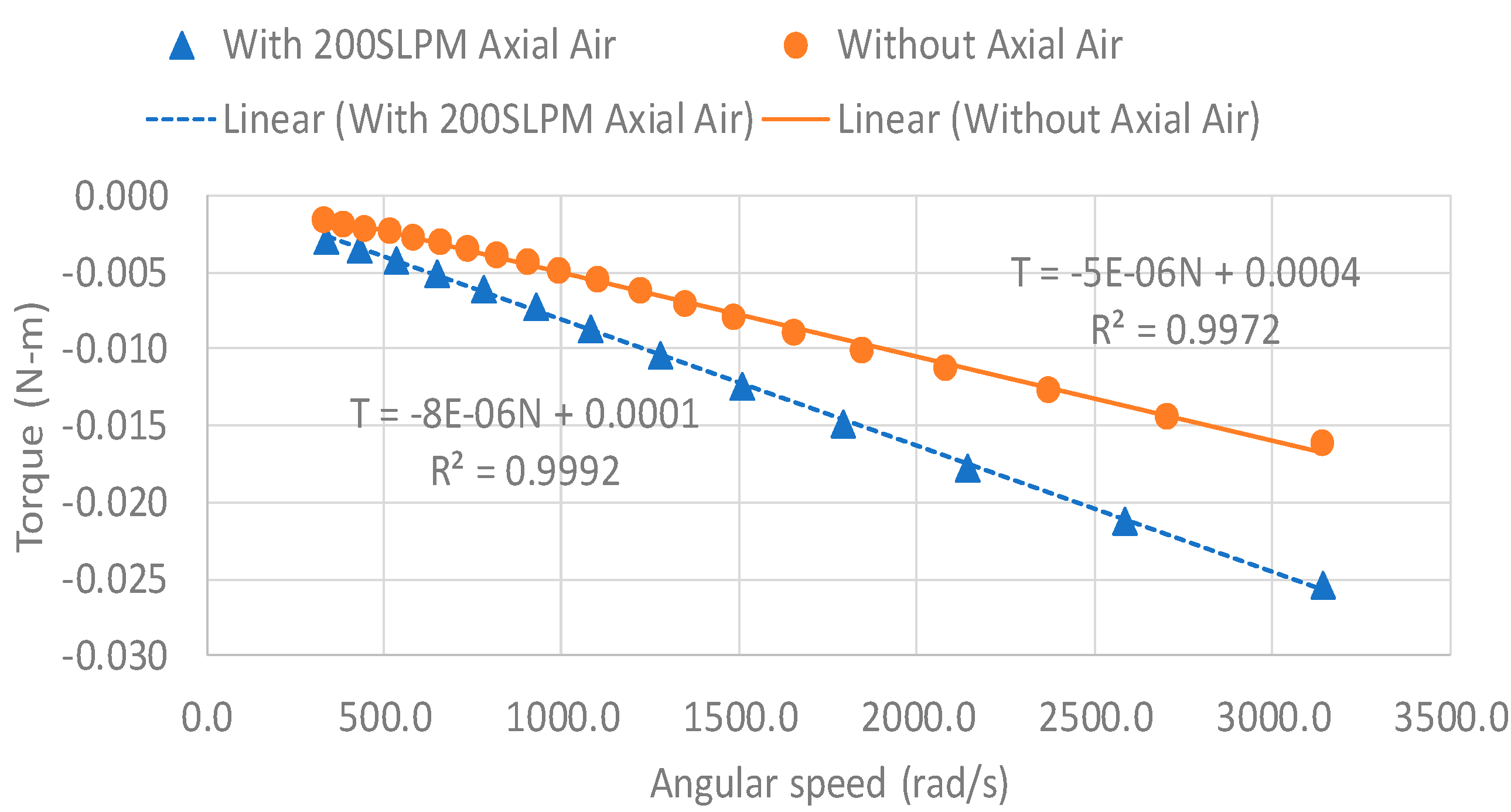
2.3. Experimental Data Reducation Procedure
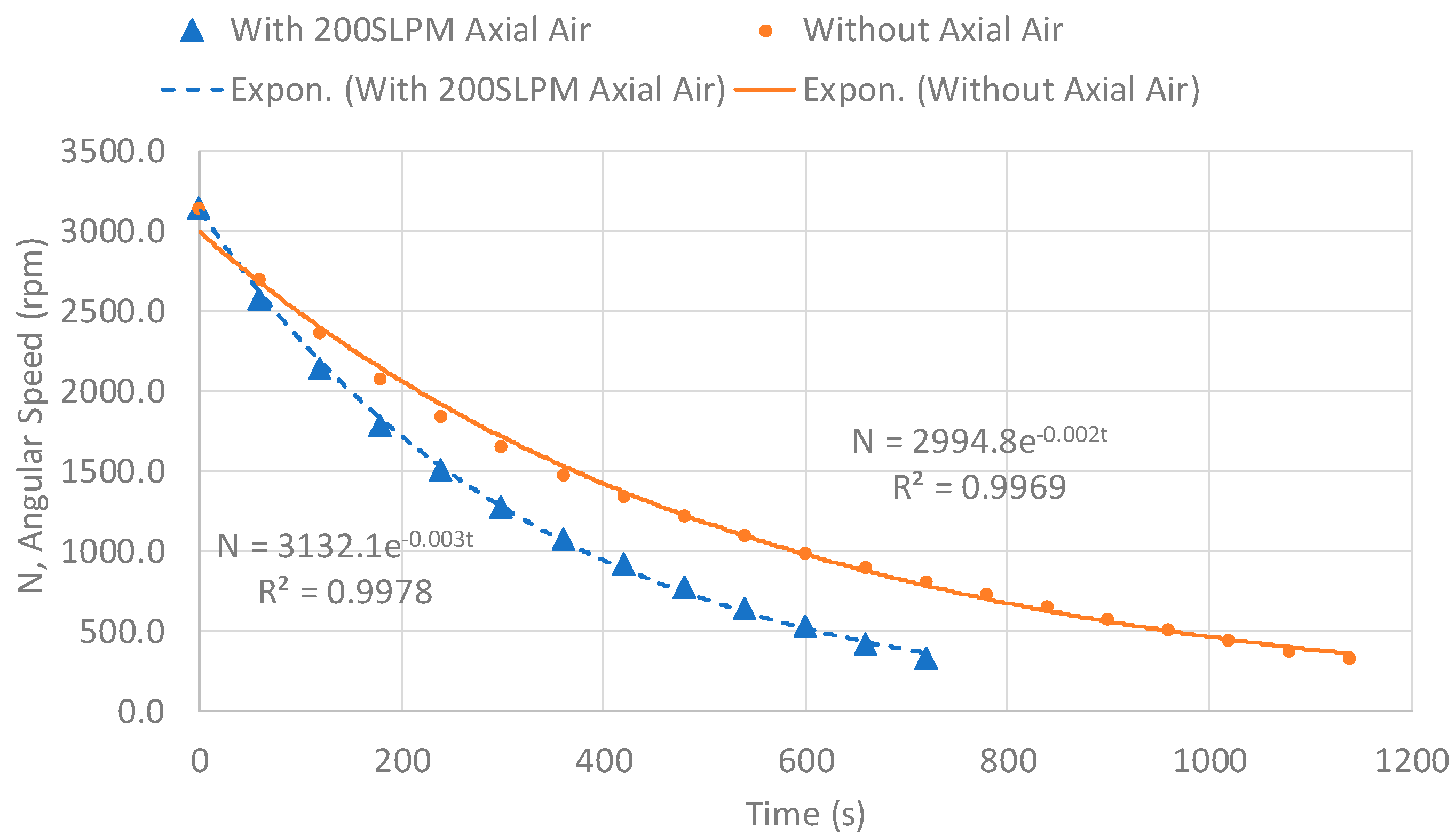
2.4. Spin Down Tests
2.5. Numerical Modeling Methodology
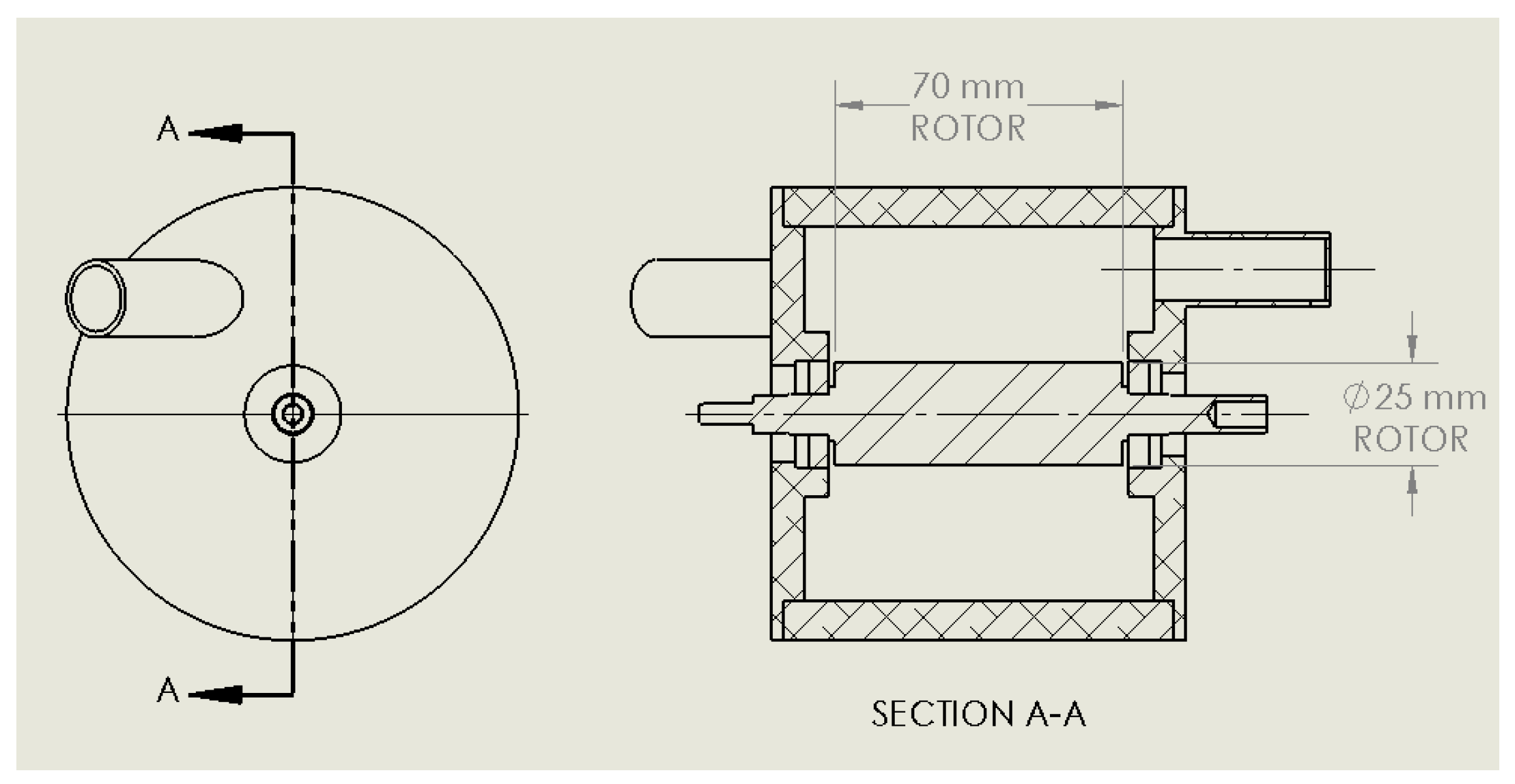
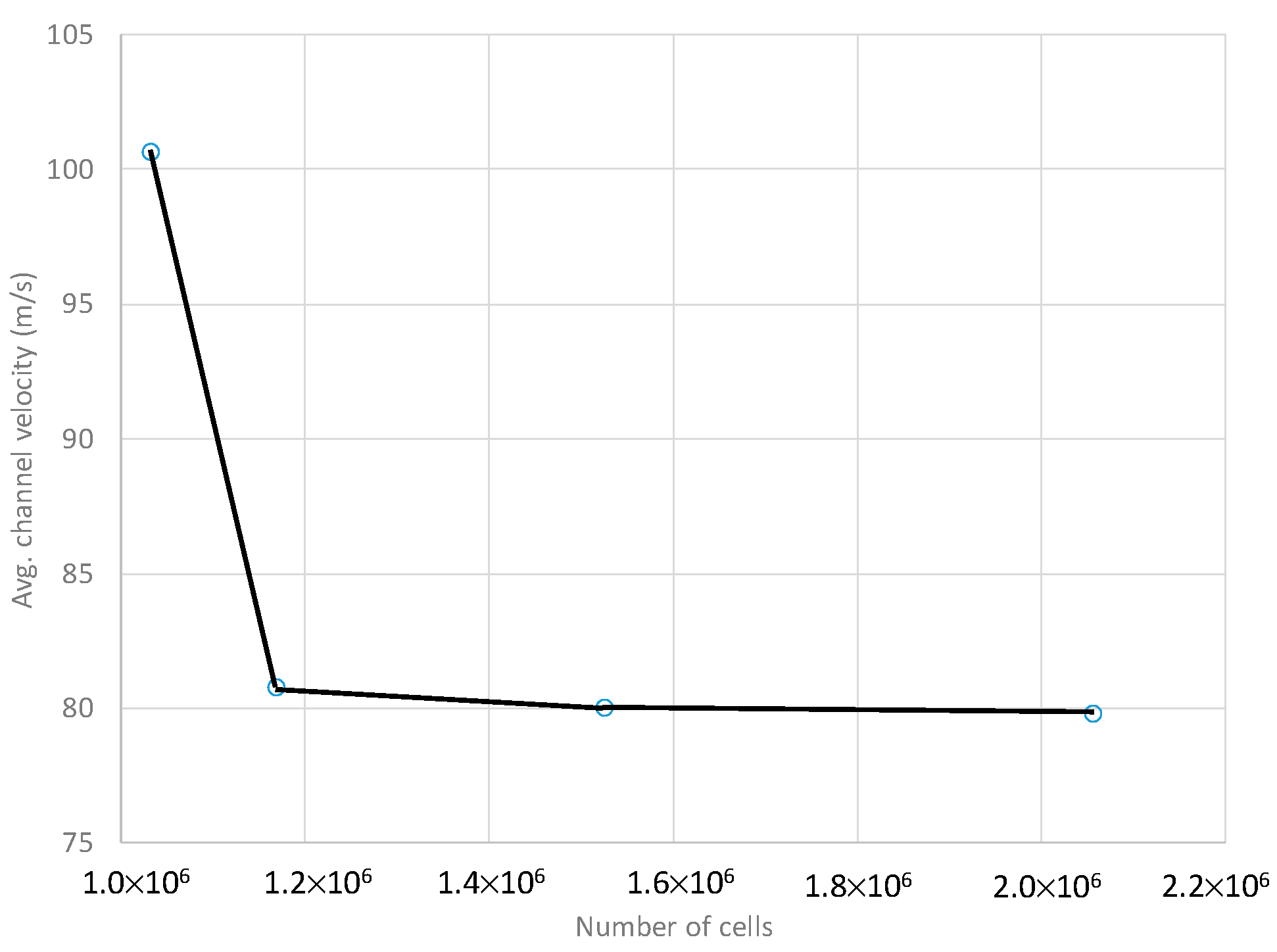
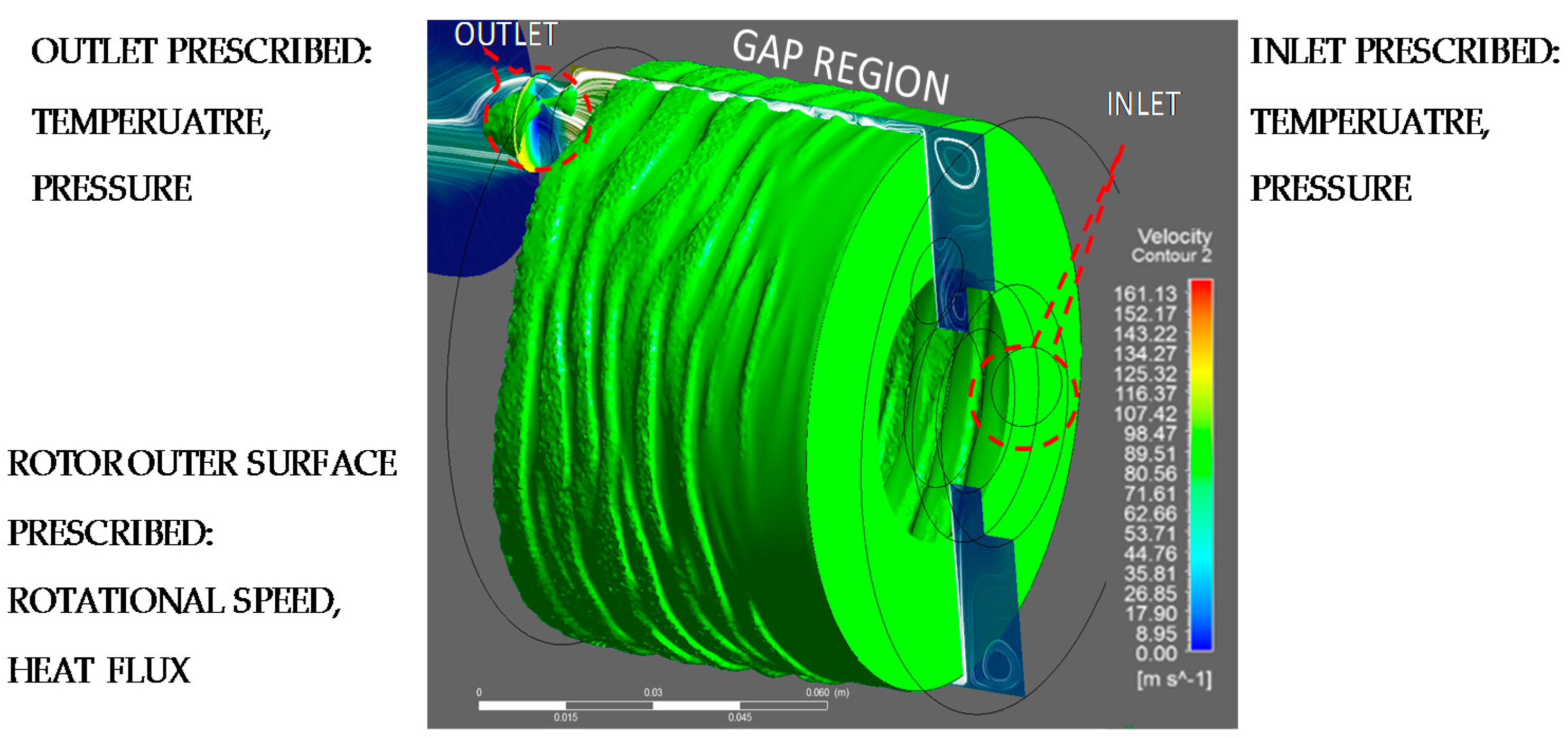
2.6. Numerical Modeling Geometry, Grid, and Boundary Conditions
3. Results
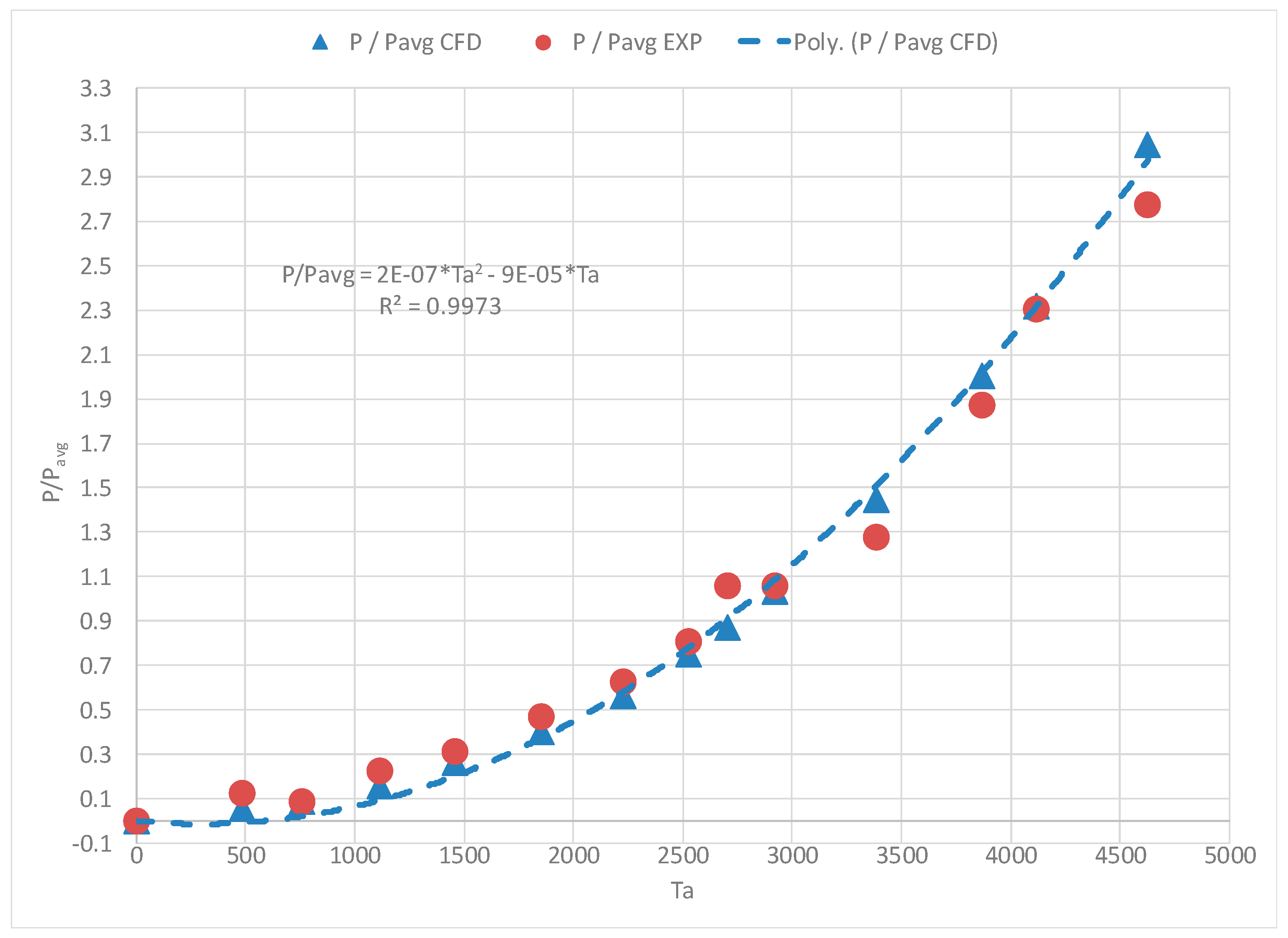
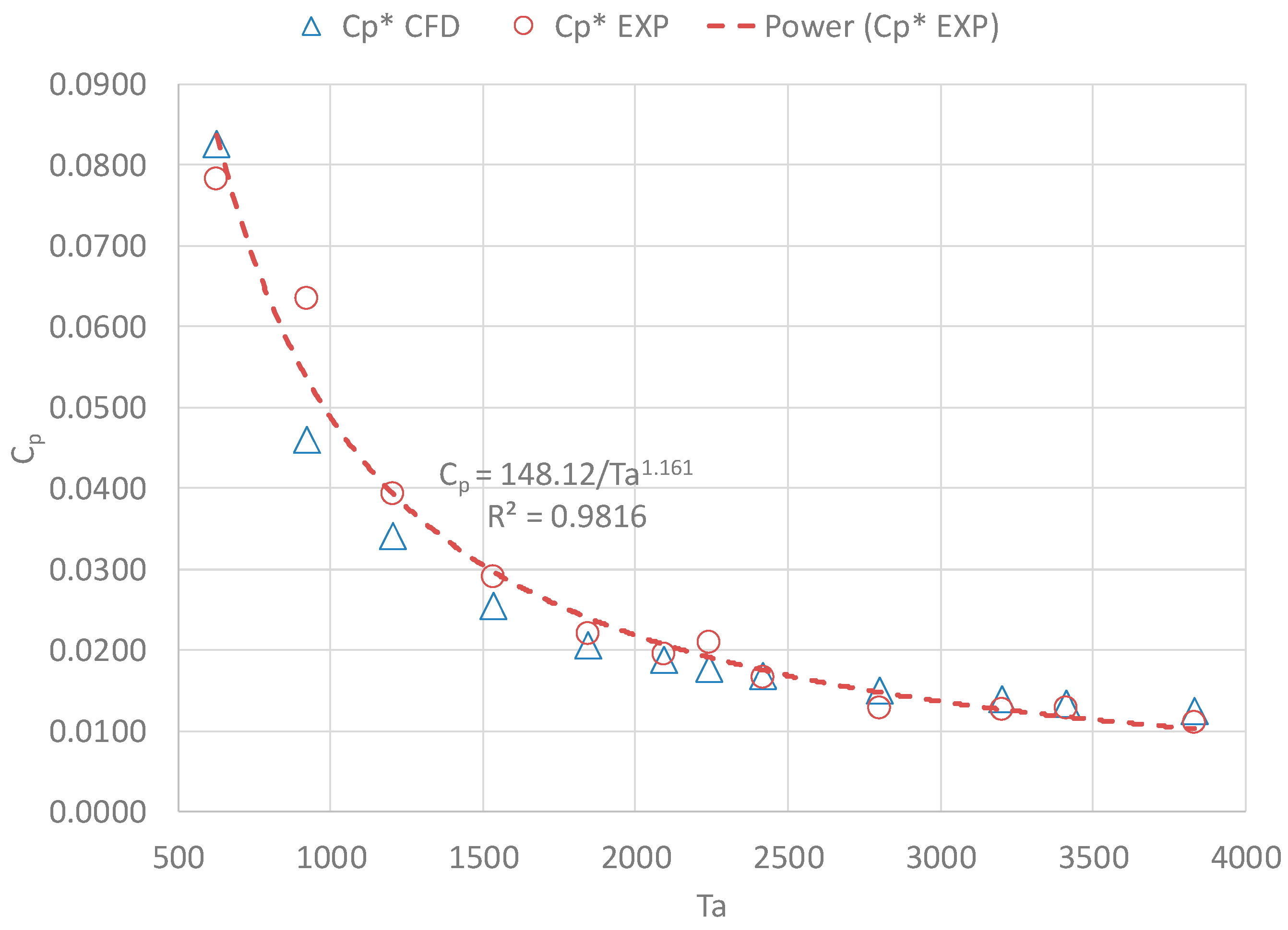
3.1. Windage Loss Results
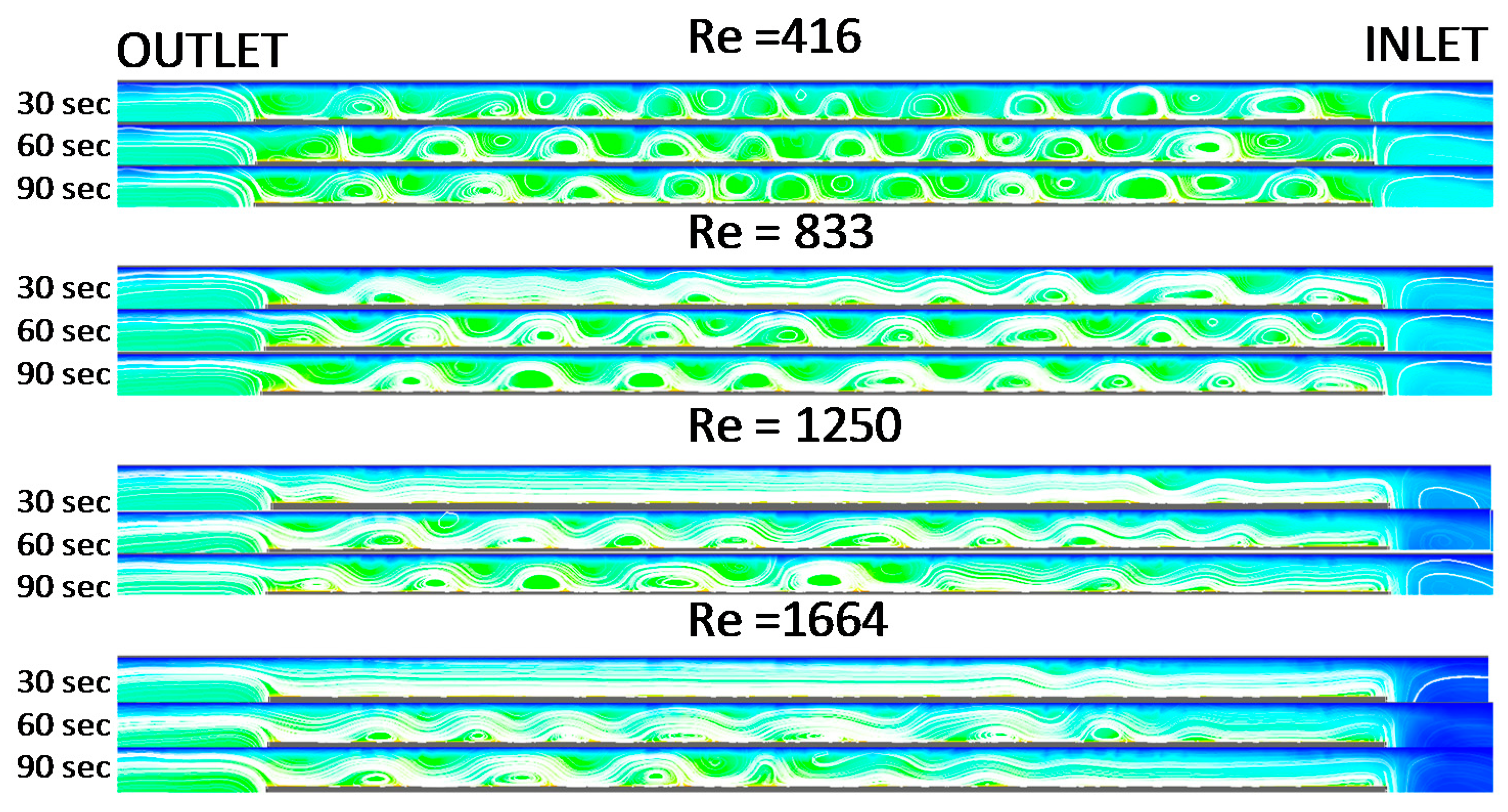
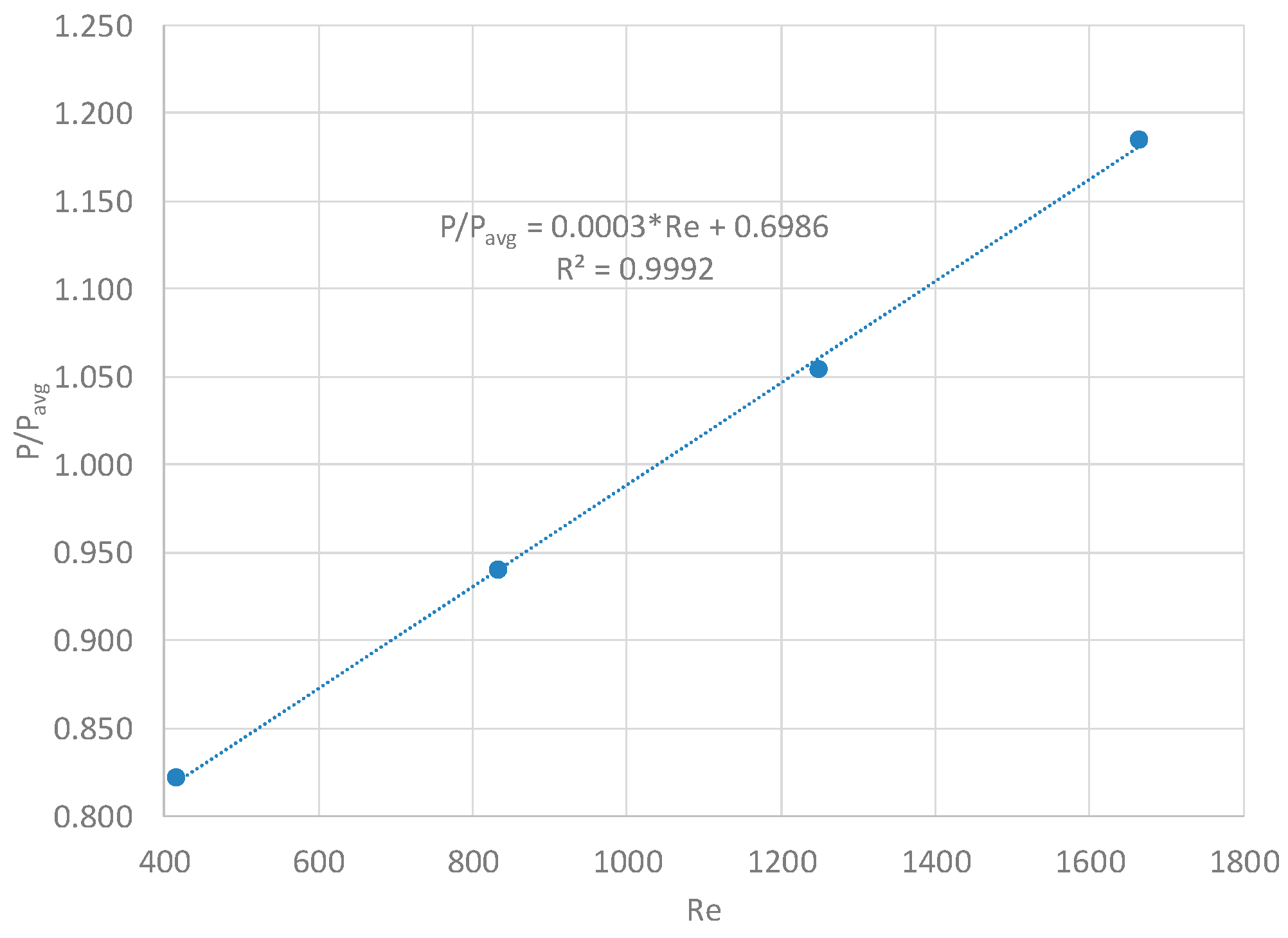
3.2. Inlet Mass Flow Rate Study
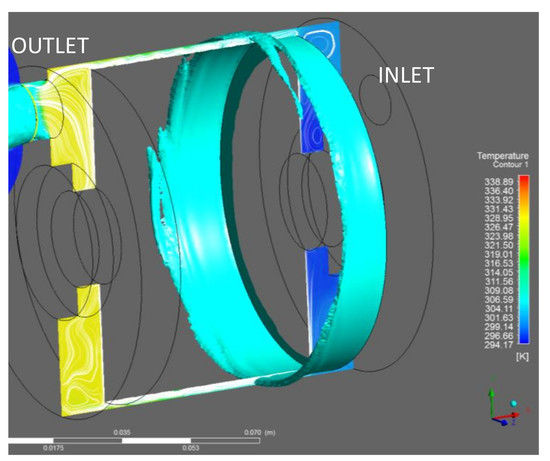
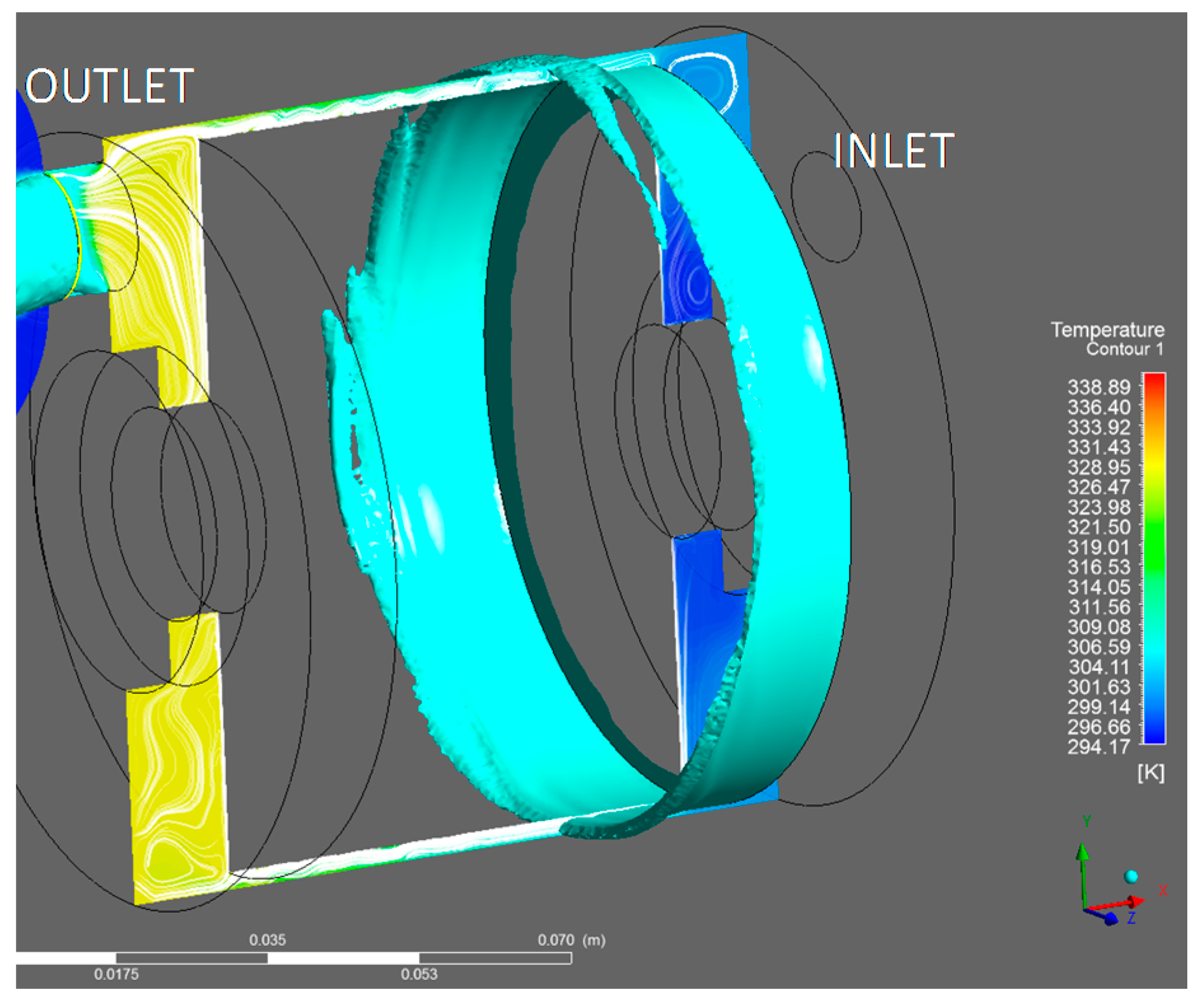
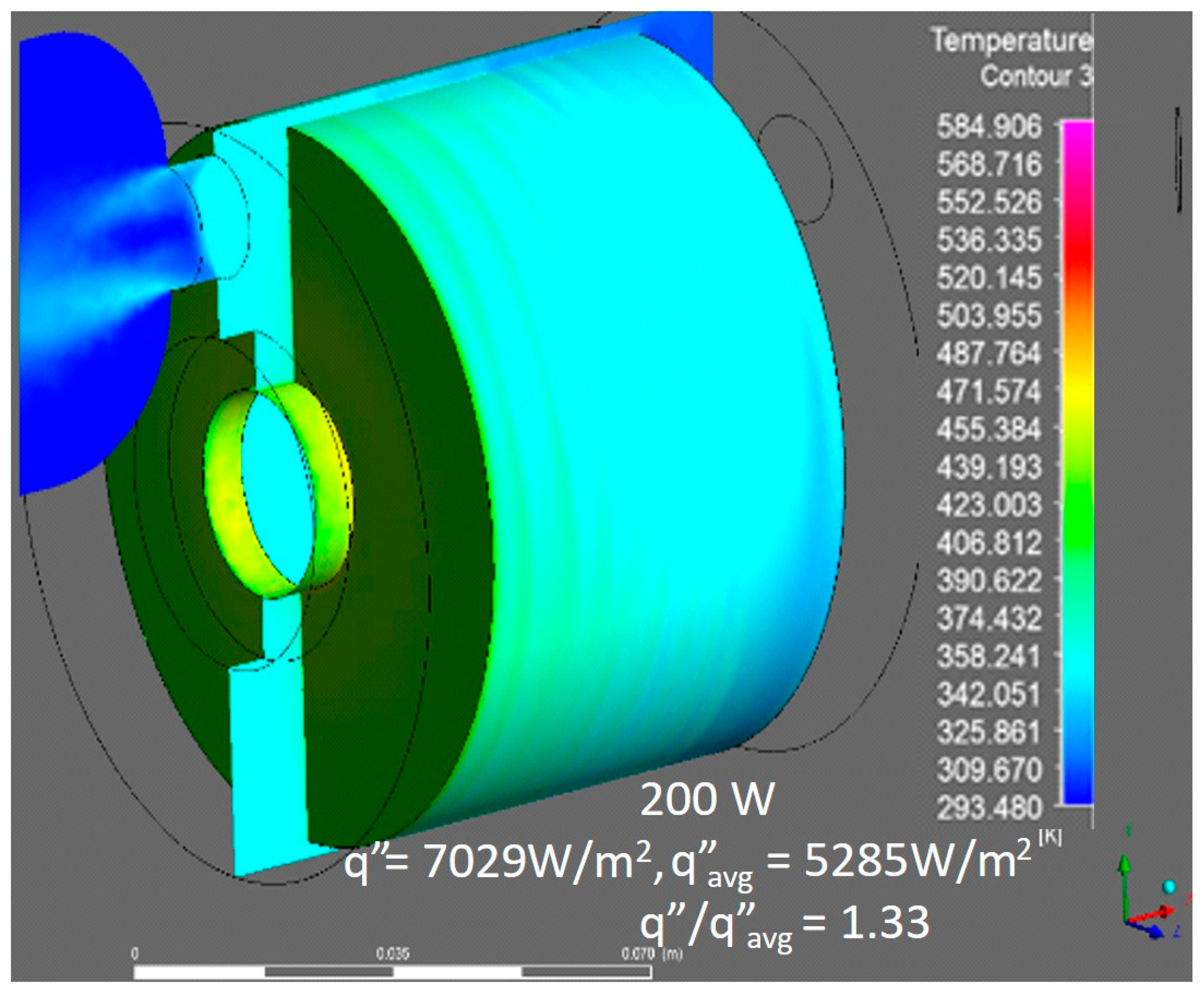
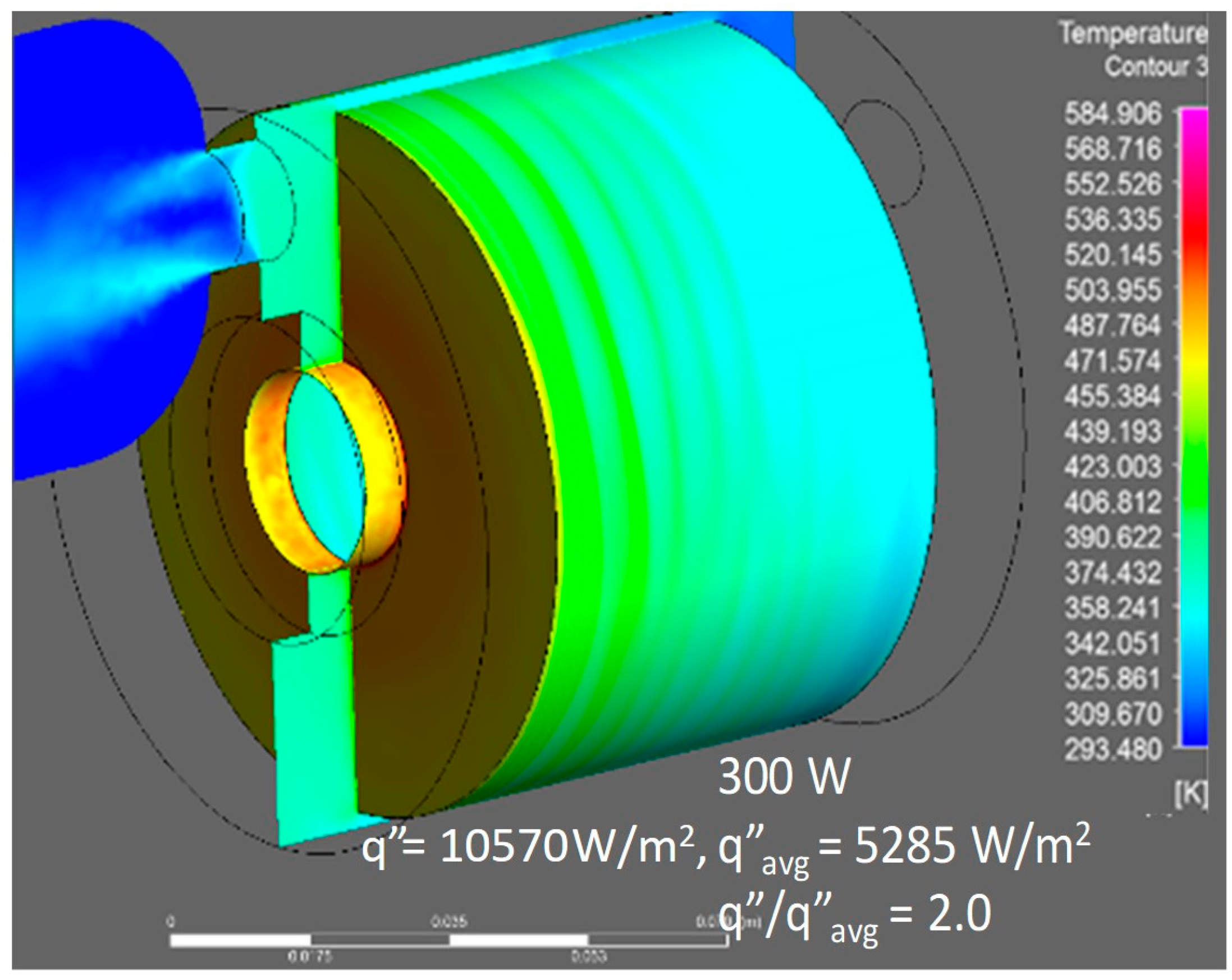
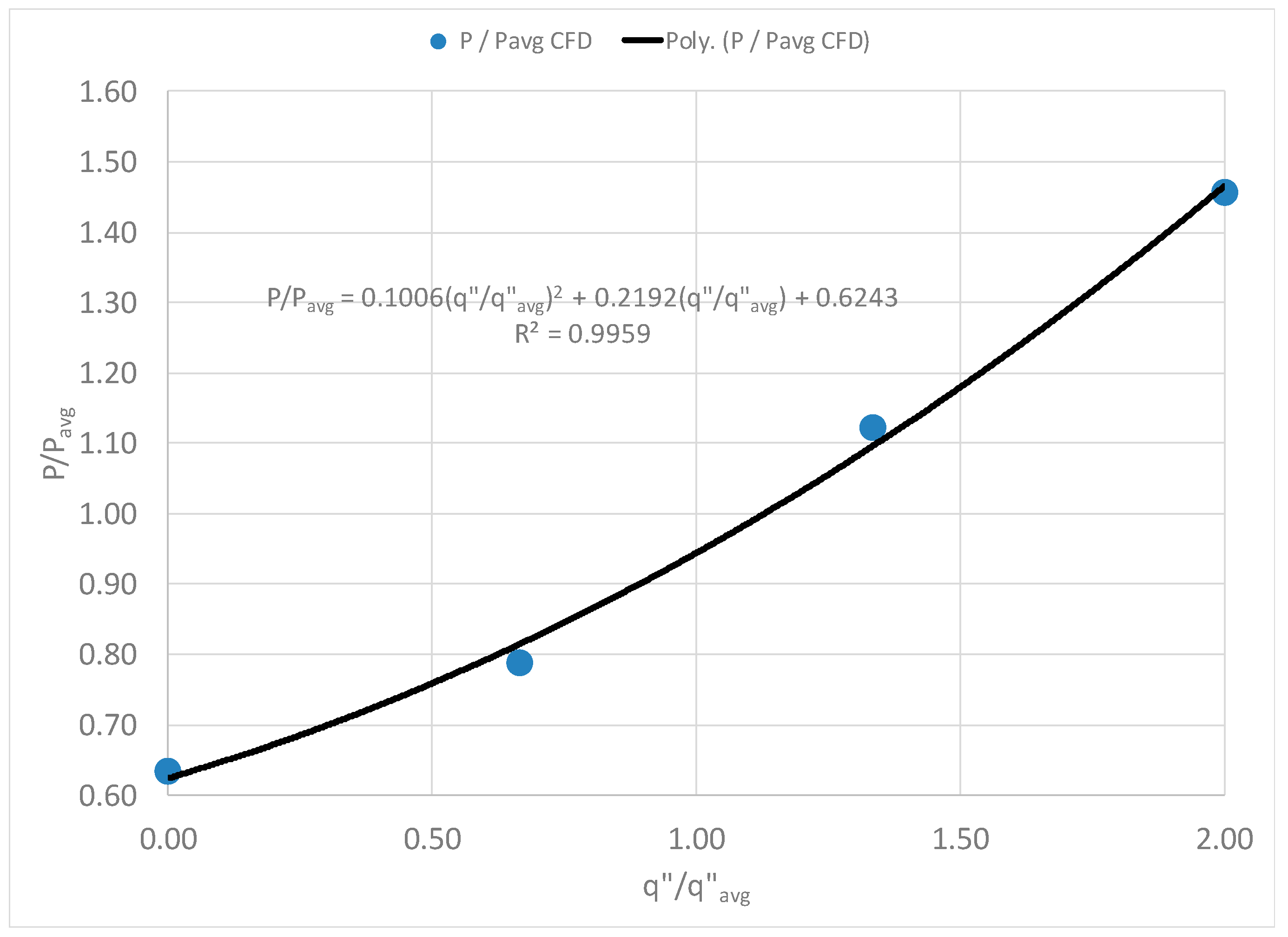
3.3. Rotor Parasitic Heat Loss Study
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Asami, F.; Miyatake, M.; Yoshimoto, S.; Tanaka, E.; Yamauchi, T. A method of reducing windage power loss of a high-speed motor using a viscous vacuum pump. Precis. Eng. 2017, 48, 60–66. [Google Scholar] [CrossRef]
- Okada, Y.; Kosaka, T.; Matsui, N. Windage Loss Reduction for Hybrid Excitation Flux Switching Motors Based on Rotor Structure Design. In Proceedings of the Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017. [Google Scholar] [CrossRef]
- Pfister, P.D.; Perriard, Y. A 200,000 RPM, 2 kW Slot-less Permanent Magnet Motor. In Proceedings of the 2008 International Conference on Electrical Machines and Systems (ICEMS), Wuhan, China, 17–20 October 2008. [Google Scholar]
- Awad, M.N.; Martin, W.J. Windage Loss Reduction Study for TFTR Pulse Generator. In Proceedings of the 17th IEEE/NPSS Symposium on Fusion Engineering, San Diego, CA, USA, 6–10 October 1997. [Google Scholar] [CrossRef]
- Seelig, T.; Harlander, U.; Kielczewski, K.; Tuliszka-Sznitko, E.; Bontoux, P.; Egbers, C. Study of Transitional and Turbulent Flows in Rotor/Stator Cavities. In Proceedings of the 19th International Couette-Taylor Workshop, Cottbus, Germany, 24–26 June 2015. [Google Scholar]
- Yu, J.S.; Cho, H.W.; Choi, J.Y.; Jang, S.M.; Lee, S.H. Stator and rotor shape optimum design of brushless permanent magnet motor for automotive cooling device. In Proceedings of the 2012 IEEE Vehicle Power and Propulsion Conference (VPPC), Seoul, Korea, 9–12 October 2012; pp. 238–243. [Google Scholar] [CrossRef]
- Lee, K.H.; Cha, H.R.; Kim, Y.B. Development of an interior permanent magnet motor through rotor cooling for electric vehicles. Appl. Therm. Eng. 2016, 95, 348–356. [Google Scholar] [CrossRef]
- Kolondzovski, Z. Determination of critical thermal operations for high-speed permanent magnet electrical machines. Int. J. Comput. Math. Electr. Electron. Eng. 2008, 27, 720–727. [Google Scholar] [CrossRef]
- Kim, C.; Lee, K.S.; Yook, S.J. Effect of air-gap fans on cooling of windings in a large-capacity, high-speed induction motor. Appl. Therm. Eng. 2016, 100, 658–667. [Google Scholar] [CrossRef]
- Anderson, K.; Lin, J.; McNamara, C.; Magri, V. CFD study of forced air cooling and windage losses in a high speed electric motor. J. Electron. Cool. Therm. Control 2015, 5, 27–44. [Google Scholar] [CrossRef]
- Kline, S.A.; McClintock, F.A. Describing uncertainties in single-sample experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Concli, F. Pressure distribution in small hydrodynamic journal bearings considering cavitation: A numerical approach based on the open-source CFD code OpenFOAM®. Lubr. Sci. 2016, 28, 329–347. [Google Scholar] [CrossRef]
- Concli, F. Thermal and efficiency characterization of a low-backlash planetary gearbox: An integrated numerical-analytical prediction model and its experimental validation. Proc. Inst. Mech. Eng. Part J J. Eng. Tribol. 2016, 230, 996–1005. [Google Scholar] [CrossRef]
- ANSYS Fluent User Manuals; V14. 0 ANSYS. ANSYS Inc.: Cannosburg, PA, USA, 2012. Available online: https://www.ansys.com/Products/Fluids/ANSYS-Fluent (accessed on 13 March 2018).
- Anderson, K.R. CFD Analysis of Inlet and Outlet Regions of Coolant Channels in an Advanced Hydrocarbon Engine Nozzle. In Proceedings of the 15th Annual Thermal and Fluids Analysis Workshop (TFAWS-04), Pasadena, CA, USA, 30 August–3 September 2004. [Google Scholar]
- Concli, F.; Gorla, C.; Della Torre, A.; Montenegro, G. Churning power losses of ordinary gears: A new approach based on the internal fluid dynamics simulations. Lubr. Sci. 2015, 27, 313–326. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1935. [Google Scholar]
- Dixon, S.L. Turbomachinery; Pergamon Press: Oxford, UK, 1975. [Google Scholar]









© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, K.R.; Lin, J.; Wong, A. Experimental and Numerical Study of Windage Losses in the Narrow Gap Region of a High-Speed Electric Motor. Fluids 2018, 3, 22. https://doi.org/10.3390/fluids3010022
Anderson KR, Lin J, Wong A. Experimental and Numerical Study of Windage Losses in the Narrow Gap Region of a High-Speed Electric Motor. Fluids. 2018; 3(1):22. https://doi.org/10.3390/fluids3010022
Chicago/Turabian StyleAnderson, Kevin R., Jun Lin, and Alexander Wong. 2018. "Experimental and Numerical Study of Windage Losses in the Narrow Gap Region of a High-Speed Electric Motor" Fluids 3, no. 1: 22. https://doi.org/10.3390/fluids3010022
APA StyleAnderson, K. R., Lin, J., & Wong, A. (2018). Experimental and Numerical Study of Windage Losses in the Narrow Gap Region of a High-Speed Electric Motor. Fluids, 3(1), 22. https://doi.org/10.3390/fluids3010022