Extended Noble–Abel Stiffened-Gas Equation of State for Sub-and-Supercritical Liquid-Gas Systems Far from the Critical Point
Abstract
1. Introduction
- -
- The first and certainly the most obvious and limiting is related to its inability to deal with liquid and non-condensable gas separated by well-defined interfaces, such as for example interfacial flows of liquid water and air. The thermodynamics of these two media being considered as discontinuous, specific theoretical and numerical treatments have been addressed. In this context, Arbitrary Lagrangian Eulerian (Hirt et al. [2]), Interface Reconstruction (Youngs [3]), Front Tracking (Glimm et al. [4]), Level-Set (Fedkiw et al. [5]), anti-diffusion (Kokh and Lagoutiere [6]) methods are possible options. Another approach relies on continuous models with extra internal variables, such as volume and mass fractions and extended equation of state. Examples of such models are the Kapila et al. [7] one and its extension with phase transition (Saurel et al. [8]) to cite a few. With these formulations, the same equations are solved everywhere routinely, in pure liquid, pure gas and interface which becomes a diffuse zone. These models are indeed often named “diffuse interface methods” (Saurel and Pantano [9]). In this approach, hyperbolic models with relaxation are considered and each phase evolves in its own volume, with its own thermodynamics. In particular, there is no need to address cubic formulations. When phase transition is addressed, it occurs through mass transfer terms that can be considered finite rate (Saurel et al. [8], Furfaro and Saurel [10]) or assumed stiff when the physical knowledge of the phase change kinetics is not enough documented (Le Métayer et al. [11], Chiapolino et al. [12,13]) or unnecessary.
- -
- The second limitation is related to the lack of convexity of cubic EOSs, having dramatic consequences on sound propagation during phase transition. The square sound speed becomes negative in the spinodal decomposition zone, such behavior not being physical.
- -
- The third limitation is related to the description of phase transition with such EOSs. Cubic equations of state consider phase transition as a thermodynamic process and not a kinetic one. It is unclear at this level whether cubic EOSs are limited to the description of global two-phase mixtures with many interfaces and not local ones, at the scale of a single interface.
- -
- The fourth, but possibly not the last, is related to the numerical treatment of boundary conditions (BC) in practical compressible flow computations. Subsonic inflow and outflow BCs rely on stagnation enthalpy and entropy invariance coupled to Riemann invariants that can be defined and computed correctly only if the equation of state is well-posed. The second issue related to EOS convexity consequently reemerges at this level. Moreover, the practical expression of Riemann invariants may be inextricable with these EOSs.
- -
- Represent the thermodynamics of pure liquid, pure vapor and supercritical fluid. Combination of the pure liquid and pure vapor EOSs must be able to represent as accurately as possible the two-phase region.
- -
- Each phase EOS must be convex in its respective domain.
- -
- The EOS must be as simple as possible, while remaining accurate, to simplify practical computations and building of mixture EOS in hyperbolic multiphase flow models.
2. Extended NASG EOS
2.1. Thermal and Caloric EOSs
2.2. Expression of the Entropy
2.3. Speed of Sound
3. Saturation Condition of the Liquid–Vapor Couple
4. Summary of the Extended NASG State Functions
5. Extended NASG Parameters
6. Transition to Supercritical Fluids
6.1. Liquid-to-Supercritical-State Transition
6.2. Vapor-to-Supercritical-State Transition
6.3. Concluding Remarks
7. Two-Phase Flow Illustrations
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Convexity of the ENASG Formulation
Appendix B. Maxwell’s Relations
Appendix C. Methodology to Determine the Various Extended NASG (ENASG) Parameters
Appendix C.1. Liquid Phase
| Fluid | N | (K) | (bar) | (m/kg) | (Pa) | (m/kg) | (m/s) | (bar) | (m/kg) |
|---|---|---|---|---|---|---|---|---|---|
| HO | 374 | 221 | 1 | ||||||
| O | 101 | 50 | 1 |
| Fluid | (K) | (Pa) | (m/kg) | (kJ/kg) | (m/kg) |
|---|---|---|---|---|---|
| HO | |||||
| O |
Appendix C.2. Gas Phase
Appendix D. Connection Temperature between the ENASG EOS and Ideal Gas Formulation
Appendix E. Toward the Critical Point
| Coefficients | ENASG | ENASG | ENASG | ENASG |
|---|---|---|---|---|
| (J/kg/K) | 3848 | 1719 | 1451 | 779 |
| 0 | 0 | |||
| (m/kg) | 0 | |||
| (Pa/K) | − 607,195 | 0 | −405,133 | 0 |
| (Pa) | 396,642,530 | 0 | 63,642,939 | 0 |
| q (J/kg) | −1,065,948 | 1,975,421 | −272,675 | |
| (J/kg/K) | −20,985 | 2224 | ||
| d (Pa m/kg) | 0 | 41,200 | 0 | 2950 |

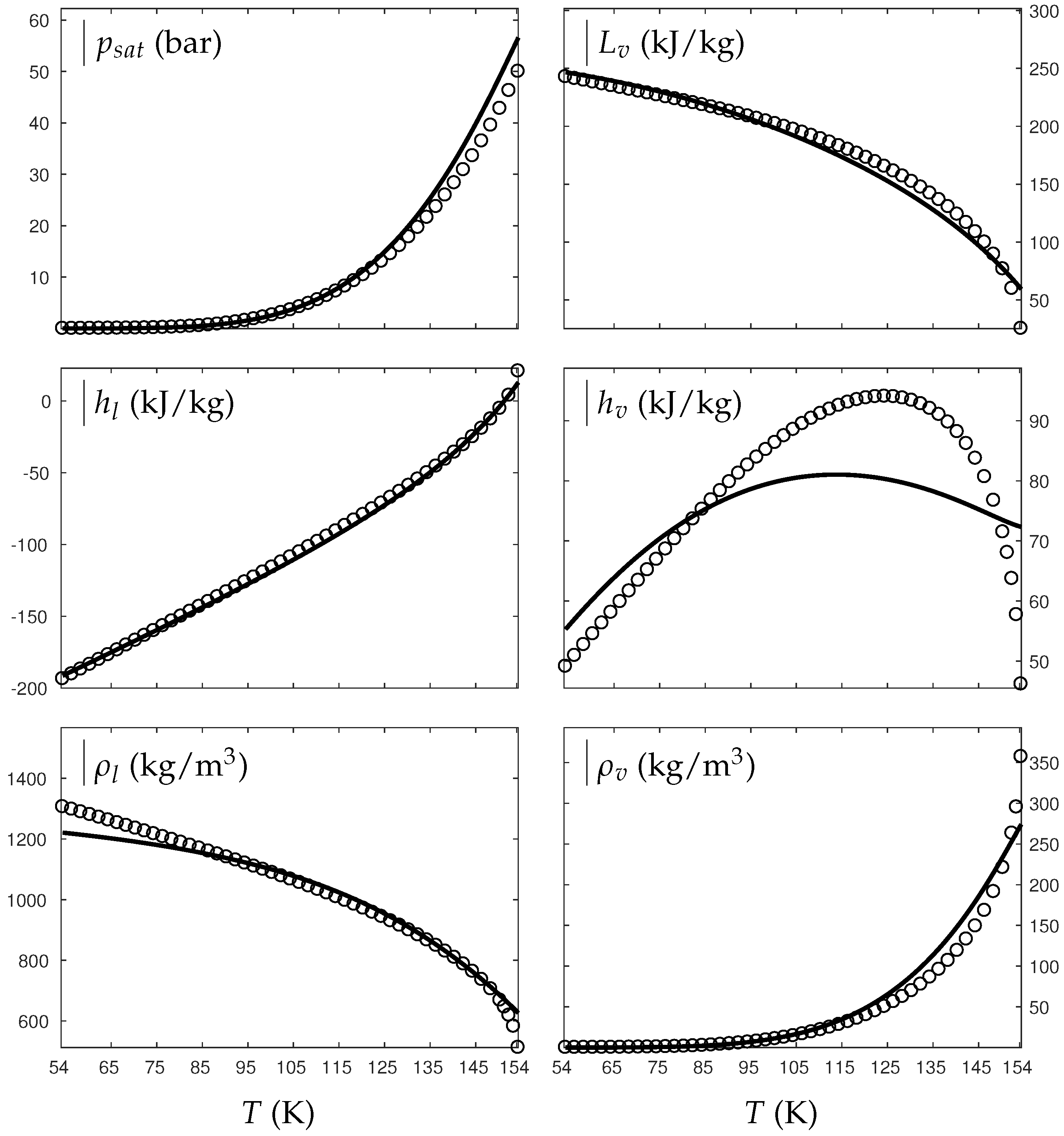
References
- Cahn, J.; Hilliard, J. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Hirt, C.; Anthony, A.; Cook, J. An arbitrary Lagrangian-Eulerian computing method for all flow speeds. J. Comput. Phys. 1974, 14, 227–253. [Google Scholar] [CrossRef]
- Youngs, D. An interface tracking method for a 3D Eulerian hydrodynamics code. In Atomic Weapons Research Establishment; Technical Report; AWRE 1984; p. 35, AWE Aldermaston (UK).
- Glimm, J.; Grove, J.; Li, X.; Shyue, K.; Zeng, Y.; Zhang, Q. Three-dimensional front tracking. SIAM J. Sci. Comput. 1998, 19, 703–727. [Google Scholar] [CrossRef]
- Fedkiw, R.; Aslam, T.; Merriman, B.; Osher, S. A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the Ghost Fluid Method). J. Comput. Phys. 1999, 152, 457–492. [Google Scholar] [CrossRef]
- Kokh, S.; Lagoutiere, F. An anti-diffusive numerical scheme for the simulation of interfaces between compressible fluids by means of a five-equation model. J. Comput. Phys. 2010, 229, 2773–2809. [Google Scholar] [CrossRef]
- Kapila, A.; Menikoff, R.; Bdzil, J.; Son, S.; Stewart, D. Two-phase modeling of deflagration-to-detonation transition in granular materials: Reduced equations. Phys. Fluids 2001, 13, 3002–3024. [Google Scholar] [CrossRef]
- Saurel, R.; Petitpas, F.; Abgrall, R. Modelling phase transition in metastable liquids: application to cavitating and flashing flows. J. Fluid Mech. 2008, 607, 313–350. [Google Scholar] [CrossRef]
- Saurel, R.; Pantano, C. Diffuse Interfaces and Capturing Methods in Compressible Two-Phase Flows. Ann. Rev. Fluid Mech. 2018, 50, 105–130. [Google Scholar] [CrossRef]
- Furfaro, D.; Saurel, R. Modeling droplet phase change in the presence of a multi-component gas mixture. Appl. Math. Comput. 2016, 272, 518–541. [Google Scholar] [CrossRef]
- Le Métayer, O.; Massoni, J.; Saurel, R. Dynamic relaxation processes in compressible multiphase flows. Application to evaporation phenomena. ESAIM Proc. 2013, 40, 103–123. [Google Scholar] [CrossRef]
- Chiapolino, A.; Boivin, P.; Saurel, R. A simple phase transition relaxation solver for liquid–vapor flows. Int. J. Numer. Methods Fluids 2017, 83, 583–605. [Google Scholar] [CrossRef]
- Chiapolino, A.; Boivin, P.; Saurel, R. A simple and fast phase transition relaxation solver for compressible multicomponent two-phase flows. Comput. Fluids 2017, 150, 31–45. [Google Scholar] [CrossRef]
- Le Métayer, O.; Saurel, R. The Noble-Abel Stiffened-Gas equation of state. Phys. Fluids 2016, 28, 046102. [Google Scholar] [CrossRef]
- Chiapolino, A.; Saurel, R.; Nkonga, B. Sharpening diffuse interfaces with compressible fluids on unstructured meshes. J. Comput. Phys. 2017, 340, 389–417. [Google Scholar] [CrossRef]
- Petitpas, F.; Saurel, R.; Franquet, E.; Chinnayya, A. Modelling detonation waves in condensed energetic materials: Multiphase CJ conditions and multidimensional computations. Shock Waves 2009, 19, 377–401. [Google Scholar] [CrossRef]
- Saurel, R.; Boivin, P.; Le Métayer, O. A general formulation for cavitating, boiling and evaporating flows. Comput. Fluids 2016, 128, 53–64. [Google Scholar] [CrossRef]
- Perigaud, G.; Saurel, R. A compressible flow model with capillary effects. J. Comput. Phys. 2005, 209, 139–178. [Google Scholar] [CrossRef]
- Favrie, N.; Gavrilyuk, S.; Saurel, R. Solid–fluid diffuse interface model in cases of extreme deformations. J. Comput. Phys. 2009, 228, 6037–6077. [Google Scholar] [CrossRef]
- Ndanou, S.; Favrie, N.; Gavrilyuk, S. Multi-solid and multi-fluid diffuse interface model: Applications to dynamic fracture and fragmentation. J. Comput. Phys. 2015, 295, 523–555. [Google Scholar] [CrossRef]
- Saurel, R.; Chinnayya, A.; Carmouze, Q. Modelling compressible dense and dilute two-phase flows. Phys. Fluids 2017, 29, 063301. [Google Scholar] [CrossRef]
- Chiapolino, A.; Saurel, R. Models and methods for two-layer shallow water flows. J. Comput. Phys. 2018. [Google Scholar] [CrossRef]
- Le Métayer, O.; Massoni, J.; Saurel, R. Elaborating equations of state of a liquid and its vapor for two-phase flow models; Élaboration des lois d’état d’un liquide et de sa vapeur pour les modèles d’écoulements diphasiques. Int. J. Therm. Sci. 2004, 43, 265–276. [Google Scholar] [CrossRef]
- Plohr, B. Shockless acceleration of thin plates modeled by a tracked random choice method. AIAA J. 1988, 26, 470–478. [Google Scholar] [CrossRef]
- Menikoff, R.; Plohr, B. The Riemann problem for fluid flow of real materials. Rev. Mod. Phys. 1989, 61, 75. [Google Scholar] [CrossRef]
- Cocchi, J.; Saurel, R. A Riemann problem based method for the resolution of compressible multimaterial flows. J. Comput. Phys. 1997, 137, 265–298. [Google Scholar] [CrossRef]
- Toro, E. Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction; Springer Science & Business Media: Berlin, Germany, 1997. [Google Scholar]
- McBride, B.; Gordon, S.; Reno, M. Coefficients for Calculating Thermodynamic and Transport Properties of Individual Species; Technical Report; NASA Technical Memorandum 4513; NASA Lewis Research Center: Cleveland, OH, USA, 1993.
- Van der Waals, J.; Rowlinson, J. J.D van der Waals: On the Continuity of the Gaseous and Liquid States; North Holland: Amsterdam, The Netherlands, 1988; Volume 14. [Google Scholar]
- Soave, G. Equilibrium constants from a modified Redlich-Kwong equation of state. Chem. Eng. Sci. 1972, 27, 1197–1203. [Google Scholar] [CrossRef]
- Wei, Y.; Sadus, R. Equations of state for the calculation of fluid-phase equilibria. AIChE J. 2000, 46, 169–196. [Google Scholar] [CrossRef]
- Downar-Zapolski, P.; Bilicki, Z.; Bolle, L.; Franco, J. The non-equilibrium relaxation model for one-dimensional flashing liquid flow. Int. J. Multiph. Flow 1996, 22, 473–483. [Google Scholar] [CrossRef]
- Godunov, S.; Platonov, V. Résolution Numérique des Problèmes Multidimensionnels de la Dynamique des Gaz (in French); Mir Publishers: Moscou, Russia, 1979. [Google Scholar]
- Callen, H.B. Thermodynamics: An Introduction to the Physical Theories of Equilibrium Thermostatics and Irreversible Thermodynamics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1960. [Google Scholar]
- NIST Chemistry WebBook. Available online: http://webbook.nist.gov/chemistry/ (accessed on 10 July 2018).












| Coefficients | ENASG | ENASG | NASG | NASG |
|---|---|---|---|---|
| (J/kg/K) | 4014 | 1500 | 3630 | 856 |
| 0 | 0 | 0 | ||
| (m/kg) | 0 | 0 | ||
| (Pa/K) | −471,025 | 0 | 0 | 0 |
| (Pa) | 307,078,403 | 0 | 664,961,465 | 0 |
| q (J/kg) | −1,112,426 | 1,947,630 | −1,178,154 | 2,176,064 |
| (J/kg/K) | −22,049 | 1136 | −10,742 | 4863 |
| Coefficients | ENASG | ENASG | NASG | NASG |
|---|---|---|---|---|
| (J/kg/K) | 1535 | 652 | 1016 | 548 |
| 0 | 0 | 0 | ||
| (m/kg) | 0 | 0 | ||
| (Pa/K) | −324,997 | 0 | 0 | 0 |
| (Pa) | 50,890,107 | 0 | 196,815,802 | 0 |
| q (J/kg) | −278,134 | −285,545 | 6528 | |
| (J/kg/K) | 4237 | 8171 | 4650 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chiapolino, A.; Saurel, R. Extended Noble–Abel Stiffened-Gas Equation of State for Sub-and-Supercritical Liquid-Gas Systems Far from the Critical Point. Fluids 2018, 3, 48. https://doi.org/10.3390/fluids3030048
Chiapolino A, Saurel R. Extended Noble–Abel Stiffened-Gas Equation of State for Sub-and-Supercritical Liquid-Gas Systems Far from the Critical Point. Fluids. 2018; 3(3):48. https://doi.org/10.3390/fluids3030048
Chicago/Turabian StyleChiapolino, Alexandre, and Richard Saurel. 2018. "Extended Noble–Abel Stiffened-Gas Equation of State for Sub-and-Supercritical Liquid-Gas Systems Far from the Critical Point" Fluids 3, no. 3: 48. https://doi.org/10.3390/fluids3030048
APA StyleChiapolino, A., & Saurel, R. (2018). Extended Noble–Abel Stiffened-Gas Equation of State for Sub-and-Supercritical Liquid-Gas Systems Far from the Critical Point. Fluids, 3(3), 48. https://doi.org/10.3390/fluids3030048




