Linear Stability Analysis of Liquid Metal Flow in an Insulating Rectangular Duct under External Uniform Magnetic Field
Abstract
:1. Introduction
2. Configuration of Problem and Governing Equations
3. Basic State and Disturbance Equations
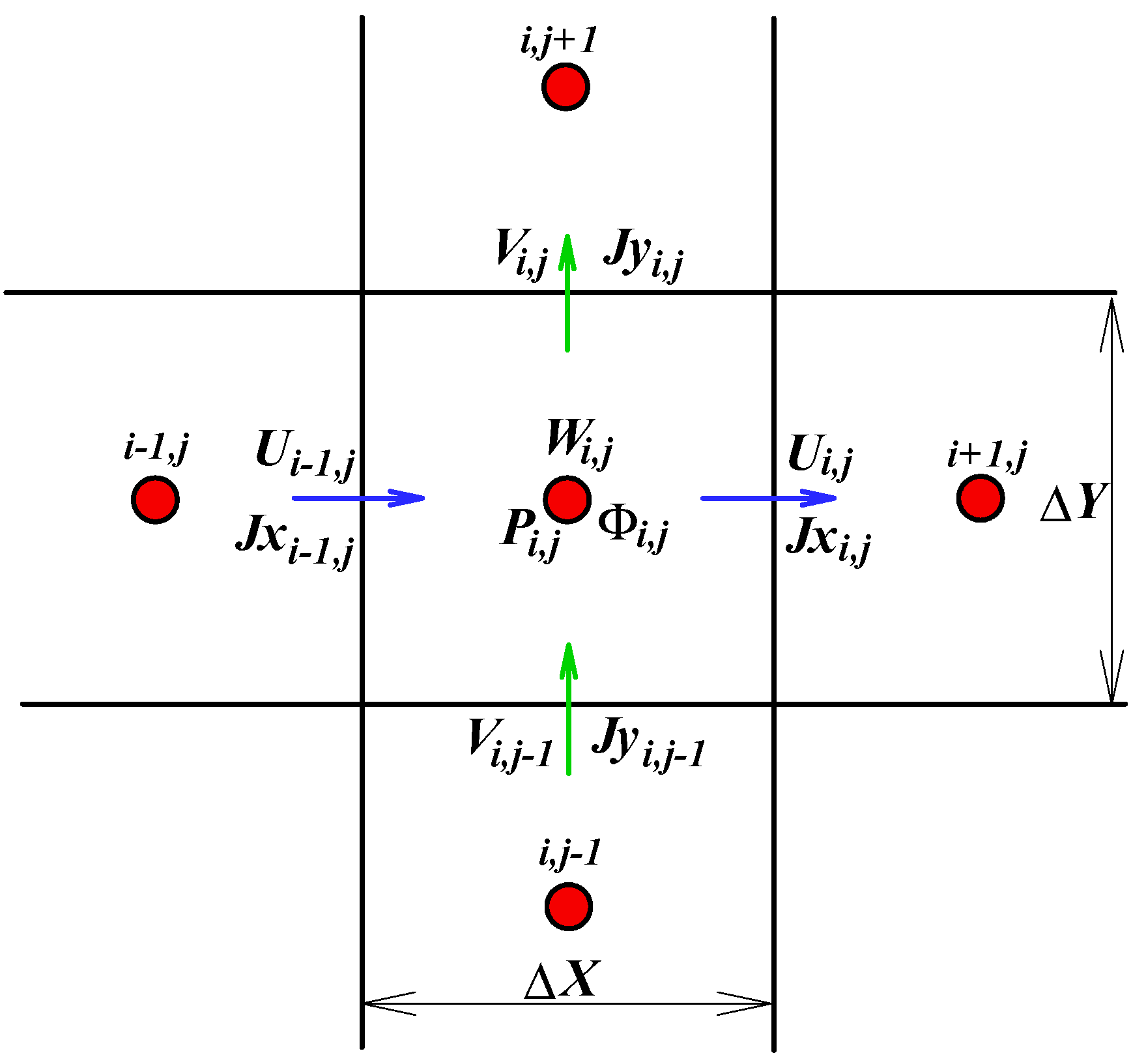
4. Numerical Methodology
5. Results and Discussion
5.1. Validation of the Code Diveloped
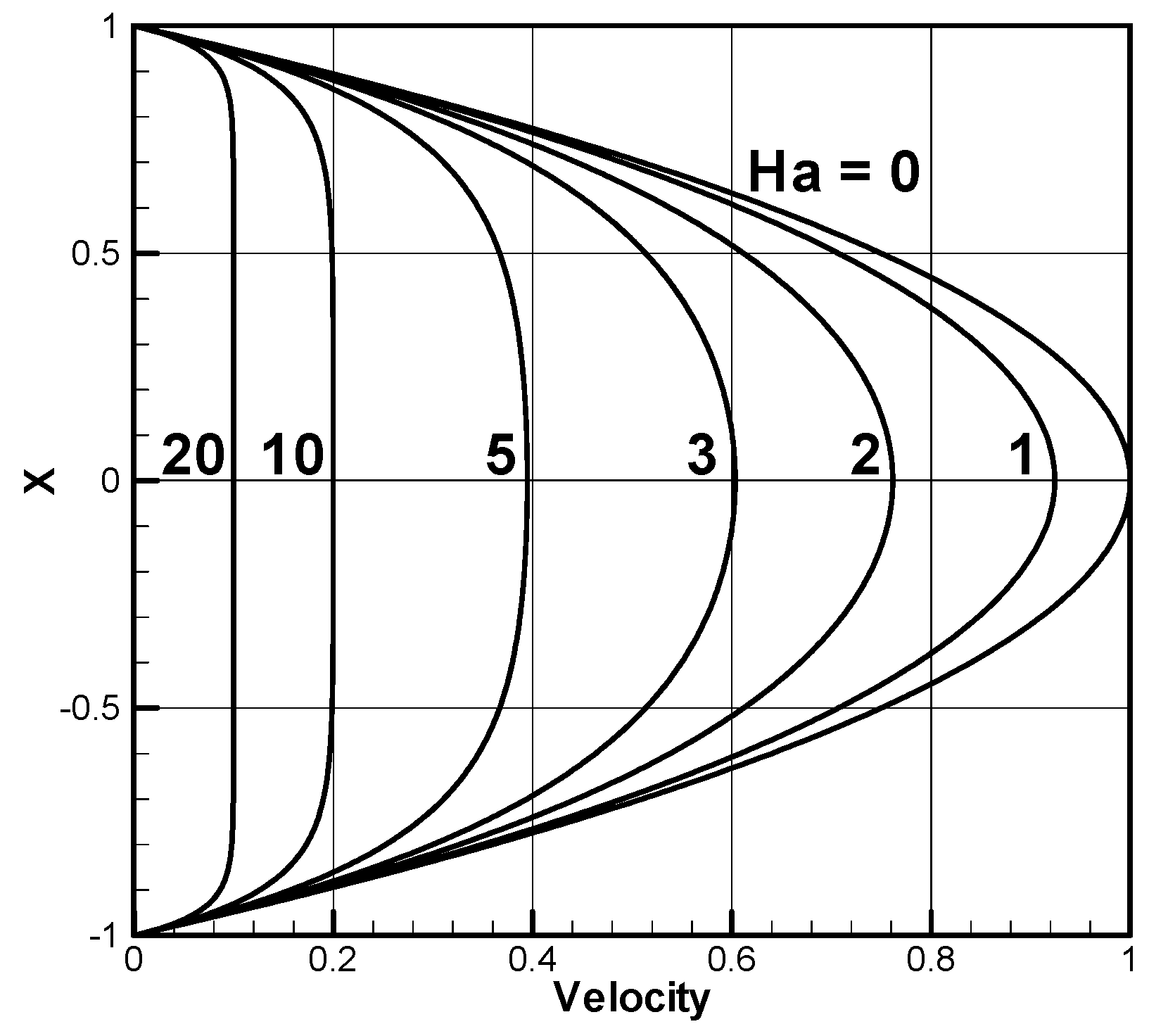
5.2. Hartmann Flow
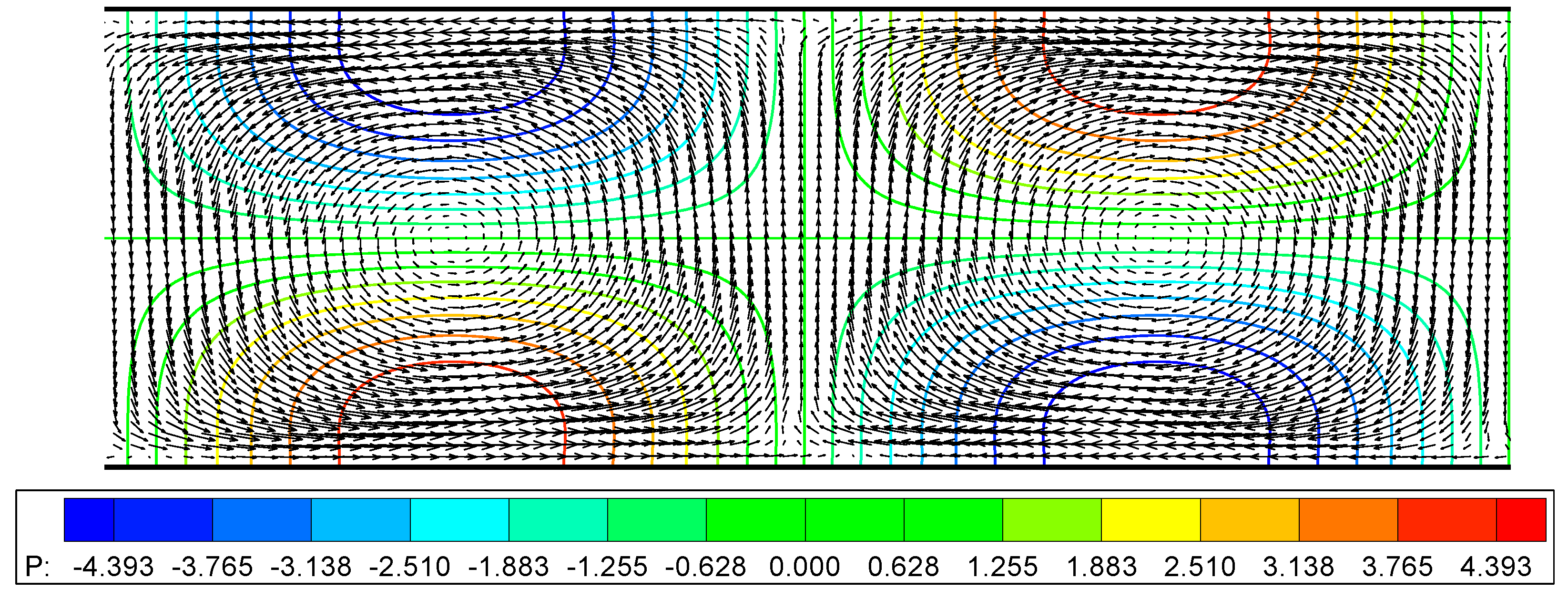
5.3. Finite Aspect Ratio
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | half spanwise length of duct (m) |
| A | aspect ratio = a/h (-) |
| b | magnetic flux density = (bx, by, 0) (T) |
| B | dimensionless magnetic flux density = b/ b0 = (BX, BY, 0) (-) |
| b0 | strength of external magnetic flux density = (bx2+ by2)1/2 (T) |
| C | coefficient of Newton—Raphson method |
| E | Electric field (V/m) |
| ex | unit vector in x direction (-) |
| ey | unit vector in y direction (-) |
| h | half length of duct height (m) |
| Ha | Hartmann number = b0h (σ/μ)1/2 (-) |
| i | imaginary unit (-) |
| j | electric current density = (jx, jy, jz) (A/m2) |
| J | dimensionless electric current density = (JX, JY, JZ) (-) |
| k | wavenumber in streamwise direction (rad/m) |
| p | pressure (Pa) |
| P | dimensionless pressure (-) |
| Prm | magnetic Prandtl number = σμmν = ν/νm (-) |
| Re | Reynolds number = uref h/ν (-) |
| Rem | magnetic Reynolds number = uref h/νm = PrmRe (-) |
| s | complex angular frequency = sr + isi (rad/s) |
| S | dimensionless complex angular frequency = SR + iSI (-) |
| SI | dimensionless angular frequency (-) |
| SR | dimensionless linear growth rate (-) |
| t | time (s) |
| u | x-directional velocity component (m/s) |
| u | velocity vector = (u, v, w) (m/s) |
| uref | reference velocity (m/s) |
| U | dimensionless x-directional velocity component = u/uref (-) |
| v | y-directional velocity component (m/s) |
| V | dimensionless y-directional velocity component = v/uref (-) |
| w | z-directional velocity component (m/s) |
| W | dimensionless z-directional velocity component = w/uref (-) |
| z | z coordinate (m) |
| Z | dimensionless z coordinate = z/h (-) |
| Greek symbols | |
| α | dimensionless wavenumber = kh (-) |
| μ | viscosity (Pa·s) |
| μm | magnetic permeability (H/m) |
| ν | kinematic viscosity = μ/ρ (m2/s) |
| νm | magnetic viscosity = 1/(σμm) (m2/s) |
| ρ | density (kg/m3) |
| σ | electric conductivity (1/(Ω·m)) |
| τ | dimensionless time (-) |
| φ | electric potential (V) |
| Φ | dimensionless electric potential (-) |
| Ψ | dimensionless stream function (-) |
| Subscripts or superscripts | |
| arb | arbitrary point |
| int | interpolation |
| c | critical |
| I | imaginary part |
| R | real part |
| i,j | grid point |
| n | time step |
| m | number of iteration |
| * | predictive |
| perturbed | |
| – | basic |
| ~ | complex amplitude |
Appendix A
Appendix A.1. Basic State
Appendix A.2. How to Solve the Eigenvalue Problem
Appendix A.3. How to Obtain Neutral Curve

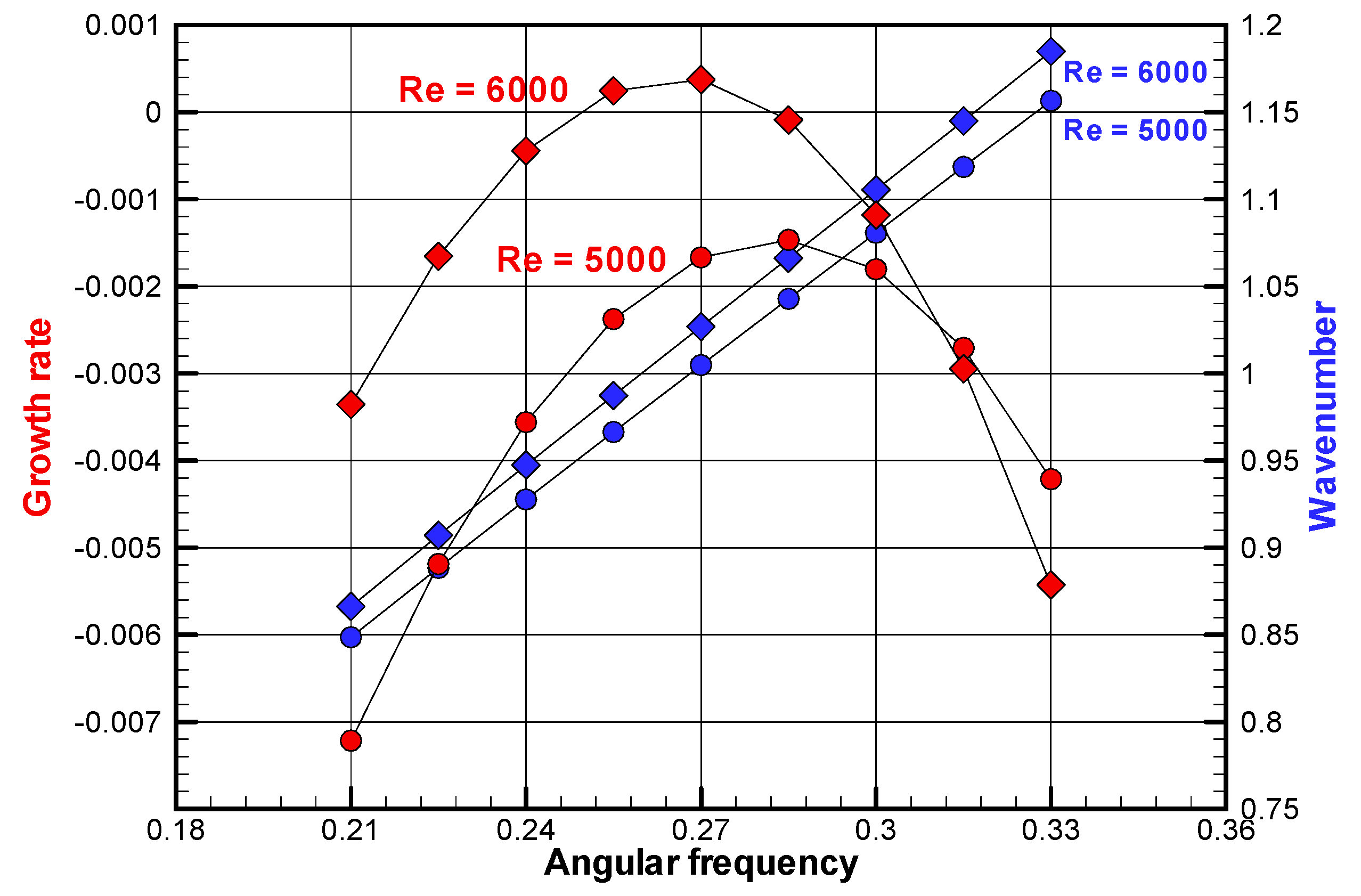
Appendix A.4. How to Determine Critical Point
References
- Moreau, R.J. Magnetohydrodynamics; Fluid Mechanics and Its Application; Kluwer Academic Publishers: Dordrecht, The Netherlands; Norwell, MA, USA, 1990; Volume 3. [Google Scholar]
- Ozoe, H. Magnetic Convection; Imperial College Press: London, UK, 2005. [Google Scholar]
- Molokov, S.; Moreau, R.; Moffatt, H.K. Magnetohydrodynamics: Historical Evolution and Trends; Fluid Mechanics and Its Application; Springer: Berlin/Heidelberg, Germany, 2007; Volume 80. [Google Scholar]
- Müller, U.; Bühler, L. Magnetofluiddynamics in Channels and Containers; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Moreau, R.; Molokov, S. Julius Hartmann and his followers: A review on the properties of the Hartmann layer. In Magnetohydrodynamics; Springer: Berlin/Heidelberg, Germany, 2007; pp. 155–170. [Google Scholar]
- Ueno, K. Inertia effect in two-dimensional MHD channel flow under a traveling sine wave magnetic field. Phys. Fluids A Fluid Dyn. 1991, 3, 3107–3116. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Dover Publication: Mineola, NY, USA, 1961. [Google Scholar]
- Stuart, J.T. On the stability of viscous flow between parallel planes in the presence of a co-planar magnetic field. Proc. R. Soc. Lond. Series A Math. Phys. Sci. 1954, 221, 189–206. [Google Scholar] [CrossRef]
- Lock, R.C. The stability of the flow of an electrically conducting fluid between parallel planes under a transverse magnetic field. Proc. R. Soc. Lond. Series A Math. Phys. Sci. 1955, 233, 105–125. [Google Scholar] [CrossRef]
- Takashima, M. The stability of the modified plane Poiseuille flow in the presence of a transverse magnetic field. Fluid Dyn. Res. 1996, 17, 293. [Google Scholar] [CrossRef]
- Tatsumi, T.; Yoshimura, T. Stability of the laminar flow in a rectangular duct. J. Fluid Mech. 1990, 212, 437–449. [Google Scholar] [CrossRef]
- Adachi, T. Linear stability of flow in rectangular ducts in the vicinity of the critical aspect ratio. Eur. J. Mech. B Fluids 2013, 41, 163–168. [Google Scholar] [CrossRef]
- Airiau, C.; Castets, M. On the amplification of small disturbances in a channel flow with a normal magnetic field. Phys. Fluids 2004, 16, 2991–3005. [Google Scholar] [CrossRef]
- Krasnov, D.S.; Zienicke, E.; Zikanov, O.; Boeck, T.; Thess, A. Numerical study of the instability of the Hartmann layer. J. Fluid Mech. 2004, 504, 183–211. [Google Scholar] [CrossRef] [Green Version]
- Krasnov, D.; Zikanov, O.; Rossi, M.; Boeck, T. Optimal linear growth in magnetohydrodynamic duct flow. J. Fluid Mech. 2010, 653, 273–299. [Google Scholar] [CrossRef]
- Dong, S.; Liu, L.; Ye, X. Linear stability analysis of magnetohydrodynamic duct flows with perfectly conducting walls. PLoS ONE 2017, 12, e0186944. [Google Scholar] [CrossRef]
- Dong, S.; Liu, L.S.; Ye, X.M. Instability of MHD Flow in the Duct with Electrically Perfectly Conducting Walls. J. Appl. Fluid Mech. 2017, 10, 1293–1304. [Google Scholar] [CrossRef]
- Tagawa, T.; Ozoe, H. Enhancement of heat transfer rate by application of a static magnetic field during natural convection of liquid metal in a cube. J. Heat Transf. 1997, 119, 265–271. [Google Scholar] [CrossRef]
- Tagawa, T.; Ozoe, H. Enhanced heat transfer rate measured for natural convection in liquid gallium in a cubical enclosure under a static magnetic field. J. Heat Transf. 1998, 120, 1027–1032. [Google Scholar] [CrossRef]
- Authié, G.; Tagawa, T.; Moreau, R. Buoyant flow in long vertical enclosures in the presence of a strong horizontal magnetic field. Part 2. Finite enclosures. Eur. J. Mech. B Fluids 2003, 22, 203–220. [Google Scholar] [CrossRef]
- Pothérat, A. Quasi-two-dimensional perturbations in duct flows under transverse magnetic field. Phys. Fluids 2007, 19, 074104. [Google Scholar] [CrossRef]
- Sommeria, J.; Moreau, R. Why, how, and when, MHD turbulence becomes two-dimensional. J. Fluid Mech. 1982, 118, 507–518. [Google Scholar] [CrossRef]
- Vo, T.; Pothérat, A.; Sheard, G.J. Linear stability of horizontal, laminar fully developed, quasi-two-dimensional liquid metal duct flow under a transverse magnetic field and heated from below. Phys. Rev. Fluids 2017, 2, 033902. [Google Scholar] [CrossRef]
- Priede, J.; Aleksandrova, S.; Molokov, S. Linear stability of Hunt’s flow. J. Fluid Mech. 2010, 649, 115–134. [Google Scholar] [CrossRef]
- Priede, J.; Aleksandrova, S.; Molokov, S. Linear stability of magnetohydrodynamic flow in a perfectly conducting rectangular duct. J. Fluid Mech. 2012, 708, 111–127. [Google Scholar] [CrossRef] [Green Version]
- Priede, J.; Arlt, T.; Bühler, L. Linear stability of magnetohydrodynamic flow in a square duct with thin conducting walls. J. Fluid Mech. 2016, 788, 129–146. [Google Scholar] [CrossRef]
- Arlt, T.; Priede, J.; Bühler, L. The effect of finite-conductivity Hartmann walls on the linear stability of Hunt’s flow. J. Fluid Mech. 2017, 822, 880–891. [Google Scholar] [CrossRef]
- Bühler, L.; Arlt, T.; Boeck, T.; Braiden, L.; Chowdhury, V.; Krasnov, D.; Mistrangelo, C.; Molokov, S.; Priede, J. Magnetically induced instabilities in duct flows. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2017; Volume 228, p. 012003. [Google Scholar]
- Hunt, J.C.R. Magnetohydrodynamic flow in rectangular ducts. J. Fluid Mech. 1965, 21, 577–590. [Google Scholar] [CrossRef]
- Qi, T.Y.; Liu, C.; Ni, M.J.; Yang, J.C. The linear stability of Hunt-Rayleigh-Bénard flow. Phys. Fluids 2017, 29, 064103. [Google Scholar] [CrossRef] [PubMed]
- Tagawa, T. Linear stability of parallel flow of liquid metal in a rectangular duct driven by a constant pressure gradient under the influence of a uniform magnetic field. In IOP Conference Series: Materials Science and Engineering; IOP Publishing: Bristol, UK, 2018; Volume 424, p. 012016. [Google Scholar]
- Tagawa, T.; Song, K. Stability of an axisymmetric liquid metal flow driven by multi-poles rotating magnetic field. Fluids 2019, 4, 77. [Google Scholar] [CrossRef]

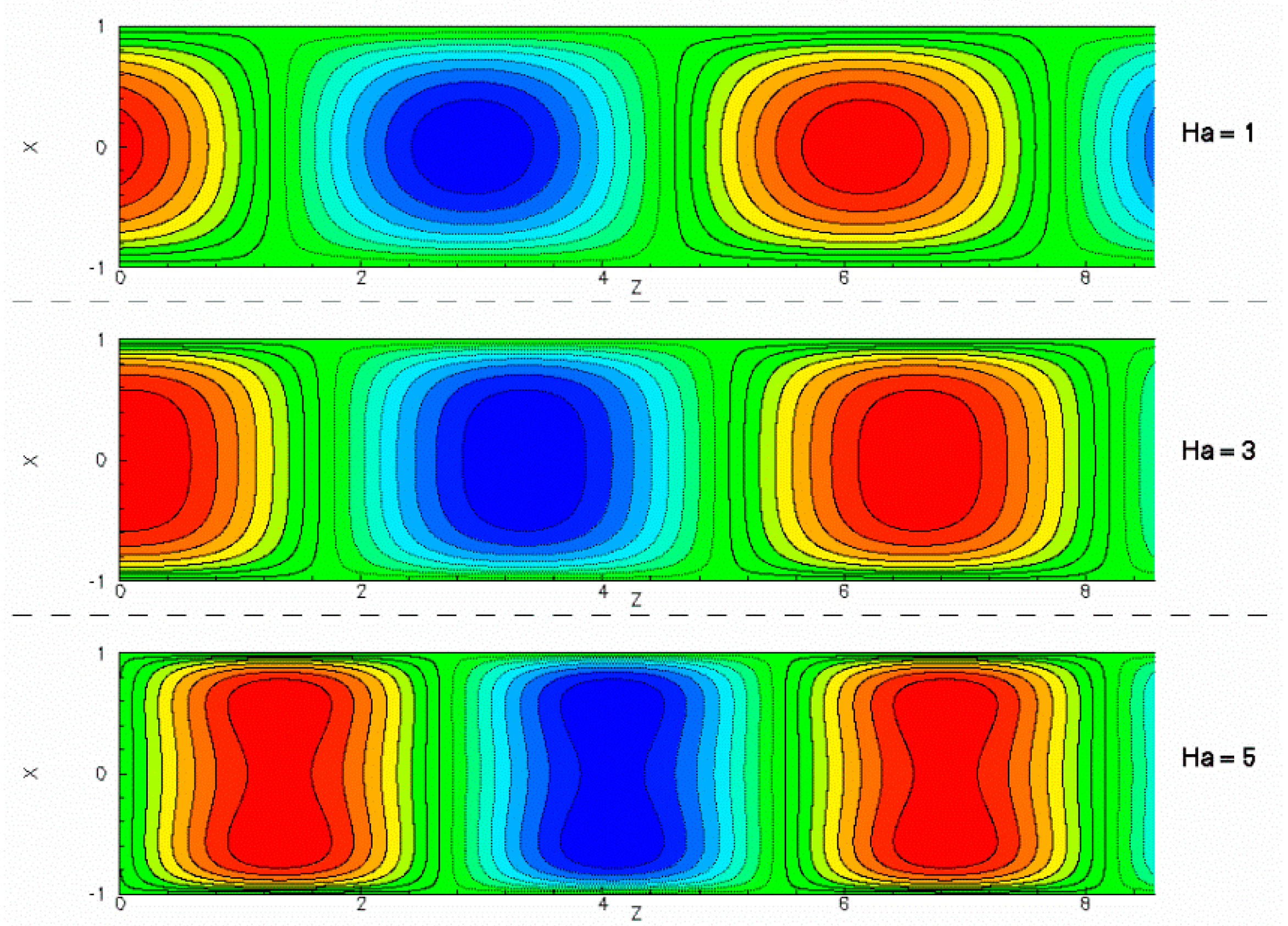
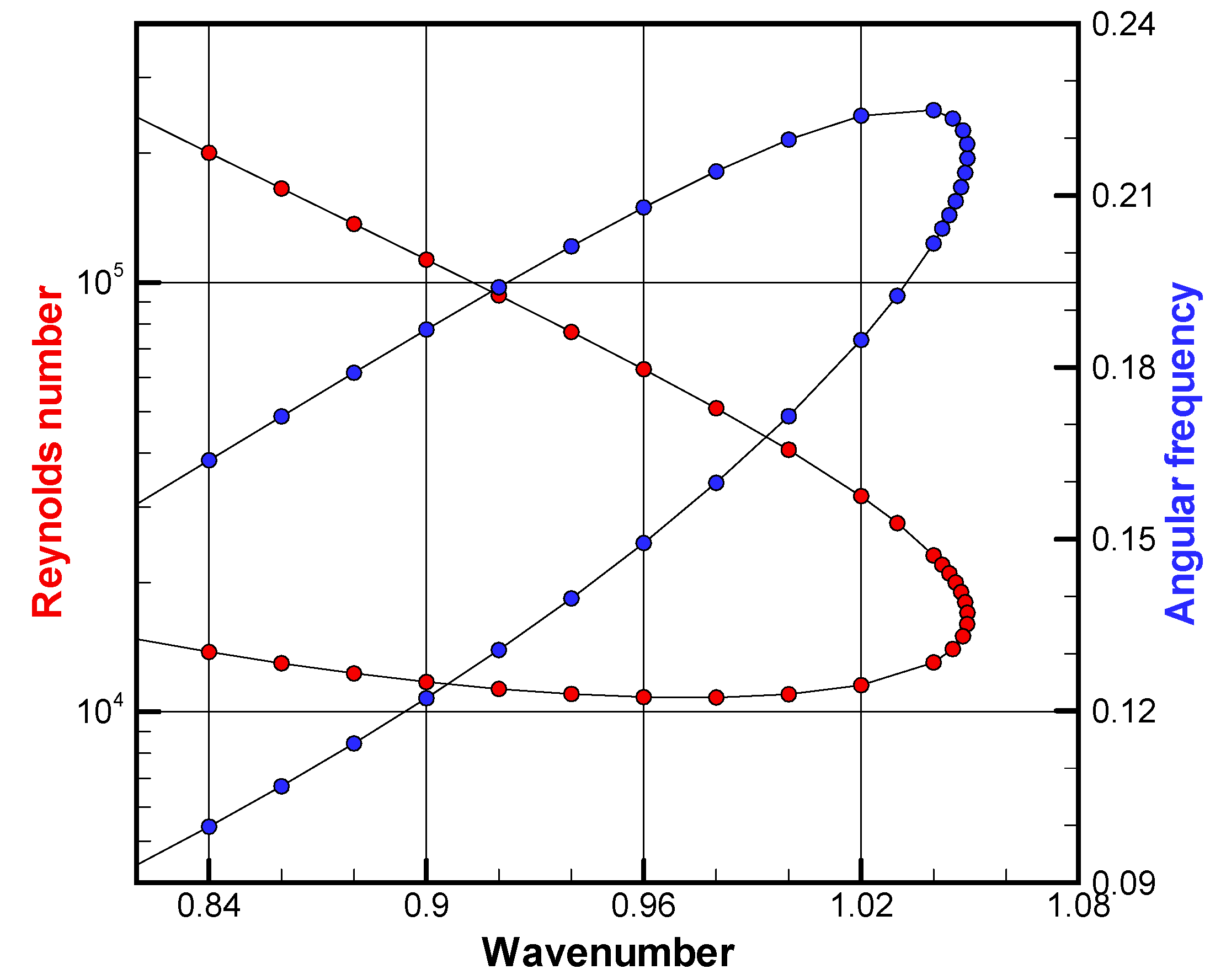

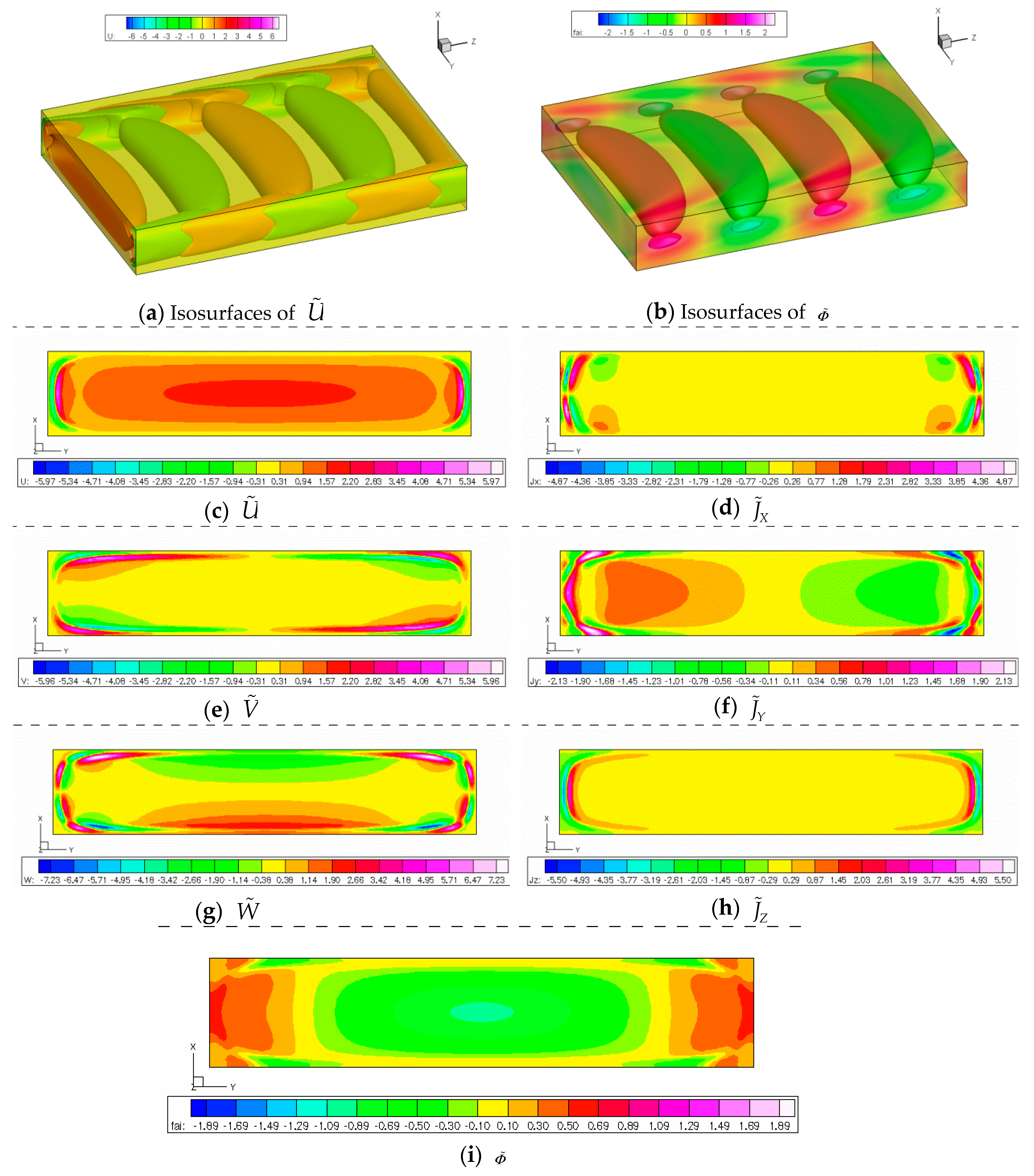
| Number of Meshes | Re | −SI | Cph | Error in Re |
|---|---|---|---|---|
| 100 | 5720.572 | 0.2699707 | 0.2645352 | 8.95 × 10−3 |
| 200 | 5767.318 | 0.2694774 | 0.2640518 | 8.50 × 10−4 |
| 400 | 5771.866 | 0.2694287 | 0.2640041 | 6.17 × 10−5 |
| 800 | 5772.198 | 0.2694250 | 0.2640005 | 4.16 × 10−6 |
| Exact value | 5772.222 | 0.2694248 | 0.2640003 | - |
| Present | Takashima [10] | ||||||
|---|---|---|---|---|---|---|---|
| Ha | Number of Meshes | αc | Rec | −SIc | αc | ReTak. | Remod |
| 0 | 200 | 1.0207 | 5767.31 | 2.695 × 10−1 | 1.0205 | 5772.22 | 5772.22 |
| 400 | 1.0206 | 5771.87 | 2.694 × 10−1 | ||||
| 1 | 200 | 0.9722 | 10,817.5 | 2.118 × 10−1 | 0.9718 | 10,016.3 | 10837.4 |
| 400 | 0.9718 | 10,835.9 | 2.116 × 10−1 | ||||
| 2 | 200 | 0.9294 | 37,274.3 | 1.363 × 10−1 | 0.9277 | 28,603.6 | 37,577.5 |
| 400 | 0.9279 | 37,532.8 | 1.358 × 10−1 | ||||
| 3 | 200 | 0.9636 | 105,614 | 9.901 × 10−2 | 0.9582 | 65,155.2 | 107,974 |
| 400 | 0.9588 | 107,702 | 9.788 × 10−2 | ||||
| 4 | 200 | 1.0476 | 224,231 | 8.180 × 10−2 | 1.0354 | 112,395 | 233,178 |
| 400 | 1.0372 | 231,617 | 8.008 × 10−2 | ||||
| 5 | 200 | 1.1527 | 399,687 | 7.230 × 10−2 | 1.1342 | 164,090 | 415,791 |
| 400 | 1.1386 | 410,155 | 7.060 × 10−2 | ||||
| Direction of Magnetic Field | Ha | αc | Rec | −SIc |
|---|---|---|---|---|
| - | 0 | 0.9255 | 9883.7 | 0.2193 |
| X | 0.5 | 0.9119 | 11,783 | 0.2051 |
| 1.0 | 0.8765 | 19,489 | 0.1700 | |
| 1.5 | 0.8797 | 36,013 | 0.1446 | |
| 2.0 | 1.0808 | 55,378 | 0.1711 | |
| Y | 0.5 | 0.9223 | 10,139 | 0.2169 |
| 1.0 | 0.9124 | 10,944 | 0.2098 | |
| 1.5 | 0.8952 | 12398 | 0.1983 | |
| 2.0 | 0.8710 | 14,582 | 0.1832 | |
| 2.5 | 0.8437 | 17,382 | 0.1672 | |
| 3.0 | 0.8214 | 20,570 | 0.1536 | |
| 3.5 | 0.8031 | 24367 | 0.1417 | |
| 4.0 | 0.8987 | 54,436 | 0.1518 | |
| XY | 1.0 | 0.8934 | 14,670 | 0.1884 |
| 2.0 | 0.8658 | 36,837 | 0.1414 |
| X-mag. (B = ex) | Y-mag. (B = ey) |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tagawa, T. Linear Stability Analysis of Liquid Metal Flow in an Insulating Rectangular Duct under External Uniform Magnetic Field. Fluids 2019, 4, 177. https://doi.org/10.3390/fluids4040177
Tagawa T. Linear Stability Analysis of Liquid Metal Flow in an Insulating Rectangular Duct under External Uniform Magnetic Field. Fluids. 2019; 4(4):177. https://doi.org/10.3390/fluids4040177
Chicago/Turabian StyleTagawa, Toshio. 2019. "Linear Stability Analysis of Liquid Metal Flow in an Insulating Rectangular Duct under External Uniform Magnetic Field" Fluids 4, no. 4: 177. https://doi.org/10.3390/fluids4040177





