Numerical Modeling of Jet at the Bottom of Tank at Moderate Reynolds Number Using Compact Hermitian Finite Differences Method
Abstract
:1. Introduction
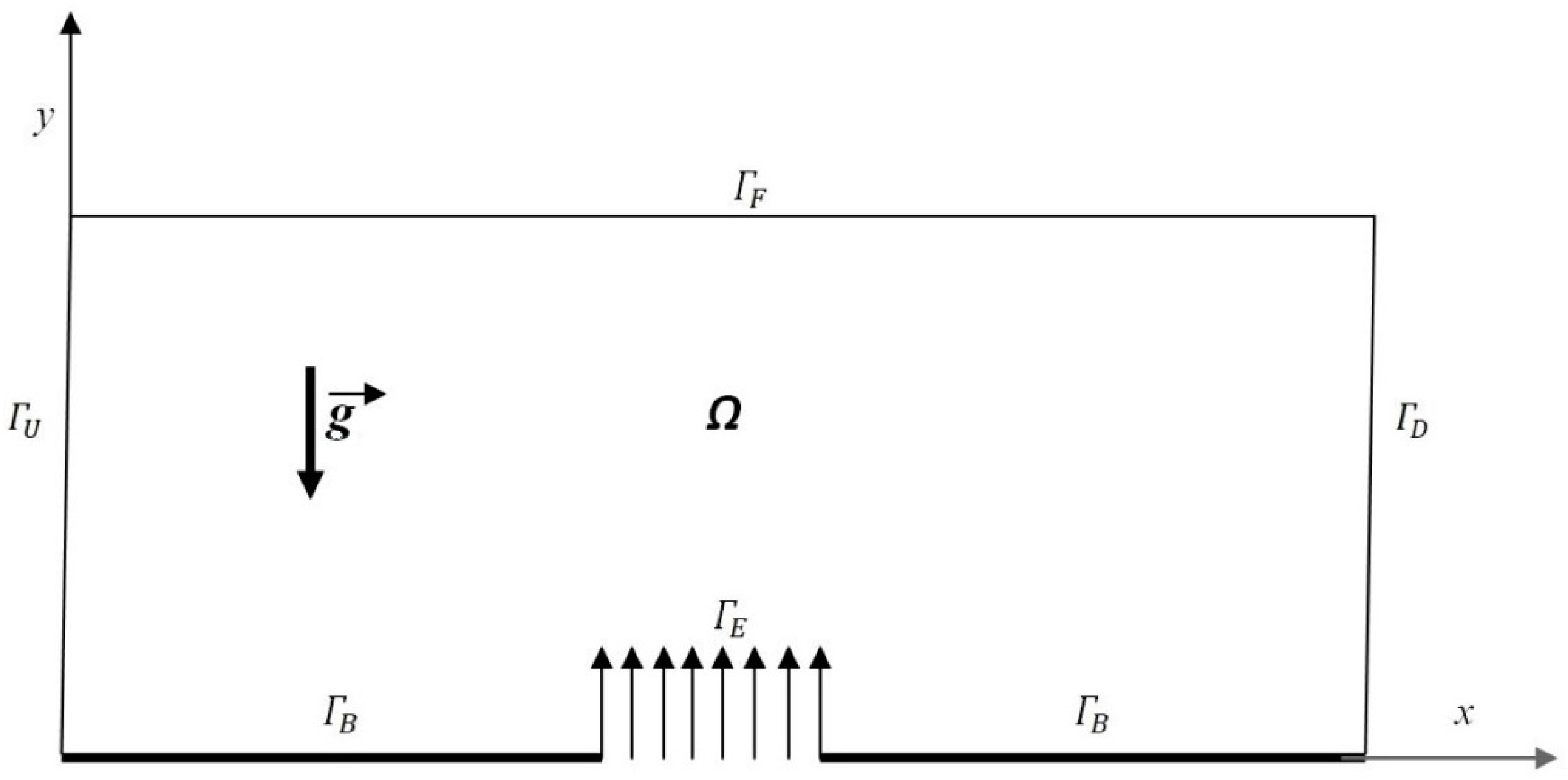
2. Problem Formulation
- -
- At the initial instant, all variables are zero except on the diffuser where C = 1;
- -
- The conditions on lateral boundaries and are expressed as:
- -
- The free surface is assumed to be flat, and therefore the condition is written as:
- -
- On the bottom of the numerical tank, two conditions are defined:
- At the nozzle , the conditions are expressed as:
- Aside from the nozzle , the conditions are expressed as:
3. Solution Procedures
- -
- The definition , is used to calculate the component v using the formula
- -
- The definition , is used to calculate the component u using the formula
- -
- in the case of , this satisfies , and ,
- -
- in the case of , this satisfies S=0 and .
- denotes the discretized operator corresponding to
- denotes the discretized operator corresponding to
- denotes the discretized operator corresponding to
- denotes the discretized operator corresponding to
- at the 1st half step:
- at the 2nd half step:
- at the 1st half step:
- at the 2nd half step:
4. Results and Discussion
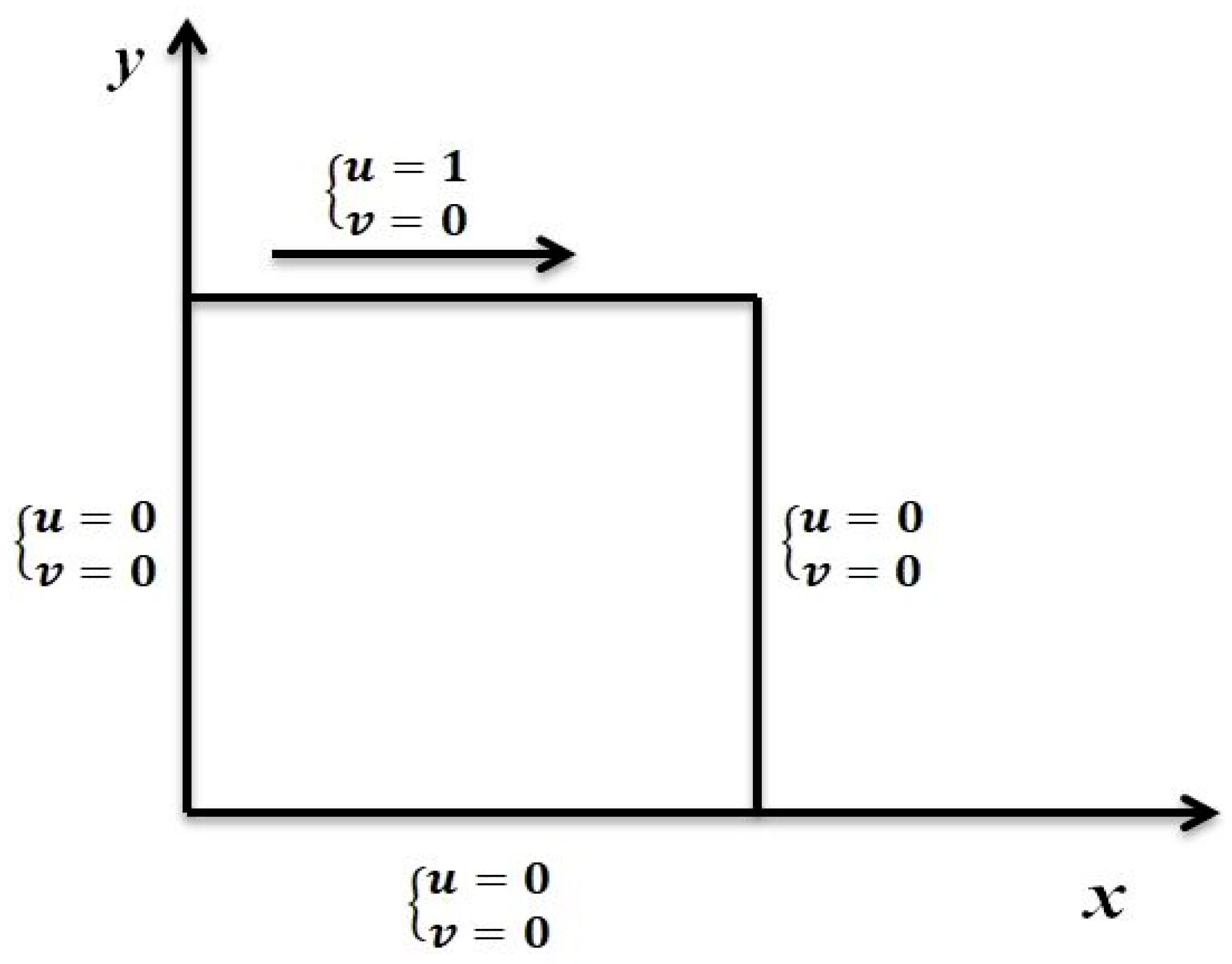
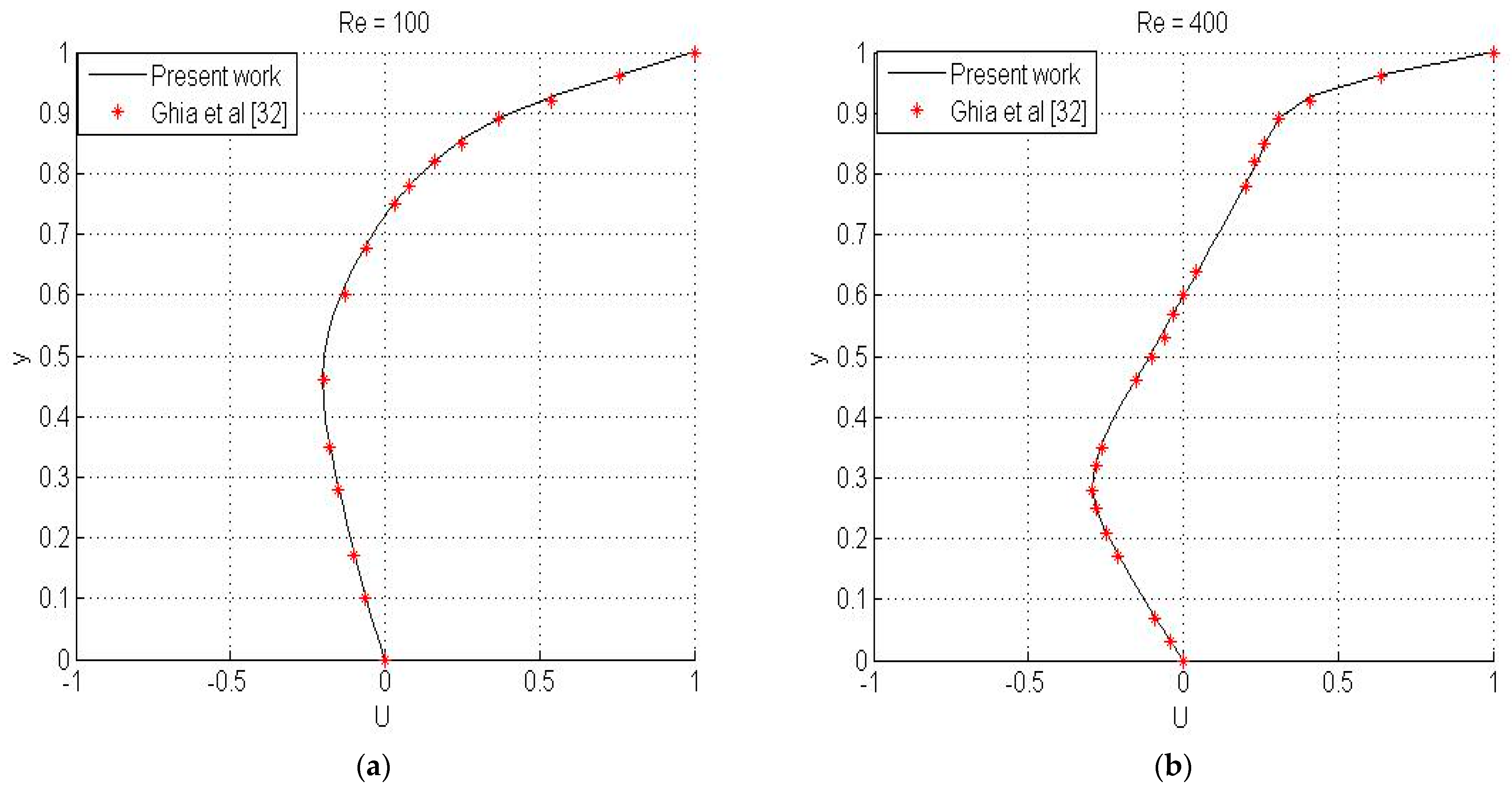
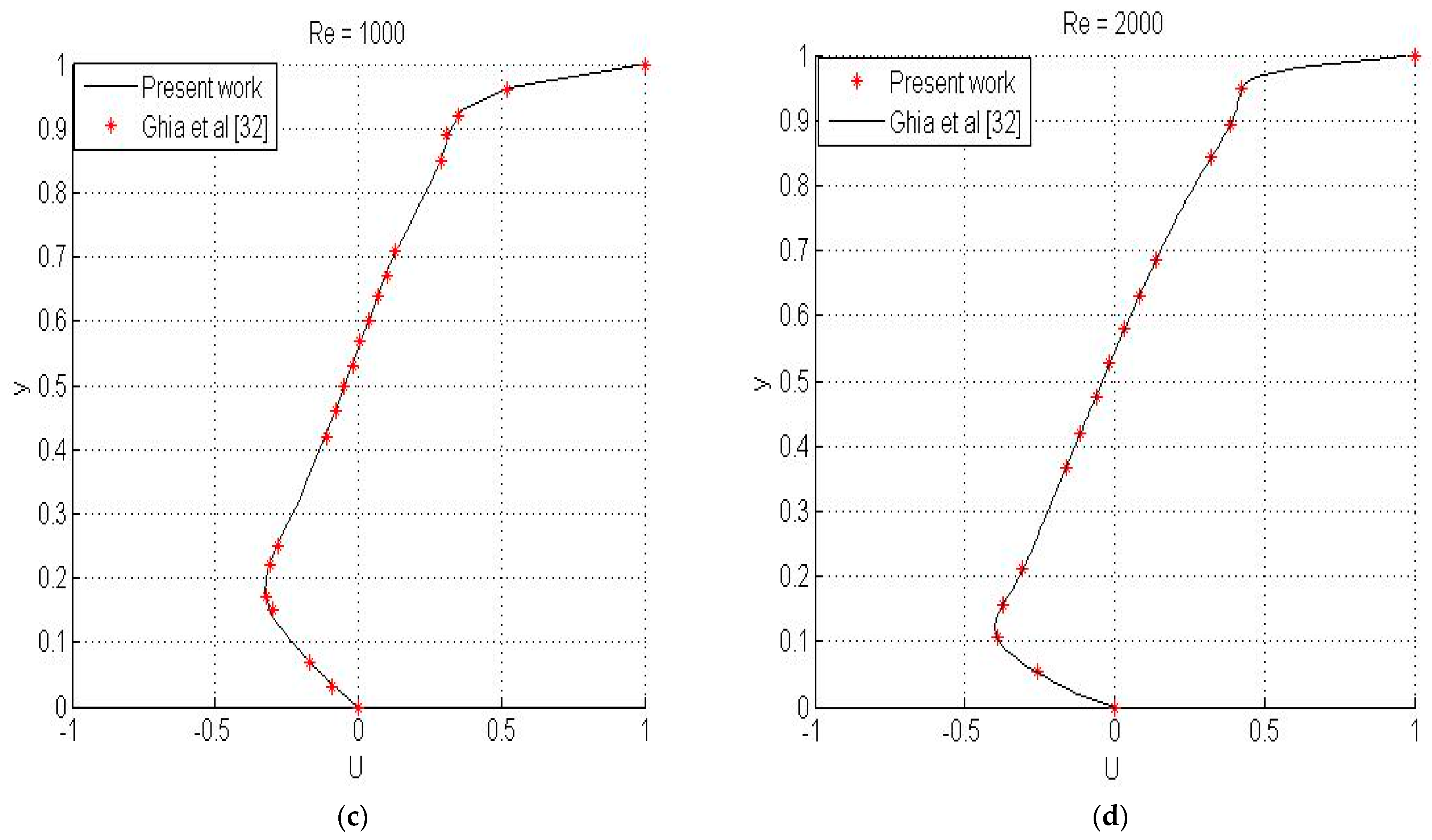
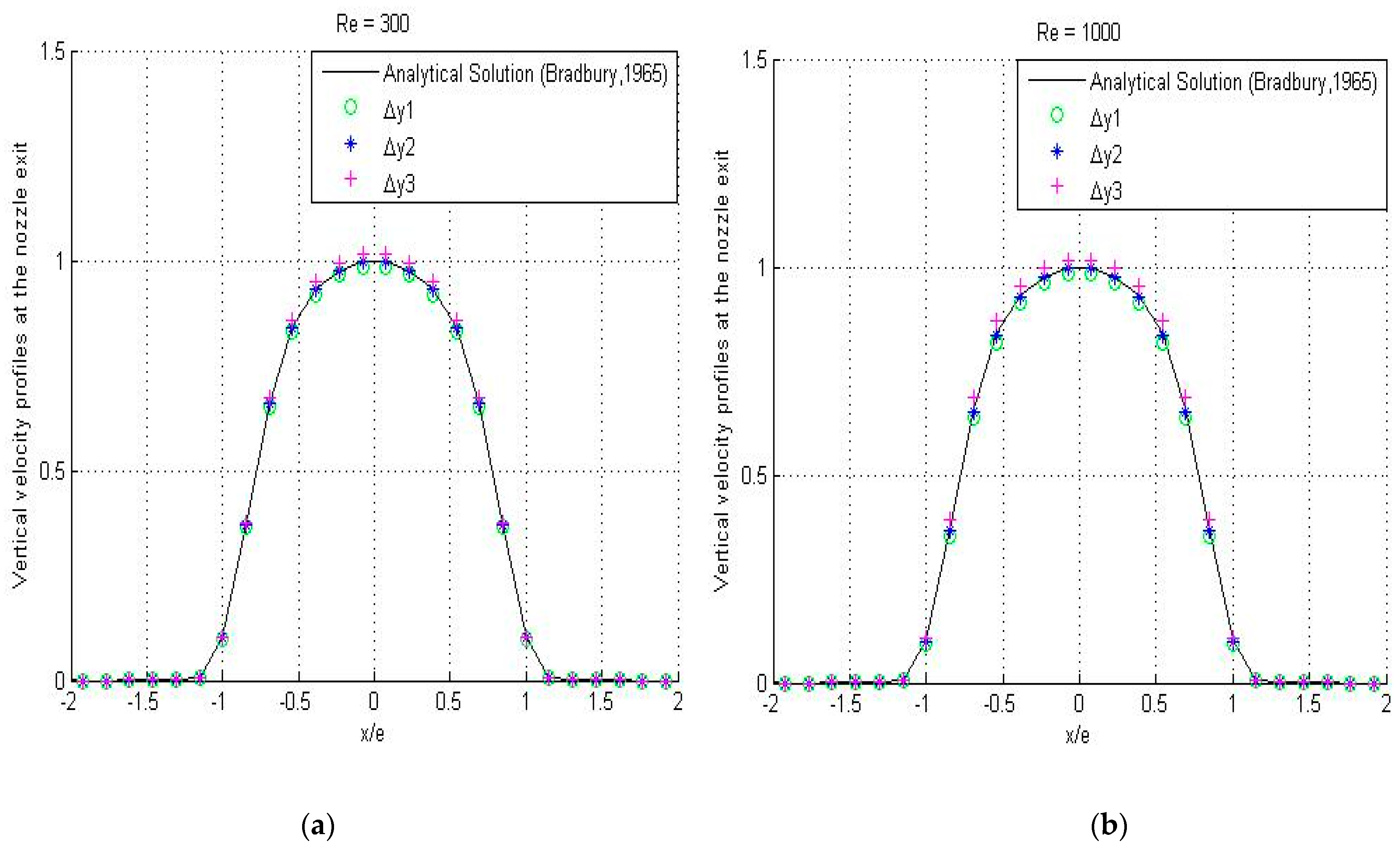
4.1. Validation Test
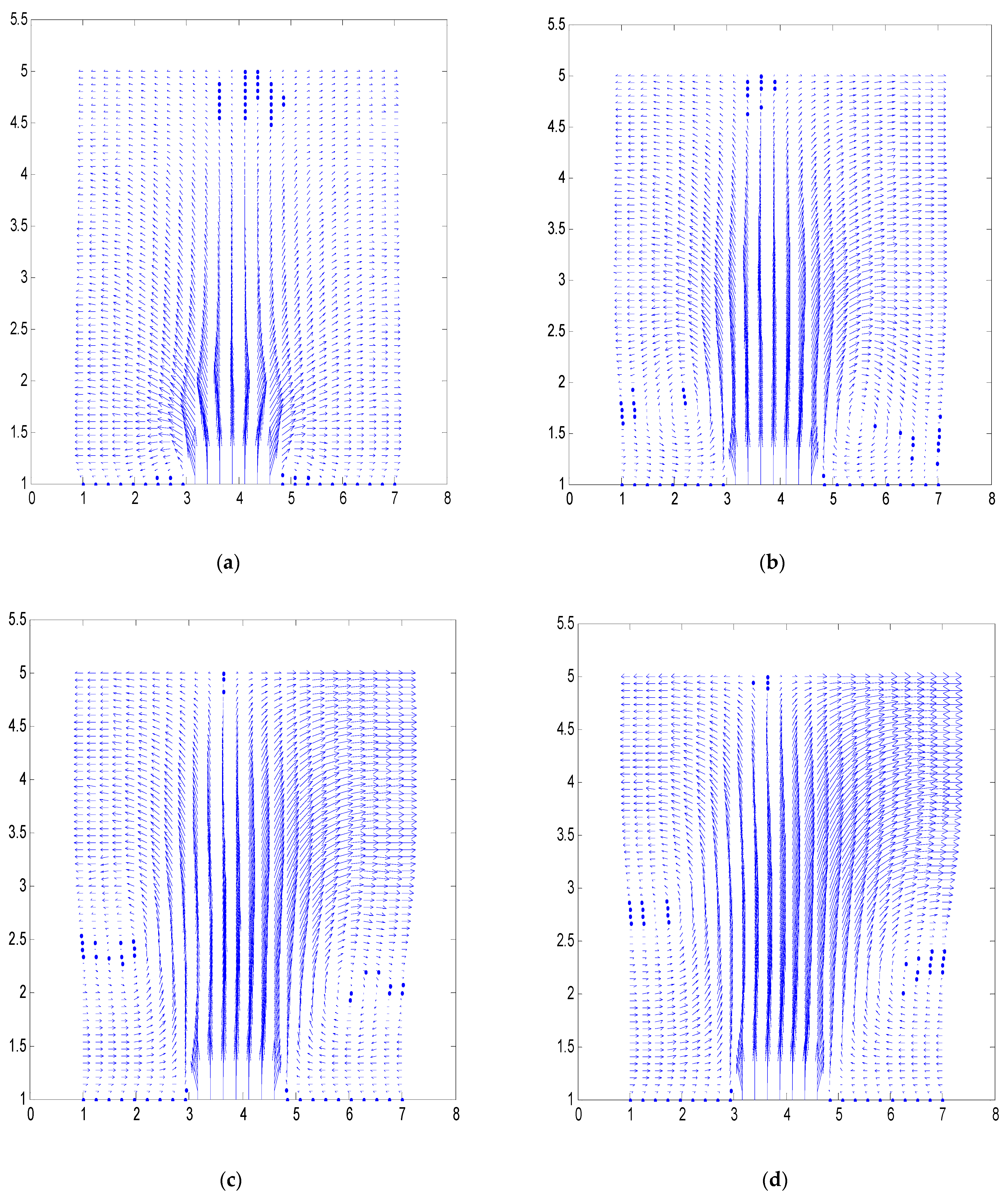
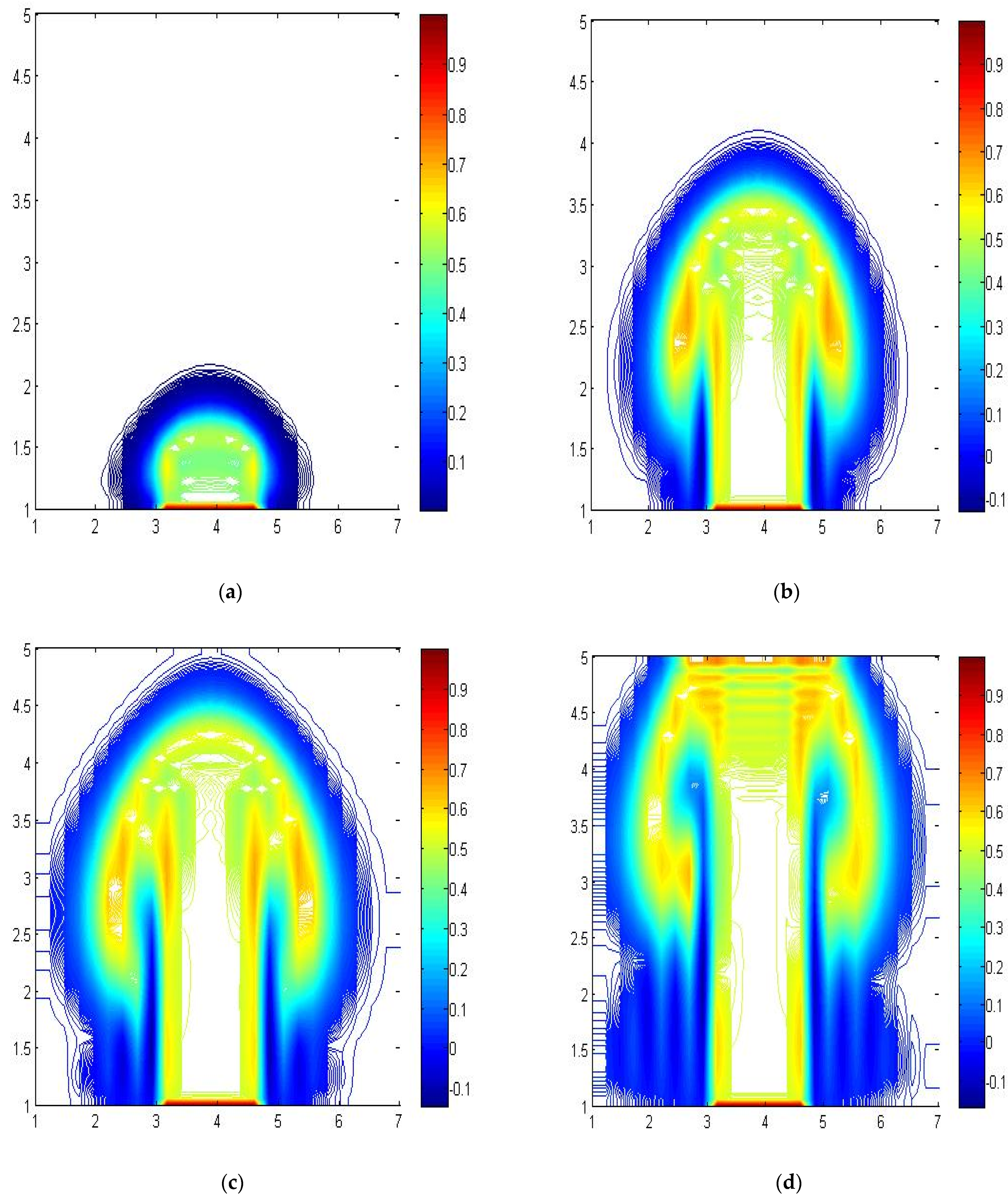
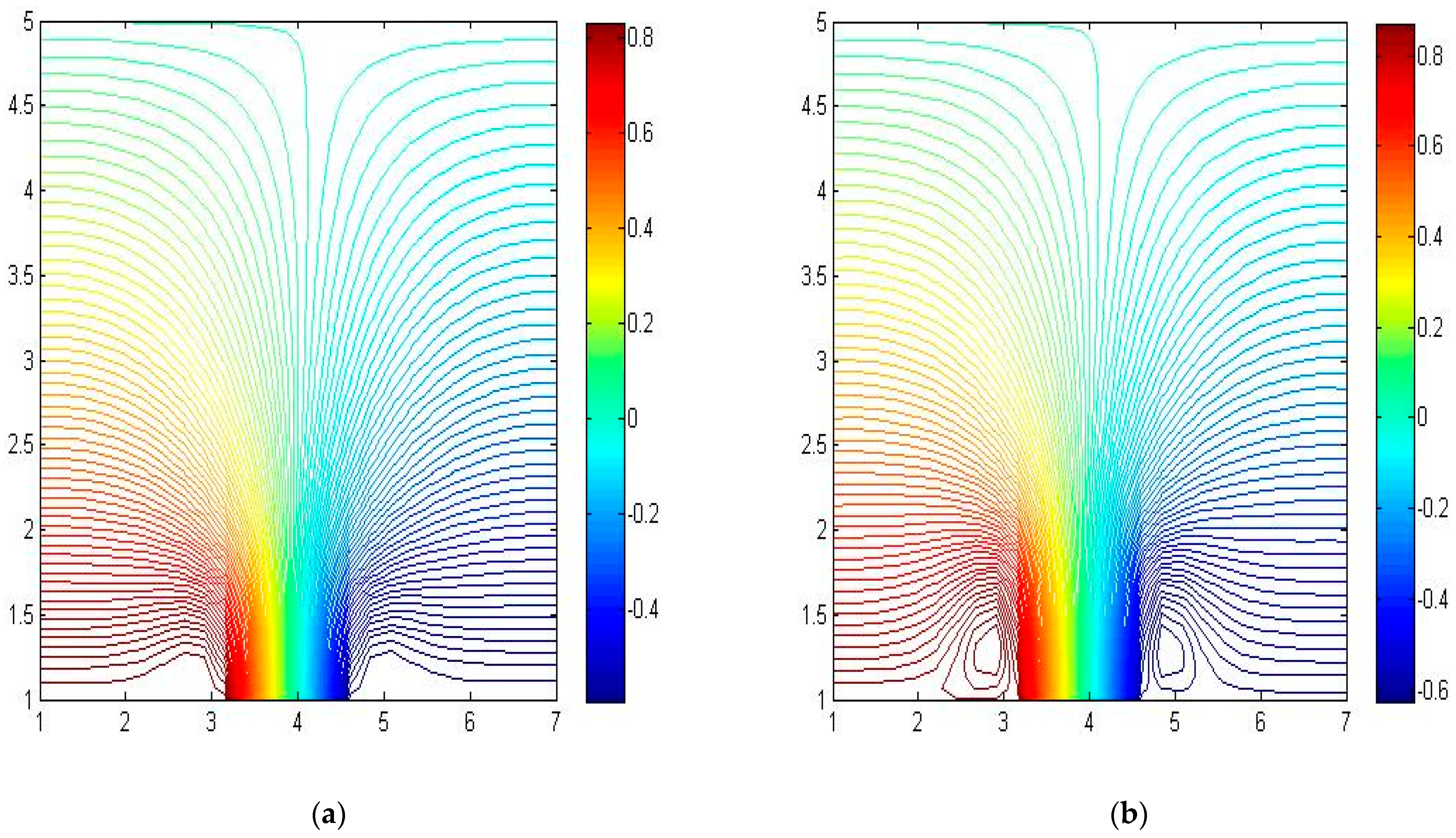
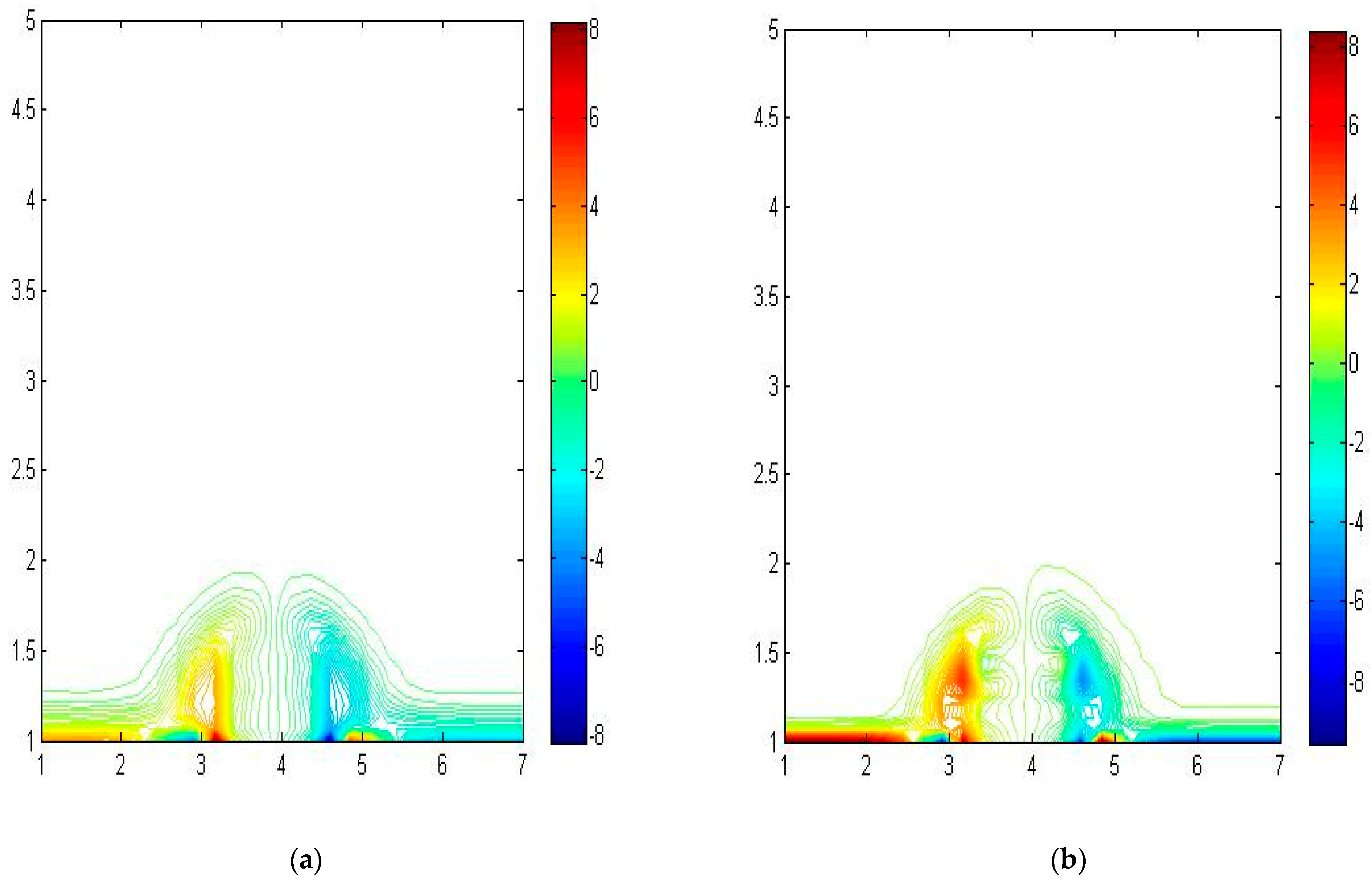
4.2. Jet Emitted from the Bottom of the Numerical Tank
4.3. Evaluation of Mesh Domain Sensitivity
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| Acceleration due to gravity | |
| x, y | Cartesian coordinates (x-axis is aligned along the stretching surface and y-axis is normal to it) |
| C | Concentration function |
| Fr | Froude number |
| Gradient operator | |
| Δ | Laplace operator |
| Normal vector | |
| Outer product operator | |
| Position of support particles | |
| Re | Reynolds number |
| Sc | Schmidt number |
| ψ | Stream function |
| Step in the x-direction coordinate | |
| Step in the y-direction coordinate | |
| Tangent vector | |
| t | Time |
| Temporal interval | |
| u | Velocity in the x-direction |
| v | Velocity in the y-direction |
| U = (u, v) | Velocity vector |
| Vorticity function, such |
References
- Miake-Lye, R.C.; Hammer, J.A. Lifted turbulent jet flames: A stability criterion based on the jet large-scale structure. Proc. Combust. Inst. 1988, 22, 817–824. [Google Scholar] [CrossRef]
- Iyogun, C.O.; Birouk, M. Effect of Fuel Nozzle Geometry on the Stability of a Turbulent Jet Methane Flame. Combust. Sci. Technol. 2008, 180, 2186–2209. [Google Scholar] [CrossRef]
- Mi, J.; Nathan, G.J.; Luxton, R.E. Cenetreline mixing characteristics of jets from nine differently shaped nozzles. Exp. Fluids. 2000, 28, 93–94. [Google Scholar] [CrossRef]
- Langman, A.S.; Nathan, G.J.; Mi, J.; Ashman, P.J. The influence of geometric nozzle profile on the global properties of a turbulent diffusion flame. Proc. Combust. Inst. 2007, 31, 1599–1607. [Google Scholar] [CrossRef]
- Zaman, K.B.M.Q. Effect of Initial Condition on Subsonic Jet Noise. AIAA 1985, 23, 1370–1373. [Google Scholar] [CrossRef]
- Antonia, R.A.; Zhao, Q. Effect of initial conditions on a circular jet. Exp. Fluids 2001, 31, 319–323. [Google Scholar] [CrossRef]
- Ferdman, E.; Otugen, M.V.; Kim, S. Effect of initial velocity profile on the development of the round jet. J. Propul. Power 2000, 16, 676–686. [Google Scholar] [CrossRef]
- Xu, G.; Antonia, R.A. Effect of different initial conditions on a turbulent round free jet. Exp. Fluids 2002, 33, 677–683. [Google Scholar] [CrossRef]
- George, W.K.; Davidson, L. Role of Initial Conditions in Establishing Asymptotic Flow Behavior. AIAA 2004, 42, 438–446. [Google Scholar] [CrossRef] [Green Version]
- Burattini, P.; Antonia, R.A.; Rajagopalan, S.; Stephens, S. Effect of initial conditions on the near-field development of a round jet. Exp. Fluids 2004, 37, 56–64. [Google Scholar] [CrossRef]
- Reynolds, A.J. Observations of a liquid-into-liquid jet. J. Fluid Mech. 1962, 14, 552–556. [Google Scholar] [CrossRef]
- Crow, S.C.; Champagne, F.H. Orderly structure in jet turbulence. J. Fluid Mech. 1971, 43, 547–591. [Google Scholar] [CrossRef]
- O’Neill, P.; Soria, J.; Honnery, D. The stability of low Reynolds number round jets. Exp. Fluids 2004, 36, 473–483. [Google Scholar] [CrossRef]
- Bogey, C.; Bailly, C. Large eddy simulations of transitional round jets: Influence of the Reynolds number on flow development and energy dissipation. Phys. Fluids 2006, 18, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Ricou, F.; Spalding, D.B. Measurements of entrainment by axisymmetric turbulent jets. J. Fluid Mech. 1961, 11, 21–32. [Google Scholar] [CrossRef]
- Grinstein, F.F.; Gutmark, E.; Parr, T. Near field dynamics of subsonic free square jets: A computational and experimental study. Phys. Fluids 1995, 7, 1483–1497. [Google Scholar] [CrossRef]
- Grinstein, F.F.; DeVore, C.R. Dynamics of coherent structures and transition to turbulence in free square jets. Phys. Fluids 1996, 8, 1237–1251. [Google Scholar] [CrossRef]
- Quinn, W.R.; Militzer, J. Experimental and numerical study of a turbulent free square jet. Phys. Fluids 1988, 31, 1017–1025. [Google Scholar] [CrossRef]
- Sankar, G.; Balachandar, R.; Carriveau, R. Characteristics of a three dimensional square jet in the vicinity of a free surface. J. Hydraul. Eng. 2009, 135, 989–994. [Google Scholar] [CrossRef]
- Tsuchiya, Y.; Horikoshi, C.; Sato, T. On the spread of rectangular jets. Exp. Fluids 1986, 4, 197–204. [Google Scholar] [CrossRef]
- Ghasemi, A.; Roussinova, V.; Balachandar, R. A study in the developing region of square jet. J. Turbul. 2013, 14, 1–24. [Google Scholar] [CrossRef]
- Ghasemi, A.; Roussinova, V.; Balachandar, R.; Barron, R.M. Reynolds number effects in the near-field of a turbulent square jet. Exp. Ther. Fluid Sci. 2015, 61, 249–258. [Google Scholar] [CrossRef]
- Casey, M.; Wintergerste, T. Special Interest Group on “Quality and Trust in Industrial CFD” Best Practice Guidelines, European Research Community On Flow, Turbulence And Combustion (ERCOFTAC), version 1; Sulzer Innotec: Winterthur, Switzerland, 2000. [Google Scholar]
- Zhiyin, Y. Large-eddy simulation: Past, present and the future. Chin. J. Aeronaut. 2015, 28, 11–24. [Google Scholar] [CrossRef] [Green Version]
- Venuta, I.D.; Petracci, I.; Angelino, M.; Boghi, A.; Gori, F. Numerical simulation of mass transfer and fluid flow evolution of a rectangular free jet of air. Int. J. Heat Mass Transfer 2018, 117, 235–251. [Google Scholar] [CrossRef] [Green Version]
- Gori, F.; Petracci, I.; Angelino, M. Flow Evolution of a Turbulent Submerged Two-Dimensional Rectangular Free Jet of Air. Average Particle Image Velocimetry (PIV) Visualizations and Measurements. Int. J. Heat Fluid Flow 2013, 44, 764–775. [Google Scholar] [CrossRef]
- Gori, F.; Petracci, I. Fluid Dynamics Measurements and Numerical Simulations around a Circular Cylinder Impinged by a Submerged Slot Jet of Air; American Society of Mechanical Engineers, Fluids Engineering Division (Publication) FED: New York, NY, USA, 2003; pp. 179–185. [Google Scholar]
- Gori, F.; Petracci, I.; Angelino, M. Influence of the Reynolds number on the instant flow evolution of a turbulent rectangular free jet of air. Int. J. Heat Fluid Flow 2014, 50, 386–401. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Zhong, D.; Guan, J.; Wang, Y. Drift velocity in sediment-laden downward jets. Environ. Fluid Mech. 2018, 19, 1–25. [Google Scholar] [CrossRef] [Green Version]
- Shukla, R.K.; Tatineni, M.; Zhong, X. Very high-order compact finite difference schemes on non-uniform grids for incompressible Navier-Stokes equations. J. Comput. Phys. 2007, 224, 1064–1094. [Google Scholar] [CrossRef]
- Yves, A. A Hermitian finite difference method for the solution of parabolic equations. Comput. Math. Appl. 1975, 1, 393–406. [Google Scholar]
- Sherer, S.E.; Scott, J.N. High-order compact finite-difference methods on general overset grids. J. Comput. Phys. 2005, 210, 459–496. [Google Scholar] [CrossRef]
- Zhang, K.K.Q.; Shotorban, B.; Minkowycz, W.J.; Mashayek, F. A compact finite difference method on staggered grid for Navier-Stokes flows. Int. J. Num. Methods Fluids 2006, 52, 867–881. [Google Scholar] [CrossRef]
- Hadjidimos, A. Successive overrelaxation (SOR) and related methods. J. Comput. Appl. Math. 2000, 123, 177–199. [Google Scholar] [CrossRef] [Green Version]
- Ghia, V.; Ghia, K.N.; Shin, C.T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method. J. Comput. Phys. 1982, 48, 387–411. [Google Scholar] [CrossRef]
- Bradbury, L.J.S. The structure of a self-preserving turbulent jet. J. Fluid Mech. 1965, 23, 31–64. [Google Scholar] [CrossRef]
- Aristodemo, F.; Marrone, S.; Federico, I. SPH modeling of plane jets into water bodies through an inflow/outflow algorithm. Ocean Eng. 2015, 105, 160–175. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T. Spectral Methods: Evolution to Complex Geometries and Applications to Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Skala, V.; Karim, S.; Zabran, M. Radial Basis Function Approximation Optimal Shape Parameters Estimation: Preliminary Experimental Results. In Computational Science-ICCS 2020, Part VI, LNCS 12142; Springer: Cham, Switzerland, 2020; pp. 309–317. [Google Scholar]
- Cervenka, M.; Skala, V. Behavioral Study of Various Radial Basis Functions for Approximation and Interpolation Purposes. In Proceedings of the IEEE 18th World Symposium on Applied Machine Intelligence and Informatics, SAMI 2020, Herl’any, Slovacia, 23–25 January 2020; pp. 135–140, ISBN 978-1-7281-314. [Google Scholar] [CrossRef]
- Loukili, M.; Mordane, S. New Numerical Investigation Using Meshless Methods Applied to the Linear Free Surface Water Waves. Adv. Intell. Syst. Comput. 2019, 765, 337–345. [Google Scholar]
- Loukili, M.; Mordane, S. Numerical Analysis of an Absorbing Boundary Condition Applied to the Free Surface Water Waves Using the Method of Fundamental Solutions. In Proceedings of the 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 15–17 April 2019. [Google Scholar]
- Loukili, M.; El Aarabi, L.; Mordane, S. Computation of Nonlinear Free-Surface Flows Using the Method of Fundamental Solutions. Adv. Intell. Syst. Comput. 2019, 763, 420–430. [Google Scholar]
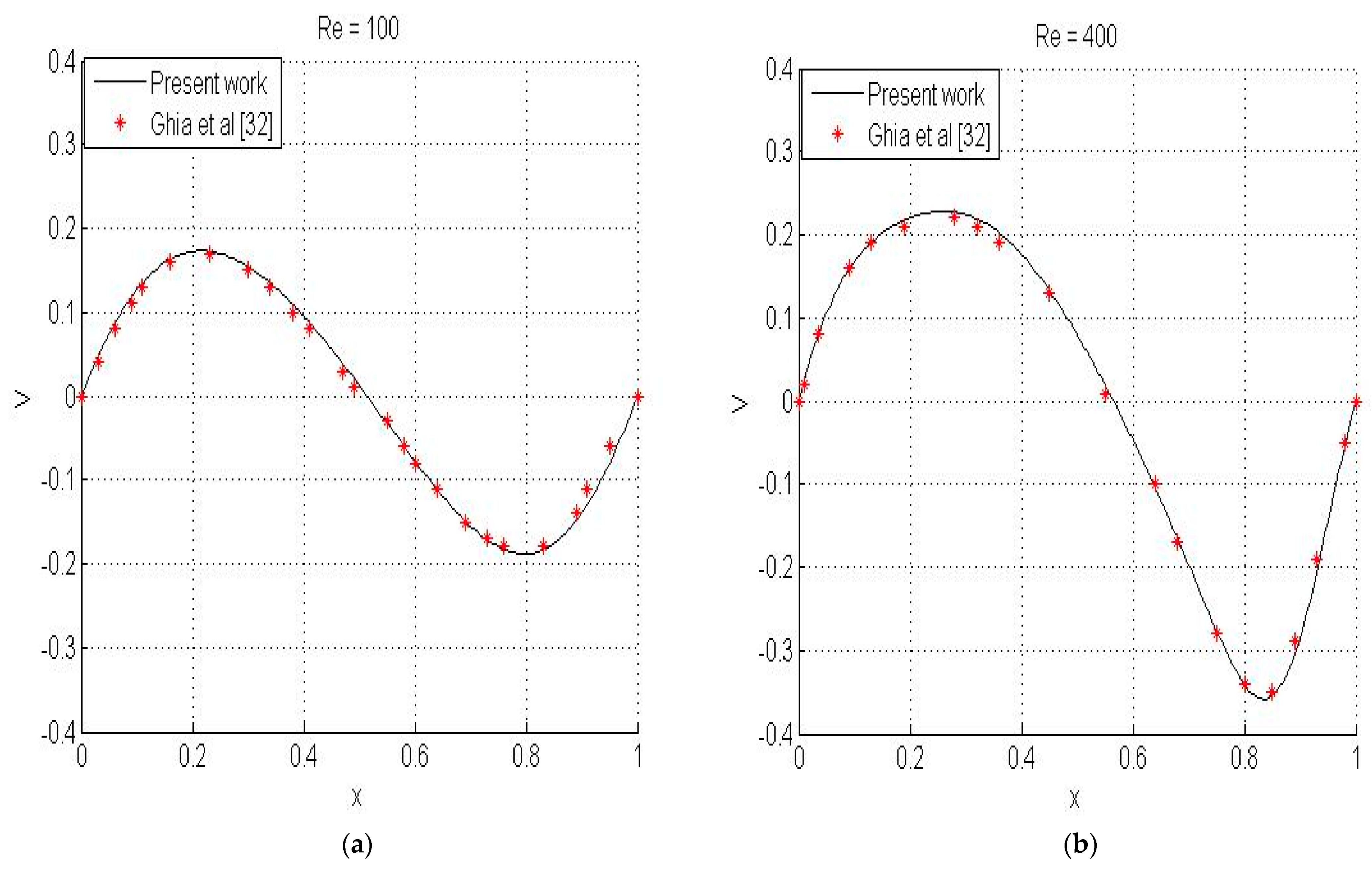
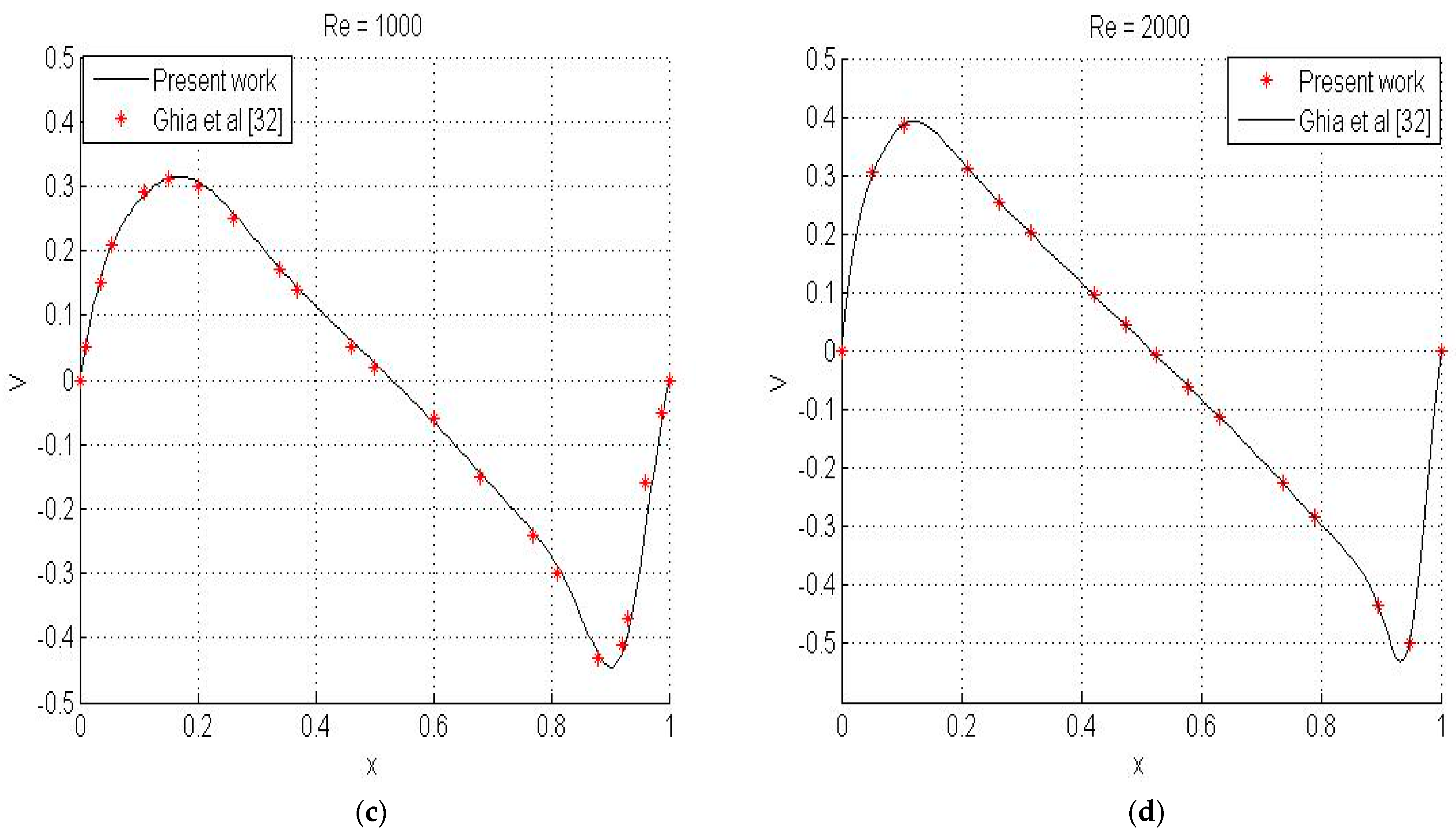
| Mean Absolute Error (MAE) | Reynolds Numbers | ||
|---|---|---|---|
| 100 | 400 | 1000 | |
| 4 × 10−5 | 3 × 10−4 | 5 × 10−3 | |
| 5 × 10−5 | 2 × 10−4 | 7 × 10−3 | |
| 2 × 10−5 | 4 × 10−4 | 9 × 10−3 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loukili, M.; Kotrasova, K.; Dutykh, D. Numerical Modeling of Jet at the Bottom of Tank at Moderate Reynolds Number Using Compact Hermitian Finite Differences Method. Fluids 2021, 6, 63. https://doi.org/10.3390/fluids6020063
Loukili M, Kotrasova K, Dutykh D. Numerical Modeling of Jet at the Bottom of Tank at Moderate Reynolds Number Using Compact Hermitian Finite Differences Method. Fluids. 2021; 6(2):63. https://doi.org/10.3390/fluids6020063
Chicago/Turabian StyleLoukili, Mohammed, Kamila Kotrasova, and Denys Dutykh. 2021. "Numerical Modeling of Jet at the Bottom of Tank at Moderate Reynolds Number Using Compact Hermitian Finite Differences Method" Fluids 6, no. 2: 63. https://doi.org/10.3390/fluids6020063







