Transient Electrophoresis of a Cylindrical Colloidal Particle
Abstract
:1. Introduction
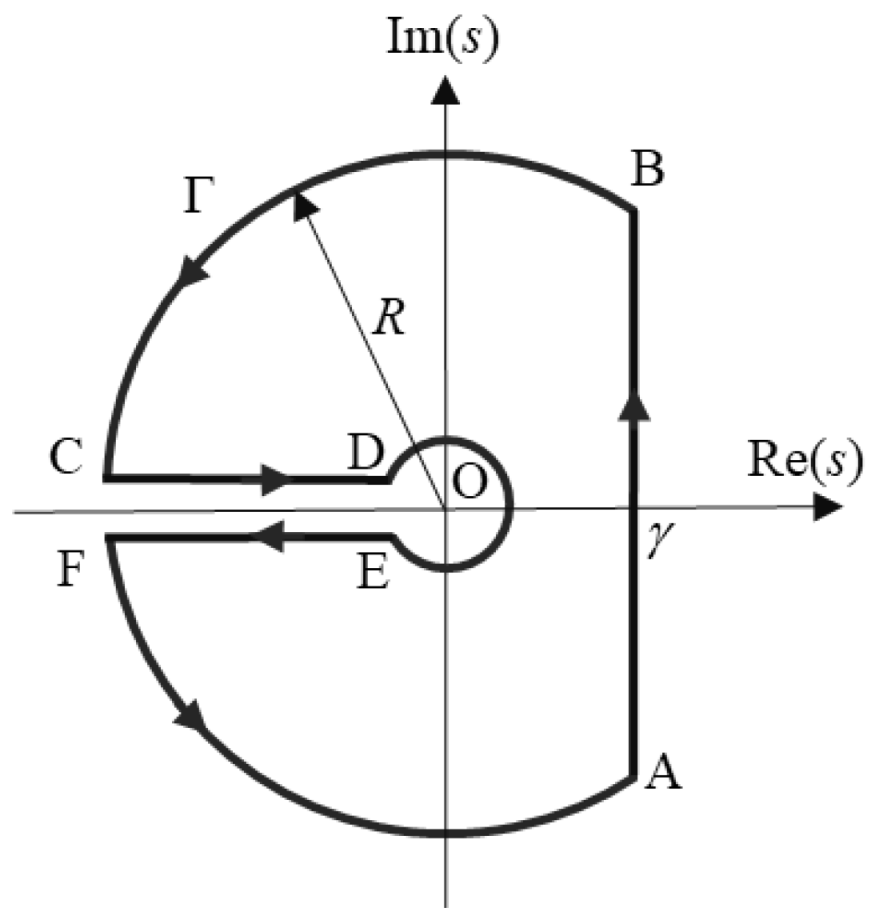
2. Theory
2.1. Cylinder in a Transverse Field
2.2. Cylinder in a Tangential Field
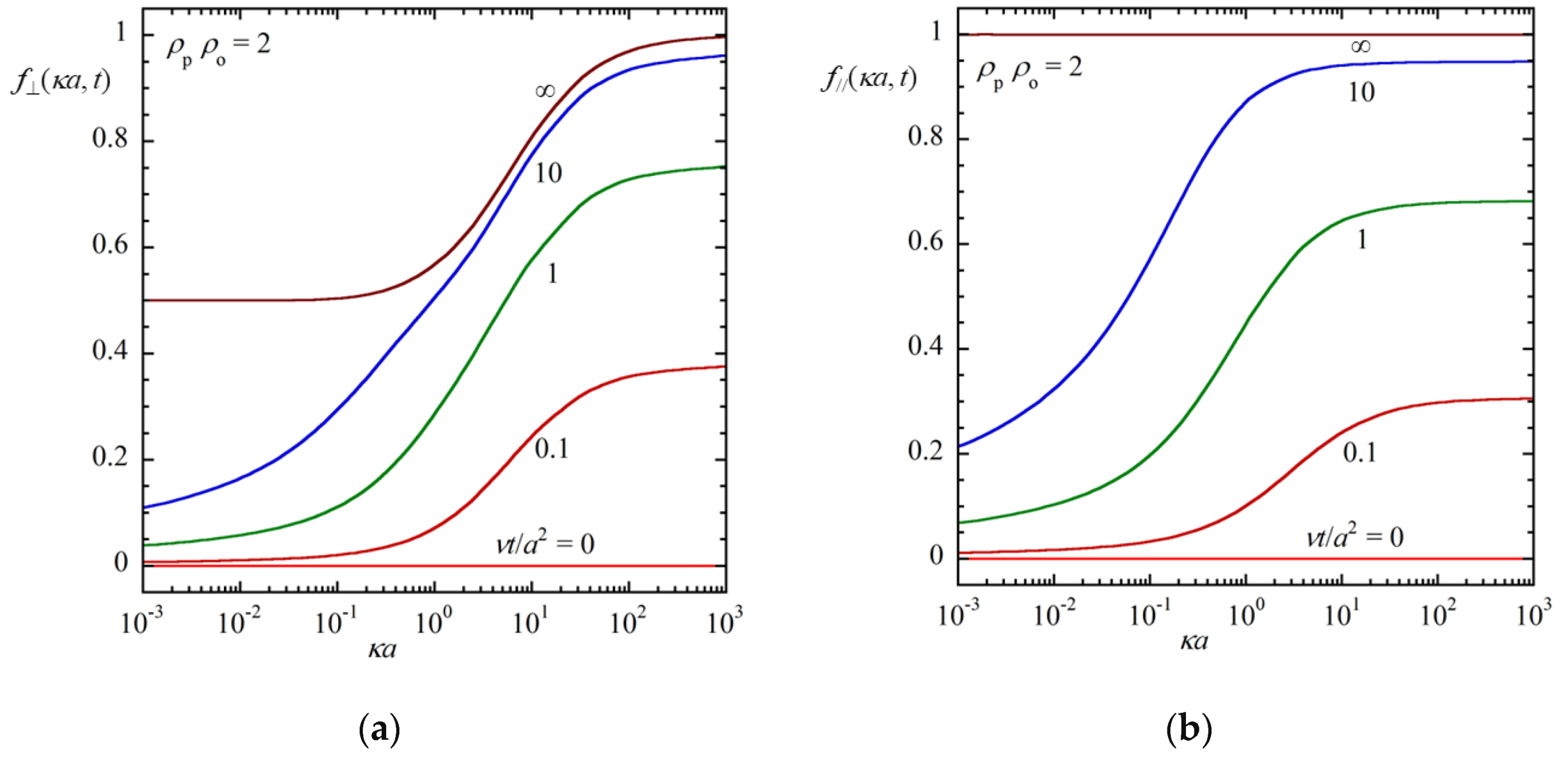
3. Results and Discussion
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Morrison, F.A. Transient electrophoresis of a dielectric sphere. J. Colloid Interface Sci. 1969, 29, 687–691. [Google Scholar] [CrossRef]
- Morrison, F.A. Transient electrophoresis of an arbitrarily oriented cylinder. J. Colloid Interface Sci. 1971, 36, 139–145. [Google Scholar] [CrossRef]
- Ivory, C.F. Transient electroosmosis: The momentum transfer coefficient. J. Colloid Interface Sci. 1983, 96, 296–298. [Google Scholar] [CrossRef]
- Ivory, C.F. Transient electrophoresis of a dielectric sphere. J. Colloid Interface Sci. 1984, 100, 239–249. [Google Scholar] [CrossRef]
- Keh, H.J.; Tseng, H.C. Transient electrokinetic flow in fine capillaries. J. Colloid Interface Sci. 2001, 242, 450–459. [Google Scholar] [CrossRef] [Green Version]
- Keh, H.J.; Huang, Y.C. Transient electrophoresis of dielectric spheres. J. Colloid Interface Sci. 2005, 291, 282–291. [Google Scholar] [CrossRef]
- Huang, Y.C.; Keh, H.J. Transient electrophoresis of spherical particles at low potential and arbitrary double-layer thickness. Langmuir 2005, 21, 11659–11665. [Google Scholar] [CrossRef]
- Khair, A.S. Transient phoretic migration of a permselective colloidal particle. J. Colloid Interface Sci. 2012, 381, 183–188. [Google Scholar] [CrossRef]
- Chiang, C.C.; Keh, H.J. Startup of electrophoresis in a suspension of colloidal spheres. Electrophoresis 2015, 36, 3002–3008. [Google Scholar] [CrossRef]
- Chiang, C.C.; Keh, H.J. Transient electroosmosis in the transverse direction of a fibrous porous medium. Colloids Surf. A Physicochem. Engin. Asp. 2015, 481, 577–582. [Google Scholar] [CrossRef]
- Saad, E.I.; Faltas, M.S. Time-dependent electrophoresis of a dielectric spherical particle embedded in Brinkman medium. Z. Angew. Math. Phys. 2018, 69, 43. [Google Scholar] [CrossRef]
- Saad, E.I. Unsteady electrophoresis of a dielectric cylindrical particle suspended in porous medium. J. Mol. Liquid 2019, 289, 111050. [Google Scholar] [CrossRef]
- Saad, E.I. Start-up Brinkman electrophoresis of a dielectric sphere for Happel and Kuwabara models. Math. Meth. Appl. Sci. 2018, 41, 9578–9591. [Google Scholar] [CrossRef]
- Li, M.X.; Keh, H.J. Start-up electrophoresis of a cylindrical particle with arbitrary double layer thickness. J. Phys. Chem. B 2020, 124, 9967–9973. [Google Scholar] [CrossRef]
- Lai, Y.C.; Keh, H.J. Transient electrophoresis of a charged porous particle. Electrophoresis 2020, 41, 259–265. [Google Scholar] [CrossRef]
- Lai, Y.C.; Keh, H.J. Transient electrophoresis in a suspension of charged particles with arbitrary electric double layers. Electrophoresis 2021, 42, 2126–2133. [Google Scholar] [CrossRef]
- Sherief, H.H.; Faltas, M.S.; Ragab, K.E. Transient electrophoresis of a conducting spherical particle embedded in an electrolyte-saturated Brinkman medium. Electrophoresis 2021, 42, 1636–1647. [Google Scholar] [CrossRef]
- Ohshima, H. Approximate analytic expression for the time-dependent transient electrophoretic mobility of a spherical colloidal particle. Molecules 2022, 27, 5108. [Google Scholar] [CrossRef]
- Ohshima, H. Transient electrophoresis of a spherical soft particle. Colloid Polym. Sci. 2022, accepted. [Google Scholar] [CrossRef]
- Ohshima, H. Dynamic electrophoretic mobility of a spherical colloidal particle. J. Colloid Interface Sci. 1996, 179, 431–438. [Google Scholar] [CrossRef]
- Ohshima, H. Dynamic electrophoretic mobility of a cylindrical colloidal particle. J. Colloid Interface Sci. 1997, 185, 131–139. [Google Scholar] [CrossRef] [PubMed]
- Ohshima, H. Henry’s function for electrophoresis of a cylindrical colloidal particle. J. Colloid Interface Sci. 1996, 180, 299–301. [Google Scholar] [CrossRef]
- Henry, D.C. The cataphoresis of suspended particles. Part I.-The equation of cataphoresis. Proc. R. Soc. Lond. A 1931, 133, 106–129. [Google Scholar]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids, 2nd ed.; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Sherwood, J.D. Electrophoresis of rods. J. Chem. Soc. Faraday Trans. 2 1982, 78, 1091–1100. [Google Scholar] [CrossRef]
- de Keizer, A.; van der Drift, W.P.J.T.; Overbeek, J.T.H.G. Electrophoresis of randomly oriented cylindrical particles. Biophys. Chem. 1975, 3, 107–108. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ohshima, H. Transient Electrophoresis of a Cylindrical Colloidal Particle. Fluids 2022, 7, 342. https://doi.org/10.3390/fluids7110342
Ohshima H. Transient Electrophoresis of a Cylindrical Colloidal Particle. Fluids. 2022; 7(11):342. https://doi.org/10.3390/fluids7110342
Chicago/Turabian StyleOhshima, Hiroyuki. 2022. "Transient Electrophoresis of a Cylindrical Colloidal Particle" Fluids 7, no. 11: 342. https://doi.org/10.3390/fluids7110342




