Are Local Heat Transfer Quantities Useful for Predicting the Working Behavior of Different Pulsating Heat Pipe Layouts? A Comparative Study

Abstract

Despite a continuous effort devoted by the scientific community, a large-scale employment of Pulsating Heat Pipes for thermal management applications is still nowadays undermined by the low reliability of such heat transfer systems. The main reason underlying this critical issue is linked to the strongly chaotic thermofluidic behavior of these devices, which prevents a robust prediction of their working behavior for different geometries and operating conditions, consequently hampering proper industrial design. The present work proposes to thoroughly compare data referring to previous infrared investigations on different Pulsating Heat Pipe layouts, which have focused on the estimation of heat fluxes locally exchanged at the wall–fluid interfaces. The aim is to understand the beneficial contribution of local heat transfer quantities in the prediction of the complex physics underlying such heat transfer systems. The results have highlighted that, regardless of the considered geometry and working conditions, wall-to-fluid heat fluxes are able to provide useful quantities to be employed, to some extent, to generalize Pulsating Heat Pipe operation and to improve their existing numerical models.

1. Introduction

Pulsating Heat Pipes (PHPs) are promising passive two-phase heat transfer devices which have achieved resounding interest among the scientific community during the last decades due to their highly advantageous technological features and are especially useful for thermal management applications [1]. Specifically, PHPs are pipes partially filled with a working fluid in saturation conditions and often constituted by three main sections, namely the evaporator (heated area), the condenser (cooled area), and the adiabatic section (transport section). Effective heat dissipation is generally obtained at the heated area thanks to self-sustained, thermally driven oscillations between the evaporator and the condenser through the adiabatic section [2]. Depending on their layout, PHPs may be classified as tubular PHPs, made of a tube arranged in a serpentine manner, and Flat Plate PHPs (FPPHPs), where the channels for the working fluid are machined on a flat plate [3,4,5]. Moreover, when the inner hydraulic diameter falls below 500 μm, devices are usually referred to as micro-PHPs [6].

PHP heat transfer performance is usually studied in terms of thermal characterizations, i.e., by evaluating equivalent thermal resistances under different operating conditions, including varying working fluid, the heat load to the evaporator, orientation, and condenser temperature [7,8,9,10,11]. Such an approach has been proven to be extremely suitable and effective from an application standpoint, i.e., when specific applications are considered, spanning from thermal management of batteries and electronic equipment to heat recovery applications and the cooling of foldable systems in both standard and microgravity conditions [12,13,14]. Nonetheless, the effectiveness of equivalent thermal resistance in terms of overall generalization of the working behavior is extremely controversial. In fact, the available literature does not provide any established methods for the prediction of PHP operation. Generalization attempts have been carried out in the past decades by means of empirical and semi-empirical correlations. Rittidech et al. [15] were among the first researchers to propose empirical correlations for PHPs. Their model aimed at predicting the transferred heat flux at horizontal orientation by evaluating the Kutateladze number. The standard deviation between the prediction and the experiments was equal to ±30%. However, the quantity of available experimental data on heat fluxes were quite limited due to the still premature literature, resulting in probably lower robustness and reliability of the proposed correlation. Khandekar et al. [16] highlighted the better fitting performances of semi-empirical models over standard empirical ones. A total of 248 data points on tubular pulsating heat pipes were used to develop, together with theoretical models, a correlation for the maximum heat flux exchangeable by a PHP device, with an overall drift in prediction of ±30%. Qu and Wang [17] used collected data on three PHPs, presenting different inner diameters and tested with different working fluids/volumetric filling ratios and previous outcomes from the literature to design an empirical correlation based on a total of 510 data points. The average standard deviation between the employed data and the predicted Kutateladze number and thermal performance was equal to ±40%.

More recently, artificial neural networks have been explored to improve the prediction capabilities of empirical and semi-empirical models, hence tackling difficulties linked to the critical definition of influencing parameters and dimensionless groups for the description of PHP complex thermo-fluid dynamics. Wang et al. [18] used 772 data points picked from previous studies on different PHPs presenting varying geometrical and operational features to build an artificial neural network model with 7 nodes in the input layer, 11 nodes in the hidden layer, and 1 node in the output layer. The prediction capability was assessed to be highly superior to traditional empirical correlations (average accuracy of about 0.22% for thermal resistance prediction), although the working fluid greatly affected model’s deviations from the experimental data. High prediction accuracies were also assessed by other neural network models, such as the ones by Jokar et al. [19] (average relative error less than 5%) and by Ahmadi et al. [20] (minimum deviation of 3.33% achieved through the least-squares support-vector machine model). However, as underlined by Kholi et al. in their review article [21], artificial neural network models per se provide no physical insight into the PHP thermo-fluid dynamics, resulting in poor flexibility and accuracy outside the training dataset ranges. Such an issue inevitably undermines a full understanding of the complex physics underlining PHP functioning as well as a robust conceptualization of design techniques to be used for reliable, large-scale employment by industries [2]. Typical figures of merit, such as equivalent thermal resistances, have been thus proven to provide viable pieces of information on PHP-influencing parameters while lacking generality probably due to almost absent standardization of experimental approaches.

In the last few years, research effort has been devoted to the comprehension of the inner thermo-fluid dynamics of PHPs through the promotion of novel figures of merit, including heat fluxes locally exchanged between the working fluid and the PHP walls. Jo et al. [22] investigated a flat micro-PHP to shed light on the debated sensible/latent heat transfer processes occurring in PHPs. The adopted multilayer structure of the walls allowed simultaneous assessment of outer and inner wall temperatures in the overall system through thermography, which resulted in the estimation of wall-to-fluid heat fluxes in all the device sections (evaporator, condenser, and adiabatic section). Additional direct visualizations enabled a one-to-one comparison between the liquid–vapor phase displacement and exchanged heat flux to ponder sensible/latent heat contributions. However, it has to be underlined that, despite the high temporal and spatial accuracy of the method, the realization of such a multilayer structure, which represents the core of the estimation of local heat fluxes in [22], would be unfeasible for tubular devices due to manufacturing difficulties. Moreover, the presented results might not be extended to the physical description of more typical PHP layouts, such as those made of metallic materials, due to intrinsic differences in terms of overall convective and conductive heat transfer. To address these issues, local wall-to-fluid heat fluxes have been evaluated in the previous literature by means of different experimental and post-processing approaches for metallic devices. Pagliarini et al. [23] proposed a novel technique for estimating heat fluxes locally exchanged between the working fluid and the walls in three-dimensional, tubular PHPs made of aluminum channels (also called “Space PHPs”) under microgravity conditions. Specifically, the experimental analysis was based on non-intrusive, infrared (IR) acquisitions on the outer wall surfaces within the adiabatic section (opportunely coated with highly emissive paints), used as inputs for the Inverse Heat Conduction Problem (IHCP) resolution approach. The results highlighted the high capability of the wall-to-fluid heat fluxes to provide insight into the inner fluid dynamics of the device. The same methodology of [23] was therefore adopted in [24] for the study of the Space PHPs at different orientations and condenser temperatures under standard gravity. Here, results on heat flux amplitudes and dominant fluid oscillation frequencies were presented. The method of [23] was extended by Iwata et al. [25] to the study of a tubular micro-PHP made of stainless-steel. IR acquisitions were carried out within the condenser section, cooled by free convection with air. Conclusions on the fluid oscillations and heat flux amplitudes were drawn. Lastly, a novel method, similarly based on the IHCP resolution approach, was proposed by Pagliarini et al. [26] for wall-to-fluid heat flux estimation in an FPPHP made of copper. Statistical reductions were performed on the resulting wall-to-fluid heat flux amplitudes. In [27], the figures of merit referred to fluid oscillations and transverse conduction in the same FPPHP device, analyzed through the same experimental and post-processing approach in [26], were collected and presented. The outcomes resulting from each experimental campaign were capable of quantitatively outlining the inner thermo-fluid dynamics of the investigated systems, even without any presence of transparent inserts for direct fluid visualizations. The main device specifics, test conditions, and quantified phenomena are listed in

Table 1. Test conditions and quantified phenomena.

Studied Device	Manufacturing Material	Working Fluid	Cooling Method	Section of Interest 1	Quantified Phenomena
Tubular PHP (Space PHP) [23,24]	Aluminum	Methanol	Prescribed temperature (Peltier cell array)	Adiabatic section	Thermal performance Heat flux amplitude against power input Working regimes Flow modes Average fluid velocity (circulatory flow on ground) Oscillation frequency (microgravity)
Micro-PHP [25]	Stainless-steel	R134a	Free convection	Condenser	Thermal performance Working regimes Oscillation frequency Flow modes
FPPHP [26,27]	Copper	Water/ethanol mixture (20% w.)	Prescribed temperature (copper heat exchanger)	Adiabatic section	Thermal performance Heat flux amplitude against power input Working regimes Oscillation frequency and transverse conduction

¹ Device section over which IR acquisitions were carried out during pseudo-steady state.

.

Due to the greatly promising results of wall-to-fluid heat fluxes for PHP descriptions, local heat transfer quantities are believed to be a straightforward and powerful tool for the generalization and prediction of the PHP operation regardless the adopted layout, the manufacturing material, the working fluid, or the operating condition. Hence, the aim of the present work is to disclose the potentiality of wall-to-fluid heat fluxes locally exchanged at the wall–fluid interfaces for PHP working behavior prediction through the comparison of results provided by the previous literature [24,25,26,27], available, to the authors’ best knowledge, for metallic devices, which are of greater manufacturing and application appeal for the general industry.

2. Materials and Methods

In the present section, the methodologies adopted in the previous works are briefly outlined. The steps belonging to the experimental procedure are summarized below:

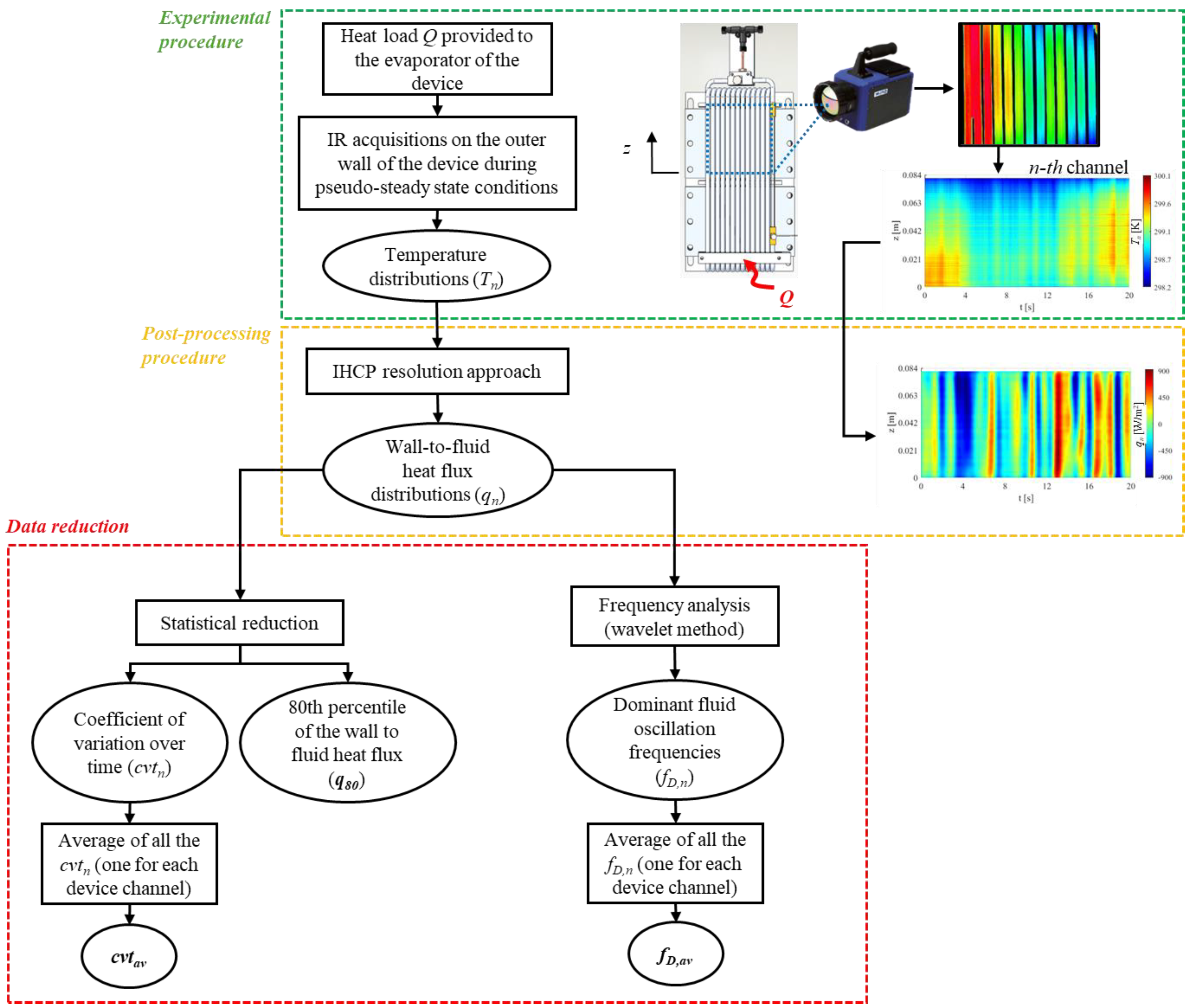
• Step heat loads are provided to the evaporator, the investigated device under specific working conditions (e.g., specific orientation, condenser temperature, etc.).
• When pseudo-steady-state conditions are reached, IR videos are taken at the outer wall surface of the section of interest (either the adiabatic section or the condenser, depending on the considered device).
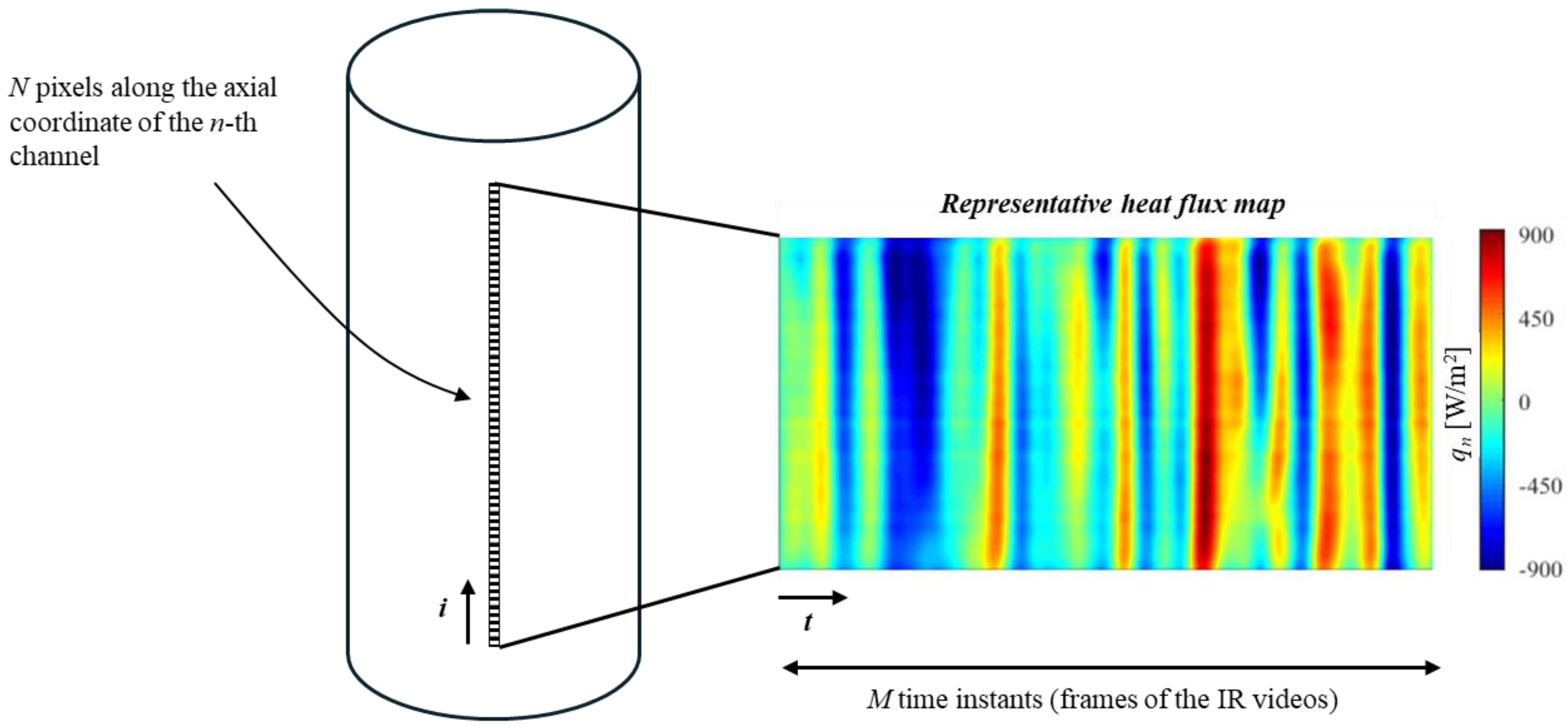
• For every framed channel, temperature distributions are collected by assuming negligible temperature variations along the circumferential direction; this results in N × M temperature distributions, with N being the number of pixels along the axial coordinate of each tube and M the number of time instants (frames).
• The temperature distributions referring to every device channel are therefore processed by means of the IHCP resolution approach, resulting in wall-to-fluid heat flux distributions q_n (for the n-th channel). For the sake of brevity and clarity, the theoretical formulations assumed by the IHCP resolution method for the geometries under investigation are left to the reader ([23] for tubular layouts, [26] for FPPHP layouts).
• The wall-to-fluid heat fluxes are processed through different reduction approaches; statistical approaches are used to provide figures of merit for all the collected wall-to-fluid heat flux distributions, while the wavelet method is adopted to assess heat flux oscillation frequencies, which directly reflect fluid oscillation frequencies.
• The above steps are replicated for every heat load step to the evaporator/all-test conditions.

All the steps referring to the experimental approach, the post-processing procedure, and the data reduction are overviewed in the flowchart in Figure 1.

The evaluated heat fluxes were proven to be inherently linked to the fluid motion, even though no information could be obtained in terms of liquid–vapor displacement due to thermal inertia and the overall thermal properties of the walls [23]. In the following subsections, the reduction methods adopted to estimate meaningful figures of merit aimed at comparing the results of previous experimental campaigns on different devices are described.

2.1. Statistical Reduction

Concerning statistical approaches, the coefficient of variation cvt was proposed to quantify heat flux variations over time. In particular, cvt is defined, for the n-th device channel, as follows [23]:

$${\mathit{cvt}}_n=\frac{\sum _{i=1}^N\left[\frac{\mathit{std}\left(\left|q_n\left(i,t=1,\dots ,M\right)\right|\right)}{\mathit{mean}\left(\left|q_n\left(i,t=1,\dots ,M\right)\right|\right)}\right]}{N}$$

(1)

where N and M are the space (axial) and time dimensions of the heat flux maps, respectively, std is the standard deviation operator, mean is the arithmetic mean operator, i is the space coordinate, and t is the time coordinate. Of note, N reflects the number of pixels in the thermographic acquisitions along the channels’ axis, while M reflects the number of frames in the IR videos (function of the adopted sampling frequency and videos length). To better highlight space and time discretization of the wall-to-fluid heat flux maps adopted in Equation (1), a representative scheme is shown in Figure 2.

Specifically, cvt was proven to provide quantitative pieces of information in terms of working regime detection, thus assuming different values during the start-up, intermittent flow, and full activation phases of the PHPs [24,26]. This represents an important improvement with respect to typical working regime identifications, which usually rely on qualitative observations of wall temperature trends at the evaporator and/or condenser sections [2,28,29].

By averaging cvt_n for the overall system, i.e., for every device channel, a new meaningful coefficient, cvt_av, is defined, quantifying differences in terms of thermofluidic interactions between the fluid and the channel wall in the whole PHP:

$${\mathit{cvt}}_{\mathit{av}}=\frac{\sum _{n=1}^{\mathit{num}}c{\mathit{vt}}_n}{\mathit{num}}$$

(2)

where num represents the total number of PHP channels.

Additionally, q₈₀ was proposed to statistically describe the wall-to-fluid heat flux magnitude in the overall devices. Such a quantity was computed as the 80th percentile [30] of the absolute value of all the estimated heat flux values. In particular, the 80th percentile of all the absolute heat flux values $q=\left\{{|q}_1\left(i=1,\dots ,N,t=1,\dots ,M\right)\right|;\dots ;{|q}_{num}\left(i=1,\dots ,N,t=1,\dots ,M\right)\left|\right\}$ represents the $q^{*}=$$\left|q_{n^{*}}(i^{*},t^{*})\right|$ value below which the 80% of $q$ falls. All the high amplitude, sporadic peaks (i.e., belonging to the remaining 20% of $q$) are therefore neglected from the analyses since they are considered meaningless in terms of statistical description of the device operation [23].

2.2. Frequency Analysis

Different techniques have been used, in the past literature, to perform frequency analyses on PHP fluid oscillations. The most typical method is represented by the fast Fourier transform, firstly applied by Jong-Soo et al. [31] to the fluid pressure signals in the evaporator section of a PHP presenting rectangular channels and filled with R-142b. The Hilbert–Huang transform [32,33] and the time strip technique [34] have also been proposed for the study of fluid oscillation frequencies. However, while some works were able to quantify PHP fluid oscillation features by assessing dominant fluid oscillation frequencies [29,35,36], others failed in such a task by means of the mentioned methods [37,38], although the operation of the investigated devices was clearly confirmed by either direct fluid visualizations or temperature/equivalent thermal resistance trends. Perna et al. [39] took advantage of fluid pressure signals and collected close to the evaporator and condenser sections of a multi-turn pulsating heat pipe filled with FC-72 to successfully quantify fluid oscillation frequencies by means of the wavelet method. In the work, the authors underlined the superiority of the wavelet-based method with respect to fast Fourier transform. In fact, the wavelet transform allows, on one hand, dynamically increased frequency resolution at lower frequencies and greater time resolution at higher frequencies. On the other hand, it provides smoother and better mathematically defined power spectra than classical Fourier spectra. Very good agreement between the dominant frequencies computed by the wavelet method on pressure signals and the thermographic data on the outer wall of the device was shown by Pagliarini et al. [23], who thus proved the full suitability of the IR data as inputs for the wavelet method for PHPs. Hence, frequency analyses were carried out by adopting, among other analysis tools, the wavelet method. Specifically, the Morlet wavelet for the dimensionless time η was used [40]:

$$\psi (\eta )={\frac{1}{\sqrt{\pi }}e}^{-\frac{{\eta }^2}{2}}{e}^{i{\omega }_0\eta }$$

(3)

Time distributions q_n(t) of the wall-to-fluid heat fluxes were thus considered as inputs for the method, which was based on the following continuous formulation [41]:

$$W_{\psi }\left(a,\tau \right)=\frac{1}{\sqrt{a}}{\int }_{-\infty }^{\infty }{q}_n\left(t\right){\psi }^{*}\left(\frac{t-\tau }{a}\right)\mathit{dt}$$

(4)

where a and τ are the wavelet scale and time shift, respectively, and the superscript * denotes the complex conjugate. The peaks in the power spectra provided by the wavelet method were referred to as dominant oscillation frequencies of the fluid oscillation phenomena f_D [39]. The average dominant fluid oscillation frequency f_D,av related to the whole device was therefore computed as:

$$f_{D,\mathit{av}}=\frac{\sum _{n=1}^{\mathit{num}}{f}_{D,n}}{\mathit{num}}$$

(5)

3. Results

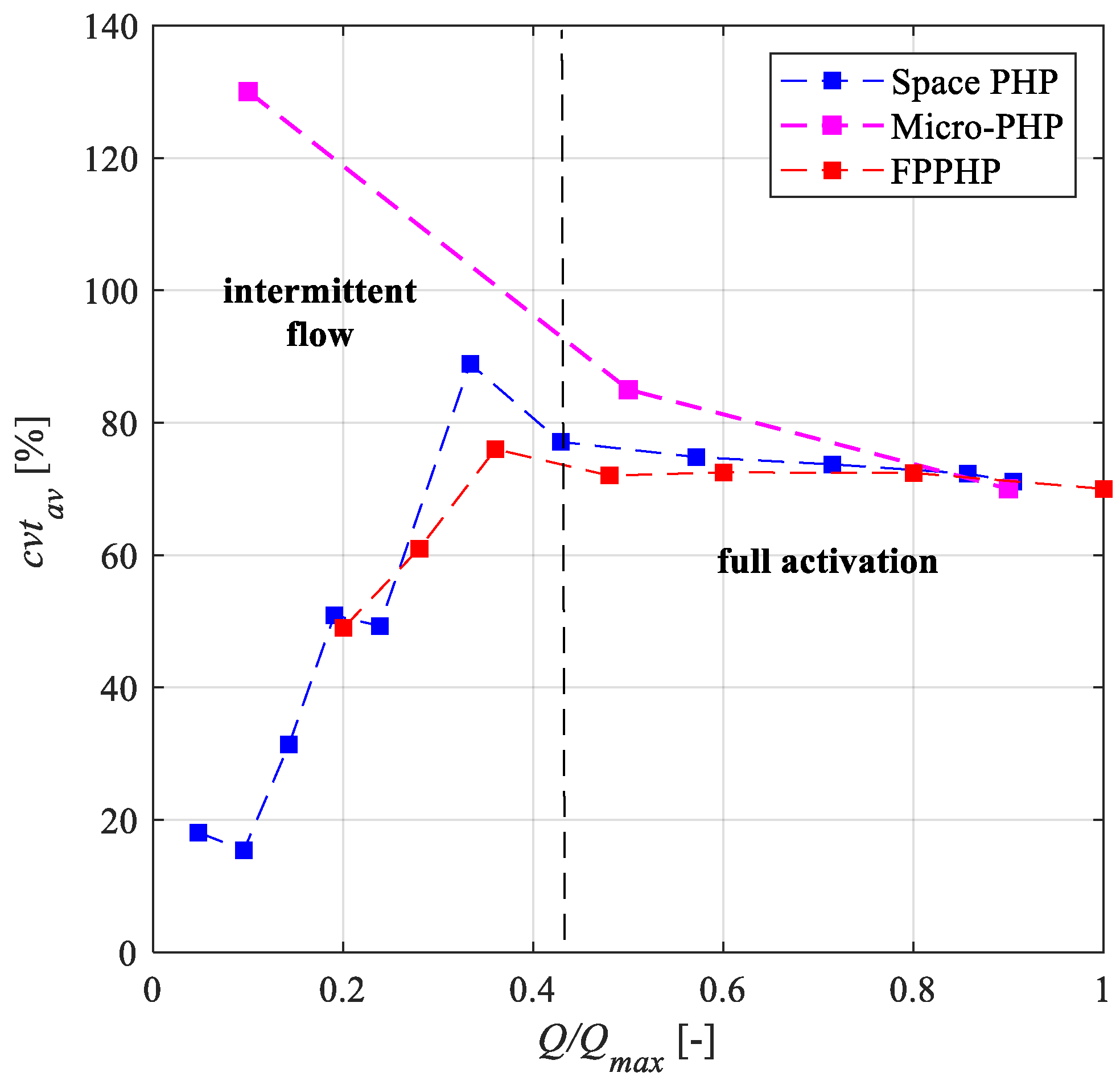
3.1. Repeatable Working Regime Detection

The first meaningful result of the comparative study refers to the working regime detection in every considered PHP device. To underline the strength and validity of such a coefficient for all the tested devices, the values of cvt_av, computed during the intermittent flow regime and the full activation, are shown for the Space PHP, the FPPHP and the micro-PHP in Figure 3. For the sake of comparison, the only vertical Bottom Heated Mode (BHM, evaporator placed below the condenser) was considered for all the PHPs, while the power input given to the evaporator was normalized with respect to the maximum provided heat loads Q_lim, equal to 190 W, 5 W, and 250 W for the Space PHPs, the micro-PHPs, and the FPPHPs, respectively. To note, all the Q_lim values are not to be intended as maximum heat loads provided to the evaporator (i.e., operational limit of the devices), but they rather reflect the safety limits chosen to prevent damage to the operators and to the experimental set-ups (the threshold evaporator temperature chosen is equal to 105 °C). In addition, the here reported data on the Space PHPs are referred to a condenser temperature equal to 20 °C (same set-point temperature given during the FPPHP investigation) to remove from the analysis any possible discrepancies due to viscous effects [24].

Here, it is interesting to notice that, despite the analyzed device, the intermittent flow is characterized by higher peaks in the cvt_av, i.e., by stronger heat flux variations over time in the overall device when heat load promotes the highest intermittency of the fluid motion. Concerning the Space PHPs and the FPPHPs, cvt_av increases up to a peak value at almost the same normalized power input to the evaporator (Q/Q_lim ≈ 0.35). The values assumed by these peaks differ by about 10%. In the micro-PHPs, cvt_av instead presents a monotonically decreasing trend from lower to higher normalized power inputs. Specifically, cvt_av assumes, within the intermittent flow, a high value at low Q/Q_lim, contrary to what was observed for the other devices. This may be due to two main factors: a different observation section (condenser, Table 1), which could result in different observed heat flux variations, and a different intermittent flow pattern occurring in micro-devices. Nonetheless, during the full activation (Q/Q_lim > 0.42), all devices exhibit a stabilization of the cvt_av around 73%, suggesting that such a value could be a significant reference for the full activation identification and prediction for every PHP geometry, regardless of the observation window and the cooling method.

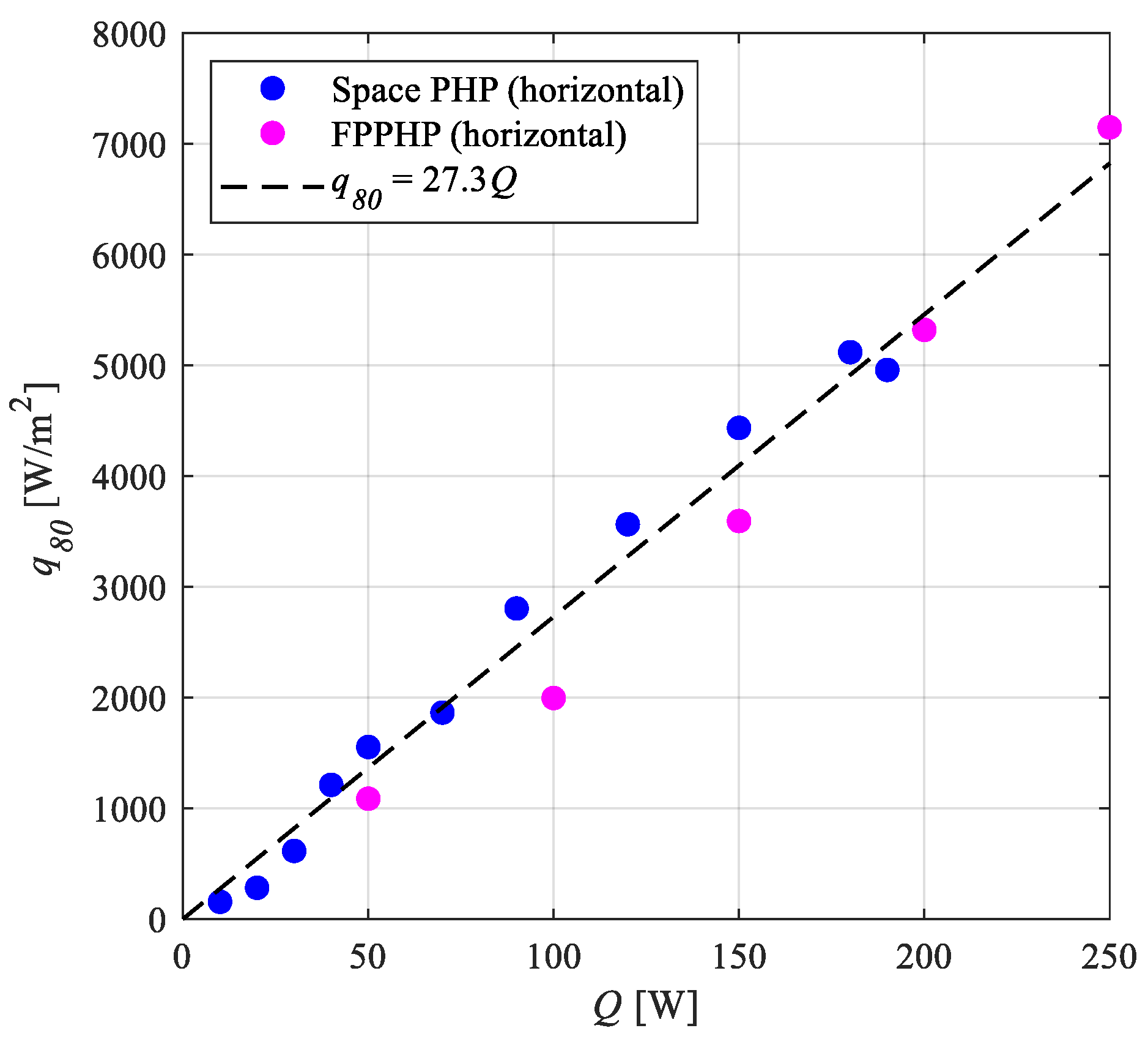
3.2. Trends in the q₈₀ Values

Another fruitful remark was achieved by comparing the values assumed by q₈₀ in the Space PHPs and the FPPHPs. These two devices were specifically chosen for comparison since the adiabatic section was investigated during pseudo-steady state conditions for both PHP layouts (Table 1). Such a comparison is shown in Figure 4. Here, the vertical BHM orientation was not considered since it promoted net fluid circulation inside the only Space PHP [24], with consequently different thermofluidic interactions between the working fluid and the device wall with respect to the FFPHPs.

Trends referring to both devices show an increase in q₈₀ both during the intermittent flow (from 20 W up to about 100 W) and the full activation regions. Such an increase in the heat load was therefore modeled by means of a linear fit of the data. Specifically, the curve which best fitted (in a least-squares sense) the data is defined by q₈₀ = 27.3 Q, with R² = 0.974. The fit was forced to pass through the origin for physical reasons (q₈₀ = 0 W/m² when no heat is given to the evaporator). The provided correlation can accurately describe the local wall-to-fluid interactions over the entire PHP operation, suggesting that, in the horizontal orientation, the amplitude of heat flux peaks does not depend either on the considered geometry or on the considered working regime. Nonetheless, it has to be stressed that the similar local heat transfer behavior experienced in both devices might also be due to a particular combination of beneficial and negative effects of the tilt angle and working fluid on the devices. In fact, on one hand, the horizontal orientation undermines the FPPHP operation in a more severe way than the tubular layouts due to stronger conductive phenomena occurring in the solid domain, which leads to a higher degree of thermalization and consequent lower pressure gradients for the fluid motion between the evaporator and the condenser [4]. On the other hand, the aqueous mixture employed during the FPPHP investigation enhances the device thermal performance [42], eventually leading to comparable local heat transfer within the adiabatic section in both the FPPHPs and the Space PHPs. The q₈₀ values and the provided model as a function of the heat load could lead to a prediction for the PHP operation in the horizontal orientation, along with a proper validation of the existing numerical models in terms of local heat transfer quantities for different PHP devices.

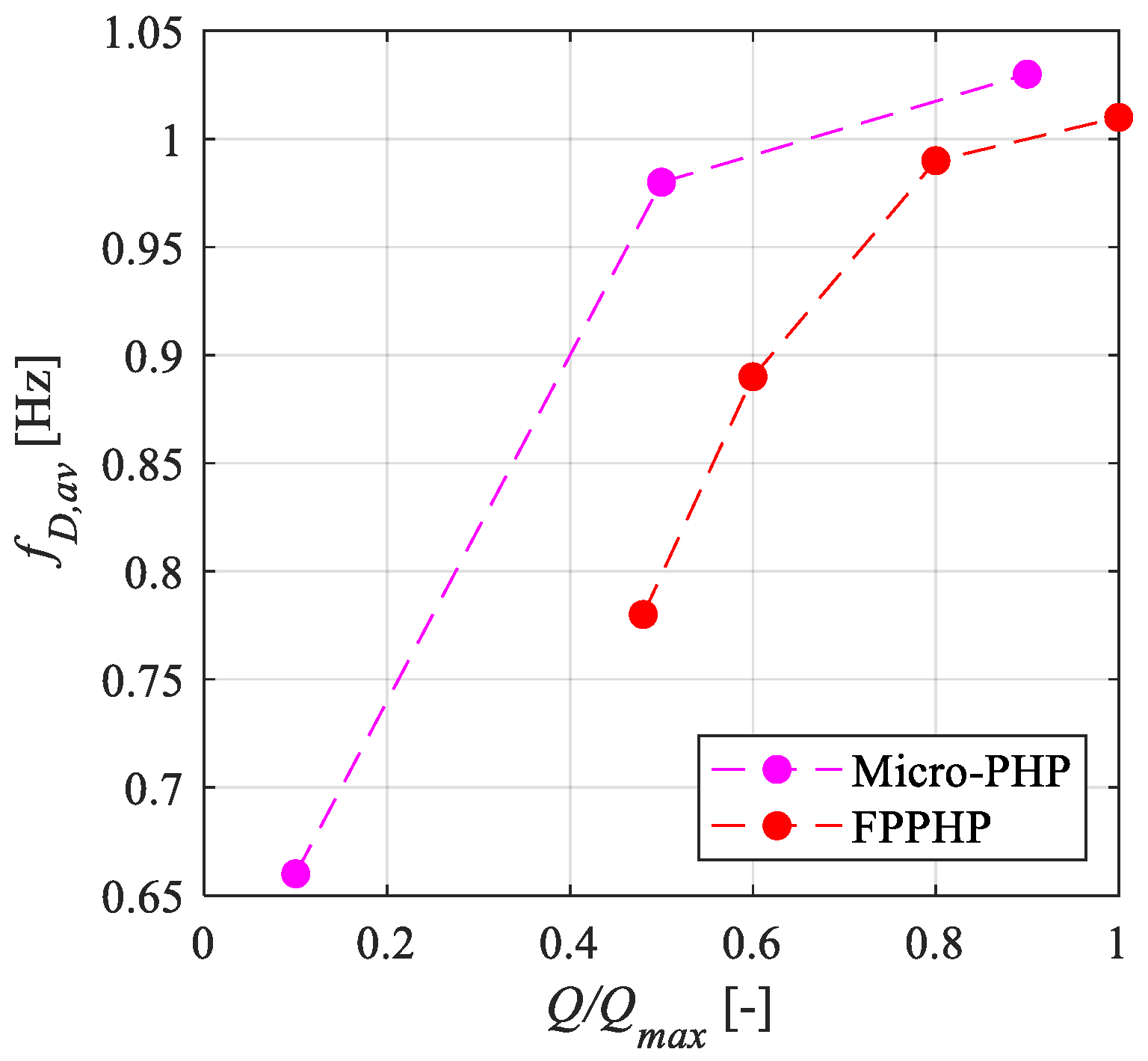
3.3. Stabilization of the Dominant Fluid Oscillation Frequency

Finally, the dominant fluid oscillation frequencies evaluated in the micro-PHPs and in the FPPHPs during the full activation were compared in the vertical BHM orientation. The Space PHP was not here taken into account due to the onset of circulatory rather than oscillatory flows [24].

The f_D,av values are shown in Figure 5 as a function of the dimensionless heat load. Here, as long as the power input to the evaporator increases, the fluid oscillation frequency tends to stabilize, regardless of the operating conditions, the geometry, the material, or the working fluid. Such a common trend opens to an interesting observation about the PHP flow pattern transition. Specifically, at high heat loads, a stabilization of the dominant fluid oscillation frequency could result in a saturation of heat transferable to the condenser, thus enabling local dry-out phenomena at the evaporator. The formation of dry spots could therefore promote the onset of annular flows, at least in some channels. This suggests that the prediction of different PHP heat transfer processes might be achieved by focusing on transitions in the fluid oscillation frequency trends at different normalized heat loads.

4. Conclusions

Results obtained by previous investigations of different PHP devices were compared with the aim of understanding the potentialities of wall-to-fluid heat flux quantities for the generalization and prediction of PHP working behaviors. In fact, the lack of effective predictive models represents a crucial gap in the literature and a phenomenological gap, especially for large-scale, industrial applications. The present comparative study focused on three different PHP layouts: a tubular PHP (Space PHP) [24], an FPPHP [26,27], and a micro-PHP (tubular channels) [25]. Two statistical quantities were considered, namely the cvt and the q₈₀, along with the dominant fluid oscillation frequencies f_D estimated by means of the wavelet method. The main outcomes of the present investigation are summarized below:

• The cvt_av coefficient succeeds in generalizing the working regime identification in different PHP layouts under the BHM orientation. In fact, it assumes comparable values for all the studied configurations, especially during the full activation phase;
• When different devices (Space PHPs and FPPHPs) tested in the horizontal orientation are compared, the correlation between the 80th percentile of the wall-to-fluid heat fluxes and the heat load provided to the systems follows a linear trend of the form q₈₀ = 27.3 Q;
• Regardless of the considered device, the dominant fluid oscillation frequencies tend to stabilize at high heat loads in vertical BHM operation, suggesting that the systems face a saturation of the heat transfer capabilities from the evaporator to the condenser due to intrinsic flow motion limitations. This could lead to the occurrence of local dry-outs at the evaporator section, resulting in the onset of annular flows.

In conclusion, the present comparative study suggests that PHP thermal behavior can be partially generalized by the reduction in wall-to-fluid heat fluxes, regardless of the geometry or the operating settings. It has to be stressed that the term “generalization” cannot fully and ultimately reflect, in the light of the proposed results, the real capabilities of wall-to-fluid heat flux reductions in terms of predicting PHP thermal behaviors. Hence, by “partially generalized”, the authors express reasonable reservations on the full effectiveness of generalizing the thermofluidic response of any kind of PHP device through the given tools, leaving the question, “Are local heat transfer quantities useful for predicting the working behavior of different Pulsating Heat Pipe layouts?”, partially open to future, in-depth investigations. Nonetheless, despite the number of available data and analyzed devices being relatively small due to a lack of works experimentally dealing with heat flux estimation in PHPs, the results exhibit clear trends that imply a concrete possibility of adopting local heat transfer features to achieve a more general quantification of PHP thermal behavior with respect to commonly employed figures of merit, such as equivalent thermal resistances. The obtained remarks can be therefore used not only as benchmarks for the improvement of PHP numerical models but also to advance the generalization and prediction of PHP thermal response, which is still hampered by the highly complex physics underlying such devices.