Numerical Study of Lateral Migration of Elliptical Magnetic Microparticles in Microchannels in Uniform Magnetic Fields
Abstract
:1. Introduction
2. Simulation Method
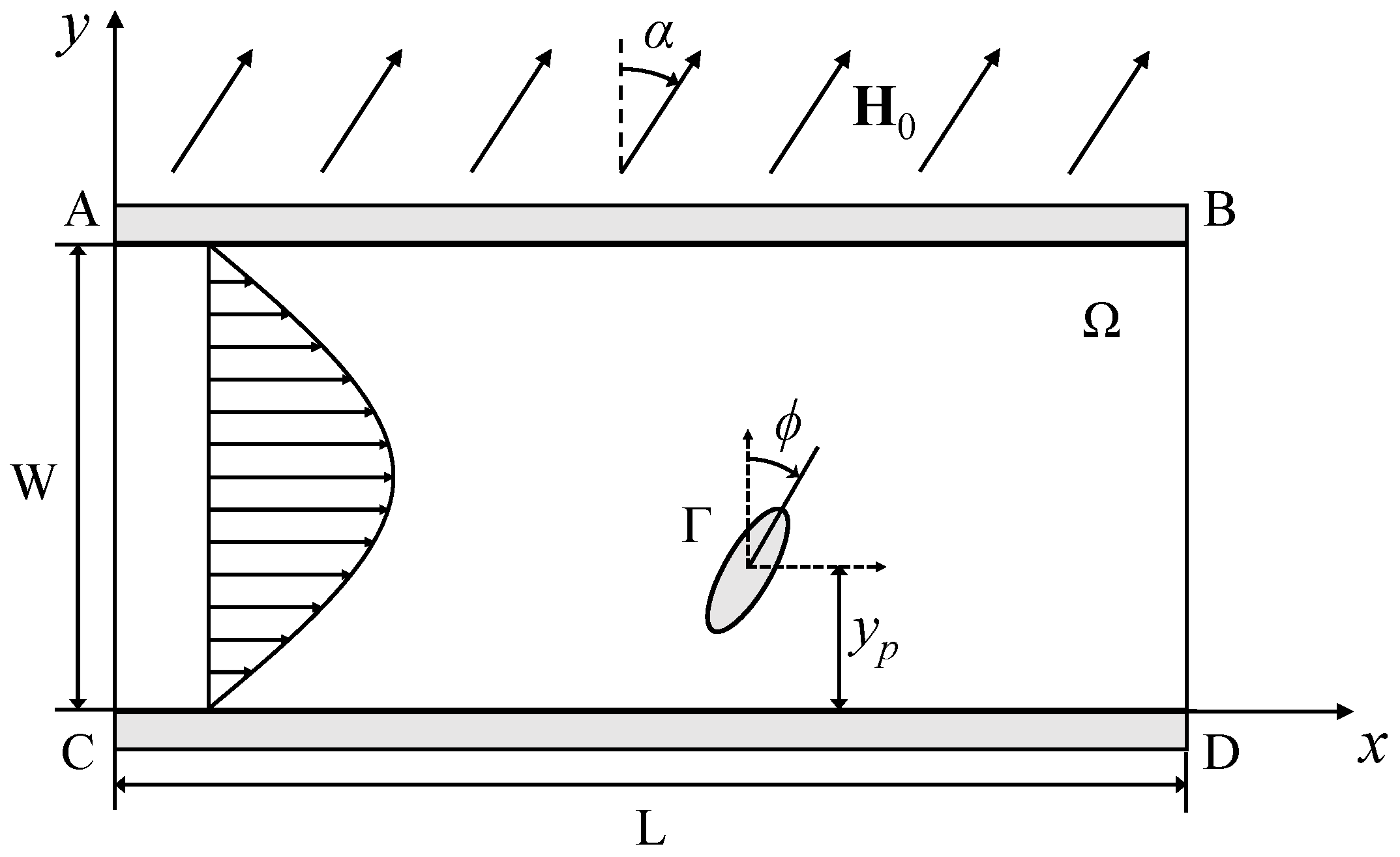
2.1. Mathematical Model
2.2. Material Properties Used in Simulations
2.3. Grid Independence Analysis
3. Results and Discussion
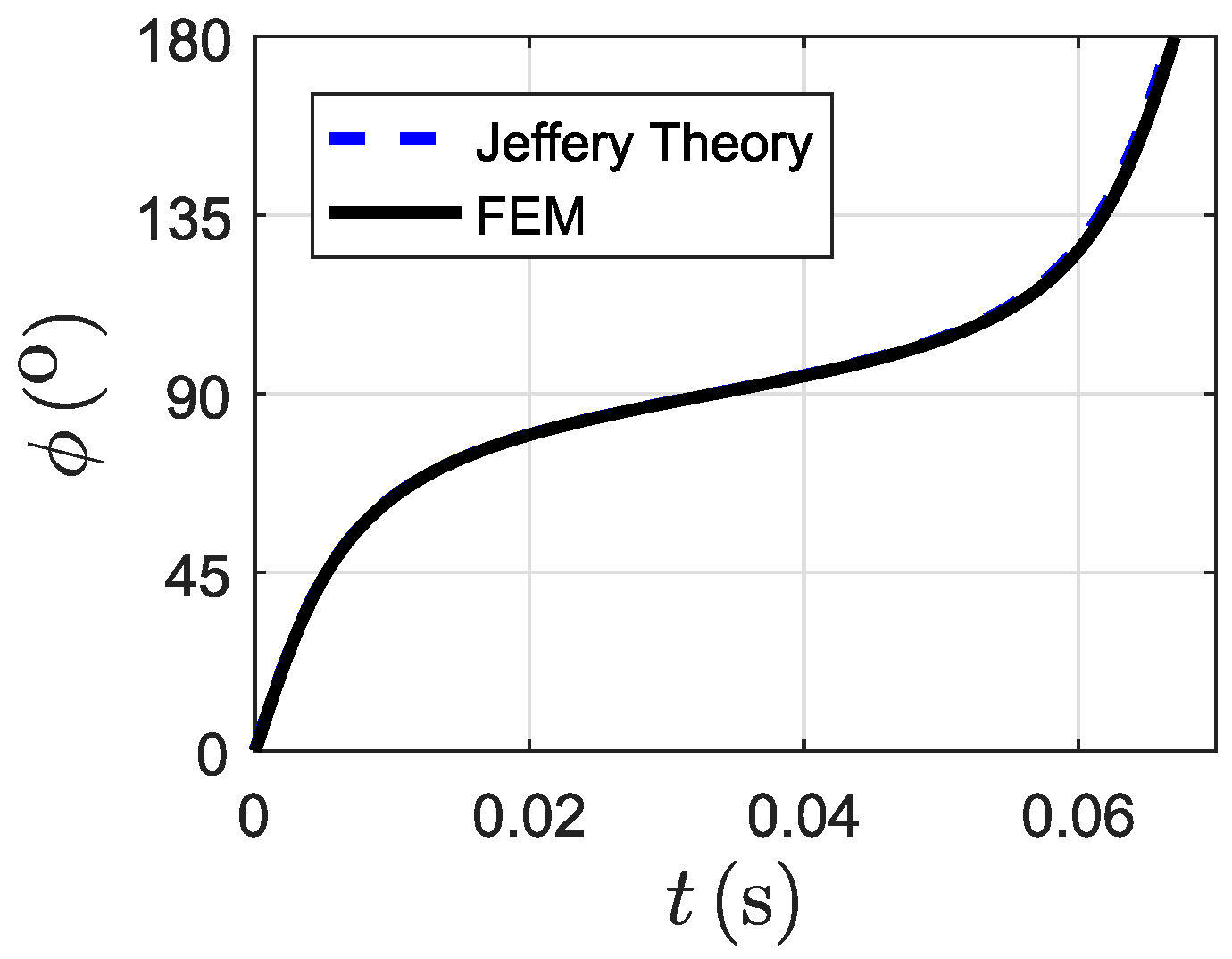
3.1. Validation of Numerical Method
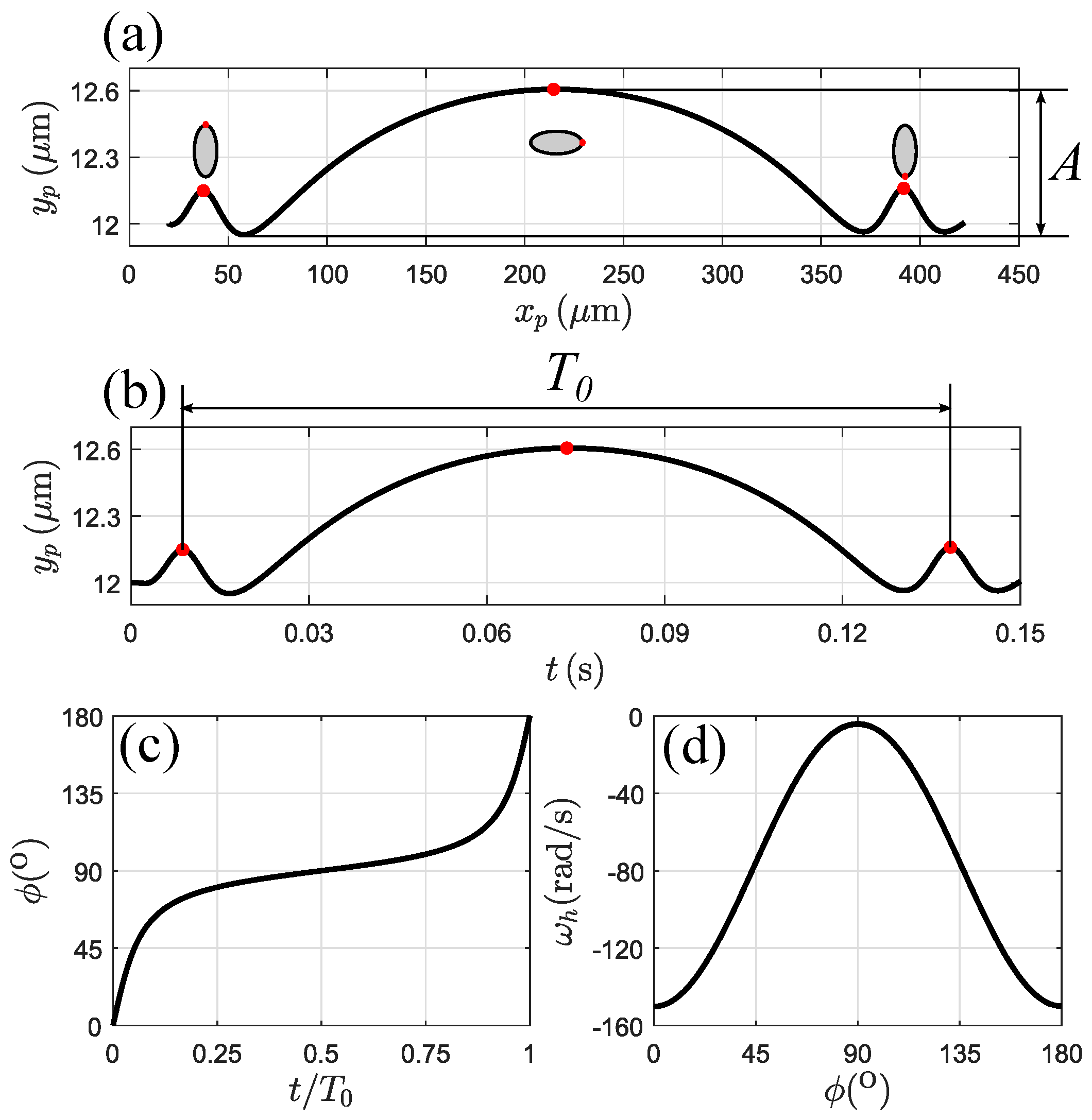
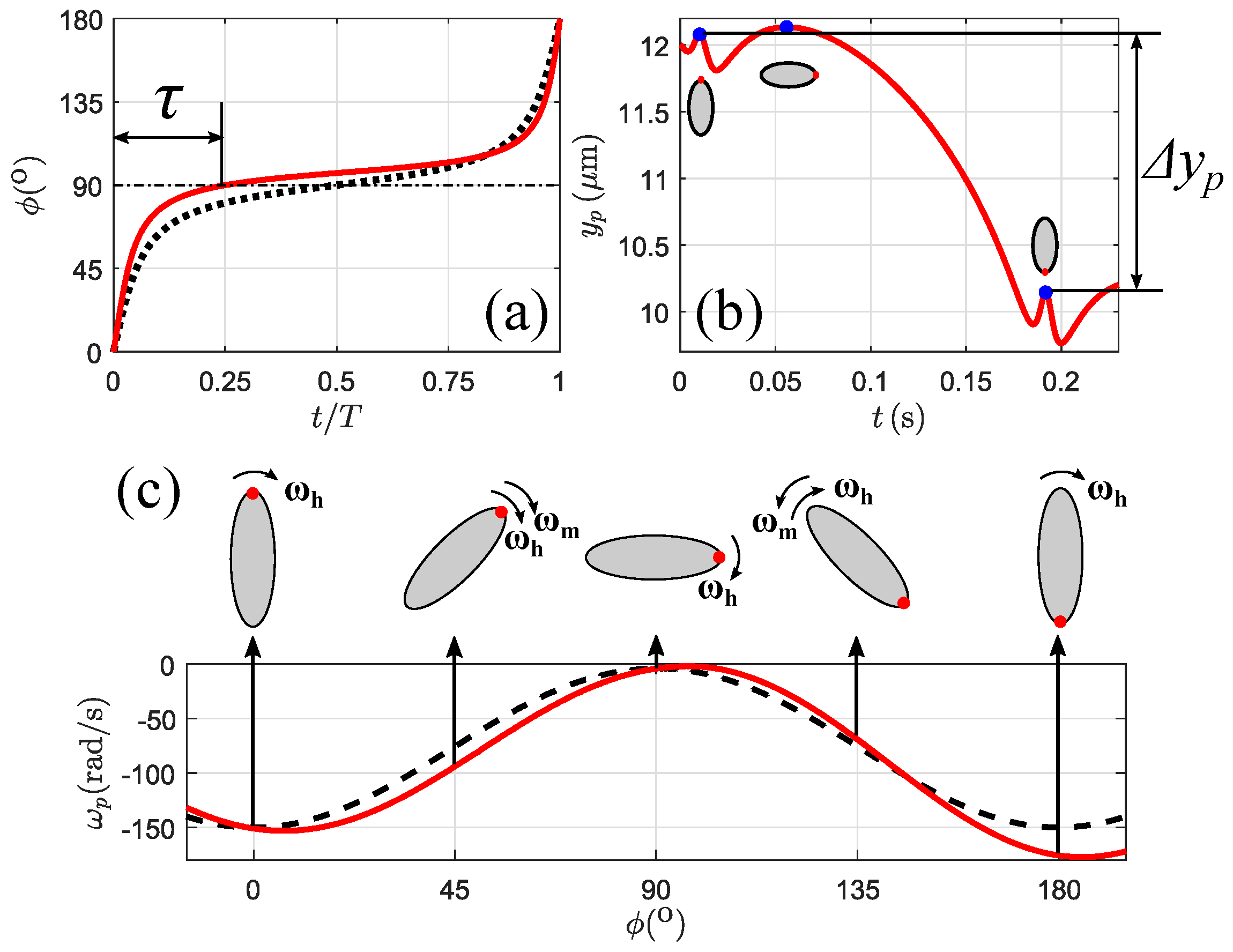
3.2. Particle Motion without a Magnetic Field
3.3. Particle Motion in a Magnetic Field
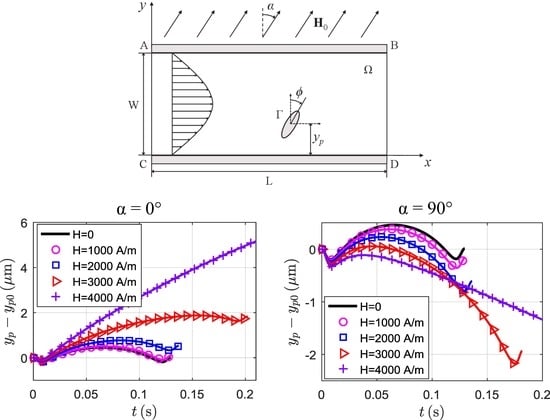
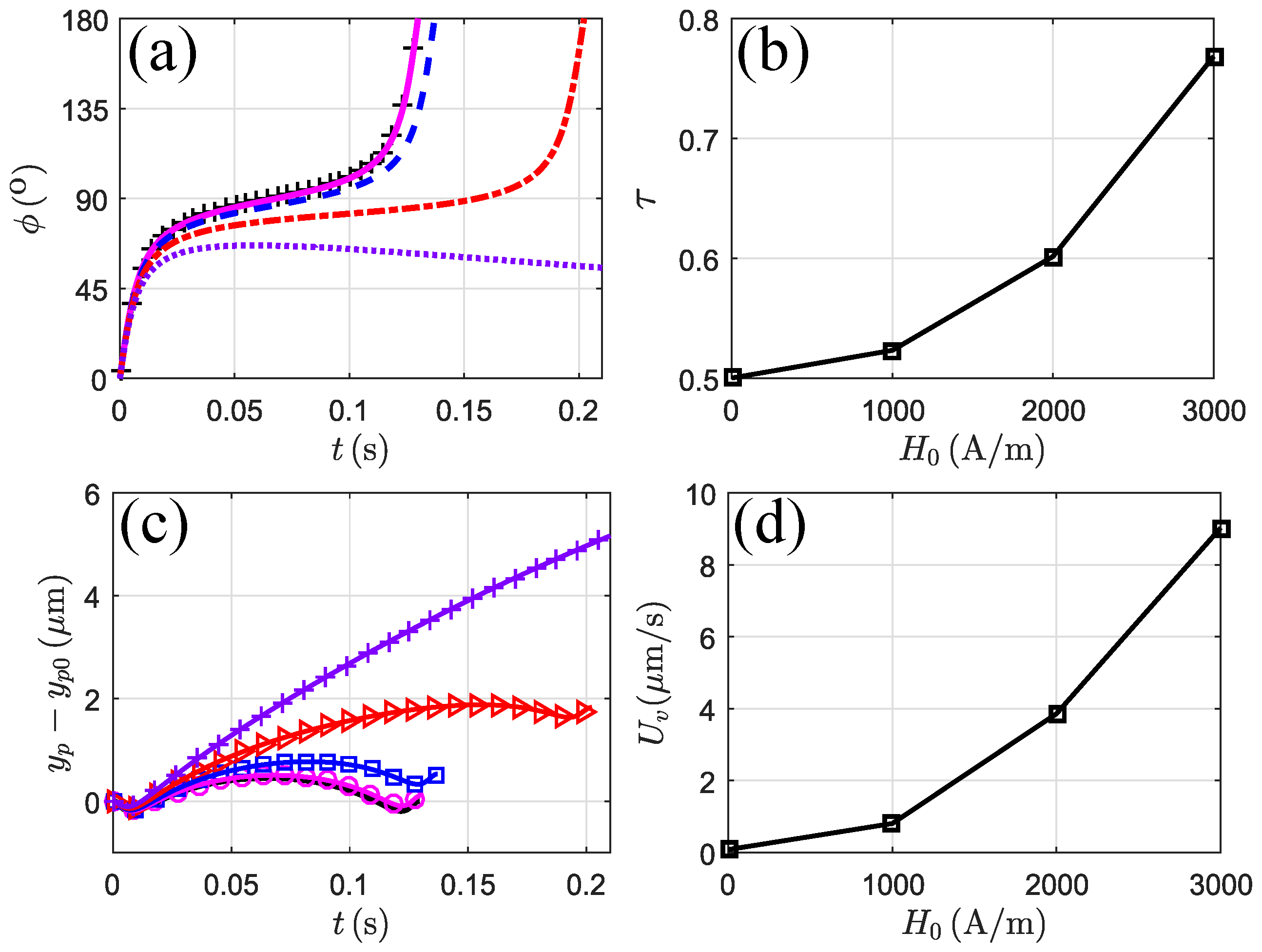
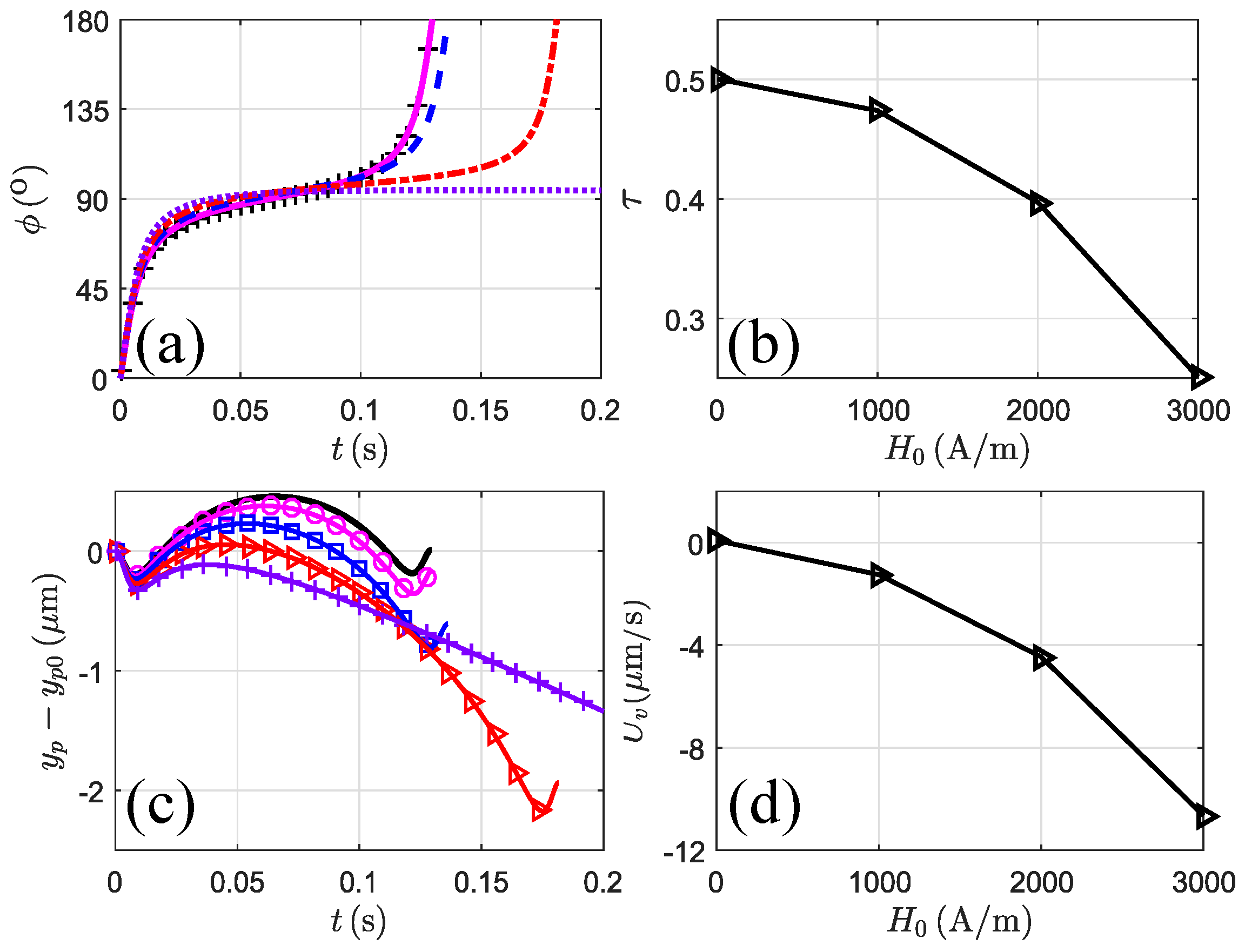
3.3.1. Magnetic Field at
3.3.2. Magnetic Field at
3.3.3. Magnetic Field at
3.3.4. Magnetic Field at
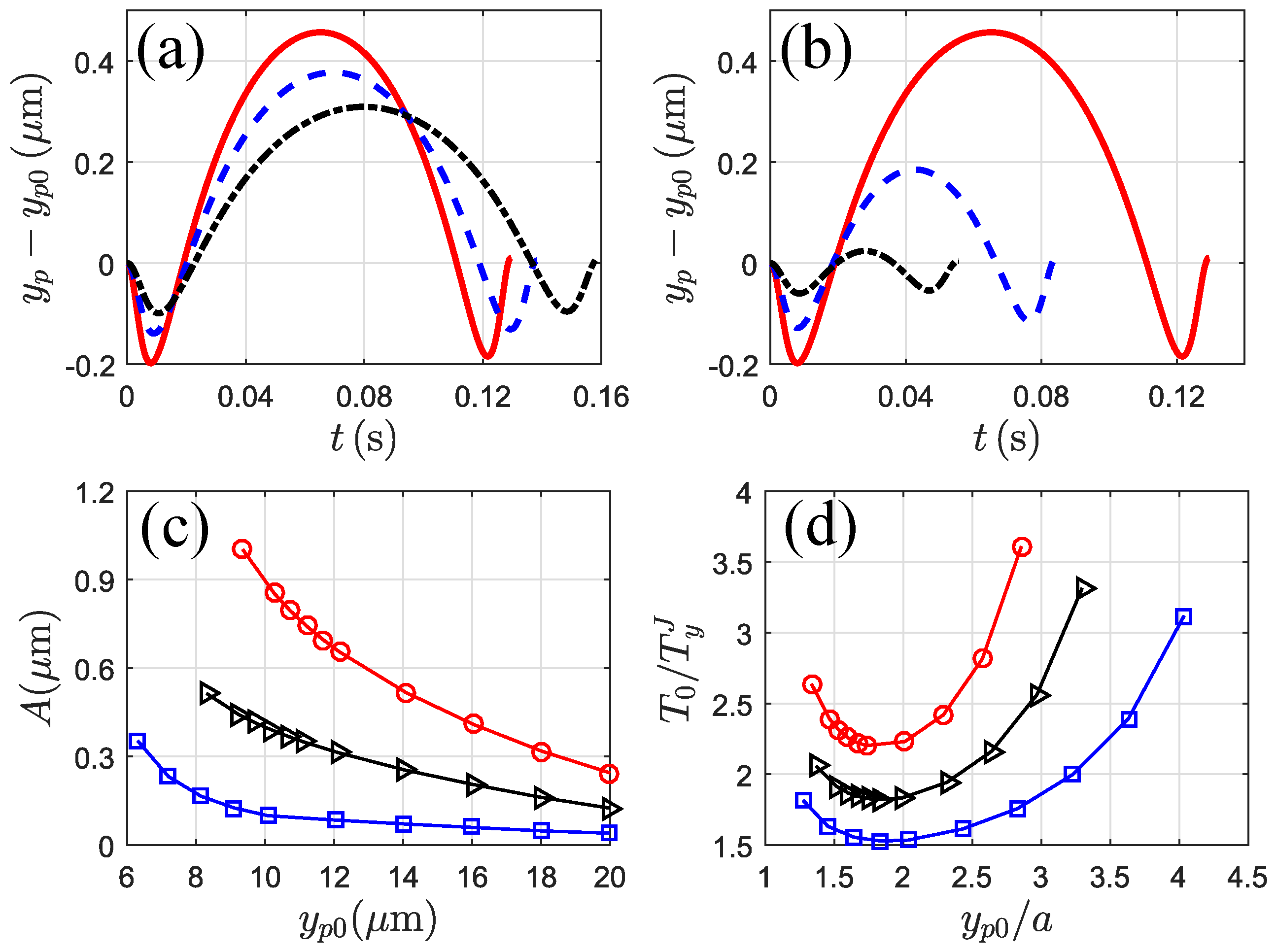
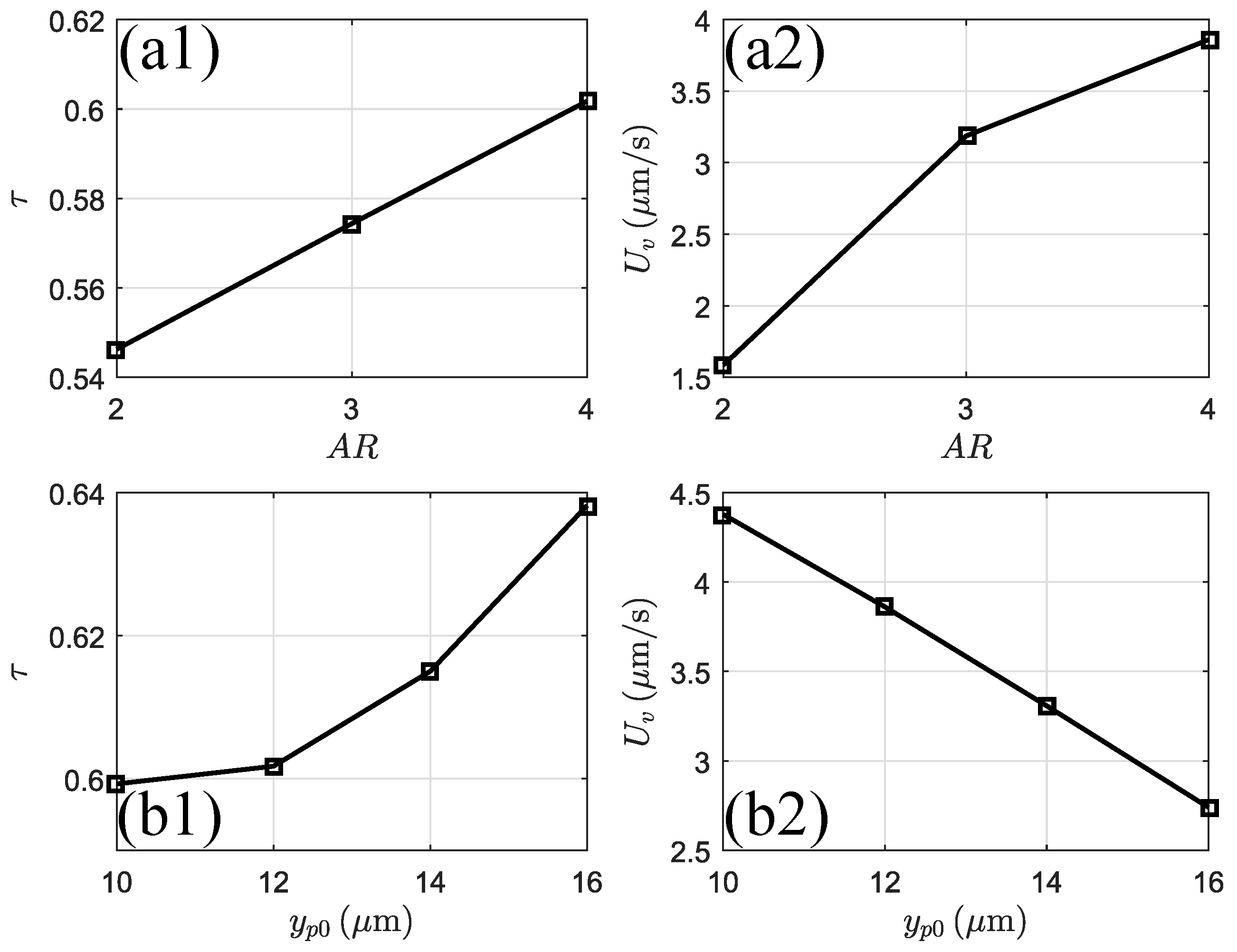
3.3.5. Effects of Particle Shape and the Wall
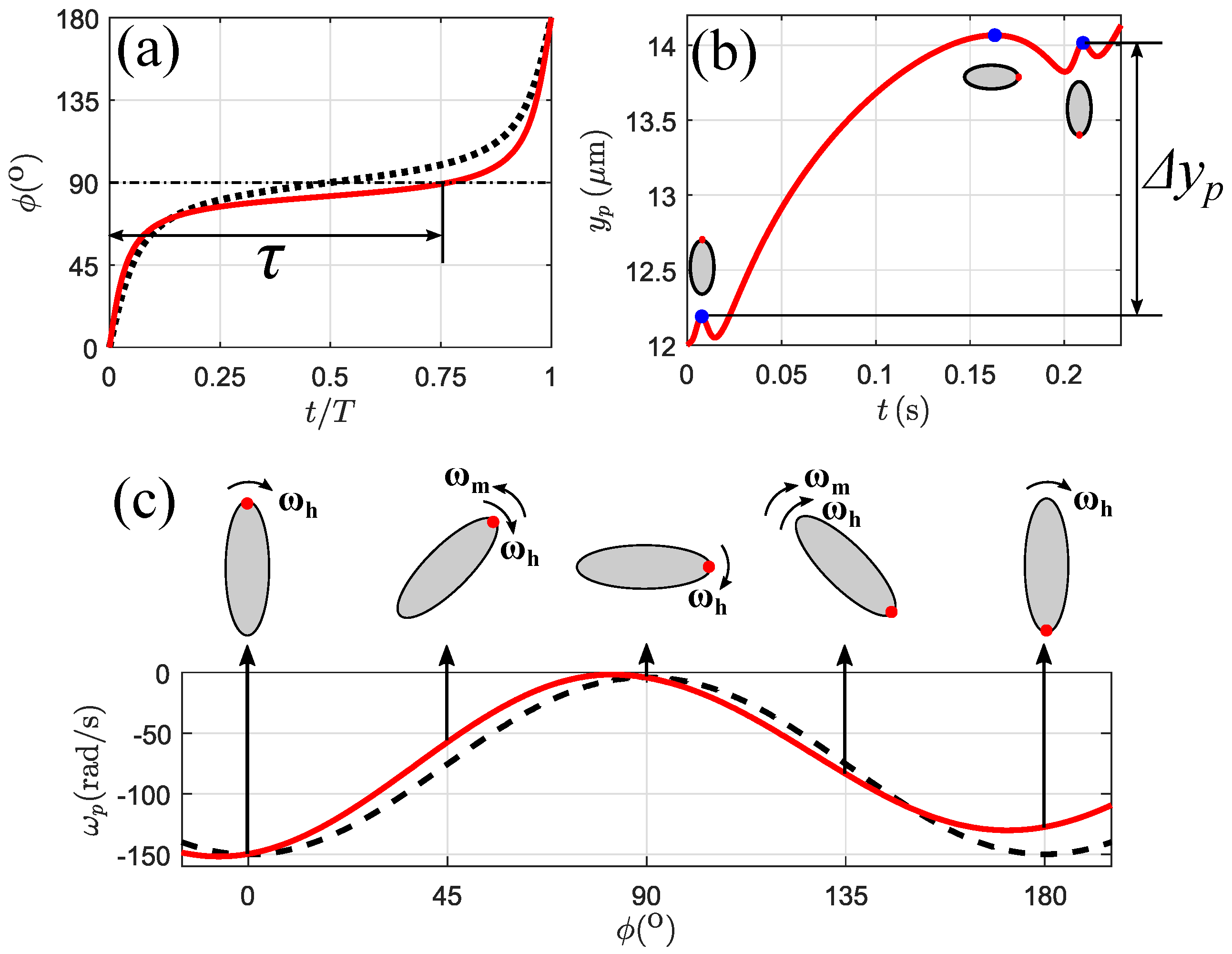
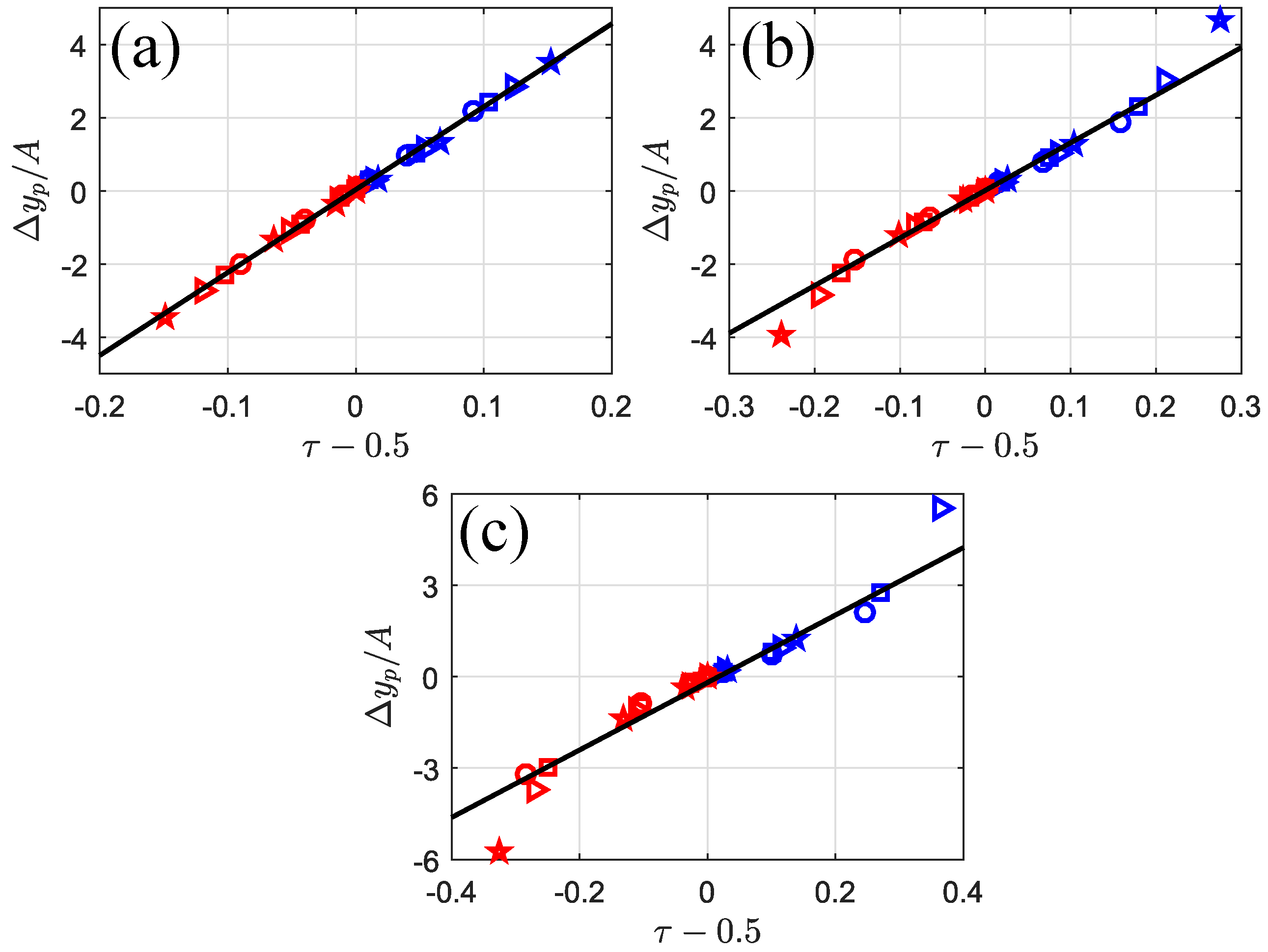
3.4. Lateral Migration Mechanism
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yavuz, C.T.; Prakash, A.; Mayo, J.; Colvin, V.L. Magnetic separations: from steel plants to biotechnology. Chem. Eng. Sci. 2009, 64, 2510–2521. [Google Scholar] [CrossRef]
- Hejazian, M.; Li, W.; Nguyen, N.T. Lab on a chip for continuous-flow magnetic cell separation. Lab Chip 2015, 15, 959–970. [Google Scholar] [CrossRef] [PubMed]
- Arruebo, M.; Fernández-Pacheco, R.; Ibarra, M.R.; Santamaría, J. Magnetic nanoparticles for drug delivery. Nano Today 2007, 2, 22–32. [Google Scholar] [CrossRef]
- Pamme, N. Magnetism and microfluidics. Lab Chip 2006, 6, 24–38. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Bai, F.; Wang, C. Magnetic separation of microparticles by shape. Lab Chip 2017, 17, 401–406. [Google Scholar] [CrossRef] [PubMed]
- Zhou, R.; Sobecki, C.A.; Zhang, J.; Zhang, Y.; Wang, C. Magnetic Control of Lateral Migration of Ellipsoidal Microparticles in Microscale Flows. Phys. Rev. Appl. 2017, 8, 024019. [Google Scholar] [CrossRef]
- Jeffery, G.B. The motion of ellipsoidal particles immersed in a viscous fluid. In Proc. R. Soc. Lond. A; 1922; Volume 102, pp. 161–179. [Google Scholar]
- Trevelyan, B.; Mason, S. Particle motions in sheared suspensions. I. Rotations. J. Colloid Sci. 1951, 6, 354–367. [Google Scholar] [CrossRef]
- Goldsmith, H.; Mason, S. Axial migration of particles in Poiseuille flow. Nature 1961, 190, 1095–1096. [Google Scholar] [CrossRef]
- Feng, J.; Hu, H.H.; Joseph, D.D. Direct simulation of initial value problems for the motion of solid bodies in a Newtonian fluid. Part 2. Couette and Poiseuille flows. J. Fluid Mech. 1994, 277, 271–301. [Google Scholar] [CrossRef]
- Gavze, E.; Shapiro, M. Particles in a shear flow near a solid wall: Effect of nonsphericity on forces and velocities. Int. J. Multiph. Flow 1997, 23, 155–182. [Google Scholar] [CrossRef]
- Pan, T.W.; Huang, S.L.; Chen, S.D.; Chu, C.C.; Chang, C.C. A numerical study of the motion of a neutrally buoyant cylinder in two dimensional shear flow. Comput. Fluids 2013, 87, 57–66. [Google Scholar] [CrossRef]
- Huang, S.L.; Chen, S.D.; Pan, T.W.; Chang, C.C.; Chu, C.C. The motion of a neutrally buoyant particle of an elliptic shape in two dimensional shear flow: A numerical study. Phys. Fluids 2015, 27, 083303. [Google Scholar] [CrossRef]
- Pan, T.W.; Glowinski, R. Direct simulation of the motion of neutrally buoyant circular cylinders in plane Poiseuille flow. J. Comput. Phys. 2002, 181, 260–279. [Google Scholar] [CrossRef]
- Chen, S.D.; Pan, T.W.; Chang, C.C. The motion of a single and multiple neutrally buoyant elliptical cylinders in plane Poiseuille flow. Phys. Fluids 2012, 24, 103302. [Google Scholar] [CrossRef]
- Yang, B.H.; Wang, J.; Joseph, D.D.; Hu, H.H.; Pan, T.W.; Glowinski, R. Migration of a sphere in tube flow. J. Fluid Mech. 2005, 540, 109–131. [Google Scholar] [CrossRef]
- Ai, Y.; Joo, S.W.; Jiang, Y.; Xuan, X.; Qian, S. Pressure-driven transport of particles through a converging-diverging microchannel. Biomicrofluidics 2009, 3, 022404. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.Y.; Ferrari, M.; Decuzzi, P. Design of bio-mimetic particles with enhanced vascular interaction. J. Biomech. 2009, 42, 1885–1890. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.Y.; Ferrari, M.; Decuzzi, P. Shaping nano-/micro-particles for enhanced vascular interaction in laminar flows. Nanotechnology 2009, 20. [Google Scholar] [CrossRef] [PubMed]
- Gijs, M.A.; Lacharme, F.; Lehmann, U. Microfluidic applications of magnetic particles for biological analysis and catalysis. Chem. Rev. 2009, 110, 1518–1563. [Google Scholar] [CrossRef] [PubMed]
- Martinez, R.; Roshchenko, A.; Minev, P.; Finlay, W. Simulation of enhanced deposition due to magnetic field alignment of ellipsoidal particles in a lung bifurcation. J. Aerosol Med. Pulm. Drug Deliv. 2013, 26, 31–40. [Google Scholar] [CrossRef] [PubMed]
- Smistrup, K.; Hansen, O.; Bruus, H.; Hansen, M.F. Magnetic separation in microfluidic systems using microfabricated electromagnets—Experiments and simulations. J. Magn. Magn. Mater. 2005, 293, 597–604. [Google Scholar] [CrossRef]
- Sinha, A.; Ganguly, R.; De, A.K.; Puri, I.K. Single magnetic particle dynamics in a microchannel. Phys. Fluids 2007, 19, 117102. [Google Scholar] [CrossRef]
- Zhou, Y.; Xuan, X. Diamagnetic particle separation by shape in ferrofluids. Appl. Phys. Lett. 2016, 109, 102405. [Google Scholar] [CrossRef]
- Chen, Q.; Li, D.; Zielinski, J.; Kozubowski, L.; Lin, J.; Wang, M.; Xuan, X. Yeast cell fractionation by morphology in dilute ferrofluids. Biomicrofluidics 2017, 11, 064102. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, D.; Meng, F.; Zöttl, A.; Golestanian, R.; Yeomans, J.M. Focusing and Sorting of Ellipsoidal Magnetic Particles in Microchannels. Phys. Rev. Lett. 2017, 119, 198002. [Google Scholar] [CrossRef] [PubMed]
- Matsunaga, D.; Zöttl, A.; Meng, F.; Golestanian, R.; Yeomans, J.M. Far-field theory for trajectories of magnetic ellipsoids in rectangular and circular channels. arXiv, 2017; arXiv:1711.00376. [Google Scholar]
- Cao, Q.; Li, Z.; Wang, Z.; Han, X. Rotational motion and lateral migration of an elliptical magnetic particle in a microchannel under a uniform magnetic field. Microfluidics Nanofluidics 2018, 22, 3. [Google Scholar] [CrossRef]
- Stratton, J.A. Electromagnetic Theory; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hu, H.H.; Patankar, N.A.; Zhu, M. Direct numerical simulations of fluid–solid systems using the arbitrary Lagrangian–Eulerian technique. J. Comput. Phys. 2001, 169, 427–462. [Google Scholar] [CrossRef]
- Ai, Y.; Beskok, A.; Gauthier, D.T.; Joo, S.W.; Qian, S. DC electrokinetic transport of cylindrical cells in straight microchannels. Biomicrofluidics 2009, 3, 044110. [Google Scholar] [CrossRef] [PubMed]
- Ai, Y.; Qian, S. DC dielectrophoretic particle—Particle interactions and their relative motions. J. Colloid Interface Sci. 2010, 346, 448–454. [Google Scholar] [CrossRef] [PubMed]
- Ai, Y.; Zeng, Z.; Qian, S. Direct numerical simulation of AC dielectrophoretic particle–particle interactive motions. J. Colloid Interface Sci. 2014, 417, 72–79. [Google Scholar] [CrossRef] [PubMed]
- Hsu, R.; Ganatos, P. Gravitational and zero-drag motion of a spheroid adjacent to an inclined plane at low Reynolds number. J. Fluid Mech. 1994, 268, 267–292. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, C. Study of rotation of ellipsoidal particles in combined simple shear flow and magnetic fields. In Proceedings of the COMSOL Conference 2017 Boston, Burlington, MA, USA, 6 October 2017. [Google Scholar]
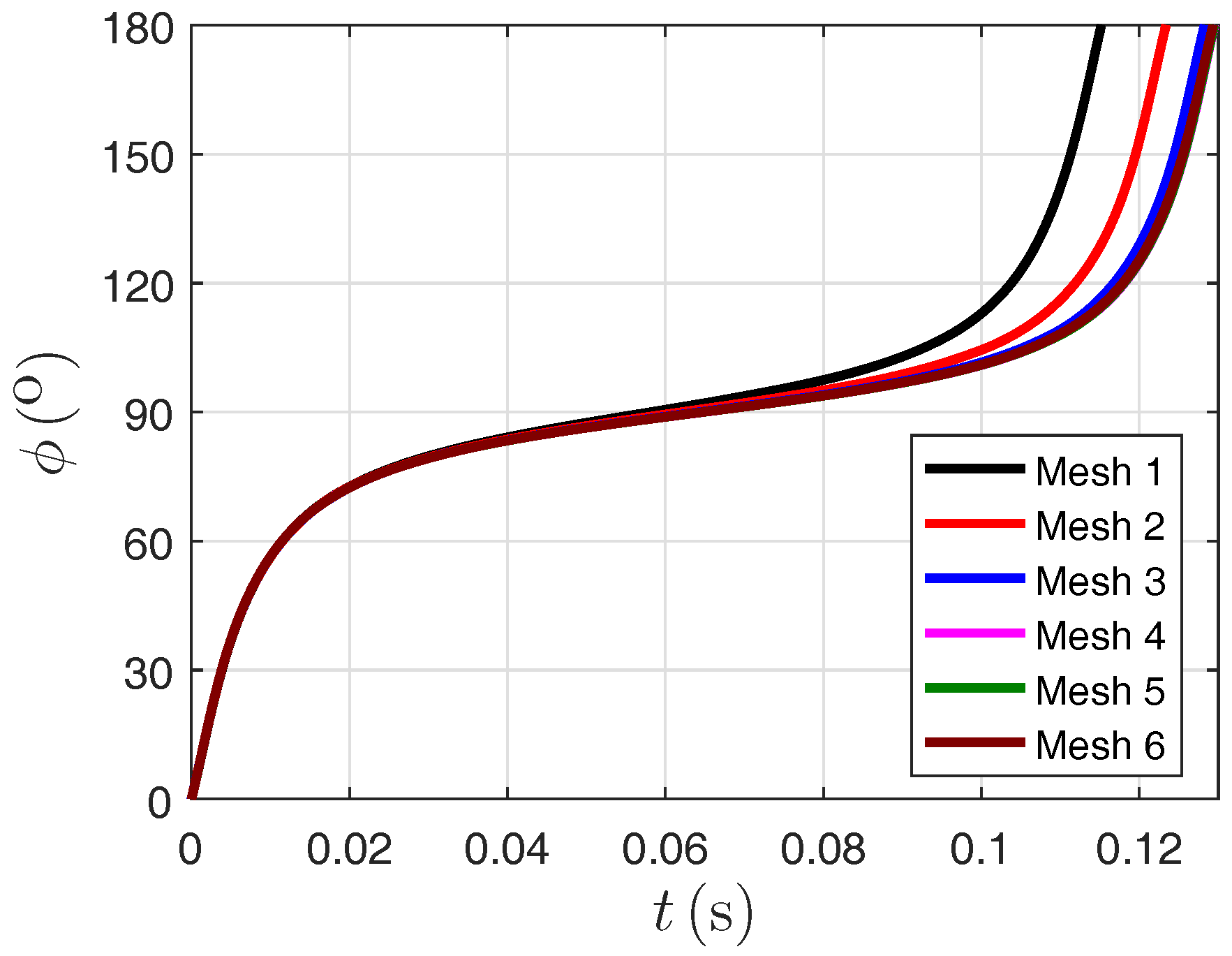


| Mesh Sizes Used for Grid Independence Analysis | Domain Elements | Boundary Elements on Particle Surface |
|---|---|---|
| Mesh 1 | 6184 | 56 |
| Mesh 2 | 7794 | 68 |
| Mesh 3 | 8281 | 92 |
| Mesh 4 | 11,608 | 116 |
| Mesh 5 | 12,359 | 152 |
| Mesh 6 | 13,079 | 184 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Wang, C. Numerical Study of Lateral Migration of Elliptical Magnetic Microparticles in Microchannels in Uniform Magnetic Fields. Magnetochemistry 2018, 4, 16. https://doi.org/10.3390/magnetochemistry4010016
Zhang J, Wang C. Numerical Study of Lateral Migration of Elliptical Magnetic Microparticles in Microchannels in Uniform Magnetic Fields. Magnetochemistry. 2018; 4(1):16. https://doi.org/10.3390/magnetochemistry4010016
Chicago/Turabian StyleZhang, Jie, and Cheng Wang. 2018. "Numerical Study of Lateral Migration of Elliptical Magnetic Microparticles in Microchannels in Uniform Magnetic Fields" Magnetochemistry 4, no. 1: 16. https://doi.org/10.3390/magnetochemistry4010016