Noncovalent Interactions in the Catechol Dimer
Abstract
:1. Introduction
2. Computational Details
- The difference ΔCC-MP2 between CCSD(T) and MP2 interaction energy is evaluated using for both calculations the Dunning’s correlated aug-cc-pvDz basis sets:
- The MP2 energy in the CBS limit, , is computed through the extrapolation scheme proposed by Halkier et al. [68], making use of the aug-cc-pvDz and aug-cc-pvTz basis sets. Despite the state-of-the-art extrapolation procedure [37,41,50] is often carried out with the larger aug-cc-pvTz and aug-cc-pvQz basis sets, it has been recently shown that, for similar aromatic dimers, the use of the smaller aug-cc-pvDz and aug-cc-pvTz affects the computed interaction energies by few hundredths of kcal/mol [66]. In consideration of the fairly large number of dimers investigated and the computational cost of a CCSD(T) calculation at the aug-cc-pvQz level, the smaller sets (Dz and Tz) were chosen as the best compromise between accuracy and feasibility.
- Finally, the CCSD(T)/CBS interaction energy, , is recovered as:
- All energies were corrected for the basis set superposition error (BSSE) with the standard counterpoise (CP) correction [69].
3. Results and Discussion
3.1. MP2mod Tuning and Validation
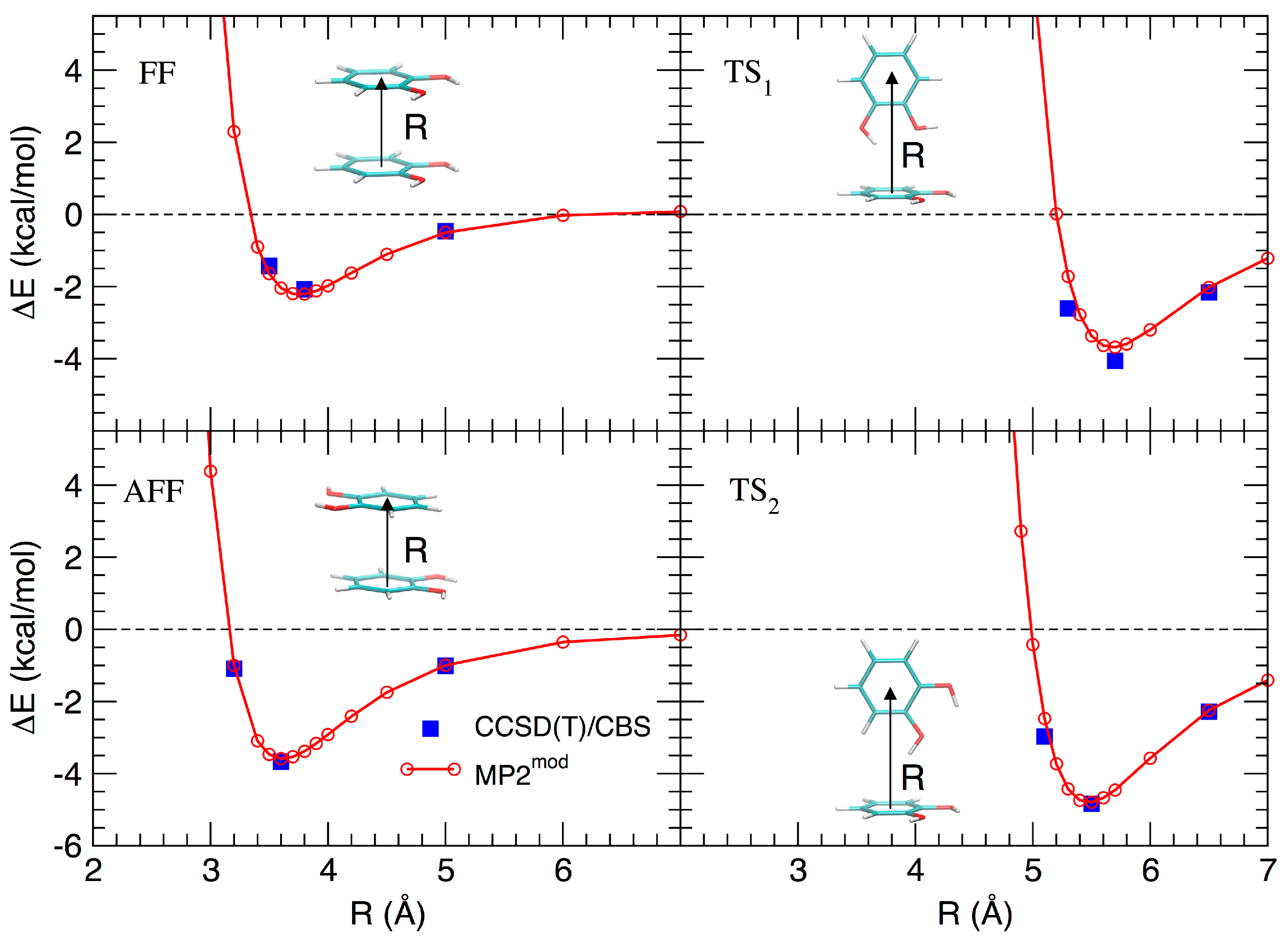
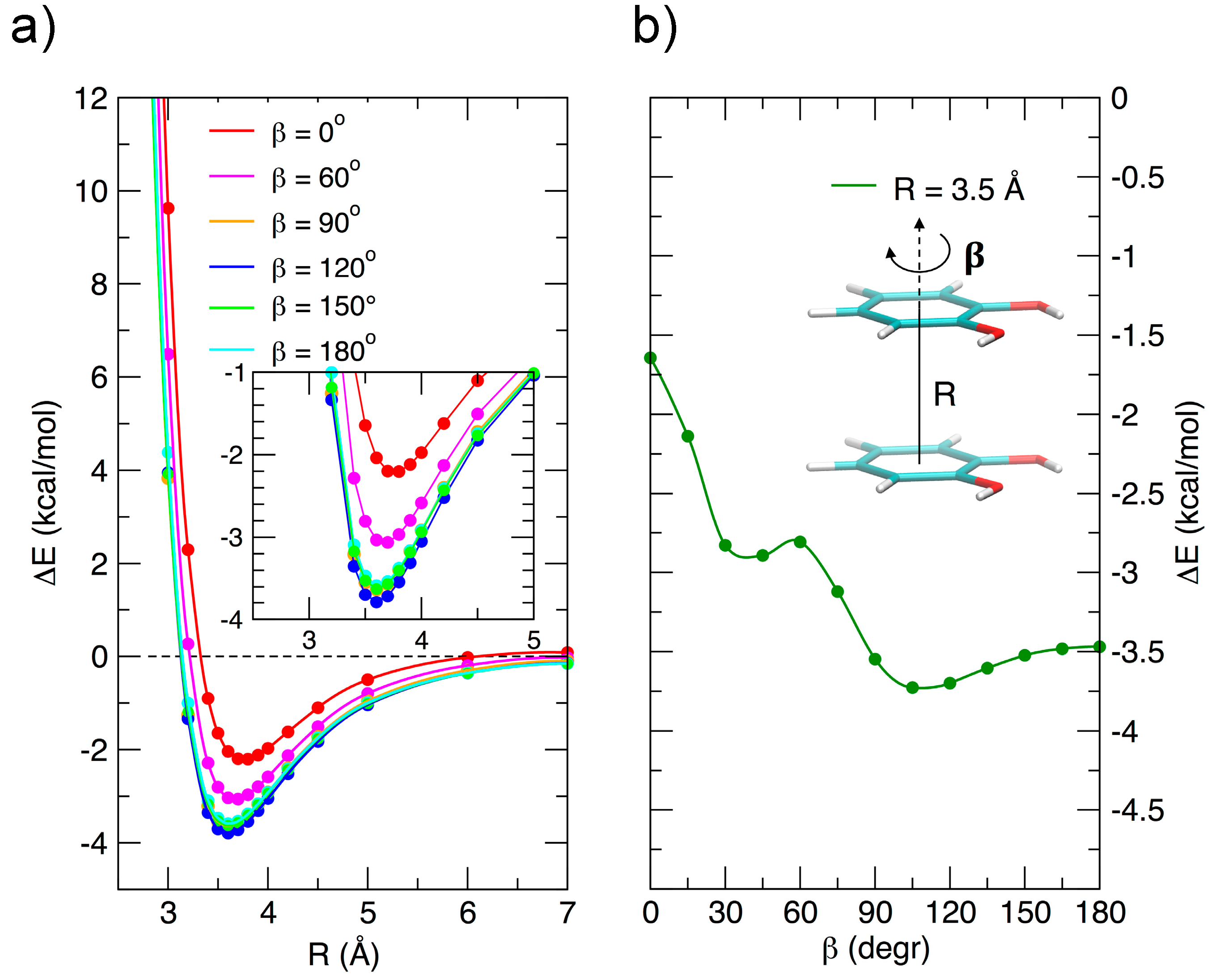
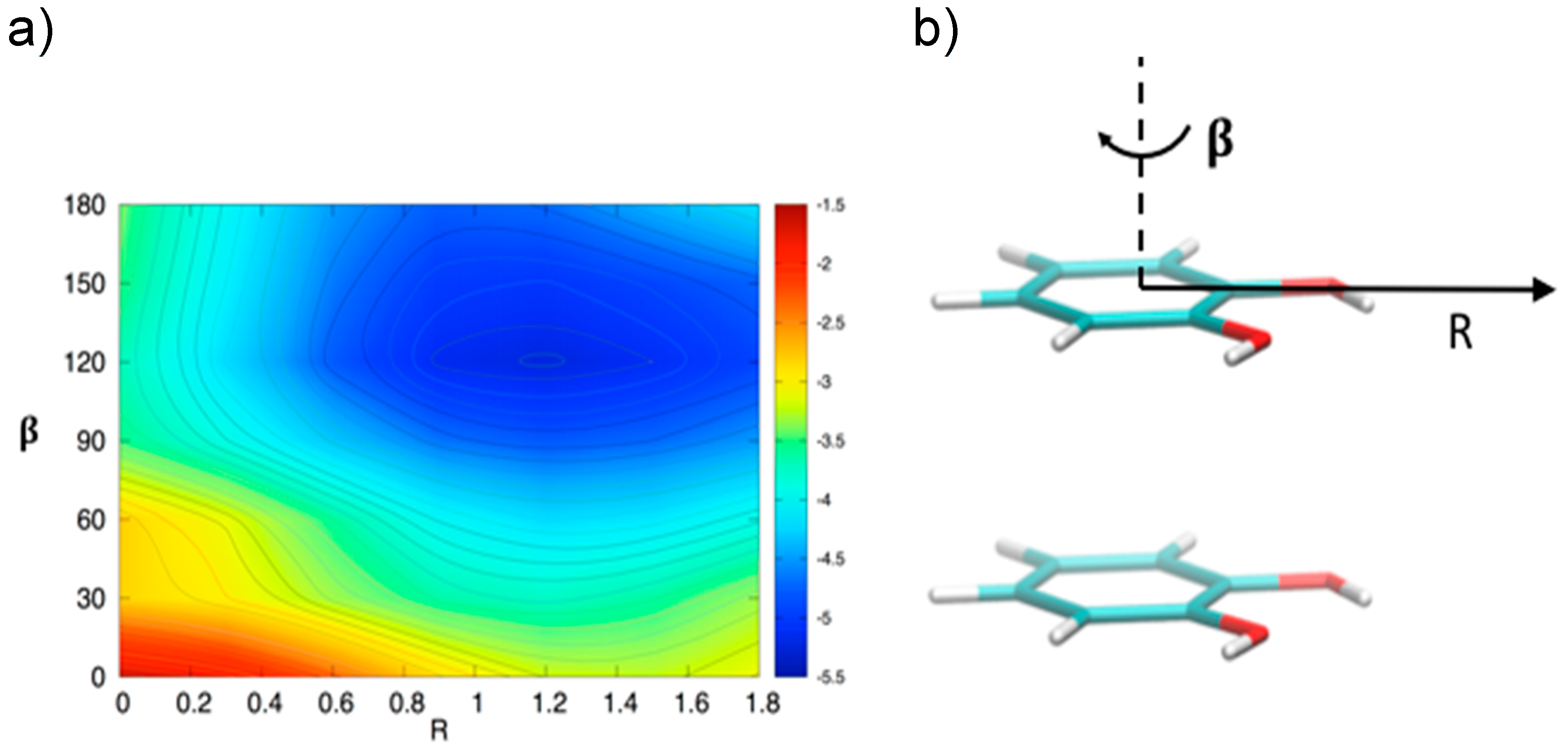
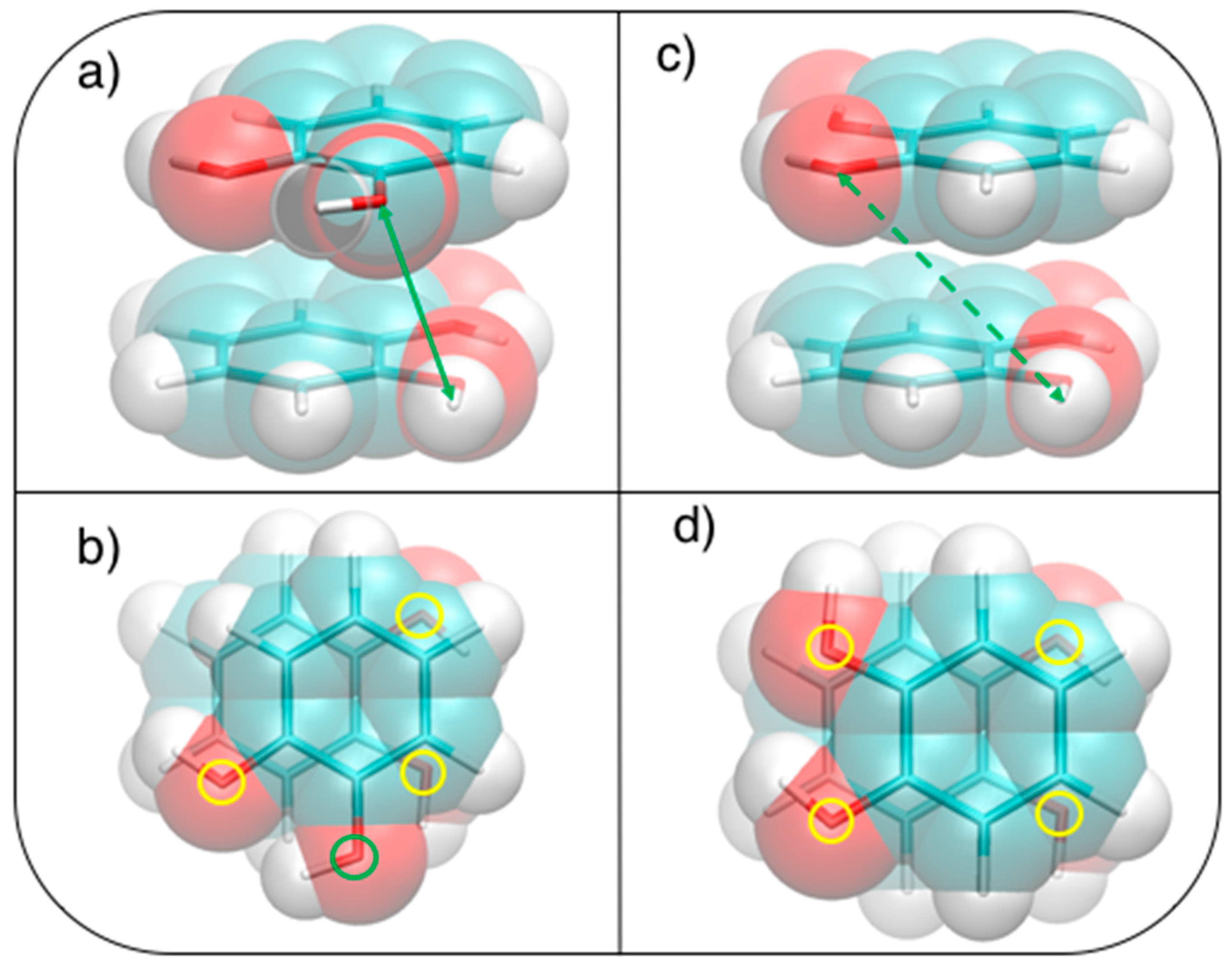
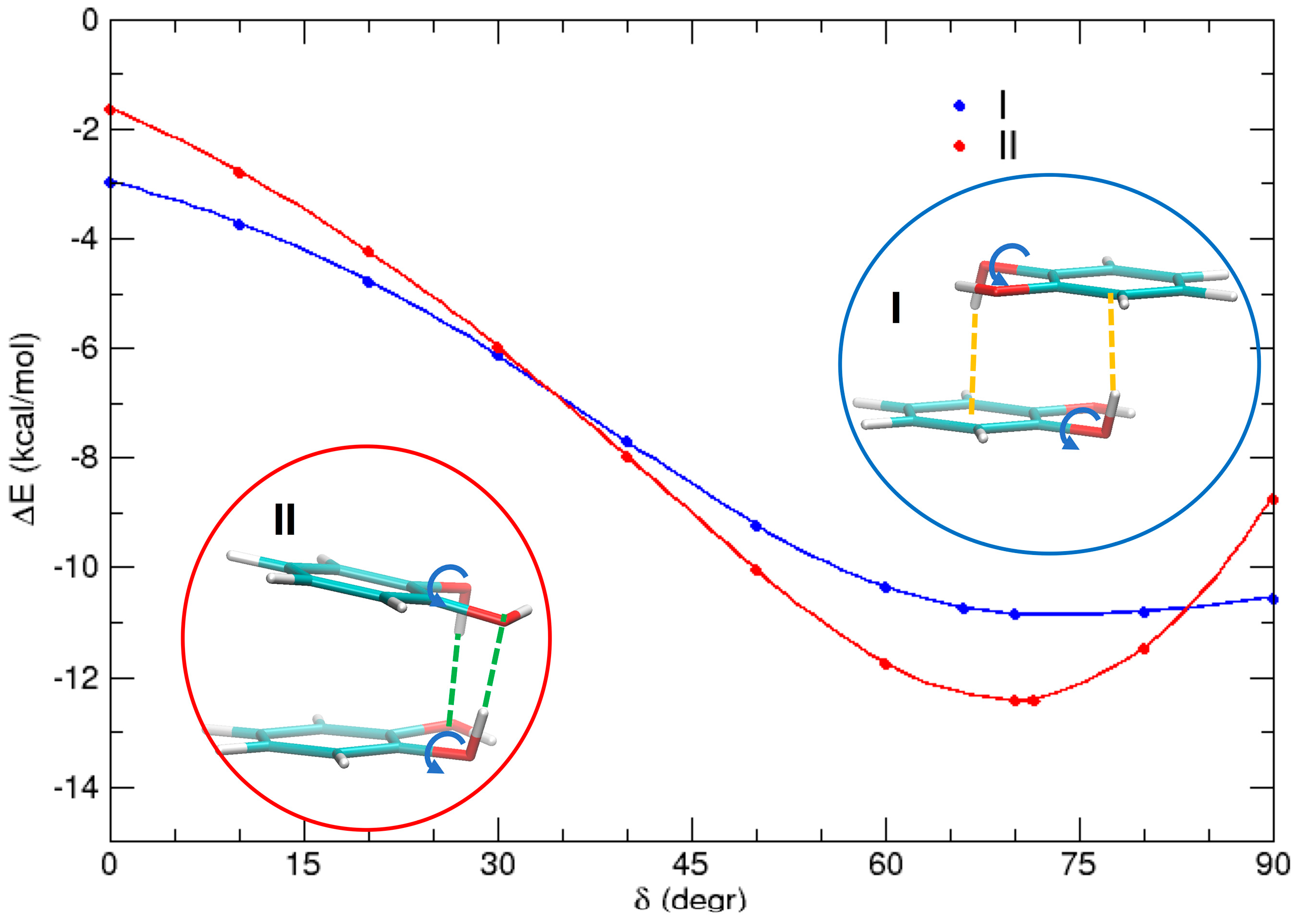
3.2. Stacked Cathecol Dimers
3.3. T-Shaped Cathecol Dimers
3.4. Effect of the Hydrogen Bond
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Mak, C.H. Unraveling base stacking driving forces in DNA. J. Phys. Chem. B 2016, 120, 6010–6020. [Google Scholar] [CrossRef] [PubMed]
- Trouillas, P.; Sancho-García, J.C.; De Freitas, V.; Gierschner, J.; Otyepka, M.; Dangles, O. Stabilizing and modulating color by copigmentation: Insights from theory and experiment. Chem. Rev. 2016, 116, 4937–4982. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lv, C.; Zhao, G.; Ning, Y. The interactions between plant proteins/enzymes and other food components and their effects on food quality. Crit. Rev. Food Sci. Nutr. 2015, 57, 1718–1728. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, S.E.; Seguin, T.J.; Guan, Y.; Doney, A.C. Noncovalent interactions in organocatalysis and the prospect of computational catalyst design. Acc. Chem. Res. 2016, 49, 1061–1069. [Google Scholar] [CrossRef] [PubMed]
- Neel, A.J.; Hilton, M.J.; Sigman, M.S.; Toste, F.D. Exploiting non-covalent π interactions for catalyst design. Nature 2017, 543, 637–646. [Google Scholar] [CrossRef] [PubMed]
- Ding, X.; Wang, Y. Weak bond-based injectable and stimuli responsive hydrogels for biomedical applications. J. Mater. Chem. B 2017, 5, 887–906. [Google Scholar] [CrossRef]
- Yilmazer, N.; Korth, M. Prospects of applying enhanced semi-empirical QM methods for 2101 virtual drug design. Curr. Med. Chem. 2016, 23, 2101–2111. [Google Scholar] [CrossRef] [PubMed]
- Meanwell, N.A. A synopsis of the properties and applications of heteroaromatic rings in medicinal chemistry. Adv. Heterocycl. Chem. 2017, 123, 245–361. [Google Scholar]
- Ghosh, T.; Panicker, J.; Nair, V. Self-assembled organic materials for photovoltaic application. Polymers 2017, 9, 112. [Google Scholar] [CrossRef]
- Würthner, F. Dipole–dipole interaction driven self-assembly of merocyanine dyes: From dimers to nanoscale objects and supramolecular materials. Acc. Chem. Res. 2016, 49, 868–876. [Google Scholar] [CrossRef] [PubMed]
- Chandra, B.K.C.; D’Souza, F. Design and photochemical study of supramolecular donor–acceptor systems assembled via metal–ligand axial coordination. Coord. Chem. Rev. 2016, 322, 104–141. [Google Scholar]
- Bredas, J.-L.; Marder, S.R.; Reichmanis, E. Preface to the chemistry of materials special issue on π-functional materials. Chem. Mater. 2011, 23, 309. [Google Scholar] [CrossRef]
- Shewmon, N.T.; Watkins, D.L.; Galindo, J.F.; Zerdan, R.B.; Chen, J.; Keum, J.; Roitberg, A.E.; Xue, J.; Castellano, R.K. Enhancement in organic photovoltaic efficiency through the synergistic interplay of molecular donor hydrogen bonding and π-stacking. Adv. Funct. Mater. 2015, 25, 5166–5177. [Google Scholar] [CrossRef]
- Rest, C.; Kandanelli, R.; Fernández, G. Strategies to create hierarchical self-assembled structures via cooperative non-covalent interactions. Chem. Soc. Rev. 2015, 44, 2543–2572. [Google Scholar] [CrossRef] [PubMed]
- Hammann, F.; Schmid, M. Determination and quantification of molecular interactions in protein films: A review. Materials 2014, 7, 7975–7996. [Google Scholar] [CrossRef] [PubMed]
- Makwana, K.M.; Mahalakshmi, R. Implications of aromatic-aromatic interactions: From protein structures to peptide models. Protein Sci. 2015, 24, 1920–1933. [Google Scholar] [CrossRef] [PubMed]
- Cragg, P.J. Supramolecular Chemistry—From Biological Inspiration to Biomedical Applications; Springer: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Wun Hwang, J.; Li, P.; Shimizu, K.D. Synergy between experimental and computational studies of aromatic stacking interactions. Org. Biomol. Chem. 2017, 15, 1554–1564. [Google Scholar] [CrossRef] [PubMed]
- Sherrill, C.D. Energy component analysis of π interactions. Acc. Chem. Res. 2013, 46, 1020–1028. [Google Scholar] [CrossRef] [PubMed]
- Heinzmann, C.; Weder, C.; de Espinosa, L.M. Supramolecular polymer adhesives: Advanced materials inspired by nature. Chem. Soc. Rev. 2015, 342, 342–358. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, C.L.; Siebert, H.M.; Wilker, J.J. Integrating mussel chemistry into a bio-based polymer to create degradable adhesives. Macromolecules 2017, 50, 561–568. [Google Scholar] [CrossRef]
- Kord Forooshani, P.; Lee, B.P. Recent approaches in designing bioadhesive materials inspired by mussel adhesive protein. J. Polym. Sci. Part A: Polym. Chem. 2017, 55, 9–33. [Google Scholar] [CrossRef] [PubMed]
- North, M.A.; Del Grosso, C.A.; Wilker, J.J. High strength underwater bonding with polymer mimics of mussel adhesive proteins. ACS Appl. Mater. Interfaces 2017, 9, 7866–7872. [Google Scholar] [CrossRef] [PubMed]
- Saiz-Poseu, J.; Sedó, J.; García, B.; Benaiges, C.; Parella, T.; Alibés, R.; Hernando, J.; Busqué, F.; Ruiz-Molina, D. Versatile nanostructured materials via direct reaction of functionalized catechols. Adv. Mater. 2013, 25, 2066–2070. [Google Scholar] [CrossRef] [PubMed]
- Sedó, J.; Saiz-Poseu, J.; Busqué, F.; Ruiz-Molina, D. Catechol-based biomimetic functional materials. Adv. Mater. 2013, 25, 653–701. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Jing, S.; Liu, Y.; Liu, S.; Tan, Y. Diblock copolymer containing bioinspired borneol and dopamine moieties: Synthesis and antibacterial coating applications. Polymer 2017, 116, 314–323. [Google Scholar] [CrossRef]
- Barone, V.; Cacelli, I.; Crescenzi, O.; D’Ischia, M.; Ferretti, A.; Prampolini, G.; Villani, G. Unraveling the interplay of different contributions to the stability of the quinhydrone dimer. RSC Adv. 2014, 4, 876–885. [Google Scholar] [CrossRef]
- Burns, L.A.; Vázquez-Mayagoitia, A.; Sumpter, B.G.; Sherrill, C.D. Density-functional approaches to noncovalent interactions: A comparison of dispersion corrections (DFT-D), exchange-hole dipole moment (XDM) theory, and specialized functionals. J. Chem. Phys. 2011, 134, 084107. [Google Scholar] [CrossRef] [PubMed]
- Corminboeuf, C. Minimizing density functional failures for non-covalent interactions beyond van der Waals complexes. Acc. Chem. Res. 2014, 47, 3217–3224. [Google Scholar] [CrossRef] [PubMed]
- Goerigk, L.; Grimme, S. Efficient and accurate double-hybrid-meta-GGA density functionals-evaluation with the extended GMTKN30 database for general main group thermochemistry, kinetics, and noncovalent interactions. J. Chem. Theory Comput. 2011, 7, 291–309. [Google Scholar] [CrossRef] [PubMed]
- Goldey, M.B.; Belzunces, B.; Head-Gordon, M. Attenuated MP2 with a long-range dispersion correction for treating nonbonded interactions. J. Chem. Theory Comput. 2015, 11, 4159–4168. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Density functional theory with London dispersion corrections. WIREsComput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S.; Hansen, A.; Brandenburg, J.G.; Bannwarth, C. Dispersion-corrected mean-field electronic structure methods. Chem. Rev. 2016, 116, 5105–5154. [Google Scholar] [CrossRef] [PubMed]
- Hobza, P.; Zahradník, R.; Müller-Dethlefs, K. The world of non-covalent interactions: 2006. Collect. Czechoslov. Chem. Commun. 2006, 71, 443–531. [Google Scholar] [CrossRef]
- Piton, M. Accurate intermolecular interaction energies from a combination of MP2 and TDDFT response theory. J. Chem. Theory Comput. 2010, 6, 168–178. [Google Scholar] [CrossRef] [PubMed]
- Prampolini, G.; Cacelli, I.; Ferretti, A. Intermolecular interactions in eumelanins: A computational bottom-up approach. I. Small building blocks. RSC Adv. 2015, 5, 38513–38526. [Google Scholar] [CrossRef]
- Řezáč, J.; Hobza, P. Describing noncovalent interactions beyond the common approximations: How accurate is the “gold standard”, CCSD(T) at the complete basis set limit? J. Chem. Theory Comput. 2013, 9, 2151–2155. [Google Scholar] [CrossRef] [PubMed]
- Řezáč, J.; Hobza, P. Benchmark calculations of interaction energies in noncovalent complexes and their applications. Chem. Rev. 2016, 116, 5038–5071. [Google Scholar] [CrossRef] [PubMed]
- Richard, R.M.; Lao, K.U.; Herbert, J.M. Achieving the CCSD(T) basis-set limit in sizable molecular clusters: Counterpoise corrections for the many-body expansion. J. Phys. Chem. Lett. 2013, 4, 2674–2680. [Google Scholar] [CrossRef] [PubMed]
- Riley, K.E.; Platts, J.A.; Řezáč, J.; Hobza, P.; Hill, J.G. Assessment of the performance of MP2 and MP2 variants for the treatment of noncovalent interactions. J. Phys. Chem. A 2012, 116, 4159–4169. [Google Scholar] [CrossRef] [PubMed]
- Sherrill, C.D.; Takatani, T.; Hohenstein, E.G. An assessment of theoretical methods for nonbonded interactions: Comparison to complete basis set limit coupled-cluster potential energy curves for the benzene dimer, the methane dimer, benzene−methane, and benzene−H2S. J. Phys. Chem. A 2009, 113, 10146–10159. [Google Scholar] [CrossRef] [PubMed]
- Tkatchenko, A.; DiStasio, R.A.; Head-Gordon, M.; Scheffler, M. Dispersion-corrected Møller–Plesset second-order perturbation theory. J. Chem. Phys. 2009, 131, 94106. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other function. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- An, Y.; Doney, A.C.; Andrade, R.B.; Wheeler, S.E. Stacking interactions between 9-methyladenine and heterocycles commonly found in pharmaceuticals. J. Chem. Inf. Model. 2016, 56, 906–914. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, S.E.; Bloom, J.W.G. Toward a more complete understanding of noncovalent interactions involving aromatic rings. J. Phys. Chem. A 2014, 118, 6133–6147. [Google Scholar] [CrossRef] [PubMed]
- Wheeler, S.E.; Houk, K.N. Substituent effects in the benzene dimer are due to direct interactions of the substituents with the unsubstituted benzene. J. Am. Chem. Soc. 2008, 130, 10854–10855. [Google Scholar] [CrossRef] [PubMed]
- Podeszwa, R.; Bukowski, R.; Szalewicz, K. Potential energy surface for the benzene dimer and perturbational analysis of π−π interactions. J. Phys. Chem. A 2006, 110, 10345–10354. [Google Scholar] [CrossRef] [PubMed]
- Sinnokrot, M.O.; Sherrill, C.D. Unexpected substituent effects in face-to-face π-stacking interactions. J. Phys. Chem. A 2003, 107, 8377–8379. [Google Scholar] [CrossRef]
- Tsuzuki, S.; Honda, K.; Uchimaru, T.; Mikami, M.; Tanabe, K. Origin of attraction and directionality of the π/π interaction: Model chemistry calculations of benzene dimer interaction. J. Am. Chem. Soc. 2002, 124, 104–112. [Google Scholar] [CrossRef] [PubMed]
- Sinnokrot, M.O.; Valeev, E.F.; Sherrill, C.D. Estimates of the ab initio limit for π−π interactions: The benzene dimer. J. Am.Chem. Soc. 2002, 124, 10887–10893. [Google Scholar] [CrossRef] [PubMed]
- Kroon-Batenburg, L.; Van Duijneveldt, F. The use of a moment-optimized DZP basis set for describing the interaction in the water dimer. J. Mol. Struct.: THEOCHEM 1985, 22, 185–199. [Google Scholar] [CrossRef]
- Hobza, P.; Zahradnik, R. Intermolecular interactions between medium-sized systems. Nonempirical and empirical calculations of interaction energies. Successes and failures. Chem. Rev. 1988, 88, 871–897. [Google Scholar] [CrossRef]
- Hobza, P.; Selzle, H.L.; Schlag, E.W. Potential energy surface for the benzene dimer. Results of ab initio CCSD(T) calculations show two nearly isoenergetic structures: T-shaped and parallel-displaced. J. Phys. Chem. 1996, 100, 18790–18794. [Google Scholar] [CrossRef]
- Sponer, J.; Leszczynski, J.; Hobza, P. Base stacking in cytosine dimer. A comparison of correlated ab initio calculations with three empirical potential models and density functional theory calculations. J. Comput. Chem. 1996, 17, 841–850. [Google Scholar] [CrossRef]
- Šponer, J.; Leszczyński, J.; Hobza, P. Nature of nucleic acid−base stacking: Nonempirical ab initio and empirical potential characterization of 10 stacked base dimers. Comparison of stacked and H-bonded base pairs. J. Phys. Chem. 1996, 100, 5590–5596. [Google Scholar] [CrossRef]
- Hobza, P.; Šponer, J. Toward true DNA base-stacking energies: MP2, CCSD(T), and complete basis set calculations. J. Am. Chem. Soc. 2002, 124, 11802–11808. [Google Scholar] [CrossRef] [PubMed]
- Cacelli, I.; Cinacchi, G.; Prampolini, G.; Tani, A. Computer simulation of solid and liquid benzene with an atomistic interaction potential derived from ab initio calculations. J. Am. Chem. Soc. 2004, 126, 14278–14286. [Google Scholar] [CrossRef] [PubMed]
- Mignon, P.; Loverix, S.; De Proft, F.; Geerlings, P. Influence of stacking on hydrogen bonding: Quantum chemical study on pyridine–benzene model complexes. J. Phys.Chem. A 2004, 108, 6038–6044. [Google Scholar] [CrossRef]
- Řeha, D.; Kabeláč, M.; Ryjáček, F.; Šponer, J.; Šponer, J.E.; Elstner, M.; Suhai, S.; Hobza, P. Intercalators. 1. Nature of stacking interactions between intercalators (ethidium, daunomycin, ellipticine, and 4′,6-diaminide-2-phenylindole) and DNA base pairs. Ab initio quantum chemical, density functional theory, and empirical potential study. J. Am. Chem. Soc. 2002, 124, 3366–3376. [Google Scholar] [CrossRef] [PubMed]
- Sponer, J.; Gabb, H.A.; Leszczynski, J.; Hobza, P. Base–base and deoxyribose–base stacking interactions in B-DNA and Z-DNA: A quantum-chemical study. Biophys. J. 1997, 73, 76–87. [Google Scholar] [CrossRef]
- Hobza, P.; Kabeláč, M.; Šponer, J.; Mejzlík, P.; Vondrášek, J. Performance of empirical potentials (AMBER, CFF95, CVFF, CHARMM, OPLS, POLTEV), semiempirical quantum chemical methods (AM1, MNDO/M, PM3), andab initio Hartree–Fock method for interaction of DNA bases: Comparison with nonempirical beyond Hartree–Fock results. J. Comput. Chem. 1997, 18, 1136–1150. [Google Scholar]
- Cacelli, I.; Prampolini, G.; Tani, A. Atomistic simulation of a nematogen using a force field derived from quantum chemical calculations. J. Phys. Chem. B 2005, 109, 3531–3538. [Google Scholar] [CrossRef] [PubMed]
- Cacelli, I.; Lami, C.F.; Prampolini, G. Force-field modeling through quantum mechanical calculations: Molecular dynamics simulations of a nematogenic molecule in its condensed phases. J. Comput. Chem. 2009, 30, 366–378. [Google Scholar] [CrossRef] [PubMed]
- Cacelli, I.; Cimoli, A.; Livotto, P.R.; Prampolini, G. An automated approach for the parameterization of accurate intermolecular force-fields: Pyridine as a case study. J. Comput. Chem. 2012, 33, 1055–1067. [Google Scholar] [CrossRef] [PubMed]
- Micillo, R.; Panzella, L.; Iacomino, M.; Prampolini, G.; Cacelli, I.; Ferretti, A.; Crescenzi, O.; Koike, K.; Napolitano, A.; D’Ischia, M. Eumelanin broadband absorption develops from aggregation-modulated chromophore interactions under structural and redox control. Sci. Rep. 2017, 7, 41532. [Google Scholar] [CrossRef] [PubMed]
- Prampolini, G.; Greff da Silveira, L.; Jacobs, M.; Livotto, P.R.; Cacelli, I. Interaction energy landscapes of aromatic heterocycles through a reliable yet affordable computational approach. J. Chem. Theory Comput. 2017. submitted. [Google Scholar]
- Estévez, L.; Otero, N.S.; Mosquera, R.A. Computational study on the stacking interaction in catechol complexes. J. Phys. Chem. A 2009, 113, 11051–11058. [Google Scholar] [CrossRef] [PubMed]
- Barone, V.; Cacelli, I.; Ferretti, A.; Prampolini, G.; Villani, G. Proton and electron transfer mechanisms in the formation of neutral and charged quinhydrone-like complexes: A multilayered computational study. J. Chem.Theory Comput. 2014, 10, 4883–4895. [Google Scholar] [CrossRef] [PubMed]
- Boys, S.F.; Bernardi, F. The calculation of small molecular interactions by the differences of separate total energies. Some procedures with reduced errors. Mol. Phys. 1970, 19, 553–566. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Prampolini, G.; Livotto, P.R.; Cacelli, I. Accuracy of quantum mechanically derived force-fields parameterized from dispersion-corrected DFT data: The benzene dimer as a prototype for aromatic interactions. J. Chem. Theory Comput. 2015, 11, 5182–5196. [Google Scholar] [CrossRef] [PubMed]
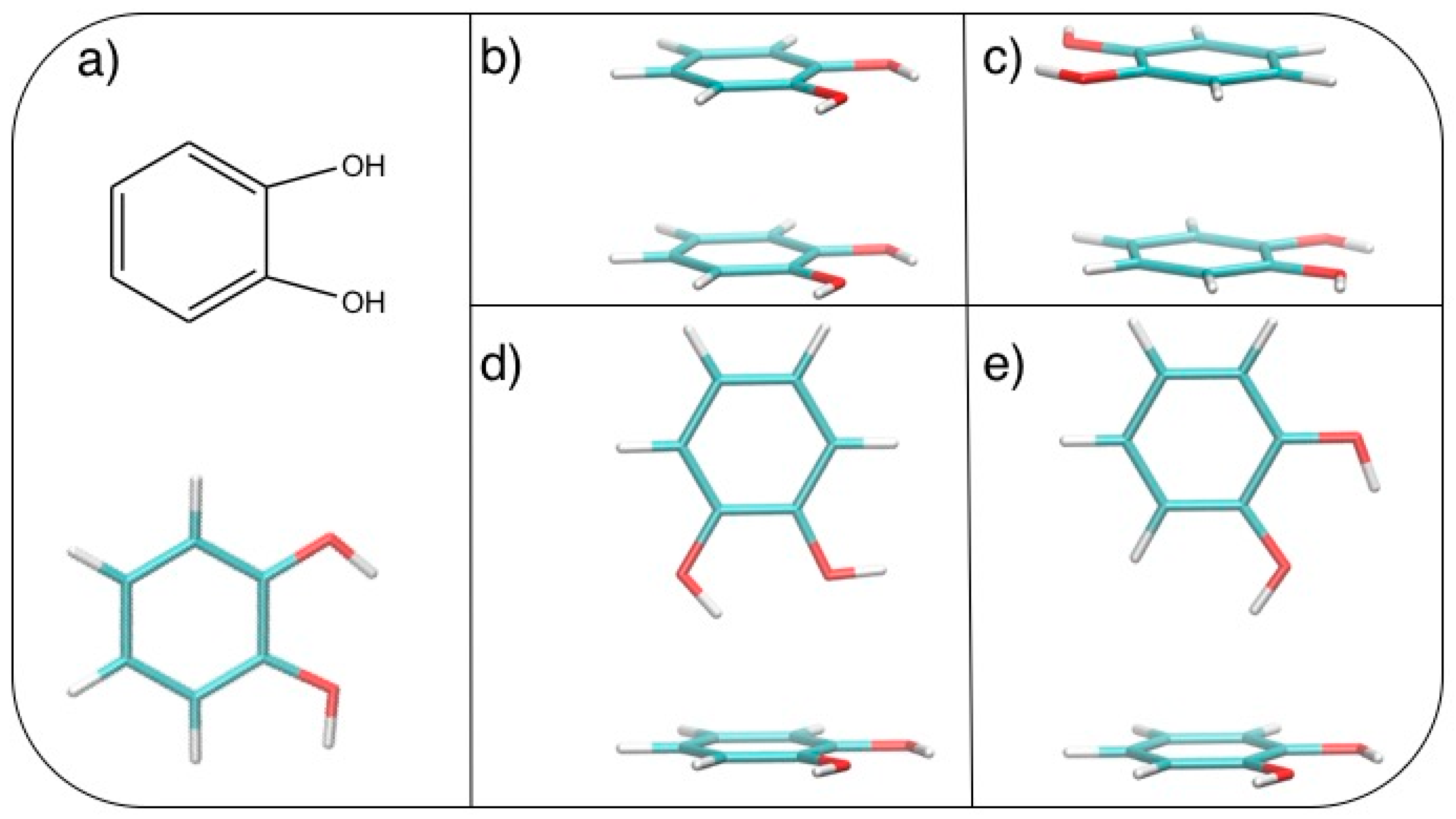


| Geometry | Energies (kcal/mol) | CPU Time (min) | ||||
|---|---|---|---|---|---|---|
| MP2mod | CCSD(T)/CBS | MPW1B95 | MP2mod | CCSD(T)/CBS | MPW1B95 | |
| I | −10.7 | −11.1 | −8.1 | 27 | 50,640 | 145 |
| II | −12.4 | −12.6 | −8.3 | 25 | 49,740 | 180 |
| III | −5.3 | −5.7 | −2.2 | 27 | 50,820 | 79 |
| IV | −6.1 | −7.3 | −5.7 | 18 | 51,720 | 142 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barone, V.; Cacelli, I.; Ferretti, A.; Prampolini, G. Noncovalent Interactions in the Catechol Dimer. Biomimetics 2017, 2, 18. https://doi.org/10.3390/biomimetics2030018
Barone V, Cacelli I, Ferretti A, Prampolini G. Noncovalent Interactions in the Catechol Dimer. Biomimetics. 2017; 2(3):18. https://doi.org/10.3390/biomimetics2030018
Chicago/Turabian StyleBarone, Vincenzo, Ivo Cacelli, Alessandro Ferretti, and Giacomo Prampolini. 2017. "Noncovalent Interactions in the Catechol Dimer" Biomimetics 2, no. 3: 18. https://doi.org/10.3390/biomimetics2030018







