Biomimetic Adaptive Pure Pursuit Control for Robot Path Tracking Inspired by Natural Motion Constraints
Abstract
:1. Introduction
2. Kinematic Model
2.1. Kinematic Analysis
- (1)
- Four wheels of the FWDDR are symmetrically distributed on the same plane;
- (2)
- None of the FWDDR’s wheels idle;
- (3)
- The FWDDR does not exhibit longitudinal skidding during steering;
- (4)
- The FWDDR possesses an ample turning radius;
- (5)
- The FWDDR’s center of mass is situated on the robot’s x-axis.
2.2. Equation of Motion
3. Path-Tracking Controller Design
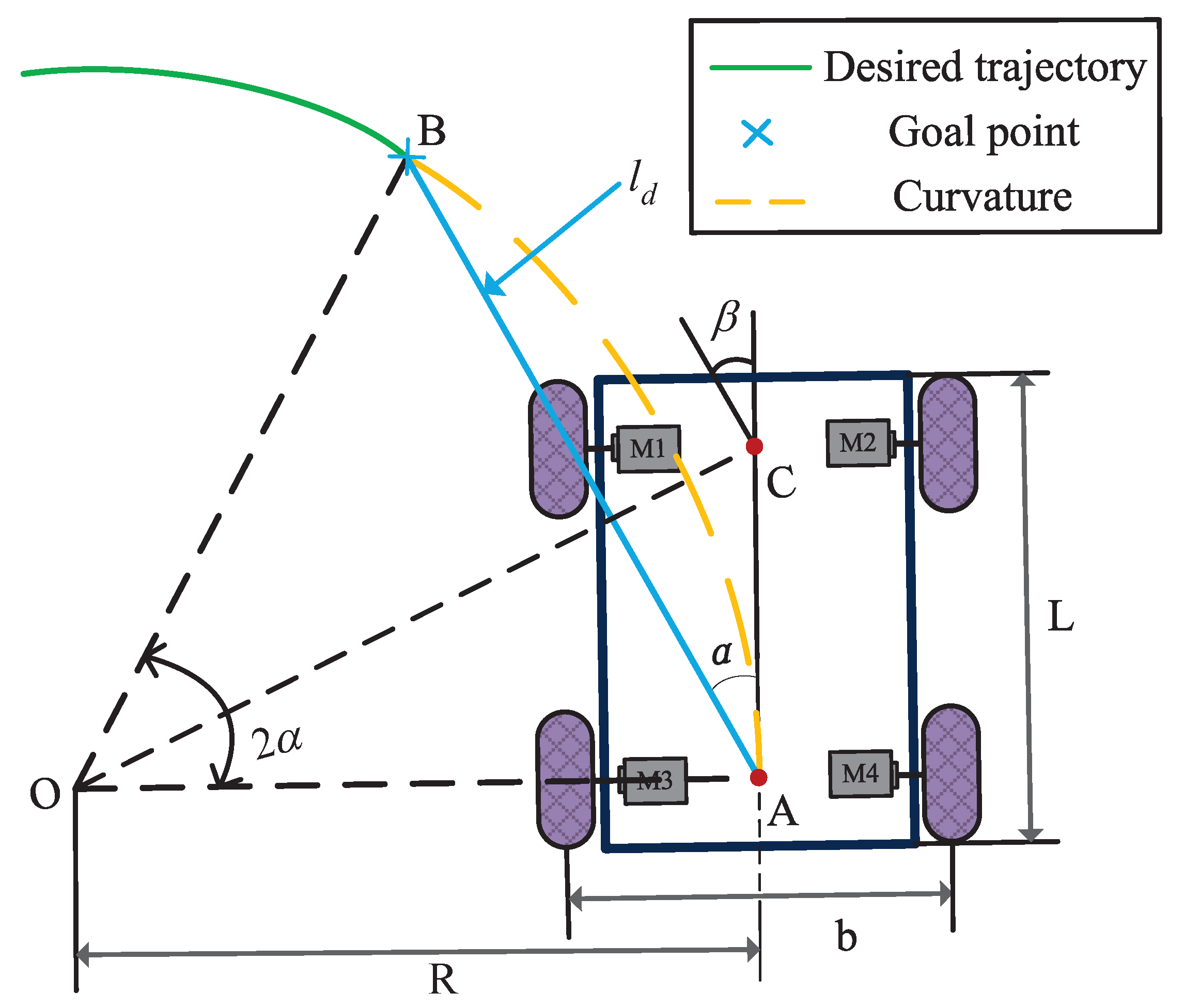
3.1. Traditional PP Control
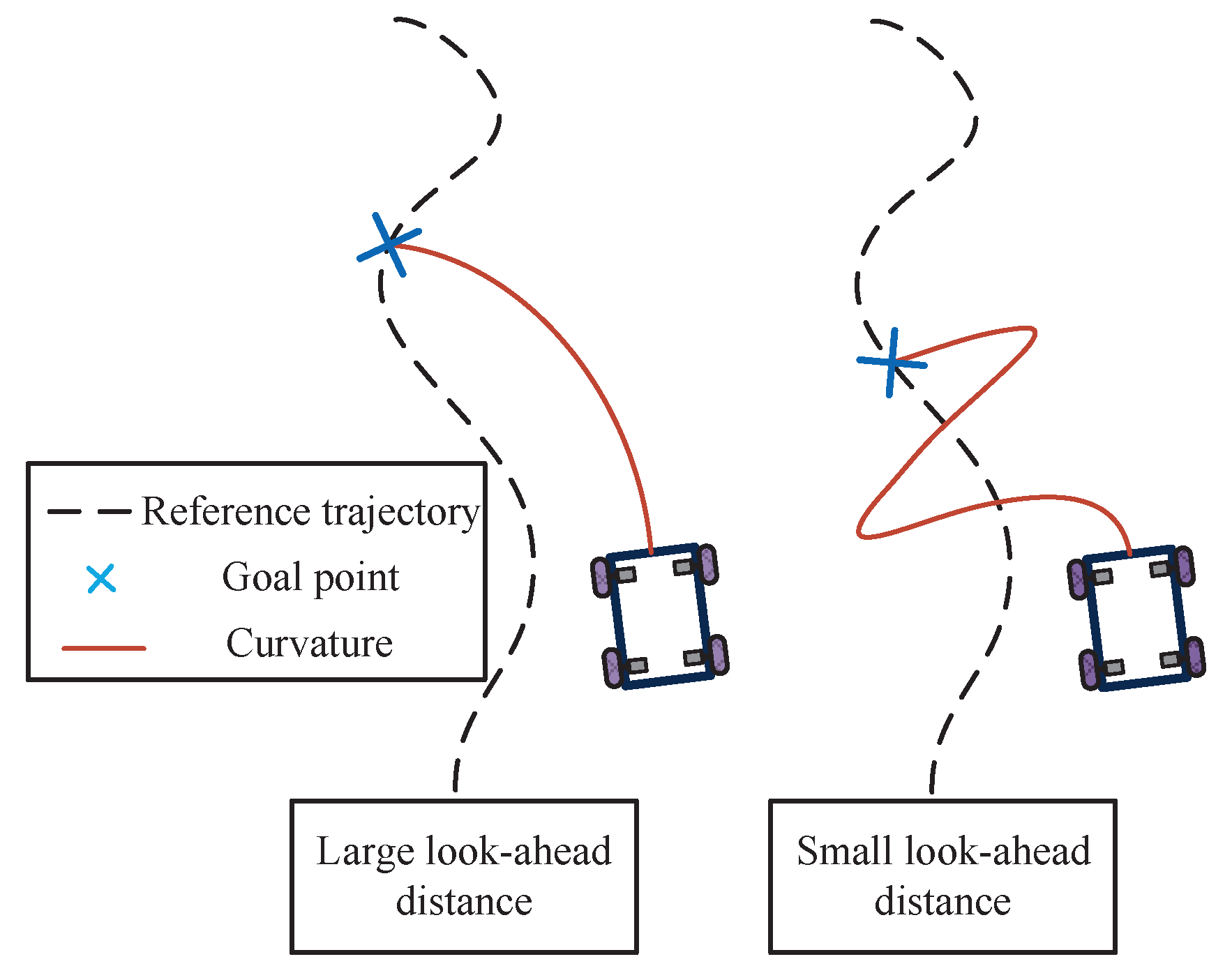
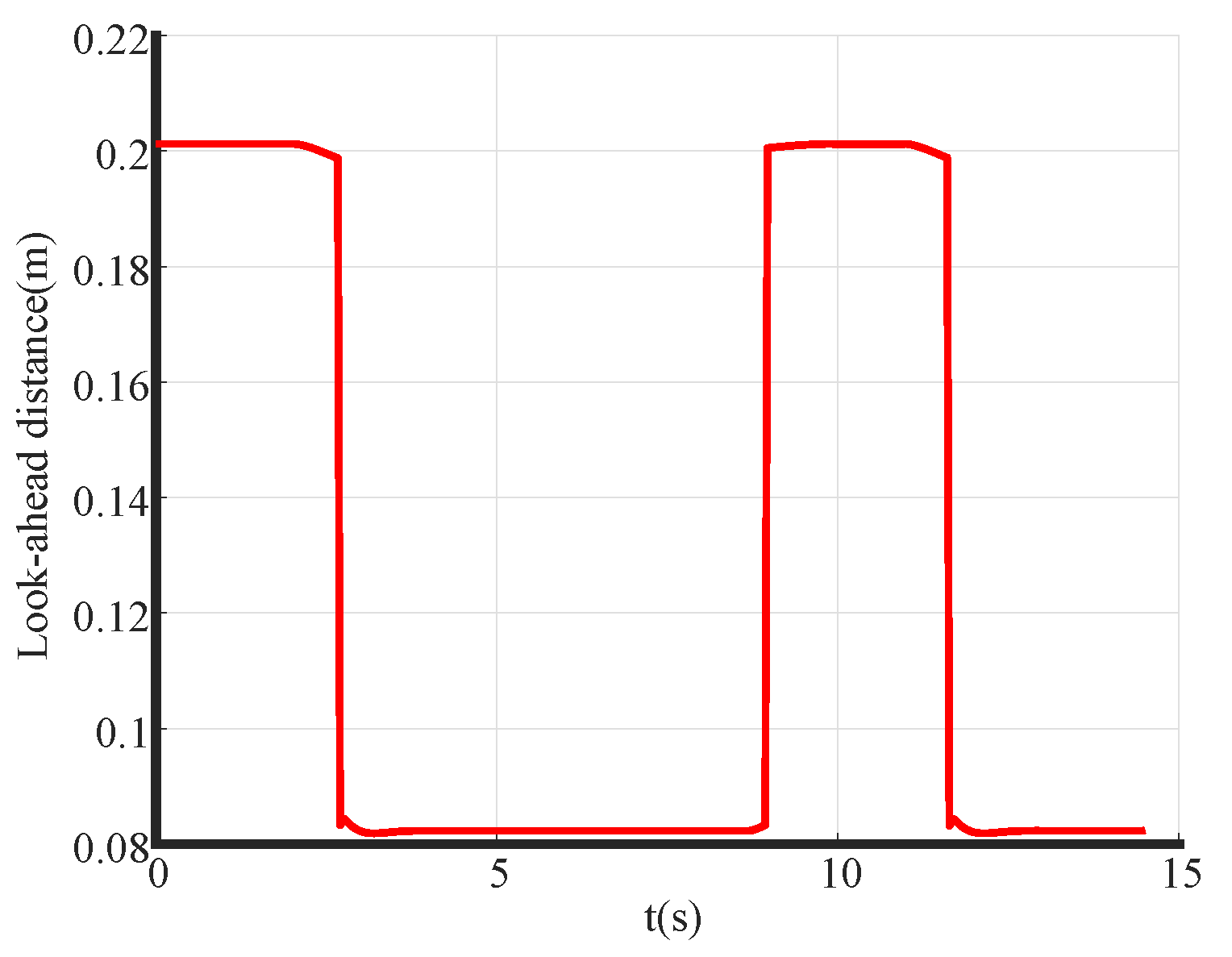
3.2. Quadratic Polynomial-Based A-PP Control
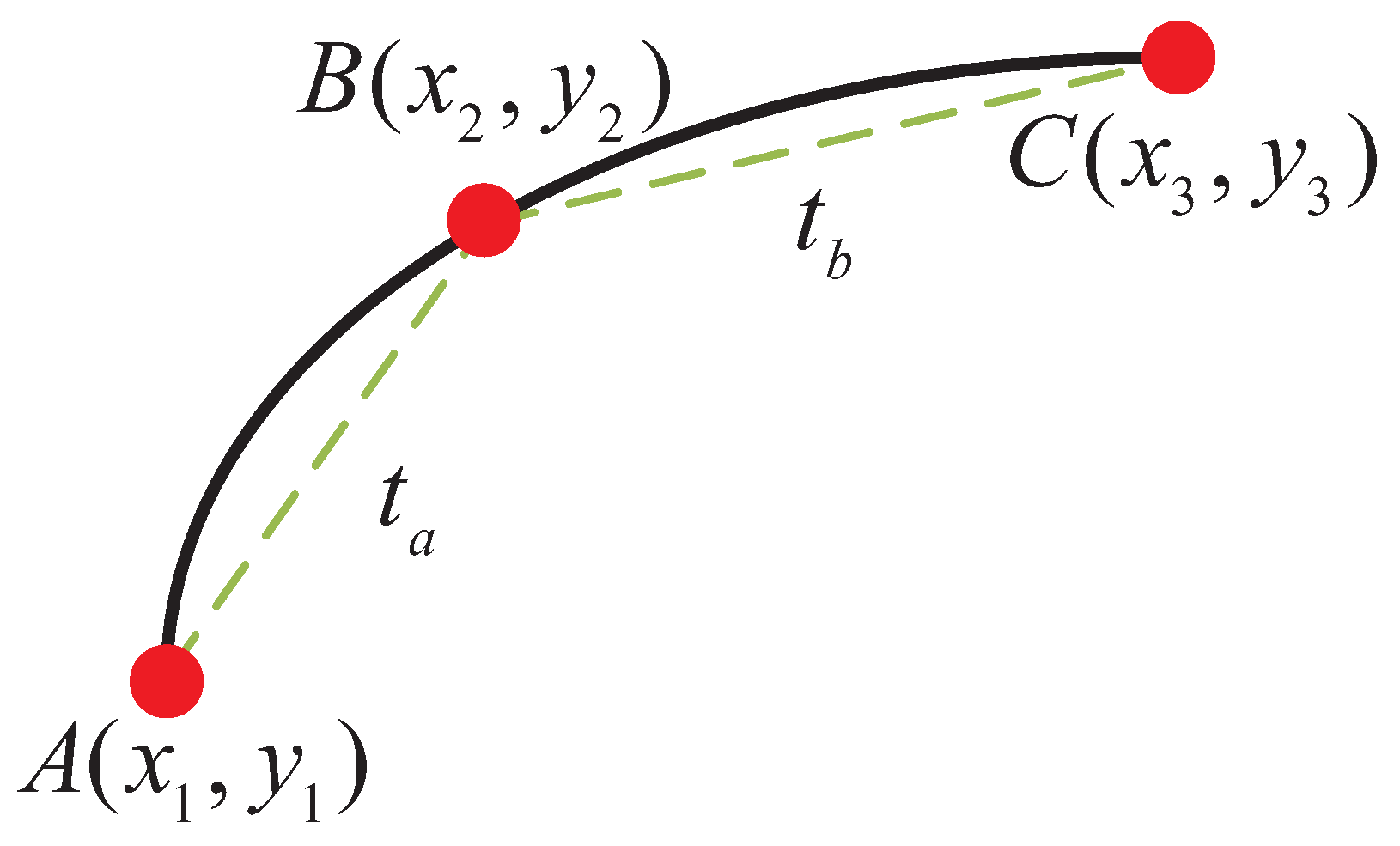
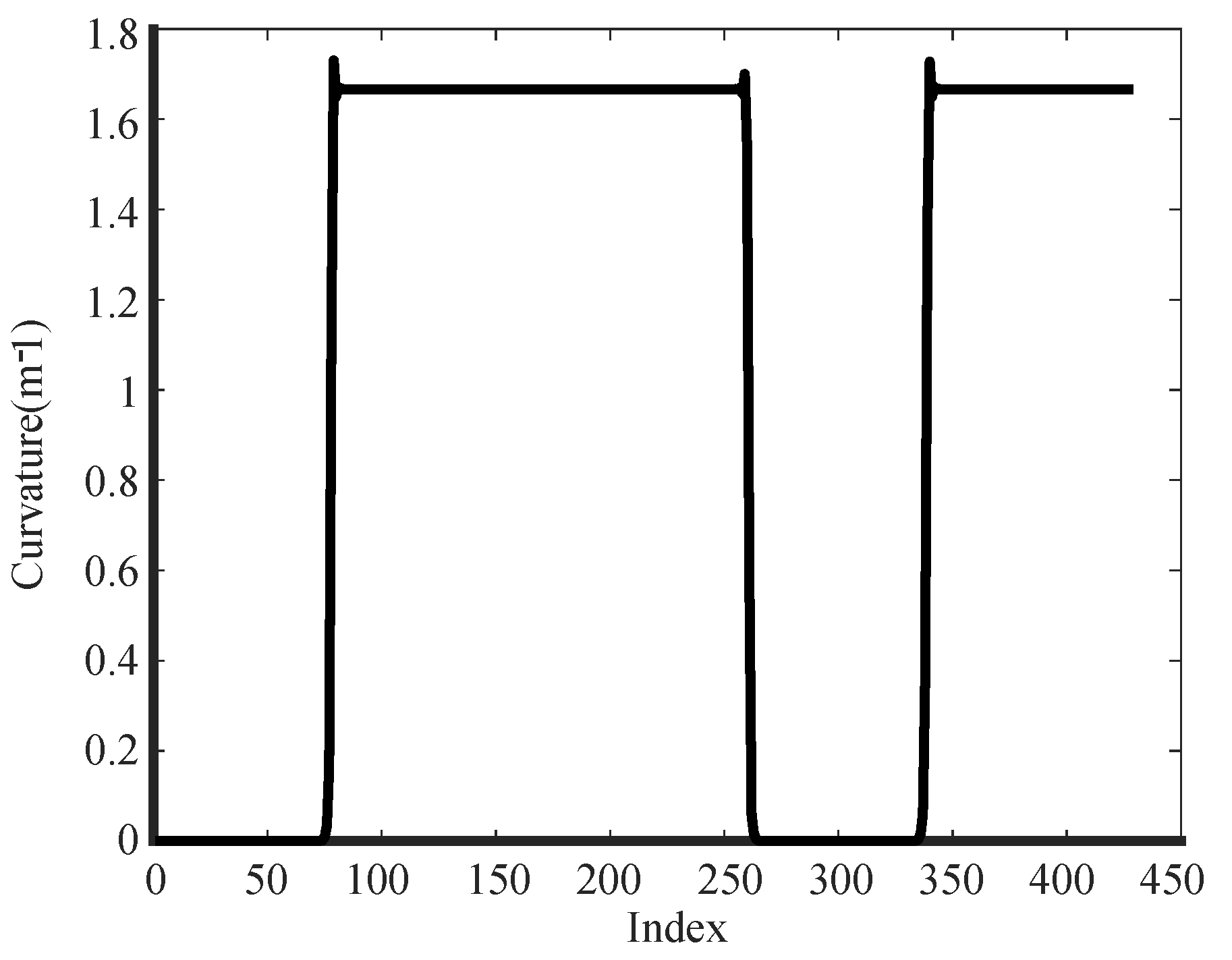
3.3. Road Curvature Calculation Method
4. Path Planning and Tracking
5. Experiment
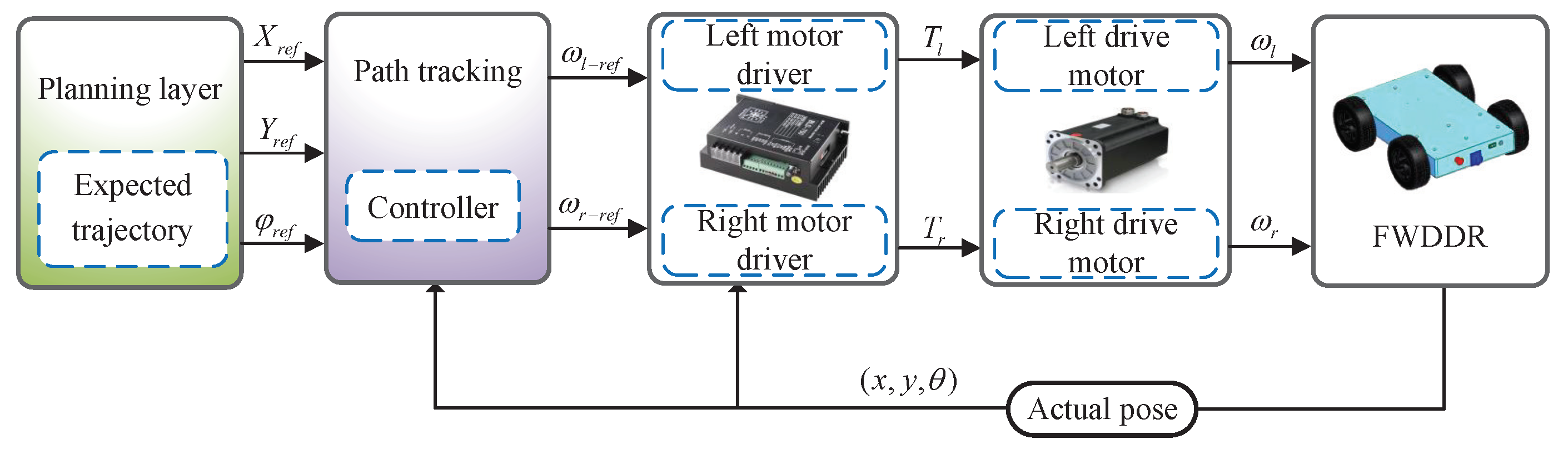
5.1. Experimental Setup
- (1)
- Control commands are sent through the PC Matlab/Simulink control interface via the RS485 bus;
- (2)
- On the PC side, E32-DTU converts commands transmitted via the RS485 bus into LoRa RF signals;
- (3)
- On the FWDDR side, E32-DTU converts LoRa signals into RS485 signals;
- (4)
- The motion controller interprets RS485 signals based on the four-wheel differential model and generates corresponding servo drive commands. These commands are then transmitted to the four servo drives through the CAN bus;
- (5)
- The motion controller transmits motor status, battery voltage, and other parameters back to the upper computer through a reverse path.
5.2. Experiment Process
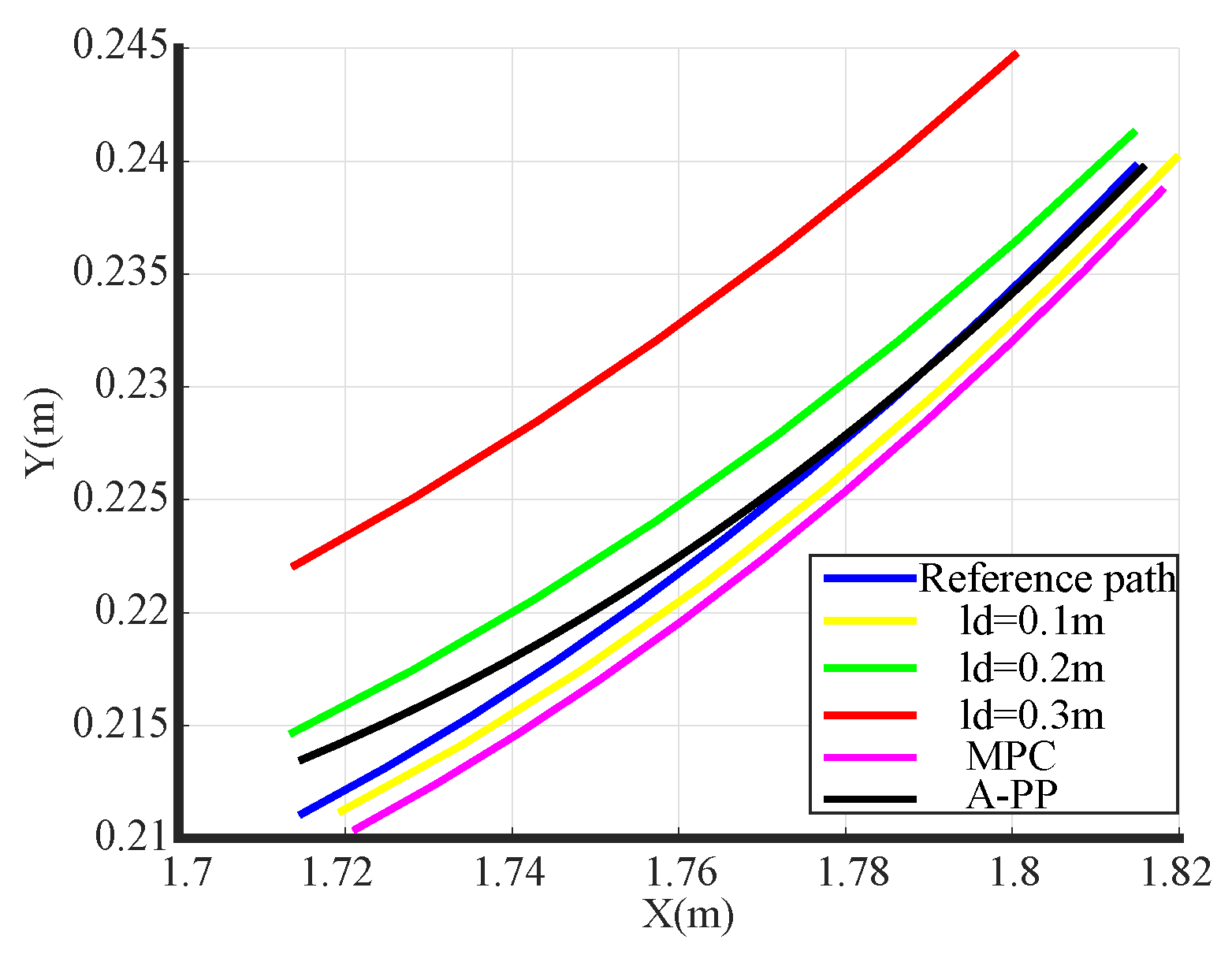
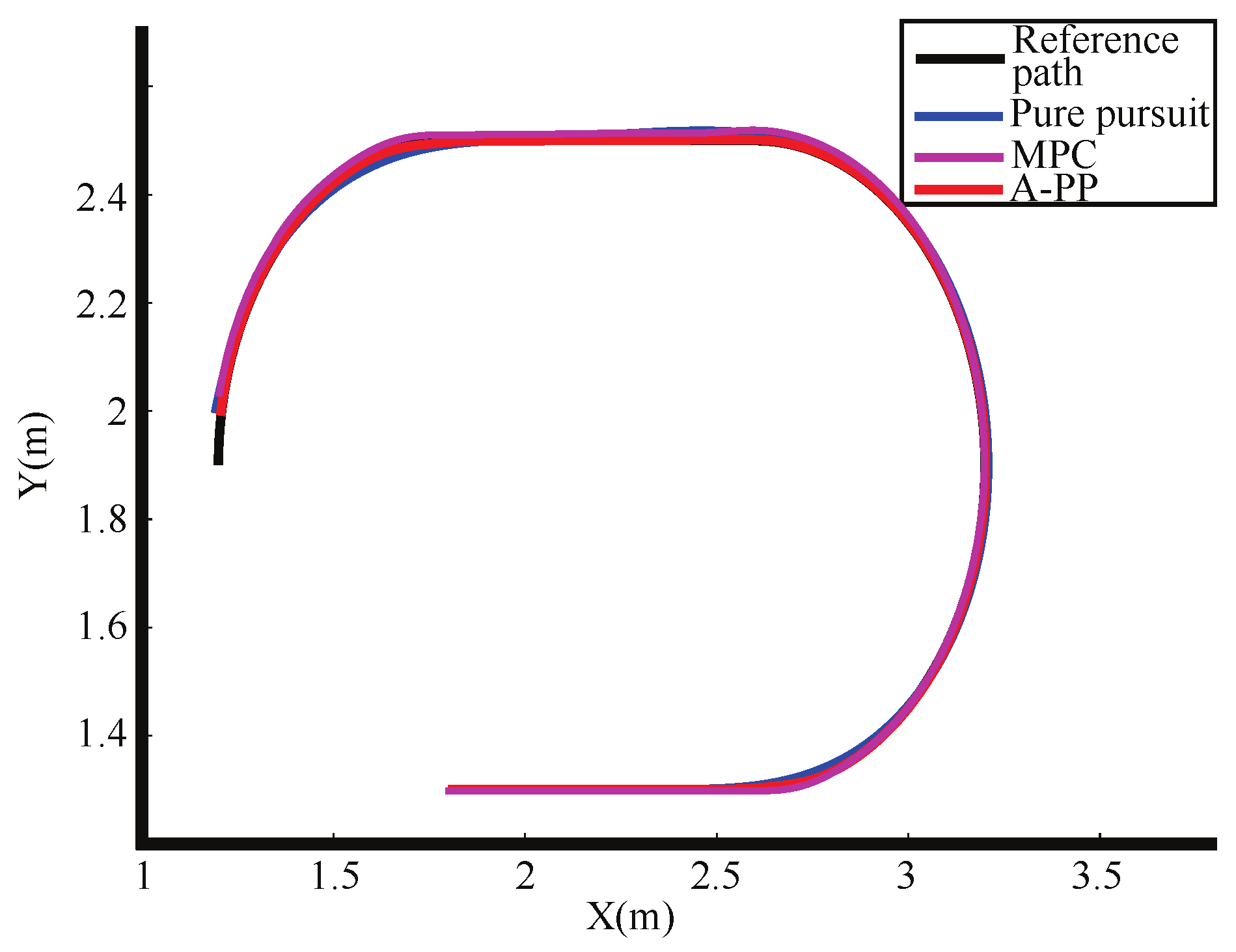
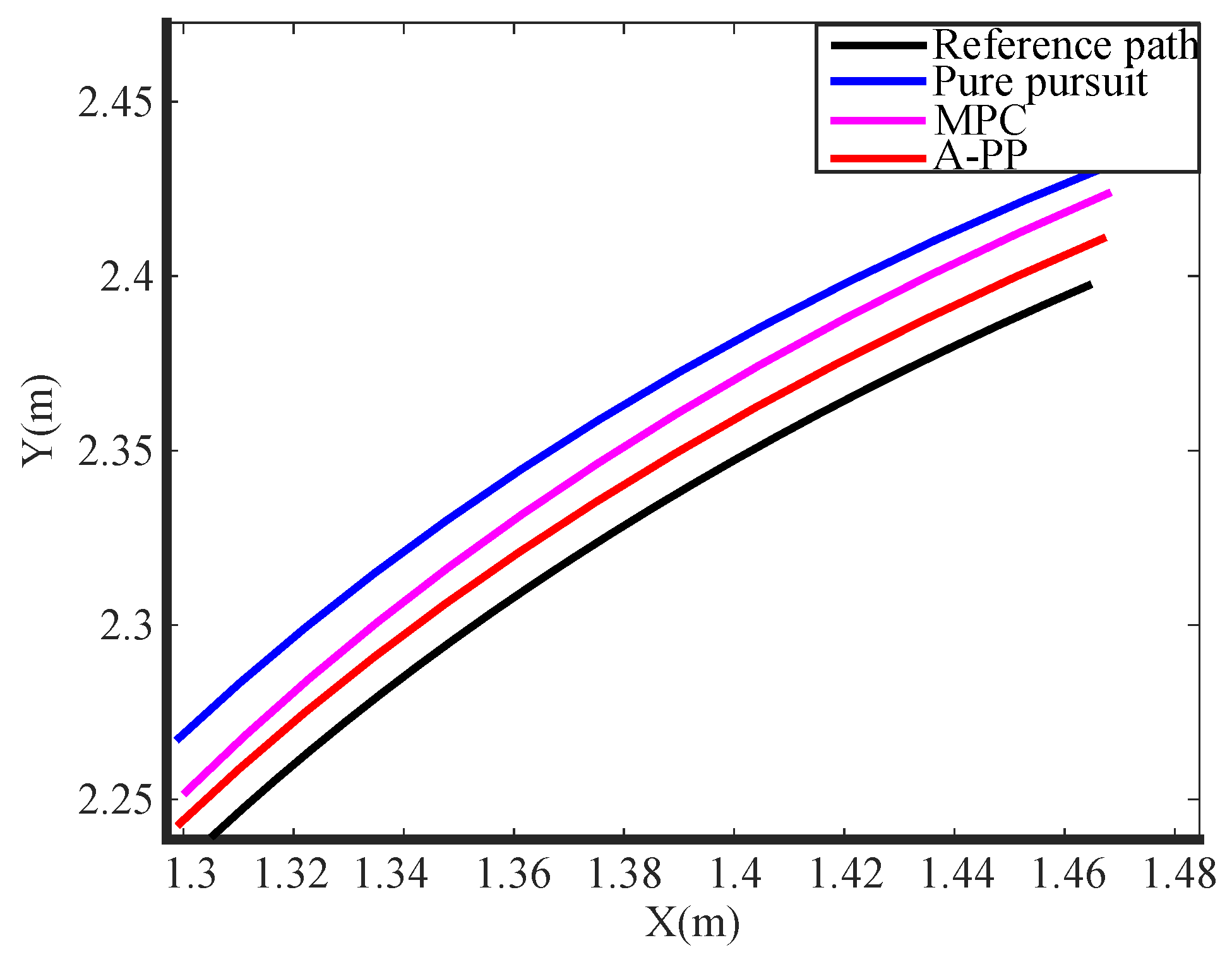
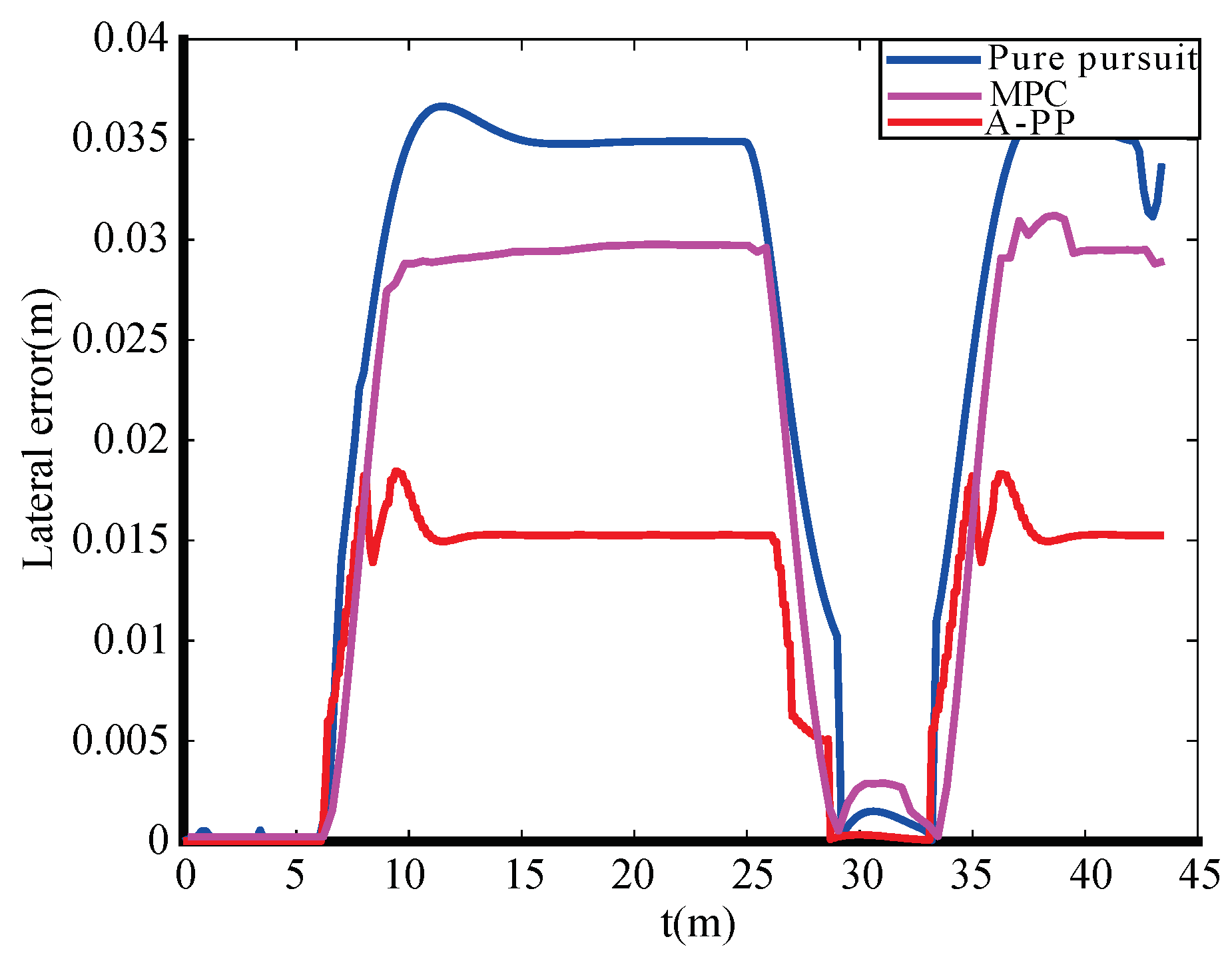
5.3. Analysis of Experimental Results
6. Conclusions
- (1)
- The quadratic polynomial is enhanced in both lateral and longitudinal dimensions to facilitate adaptive dynamic adjustment of the forward-looking distance. This enhancement reduces the lateral deviation of the FWDDR during path tracking and enhances both tracking accuracy and operational stability.
- (2)
- The A-PP algorithm is simulated and verified by Matlab/Simulink, and the results indicate that the A-PP algorithm achieves a mean lateral error of 0.00694 m, a variance of 0.004663 m, and a maximum lateral error of 0.012837 m during path tracking, which represent a significant enhancement in stability and accuracy when compared to the traditional PP and MPC algorithms.
- (3)
- Experimental tests further validated the A-PP algorithm. The results showed a mean lateral error of 0.01070 m, a variance of 0.006663 m, and a maximum lateral error of 0.019443 m. In comparison with the PP algorithm, the A-PP algorithm achieved faster convergence of deviations, enhanced lateral errors in turning sections, and heightened driving smoothness, all while maintaining low computational time.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Yan, Y.; Geng, K.; Liu, S.; Ren, Y. A New Path Tracking Algorithm for Four-Wheel Differential Steering Vehicle. In Proceedings of the 2019 Chinese Control Furthermore, Decision Conference (CCDC), Nanchang, China, 3–5 June 2019; pp. 1527–1532. [Google Scholar] [CrossRef]
- Shojaei, K.; Shahri, A.M.; Tarakameh, A.; Tabibian, B. Adaptive trajectory tracking control of a differential drive wheeled mobile robot. Robotica 2011, 29, 391–402. [Google Scholar] [CrossRef]
- Gao, H.; Song, X.; Ding, L.; Xia, K.; Li, N.; Deng, Z. Adaptive motion control of wheeled mobile robot with unknown slippage. Int. J. Control 2014, 87, 1513–1522. [Google Scholar] [CrossRef]
- Deng, M.; Inoue, A.; Sekiguchi, K.; Jiang, L. Two-wheeled mobile robot motion control in dynamic environments. Robot. Comput.-Integr. Manuf. 2010, 26, 268–272. [Google Scholar] [CrossRef]
- Coelho, P.; Nunes, U. Path-following control of mobile robots in presence of uncertainties. IEEE Trans. Robot. 2005, 21, 252–261. [Google Scholar] [CrossRef]
- Samson, C.; Morin, P.; Lenain, R. Modeling and control of wheeled mobile robots. In Springer Handbook of Robotics; Springer: Berlin, Germany, 2016; pp. 1235–1266. [Google Scholar] [CrossRef]
- Cui, M. Observer-based adaptive tracking control of wheeled mobile robots with unknown slipping parameters. IEEE Access 2019, 7, 169646–169655. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, B. Development and key technologies of dynamic wireless power transfer system for mobile load. Electr. Power Eng. Technol. 2020, 39, 21–30. [Google Scholar]
- Xie, L.; Jiang, C.; Sun, Q.; Wang, H.; Song, Q.; Guan, G. The global map’s creating and positioning of substation inspection robot based on adaptive Monte Carlo particle filter algorithm. Electr. Power Eng. Technol. 2019, 38, 16–23. [Google Scholar]
- Dong, L.; Geng, Z.; Liu, H.; Li, H. High accuracy and high efficiency model of non-standard ratio transformer. Electr. Power Eng. Technol. 2021, 40, 60–65. [Google Scholar]
- Moudoud, B.; Aissaoui, H.; Diany, M. Robust trajectory tracking control based on sliding mode of Differential Driving Four-Wheeled Mobile Robot. In Proceedings of the 2020 IEEE 6th International Conference on Optimization and Applications (ICOA), Beni Mellal, Morocco, 20–21 April 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Wang, S.; Yin, X.; Li, P.; Zhang, M.; Wang, X. Trajectory tracking control for mobile robots using reinforcement learning and PID. Iran. J. Sci. Technol. Trans. Electr. Eng. 2020, 44, 1059–1068. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, M. Fuzzy control systems: Past, present and future. IEEE Comput. Intell. Mag. 2019, 14, 56–68. [Google Scholar] [CrossRef]
- Alouache, A.; Wu, Q. Genetic algorithms for trajectory tracking of mobile robot based on PID controller. In Proceedings of the 2018 IEEE 14th International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 6–8 September 2018; pp. 237–241. [Google Scholar] [CrossRef]
- Jiang, X.; Motai, Y.; Zhu, X. Predictive fuzzy logic controller for trajectory tracking of a mobile robot. In Proceedings of the 2005 IEEE Midnight-Summer Workshop on Soft Computing in Industrial Applications, Espoo, Finland, 28–30 June 2005; pp. 29–32. [Google Scholar] [CrossRef]
- Nguyen, T.V.; Huynh, N.T.; Vu, N.C.; Kieu, V.N.; Huang, S.C. Optimizing compliant gripper mechanism design by employing an effective bi-algorithm: Fuzzy logic and ANFIS. Microsyst. Technol. 2021, 27, 1–24. [Google Scholar] [CrossRef]
- Huynh, N.T.; Nguyen, T.V.; Tam, N.T.; Nguyen, Q.M. Optimizing magnification ratio for the flexible hinge displacement amplifier mechanism design. In Proceedings of the 2nd Annual International Conference on Material, Machines and Methods for Sustainable Development (MMMS2020); Springer: Berlin/Heidelberg, Germany, 2021; pp. 769–778. [Google Scholar] [CrossRef]
- Cheng, S.; Li, L.; Guo, H.Q.; Chen, Z.G.; Song, P. Longitudinal collision avoidance and lateral stability adaptive control system based on MPC of autonomous vehicles. IEEE Trans. Intell. Transp. Syst. 2019, 21, 2376–2385. [Google Scholar] [CrossRef]
- Xu, C.; Li, M.; Pan, F. The system design and LQR control of a two-wheels self-balancing mobile robot. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Nanchang, China, 20–22 June 2011; pp. 2786–2789. [Google Scholar] [CrossRef]
- Xu, H.; Zhu, J. Interval trajectory tracking for AGV based on MPC. In Proceedings of the 2019 Chinese Control Conference (CCC), Guangzhou, China, 27–30 July 2019; pp. 2835–2839. [Google Scholar] [CrossRef]
- Ni, J.; Wang, Y.; Li, H.; Du, H. Path Tracking Motion Control Method Of Tracked Robot Based On Improved LQR Control. In Proceedings of the 2022 41st Chinese Control Conference (CCC), Hefei, China, 25–27 July 2022; pp. 2888–2893. [Google Scholar] [CrossRef]
- Wang, W.J.; Hsu, T.M.; Wu, T.S. The improved pure pursuit algorithm for autonomous driving advanced system. In Proceedings of the 2017 IEEE 10th International Workshop on Computational Intelligence and Applications (IWCIA), Hiroshima, Japan, 11–12 November 2017; pp. 33–38. [Google Scholar] [CrossRef]
- Sun, Q.; Wang, Z.; Li, M.; Liu, B.; Cheng, J.; Tai, J. Path tracking control of wheeled mobile robot based on improved pure pursuit algorithm. In Proceedings of the 2019 Chinese Automation Congress (CAC), Hangzhou, China, 22–24 November 2019; pp. 4239–4244. [Google Scholar] [CrossRef]
- Amer, N.H.; Hudha, K.; Zamzuri, H.; Aparow, V.R.; Abidin, A.F.Z.; Abd Kadir, Z.; Murrad, M. Adaptive modified Stanley controller with fuzzy supervisory system for trajectory tracking of an autonomous armoured vehicle. Robot. Auton. Syst. 2018, 105, 94–111. [Google Scholar] [CrossRef]
- Ding, H.; Liu, H.; Zhuang, Y.; Kan, M.; Xia, D.; Ding, S. Multi-robot path planning based on four-wheel differential speed model. Control Eng. China 2023, 30, 730–738. [Google Scholar] [CrossRef]
- Zhang, K.; Yen, G.G.; He, Z. Evolutionary algorithm for knee-based multiple criteria decision making. IEEE Trans. Cybern. 2019, 51, 722–735. [Google Scholar] [CrossRef]
- Hu, Y.; Chen, G.; Li, Z.; Knoll, A. Robot policy improvement with natural evolution strategies for stable nonlinear dynamical system. IEEE Trans. Cybern. 2022, 2022, 4002–4014. [Google Scholar] [CrossRef]
- Kozłowski, K.; Pazderski, D. Modeling and control of a 4-wheel skid-steering mobile robot. Int. J. Appl. Math. Comput. Sci. 2004, 14, 477–496. [Google Scholar]
- Li, P.; Wang, H.; Zhu, M.; Liu, J. Maneuver control of a four-wheel differentially driven robot based on instantaneous center of rotation. In Proceedings of the 2018 Chinese Control Furthermore, Decision Conference (CCDC), Shenyang, China, 9–11 June 2018; pp. 4917–4922. [Google Scholar] [CrossRef]
- Liu, Y.; Jiang, Y. Motion planning of differential driven robot based on tracking. Control Decis. 2023, 38, 2529–2536. [Google Scholar] [CrossRef]
- Coulter, R.C. Implementation of the Pure Pursuit Path Tracking Algorithm; Carnegie Mellon University, The Robotics Institute: Pittsburgh, PA, USA, 1992. [Google Scholar]
- Wu, X.; Angeles, J.; Zou, T.; Sun, C.; Sun, Q.; Wang, L. Receding-horizon vision guidance with smooth trajectory blending in the field of view of mobile robots. Appl. Sci. 2020, 10, 676. [Google Scholar] [CrossRef]
- Duan, J.; Yang, C.; Shi, H. Path tracking based on pure pursuit algorithm for intelligent vehicles. J. Beijing Univ. Technol. 2016, 42, 1301–1306. [Google Scholar]
- Li, G.; Wang, Y.; Guo, L.; Tong, J. Improved pure pursuit algorithm for rice transplanter path tracking. Nongye Jixie Xuebao/Trans. Chin. Soc. Agric. Mach. 2018, 49, 21–26. [Google Scholar]



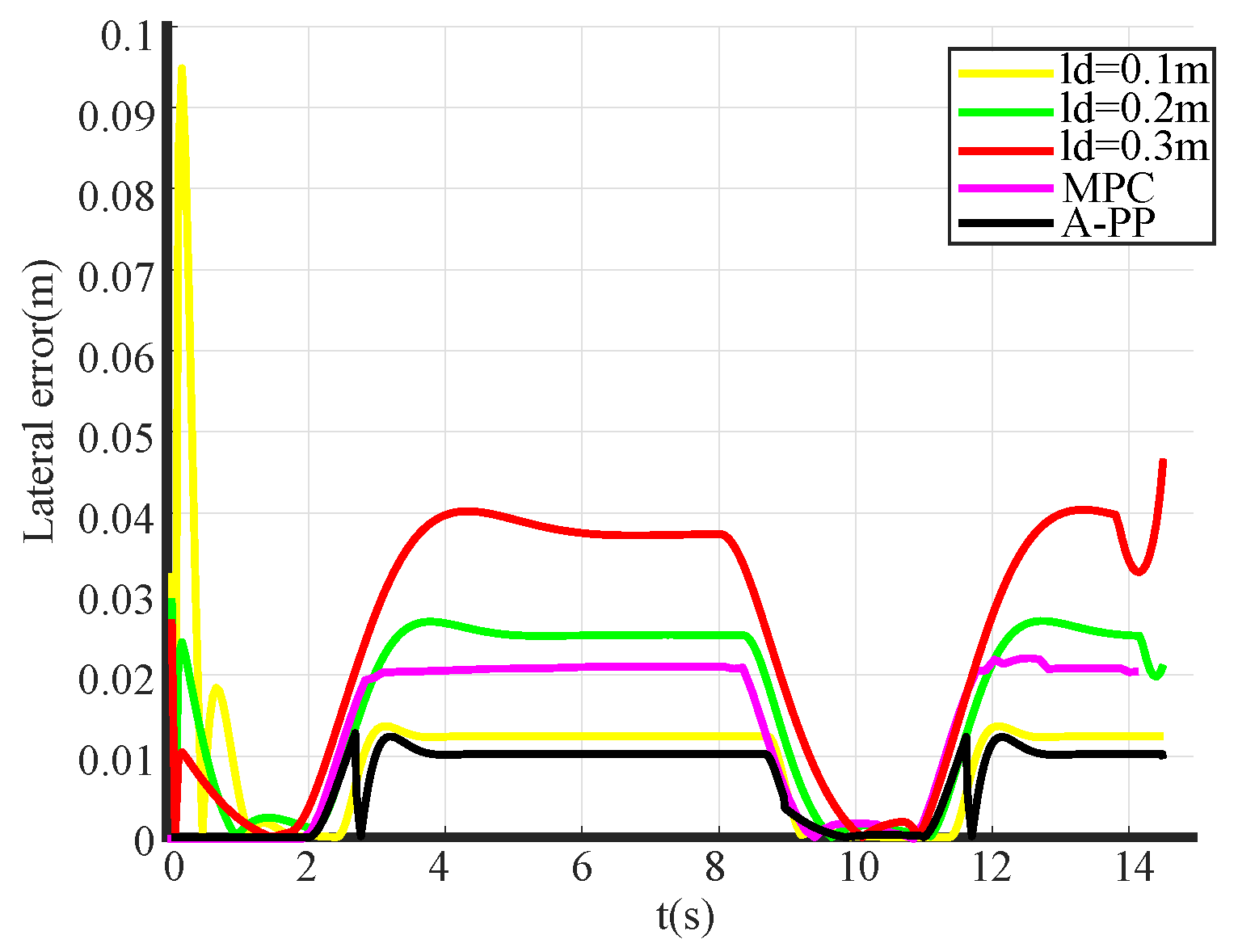

| Method | Average Value of Lateral Error (m) | Variance (m) | Maximum Lateral Error (m) |
|---|---|---|---|
| = 0.1 m | 0.01007 | 0.010075 | 0.094842 |
| = 0.2 m | 0.01688 | 0.010333 | 0.029417 |
| = 0.3 m | 0.02462 | 0.015404 | 0.046663 |
| MPC | 0.01467 | 0.010247 | 0.021854 |
| A-PP | 0.00694 | 0.004663 | 0.012837 |
| Parameters | Value | Units |
|---|---|---|
| Length | 770 | mm |
| Width | 658 | mm |
| Wheelbase | 470 | mm |
| Wheel tread | 573 | mm |
| Minimum turning | 1015 | mm |
| Tire size (diameter) | 260 | mm |
| Maximum motor speed | 3600 | rpm |
| Maximum driving torque | 47.5 | N·m |
| Maximum load | ≥50 | kg |
| Method | Average Value of Lateral Error (m) | Variance (m) | Maximum Lateral Error (m) |
|---|---|---|---|
| Pure pursuit | 0.02372 | 0.016588 | 0.036705 |
| MPC | 0.02069 | 0.014416 | 0.031628 |
| A-PP | 0.01070 | 0.006663 | 0.019443 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Zhao, G.; He, Y.; Diao, Z.; He, Z.; Cui, Y.; Jiang, L.; Shen, Y.; Cheng, C. Biomimetic Adaptive Pure Pursuit Control for Robot Path Tracking Inspired by Natural Motion Constraints. Biomimetics 2024, 9, 41. https://doi.org/10.3390/biomimetics9010041
Zhao S, Zhao G, He Y, Diao Z, He Z, Cui Y, Jiang L, Shen Y, Cheng C. Biomimetic Adaptive Pure Pursuit Control for Robot Path Tracking Inspired by Natural Motion Constraints. Biomimetics. 2024; 9(1):41. https://doi.org/10.3390/biomimetics9010041
Chicago/Turabian StyleZhao, Suna, Guangxin Zhao, Yan He, Zhihua Diao, Zhendong He, Yingxue Cui, Liying Jiang, Yongpeng Shen, and Chao Cheng. 2024. "Biomimetic Adaptive Pure Pursuit Control for Robot Path Tracking Inspired by Natural Motion Constraints" Biomimetics 9, no. 1: 41. https://doi.org/10.3390/biomimetics9010041






