Static Robust Design Optimization Using the Stochastic Frontier Method: A Case Study of Pulsed EPD Process on TiO2 Films
Abstract
:1. Introduction
1.1. Robust Design of Products and Processes
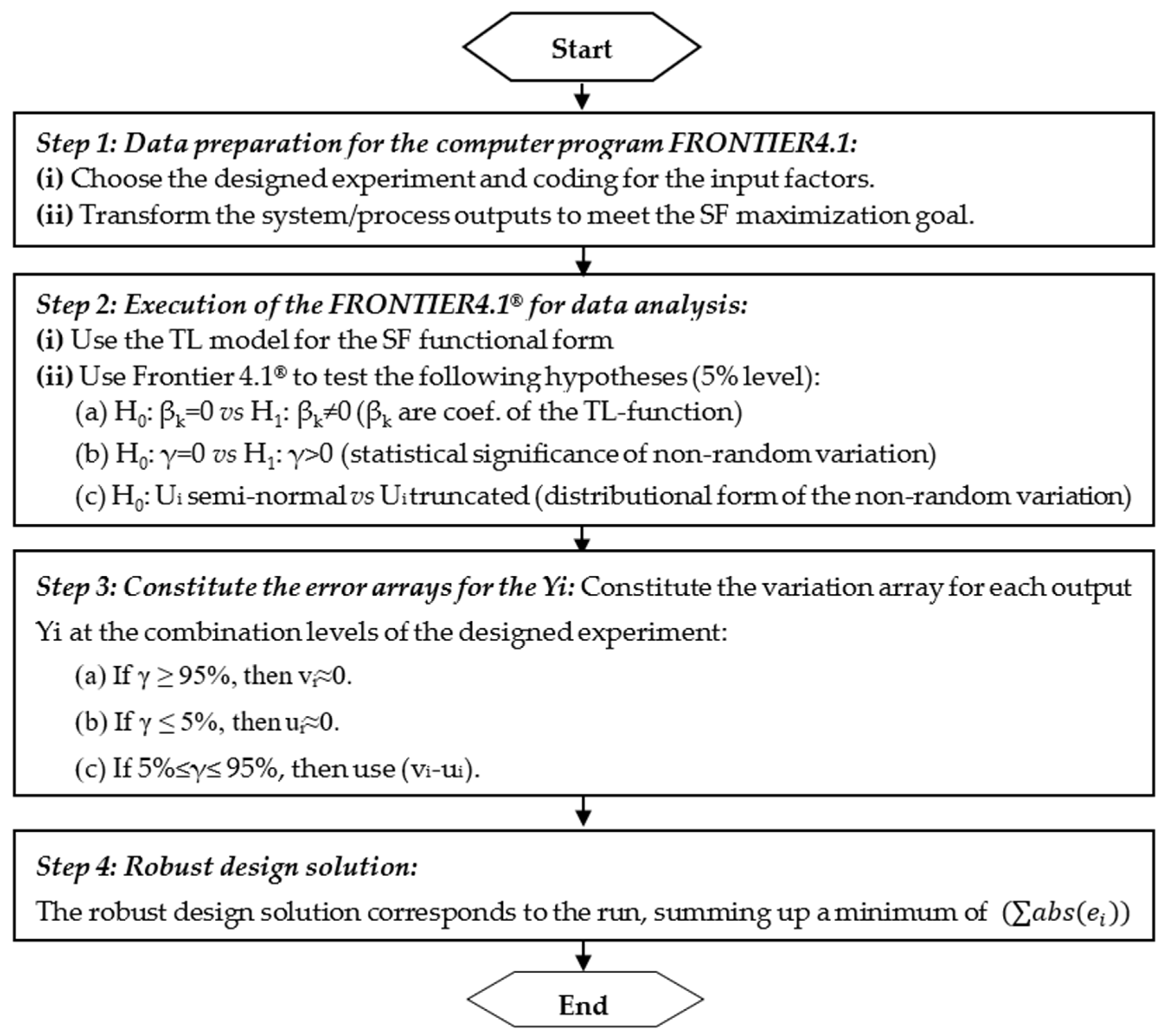
1.2. Static RDPP-SF Method
- (a)
- vi~N(0,).
- (b)
- ui~N+(0,).
- (c)
- vi and ui are independent and uncorrelated with the input variables.
- H0: βk = 0 vs. H1: βk ≠ 0. This is to check the statistical significance of the coefficients of the frontier model.
- H0: γ = 0 vs. H1: γ > 0. This is to assess the fitness of the average line model (RSM) and investigate the statistical significance of the special cause error for the (Yi).
- H0: Ui~Half-normal vs. H1: Ui~truncated normal distribution.
- If γ ≥ 95%, then vi ≈ 0 and special cause variation prevails. The error array (ei) is then composed of the ui(s) values of the output (Yi) for each run.
- If γ ≤ 5%, then ui ≈ 0 and the bulk of variation is due to only random unit-to-unit variation. The error array (ei) is composed of the vi(s) values of the output (Yi) for each run. In this situation, the average line model (RMS) is confounding with the SF model.
- If 5% ≤ γ ≤ 95%, both random and special cause variation sources are accountable for the result. The error array (ei) is then composed of the Abs(vi–ui) values of the output (Yi) for each run. The (vi–ui) values represent the observable variation in Yi.
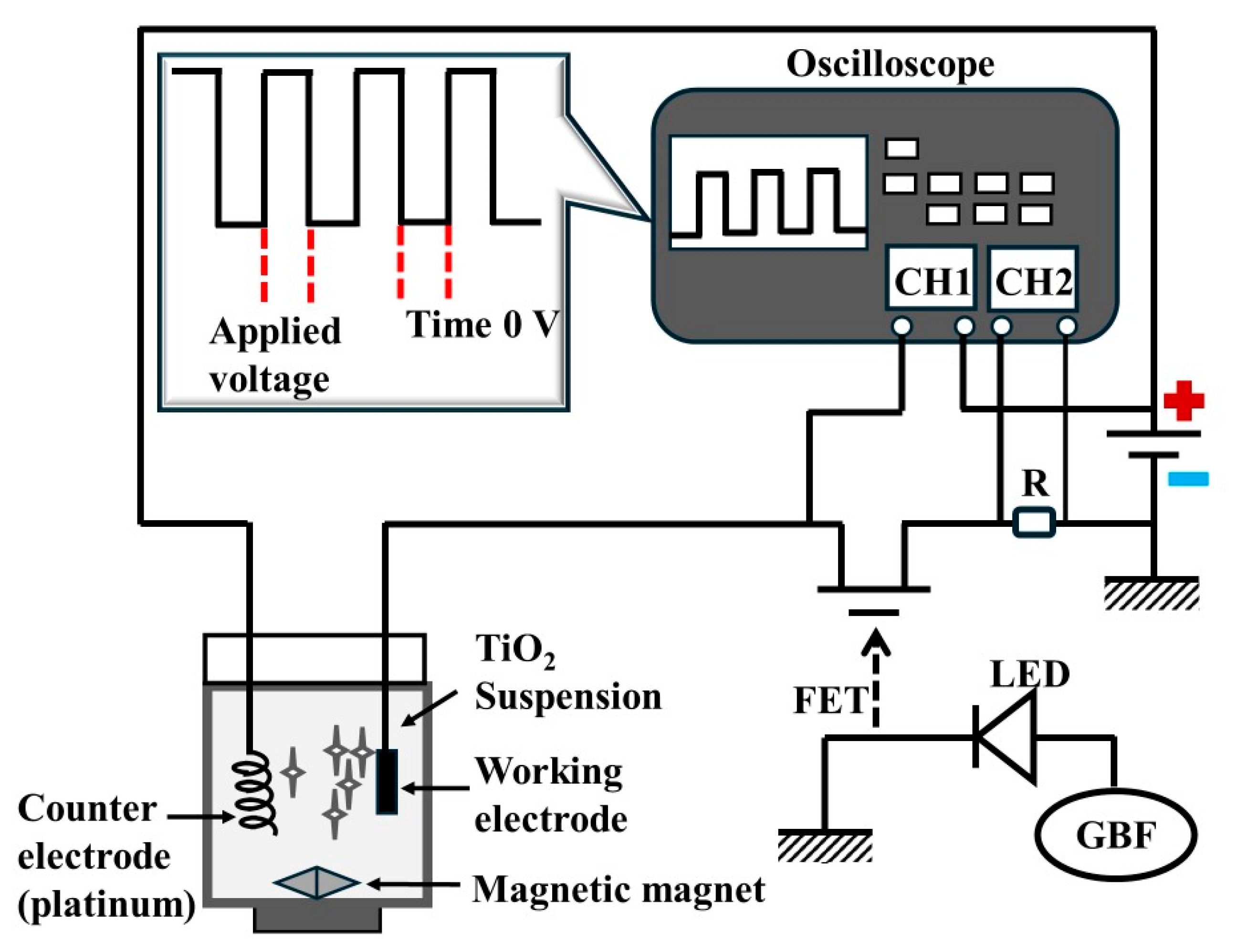
2. Materials and Methods
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zeribi, F.; Attaf, A.; Derbali, A.; Saidi, H.; Benmebrouk, L.; Aida, M.S.; Dahnoun, M.; Nouadji, R.; Ezzaouia, H. Dependence of the physical properties of titanium dioxide (TiO2) thin films grown by sol-gel (spin-coating) process on thickness. ECS J. Solid State Sci. Technol. 2022, 11, 023003. [Google Scholar] [CrossRef]
- Xu, J.; Nagasawa, H.; Kanezashi, M.; Tsuru, T. TiO2 coatings via atmospheric-pressure plasma-enhanced chemical vapor deposition for enhancing the UV-resistant properties of transparent plastics. ACS Omega 2021, 6, 1370–1377. [Google Scholar] [CrossRef]
- Puga, M.L.; Venturini, J.; Ten Caten, C.S.; Bergmann, C.P. Influencing parameters in the electrochemical anodization of TiO2 nanotubes: Systematic review and meta-analysis. Ceram. Int. 2022, 48, 19513–19526. [Google Scholar] [CrossRef]
- Barbana, N.; Ben Youssef, A.; Dhiflaoui, H.; Bousselmi, L. Preparation and characterization of photocatalytic TiO2 films on functionalized stainless steel. J. Mater. Sci. 2018, 53, 3341–3364. [Google Scholar] [CrossRef]
- Ben Youssef, A.; Barbana, N.; Al-Addous, M.; Bousselmi, L. Preparation and characterization of photocatalytic TiO2/WO3 films on functionalized stainless steel. J. Mater. Sci. Mater. Electron. 2018, 29, 19909–19922. [Google Scholar] [CrossRef]
- Santillán, M.; Membrives, F.; Quaranta, N.; Boccaccini, A. Characterization of TiO2 nanoparticle suspensions for electrophoretic deposition. J. Nanopart. Res. 2008, 10, 787–793. [Google Scholar] [CrossRef]
- Hanaor, D.; Michelazzi, M.; Veronesi, P.; Leonelli, C.; Romagnoli, M.; Sorrell, C. Anodic aqueous electrophoretic deposition of titanium dioxide using carboxylic acids as dispersing agents. J. Eur. Ceram. Soc. 2011, 31, 1041–1047. [Google Scholar] [CrossRef]
- de Sousa, R.R.M.; de Araújo, F.O.; da Costa, J.A.P.; Nishimoto, A.; Viana, B.C.; Alves, C., Jr. Deposition of TiO2 film on duplex stainless-steel substrate using the cathodic cage plasma technique. Mater. Res. 2016, 19, 1207–1212. [Google Scholar] [CrossRef]
- Gao, F.; Sherwood, P. Photoelectron spectroscopic studies of the formation of hydroxyapatite films on 316L. Surf. Interface Anal. 2012, 44, 1587–1600. [Google Scholar] [CrossRef]
- Krishna, D.; Chena, Y.; Sun, Z. Magnetron sputtered TiO2 films on a stainless-steel substrate: Selective rutile phase formation and its tribological and anti-corrosion performance. Thin Solid Films 2011, 519, 4860–4864. [Google Scholar] [CrossRef]
- Tang, F.; Uchikoshi, T.; Ozawa, K.; Sakka, Y. Effect of polyethyleneimine on the dispersion and electrophoretic deposition of nano-sized titania aqueous suspensions. J. Eur. Ceram. Soc. 2006, 26, 1555–1560. [Google Scholar] [CrossRef]
- Nurhayati, E.; Yang, H.; Chen, C.; Liu, C.; Juang, Y.; Huang, C.; Hu, C. Electro-photocatalytic fenton decolorization of orange G using mesoporous TiO2/stainless steel mesh photo-electrode prepared by the sol-gel dip-coating method. Int. J. Electrochem. Sci. 2016, 11, 3615–3632. [Google Scholar] [CrossRef]
- Trabelsi, A.; Rezgui, M.-A. Robust design of processes and products using the mathematics of the stochastic frontier. Int. J. Adv. Manuf. Technol. 2020, 106, 2829–2841. [Google Scholar] [CrossRef]
- Rezgui, M.-A.; Trabelsi, A. Use of the stochastic frontier and the grey relational analysis in robust design of multi-objective problems. Concurr. Eng. Res. Appl. 2020, 28, 110–129. [Google Scholar] [CrossRef]
- Taguchi, G. System of Experimental Design; UNIPUB/Kraus International Publications: White Plains, NY, USA, 1987. [Google Scholar]
- Del Castillo, E.; Montgomery, D.; McCarville, D.R. Modified desirability functions for multiple response optimization. J. Qual. Technol. 1996, 28, 337–345. [Google Scholar] [CrossRef]
- Chen, L.H. Designing robust products with multiple quality characteristics. Comput. Oper. Res. 1997, 24, 937–944. [Google Scholar] [CrossRef]
- Su, C.T.; Tong, L.I. Multi-response robust design by principal component analysis. Total Qual. Manag. 1997, 8, 409–416. [Google Scholar] [CrossRef]
- Tong, L.-I.; Su, C.T. Optimizing multi-response problems in the Taguchi method by fuzzy multiple attribute decision making. Qual. Reliab. Eng. Int. 1997, 13, 25–34. [Google Scholar] [CrossRef]
- Antony, J. Simultaneous optimization of multiple quality characteristics in manufacturing processes using Taguchi’s quality loss function. Int. J. Adv. Manuf. Technol. 2001, 17, 134–138. [Google Scholar] [CrossRef]
- Kim, K.J.; Lin, D.K.J. Simultaneous optimization of mechanical properties of steel by maximizing exponential desirability functions. J. R. Stat. Soc. Ser. C Appl. Stat. 2000, 49, 311–325. [Google Scholar] [CrossRef]
- Liao, H.-C.; Chen, Y.K. Optimizing multi-response problem in the Taguchi method by DEA-based ranking method. Int. J. Qual. Reliab. Manag. 2002, 19, 825–837. [Google Scholar] [CrossRef]
- Liao, H.-C. Using PCR-TOPSIS to optimize Taguchi’s multi-response problem. Int. J. Adv. Manuf. Technol. 2003, 22, 649–655. [Google Scholar] [CrossRef]
- Hsu, C.M.; Su, C.T.; Liao, D. Simultaneous of the broadband tap coupler optical performance based on neural networks and exponential desirability functions. Int. J. Adv. Manuf. Technol. 2004, 23, 896–902. [Google Scholar] [CrossRef]
- Ortiz, F.J.R.; Simpson, J.R.; Pignatiello, J.R.; Alejandro, H.L. A genetic algorithm approach to multiple-response optimization. J. Qual. Technol. 2004, 36, 432–449. [Google Scholar] [CrossRef]
- Liao, H.-C. Using N-D method to solve multi-response problem in Taguchi. J. Intell. Manuf. 2005, 16, 331–347. [Google Scholar] [CrossRef]
- Fung, C.P.; Kang, P.C. Multi-response optimization in friction properties of PBT composites using Taguchi method and principle component analysis. J. Mater. Process. Technol. 2005, 170, 602–610. [Google Scholar] [CrossRef]
- Liao, H.-C. Multi-response optimization using weighted principal component. Int. J. Adv. Manuf. Technol. 2006, 27, 720–725. [Google Scholar] [CrossRef]
- Liao, H.-C.; Chang, H.H.; Hsu, C.M. Using canonical correlation to optimize Taguchi’s multiresponse problem. Concurr. Eng. Res. Appl. 2006, 14, 141–149. [Google Scholar] [CrossRef]
- Köksoy, O.A. Nonlinear programming solution to robust multi-response quality problem. Appl. Math. Comput. 2008, 196, 603–612. [Google Scholar] [CrossRef]
- Al-Refaie, A. Grey-data envelopment analysis approach for solving the multi-response problem in the Taguchi method. Proc. IMechE Part B J. Eng. Manuf. 2010, 224, 147–158. [Google Scholar] [CrossRef]
- Pal, S.; Gauri, S.K. Multi-response optimization using multiple regression-based weighted signal-to-noise ratio (MRWSN). Qual. Eng. 2010, 22, 336–350. [Google Scholar] [CrossRef]
- Al-Refaie, A.; Rawabdeh, I.; Abu-Alhaj, R.; Jalham, I. A fuzzy multiple regressions approach for optimizing multiple responses in the Taguchi method. Int. J. Fuzzy Syst. Appl. 2012, 2, 13–34. [Google Scholar] [CrossRef]
- Canessa, E.; Bielenberg, G.; Allende, H. Robust design in multiobjective systems using Taguchi’s parameter design approach and Pareto genetic algorithm. Rev. Fac. Ing. Univ. Antioq. 2014, 72, 73–85. [Google Scholar] [CrossRef]
- Sylajakumari, P.A.; Ramakrishnasamy, R.; Palaniappan, G. Taguchi grey relational analysis for multi-response optimization of wear in co-continuous composite. Materials 2018, 11, 1743. [Google Scholar] [CrossRef] [PubMed]
- Sutono, S.B. Grey-based Taguchi method to optimize the multi-response design of product form design. J. Optimasi Sist. Ind. 2021, 20, 136–146. [Google Scholar] [CrossRef]
- Huang, W.-T.; Tasi, Z.-Y.; Ho, W.-H.; Chou, J.-H. Integrating Taguchi method and gray relational analysis for auto locks by using multiobjective design in computer-aided engineering. Polymers 2022, 14, 644. [Google Scholar] [CrossRef]
- Muthana, S.A.; Ku-Mahamud, K.R. Taguchi-Grey relational analysis method for parameter tuning of multi-objective pareto ant colony system algorithm. J. Inf. Commun. Technol. 2023, 22, 149–181. [Google Scholar] [CrossRef]
- Parinam, S.; Kumar, M.; Kumari, N.; Karar, V.; Sharma, A.L. An improved optical parameter optimisation approach using taguchi and genetic algorithm for high transmission optical filter design. Optik 2019, 182, 382–392. [Google Scholar] [CrossRef]
- Parnianifard, A.; Azfanizam, A.S.; Ariffin, M.K.A.; Ismail, M.I.S. Trade-off in robustness, cost and performance by a multi-objective robust production optimization method. Int. J. Ind. Eng. Comput. 2019, 10, 133–148. [Google Scholar] [CrossRef]
- Viswanathan, R.; Ramesh, S.; Maniraj, S.; Subburam, V. Measurement and Multiresponse Optimization of Turning Parameters for Magnesium Alloy Using Hybrid Combination of Taguchi GRA- PCA Technique. Measurement 2020, 159, 107800. [Google Scholar] [CrossRef]
- Sreedharan, J.; Jeevanantham, A.K.; Rajeshkannan, A. Multi-objective optimization for multi-stage sequential plastic injection molding with plating process using RSM and PCA-based weighted-GRA. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2020, 234, 1014–1030. [Google Scholar] [CrossRef]
- Kumar, D.; Mondal, M. Process parameters optimization of AISI M2 steel in EDM using Taguchi based TOPSIS and GRA. Mater. Today-Proc. 2020, 26, 2477–2484. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, L. Multi-objective optimisation of user experience in mobile application design via a grey-fuzzy-based Taguchi approach. Concurr. Eng.-Res. A 2020, 28, 175–188. [Google Scholar] [CrossRef]
- Huang, W.-T.; Tsai, C.-L.; Ho, W.-H.; Chou, J.-H. Application of intelligent modeling method to optimize the multiple quality characteristics of the injection molding process of automobile lock parts. Polymers 2021, 13, 2515. [Google Scholar] [CrossRef]
- Lin, C.-M.; Hung, Y.-T.; Tan, C.-M. Hybrid Taguchi–gray relation analysis method for design of metal powder injection-molded artificial knee joints with optimal powder concentration and volume shrinkage. Polymers 2021, 13, 865. [Google Scholar] [CrossRef]
- Jiang, R.; Zou, B. A DEA-based multi-response fusion model in the context of Taguchi method. In Proceedings of the Fourth International Conference on Mechanical, Electric and Industrial Engineering, Kunming, China, 22–24 May 2021; Volume 1983, p. 012108. [Google Scholar]
- Tanash, M.; Al Athamneh, R.; Bani Hani, D.; Rababah, M.; Albataineh, Z. A PDCA framework towards a multi-response optimization of process parameters based on Taguchi-fuzzy model. Processes 2022, 10, 1894. [Google Scholar] [CrossRef]
- Li, J.; Horber, D.; Keller, C.; Grauberger, P.; Goetz, S.; Wartzack, S.; Matthiesen, S. Utilizing the embodiment function relation and tolerance model for robust concept design. In Proceedings of the International Conference On Engineering Design, ICED23, Bordeaux, France, 24–28 July 2023. [Google Scholar]
- Chen, L.; Rottmayer, J.; Kusch, L.; Gauger, N.R.; Ye, Y. Data-driven aerodynamic shape design with distributionally robust optimization approaches. arXiv 2023, arXiv:2310.08931v1. [Google Scholar]
- Shrimali, R.; Kumar, M.; Pandey, S.; Sharma, V.; Kaushik, L.; Singh, K. A robust Taguchi combined AHP approach for optimizing AISI1023 low carbon steel weldments in the SAW process. Int. J. Interact. Des. Manuf. 2023, 17, 1959–1977. [Google Scholar] [CrossRef]
- Zheng, M.; Teng, H.; Wang, Y. Application of new robust design by means of probability-based multi-objective optimization to machining process parameters. Vojnoteh. Glas. Mil. Tech. Cour. 2023, 71, 84–99. [Google Scholar] [CrossRef]
- Zheng, M.; Yu, J. Probabilistic approach for robust design with orthogonal experimental methodology in case of target the best. J. Umm Al-Qura Univ. Eng. Archit. 2024, 15, 55–59. [Google Scholar] [CrossRef]
- Parnianifard, A.; Azfanizam, A.S.; Ariffin, M.K.A.; Ismail, M.I.S. An overview on robust design hybrid metamodeling: Advanced methodology in process optimization under uncertainty. Int. J. Ind. Eng. Comput. 2018, 9, 1–32. [Google Scholar] [CrossRef]
- Coelli, J.T.; Rao, P.; Christopher, O.J.; Battese, E.G. An Introduction to Efficiency and Productivity Analysis, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Aigner, D.; Knox Lovell, C.A.; Peter, S. Formulation and estimation of stochastic frontier production function models. J. Econ. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; Van Den Broeck, J. Efficiency estimation from Cobb–Douglas production functions with composed error. Int. Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Schmidt, P.; Knox Lovell, C.A. Estimating stochastic production and cost frontiers when technical and allocative inefficiency are correlated. J. Econ. 1980, 13, 83–100. [Google Scholar] [CrossRef]
- Von Hirschhausen, C.R.; Cullmann, A.; Kappeler, A. Efficiency analysis of German electricity distribution utilities–non–parametric and parametric tests. Appl. Econ. 2006, 38, 2553–2566. [Google Scholar] [CrossRef]
- Montgomery, D.C. Design and Analysis of Experiments, 9th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA; Arizona State University: Tempe, AZ, USA, 2017; p. 749. [Google Scholar]
- Coelli, J.T. A Guide to FRONTIER Version 4.1: A Computer Program for Stochastic Frontier Production and Cost Function Estimation; Centre for Efficiency and Productivity Analysis, University of New England: Armidale, Australia, 1996. [Google Scholar]
- Barbana, N.; Ben Youssef, A.; Rezgui, M.-A.; Bousselmi, L.; Al-Addous, M. Modelling, analysis, and optimization of the effects of pulsed electrophoretic deposition parameters on TiO2 films properties using desirability optimization methodology. Materials 2020, 13, 5160. [Google Scholar] [CrossRef]
- Box, G.E.P.; Wilson, K.B. On the experimental attainment of optimum conditions. J. R. Stat. Soc. Ser. B 1951, 13, 1–45. [Google Scholar] [CrossRef]
| Econometric Model | RDPP-SF Method | Performance Metric |
|---|---|---|
| DMUs | Design plan (DoE) | |
| DMUi | Execution i in the DoE | |
| Cross/panel data | Nonreplicated/replicated | |
| vi: Random variation | Natural noise (experimental and unit-to-unit variation) | |
| ui: TE | Non-natural noise (environment and degradation) |
| Operating Factors | Units | Levels | ||||
|---|---|---|---|---|---|---|
| −α | −1 | 0 | +1 | +α | ||
| x1: Initial concentration | g/L | 2 | 8 | 14 | 20 | 26 |
| x2: Deposition time | s | 150 | 300 | 450 | 600 | 750 |
| x3: Duty cycle (DC) | % | 10 | 30 | 50 | 70 | 90 |
| x4: Voltage | V | 4 | 22 | 40 | 58 | 76 |
| Run | Operating Parameters (Coded Values) | Performance Characteristics (PCHs) | ||||||
|---|---|---|---|---|---|---|---|---|
| x1 (g/L) | x2 (s) | x3 (%) | x4 (V) | De (%) | LC1 (N) | LC2 (N) | LC3 (N) | |
| 1 | −1 | −1 | −1 | −1 | 76.39 | 4.69 | 8.88 | 9.23 |
| 2 | 1 | −1 | −1 | −1 | 83.57 | 3.89 | 7.56 | 9.56 |
| 3 | −1 | 1 | −1 | −1 | 68.77 | 4.67 | 7.32 | 10.74 |
| 4 | 1 | 1 | −1 | −1 | 58.87 | 2.32 | 6.89 | 13.84 |
| 5 | −1 | −1 | 1 | −1 | 57.58 | 4.78 | 9.29 | 11.21 |
| 6 | 1 | −1 | 1 | −1 | 61.96 | 3.24 | 7.52 | 11.47 |
| 7 | −1 | 1 | 1 | −1 | 31.82 | 5.19 | 10.05 | 10.78 |
| 8 | 1 | 1 | 1 | −1 | 29.23 | 2.92 | 6.59 | 12.85 |
| 9 | −1 | −1 | −1 | 1 | 30.96 | 3.61 | 6.53 | 9.64 |
| 10 | 1 | −1 | −1 | 1 | 38.36 | 4.39 | 7.94 | 8.96 |
| 11 | −1 | 1 | −1 | 1 | 43.90 | 2.56 | 5.32 | 10.92 |
| 12 | 1 | 1 | −1 | 1 | 41.68 | 3.25 | 6.36 | 10.45 |
| 13 | −1 | −1 | 1 | 1 | 42.26 | 2.97 | 5.51 | 11.85 |
| 14 | 1 | −1 | 1 | 1 | 50.09 | 3.80 | 6.25 | 9.35 |
| 15 | −1 | 1 | 1 | 1 | 34.42 | 2.94 | 4.48 | 10.30 |
| 16 | 1 | 1 | 1 | 1 | 34.62 | 2.75 | 4.35 | 10.26 |
| 17 | 0 | 0 | 0 | 0 | 52.09 | 3.46 | 6.35 | 9.56 |
| 18 | 0 | 0 | 0 | 0 | 51.89 | 3.56 | 7.34 | 9.17 |
| 19 | 0 | 0 | 0 | 0 | 50.57 | 3.55 | 6.14 | 9.75 |
| 20 | 0 | 0 | 0 | 0 | 53.24 | 3.87 | 6.71 | 9.64 |
| 21 | 0 | 0 | 0 | 0 | 55.09 | 3.52 | 5.98 | 9.43 |
| 22 | 0 | 0 | 0 | 0 | 51.84 | 3.77 | 6.85 | 9.58 |
| 23 | −α | 0 | 0 | 0 | 36.13 | 3.50 | 5.26 | 8.41 |
| 24 | +α | 0 | 0 | 0 | 35.52 | 2.60 | 4.97 | 8.53 |
| 25 | 0 | −α | 0 | 0 | 60.96 | 5.89 | 8.92 | 9.30 |
| 26 | 0 | +α | 0 | 0 | 41.31 | 3.96 | 6.44 | 10.33 |
| 27 | 0 | 0 | −α | 0 | 70.95 | 3.24 | 6.92 | 10.45 |
| 28 | 0 | 0 | +α | 0 | 45.37 | 3.06 | 6.911 | 11.94 |
| 29 | 0 | 0 | 0 | −α | 57.62 | 4.86 | 9.96 | 14.46 |
| 30 | 0 | 0 | 0 | +α | 24.56 | 2.92 | 5.98 | 12.05 |
| Hypotheses (α = 5%) | LR-stat. | χ20.95-Value | Decision | ||
|---|---|---|---|---|---|
| De | Test 1 | Linear vs. quadratic | 37.98 | 18.31 | Reject |
| Test 2 | γ = 0 | 13.67 | 2.71 | Reject | |
| LC1 | Test 1 | Linear vs. quadratic | 50.94 | 18.31 | Reject |
| Test 2 | γ = 0 | 0.00 | 2.71 | Fail to Reject | |
| LC2 | Test 1 | Linear vs. quadratic. | 48.92 | 18.31 | Reject |
| Test 2 | γ = 0 | 42.40 | 2.71 | Reject | |
| LC3 | Test 1 | Linear vs. quadratic. | 27.36 | 18.31 | Reject |
| Test 2 | γ = 0 | 0.00 | 2.71 | Fail to reject |
| Variables | Param. | De(%) (γ ≠ 0; µ = η = 0) | LC1(N) (γ ≠ 0; µ = η = 0) | LC2(N) (γ = 0, OLS) | LC3(N) (γ = 0, OLS) | ||||
|---|---|---|---|---|---|---|---|---|---|
| Est. | t-test. | Est. | t-test. | Est. | t-test. | Est. | t-test. | ||
| Cte. | β0 | −1.244 | −1.269 | 14.016 | 14.016 | −4.185 | 4.280 | −3.777 | 1.579 |
| ln(x1) | β1 | 2.409 | 2.578 * | 0.703 | 0.703 | 0.685 | 0.730 | −0.019 | −0.026 |
| ln(x2) | β2 | 4.070 | 6.575 * | −3.508 | −3.508 * | 0.578 | 1.082 | 0.385 | 0.586 |
| ln(x3) | β3 | 1.679 | 1.981 | −0.613 | −0.613 | 1.419 | 1.645 | 1.512 | 1.719 |
| ln(x4) | β4 | −6.007 | −6.858 * | −0.284 | −0.284 | 1.139 | 1.378 | 0.875 | 1.321 |
| ln(x1)^2 | β5 | −0.153 | −3.602 * | −0.098 | −0.098 | −0.141 | −4.960 * | −0.072 | −2.536 |
| ln(x1)*ln(x2) | β6 | −0.294 | −1.804 | −0.373 | −0.373 | −0.092 | −0.758 | 0.234 | 2.267 |
| ln(x1)*ln(x3) | β7 | 0.010 | 0.061 | −0.138 | −0.138 | −0.230 | −2.259 * | −0.063 | −0.763 |
| ln(x1)*ln(x4) | β8 | 0.020 | 0.138 | 0.664 | 0.664 | 0.383 | 4.390* | −0.224 | −3.027 |
| ln(x2)^2 | β9 | −0.290 | −3.644 * | 0.279 | 0.279 | −0.011 | −0.196 | 0.063 | 1.014 |
| ln(x2)*Ln(x3) | β10 | −0.670 | −5.869 * | 0.362 | 0.362 | 0.055 | 0.430 | −0.315 | −2.706 |
| ln(x2)*Ln(x4) | β11 | 0.666 | 4.660 * | −0.144 | −0.144 | −0.166 | −1.549 | −0.114 | −1.215 |
| ln(x3)^2 | β12 | −0.047 | −1.110 | −0.080 | −0.080 | −0.031 | −0.724 | 0.084 | 2.152 |
| ln(x3)*ln(x4) | β13 | 0.682 | 4.155 * | −0.185 | −0.185 | −0.258 | −2.916 * | 0.002 | 0.027 |
| ln(x4)^2 | β14 | −0.159 | −4.281 * | −0.002 | −0.002 | −0.055 | −2.265 * | 0.046 | 2.161 |
| 0.03 | 0.005 | 0.012 | 0.005 | ||||||
| γ-value | 1.000 | 0.05 | 1.000 | 0.000 | |||||
| µ, η | - | - | - | - | |||||
| Log (likelihood) | 31.79 | 36.48 | 42.40 | 38.44 | |||||
| Critical t-value (5%) = 1.753 | |||||||||
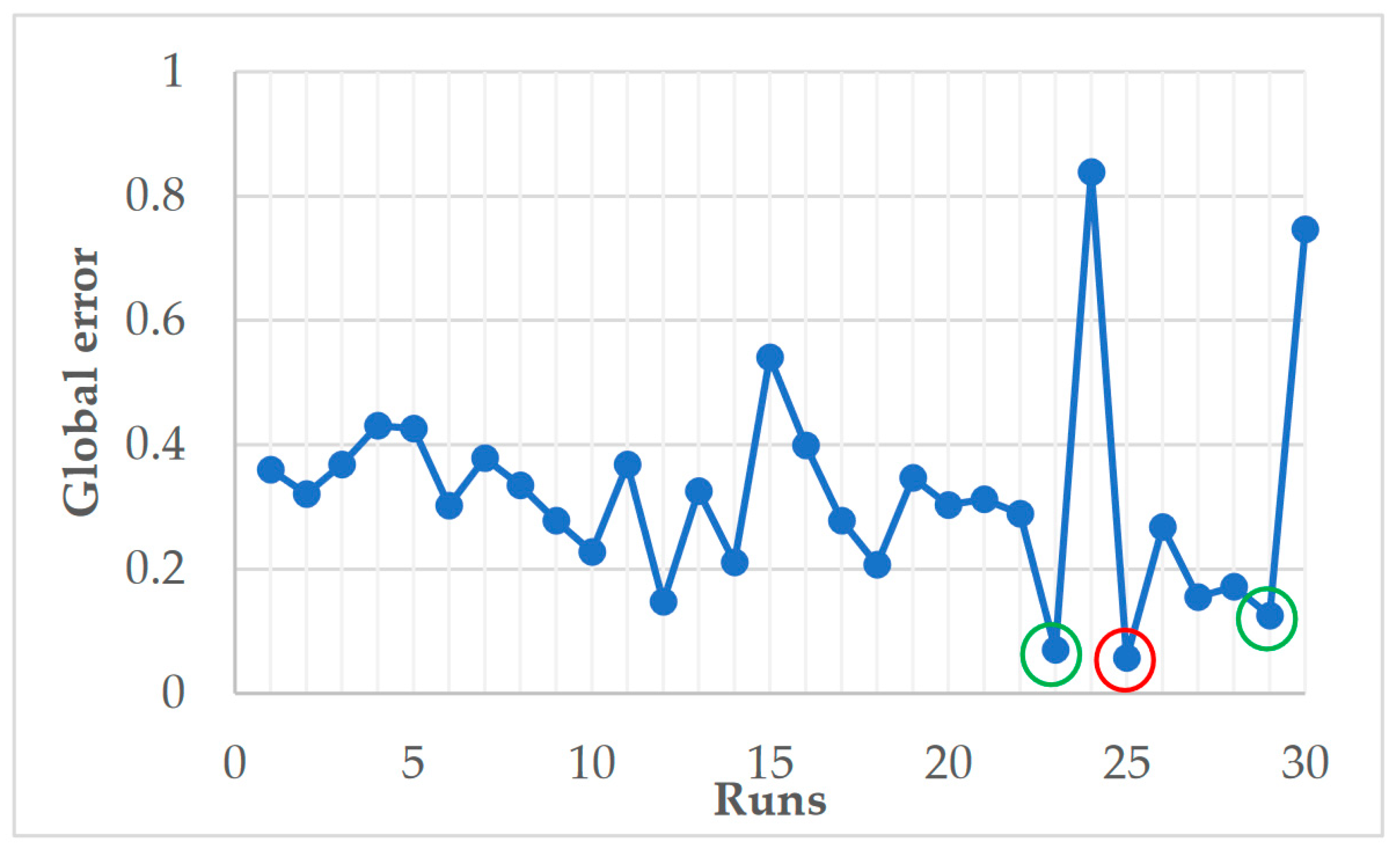
| Run | Operating Factors | PCHs | Global Error | Ranking | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| x1 (g/L) | x2 (s) | x3 (%) | x4 (V) | De(%) | LC1(N) | LC2(N) | LC3(N) | |||
| ui | Abs(vi) | ui | Abs(vi) | |||||||
| 1 | 8 | 300 | 30 | 22 | 0.253 | 0.066 | 0.004 | 0.038 | 0.360 | 21 |
| 2 | 20 | 300 | 30 | 22 | 0.209 | 0.055 | 0.021 | 0.036 | 0.321 | 17 |
| 3 | 8 | 600 | 30 | 22 | 0.171 | 0.014 | 0.144 | 0.040 | 0.368 | 23 |
| 4 | 20 | 600 | 30 | 22 | 0.185 | 0.136 | 0.002 | 0.108 | 0.431 | 27 |
| 5 | 8 | 300 | 70 | 22 | 0.220 | 0.032 | 0.143 | 0.032 | 0.426 | 26 |
| 6 | 20 | 300 | 70 | 22 | 0.199 | 0.004 | 0.032 | 0.067 | 0.302 | 14 |
| 7 | 8 | 600 | 70 | 22 | 0.232 | 0.076 | 0.043 | 0.028 | 0.379 | 24 |
| 8 | 20 | 600 | 70 | 22 | 0.183 | 0.001 | 0.084 | 0.067 | 0.335 | 19 |
| 9 | 8 | 300 | 30 | 58 | 0.202 | 0.025 | 0.040 | 0.011 | 0.278 | 11 |
| 10 | 20 | 300 | 30 | 58 | 0.050 | 0.059 | 0.041 | 0.078 | 0.228 | 9 |
| 11 | 8 | 600 | 30 | 58 | 0.113 | 0.134 | 0.081 | 0.040 | 0.368 | 22 |
| 12 | 20 | 600 | 30 | 58 | 0.041 | 0.057 | 0.040 | 0.010 | 0.148 | 4 |
| 13 | 8 | 300 | 70 | 58 | 0.134 | 0.002 | 0.182 | 0.007 | 0.326 | 18 |
| 14 | 20 | 300 | 70 | 58 | 0.035 | 0.070 | 0.074 | 0.033 | 0.211 | 8 |
| 15 | 8 | 600 | 70 | 58 | 0.206 | 0.043 | 0.257 | 0.035 | 0.541 | 28 |
| 16 | 20 | 600 | 70 | 58 | 0.084 | 0.046 | 0.245 | 0.023 | 0.399 | 25 |
| 17 | 14 | 450 | 50 | 40 | 0.056 | 0.012 | 0.145 | 0.065 | 0.278 | 12 |
| 18 | 14 | 450 | 50 | 40 | 0.060 | 0.040 | 0.000 | 0.107 | 0.207 | 7 |
| 19 | 14 | 450 | 50 | 40 | 0.086 | 0.037 | 0.179 | 0.046 | 0.347 | 20 |
| 20 | 14 | 450 | 50 | 40 | 0.034 | 0.122 | 0.090 | 0.057 | 0.303 | 15 |
| 21 | 14 | 450 | 50 | 40 | 0.000 | 0.029 | 0.205 | 0.079 | 0.313 | 16 |
| 22 | 14 | 450 | 50 | 40 | 0.061 | 0.096 | 0.069 | 0.063 | 0.289 | 13 |
| 23 | 2 | 450 | 50 | 40 | 0.005 | 0.040 | 0.016 | 0.010 | 0.070 | 2 |
| 24 | 26 | 450 | 50 | 40 | 0.328 | 0.121 | 0.267 | 0.123 | 0.839 | 30 |
| 25 | 14 | 150 | 50 | 40 | 0.003 | 0.011 | 0.012 | 0.032 | 0.057 | 1 |
| 26 | 14 | 750 | 50 | 40 | 0.001 | 0.173 | 0.025 | 0.068 | 0.268 | 10 |
| 27 | 14 | 450 | 10 | 40 | 0.013 | 0.036 | 0.057 | 0.050 | 0.155 | 5 |
| 28 | 14 | 450 | 90 | 40 | 0.037 | 0.039 | 0.021 | 0.075 | 0.172 | 6 |
| 29 | 14 | 450 | 50 | 4 | 0.014 | 0.025 | 0.042 | 0.044 | 0.125 | 3 |
| 30 | 14 | 450 | 50 | 76 | 0.491 | 0.062 | 0.005 | 0.189 | 0.747 | 29 |
| Operating Factors | Process Responses | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| x1 (g/L) | x2 (s) | x3 (%) | x4 (V) | De (%) | LC1 (N) | LC2 (N) | LC3 (N) | ||
| γ-Value | - | - | - | - | 1.000 | 0.050 | 1.000 | 0.000 | |
| RDPP-SF | run 25 | 14 | 150 | 50 | 40 | 60.960 | 5.890 | 8.920 | 9.300 |
| run 23 | 2 | 450 | 50 | 40 | 36.130 | 3.500 | 5.260 | 8.410 | |
| run 29 | 14 | 450 | 50 | 4 | 57.620 | 4.860 | 9.960 | 14.460 | |
| RSM-Desirability [41] method | 16.34 | 150 | 90 | 4 | 82.757 | 5.895 | 12.584 | 16.773 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rezgui, M.A.; Trabelsi, A.; Barbana, N.; Ben Youssef, A.; Al-Addous, M. Static Robust Design Optimization Using the Stochastic Frontier Method: A Case Study of Pulsed EPD Process on TiO2 Films. Inventions 2024, 9, 31. https://doi.org/10.3390/inventions9020031
Rezgui MA, Trabelsi A, Barbana N, Ben Youssef A, Al-Addous M. Static Robust Design Optimization Using the Stochastic Frontier Method: A Case Study of Pulsed EPD Process on TiO2 Films. Inventions. 2024; 9(2):31. https://doi.org/10.3390/inventions9020031
Chicago/Turabian StyleRezgui, Mohamed Ali, Ali Trabelsi, Nesrine Barbana, Adel Ben Youssef, and Mohammad Al-Addous. 2024. "Static Robust Design Optimization Using the Stochastic Frontier Method: A Case Study of Pulsed EPD Process on TiO2 Films" Inventions 9, no. 2: 31. https://doi.org/10.3390/inventions9020031





