The Biomechanical Analysis of Tibial Implants Using Meshless Methods: Stress and Bone Tissue Remodeling Analysis
Abstract
:1. Introduction
2. Numerical Formulation
2.1. Meshless Methods Formulation
2.1.1. Influence Domains
2.1.2. Shape Functions
2.2. Weak Form and Discrete System of Equations
2.3. Bone Tissue Remodeling Algorithm
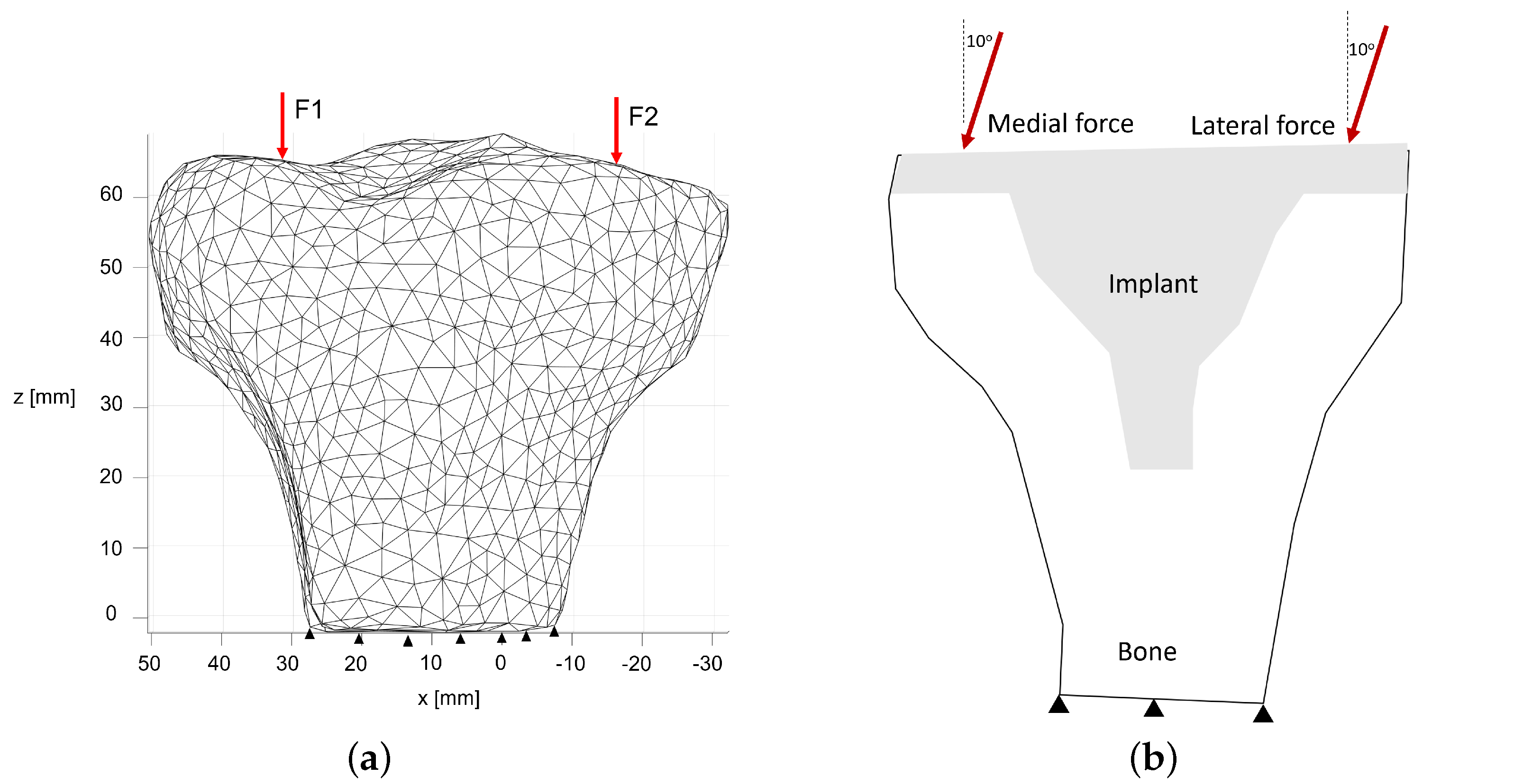
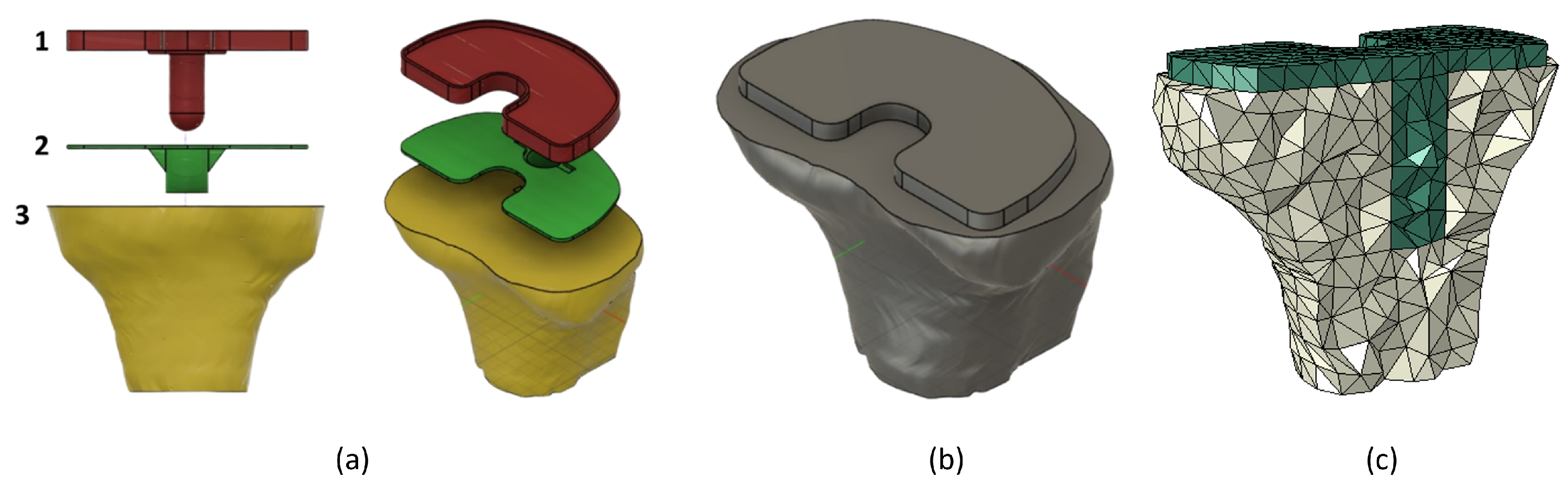
3. Tibia and Implant Numerical Models
4. Results and Discussion
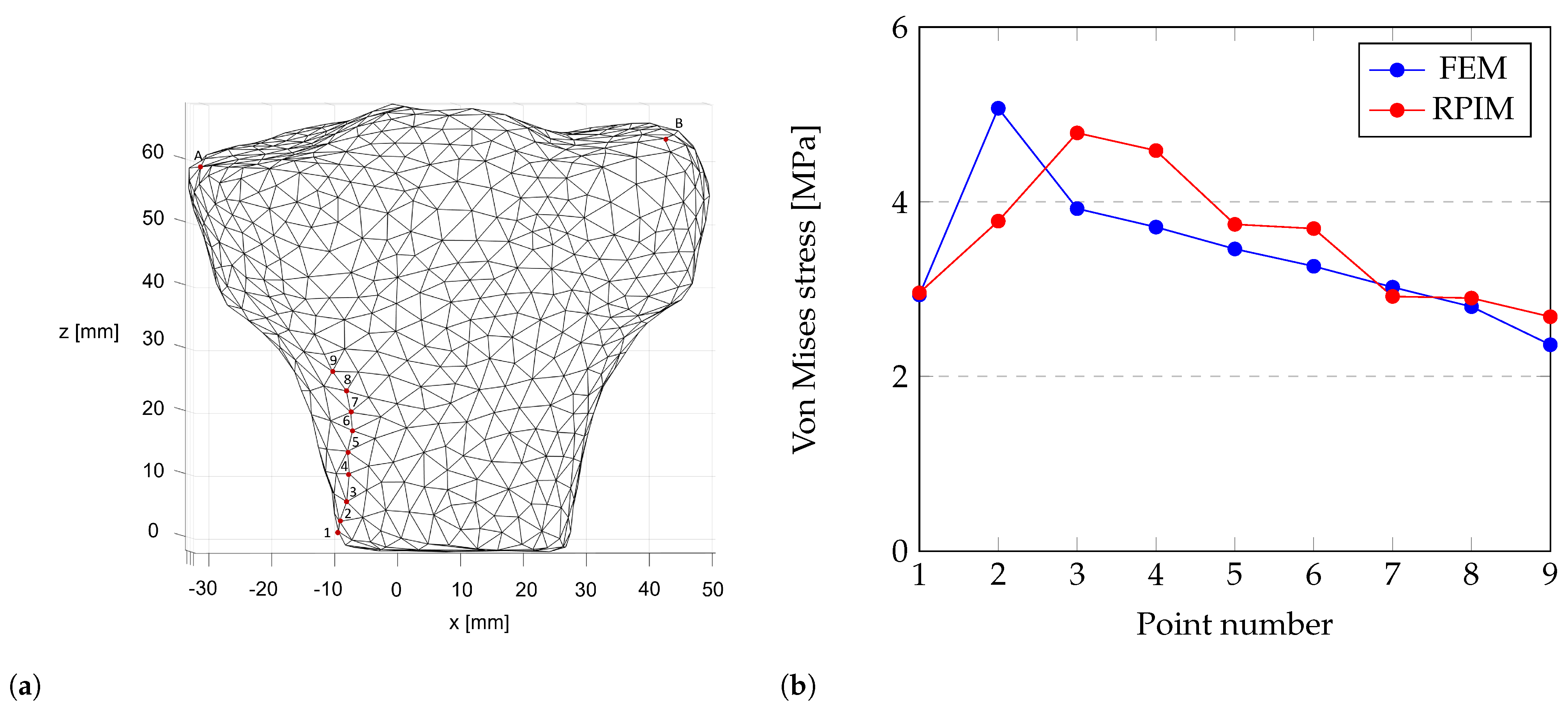
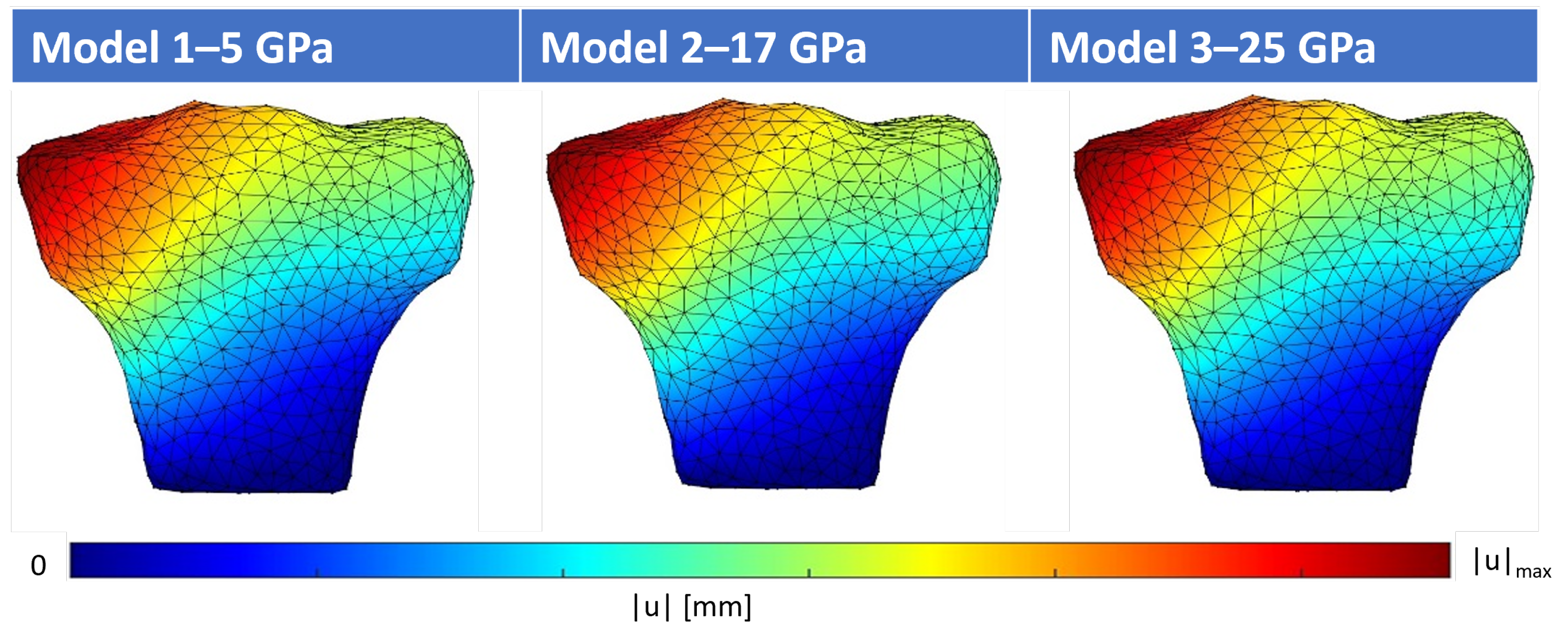
4.1. Structural Analysis of the Proximal Tibia
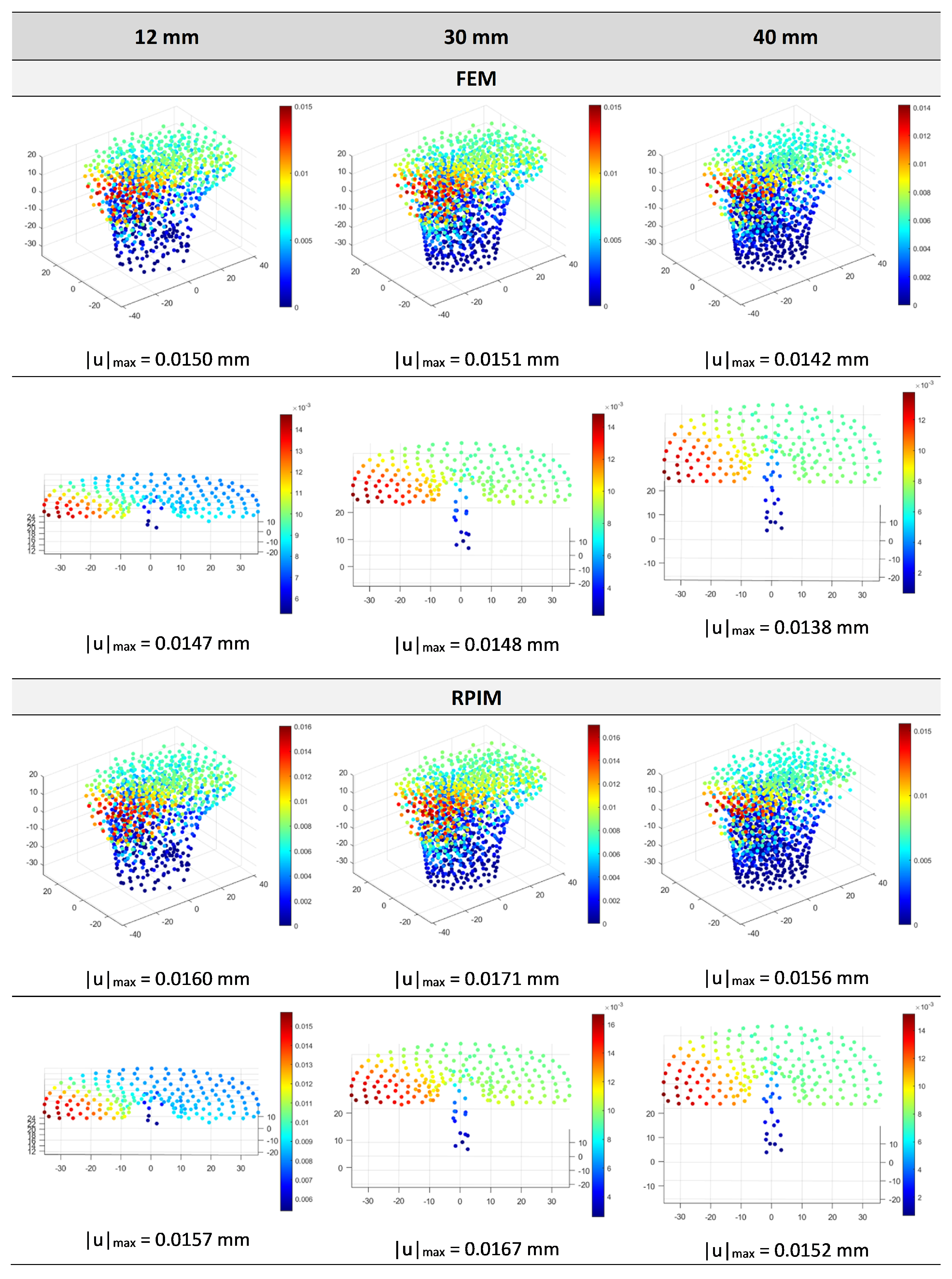
4.2. Structural Analysis of the Implant and Influence of Implant Length
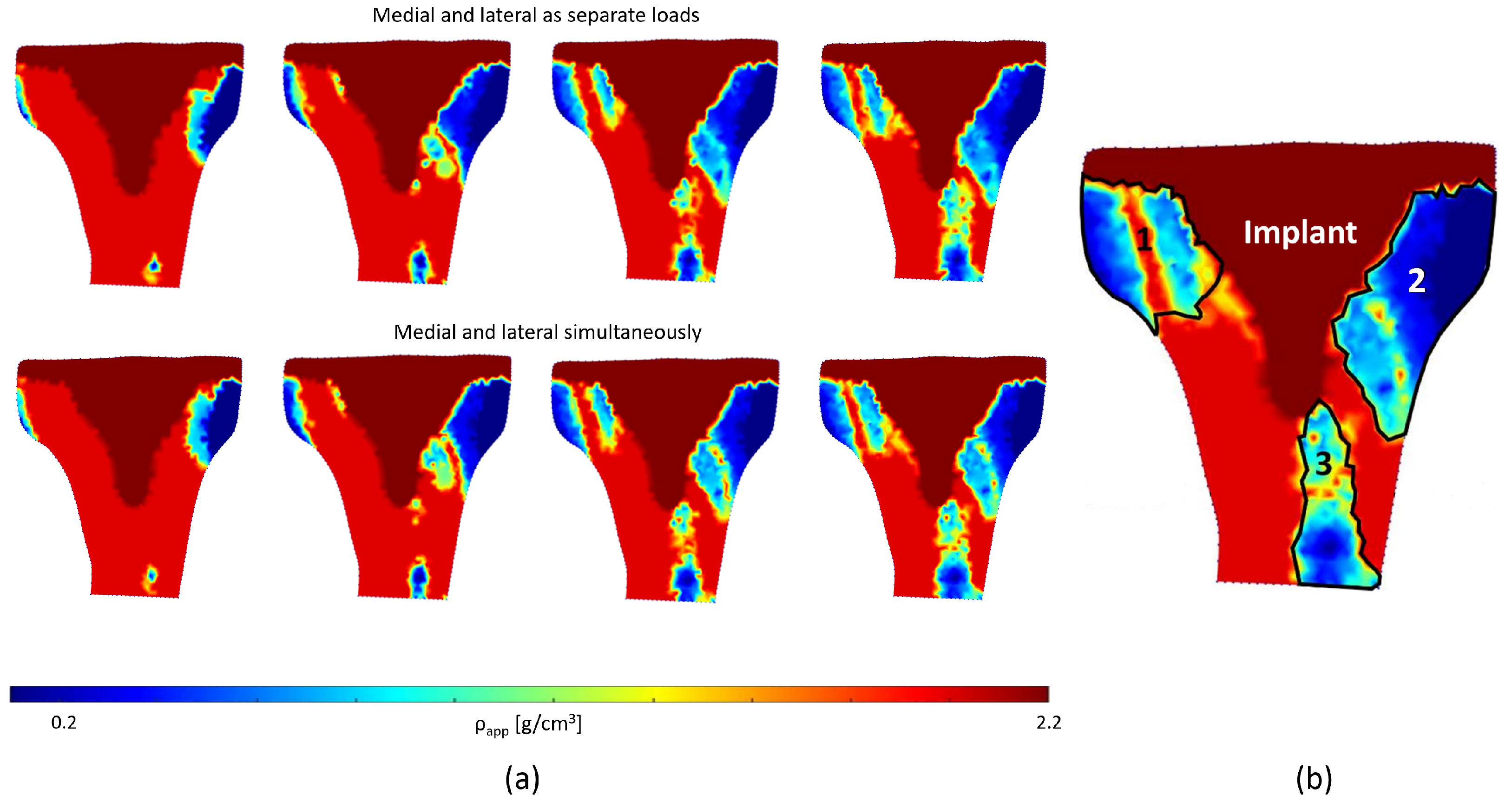
4.3. Bone Remodeling Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fernandes, D.A.; Poeta, L.S.; Martins, C.A.d.Q.; Lima, F.d.; Rosa Neto, F. Balance and quality of life after total knee arthroplasty. Rev. Bras. Ortop. (Engl. Ed.) 2018, 53, 747–753. [Google Scholar] [CrossRef]
- Yueh, S.; Noori, M.; Mahadev, S.; Noori, N.B. Finite Element Analysis of Total Knee Arthroplasty. Am. J. Biomed. Sci. Res. 2021, 14, 6–15. [Google Scholar] [CrossRef]
- Filip, A.C.; Cuculici, S.A.; Cristea, S.; Filip, V.; Negrea, A.D.; Mihai, S.; Pantu, C.M. Tibial Stem Extension versus Standard Configuration in Total Knee Arthroplasty: A Biomechanical Assessment According to Bone Properties. Medicina 2022, 58, 634. [Google Scholar] [CrossRef] [PubMed]
- Peters, C.L.; Erickson, J.; Kloepper, R.G.; Mohr, R.A. Revision total knee arthroplasty with modular components inserted with metaphyseal cement and stems without cement. J. Arthroplast. 2005, 20, 302–308. [Google Scholar] [CrossRef]
- Cintra, F.F.; Yepéz, A.K.; Rasga, M.G.S.; Abagge, M.; Alencar, P.G.C. Tibial Component in Revision of Total Knee Arthroplasty: Comparison Between Cemented and Hybrid Fixation. Rev. Bras. Ortop. (Engl. Ed.) 2011, 46, 585–590. [Google Scholar] [CrossRef]
- Lonner, J.H.; Klotz, M.; Levitz, C.; Lotke, P.A. Changes in bone density after cemented total knee arthroplasty: Influence of stem design. J. Arthroplast. 2001, 16, 107–111. [Google Scholar] [CrossRef] [PubMed]
- Shannon, B.D.; Klassen, J.F.; Rand, J.A.; Berry, D.J.; Trousdale, R.T. Revision total knee arthroplasty with cemented components and uncemented intramedullary stems. J. Arthroplast. 2003, 18, 27–32. [Google Scholar] [CrossRef] [PubMed]
- Kang, S.G.; Park, C.H.; Song, S.J. Stem fixation in revision total knee arthroplasty: Indications, stem dimensions, and fixation methods. Knee Surg. Relat. Res. 2018, 30, 187–192. [Google Scholar] [CrossRef]
- Crawford, D.A.; Berend, K.R.; Morris, M.J.; Adams, J.B.; Lombardi, A.V. Results of a Modular Revision System in Total Knee Arthroplasty. J. Arthroplast. 2017, 32, 2792–2798. [Google Scholar] [CrossRef]
- Bottner, F.; Laskin, R.; Windsor, R.E.; Haas, S.B. Hybrid component fixation in revision total knee arthroplasty. Clin. Orthop. Relat. Res. 2006, 446, 127–131. [Google Scholar] [CrossRef]
- Ni, G.X.; Lu, W.W.; Chiu, K.Y.; Fong, D.Y. Cemented or uncemented femoral component in primary total hip replacement? A review from a clinical and radiological perspective. J. Orthop. Surg. (Hong Kong) 2005, 13, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Kadir, M.R.A. Computational Biomechanics of the Hip Joint; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Dorr, L.D.; Wan, Z.; Gruen, T. Functional results in total hip replacement in patients 65 years and older. Clin. Orthop. Relat. Res. 1997, 336, 143–151. [Google Scholar] [CrossRef] [PubMed]
- Kozelskaya, A.I.; Rutkowski, S.; Frueh, J.; Gogolev, A.S.; Chistyakov, S.G.; Gnedenkov, S.V.; Sinebryukhov, S.L.; Frueh, A.; Egorkin, V.S.; Choynzonov, E.L.; et al. Surface Modification of Additively Fabricated Titanium-Based Implants by Means of Bioactive Micro-Arc Oxidation Coatings for Bone Replacement. J. Funct. Biomater. 2022, 13, 285. [Google Scholar] [CrossRef] [PubMed]
- Completo, A.; Simões, J.A.; Fonseca, F.; Oliveira, M. The influence of different tibial stem designs in load sharing and stability at the cement-bone interface in revision TKA. Knee 2008, 15, 227–232. [Google Scholar] [CrossRef] [PubMed]
- Quevedo González, F.J.; Sculco, P.K.; Kahlenberg, C.A.; Mayman, D.J.; Lipman, J.D.; Wright, T.M.; Vigdorchik, J.M. Undersizing the Tibial Baseplate in Cementless Total Knee Arthroplasty has Only a Small Impact on Bone-Implant Interaction: A Finite Element Biomechanical Study. J. Arthroplast. 2023, 38, 757–762. [Google Scholar] [CrossRef] [PubMed]
- Quevedo Gonzalez, F.J.; Lipman, J.D.; Sculco, P.K.; Sculco, T.P.; De Martino, I.; Wright, T.M. An Anterior Spike Decreases Bone-Implant Micromotion in Cementless Tibial Baseplates for Total Knee Arthroplasty: A Biomechanical Study. J. Arthroplast. 2023, 4–8. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Chen, B.; Wang, C.; Chen, H.; Zhang, A.; Yin, W.; Wu, N.; Han, Q.; Wang, J. Design of Porous Metal Block Augmentation to Treat Tibial Bone Defects in Total Knee Arthroplasty Based on Topology Optimization. Front. Bioeng. Biotechnol. 2021, 9, 765438. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Zhang, A.; Wang, C.; Yin, W.; Wu, N.; Chen, H.; Chen, B.; Han, Q.; Wang, J. Biomechanical comparison between metal block and cement-screw techniques for the treatment of tibial bone defects in total knee arthroplasty based on finite element analysis. Comput. Biol. Med. 2020, 125, 104006. [Google Scholar] [CrossRef]
- Bhandarkar, S.; Dhatrak, P. Optimization of a knee implant with different biomaterials using finite element analysis. Mater. Today Proc. 2022, 59, 459–467. [Google Scholar] [CrossRef]
- Apostolopoulos, V.; Tomáš, T.; Boháč, P.; Marcián, P.; Mahdal, M.; Valoušek, T.; Janíček, P.; Nachtnebl, L. Biomechanical analysis of all-polyethylene total knee arthroplasty on periprosthetic tibia using the finite element method. Comput. Methods Programs Biomed. 2022, 220, 106834. [Google Scholar] [CrossRef]
- Mondal, S.; Ghosh, R. The role of the depth of resection of the distal tibia on biomechanical performance of the tibial component for TAR: A finite element analysis with three implant designs. Med. Eng. Phys. 2023, 119, 104034. [Google Scholar] [CrossRef]
- Mondal, S.; Ghosh, R. Biomechanical analysis of three popular tibial designs for TAR with different implant-bone interfacial conditions and bone qualities: A finite element study. Med. Eng. Phys. 2022, 104, 103812. [Google Scholar] [CrossRef]
- ISO 22926:2023; Implants for Surgery Specification and Verification of Synthetic Anatomical Bone Models for Testing. ISO: Geneva, Switzerland, 2023.
- ISO/CD 5092:2023; Additive Manufacturing for Medical. ISO: Geneva, Switzerland, 2023.
- Belinha, J. Meshless Methods in Biomechanics—Bone Tissue Remodelling Analysis; Springer: Porto, Portugal, 2014. [Google Scholar]
- Belinha, J. Meshless Methods in Biomechanics: Bone Tissue Remodelling Analysis; Lecture Notes in Computational Vision and Biomechanics; Springer International Publishing: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Hardy, R.L. Theory and applications of the multiquadric-biharmonic method 20 years of discovery 1968–1988. Comput. Math. Appl. 1990, 19, 163–208. [Google Scholar] [CrossRef]
- Raggatt, L.J.; Partridge, N.C. Cellular and molecular mechanisms of bone remodeling. J. Biol. Chem. 2010, 285, 25103–25108. [Google Scholar] [CrossRef] [PubMed]
- Sabet, F.A.; Najafi, A.R.; Hamed, E.; Jasiuk, I. Modelling of bone fracture and strength at different length scales: A review. Interface Focus 2016, 6, 20–30. [Google Scholar] [CrossRef] [PubMed]
- Carter, D.R.; Hayes, W.C. The compressive behavior of bone as a two-phase porous structure. J. Bone Jt. Surgery. Am. Vol. 1977, 59, 954–962. [Google Scholar] [CrossRef]
- Goldstein, S.A. The mechanical properties of trabecular bone: Dependence on anatomic location and function. J. Biomech. 1987, 20, 1055–1061. [Google Scholar] [CrossRef]
- Rice, J.C.; Cowin, S.C.; Bowman, J.A. On the dependence of the elasticity and strength of cancellous bone on apparent density. J. Biomech. 1988, 21, 155–168. [Google Scholar] [CrossRef]
- Martin, R.B. Determinants of the mechanical properties of bones. J. Biomech. 1991, 24, 79–88. [Google Scholar] [CrossRef]
- Pauwels, F. Gesammelte Abhandlungen zur Funktionellen Anatomie des Bewegungsapparates; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Cowin, S.C.; Hegedus, D.H. Bone remodeling I: Theory of adaptive elasticity. J. Elast. 1976, 6, 313–326. [Google Scholar] [CrossRef]
- Cowin, S.C.; Sadegh, A.M.; Luo, G.M. An Evolutionary Wolff’s Law for Trabecular Architecture. J. Biomech. Eng. 1992, 114, 129–136. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, H.; Jacobs, C.; Guedes, J.M.; Bendsøe, M.P. Global and local material optimization models applied to anisotropic bone adaptation. In Proceedings of the IUTAM Symposium on Synthesis in Bio Solid Mechanics, Copenhagen, Denmark, 24–27 May 1998; Springer: Berlin/Heidelberg, Germany, 1999; pp. 209–220. [Google Scholar]
- Carter, D.R.; Fyhrie, D.P.; Whalen, R.T. Trabecular bone density and loading history: Regulation of connective tissue biology by mechanical energy. J. Biomech. 1987, 20, 785–794. [Google Scholar] [CrossRef] [PubMed]
- Whalen, R.T.; Carter, D.R.; Steele, C.R. Influence of physical activity on the regulation of bone density. J. Biomech. 1988, 21, 825–837. [Google Scholar] [CrossRef]
- Carter, D.R.; Orr, T.E.; Fyhrie, D.P. Relationships between loading history and femoral cancellous bone architecture. J. Biomech. 1989, 22, 231–244. [Google Scholar] [CrossRef] [PubMed]
- Belinha, J.; Natal Jorge, R.M.; Dinis, L.M. Bone tissue remodelling analysis considering a radial point interpolator meshless method. Eng. Anal. Bound. Elem. 2012, 36, 1660–1670. [Google Scholar] [CrossRef]
- Belinha, J.; Jorge, R.M.N.; Dinis, L.M.J.S. A meshless microscale bone tissue trabecular remodelling analysis considering a new anisotropic bone tissue material law. Comput. Methods Biomech. Biomed. Eng. 2013, 16, 1170–1184. [Google Scholar] [CrossRef]
- Taddei, F.; Pani, M.; Zovatto, L.; Tonti, E.; Viceconti, M. A new meshless approach for subject-specific strain prediction in long bones: Evaluation of accuracy. Clin. Biomech. 2008, 23, 1192–1199. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.; Wang, H.; Zhang, N.; Zhang, M.; Cheng, C.K. Femoral Stems With Porous Lattice Structures: A Review. Front. Bioeng. Biotechnol. 2021, 9, 772539. [Google Scholar] [CrossRef]
- Marques, M.; Belinha, J.; Dinis, L.M.J.S.; Natal Jorge, R. A brain impact stress analysis using advanced discretization meshless techniques. Proc. Inst. Mech. Eng. Part H J. Eng. Med. 2018, 232, 257–270. [Google Scholar] [CrossRef]



| Implant Length | Element Type | Nodes | Elements |
|---|---|---|---|
| 0 | 4-node tetrahedral | 2083 | 9522 |
| 12 mm | 4-node tetrahedral | 5273 | 1171 |
| 30 mm | 4-node tetrahedral | 6908 | 1487 |
| 40 mm | 3-node plane stress | 1901 | 3630 |
| 40 mm | 4-node tetrahedral | 6299 | 1360 |
| Young’s Modulus [GPa] | Poisson’s Ratio | |
|---|---|---|
| Implant—Ti-6Al-4V | 110 | 0.34 |
| Low-stiffness bone | 5 | 0.33 |
| Healthy cortical bone | 17 | 0.33 |
| High-stiffness bone | 25 | 0.33 |
| Method | Young’s Modulus | Point | ux [mm] | uy [mm] | uz [mm] | |u| [mm] |
|---|---|---|---|---|---|---|
| FEM | 5 GPa | A | −0.0281 | −0.0158 | −0.0451 | 0.0555 |
| B | −0.0241 | −0.0193 | −0.0035 | 0.031 | ||
| 17 GPa | A | −0.0082 | −0.0046 | −0.0132 | 0.0163 | |
| B | −0.007 | −0.0056 | −0.001 | 0.0091 | ||
| 25 GPa | A | −0.0056 | −0.0031 | −0.009 | 0.0111 | |
| B | −0.0048 | −0.0038 | −0.0007 | 0.0062 | ||
| RPIM | 5 GPa | A | −0.0286 | −0.0161 | −0.0471 | 0.0575 |
| B | −0.0246 | −0.0203 | −0.004 | 0.0322 | ||
| 17 GPa | A | −0.0084 | −0.0047 | −0.0138 | 0.0169 | |
| B | −0.0072 | −0.0059 | −0.0011 | 0.0094 | ||
| 25 GPa | A | −0.0057 | −0.0032 | −0.0094 | 0.0115 | |
| B | −0.0049 | −0.004 | −0.0008 | 0.0064 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pais, A.; Moreira, C.; Belinha, J. The Biomechanical Analysis of Tibial Implants Using Meshless Methods: Stress and Bone Tissue Remodeling Analysis. Designs 2024, 8, 28. https://doi.org/10.3390/designs8020028
Pais A, Moreira C, Belinha J. The Biomechanical Analysis of Tibial Implants Using Meshless Methods: Stress and Bone Tissue Remodeling Analysis. Designs. 2024; 8(2):28. https://doi.org/10.3390/designs8020028
Chicago/Turabian StylePais, Ana, Catarina Moreira, and Jorge Belinha. 2024. "The Biomechanical Analysis of Tibial Implants Using Meshless Methods: Stress and Bone Tissue Remodeling Analysis" Designs 8, no. 2: 28. https://doi.org/10.3390/designs8020028
APA StylePais, A., Moreira, C., & Belinha, J. (2024). The Biomechanical Analysis of Tibial Implants Using Meshless Methods: Stress and Bone Tissue Remodeling Analysis. Designs, 8(2), 28. https://doi.org/10.3390/designs8020028








