Integrating Satellite-Derived Data as Spatial Predictors in Multiple Regression Models to Enhance the Knowledge of Air Temperature Patterns
Abstract
1. Introduction
2. Methodology
2.1. The Spatial and Temporal Extent of the Study
2.2. Twenty-Eight Explanatory Variables Selected from the Literature
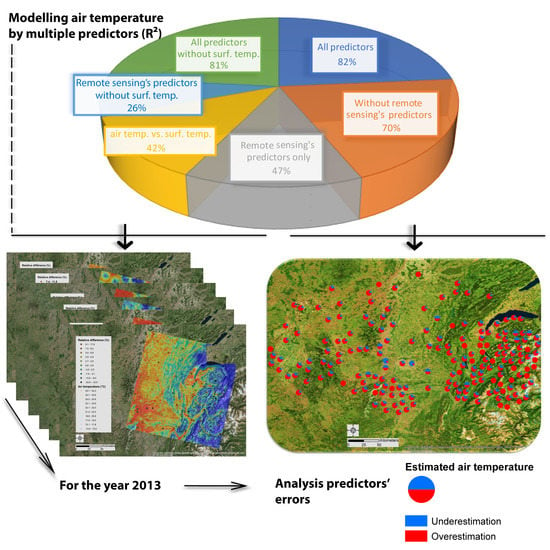
2.3. A Sensitivity Analysis to Measure the Contribution of Remote Sensing Variables to Air Temperature Estimation
- air temperature modelling with all variables,
- air temperature modelling with only remote sensing variables,
- air temperature modelling without remote sensing variables,
- air temperature modelling with remote sensing variables but without surface temperature,
- air temperature modelling with all variables except surface temperature,
- simple linear regression between air temperature and surface temperature.
2.4. Location of the Underestimation or Overestimation of Air Temperature Modelling Compared to In Situ Measurements at Météo France’s Weather Stations
2.4.1. Quantifying the Underestimation or Overestimation of Air Temperatures through a Statistical Model
2.4.2. Geographical Identification of Statistically Similar Zones: The Use of LISA and Getis Ord Gi*
3. Results for the Year 2013
4. Discussion
4.1. Characterization of Error Location and Intensity
4.2. The Contribution of Remote Sensing Variables to the Quality of the Air Temperature Prediction Model
4.3. Limits and Outlooks
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jouzel, J. Le Climat de la France au XXIe Siècle—Volume 4—Scénarios Régionalisés: Publishing in 2014 for Metropolitan France and Overseas Regions. 2014. Available online: http://www.ladocumentationfrancaise.fr/rapports-publics/144000543/index.shtml (accessed on 19 April 2019).
- Météo-France. Changement Climatique en Rhône-Alpes; Météo-France: Bron, France, 2011. [Google Scholar]
- ORECC. Fiche Indicateur—Climat: Changement Climatique en Auvergne Rhône-Alpes—Températures Moyennes Annuelles et Saisonnières; ORECC: Lyon, France, 2017; Available online: http://orecc.auvergnerhonealpes.fr/fileadmin/user_upload/mediatheque/orecc/Documents/Donnees_territoriales/Indicateurs/ORECC_FicheIndicateur_2017_V20170929_CumulPrecipitations.pdf (accessed on 20 September 2019).
- Keeratikasikorn, C.; Bonafoni, S. Urban Heat Island Analysis over the Land Use Zoning Plan of Bangkok by Means of Landsat 8 Imagery. Remote Sens. 2018, 10, 440. [Google Scholar] [CrossRef]
- Fallmann, J.; Forkel, R.; Emeis, S. Secondary effects of urban heat island mitigation measures on air quality. Atmos. Environ. 2016, 125, 199–211. [Google Scholar] [CrossRef]
- Benas, N.; Chrysoulakis, N.; Cartalis, C. Trends of urban surface temperature and heat island characteristics in the Mediterranean. Theor. Appl. Climatol. 2017, 130, 807–816. [Google Scholar] [CrossRef]
- Heino, R. Urban effect on climatic elements in Finland. Geophysica 1978, 15, 171–188. [Google Scholar]
- Giguère, M.; National Institute of Public Health of Québec, Environmental and Occupational Biological Risks Directorate. Mesures de Lutte aux Îlots de Chaleur Urbains Revue de Littérature; Environmental and Occupational Biological Risks Directorate, I National Institute of Public Health of Québec: Québec, QC, Canada, 2010. [Google Scholar]
- Wang, M.; He, G.; Zhang, Z.; Wang, G.; Zhang, Z.; Cao, X.; Wu, Z.; Liu, X. Comparison of Spatial Interpolation and Regression Analysis Models for an Estimation of Monthly near Surface Air Temperature in China. Remote Sens. 2017, 9, 1278. [Google Scholar] [CrossRef]
- Zhang, Z.; Du, Q. A Bayesian Kriging Regression Method to Estimate Air Temperature Using Remote Sensing Data. Remote Sens. 2019, 11, 767. [Google Scholar] [CrossRef]
- Chen, Y.; Quan, J.; Zhan, W.; Guo, Z. Enhanced Statistical Estimation of Air Temperature Incorporating Nighttime Light Data. Remote Sens. 2016, 8, 656. [Google Scholar] [CrossRef]
- Zhao, C.; Jensen, J.; Weng, Q.; Weaver, R. A Geographically Weighted Regression Analysis of the Underlying Factors Related to the Surface Urban Heat Island Phenomenon. Remote Sens. 2018, 10, 1428. [Google Scholar] [CrossRef]
- Wicki, A.; Parlow, E. Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment. Remote Sens. 2017, 9, 684. [Google Scholar] [CrossRef]
- Mira, M.; Ninyerola, M.; Batalla, M.; Pesquer, L.; Pons, X. Improving Mean Minimum and Maximum Month-to-Month Air Temperature Surfaces Using Satellite-Derived Land Surface Temperature. Remote Sens. 2017, 9, 1313. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, C.; Li, J.; Wang, R.; Liu, J. Quantifying the Effects of Urban Form on Land Surface Temperature in Subtropical High-Density Urban Areas Using Machine Learning. Remote Sens. 2019, 11, 959. [Google Scholar] [CrossRef]
- The Senate. Closures of Météo-France Weather Stations and the Future of the French Public Weather Service—The Senate. Available online: https://www.senat.fr/questions/base/2011/qSEQ110317685.html (accessed on 25 April 2019).
- Barroux, R. Météo France’s Forecasts in the Budgetary Crisis. Published 15 December 2014. Available online: https://www.lemonde.fr/planete/article/2014/12/15/les-previsions-de-meteo-france-dans-la-tourmente-budgetaire_4540743_3244.html (accessed on 25 April 2019).
- Stewart, I.D. A systematic review and scientific critique of methodology in modern urban heat island literature. Int. J. Climatol. 2011, 31, 200–217. [Google Scholar] [CrossRef]
- Oyler, J.W.; Dobrowski, S.Z.; Holden, Z.A.; Running, S.W. Remotely Sensed Land Skin Temperature as a Spatial Predictor of Air Temperature across the Conterminous United States. J. Appl. Meteorol. Climatol. 2016, 55, 1441–1457. [Google Scholar] [CrossRef]
- Parmentier, B.; McGill, B.J.; Wilson, A.M.; Regetz, J.; Jetz, W.; Guralnick, R.; Tuanmu, M.-N.; Schildhauer, M. Using multi-timescale methods and satellite-derived land surface temperature for the interpolation of daily maximum air temperature in Oregon. Int. J. Climatol. 2015, 35, 3862–3878. [Google Scholar] [CrossRef]
- Hashimoto, H.; Wang, W.; Melton, F.S.; Moreno, A.L.; Ganguly, S.; Michaelis, A.R.; Nemani, R.R. High-resolution mapping of daily climate variables by aggregating multiple spatial data sets with the random forest algorithm over the conterminous United States. Int. J. Climatol. 2019, 39, 2964–2983. [Google Scholar] [CrossRef]
- Hasanlou, M.; Mostofi, N. Investigating Urban Heat Island Estimation and Relation between Various Land Cover Indices in Tehran City Using Landsat 8 Imagery. In Proceedings of the 1st International Electronic Conference on Remote Sensing, online, 22 June–5 July 2015. [Google Scholar]
- Chen, X.-L.; Zhao, H.-M.; Li, P.-X.; Yin, J. Remote sensing image-based analysis of the relationship between urban heat island and land use/cover changes. Remote Sens. Environ. 2006, 104, 133–146. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S. Comparison of time series Tasseled Cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ. 2005, 94, 364–372. [Google Scholar] [CrossRef]
- Nguyen, K.-A.; Liou, Y.-A.; Li, M.-H.; Anh Tran, T. Zoning eco-environmental vulnerability for environmentalmanagement and protection. Ecol. Indic. 2016, 69. [Google Scholar] [CrossRef]
- Tsin, P.K.; Knudby, A.; Krayenhoff, E.S.; Ho, H.C.; Brauer, M.; Henderson, S.B. Microscale mobile monitoring of urban air temperature. Urban Clim. 2016, 18, 58–72. [Google Scholar] [CrossRef]
- Nichol, J.E.; To, P.H. Temporal characteristics of thermal satellite images for urban heat stress and heat island mapping. ISPRS J. Photogramm. Remote Sens. 2012, 74, 153–162. [Google Scholar] [CrossRef]
- Renard, F.; Alonso, L.; Fitts, Y.; Hadjiosif, A.; Comby, J. Evaluation of the Effect of Urban Redevelopment on Surface Urban Heat Islands. Remote Sens. 2019, 11, 299. [Google Scholar] [CrossRef]
- Kim, Y.-H.; Baik, J.-J. Daily maximum urban heat island intensity in large cities of Korea. Theor. Appl. Climatol. 2004, 79, 151–164. [Google Scholar] [CrossRef]
- Météo-France. METEO-FRANCE: Publithèque. Available online: https://publitheque.meteo.fr/okapi/accueil/okapiWebPubli/index.jsp (accessed on 19 September 2019).
- Corine Land Cover. European Environment Agency. 2012. Available online: https://www.eea.europa.eu/publications/COR0-landcover (accessed on 19 September 2019).
- Hafner, J.; Kidder, S.Q. Urban Heat Island Modeling in Conjunction with Satellite-Derived Surface/Soil Parameters. J. Appl. Meteorol. 1999, 38, 448–465. [Google Scholar] [CrossRef]
- Sobrino, J.; Jimenez-Munoz, J.-C.; Paolini, L. Land surface temperature retrieval from LANDSAT TM 5. Remote Sens. Environ. 2004, 90, 434–440. [Google Scholar] [CrossRef]
- Tran, H.; Uchihama, D.; Ochi, S.; Yasuoka, Y. Assessment with satellite data of the urban heat island effects in Asian mega cities. Int. J. Appl. Earth Obs. Geoinf. 2006, 8, 34–48. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y. Urban Heat Island Analysis Using the Landsat TM Data and ASTER Data: A Case Study in Hong Kong. Remote Sens. 2011, 3, 1535–1552. [Google Scholar] [CrossRef]
- Shohei, K.; Takeki, I.; Hideo, T. Relationship between Terra/ASTER Land Surface Temperature and Ground-observed Air Temperature. Geogr. Rev. Jpn. Ser. B 2016, 88, 38–44. [Google Scholar] [CrossRef]
- Iizawa, I.; Umetani, K.; Ito, A.; Yajima, A.; Ono, K.; Amemura, N.; Onishi, M.; Sakai, S. Time evolution of an urban heat island from high-density observations in Kyoto city. Sci. Online Lett. Atmos. 2016, 12, 51–54. [Google Scholar] [CrossRef]
- Madelin, M.; Bigot, S.; Duché, S.; Rome, S. Intensité et délimitation de l’îlot de chaleur nocturne de surface sur l’agglomération parisienne. In Proceedings of the Colloque International de l’Association Internationale de Climatologie (AIC), Sfax, Tunisia, 3–6 July 2017. [Google Scholar]
- Roşca, C.F.; Harpa, G.V.; Croitoru, A.-E.; Herbel, I.; Imbroane, A.M.; Burada, D.C. The impact of climatic and non-climatic factors on land surface temperature in southwestern Romania. Theor. Appl. Climatol. 2017, 130, 775–790. [Google Scholar] [CrossRef]
- Weng, Q.; Firozjaei, M.K.; Sedighi, A.; Kiavarz, M.; Alavipanah, S.K. Statistical analysis of surface urban heat island intensity variations: A case study of Babol city, Iran. GIScience Remote Sens. 2019, 56, 576–604. [Google Scholar] [CrossRef]
- Weng, Q.; Quattrochi, D. Thermal remote sensing of urban areas: An introduction to the special issue. Remote Sens. Environ. 2006, 104, 119–122. [Google Scholar] [CrossRef]
- Alfraihat, R.; Mulugeta, G.; Gala, T.S. Ecological Evaluation of Urban Heat Island in Chicago City, USA. J. Atmos. Pollut. 2016, 4, 23–29. [Google Scholar] [CrossRef]
- Gallo, K.; Hale, R.; Tarpley, D.; Yu, Y. Evaluation of the Relationship between Air and Land Surface Temperature under Clear- and Cloudy-Sky Conditions. J. Appl. Meteorol. Climatol. 2010, 50, 767–775. [Google Scholar] [CrossRef]
- Taha, H. Urban climates and heat islands: Albedo, evapotranspiration, and anthropogenic heat. Energy Build. 1997, 25, 99–103. [Google Scholar] [CrossRef]
- Ali-Toudert, F.; Mayer, H. Effects of asymmetry, galleries, overhanging façades and vegetation on thermal comfort in urban street canyons. Sol. Energy 2007, 81, 742–754. [Google Scholar] [CrossRef]
- Barsi, J.A.; Lee, K.; Kvaran, G.; Markham, B.L.; Pedelty, J.A. The Spectral Response of the Landsat-8 Operational Land Imager. Remote Sens. 2014, 6, 10232–10251. [Google Scholar] [CrossRef]
- Shapiro, S.S.; Wilk, M.B. An analysis of variance test for normality (complete samples). Biometrika 1965, 52, 591–611. [Google Scholar] [CrossRef]
- OECD. Handbook on Constructing Composite Indicators: Methodology and User Guide. Available online: http://www.oecd.org/fr/els/soc/handbookonconstructingcompositeindicatorsmethodologyanduserguide.htm (accessed on 17 April 2019).
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B Methodol. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Reid, S.; Tibshirani, R.; Friedman, J. A study of error variance estimation in lasso regression. Stat. Sin. 2016, 26, 35–67. [Google Scholar] [CrossRef]
- Voelkel, J.; Shandas, V.; Haggerty, B. Developing High-Resolution Descriptions of Urban Heat Islands: A Public Health Imperative. Prev. Chronic Dis. 2016, 13. [Google Scholar] [CrossRef]
- Shandas, V.; Voelkel, J.; Williams, J.; Hoffman, J. Integrating Satellite and Ground Measurements for Predicting Locations of Extreme Urban Heat. Climate 2019, 7, 5. [Google Scholar] [CrossRef]
- Durbin, J.; Watson, G.S. Testing for serial correlation in least squares regression. I. Biometrika 1950, 37, 409–428. [Google Scholar] [CrossRef] [PubMed]
- Anselin, L. Local Indicators of Spatial Association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Getis, A.; Ord, J. A Research Agenda for Geographic Information Science. In Spatial Analysis and Modeling in a GIS Environment; McMaster, R.B., Usery, E.L., Eds.; CRC Press: Boca Raton, FL, USA, 1996; p. 416. Available online: https://books.google.fr/books?hl=fr&lr=&id=k9x0B3V3op0C&oi=fnd&pg=PA157&ots=cOnYyDRjKL&sig=nW-5WZ7_04hBe-lbgv2MdwBABBM&redir_esc=y#v=onepage&q&f=false (accessed on 3 May 2019).
- Getis, A.; Ord, J.K. The Analysis of Spatial Association by Use of Distance Statistics. Geogr. Anal. 1992, 24. [Google Scholar] [CrossRef]
- Qaid, A.; Lamit, H.B.; Ossen, D.R.; Rasidi, M.H. Effect of the position of the visible sky in determining the sky view factor on micrometeorological and human thermal comfort conditions in urban street canyons. Theor. Appl. Climatol. 2018, 131, 1083–1100. [Google Scholar] [CrossRef]
- Chen, L.; Ng, E.; An, X.; Ren, C.; Lee, M.; Wang, U.; He, Z. Sky view factor analysis of street canyons and its implications for daytime intra-urban air temperature differentials in high-rise, high-density urban areas of Hong Kong: A GIS-based simulation approach. Int. J. Climatol. 2012, 32, 121–136. [Google Scholar] [CrossRef]
- Hodul, M.; Knudby, A.; Ho, H.C. Estimation of Continuous Urban Sky View Factor from Landsat Data Using Shadow Detection. Remote Sens. 2016, 8, 568. [Google Scholar] [CrossRef]
- Dong, Y.; Varquez, A.C.G.; Kanda, M. Global anthropogenic heat flux database with high spatial resolution. Atmos. Environ. 2017, 150, 276–294. [Google Scholar] [CrossRef]
- Chrysoulakis, N.; Grimmond, S.; Feigenwinter, C.; Lindberg, F.; Gastellu-Etchegorry, J.-P.; Marconcini, M.; Mitraka, Z.; Stagakis, S.; Crawford, B.; Olofson, F.; et al. Urban energy exchanges monitoring from space. Sci. Rep. 2018, 8, 1–8. [Google Scholar] [CrossRef]
- Lin, X.; Su, Y.-C.; Shang, J.; Sha, J.; Li, X.; Sun, Y.-Y.; Ji, J.; Jin, B. Geographically Weighted Regression Effects on Soil Zinc Content Hyperspectral Modeling by Applying the Fractional-Order Differential. Remote Sens. 2019, 11, 636. [Google Scholar] [CrossRef]




| Location of Weather Stations | Number | Proportion (%) |
|---|---|---|
| artificialized area | 151 | 38.6 |
| agricultural area | 178 | 45.5 |
| forest and semi-natural environment | 61 | 15.6 |
| wet area | 1 | 0.3 |
| total | 391 | 100 |
| Date | Temperature (°C) | Humidity (%) | Rain (mm/h) | Wind Average (km/h) | Pressure (hPa) | Cloud Cover (%) |
|---|---|---|---|---|---|---|
| 25 April 2013 | 21.3 | 47 | 0 | 4 | 1024.5 | 1.63 |
| 14 July 2013 | 24.5 | 52 | 0 | 14 | 1019.5 | 1.8 |
| 21 July 2013 | 29.4 | 45 | 0 | 6 | 1016.7 | 1.96 |
| 15 August 2013 | 21.2 | 51 | 0 | 7 | 1021.4 | 0.56 |
| 22 August 2013 | 24.4 | 44 | 0 | 4 | 1016.8 | 0.04 |
| 23 September 2013 | 17.8 | 71 | 0 | 4 | 1024 | 10.01 |
| Mean | 23.1 | 51.7 | 0 | 6.5 | 1020.5 | 2.7 |
| Standard deviation | 4.0 | 10.0 | 0 | 3.9 | 3.4 | 3.7 |
| Data Name | Variables Used for the Input (Units) | Acquisition Method | Acquisition Source | Reference |
|---|---|---|---|---|
| Meteorological data from remote sensing | Surface temperature (°C) | Satellite Landsat 8 | USGS EarthExplorer | [26,33,34,43] |
| Brightness temperatures (°C) | ||||
| UTFVI Urban Thermal Field Variation Index | [35,42] | |||
| Vegetation index | NDVI Normalized Difference Vegetation Index | Satellite Landsat 8 | USGS EarthExplorer | [22,23,39] |
| SAVI Soil Adjusted Vegetation Index | [22] | |||
| EVI Enhanced Vegetation Index | ||||
| Tasseled cap greeness or GVI | ||||
| Water presence index | NDWI Normalized Difference Water Index | [22,23] | ||
| MNDWI Modified Normalized Difference Water Index | [22] | |||
| Humidity index | Tasseled cap Wetness | |||
| NDMI Normalized Difference Moisture Index | [24,25] | |||
| Bare soil index | NDBaI Normalized Difference Bareness Index | Satellite Landsat 8 | USGS EarthExplorer | [22,23] |
| BI Bare Soil Index | [22] | |||
| EBBI Enhanced Built-Up and Bareness Index | ||||
| Building index | NDBI Normalized Difference Built-Up Index | [22,23] | ||
| UI Urban Index | [22] | |||
| IBI Index-based Built-Up Index | ||||
| Topographical | Altitude (m) | GIS processing | IGN | [29,40] |
| Slope (%) | ||||
| Exposure (°N) | [45] | |||
| Curvature | [32,41] | |||
| Latitude (°N) | ESRI | [40] | ||
| Longitude (°E) | ||||
| Proximity to land occupations | Proximity of water surfaces (m) | GIS processing | Corine Land Cover | [36,38] |
| Proximity to a forest or a semi-natural environment (m) | ||||
| Proximity to an agricultural area (m) | ||||
| Proximity to a wet area (m) | ||||
| Proximity to an artificial area (m) | ||||
| Radiation index | Spectral Radiance | Satellite Landsat 8 | USGS EarthExplorer | [37] |
| Emissivity | [44] | |||
| Tasseled Cap Brightness |
| 25 April 2013 | 14 July 2013 | 21 July 2013 | 15 August 2013 | 22 August 2013 | 23 September 2013 | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pearson Test & VIF | MLR | Pearson Test & VIF | MLR | Pearson Test & VIF | MLR | Pearson Test & VIF | MLR | Pearson Test & VIF | MLR | Pearson Test & VIF | MLR | |
| Altitude | X | X | X | X | X | X | X | X | X | X | ||
| Latitude | X | X | X | X | X | X | X | X | X | |||
| Longitude | X | X | X | X | X | X | X | |||||
| Slope | X | X | X | X | X | X | X | X | ||||
| Exposure | X | X | X | X | X | X | X | |||||
| Curvature | X | X | X | X | X | X | X | |||||
| Surface T °C | X | X | X | X | X | X | X | X | X | X | X | X |
| Brightness T °C | ||||||||||||
| UTFVI | ||||||||||||
| Emissivity | X | X | ||||||||||
| Radiance | X | X | ||||||||||
| TCT Brightness | ||||||||||||
| Proximity to a wet area | X | X | X | X | X | X | X | X | X | |||
| Proximity to an artificial area | X | X | X | X | X | X | X | X | ||||
| Proximity to an agricultural area | X | X | X | X | X | X | X | |||||
| Proximity to a water area | X | X | X | X | X | X | X | |||||
| Proximity to a forest or a semi-natural environment | X | X | X | X | X | X | X | X | ||||
| EVI | X | X | X | X | X | |||||||
| MNDWI | X | X | X | X | ||||||||
| EBBI | ||||||||||||
| NDBaI | X | X | X | X | X | X | ||||||
| NDBI | X | X | ||||||||||
| UI | ||||||||||||
| IBI | ||||||||||||
| NDWI | X | |||||||||||
| NDVI | X | X | X | X | X | X | X | X | ||||
| SAVI | ||||||||||||
| GVI | ||||||||||||
| NDMI | X | X | X | |||||||||
| TCT Wetness | ||||||||||||
| Retained variables (/28) | 19 | 5 | 17 | 4 | 15 | 5 | 16 | 6 | 16 | 6 | 16 | 5 |
| Scale | Coefficient of Determination (R2) Mean | Root-Mean-Square Error (RMSE) Mean | Variables | Number of Times Included in Model Settings | Average Normalized Coefficients | Impact on the Model |
|---|---|---|---|---|---|---|
| Weather stations throughout the study area | 0.82 | 1.20 | Surface temperature | 6 | 0.30 | Positive trend |
| Altitude | 5 | 0.80 | Negative trend | |||
| Proximity to a wet area | 3 | 0.17 | Negative trend | |||
| Latitude | 3 | 0.16 | Negative trend | |||
| Slope | 2 | 0.16 | Negative trend | |||
| Proximity to an artificial area | 2 | 0.13 | Negative trend | |||
| NDVI | 2 | 0.12 | Positive trend | |||
| Proximity to a forest or a semi-natural environment | 2 | 0.07 | Negative trend | |||
| Longitude | 2 | 0.01 | Both trends | |||
| Proximity to an agricultural area | 1 | 0.12 | Negative trend | |||
| Roughness | 1 | 0.12 | Negative trend | |||
| Proximity of water surfaces | 1 | 0.11 | Positive trend | |||
| Exposure | 1 | 0.11 | Positive trend | |||
| Weather stations located in an artificialized area | 0.73 | 1.21 | Altitude | 5 | 0.75 | Negative trend |
| Surface temperature | 4 | 0.41 | Negative trend | |||
| Proximity to a wet area | 4 | 0.28 | Positive trend | |||
| Latitude | 2 | 0.40 | Negative trend | |||
| Longitude | 2 | 0.24 | Negative trend | |||
| Roughness | 2 | 0.24 | Negative trend | |||
| EVI | 2 | 0.24 | Negative trend | |||
| Slope | 1 | 0.30 | Negative trend | |||
| NDVI | 1 | 0.25 | Positive trend | |||
| Proximity of water surfaces | 1 | 0.23 | Negative trend | |||
| Proximity to a forest or a semi-natural environment | 1 | 0.10 | Negative trend | |||
| Weather stations located in an agricultural area | 0.74 | 0.95 | Altitude | 5 | 0.80 | Negative trend |
| Surface temperature | 4 | 0.30 | Positive trend | |||
| Proximity of water surfaces | 2 | 0.04 | Both trends | |||
| Slope | 1 | 0.45 | Negative trend | |||
| MNDWI | 1 | 0.30 | Positive trend | |||
| Proximity to an artificial area | 1 | 0.28 | Negative trend | |||
| Latitude | 1 | 0.12 | Negative trend | |||
| Weather stations located in forest and semi-natural environment | 0.92 | 1.01 | Altitude | 3 | 0.86 | Negative trend |
| Proximity to an artificial area | 2 | 0.59 | Negative trend | |||
| Surface temperature | 2 | 0.35 | Positive trend | |||
| Radiance | 1 | 0.97 | Positive trend | |||
| NDBAI | 1 | 0.35 | Negative trend | |||
| NDVI | 1 | 0.33 | Positive trend | |||
| Proximity to a wet area | 1 | 0.13 | Positive trend |
| MLR over the Entire Area | MLR over Artificialized Area | MLR over Agricultural Area | MLR over Forest and Semi-Natural Environment | |||||
|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | R2 | RMSE | |
| 25 April 2013 | 0.85 | 1.31 | 0.71 | 1.66 | 0.72 | 1.08 | 0.92 | 1.00 |
| 14 July 2013 | 0.81 | 1.95 | 0.68 | 1.56 | 0.66 | 1.14 | 0.89 | 1.94 |
| 21 July 2013 | 0.87 | 0.86 | 0.83 | 0.73 | 0.87 | 0.82 | 0.99 | 0.06 |
| 15 August 2013 | 0.92 | 1.04 | 0.75 | 1.18 | 0.71 | 0.91 | 0.95 | 1.11 |
| 22 August 2013 | 0.80 | 0.86 | 0.72 | 0.85 | 0.83 | 0.78 | 0.95 | 0.66 |
| 23 September 2013 | 0.66 | 1.17 | 0.73 | 1.24 | 0.63 | 0.99 | 0.81 | 1.24 |
| Mean | 0.82 | 1.20 | 0.74 | 1.20 | 0.74 | 0.95 | 0.92 | 1.00 |
| Minimum | 0.66 | 0.86 | 0.68 | 0.73 | 0.63 | 0.78 | 0.81 | 0.06 |
| Maximum | 0.92 | 1.95 | 0.83 | 1.66 | 0.87 | 1.14 | 0.99 | 1.94 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alonso, L.; Renard, F. Integrating Satellite-Derived Data as Spatial Predictors in Multiple Regression Models to Enhance the Knowledge of Air Temperature Patterns. Urban Sci. 2019, 3, 101. https://doi.org/10.3390/urbansci3040101
Alonso L, Renard F. Integrating Satellite-Derived Data as Spatial Predictors in Multiple Regression Models to Enhance the Knowledge of Air Temperature Patterns. Urban Science. 2019; 3(4):101. https://doi.org/10.3390/urbansci3040101
Chicago/Turabian StyleAlonso, Lucille, and Florent Renard. 2019. "Integrating Satellite-Derived Data as Spatial Predictors in Multiple Regression Models to Enhance the Knowledge of Air Temperature Patterns" Urban Science 3, no. 4: 101. https://doi.org/10.3390/urbansci3040101
APA StyleAlonso, L., & Renard, F. (2019). Integrating Satellite-Derived Data as Spatial Predictors in Multiple Regression Models to Enhance the Knowledge of Air Temperature Patterns. Urban Science, 3(4), 101. https://doi.org/10.3390/urbansci3040101