Unsteady Flows and Component Interaction in Turbomachinery
Abstract
1. Introduction
2. Unsteady Flows in Gas Turbine Stages
2.1. Introduction to Unsteady Interaction in Turbomachinery
- Inlet flow distortions: Boundary conditions affect the performance of the gas turbine (e.g., hot spots and residual swirl from the combustion chamber modify the turbine aerothermal field).
- Potential (inviscid) interaction: It is caused by pressure waves travelling and reflecting across the vane/blade gap.
- Wake unsteadiness: It is mainly represented by vortices developing from vane and blade trailing edges and has an impact on mixing losses and boundary layer development.
- Secondary flows: They are flow structures that deviate from the expected behavior of the flow, and their interaction can produce detrimental effects on turbine performance.
- Oblique shocks from blade trailing edge: In transonic stages, a complex reflecting shock system affects the heat transfer rate due to the generation of separation bubbles.
- Rotating stall: It is caused by the blockage of some vanes due to the wrong incidence, which causes flow separation.
- Aeroelastic instability: Generally called “flutter”, it is generated by the blade mechanical response to the unsteady disturbance.
2.2. Potential Interaction in Turbine Stages
- Entropy and velocity fluctuations are convected downstream of the vane row at the local flow velocity v.
- Pressure fluctuations travel as acoustic waves at and velocities (a being the local speed of sound), then the direction changes depending on flow regime, which can be either subsonic (, where is the Mach number) or supersonic ().
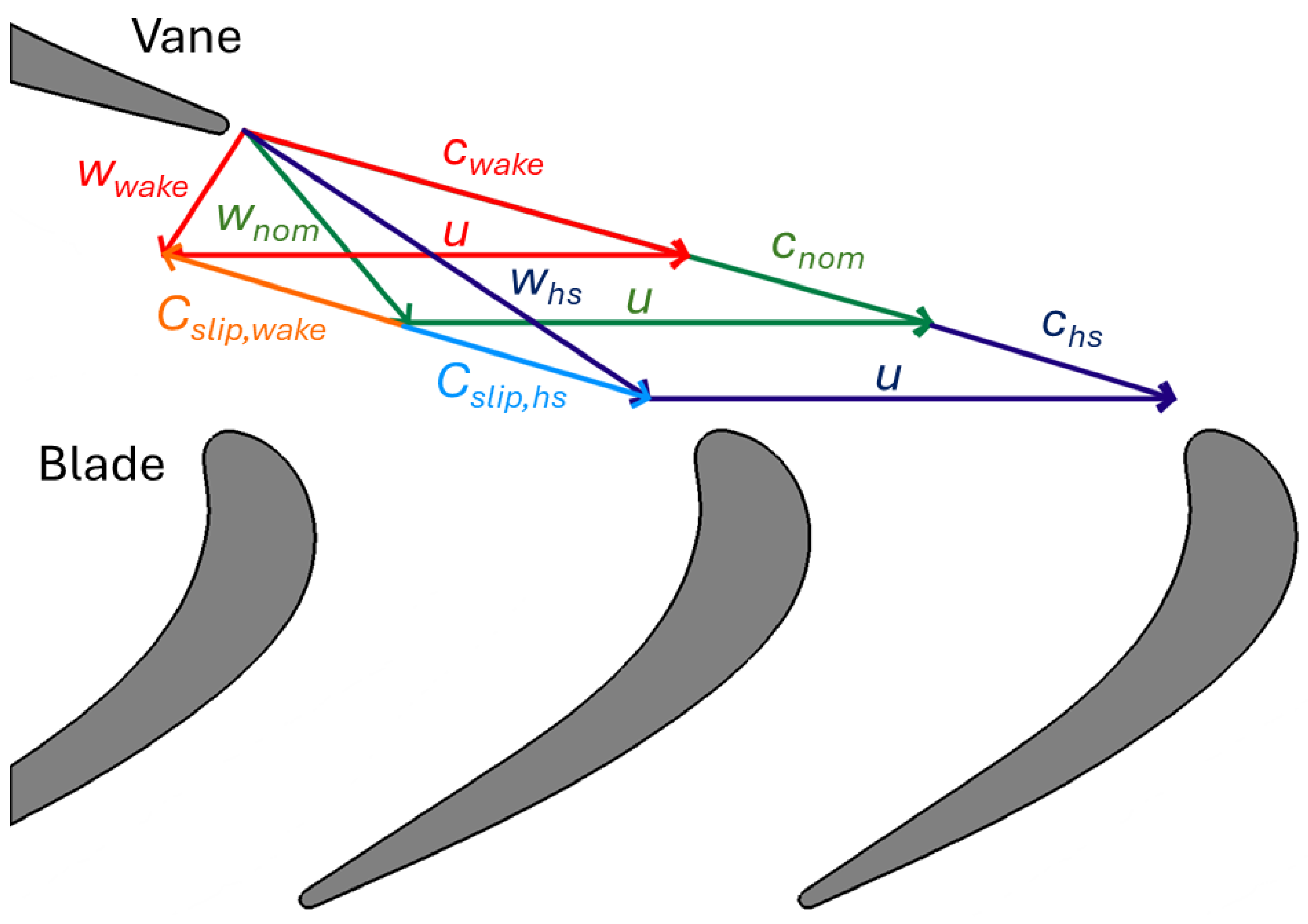
- Wakes generated by vanes represent a source of unsteadiness for the blade row. Since the pressure gradient across a wake is negligible, wake disturbance travels at a velocity that is lower than the one associated with the main flow. This is the driving mechanism for the “negative jet” effect, which is responsible for a fundamental interaction phenomenon occurring in aero-engines at cruise conditions in low-pressure turbine stages (see Section 2.8).
- Steady pressure field associated with the blade load is a source of unsteadiness for the adjacent rows. Since this mechanism is purely inviscid, this kind of interaction is referred to as “potential”.
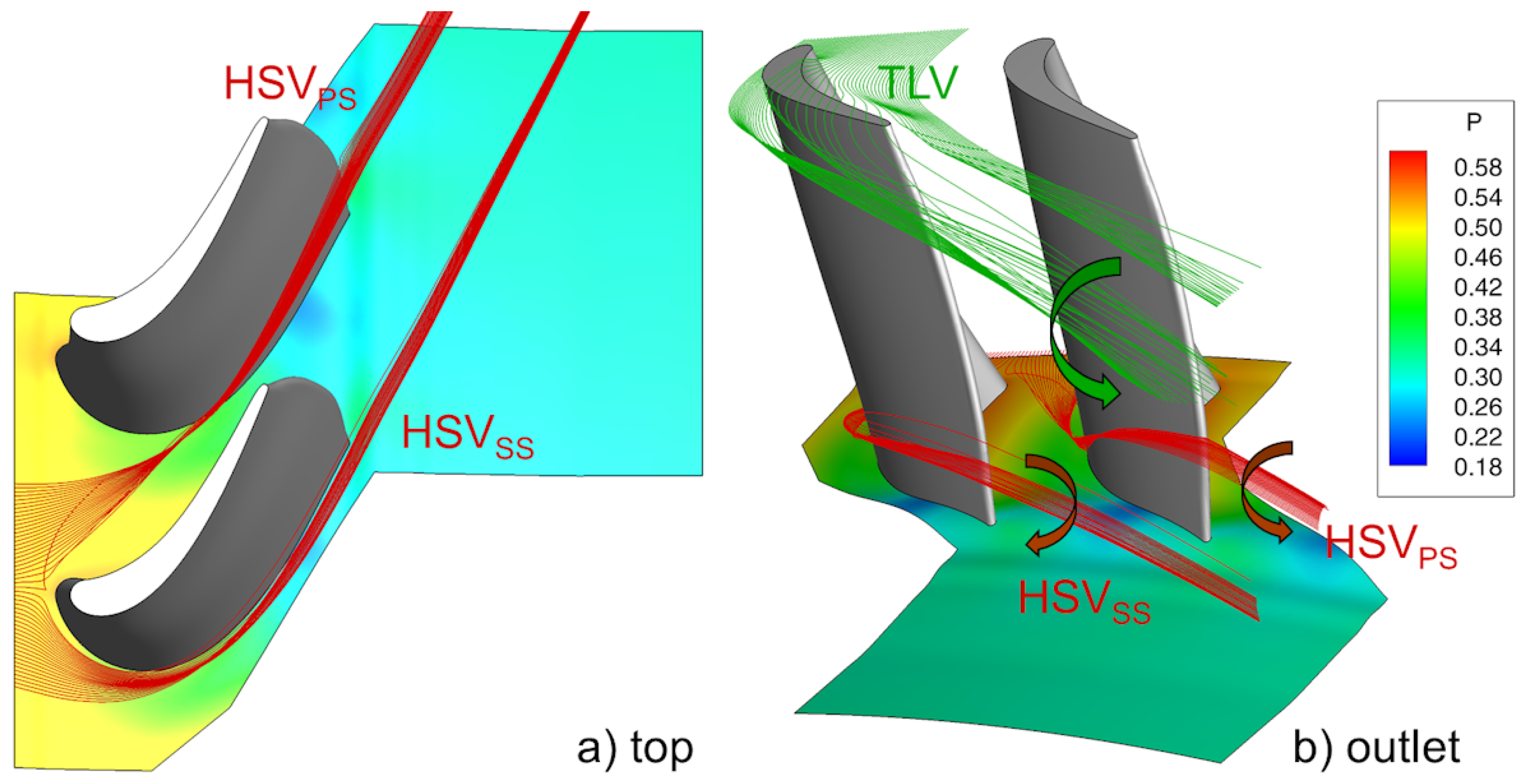
2.3. Secondary Flows in Turbomachinery
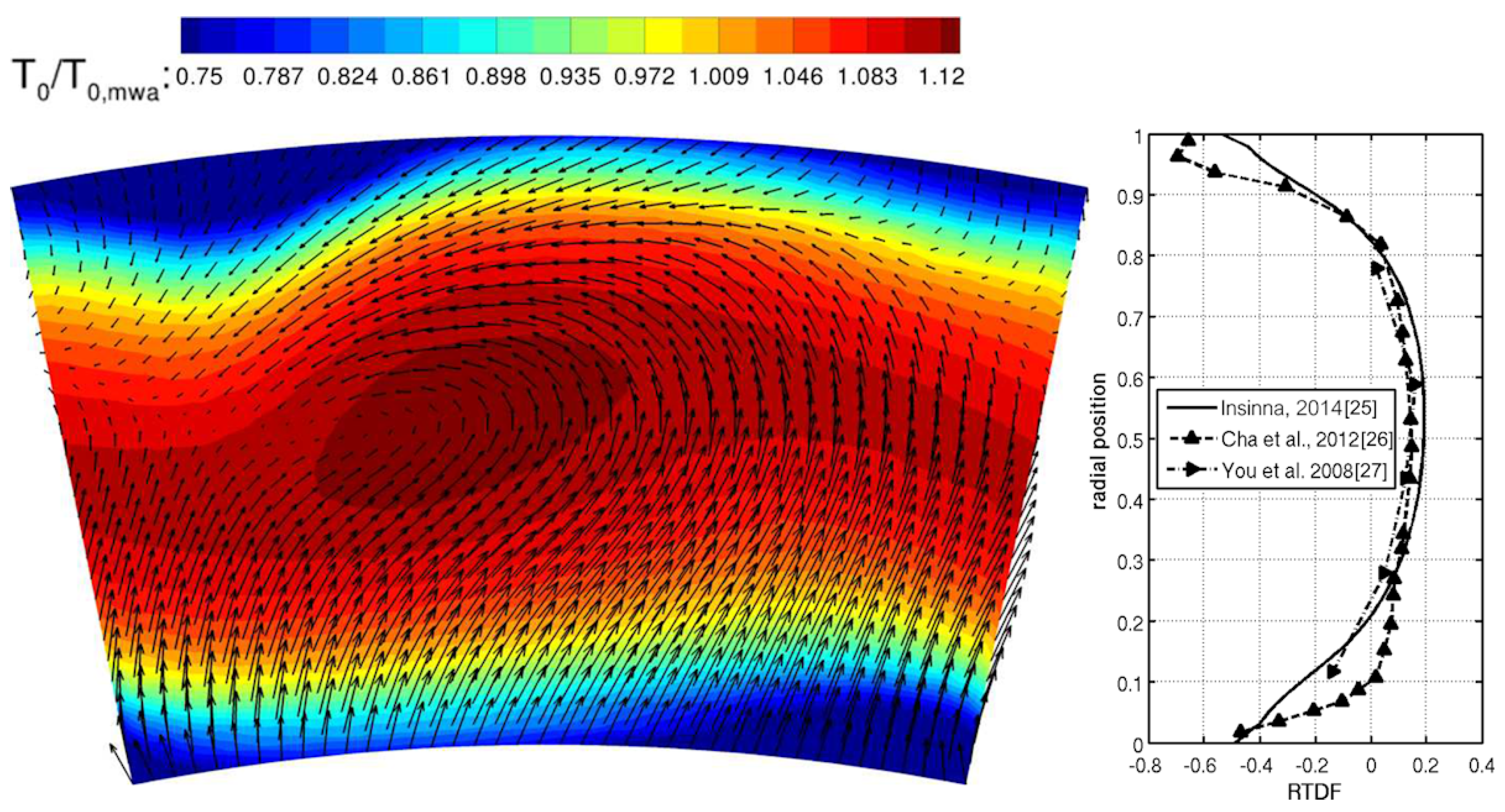
2.4. Stagnation Pressure Non-Uniformity at the Combustor Exit
2.5. Hot Spot Migration in the High-Pressure Turbine Stage
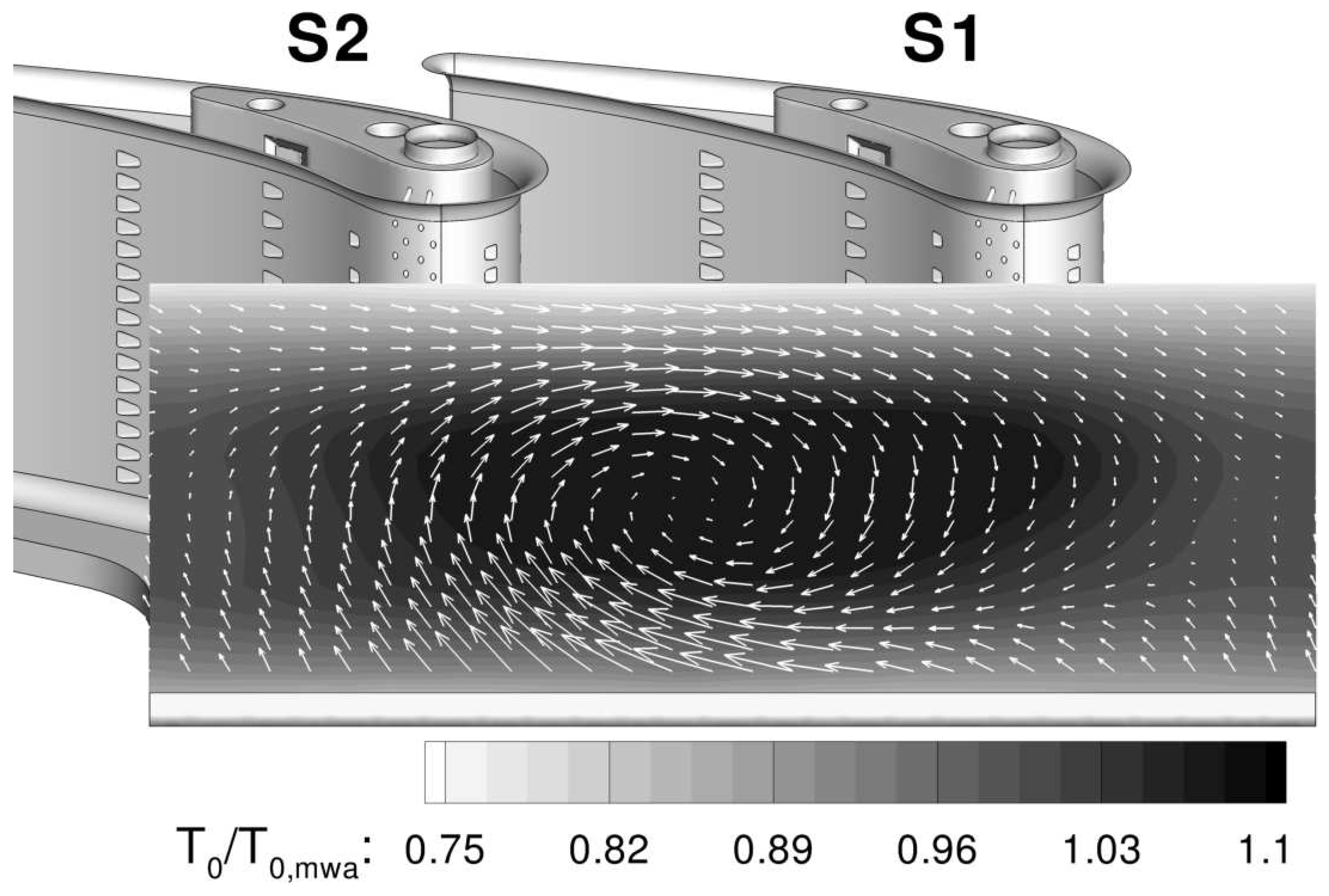
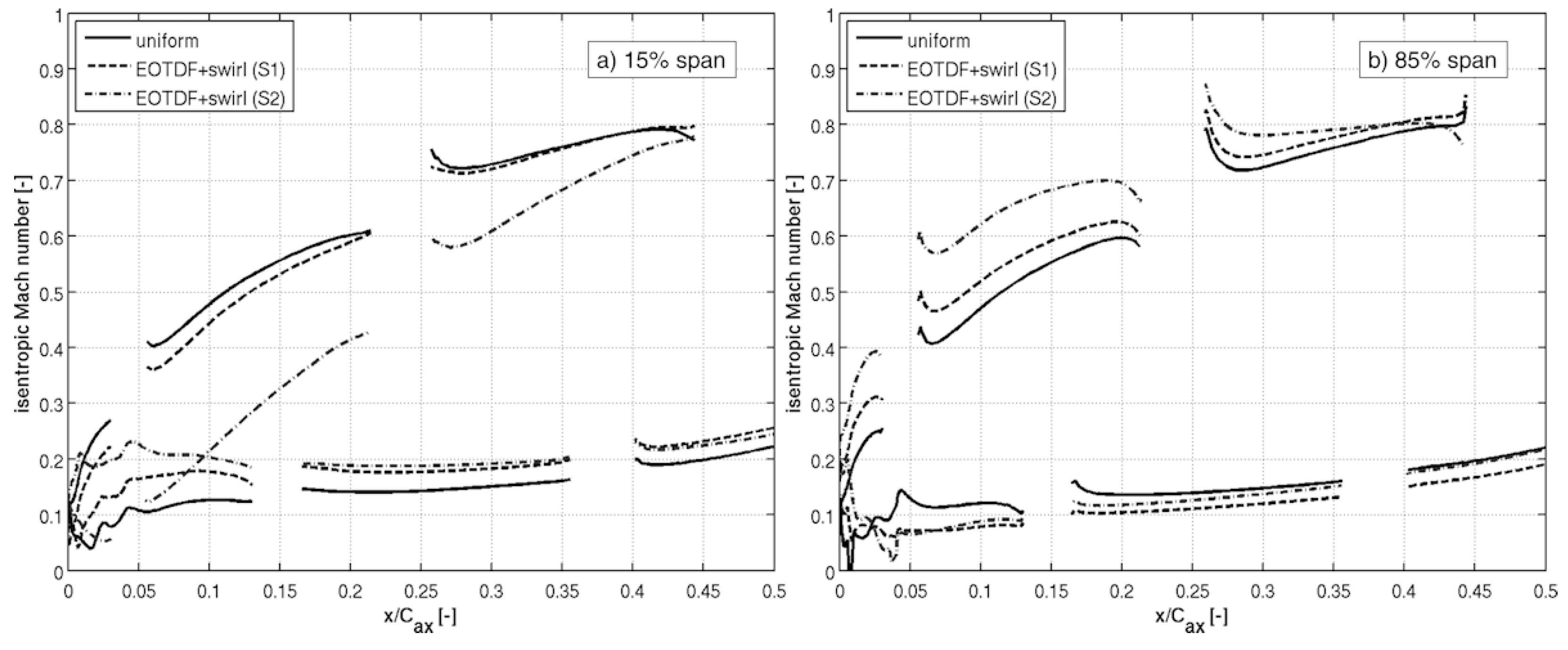
2.6. Residual Swirl on Turbine Inlet Section
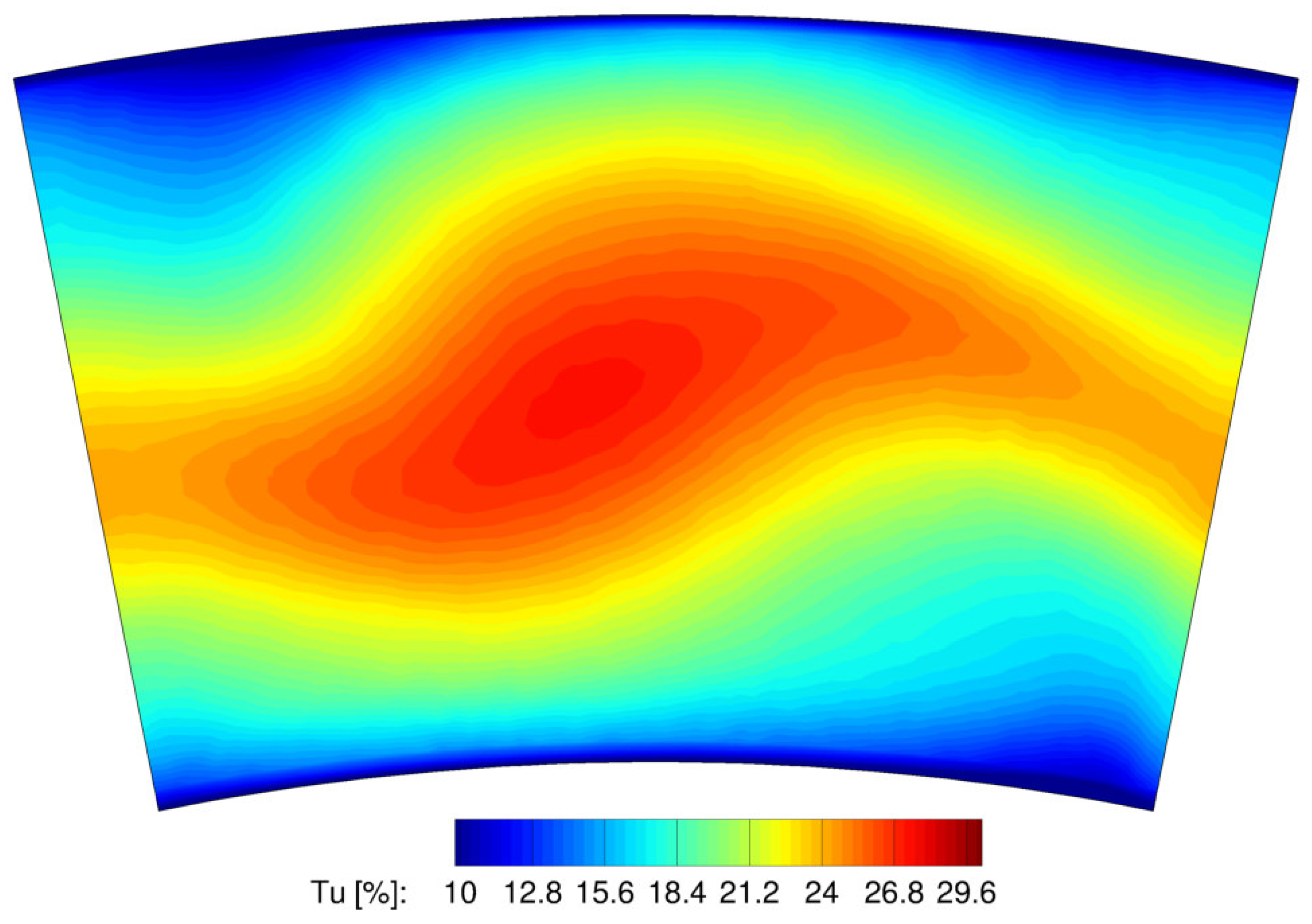
2.7. Turbulence Intensity and Length Scale on Turbine Inlet Section
2.8. Wake/Blade Interaction
2.9. Shock/Blade Interaction
- At time , the oblique shocks and (both generated from vane ) are visible. Shock impinges on the suction side of vane and shock impinges on the suction side of blade close to the leading edge (and is weakly reflected).
- At time , the oblique shock is reflected through the axial gap () and impinges on blade (which, in the meantime, moves in the direction of rotation). Moreover, the shock interacts with blade , generating locally the normal shock and causing a local instability in the boundary layer.
- At time , the shock does not reach any blade, while a new reflected shock () appears, originating from thanks to the “shock-sweeping” mechanism. The reflected shocks along with the oblique shocks generate a region delimited by high-density gradients in the vane/blade gap.
- At time , a configuration similar to the one occurring at time occurs, but with a weaker intensity of .
- At time , a configuration similar to the one occurring at time occurs, but without the formation of the normal shock.
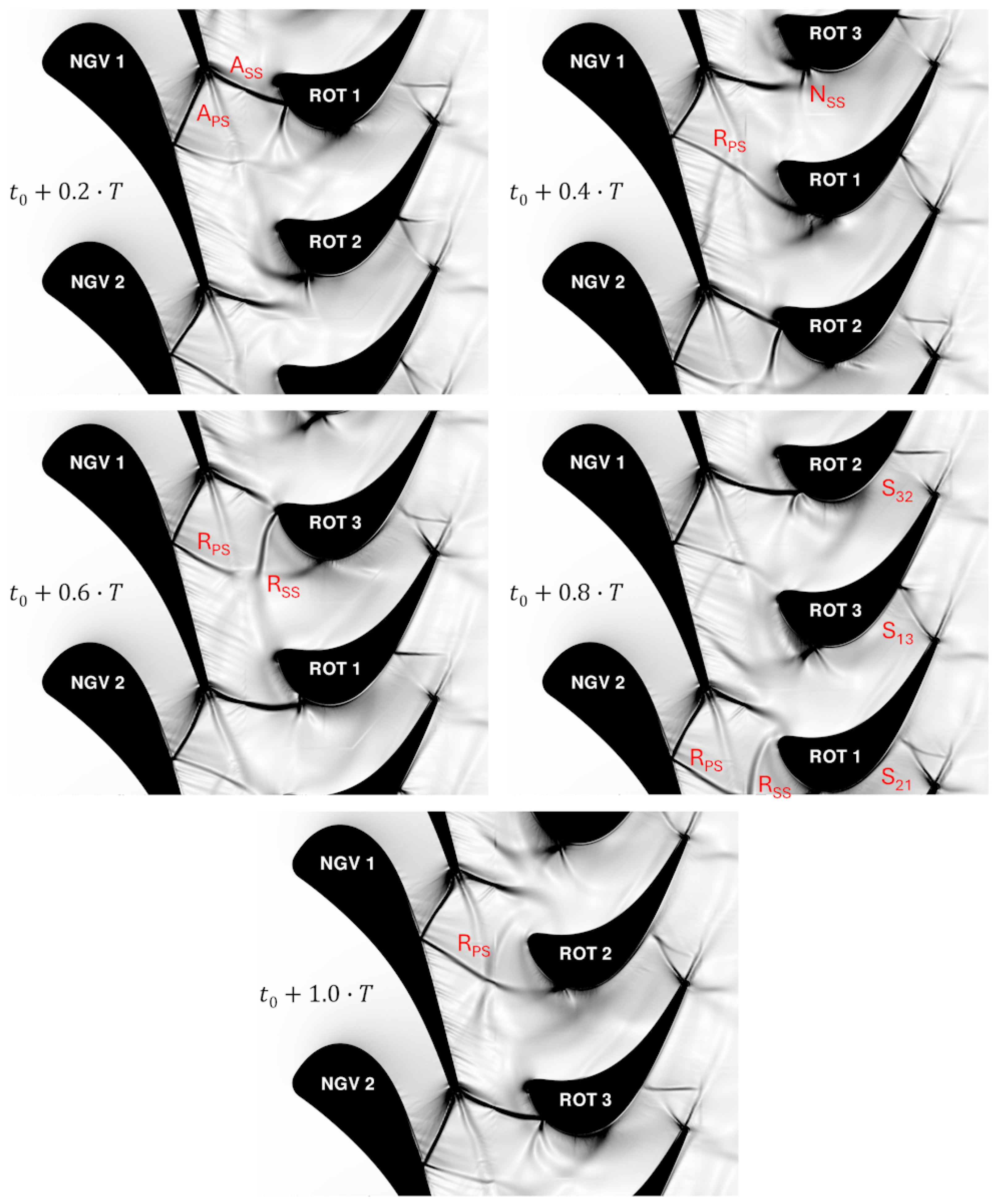
2.10. Clocking Effects between Blade Rows
2.11. The Role of Unsteadiness in the Generation of Losses
2.12. Aerodynamic Instability and Aeroelastic Effects
3. Component Interaction Analysis
3.1. Compressor/Combustor Interaction
- to ensure uniform air feeding to burners;
- to ensure effective air redistribution to the combustor walls;
- to increase pressure recovery across the pre-diffuser, avoiding its stall;
- to reduce overall stagnation pressure losses;
- to avoid unexpected working conditions or instabilities of the reacting flow due to disturbances coming from the compressor.
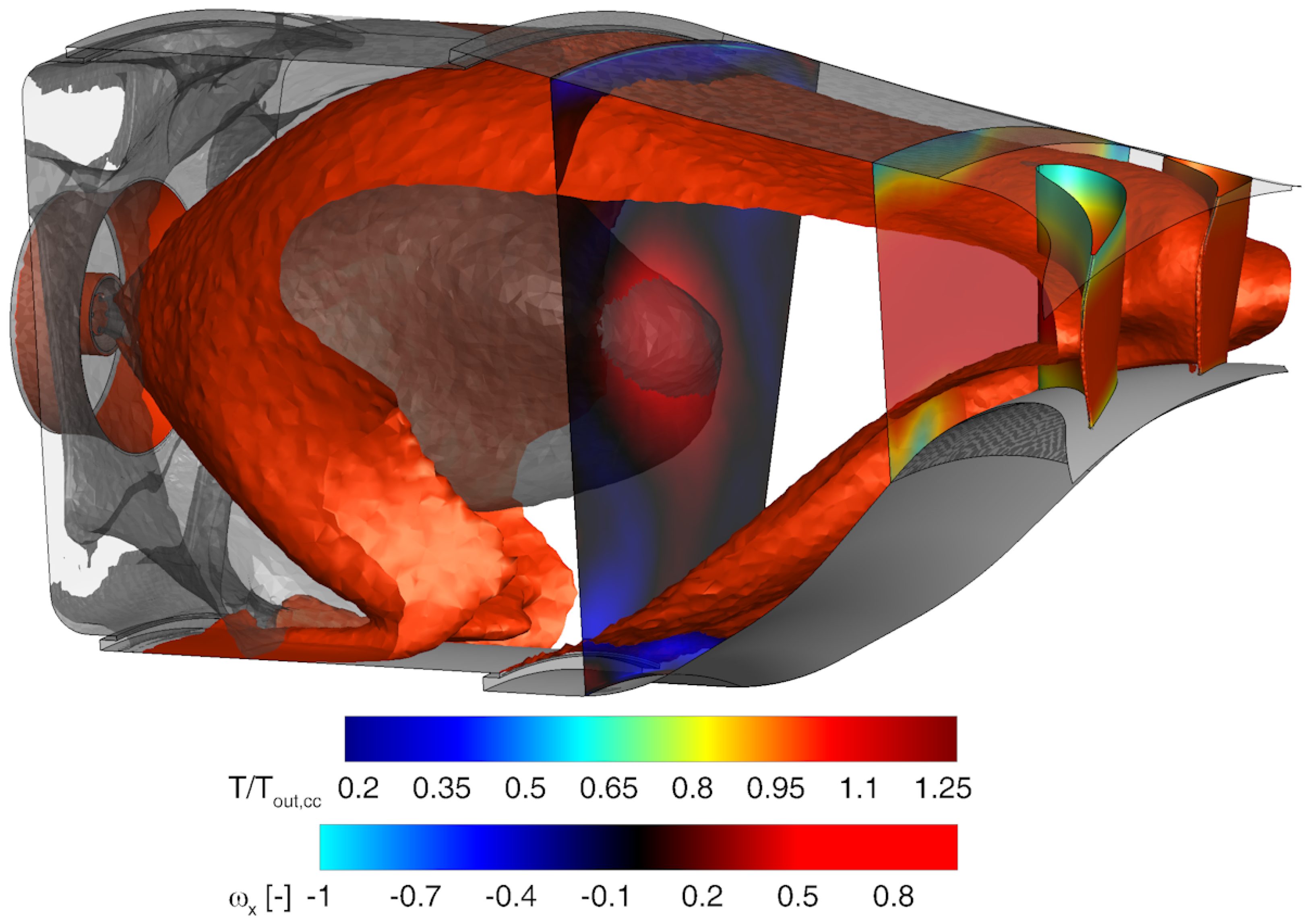
3.2. Combustor/Turbine Interaction
3.2.1. Combustor Simulators for Combustor/Turbine Interaction Analysis
- The most intense temperature gradients were mainly directed radially.
- Actual combustor geometries had remarkable tangential non-uniformities near the end-walls. The presence of tangential gradients in the center of the height of the channel was strongly dependent on the combustor architecture.
- Hot streaks coming from actual geometries were distorted. The same was not true for the profile shown in [18], coming from the hot streak generator presented in the work by Povey and Qureshi [37], where well-defined hot spots were present. Nevertheless, this consideration cannot be generalized to all the hot streak generators.
- In quantitative terms, the most representative hot streak generators aiming to reproduce aero-engine combustors are characterized by .
3.2.2. Numerical Methods for Combustor/Turbine Interaction Analysis
- A single CFD solver that resolves the reactive flow through combustor and turbine. In this case, a single computational grid, including combustion chamber and turbine, was considered.
- The computational domain was divided into multiple sub-domains and hence multiple grids. Each of these was handled by a specific solver. A mechanism for the exchange of information across the domain interfaces ensured the spatial and temporal consistency between the solutions in the sub-domains and the synchronization of the solvers.
- Solver 1 is initially at the state , which corresponds to the time , and, after receiving the feedback B from solver 2, starts to advance in time until reaching the state , which corresponds to the time ; solver 2 waits.
- Solver 1 passes F to solver 2. F contains time-averaged data, taken on a moving window, the amplitude of which can also be larger than the time interval .
- Solver 2 is initially at the state , which corresponds to the time and, after receiving the time-averaged F from solver 1, advances in time until reaching the state , which corresponds to the time ; solver 1 waits.
- Solver 2 passes B to solver 1 and the cycle restarts.
3.3. Numerical Methods for Blade Row Interaction Analysis
- Unsteady modelling using deterministic stresses.
- Quasi-unsteady simulations with unsteady boundary condition updating.
- Full unsteady simulations in time or frequency domains.
3.3.1. Deterministic Stresses
3.3.2. Loosely Coupled Approach
3.3.3. Domain Scaling Approach
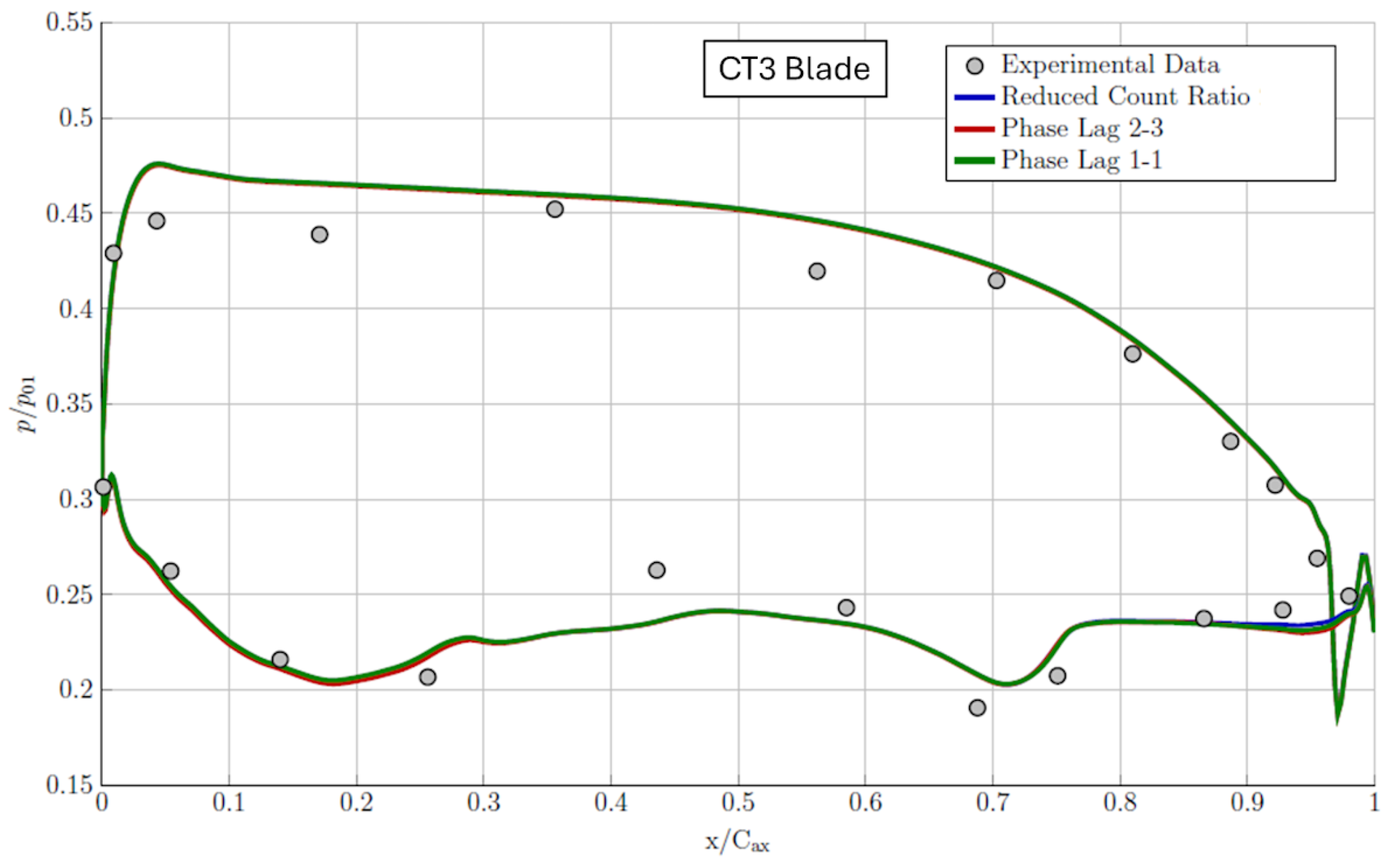
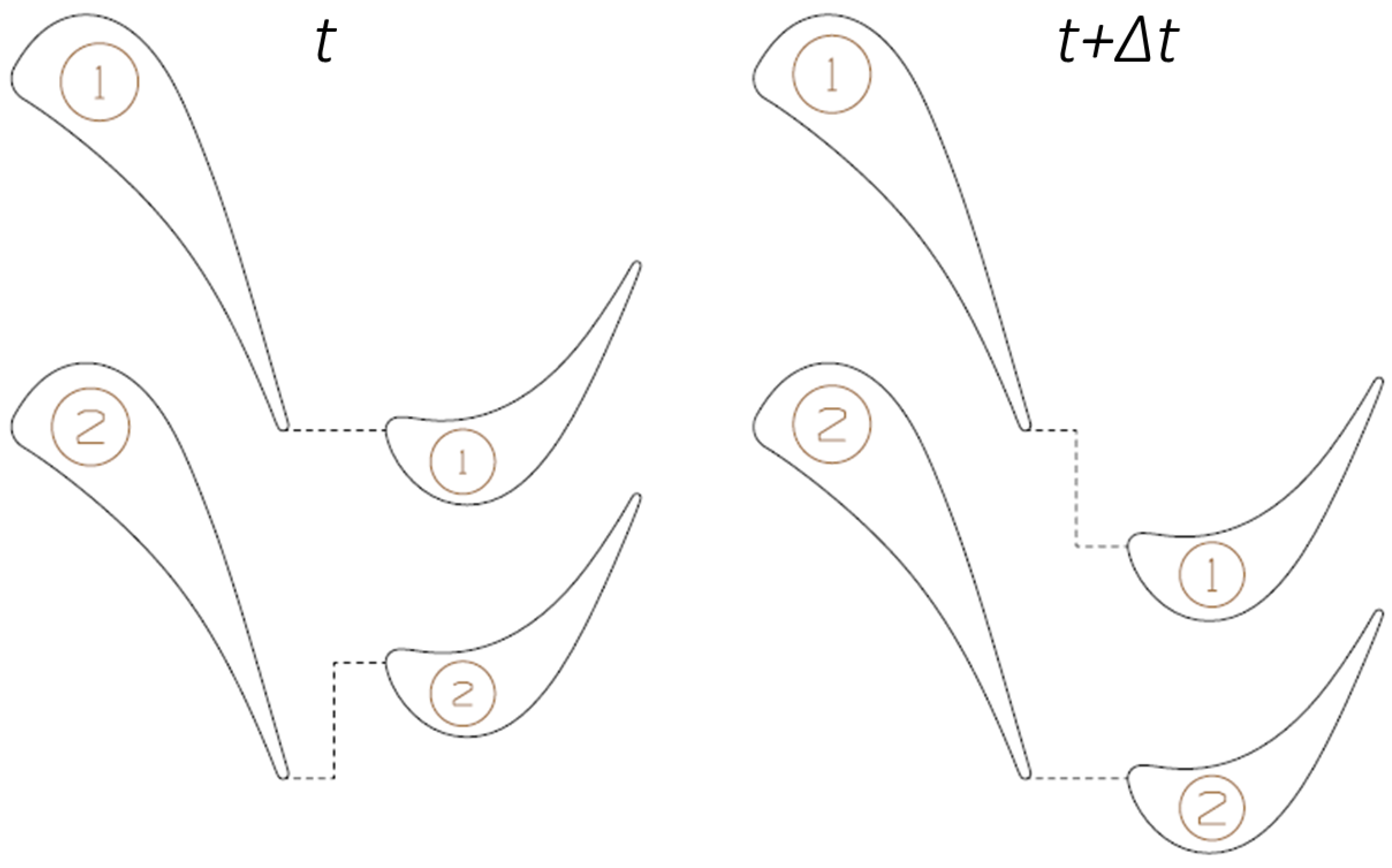
3.3.4. Time Lag or Time Inclining
3.3.5. Direct Storage and Shape Correction Methods
4. Conclusions
- The impact of stagnation pressure non-uniformities on the turbine performance is negligible, with the maximum non-uniformity being lower than . However, non-negligible effects were found when an increase in stagnation pressure was found close to the end-walls because it affected the development of secondary flows.
- The stagnation line on high-pressure vanes is modified by the presence of a residual swirl from the combustor, especially in lean-burn configurations. In fact, fluctuations of in the incidence were found close to the end-walls, thus causing the modification of the stagnation point location up to axial chords. The radial variation of incidence also generates a radial distribution of loading.
- Stagnation temperature circumferential non-uniformities are responsible for the migration of hot flow towards the high-pressure blade suction side due to the “positive jet” effect that interacts with the passage vortex. An increase in Nusselt number value by was observed on the blade pressure side at mid-span. Moreover, a reduction in the residual blade life up to ≈ was associated with an increase of ≈+40 K in metal temperature. The passage vortex is also responsible for the migration of the hot flow towards the tip clearance and for its interaction with the tip leakage vortex.
- Coolant flow distribution is driven both by the non-uniform cooling hole outlet pressure distribution generated by residual swirls and by the modified development of secondary flows. Variations in coolant mass flow rate of were found in a linear case with a strong residual inlet swirl profile. Moreover, the usage of a mean driving temperature value for heat transfer calculations may provide inaccurate results during the design process.
- Existing test rigs for compressor/combustor and combustor/turbine interaction analysis allowed for accurately studying the most relevant phenomena occurring in gas turbines in engine-relevant conditions. Experimental results were also of great relevance for the solver verification, calculation validation, and uncertainty quantification.
- Even though non-uniform air feeding to burners was experimentally found, compressor/combustor interaction generated negligible effects when compared with combustor/turbine interaction (at least for the investigated configurations). However, it was possible to individuate the high-pressure compressor rotor passing frequency in the primary zone of the combustor through a frequency domain analysis, thus hinting at an interaction with combustion instabilities.
- Either fully coupled or integrated simulations were necessary to correctly analyze the aerothermal characteristics of cooled high-pressure turbine stages due to the impact associated with the unsteadiness and the turbulence on both loading and heat transfer. Concerning the latter, scale-resolving methods were necessary to correctly simulate heat transfer coefficients on cooled vane surfaces, with SBES being the most promising approach thanks to its reduced computational cost with respect to LES. Such approaches were also necessary to take into account the “net circulation” phenomenon, which was responsible for the circumferential movement of the residual swirl.
- Concerning vane/blade interaction, frequency domain methods proved to be accurate methods for the analysis of a wide range of phenomena and showed a remarkable convergence rate. However, all the methods presented here were sufficiently accurate for the study of turbine stages and the selection of the most suitable one mostly depended on the problem that was investigated and on the available computational resources.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | sound speed [m/s] |
| A | amplitude of an oscillation [m] |
| b | bi-normal direction [−] |
| B | vector of variables |
| c | absolute velocity [m/s] |
| C | chord |
| d | dump gap [m] |
| f | frequency [Hz] |
| F | force [N/m2], vector of variables |
| axial flux of momentum [(kg · m)/s2] | |
| axial flux of momentum [(kg · m2)/s2] | |
| h | enthalpy [kJ/(kg · K)], pre-diffuser exit radius [m] |
| H | total enthalpy [kJ/(kg · K)] |
| k | kinetic energy [m2/s2], turbulent kinetic energy [m2/s2] |
| n | normal direction [−] |
| N | number of airfoils, number |
| p | pressure [Pa] |
| P | pressure [Pa], pitch [m] |
| Q | tensor |
| r | radius [m] |
| R | radius [m], tensor, Fourier series residual [m/s] |
| s | stream-wise direction [−] |
| S | blade pitch [m], entropy [kJ/kg] |
| swirl number [−] | |
| t | time [s] |
| T | temperature [K], time period [s] |
| turbulence level [−] | |
| u | velocity [m/s], tangential velocity [m/s], velocity component [m/s] |
| U | velocity [m/s] |
| v | velocity [m/s] |
| V | tangential velocity [m/s] |
| w | relative velocity [m/s] |
| W | work [J] |
| x | axial gap [m], displacement [m] |
| y | Cartesian y-direction value [m] |
| Subscripts and Superscripts | |
| average value, deterministic value | |
| double average, deterministic value | |
| steady solution | |
| ′ | fluctuating value, stochastic value |
| ″ | double fluctuating value, stochastic value |
| 0 | stagnation condition, initial time step, averaged value |
| stationary reference frame | |
| moving reference frame | |
| both stationary and moving reference frame | |
| A | Fourier series coefficient [m/s] |
| axial | |
| B | vibrational, Fourier series coefficient [m/s] |
| turbine blade | |
| turbine casing | |
| combustion chamber | |
| fluid–blade | |
| harmonics | |
| turbine hub | |
| hot spot | |
| i | counter |
| j | counter |
| L | laminar |
| lower periodic | |
| maximum value | |
| mean value | |
| minimum value | |
| mass-weighted averaged | |
| n | counter |
| modified value | |
| nominal condition | |
| outlet section | |
| perturbation | |
| R | rotor |
| actual value | |
| slip flow | |
| s | stall condition |
| stall condition | |
| swirl | |
| T | turbulent |
| time averaged | |
| tangential | |
| total | |
| time step | |
| upper periodic | |
| turbine vane | |
| turbine wake | |
| x | axial direction |
| z | axial direction |
| Greek Letters | |
| dissipation rate [m2/s3] | |
| density [kg/m3] | |
| phase shift | |
| PI Greek | |
| phase shift | |
| tangential | |
| vane angle [deg] | |
| vorticity [1/s], specific dissipation rate [1/s], pulsation [1/s], rotational speed [rad/s] | |
| rotational speed [RPM] | |
| Abbreviations | |
| CFD | Computational Fluid Dynamics |
| CHT | Conjugate Heat Transfer |
| DES | Detached Eddy Simulation |
| DLN | Dry Low |
| DS | Domain Scaling |
| HSV | Horseshoe Vortex |
| HWA | Hot Wire Anemometer |
| ITD | Inlet Temperature Distortion |
| LES | Large-Eddy Simulation |
| NRBC | Non-Reflecting Boundary Conditions |
| OGV | Outlet Guide Vane |
| OTDF | Overall Temperature Distortion Factor |
| PIV | Particle Image Velocimetry |
| POD | Proper Orthogonal Decomposition |
| PV | Passage Vortex |
| PVC | Precessing Vortex Core |
| PS | Pressure Side |
| PSP | Pressure-Sensitive Paint |
| RTDF | Radial Temperature Distortion Factor |
| RANS | Reynolds-Averaged Navier–Stokes |
| RQL | Rich–Quench–Lean |
| RSM | Reynolds-Stress Model |
| SAS | Scale-Adaptive Simulation |
| SBES | Stress-Blended Eddy Simulation |
| SF | Scaling Factor |
| SS | Suction Side |
| SSG | Speziale–Sarkar–Gatski |
| SST | Shear Stress Transport |
| TLV | Tip Leakage Vortex |
| URANS | Unsteady Reynolds-Averaged Navier–Stokes |
References
- Lakshminarayana, B. Fluid Dynamics and Heat Transfer of Turbomachinery; Wiley: Hoboken, NJ, USA, 1995. [Google Scholar] [CrossRef]
- Rolls-Royce. The Jet Engine; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Paniagua, G. Investigation of the Steady and Unsteady Performance of a Transonic hp Turbine. Ph.D. Thesis, Université Libre de Bruxelles, Bruxelles, Belgium, 2002. [Google Scholar]
- Montomoli, F.; Carnevale, M.; D’Ammaro, A.; Massini, M.; Salvadori, S. Uncertainty Quantification in Computational Fluid Dynamics and Aircraft Engines; Springer International Publishing: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Parker, R. Paper 1: Relation between Blade Row Spacing and Potential Flow Interaction Effects in Turbomachines. Proc. Inst. Mech. Eng. Conf. Proc. 1969, 184, 1–8. [Google Scholar] [CrossRef]
- Greitzer, E. Introduction to unsteady flow in turbomachines. Unsteady Flow Turbomach. 1984, 1–62. [Google Scholar]
- Sieverding, C.H. Recent Progress in the Understanding of Basic Aspects of Secondary Flows in Turbine Blade Passages. J. Eng. Gas Turbines Power 1985, 107, 248–257. [Google Scholar] [CrossRef]
- Langston, L. Secondary Flows in Axial Turbines—A Review. Ann. N. Y. Acad. Sci. 2006, 934, 11–26. [Google Scholar] [CrossRef]
- Salvadori, S.; Montomoli, F.; Martelli, F.; Adami, P.; Chana, K.S.; Castillon, L. Aerothermal Study of the Unsteady Flow Field in a Transonic Gas Turbine With Inlet Temperature Distortions. J. Turbomach. 2011, 133, 031030. [Google Scholar] [CrossRef]
- Langston, L.S. Crossflows in a Turbine Cascade Passage. J. Eng. Power 1980, 102, 866–874. [Google Scholar] [CrossRef]
- Délery, J.M. Robert Legendre and Henri Werlé: Toward the Elucidation of Three-Dimensional Separation. Annu. Rev. Fluid Mech. 2001, 33, 129–154. [Google Scholar] [CrossRef]
- Lakshminarayana, B.; Horlock, J.H. Generalized expressions for secondary vorticity using intrinsic co-ordinates. J. Fluid Mech. 1973, 59, 97–115. [Google Scholar] [CrossRef]
- Denton, J.D. Loss Mechanisms in Turbomachines; American Society of Mechanical Engineers: New York, NY, USA, 1993; Volume 78897. [Google Scholar] [CrossRef]
- Kerrebrock, J.L.; Mikolajczak, A.A. Intra-Stator Transport of Rotor Wakes and Its Effect on Compressor Performance. J. Eng. Power 1970, 92, 359–368. [Google Scholar] [CrossRef]
- Dorney, D.; Davis, R.; Edwards, D.; Madavan, N. Unsteady analysis of hot streak migration in a turbine stage. J. Propuls. Power 1990, 8, 520–529. [Google Scholar] [CrossRef]
- Pullan, G. Secondary Flows and Loss Caused by Blade Row Interaction in a Turbine Stage. J. Turbomach. 2006, 128, 484–491. [Google Scholar] [CrossRef]
- Payne, S.; Ainsworth, R.; Miller, R.; Moss, R.; Harvey, N. Unsteady loss in a high pressure turbine stage. Int. J. Heat Fluid Flow 2003, 24, 698–708. [Google Scholar] [CrossRef]
- Qureshi, I.; Beretta, A.; Povey, T. Effect of Simulated Combustor Temperature Nonuniformity on HP Vane and End Wall Heat Transfer: An Experimental and Computational Investigation. J. Eng. Gas Turbines Power 2011, 133, 031901. [Google Scholar] [CrossRef]
- Shahpar, S.; Caloni, S. Aerodynamic Optimization of High-Pressure Turbines for Lean-Burn Combustion System. J. Eng. Gas Turbines Power 2013, 135, 055001. [Google Scholar] [CrossRef]
- Hall, B.F.; Chana, K.S.; Povey, T. Design of a Non-Reacting Combustor Simulator with Swirl and Temperature Distortion with Experimental Validation. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. ASME Paper No. GT2013-95499. [Google Scholar] [CrossRef]
- Barringer, M.D.; Thole, K.A.; Polanka, M.D. An Experimental Study of Combustor Exit Profile Shapes on Endwall Heat Transfer in High Pressure Turbine Vanes. J. Turbomach. 2009, 131, 021009. [Google Scholar] [CrossRef]
- Barringer, M.D.; Thole, K.A.; Polanka, M.D.; Clark, J.P.; Koch, P.J. Migration of Combustor Exit Profiles Through High Pressure Turbine Vanes. J. Turbomach. 2009, 131, 021010. [Google Scholar] [CrossRef]
- Insinna, M.; Salvadori, S.; Martelli, F.; Adami, P.; Vazquez, R. Aero-Thermal Analysis of Combustor/Turbine Interaction in Aero-Engines: The Challenge of Today. Available online: https://aerospace-europe.eu/case-studies/aero-thermal-analysis-of-combustorturbine-interaction-in-aero-engines-the-challenge-of-today/abstract/ (accessed on 25 January 2024).
- Insinna, M.; Salvadori, S.; Martelli, F. Simulation of Combustor/NGV Interaction Using Coupled RANS Solvers: Validation and Application to a Realistic Test Case. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; Volume 45622, p. V02CT38A010. [Google Scholar] [CrossRef]
- Insinna, M. Investigation of the Aero-Thermal Aspects of Combustor/Turbine Interaction in Gas Turbines. Ph.D. Thesis, Department of Industrial Engineering, University of Florence, Florence, Italy, 2014. [Google Scholar]
- Cha, C.M.; Hong, S.; Ireland, P.T.; Denman, P.; Savarianandam, V. Experimental and Numerical Investigation of Combustor–Turbine Interaction Using an Isothermal, Nonreacting Tracer. J. Eng. Gas Turbines Power 2012, 134, 081501. [Google Scholar] [CrossRef]
- You, D.; Ham, F.; Moin, P. Large-Eddy Simulation Analysis of Turbulent Combustion in a Gas Turbine Engine Combustor; Annual Research Briefs 2008; Center for Turbulence Research: Stanford, CA, USA, 2008; pp. 219–230. [Google Scholar]
- Butler, T.; Sharma, O.; Joslyn, H.; Dring, R. Redistribution of an inlet temperature distortion in an axial flow turbine stage. J. Propuls. Power 1986, 5, 64–71. [Google Scholar] [CrossRef]
- Munk, M.; Prim, R. On the Multiplicity of Steady Gas Flows Having the Same Streamline Pattern. Proc. Natl. Acad. Sci. USA 1947, 33, 137–141. [Google Scholar] [CrossRef]
- Simone, S.; Montomoli, F.; Martelli, F.; Chana, K.S.; Qureshi, I.; Povey, T. Analysis on the Effect of a Nonuniform Inlet Profile on Heat Transfer and Fluid Flow in Turbine Stages. J. Turbomach. 2012, 134, 011012. [Google Scholar] [CrossRef]
- Rai, M.; Dring, R. Navier–Stokes analyses of the redistribution of inlet temperature distortions in a turbine. J. Propuls. Power 1987, 6, 276–282. [Google Scholar] [CrossRef]
- Povey, T.; Chana, K.; Jones, T.V.; Hurrion, J. The Effect of Hot-Streaks on HP Vane Surface and Endwall Heat Transfer: An Experimental and Numerical Study. J. Turbomach. 2005, 129, 1483–1497. [Google Scholar] [CrossRef]
- Adami, P.; Salvadori, S.; Chana, K.S. Unsteady Heat Transfer Topics in Gas Turbine Stages Simulations. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 6, pp. 1733–1744. [Google Scholar] [CrossRef]
- Hilditch, M.A.; Fowler, A.; Jones, T.V.; Chana, K.S.; Oldfield, M.L.G.; Ainsworth, R.W.; Hogg, S.I.; Anderson, S.J.; Smith, G.C. Installation of a Turbine Stage in the Pyestock Isentropic Light Piston Facility. In Proceedings of the ASME 1994 International Gas Turbine and Aeroengine Congress and Exposition, Hague, The Netherlands, 13–16 June 1994. [Google Scholar] [CrossRef]
- Chana, K.; Mole, A. Summary of Cooled NGV and Uncooled Rotor Measurements from the MT1 Single Stage High Pressure Turbine in the DERA Isentropic Light Piston Facility; Brite-EuRam Turbine Aero-Thermal External Flow project (BRPR-CT97-0519); DERA: London, UK, 2002. [Google Scholar]
- Chana, K.S.; Jones, T.V. An Investigation on Turbine Tip and Shroud Heat Transfer. J. Turbomach. 2003, 125, 513–520. [Google Scholar] [CrossRef]
- Povey, T.; Qureshi, I. Developements in Hot-Streak Simulators for Turbine Testing. J. Turbomach. 2009, 131, 031009. [Google Scholar] [CrossRef]
- Chana, K.S.; Hurrion, J.R.; Jones, T.V. The Design, Development and Testing of a Non-Uniform Inlet Temperature Generator for the QinetiQ Transient Turbine Research Facility. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA, 16–19 June 2003; Volume 36894, pp. 273–280. [Google Scholar] [CrossRef]
- Gerolymos, G.A.; Michon, G.J.; Neubauer, J. Analysis and Application of Chorochronic Periodicity in Turbomachinery Rotor/Stator Interaction Computations. J. Propuls. Power 2002, 18, 1139–1152. [Google Scholar] [CrossRef]
- Castillon, L. Evaluation of a multiple frequency phase lagged method for unsteady numerical simulations of multistage turbomachinery. In Proceedings of the 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012. [Google Scholar]
- Thorpe, S.J.; Miller, R.J.; Yoshino, S.; Ainsworth, R.W.; Harvey, N.W. The Effect of Work Processes on the Casing Heat Transfer of a Transonic Turbine. J. Turbomach. 2007, 129, 84–91. [Google Scholar] [CrossRef]
- Roback, R.J.; Dring, R.P. Hot Streaks and Phantom Cooling in a Turbine Rotor Passage: Part 1—Separate Effects. J. Turbomach. 1993, 115, 657–666. [Google Scholar] [CrossRef]
- Roback, R.J.; Dring, R.P. Hot Streaks and Phantom Cooling in a Turbine Rotor Passage: Part 2—Combined Effects and Analytical Modeling. J. Turbomach. 1993, 115, 667–674. [Google Scholar] [CrossRef]
- Dorney, D.J.; Gundy-Burlet, K. Hot-streak clocking effects in a 1-1/2 stage turbine. J. Propuls. Power 1996, 12, 619–620. [Google Scholar] [CrossRef]
- Gundy-Burlet, K.L.; Dorney, D.J. Influence of 3D Hot Streaks on Turbine Heat Transfer. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997; Volume 14, pp. 123–132. [Google Scholar] [CrossRef]
- Shang, T.; Epstein, A.H. Analysis of Hot Streak Effects on Turbine Rotor Heat Load. J. Turbomach. 1997, 119, 544–553. [Google Scholar] [CrossRef]
- He, L.; Menshikova, V.; Haller, B.R. Influence of Hot Streak Circumferential Length-Scale in Transonic Turbine Stage. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; ASME Paper No. GT2004-53370. pp. 1117–1126. [Google Scholar]
- Saxer, A.P.; Felici, H.M. Numerical Analysis of Three-Dimensional Unsteady Hot Streak Migration and Shock Interaction in a Turbine Stage. J. Turbomach. 1996, 118, 268–277. [Google Scholar] [CrossRef]
- Dorney, D.J.; Gundy-Buriet, K.L. Effects of Hot Streak Shape on Rotor Heating in a High-Subsonic Single-Stage Turbine. Int. J. Turbo Jet Engines 2001, 18, 15–30. [Google Scholar] [CrossRef]
- Dorney, D.J.; Sondak, D.L. Effects of Tip Clearance on Hot Streak Migration in a High-Subsonic Single-Stage Turbine. J. Turbomach. 2000, 122, 613–620. [Google Scholar] [CrossRef]
- Bohn, D.; Funke, H.; Heuer, T.; Bütikofer, J. Numerical and Experimental Investigations of the Influence of Different Swirl Ratios on the Temperature Streak Development in a 4-Stage Turbine. In Proceedings of the ASME Turbo Expo 2000: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000; Volume 78569, p. V003T01A056. [Google Scholar] [CrossRef]
- Ji, L.C.; Xu, J.Z.; Chen, J. Study of Hot Streak Effects in a Counter-Rotating Turbine. In Proceedings of the ASME Turbo Expo 2001: Power for Land, Sea, and Air, New Orleans, LA, USA, 4–7 June 2001; Volume 78521, p. V003T01A051. [Google Scholar] [CrossRef]
- Barringer, M.D.; Thole, K.A.; Polanka, M.D. Experimental Evaluation of an Inlet Profile Generator for High-Pressure Turbine Tests. J. Turbomach. 2007, 129, 382–393. [Google Scholar] [CrossRef]
- Barringer, M.D.; Thole, K.A.; Polanka, M.D. Effects of Combustor Exit Profiles on Vane Aerodynamic Loading and Heat Transfer in a High Pressure Turbine. J. Turbomach. 2009, 131, 021008. [Google Scholar] [CrossRef]
- Mathison, R.M.; Haldeman, C.W.; Dunn, M.G. Aerodynamics and Heat Transfer for a Cooled One and One-Half Stage High-Pressure Turbine—Part I: Vane Inlet Temperature Profile Generation and Migration. J. Turbomach. 2012, 134, 011006. [Google Scholar] [CrossRef]
- Mathison, R.M.; Haldeman, C.W.; Dunn, M.G. Aerodynamics and Heat Transfer for a Cooled One and One-Half Stage High-Pressure Turbine: Part II—Influence of Inlet Temperature Profile on Blade Row and Shroud. J. Turbomach. 2010, 134, 011007. [Google Scholar] [CrossRef]
- Mathison, R.M.; Haldeman, C.W.; Dunn, M.G. Aerodynamics and Heat Transfer for a Cooled One and One-Half Stage High-Pressure Turbine—Part III: Impact of Hot-Streak Characteristics on Blade Row Heat Flux. J. Turbomach. 2012, 134, 011008. [Google Scholar] [CrossRef]
- Gaetani, P.; Persico, G. Transport of Entropy Waves Within a High Pressure Turbine Stage. J. Turbomach. 2019, 141, 031006. [Google Scholar] [CrossRef]
- Gaetani, P.; Persico, G.; Pinelli, L.; Marconcini, M.; Pacciani, R. Computational and Experimental Study of Hot Streak Transport Within the First Stage of a Gas Turbine. J. Turbomach. 2019, 142, 081002. [Google Scholar] [CrossRef]
- Pinelli, L.; Marconcini, M.; Pacciani, R.; Gaetani, P.; Persico, G. Computational and Experimental Study of the Unsteady Convection of Entropy Waves within a High-Pressure Turbine Stage. J. Turbomach. 2021, 143, 091011. [Google Scholar] [CrossRef]
- Notaristefano, A.; Gaetani, P. Transport of Swirling Entropy Waves through an Axial Turbine Stator. Int. J. Turbomach. Propuls. Power 2021, 6, 45. [Google Scholar] [CrossRef]
- Notaristefano, A.; Gaetani, P. The Role of Turbine Operating Conditions on Combustor–Turbine Interaction—Part I: Change in Expansion Ratio. J. Turbomach. 2023, 145, 051001. [Google Scholar] [CrossRef]
- Notaristefano, A.; Gaetani, P. The Role of Turbine Operating Conditions on Combustor–Turbine Interaction—Part II: Loading Effects. J. Turbomach. 2023, 145, 051002. [Google Scholar] [CrossRef]
- Pinelli, L.; Marconcini, M.; Pacciani, R.; Notaristefano, A.; Gaetani, P. The Effects of Swirling Flows in Entropy Wave Convection Through High-Pressure Turbine Stage. J. Turbomach. 2023, 145, 031004. [Google Scholar] [CrossRef]
- Qureshi, I.; Smith, A.D.; Povey, T. HP Vane Aerodynamics and Heat Transfer in the Presence of Aggressive Inlet Swirl. J. Turbomach. 2013, 135, 1925–1942. [Google Scholar] [CrossRef]
- Qureshi, I.; Beretta, A.; Chana, K.; Povey, T. Effect of Aggressive Inlet Swirl on Heat Transfer and Aerodynamics in an Unshrouded Transonic HP Turbine. J. Turbomach. 2011, 134, 1457–1469. [Google Scholar] [CrossRef]
- Schmid, G.; Schiffer, H.P. Numerical Investigation of Inlet Swirl in a Turbine Cascade. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; ASME Paper No. GT2012-69397. pp. 543–552. [Google Scholar] [CrossRef]
- Khanal, B.; He, L.; Northall, J.; Adami, P. Analysis of Radial Migration of Hot-Streak in Swirling Flow Through HP Turbine Stage. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; ASME Paper No. GT2012-68983. pp. 1287–1299. [Google Scholar] [CrossRef]
- Giller, L.; Schiffer, H.P. Interactions Between the Combustor Swirl and the High Pressure Stator of a Turbine. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; ASME Paper No. GT2012-69157. pp. 1401–1415. [Google Scholar] [CrossRef]
- Hong, Y.; Yanmin, Q.; Jing, R.; Hongde, J. Effect of Inlet Swirl on the Model Leading Edge of Turbine Vane. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. ASME Paper No. GT2013-94471. [Google Scholar]
- Turrell, M.D.; Stopford, P.J.; Syed, K.J.; Buchanan, E. CFD Simulation of the Flow Within and Downstream of a High-Swirl Lean Premixed Gas Turbine Combustor. In Proceedings of the ASME Turbo Expo 2004: Power for Land, Sea, and Air, Vienna, Austria, 14–17 June 2004; ASME Paper No. GT2004-53112. pp. 31–38. [Google Scholar] [CrossRef]
- Insinna, M.; Griffini, D.; Salvadori, S.; Martelli, F. On the Effect of an Aggressive Inlet Swirl Profile on the Aero-thermal Performance of a Cooled Vane. Energy Procedia 2015, 81, 1113–1120. [Google Scholar] [CrossRef][Green Version]
- Jonsson, M.; Ott, P. Heat Transfer Experiments on an Heavily Film Cooled Nozzle Guide Vane. In Proceedings of the 7th European Turbomachinery Conference-ETC7, Athens, Greece, 5–9 March 2007; pp. 1011–1020. [Google Scholar]
- Charbonnier, D.; Ott, P.; Jonsson, M.; Köbke, T.; Cottier, F. Comparison of Numerical Investigations With Measured Heat Transfer Performance of a Film Cooled Turbine Vane. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 43147, pp. 571–582. [Google Scholar] [CrossRef]
- Insinna, M.; Griffini, D.; Salvadori, S.; Martelli, F. Effects of Realistic Inflow Conditions on the Aero-Thermal Performance of a Film-Cooled Vane. In Proceedings of the 11th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Madrid, Spain, 23–27 March 2015; European Turbomachinery Society: Florence, Italy, 2015; pp. 1–13. [Google Scholar]
- Griffini, D.; Insinna, M.; Salvadori, S.; Martelli, F. Clocking Effects of Inlet Nonuniformities in a Fully Cooled High-Pressure Vane: A Conjugate Heat Transfer Analysis. J. Turbomach. 2016, 138, 021006. [Google Scholar] [CrossRef]
- Walters, D.K.; Cokljat, D. A Three-Equation Eddy-Viscosity Model for Reynolds-Averaged Navier–Stokes Simulations of Transitional Flow. J. Fluids Eng. 2008, 130, 121401. [Google Scholar] [CrossRef]
- Salvadori, S.; Ottanelli, L.; Jonsson, M.; Ott, P.; Martelli, F. Investigation of High-Pressure Turbine Endwall Film-Cooling Performance Under Realistic Inlet Conditions. J. Propuls. Power 2012, 28, 799–810. [Google Scholar] [CrossRef]
- Cubeda, S.; Bacci, T.; Mazzei, L.; Salvadori, S.; Facchini, B.; Fiorineschi, L.; Volpe, Y. Design of a Non-Reactive Warm Rig With Real Lean-Premix Combustor Swirlers and Film-Cooled First Stage Nozzles. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, 21–25 September 2020; Volume 84164, p. V07AT11A001. [Google Scholar] [CrossRef]
- Babazzi, G.; Bacci, T.; Picchi, A.; Facchini, B.; Cubeda, S. Film Cooling and Cold Streaks Tracking on a Fully Cooled Nozzle Guide Vane Under Representative Combustor Outflow Conditions. J. Turbomach. 2022, 145, 021005. [Google Scholar] [CrossRef]
- Bacci, T.; Picchi, A.; Babazzi, G.; Facchini, B.; Cubeda, S. Heat Transfer Coefficient and Adiabatic Wall Temperature Measurements on High-Pressure Turbine Nozzle Guide Vanes With Representative Inlet Swirl and Temperature Distortions. J. Turbomach. 2023, 145, 071010. [Google Scholar] [CrossRef]
- Tomasello, S.G.; Andreini, A.; Meloni, R.; Cubeda, S.; Andrei, L.; Michelassi, V. Numerical Study of Combustor–Turbine Interaction by Using Hybrid RANS-LES Approach. In Proceedings of the ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022; Volume 86038, p. V06AT11A005. [Google Scholar] [CrossRef]
- Cubeda, S.; Mazzei, L.; Andreini, A. External heat transfer on nozzle guide vanes under highly swirled combustor outlet flow. In Proceedings of the European Conference on Turbomachinery Fluid Dynamics and Hermodynamics, Lausanne, Switzerland, 8–12 April 2019; European Turbomachinery Society: Florence, Italy, 2019. [Google Scholar] [CrossRef]
- Adams, M.G.; Beard, P.F.; Stokes, M.R.; Wallin, F.; Chana, K.S.; Povey, T. Effect of a Combined Hot-Streak and Swirl Profile on Cooled 1.5-Stage Turbine Aerodynamics: An Experimental and Computational Study. J. Turbomach. 2021, 143, 1–24. [Google Scholar] [CrossRef]
- Hall, B.F.; Chana, K.S.; Povey, T. Design of a Nonreacting Combustor Simulator with Swirl and Temperature Distortion with Experimental Validation. J. Eng. Gas Turbines Power 2014, 136, 081501. [Google Scholar] [CrossRef]
- Hall, B.F.; Povey, T. Experimental Study of Non-Reacting Low NOx Combustor Simulator for Scaled Turbine Experiments. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; Volume 56697, p. V04BT04A040. [Google Scholar] [CrossRef]
- Beard, P.; Adams, M.; Nagawakar, J.; Stokes, M.; Wallin, F.; Cardwell, D.; Povey, T.; Chana, K. The LEMCOTEC 11/2 stage film-cooled HP turbine: Design, integration and testing in the Oxford turbine research facility. In Proceedings of the 13th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Lausanne, Switzerland, 8–12 April 2019. [Google Scholar]
- Radomsky, R.W.; Thole, K.A. Flowfield Measurements for a Highly Turbulent Flow in a Stator Vane Passage. J. Turbomach. 2000, 122, 255–262. [Google Scholar] [CrossRef]
- Cha, C.M.; Ireland, P.T.; Denman, P.A.; Savarianandam, V. Turbulence Levels are High at the Combustor–Turbine Interface. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; ASME Paper No. GT2012-69130. pp. 1371–1390. [Google Scholar] [CrossRef]
- Notaristefano, A.; Persico, G.; Gaetani, P. Turbulence Measurements Downstream of a Combustor Simulator Designed for Studies on the Combustor–Turbine Interaction. Int. J. Turbomach. Propuls. Power 2024, 9, 4. [Google Scholar] [CrossRef]
- Koupper, C.; Caciolli, G.; Gicquel, L.; Duchaine, F.; Bonneau, G.; Tarchi, L.; Facchini, B. Development of an Engine Representative Combustor Simulator Dedicated to Hot Streak Generation. J. Turbomach. 2014, 136, 111007. [Google Scholar] [CrossRef]
- Zarrillo, M. Assessment of an Integrated Numerical Methodology Oriented to the Study of Combustor/Turbine Interaction. Master’s Thesis, Department of Industrial Engineering, University of Florence, Florence, Italy, 2015. [Google Scholar]
- Smith, L.H. Wake Dispersion in Turbomachines. J. Basic Eng. 1966, 88, 688–690. [Google Scholar] [CrossRef]
- Adamczyk, J.J. Wake Mixing in Axial Flow Compressors. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition, Birmingham, UK, 10–13 June 1996; Volume 78729, p. V001T01A002. [Google Scholar] [CrossRef]
- Kemp, N.H.; Sears, W.R. Aerodynamic Interference Between Moving Blade Rows. J. Aeronaut. Sci. 1953, 20, 585–597. [Google Scholar] [CrossRef]
- Letcourt, M. An investigation into unsteady blade forces in turbomachinery. ASME J. Eng. Power 1965, 87, 345–354. [Google Scholar]
- Doorly, D.J.; Oldfield, M.L.G. Simulation of the Effects of Shock Wave Passing on a Turbine Rotor Blade. J. Eng. Gas Turbines Power 1985, 107, 998–1006. [Google Scholar] [CrossRef]
- Hodson, H.P.; Addison, J.S. Wake–Boundary Layer Interactions in an Axial Flow Turbine Rotor at Off-Design Conditions. J. Turbomach. 1989, 111, 181–192. [Google Scholar] [CrossRef]
- Hummel, F. Wake–Wake Interaction and Its Potential for Clocking in a Transonic High-Pressure Turbine. J. Turbomach. 2002, 124, 69–76. [Google Scholar] [CrossRef]
- He, L. Method of simulating unsteady turbomachinery flows with multiple perturbations. AIAA J. 1992, 30, 2730–2735. [Google Scholar] [CrossRef]
- Kurosaka, M.; Gertz, J.B.; Graham, J.E.; Goodman, J.R.; Sundaram, P.; Riner, W.C.; Kuroda, H.; Hankey, W.L. Energy separation in a vortex street. J. Fluid Mech. 1987, 178, 1–29. [Google Scholar] [CrossRef]
- Han, B.; Goldstein, R.; Choi, H. Energy separation in shear layers. Int. J. Heat Mass Transf. 2002, 45, 47–55. [Google Scholar] [CrossRef]
- Miller, R.J.; Moss, R.W.; Ainsworth, R.W.; Horwood, C.K. Time-Resolved Vane-Rotor Interaction in a High-Pressure Turbine Stage. J. Turbomach. 2003, 125, 1–13. [Google Scholar] [CrossRef]
- Schlienger, J.; Kalfas, A.I.; Abhari, R.S. Vortex-Wake-Blade Interaction in a Shrouded Axial Turbine. J. Turbomach. 2005, 127, 699–707. [Google Scholar] [CrossRef]
- Qiu, S.; Simon, T.W. An Experimental Investigation of Transition as Applied to Low Pressure Turbine Suction Surface Flows; American Society of Mechanical Engineers: New York, NY, USA, 1997; Volume 78682. [Google Scholar] [CrossRef]
- Stieger, R.D.; Hollis, D.; Hodson, H.P. Unsteady Surface Pressures Due to Wake-Induced Transition in a Laminar Separation Bubble on a Low-Pressure Cascade. J. Turbomach. 2004, 126, 544–550. [Google Scholar] [CrossRef]
- Hodson, H.P.; Howell, R.J. Bladerow Interactions, Transition, and High-Lift Aerofoils in Low-Pressure Turbines. Annu. Rev. Fluid Mech. 2005, 37, 71–98. [Google Scholar] [CrossRef]
- Suzen, Y.B.; Huang, P.G. Numerical Simulation of Unsteady Wake/Blade Interactions in Low-Pressure Turbine Flows Using an Intermittency Transport Equation. J. Turbomach. 2005, 127, 431–444. [Google Scholar] [CrossRef]
- Sarkar, S.; Voke, P.R. Large-Eddy Simulation of Unsteady Surface Pressure Over a Low-Pressure Turbine Blade due to Interactions of Passing Wakes and Inflexional Boundary Layer. J. Turbomach. 2006, 128, 221–231. [Google Scholar] [CrossRef]
- Mahallati, A.; McAuliffe, B.R.; Sjolander, S.A.; Praisner, T.J. Aerodynamics of a Low-Pressure Turbine Airfoil at Low Reynolds Numbers—Part I: Steady Flow Measurements. J. Turbomach. 2013, 135, 011010. [Google Scholar] [CrossRef]
- Mahallati, A.; Sjolander, S.A. Aerodynamics of a Low-Pressure Turbine Airfoil at Low Reynolds Numbers—Part II: Blade-Wake Interaction. J. Turbomach. 2013, 135, 011011. [Google Scholar] [CrossRef]
- Michelassi, V.; Wissink, J.; Rodi, W. Analysis of DNS and LES of Flow in a Low Pressure Turbine Cascade with Incoming Wakes and Comparison with Experiments. Flow Turbul. Combust. 2002, 69, 295–329. [Google Scholar] [CrossRef]
- Pichler, R.; Zhao, Y.; Sandberg, R.; Michelassi, V.; Pacciani, R.; Marconcini, M.; Arnone, A. Large-Eddy Simulation and RANS Analysis of the End-Wall Flow in a Linear Low-Pressure Turbine Cascade, Part I: Flow and Secondary Vorticity Fields Under Varying Inlet Condition. J. Turbomach. 2019, 141, 121005. [Google Scholar] [CrossRef]
- Marconcini, M.; Pacciani, R.; Arnone, A.; Michelassi, V.; Pichler, R.; Zhao, Y.; Sandberg, R. Large Eddy Simulation and RANS Analysis of the End-Wall Flow in a Linear Low-Pressure-Turbine Cascade—Part II: Loss Generation. J. Turbomach. 2019, 141, 051004. [Google Scholar] [CrossRef]
- Simonassi, L.; Lopes, G.; Gendebien, S.; Torre, A.F.M.; Patinios, M.; Lavagnoli, S.; Zeller, N.; Pintat, L. An Experimental Test Case for Transonic Low-Pressure Turbines—Part I: Rig Design, Instrumentation and Experimental Methodology. In Proceedings of the ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022; Volume 86106, p. V10BT30A012. [Google Scholar] [CrossRef]
- Lopes, G.; Simonassi, L.; Torre, A.F.M.; Patinios, M.; Lavagnoli, S. An Experimental Test Case for Transonic Low-Pressure Turbines—Part 2: Cascade Aerodynamics at On- and Off-Design Reynolds and Mach Numbers. In Proceedings of the ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022; Volume 86106, p. V10BT30A027. [Google Scholar] [CrossRef]
- Dénos, R.; Arts, T.; Paniagua, G.; Michelassi, V.; Martelli, F. Investigation of the Unsteady Rotor Aerodynamics in a Transonic Turbine Stage. J. Turbomach. 2000, 123, 81–89. [Google Scholar] [CrossRef]
- De la Loma, A.; Paniagua, G.; Verrastro, D.; Adami, P. Transonic Turbine Stage Heat Transfer Investigation in Presence of Strong Shocks. J. Turbomach. 2008, 130, 031019. [Google Scholar] [CrossRef]
- Paniagua, G.; Yasa, T.; de la Loma, A.; Castillon, L.; Coton, T. Unsteady Strong Shock Interactions in a Transonic Turbine: Experimental and Numerical Analysis. J. Propuls. Power 2008, 24, 722–731. [Google Scholar] [CrossRef]
- Miller, R.J.; Moss, R.W.; Ainsworth, R.W.; Harvey, N.W. Wake, Shock, and Potential Field Interactions in a 1.5 Stage Turbine—Part I: Vane-Rotor and Rotor-Vane Interaction. J. Turbomach. 2003, 125, 33–39. [Google Scholar] [CrossRef]
- Miller, R.J.; Moss, R.W.; Ainsworth, R.W.; Harvey, N.W. Wake, Shock, and Potential Field Interactions in a 1.5 Stage Turbine—Part II: Vane-Vane Interaction and Discussion of Results. J. Turbomach. 2003, 125, 40–47. [Google Scholar] [CrossRef]
- Li, H.D.; He, L. Blade Count and Clocking Effects on Three-Bladerow Interaction in a Transonic Turbine. J. Turbomach. 2003, 125, 632–640. [Google Scholar] [CrossRef]
- Ottanelli, L. Development and Testing of a Phase Lag Methodology for Unsteady Simulation of Turbine Stages. Master’s Thesis, Department of Industrial Engineering, University of Florence, Florence, Italy, 2013. [Google Scholar]
- Salvadori, S.; Martelli, F.; Adami, P. Development of a Phase Lag Approach for the Numerical Evaluation of Unsteady Flows. In Proceedings of the Tenth International Congress of Fluid Dynamics, Ain Soukhna, Egypt, 16–19 December 2010; pp. 1–10. [Google Scholar]
- Salvadori, S.; Adami, P.; Martelli, F. On the Implementation of a Phase Lag Approach for Multi-Row Simulations. In Proceedings of the 10th International Symposium on Experimental Computational Aerothermodynamics of Internal Flows, Brussels, Belgium, 4–7 July 2011; pp. 1–9. [Google Scholar]
- Saracoglu, B.; Paniagua, G.; Salvadori, S.; Tomasoni, F.; Duni, S.; Yasa, T.; Miranda, A. Trailing edge shock modulation by pulsating coolant ejection. Appl. Therm. Eng. 2012, 48, 1–10. [Google Scholar] [CrossRef]
- Saracoglu, B.H.; Paniagua, G.; Salvadori, S. Energy Analysis of Pulsating Coolant Ejection. In Proceedings of the V ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; Volume 45639, p. V02DT44A016. [Google Scholar] [CrossRef]
- He, L. Computation of unsteady flow through steam turbine blade rows at partial admission. Proc. Inst. Mech. Eng. Part A J. Power Energy 1997, 211, 197–205. [Google Scholar] [CrossRef]
- He, L.; Chen, T.; Wells, R.G.; Li, Y.S.; Ning, W. Analysis of Rotor-Rotor and Stator-Stator Interferences in Multi-Stage Turbomachines. J. Turbomach. 2002, 124, 564–571. [Google Scholar] [CrossRef]
- He, L. Modelling Issues for Computations of Unsteady Turbomachinery Flows. In Lecture Series 1996; Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 1996. [Google Scholar]
- He, L. Time Marching Calculations For Blade Row Interaction and Flutter. In Lecture Series 1996; Von Karman Institute for Fluid Dynamics: Sint-Genesius-Rode, Belgium, 1996. [Google Scholar]
- Hall, K.; Crawley, E. Calculation of unsteady flows in turbomachinery using the linearized Euler equations. AIAA J. 1989, 27, 777–787. [Google Scholar] [CrossRef]
- Sieverding, C.H.; Richard, H.; Desse, J.M. Turbine Blade Trailing Edge Flow Characteristics at High Subsonic Outlet Mach Number. J. Turbomach. 2003, 125, 298–309. [Google Scholar] [CrossRef]
- Day, I.; Greitzer, E.M.; Cumpsty, N. Prediction of compressor performance in rotating stall. J. Eng. Gas Turbines Power 1978, 100, 1–12. [Google Scholar] [CrossRef]
- Stenning, A. Rotating stall and surge. J. Fluids Eng. 1980, 102, 14–20. [Google Scholar] [CrossRef]
- Emmons, H.; Pearson, C.; Grant, H. Compressor surge and stall propagation. Trans. Am. Soc. Mech. Eng. 1955, 77, 455–467. [Google Scholar] [CrossRef]
- He, L. Computational Study of Rotating-Stall Inception in Axial Compressors. J. Propuls. Power 1997, 13, 31–38. [Google Scholar] [CrossRef]
- He, L.; Ismael, J.O. Computations of bladerow stall inception in transonic flows. Aeronaut. J. 1999, 103, 317–324. [Google Scholar] [CrossRef]
- Greitzer, E.M. Surge and rotating stall in axial flow compressors—Part I: Theoretical compression system model. J. Eng. Gas Turbines Power 1976, 98, 190–198. [Google Scholar] [CrossRef]
- Greitzer, E.M. Surge and rotating stall in axial flow compressors—Part II: Experimental results and comparison with theory. J. Eng. Gas Turbines Power 1976, 98, 199–211. [Google Scholar] [CrossRef]
- Ford, C.L.; Carrotte, J.F.; Walker, A.D. The Impact of Compressor Exit Conditions on Fuel Injector Flows. J. Eng. Gas Turbines Power 2012, 134, 111504. [Google Scholar] [CrossRef]
- Walker, A.D.; Carrotte, J.F.; McGuirk, J.J. Enhanced External Aerodynamic Performance of a Generic Combustor Using An Integrated OGV/Prediffuser Design Technique. J. Eng. Gas Turbines Power 2007, 129, 80–87. [Google Scholar] [CrossRef]
- Stevens, S.J.; Harasgama, S.P.; Wray, P. The influence of blade wakes on the performance of combustor shortened prediffusers. J. Aircr. 1984, 21, 641–648. [Google Scholar] [CrossRef]
- Walker, A.D.; Carrotte, J.F.; McGuirk, J.J. The Influence of Dump Gap on External Combustor Aerodynamics at High Fuel Injector Flow Rates. J. Eng. Gas Turbines Power 2009, 131, 031506. [Google Scholar] [CrossRef]
- Walker, A.; Graham, P.L.; Carrotte, J.F.; Spencer, A.; McGuirk, J.J. Experimental Study of the Unsteady Aerodynamics the Compressor-Combustor Interface of a Lean Burn Combustion System. In Proceedings of the 49th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, San Jose, CA, USA, 14–17 July 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar] [CrossRef][Green Version]
- Karki, K.C.; Oechsle, V.L.; Mongia, H.C. A Computational Procedure for Diffuser-Combustor Flow Interaction Analysis. J. Eng. Gas Turbines Power 1992, 114, 1–7. [Google Scholar] [CrossRef]
- Kannan, K.; Page, G. Coupling of Compressible Turbomachinery and Incompressible Combustor Flow Solvers for Aerothermal Applications. In Proceedings of the V ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; Volume 45608, p. V02AT40A004. [Google Scholar] [CrossRef]
- Kannan, K.V.; Page, G.J. Automated Multi-Code URANS Simulation of Compressor-Combustor Components. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; Volume 49699, p. V02AT40A005. [Google Scholar] [CrossRef]
- Collado Morata, E. Impact of the Unsteady Aerothermal Environment on the Turbine Blades Temperature. Ph.D. Thesis, Institut National Polytechnique de Toulouse, Toulouse, France, 2012. [Google Scholar]
- Insinna, M.; Griffini, D.; Salvadori, S.; Martelli, F. Conjugate Heat Transfer Analysis of a Film Cooled High-Pressure Turbine Vane Under Realistic Combustor Exit Flow Conditions. In Proceedings of the V ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. ASME Paper No. GT2014-25280. [Google Scholar] [CrossRef]
- Schlüter, J.; Wu, X.; Kim, S.; Alonso, J.; Pitsch, H. Coupled RANS-LES Computation of a Compressor and Combustor in a Gas Turbine Engine. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2013; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013; p. 3417. [Google Scholar] [CrossRef]
- Schlüter, J.; Wu, X.; Pitsch, H.; Kim, S.; Alonso, J. Integrated Simulations of a Compressor/Combustor Assembly of a Gas Turbine Engine. In Proceedings of the ASME Turbo Expo 2005: Power for Land, Sea, and Air, Reno, NV, USA, 6–9 June 2005; Volume 47306, pp. 971–982. [Google Scholar] [CrossRef]
- Soli, A.; Adoua, R.; Langella, I.; Denman, P.; Garmory, A.; Page, G.J. Effect of Compressor Unsteady Wakes on a Gas Turbine Combustor Flow. J. Eng. Gas Turbines Power 2022, 144, 121018. [Google Scholar] [CrossRef]
- Denman, P.A. Aerodynamic Evaluation of Double Annular Combustion Systems. In Proceedings of the ASME Turbo Expo 2002: Power for Land, Sea, and Air, Amsterdam, The Netherlands, 3–6 June 2002; Volume 36061, pp. 749–757. [Google Scholar] [CrossRef]
- Carusotto, S.; Goel, P.; Baratta, M.; Misul, D.A.; Salvadori, S.; Cardile, F.; Forno, L.; Toppino, M.; Valsania, M. Combustion Characterization in a Diffusive Gas Turbine Burner for Hydrogen-Compliant Applications. Energies 2022, 15, 4117. [Google Scholar] [CrossRef]
- Zeldovich, Y.B. To the Question of Energy Use of Detonation Combustion. J. Propuls. Power 2006, 22, 588–592. [Google Scholar] [CrossRef]
- Sousa, J.; Paniagua, G.; Collado Morata, E. Thermodynamic analysis of a gas turbine engine with a rotating detonation combustor. Appl. Energy 2017, 195, 247–256. [Google Scholar] [CrossRef]
- Ong, J.; Miller, R. Hot Streaks and Vane Coolant Migration in a Downstream Rotor. J. Turbomach. 2012, 134. [Google Scholar] [CrossRef]
- Kilik, E. The Influence of Swirler Design Parameters on the Aerodynamics of Downstream Recirculation Region. Ph.D. Thesis, Cranfield University, Bedford, UK, 1976. [Google Scholar]
- Amend, J.; Lubbock, R.; Ornano, F.; Povey, T. Lean-Burn Combustor Simulator for an Engine-Component Test Facility: An Experimental and Computational Study. J. Turbomach. 2023, 145, 061014. [Google Scholar] [CrossRef]
- Kirollos, B.; Lubbock, R.; Beard, P.; Goenaga, F.; Rawlinson, A.; Janke, E.; Povey, T. ECAT: An Engine Component Aerothermal Facility at the University of Oxford. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; Volume 50787, p. V02AT40A032. [Google Scholar]
- Wilcox, D. Turbulence Modeling for CFD; DCW Industries: La Canada, CA, USA, 1998; Volume 2. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the pressure–Strain correlation of turbulence: An invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Bacci, T.; Caciolli, G.; Facchini, B.; Tarchi, L.; Koupper, C.; Champion, J.L. Flowfield and Temperature Profiles Measurements on a Combustor Simulator Dedicated to Hot Streaks Generation. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; Volume 56734, p. V05CT17A001. [Google Scholar] [CrossRef]
- Bacci, T.; Facchini, B.; Picchi, A.; Tarchi, L.; Koupper, C.; Champion, J.L. Turbulence Field Measurements at the Exit of a Combustor Simulator Dedicated to Hot Streaks Generation. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; Volume 56734, p. V05CT17A002. [Google Scholar] [CrossRef]
- Koupper, C.; Bacci, T.; Facchini, B.; Picchi, A.; Tarchi, L.; Gicquel, L.; Duchaine, F.; Bonneau, G. Experimental and Numerical Calculation of Turbulent Timescales at the Exit of an Engine Representative Combustor Simulator. J. Eng. Gas Turbines Power 2015, 138, 021503. [Google Scholar] [CrossRef]
- Krumme, A.; Buske, C.; Bachner, J.R.; Dähnert, J.; Tegeler, M.; Ferraro, F.; Gövert, S.; Kocian, F.; di Mare, F.; Pahs, A. Investigation of Combustor–Turbine-Interaction in a Rotating Cooled Transonic High-Pressure Turbine Test Rig: Part 1—Experimental Results. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; Volume 58561, p. V02BT42A004. [Google Scholar] [CrossRef]
- Gövert, S.; Ferraro, F.; Krumme, A.; Buske, C.; Tegeler, M.; Kocian, F.; di Mare, F. Investigation of Combustor–Turbine-Interaction in a Rotating Cooled Transonic High-Pressure Turbine Test Rig: Part 2—Numerical Modelling and Simulation. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; Volume 58561, p. V02BT42A005. [Google Scholar] [CrossRef]
- Koupper, C.; Bonneau, G.; Gicquel, L.; Duchaine, F. Large Eddy Simulations of the Combustor Turbine Interface: Study of the Potential and Clocking Effects. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Republic of Korea, 13–17 June 2016; Volume 49798, p. V05BT17A003. [Google Scholar] [CrossRef]
- Andreini, A.; Facchini, B.; Insinna, M.; Mazzei, L.; Salvadori, S. Hybrid RANS-LES Modeling of a Hot Streak Generator Oriented to the Study of Combustor–Turbine Interaction. In Proceedings of the ASME Turbo Expo 2015: Turbine Technical Conference and Exposition, Montreal, QC, Canada, 15–19 June 2015; Volume 56734, p. V05CT17A004. [Google Scholar] [CrossRef]
- Menter, F.R.; Egorov, Y. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 1: Theory and Model Description. Flow Turbul. Combust. 2010, 85, 113–138. [Google Scholar] [CrossRef]
- Andreini, A.; Bacci, T.; Insinna, M.; Mazzei, L.; Salvadori, S. Hybrid RANS-LES Modeling of the Aerothermal Field in an Annular Hot Streak Generator for the Study of Combustor–Turbine Interaction. J. Eng. Gas Turbines Power 2017, 139, 021508. [Google Scholar] [CrossRef]
- Andreini, A.; Da Soghe, R.; Facchini, B.; Mazzei, L.; Colantuoni, S.; Turrini, F. Local Source Based CFD Modeling of Effusion Cooling Holes: Validation and Application to an Actual Combustor Test Case. J. Eng. Gas Turbines Power 2013, 136, 011506. [Google Scholar] [CrossRef]
- Cubeda, S.; Mazzei, L.; Bacci, T.; Andreini, A. Impact of Predicted Combustor Outlet Conditions on the Aerothermal Performance of Film-Cooled High Pressure Turbine Vanes. J. Eng. Gas Turbines Power 2019, 141, 051011. [Google Scholar] [CrossRef]
- Andreini, A.; Bacci, T.; Insinna, M.; Mazzei, L.; Salvadori, S. Modelling strategies for the prediction of hot streak generation in lean burn aeroengine combustors. Aerosp. Sci. Technol. 2018, 79, 266–277. [Google Scholar] [CrossRef]
- Mendez, S.; Nicoud, F. Adiabatic Homogeneous Model for Flow Around a Multiperforated Plate. AIAA J. 2008, 46, 2623–2633. [Google Scholar] [CrossRef]
- Thomas, M.; Dauptain, A.; Duchaine, F.; Gicquel, L.; Koupper, C.; Nicoud, F. Comparison of Heterogeneous and Homogeneous Coolant Injection Models for Large Eddy Simulation of Multiperforated Liners Present in a Combustion Simulator. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; Volume 50794, p. V02BT41A038. [Google Scholar] [CrossRef]
- Thomas, M.; Dombard, J.; Duchaine, F.; Gicquel, L.; Koupper, C. Large Eddy Simulation of Combustor and Complete Single-Stage High-Pressure Turbine of the FACTOR Test Rig. In Proceedings of the ASME Turbo Expo 2019: Turbomachinery Technical Conference and Exposition, Phoenix, AZ, USA, 17–21 June 2019; Volume 58554, p. V02AT45A016. [Google Scholar] [CrossRef]
- Bacci, T.; Picchi, A.; Facchini, B.; Cubeda, S. A New Experimental Approach for Heat Transfer Coefficient and Adiabatic Wall Temperature Measurements on a Nozzle Guide Vane With Inlet Temperature Distortions. J. Turbomach. 2021, 144, 031007. [Google Scholar] [CrossRef]
- Schwab, J.; Stabe, R.; Whitney, W. Analytical and experimental study of flow through an axial turbine stage with a nonuniform inlet radial temperature profile. In Proceedings of the 19th Joint Propulsion Conference, Seattle, WA, USA, 27–29 June 1983; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1983; p. 1175. [Google Scholar] [CrossRef][Green Version]
- Stabe, R.; Whitney, W.; Moffitt, T. Performance of a high-work low aspect ratio turbine tested with a realistic inlet radial temperature profile. In Proceedings of the 20th AIAA Joint Propulsion Conference, Cincinnati, OH, USA, 11–13 June 1984. AIAA-84-1161. [Google Scholar]
- Joslyn, H.D.; Dring, R.P. A Trace Gas Technique to Study Mixing in a Turbine Stage. J. Turbomach. 1988, 110, 38–43. [Google Scholar] [CrossRef]
- Chana, K.; Cardwell, D.; Jones, T. A Review of the Oxford Turbine Research Facility. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013. [Google Scholar] [CrossRef]
- Shang, T.; Guenette, G.; Epstein, A.; Saxer, A. The influence of inlet temperature distortion on rotor heat transfer in a transonic turbine. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10–12 July 1995; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1995; p. 3042. [Google Scholar] [CrossRef]
- Anthony, R.J.; Clark, J.P. A Review of the AFRL Turbine Research Facility. In Proceedings of the ASME Turbo Expo 2013: Turbine Technical Conference and Exposition, San Antonio, TX, USA, 3–7 June 2013; Volume 55164, p. V03CT14A010. [Google Scholar] [CrossRef]
- Dunn, M.; Mathison, R. History of Short-Duration Measurement Programs Related to Gas Turbine Heat Transfer, Aerodynamics, and Aeroperformance at Calspan and The Ohio State University. J. Turbomach. 2014, 136, 041004. [Google Scholar] [CrossRef]
- Adams, M.G.; Povey, T.; Hall, B.F.; Cardwell, D.N.; Chana, K.S.; Beard, P.F. Commissioning of a Combined Hot-Streak and Swirl Profile Generator in a Transonic Turbine Test Facility. J. Eng. Gas Turbines Power 2020, 142, 031008. [Google Scholar] [CrossRef]
- Shankaran, S.; Alonso, J.; Liou, M.; Liu, N.S.; Davis, R. A multi-code-coupling interface for combustor/turbomachinery simulations. In Proceedings of the 39th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 8–11 January 2001. AIAA 01-0974. [Google Scholar]
- Schlüter, J.; Pitsch, H.; Moin, P.; Shankaran, S.; Kim, S.; Alonso, J. Towards Multi-Component Analysis of Gas Turbines by CFD: Integration of RANS and LES Flow Solvers. In Proceedings of the ASME Turbo Expo 2003, Collocated with the 2003 International Joint Power Generation Conference, Atlanta, GA, USA, 16–19 June 2003; ASME Paper No. GT2003-38350. Volume 1, pp. 101–109. [Google Scholar] [CrossRef]
- Schlüter, J.; Wu, X.; Kim, S.; Alonso, J.; Pitsch, H. Integrated RANS-LES Computations of Turbomachinery Components: Generic Compressor/Diffuser; Annual Research Briefs 2003; Center for Turbulence Research: Stanford, CA, USA, 2003; pp. 357–368. [Google Scholar]
- Kim, S.; Alonso, J.; Schlüter, J.; Wu, X.; Pitsch, H. Integrated Simulations for Multi-Component Analysis of Gas Turbines: RANS Boundary Conditions. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. AIAA Paper 2004-3415. [Google Scholar]
- Schlüter, J.; Wu, X.; Weide, E.V.D.; Hahn, S.; Alonso, J.; Pitsch, H. Multi-code simulations: A generalized coupling approach. In Proceedings of the 17th AIAA Computational Fluid Dynamics Conference, June 43rd AIAA Aerospace Sciences Meeting and Exhibit, Toronto, ON, Canada, 6–9 June 2005; AIAA Paper 2005-4997. pp. 1–12. [Google Scholar]
- Schlüter, J.; Apte, S.; Kalitzin, G.; Weide, E.V.D.; Alonso, J.; Pitsch, H. Large-Scale Integrated LES-RANS Simulations of a Gas Turbine Engine; Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2005; pp. 111–120. [Google Scholar]
- Medic, G.; Kalitzin, G.; You, D.; Herrmann, M.; Ham, F.; Weide, E.; Pitsch, H.; Alonso, J. Integrated RANS/LES Computations of Turbulent Flow Through a Turbofan Jet Engine; Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2006; pp. 275–285. [Google Scholar]
- Medic, G.; You, D.; Kalitzin, G. An Approach for Coupling RANS and LES in Integrated Computations of Jet Engines; Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2006; pp. 287–298. [Google Scholar]
- Klapdor, E.V. Simulation of Combustor–Turbine Interaction in a Jet Engine. Ph.D. Thesis, TU Darmstadt, Institut für Energie und Kraftwerkstechnik, Darmstadt, Germany, 2011. [Google Scholar]
- Klapdor, E.V.; di Mare, F.; Kollmann, W.; Janicka, J. A Compressible Pressure-based Solution Algorithm for Gas Turbine Combustion Chambers Using the PDF/FGM Model. Flow Turbul. Combust. 2013, 91, 209–247. [Google Scholar] [CrossRef]
- Piomelli, U. Large-eddy simulation: Achievements and challenges. Prog. Aerosp. Sci. 1999, 35, 335–362. [Google Scholar] [CrossRef]
- Menter, F. Stress-Blended Eddy Simulation (SBES)—A New Paradigm in Hybrid RANS-LES Modeling. In Progress in Hybrid RANS-LES Modelling; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 27–37. [Google Scholar] [CrossRef]
- Spalart, P.R. Detached-Eddy Simulation. Annu. Rev. Fluid Mech. 2009, 41, 181–202. [Google Scholar] [CrossRef]
- Egorov, Y.; Menter, F.R.; Lechner, R.; Cokljat, D. The Scale-Adaptive Simulation Method for Unsteady Turbulent Flow Predictions. Part 2: Application to Complex Flows. Flow Turbul. Combust. 2010, 85, 139–165. [Google Scholar] [CrossRef]
- Givoli, D. Non-reflecting boundary conditions. J. Comput. Phys. 1991, 94, 1–29. [Google Scholar] [CrossRef]
- Martelli, F.; Salvadori, S.; Cappelletti, A.; Insinna, M.; Griffini, D.; Chiaramonti, D.; Prussi, M.; Buffi, M. Turbomachinery and Combustion Research (TCR) group and RE-CORD consortium. ERCOFTAC Bull. 2016, 107, 29–32. [Google Scholar]
- Miki, K.; Wey, T.; Moder, J. Computational Study on Fully Coupled Combustor–Turbine Interactions. J. Propuls. Power 2023, 39, 540–553. [Google Scholar] [CrossRef]
- Burrus, D.; Chahrour, C.A.; Foltz, H.; Sabla, P.E.; Seto, S.; Taylor, J.R. Energy Efficient Engine Combustor Test Hardware Detailed Design Report; Technical Report; NASA: Washington, DC, USA, 1984.
- Timko, L.P. Energy Efficient Engine High Pressure Turbine Component Test Performance Report; Technical Report; NASA: Washington, DC, USA, 1984.
- Duchaine, F.; Dombard, J.; Gicquel, L.; Koupper, C. On the importance of inlet boundary conditions for aerothermal predictions of turbine stages with large eddy simulation. Comput. Fluids 2017, 154, 60–73. [Google Scholar] [CrossRef]
- Thomas, M.; Duchaine, F.; Gicquel, L.; Koupper, C. Advanced Statistical Analysis Estimating the Heat Load Issued by Hot Streaks and Turbulence on a High-Pressure Vane in the Context of Adiabatic Large Eddy Simulations. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; Volume 50794, p. V02BT41A041. [Google Scholar] [CrossRef]
- Tomasello, S.G.; Meloni, R.; Andrei, L.; Andreini, A. Study of Combustor–Turbine Interactions by Performing Coupled and Decoupled Hybrid RANS-LES Simulations under Representative Engine-like Conditions. Energies 2023, 16, 5395. [Google Scholar] [CrossRef]
- Gründler, J.; Schiffer, H.P.; Lehmann, K. An Efficient Unsteady 1-Way Coupling Method of Combustor and Turbine. In Proceedings of the ASME Turbo Expo 2022: Turbomachinery Technical Conference and Exposition, Rotterdam, The Netherlands, 13–17 June 2022; Volume 86120, p. V10DT37A003. [Google Scholar] [CrossRef]
- Hall, K.C.; Thomas, J.P.; Dowell, E.H. Proper Orthogonal Decomposition Technique for Transonic Unsteady Aerodynamic Flows. AIAA J. 2000, 38, 1853–1862. [Google Scholar] [CrossRef]
- Giangiacomo, P.; Michelassi, V.; Martelli, F. Analysis of the mixing plane interface between stator and rotor of a transonic axial turbine stage. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Munich, Germany, 8–11 May 2000; Volume 78545, p. V001T03A107. [Google Scholar]
- Holmes, D.G. Mixing planes revisited: A steady mixing plane approach designed to combine high levels of conservation and robustness. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Berlin, Germany, 9–13 June 2008; Volume 43161, pp. 2649–2658. [Google Scholar]
- Denton, J.D. Some limitations of turbomachinery CFD. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010; Volume 44021, pp. 735–745. [Google Scholar]
- Hanimann, L.; Mangani, L.; Casartelli, E.; Mokulys, T.; Mauri, S. Development of a novel mixing plane interface using a fully implicit averaging for stage analysis. J. Turbomach. 2014, 136, 081010. [Google Scholar] [CrossRef]
- Adamczyk, J.J.; Mulac, R.A.; Celestina, M.L. A Model for Closing the Inviscid Form of the Average-Passage Equation System; American Society of Mechanical Engineers: New York, NY, USA, 1986; Volume 5. [Google Scholar] [CrossRef]
- Busby, J.; Sondak, D.; Staubach, B.; Davis, R. Deterministic Stress Modeling of Hot Gas Segregation in a Turbine. J. Turbomach. 1999, 122, 62–67. [Google Scholar] [CrossRef]
- Hall, K.C.; Thomas, J.P.; Clark, W.S. Computation of unsteady nonlinear flows in cascades using a harmonic balance technique. AIAA J. 2002, 40, 879–886. [Google Scholar] [CrossRef]
- Hall, K.C.; Ekici, K. Multistage Coupling for Unsteady Flows in Turbomachinery. AIAA J. 2005, 43, 624–632. [Google Scholar] [CrossRef]
- Vilmin, S.; Lorrain, E.; Hirsch, C.; Swoboda, M. Unsteady Flow Modeling Across the Rotor/Stator Interface Using the Nonlinear Harmonic Method. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 4241, pp. 1227–1237. [Google Scholar] [CrossRef]
- Dorney, D.J.; Davis, R.L.; Sharma, O.P. Unsteady multistage analysis using a loosely coupled blade row approach. J. Propuls. Power 1996, 12, 274–282. [Google Scholar] [CrossRef]
- Rai, M.M.; Madavan, N.K. Multi-Airfoil Navier–Stokes Simulations of Turbine Rotor–Stator Interaction. J. Turbomach. 1990, 112, 377–384. [Google Scholar] [CrossRef]
- Dawes, W.N. The Simulation of Three-Dimensional Viscous Flow in Turbomachinery Geometries Using a Solution-Adaptive Unstructured Mesh Methodology. J. Turbomach. 1992, 114, 528–537. [Google Scholar] [CrossRef]
- Rai, M.M. Navier–Stokes simulations of rotor/stator interaction using patched and overlaid grids. J. Propuls. Power 1987, 3, 387–396. [Google Scholar] [CrossRef]
- Rai, M.M. Three-dimensional Navier–Stokes simulations of turbine rotor–stator interaction. Part I—Methodology. J. Propuls. Power 1989, 5, 305–311. [Google Scholar] [CrossRef]
- Rai, M.M. Three-Dimensional Navier–Stokes Simulations of Turbine Rotor–Stator Interaction; Part II—Results. J. Propuls. Power 1989, 5, 312–319. [Google Scholar] [CrossRef]
- Arnone, A.; Pacciani, R. Rotor–Stator Interaction Analysis Using the Navier–Stokes Equations and a Multigrid Method. J. Turbomach. 1995, 118, 679–689. [Google Scholar] [CrossRef]
- Salvadori, S.; Riccio, G.; Insinna, M.; Martelli, F. Analysis of Combustor/Vane Interaction With Decoupled and Loosely Coupled Approaches. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; Volume 8, pp. 2641–2652. [Google Scholar] [CrossRef]
- Wang, G.; Duchaine, F.; Papadogiannis, D.; Duran, I.; Moreau, S.; Gicquel, L.Y. An overset grid method for large eddy simulation of turbomachinery stages. J. Comput. Phys. 2014, 274, 333–355. [Google Scholar] [CrossRef]
- Galpin, P.; Broberg, R.; Hutchinson, B. Three-dimensional Navier Stokes predictions of steady state rotor/stator interaction with pitch change. In Proceedings of the 3rd Annual Conference of the CFD Society of Canada, Banff, AB, Canada, 25–27 June 1995; Volume 3, pp. 305–319. [Google Scholar]
- Connell, S.; Hutchinson, B.; Galpin, P.; Campregher, R.; Godin, P. The Efficient Computation of Transient Flow in Turbine Blade Rows Using Transformation Methods. In Proceedings of the ASME Turbo Expo 2012: Turbine Technical Conference and Exposition, Copenhagen, Denmark, 11–15 June 2012; Volume 44748, pp. 2631–2640. [Google Scholar] [CrossRef]
- Giles, M. Calculation of unsteady wake/rotor interaction. J. Propuls. Power 1987, 4, 356–362. [Google Scholar] [CrossRef]
- Giles, M. Stator/rotor interaction in a transonic turbine. J. Propuls. Power 1988, 6, 621–627. [Google Scholar] [CrossRef]
- Giles, M. UNSFLO: A Numerical Method for Unsteady Inviscid Flow in Turbomachinery; Technical Report; Gas Turbine Laboratory: Cambridge, MA, USA, 1988. [Google Scholar]
- Erdos, J.; Alzner, E.; McNally, W. Numerical solution of periodic transonic flow through a fan stage. AIAA J. 1976, 15, 1559–1568. [Google Scholar] [CrossRef]
- Koya, M.; Kotake, S. Numerical Analysis of Fully Three-Dimensional Periodic Flows Through a Turbine Stage. J. Eng. Gas Turbines Power 1985, 107, 945–952. [Google Scholar] [CrossRef]
- He, L. An Euler Solution for Unsteady Flows Around Oscillating Blades. J. Turbomach. 1990, 112, 714–722. [Google Scholar] [CrossRef]
- Li, H.; He, L. Single-Passage Analysis of Unsteady Flows Around Vibrating Blades of a Transonic Fan Under Inlet Distortion. J. Turbomach. 2002, 124, 285–292. [Google Scholar] [CrossRef]
- Giovannini, M.; Marconcini, M.; Arnone, A.; Bertini, F. Evaluation of unsteady computational fluid dynamics models applied to the analysis of a transonic high-pressure turbine stage. Proc. Inst. Mech. Eng. Part A J. Power Energy 2014, 228, 813–824. [Google Scholar] [CrossRef]
- Rubechini, F.; Marconcini, M.; Giovannini, M.; Bellucci, J.; Arnone, A. Accounting for Unsteady Interaction in Transonic Stages. J. Eng. Gas Turbines Power 2015, 137, 052602. [Google Scholar] [CrossRef]
- Issa, R.I.; Sadri, M.A. Numerical Modeling of Unsteady Flow Through a Turbomachine Stage. In Proceedings of the ASME 1998 International Gas Turbine and Aeroengine Congress and Exhibition, Stockholm, Sweden, 2–5 June 1998; Volume 78620, p. V001T01A068. [Google Scholar] [CrossRef]


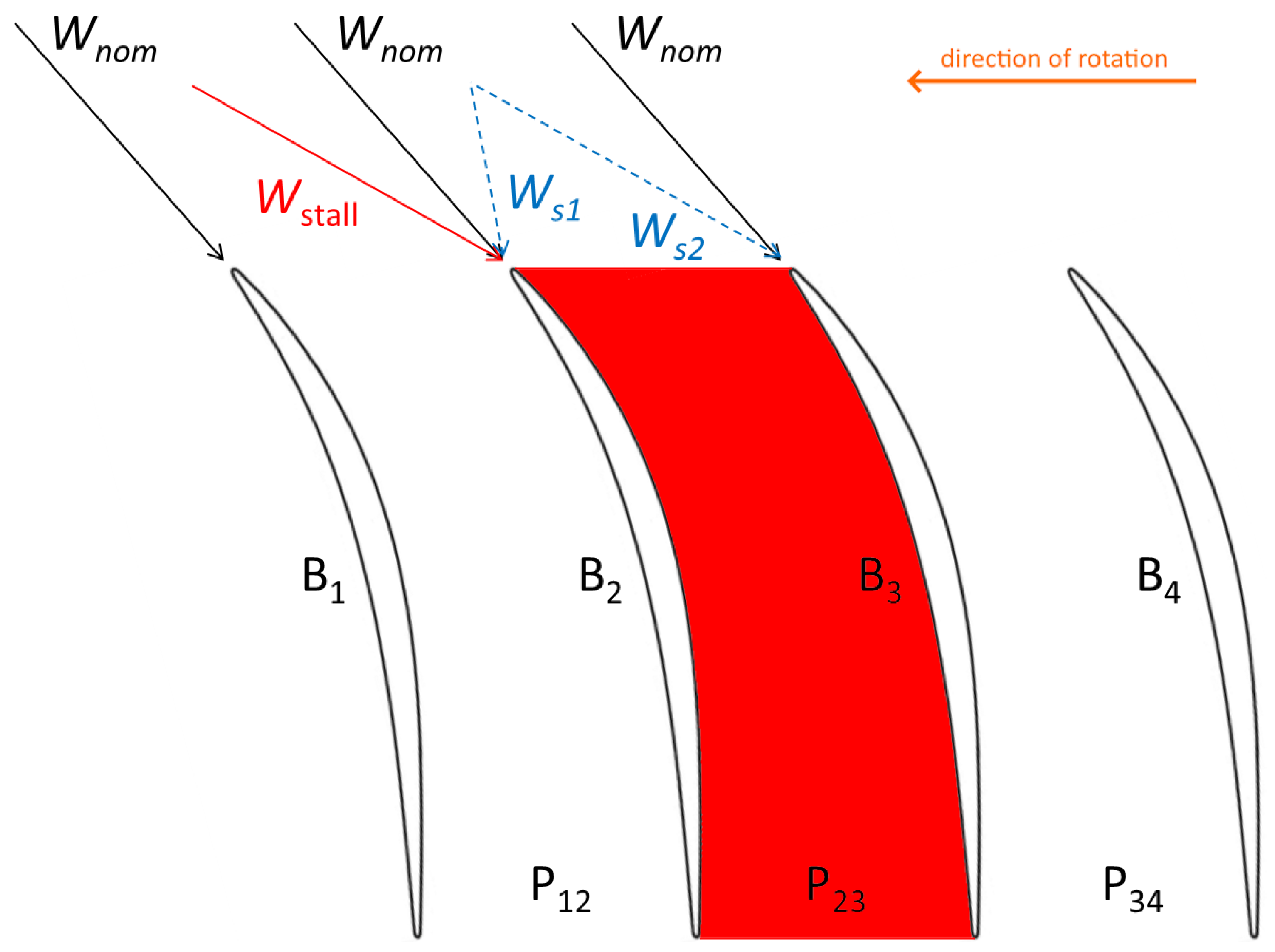
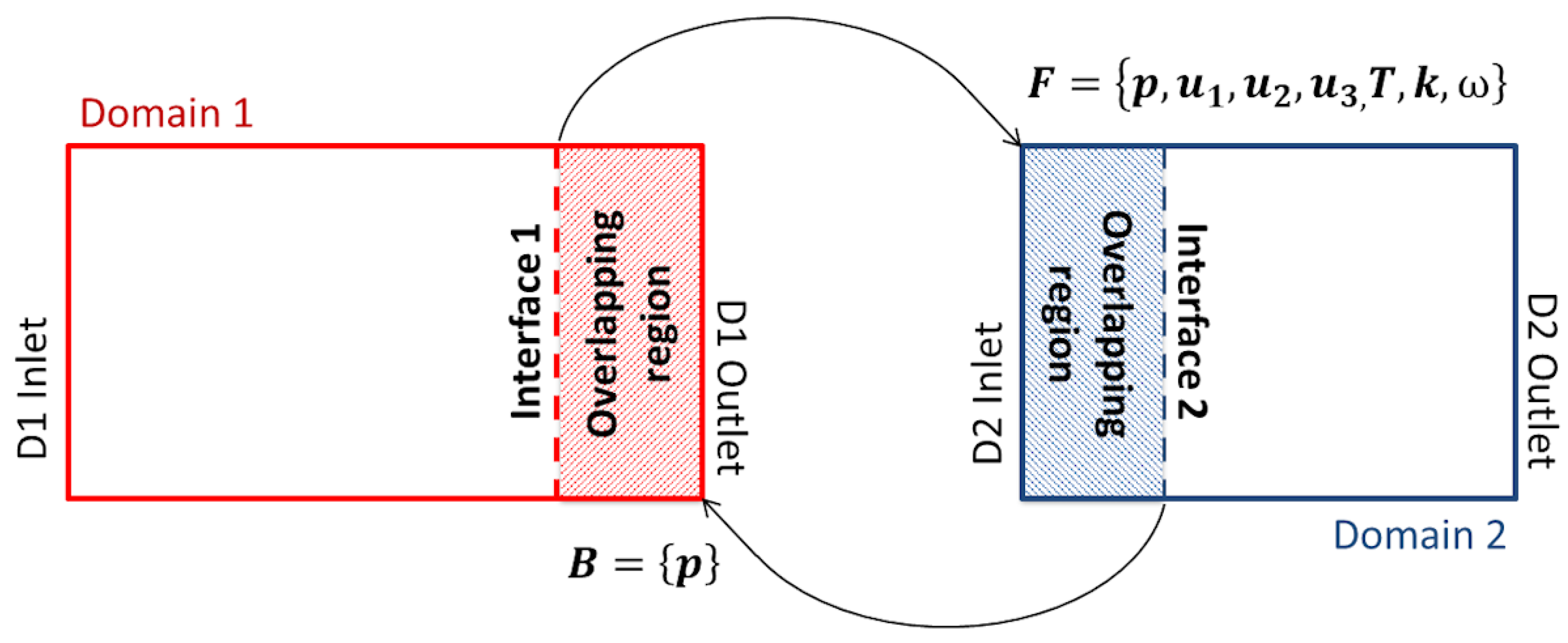
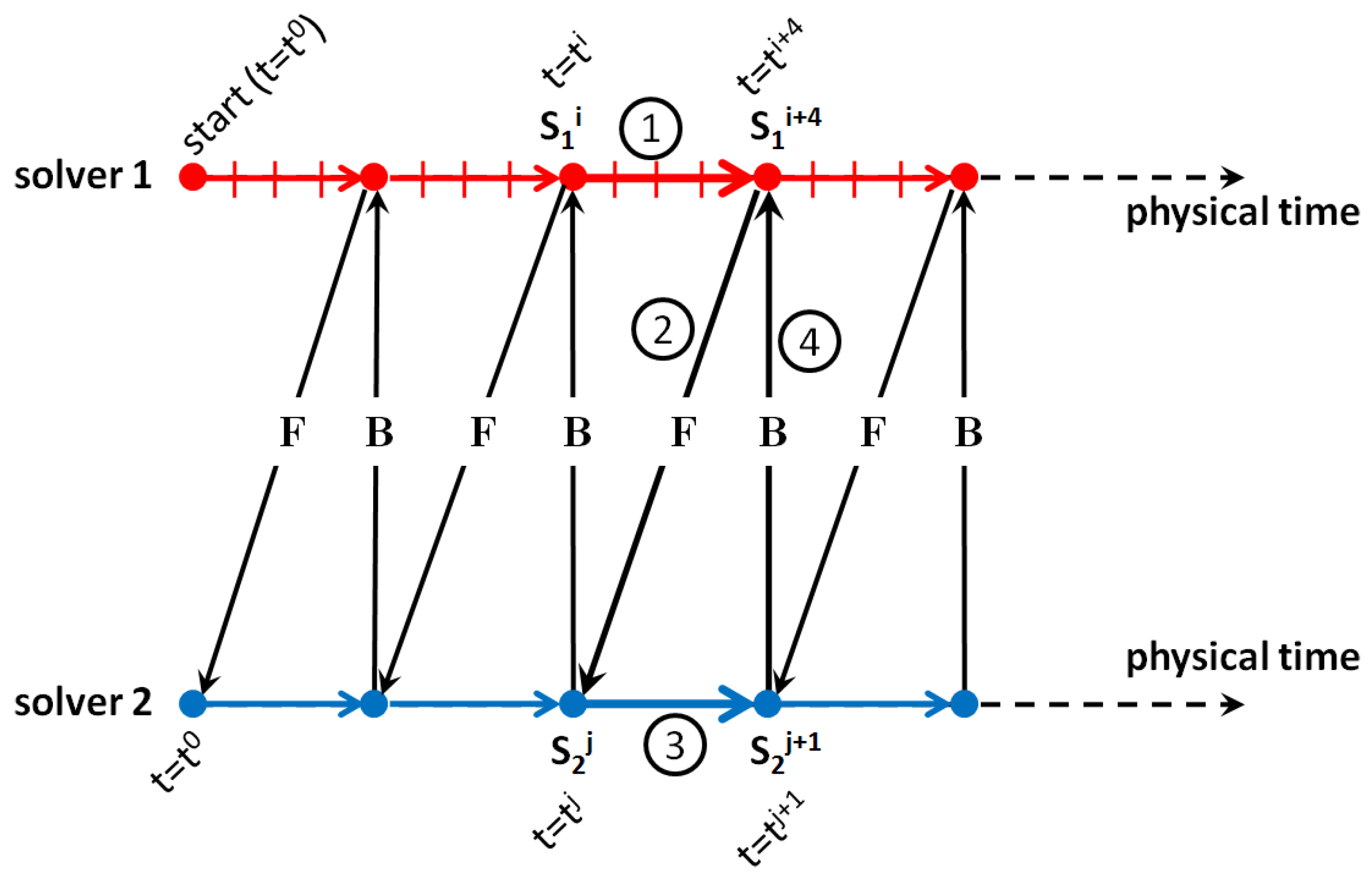
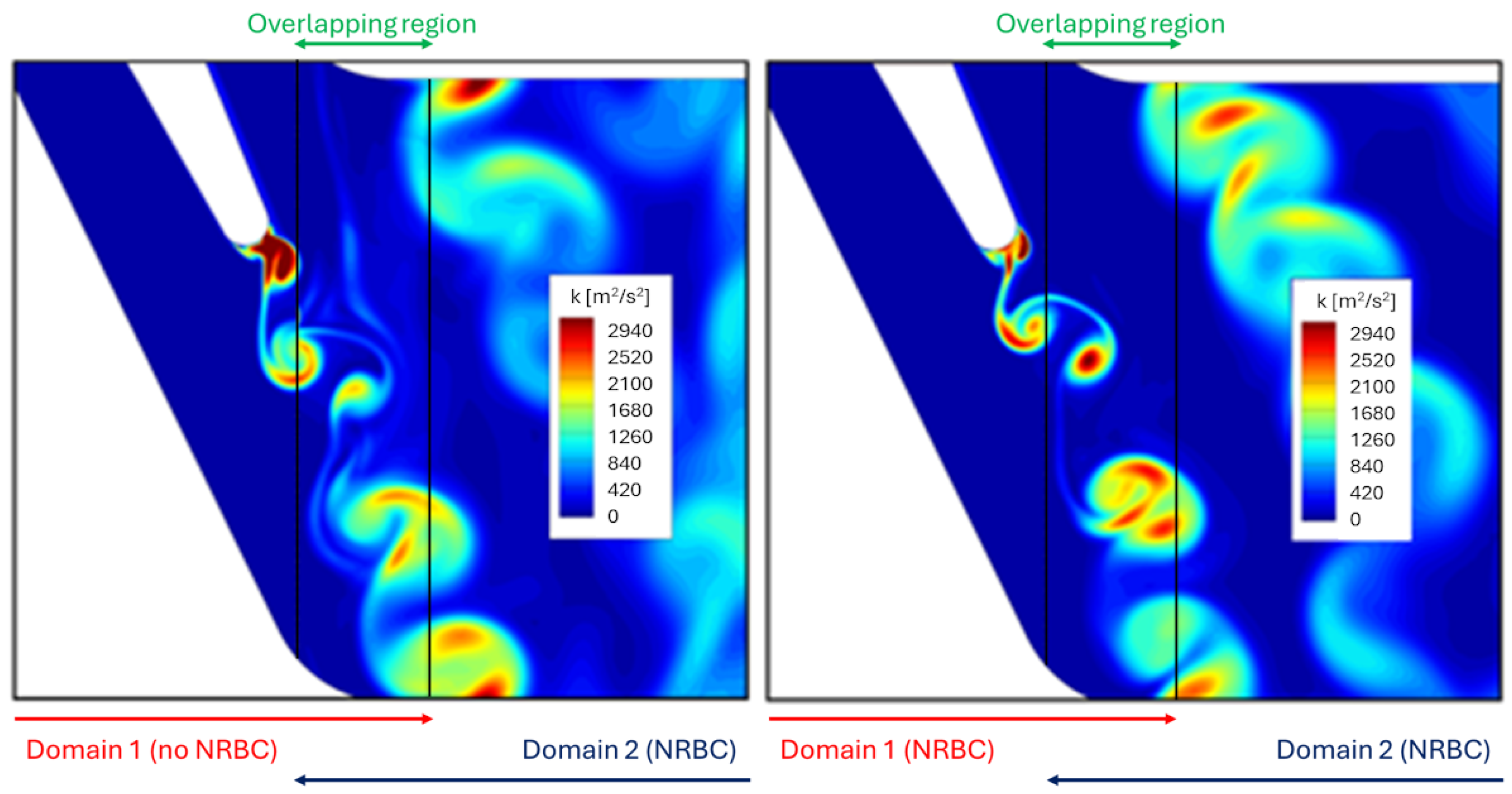



| Class of Phenomena | Interaction (Mainly Deterministic) | Instability (Usually Stochastic) |
|---|---|---|
| Unsteady aerodynamics | Entropy/ decoupling, Wake/Blade interaction, Shock/Blade interaction, Clocking effects | Vortex Shedding, Shock Oscillation, Rotating Stall |
| Aeroelastic effects | Blade Forced Response | Flutter |
| Facility/Project Name | Main References |
|---|---|
| WCTF (Warm Core Turbine Facility) | [181,182] |
| LSRR (Large Scale Rotating Rig) | [183] |
| TATEF (Turbine Aero-Thermal External Flows) & TATEF2 | [34,37,38,184] |
| RTBDF at Gas Turbine Laboratory (MIT, Cambridge, MA, USA) | [185] |
| TRF (Turbine Research Facility) at Air Force Research Laboratory (AFRL) | [53,186] |
| SILOET (Strategic Investment in Low–carbon Engine Technology) | [19] |
| TTF (Turbine Test Facility) | [55,187] |
| LEMCOTEC (Low Emissions Core-Engine Technologies) | [87,188] |
| OTRF (Oxford Turbine Research Facility) | [85,86] |
| FACTOR (Full Aerothermal Combustor–Turbine interactiOns Research) | [91,165,166,167,168] |
| ECAT (Engine Component Aerothermal Facility) | [160,161] |
| STech (Smart Turbine Technologies) | [79] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Salvadori, S.; Insinna, M.; Martelli, F. Unsteady Flows and Component Interaction in Turbomachinery. Int. J. Turbomach. Propuls. Power 2024, 9, 15. https://doi.org/10.3390/ijtpp9020015
Salvadori S, Insinna M, Martelli F. Unsteady Flows and Component Interaction in Turbomachinery. International Journal of Turbomachinery, Propulsion and Power. 2024; 9(2):15. https://doi.org/10.3390/ijtpp9020015
Chicago/Turabian StyleSalvadori, Simone, Massimiliano Insinna, and Francesco Martelli. 2024. "Unsteady Flows and Component Interaction in Turbomachinery" International Journal of Turbomachinery, Propulsion and Power 9, no. 2: 15. https://doi.org/10.3390/ijtpp9020015
APA StyleSalvadori, S., Insinna, M., & Martelli, F. (2024). Unsteady Flows and Component Interaction in Turbomachinery. International Journal of Turbomachinery, Propulsion and Power, 9(2), 15. https://doi.org/10.3390/ijtpp9020015