Enhancing Supervised Model Performance in Credit Risk Classification Using Sampling Strategies and Feature Ranking
Abstract
1. Introduction
2. Related Works
2.1. Literature Review
2.2. Machine Learning Approaches
2.2.1. Logistic Regression (LR)
2.2.2. Random Forest (RF)
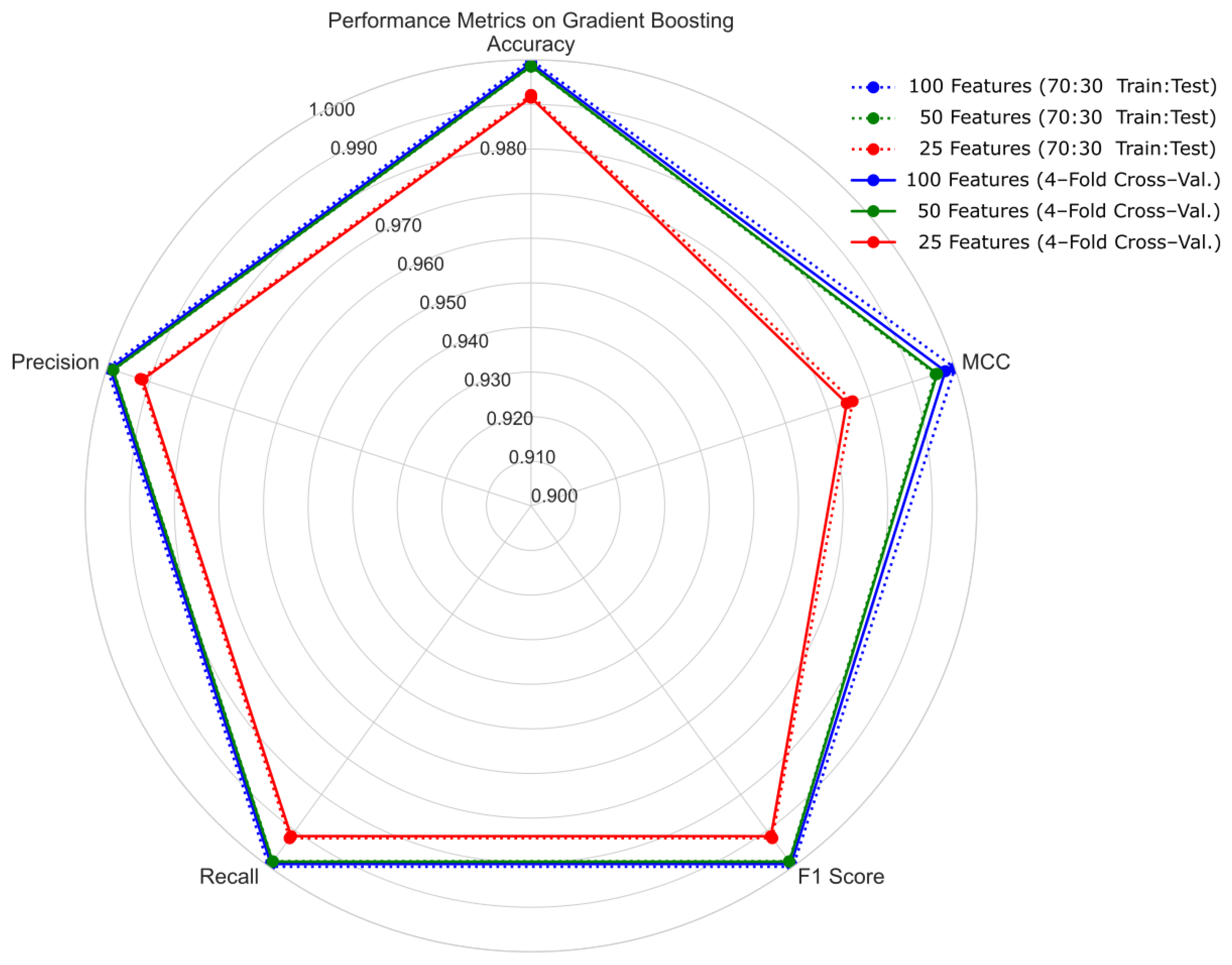
2.2.3. Gradient Boosting (GB)
2.3. Resampling Imbalanced Data
2.3.1. Over-Sampling Approach
- (1)
- Select a minority class data point .
- (2)
- Find its k nearest neighbors (e.g., ).
- (3)
- Randomly select one of the neighbors .
- (4)
- Generate a random number between 0 and 1.
- (5)
- Use the formula to create a synthetic instance .
- (6)
- Repeat steps (1)–(5) for the desired number of synthetic data points.
2.3.2. Under-Sampling Approach
- (1)
- Calculate the sampling ratio: .
- (2)
- For each data point in the majority class:
- (2.1)
- With probability ratio, keep .
- (2.2)
- With probability , discard .
2.3.3. Combined Sampling Approach
- (1)
- Identify data points in the dataset that are misclassified.
- (2)
- For each misclassified data point, check its k nearest neighbors.
- (2.1)
- If the majority of the neighbors have a different class label, remove the misclassified data point.
3. Materials and Methodology
3.1. Data Description and Preprocessing
- (1)
- Drop column “id” because it typically serves as a unique identifier for each row, and including it as a feature could lead the model to incorrectly learn patterns that are specific to certain ids rather than generalizing well to new data.
- (2)
- Drop “url” because it might not provide meaningful information for your model, or its content might be better represented in a different format.
- (3)
- Drop columns “pymnt_plan” and “policy_code” because every record in the “pymnt_plan” column has the value “n” and every record in the “policy_code” column has the value 1. These columns contain constant values, resulting in the model being unable to differentiate between different data inputs.
- (4)
- Drop columns that have missing values exceeding 50%. The selected dataset now comprises 101 columns, including 100 features and the loan status.
- (5)
- In the “int_rate” and “revol_util” columns, convert the percentage values from string format to float.
- (6)
- For categorical data, fill the missing values with the mode and transform them into numerical values.
- (7)
- For real value data, fill the missing values with the mean of the existing values.
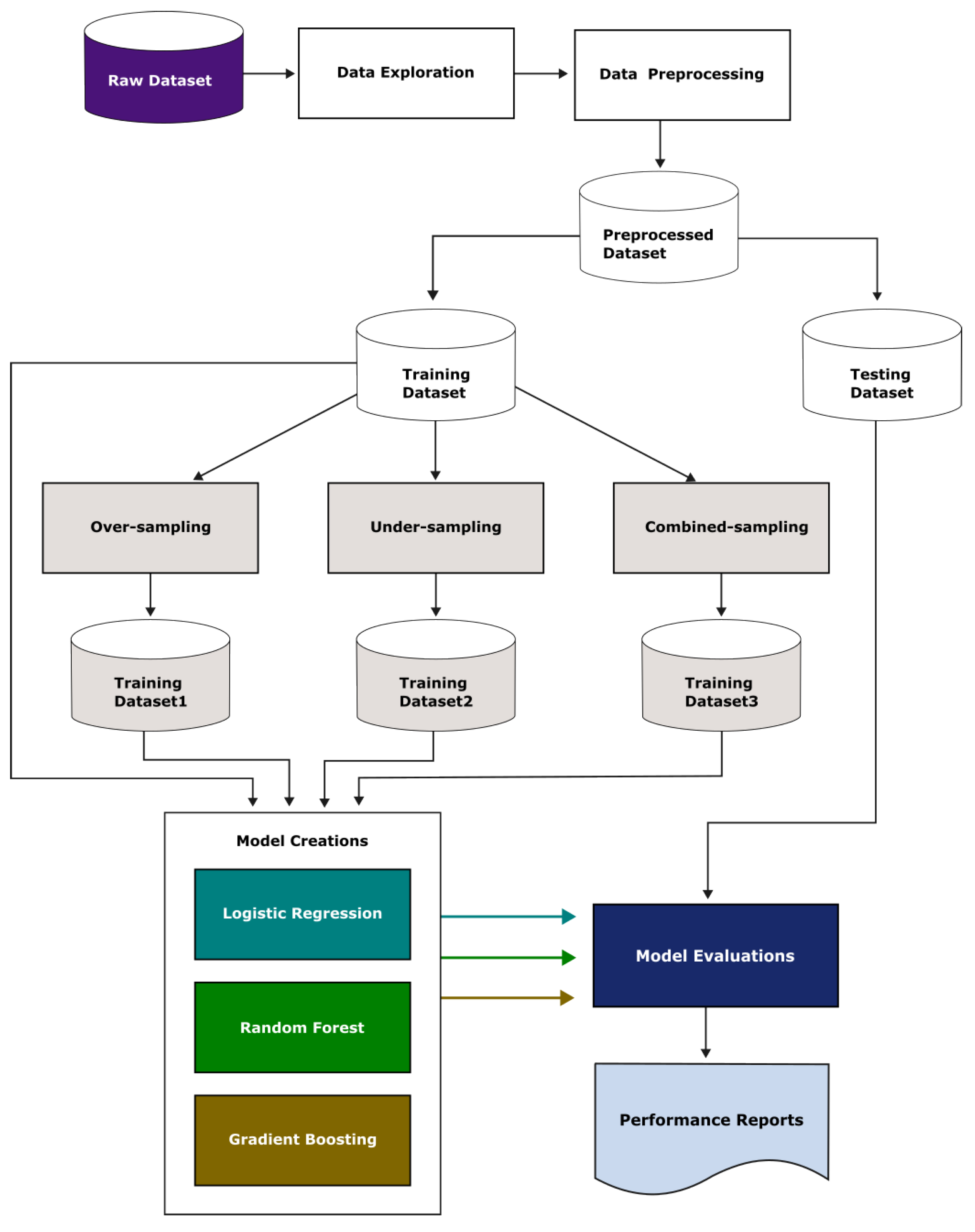
3.2. Model Creations and Evaluations
4. Results and Discussion
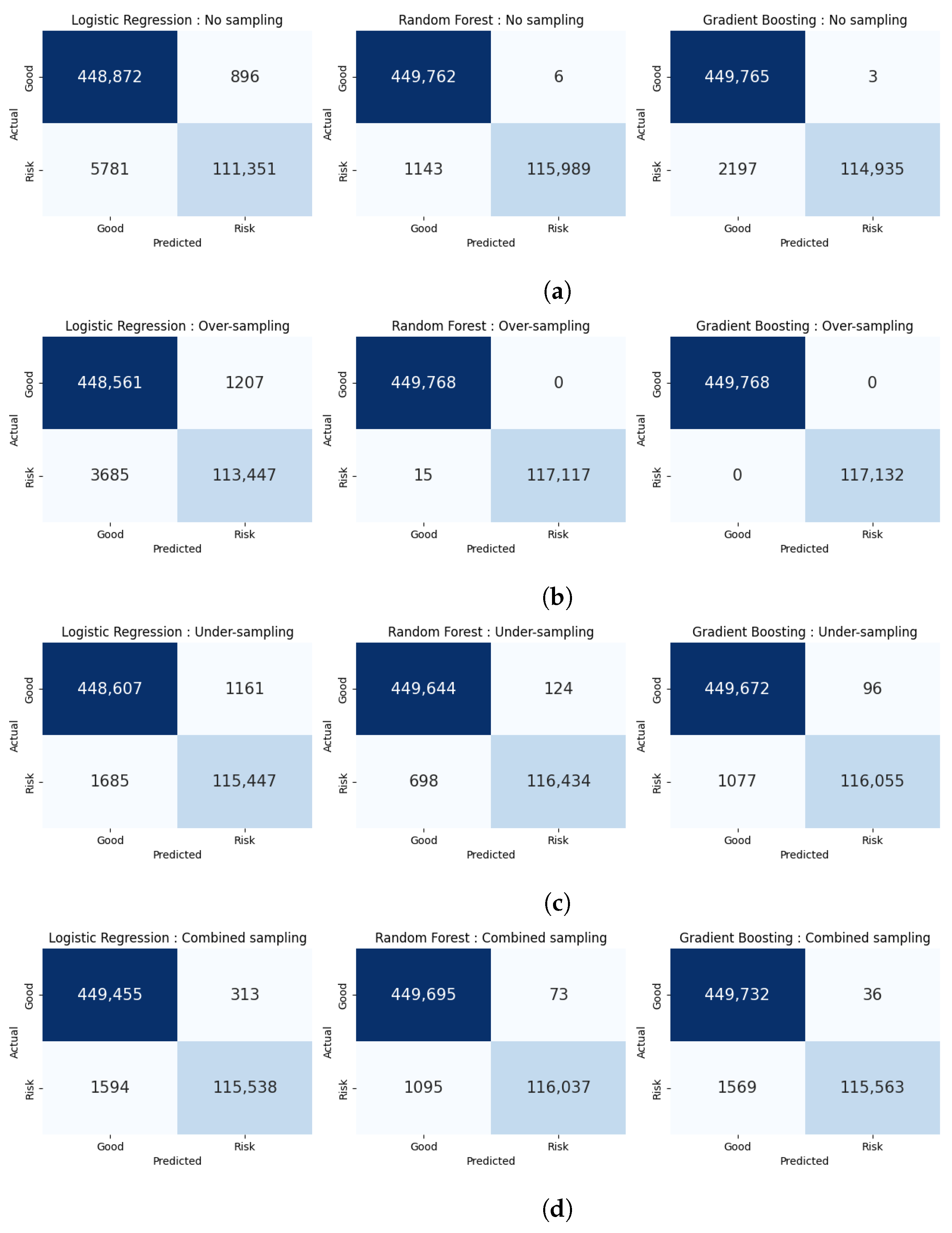
4.1. Hold-Out Cross-Validation with 70:30 Ratio of Training and Testing Sets
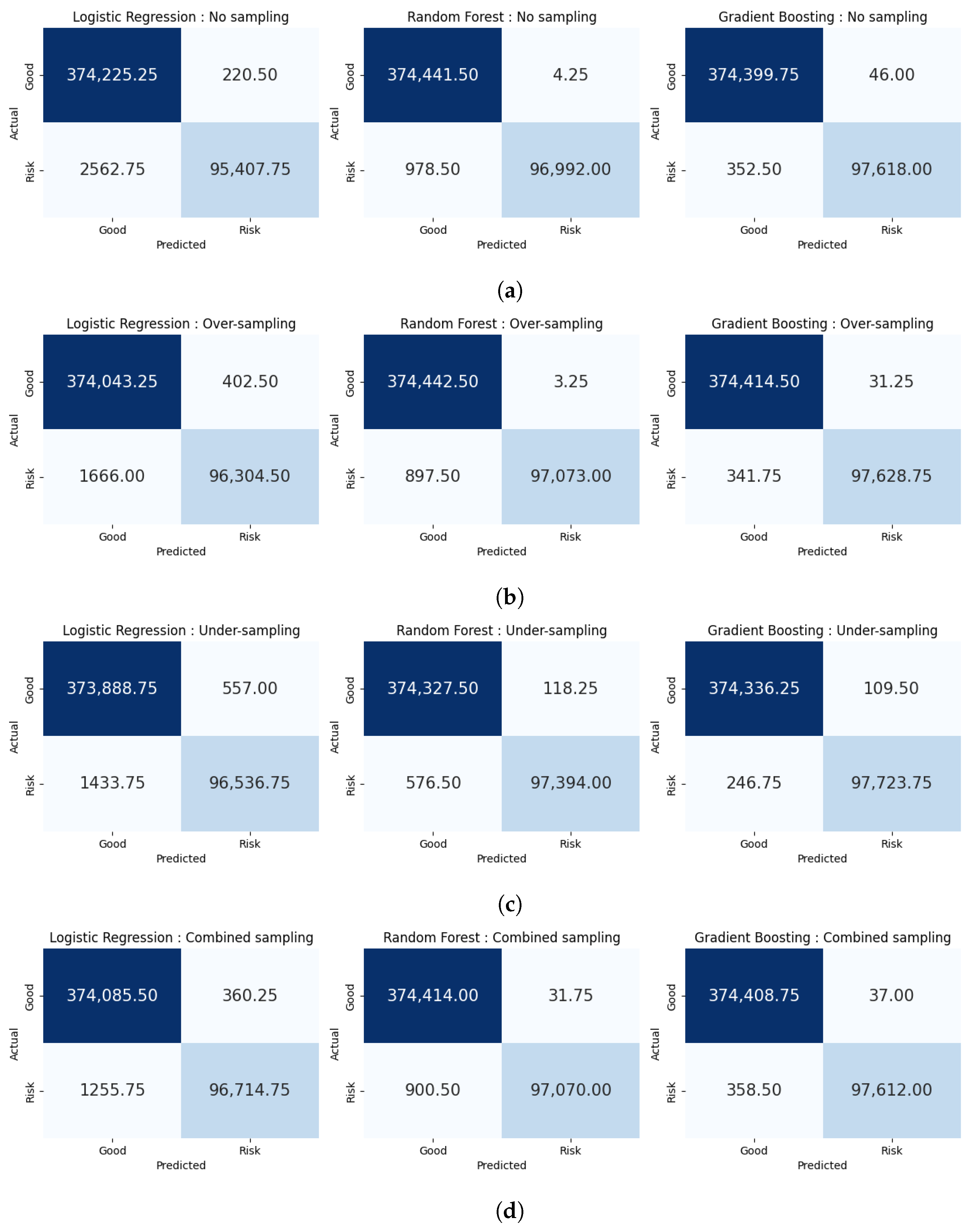
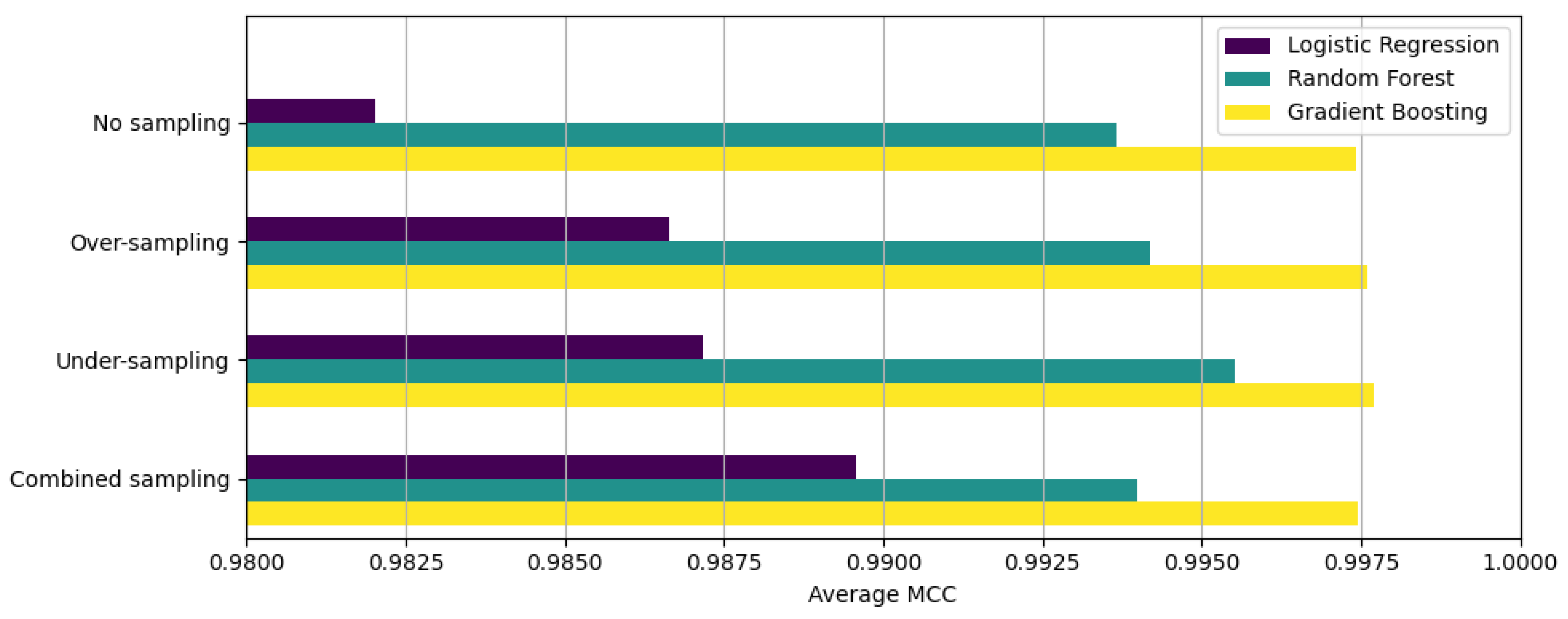
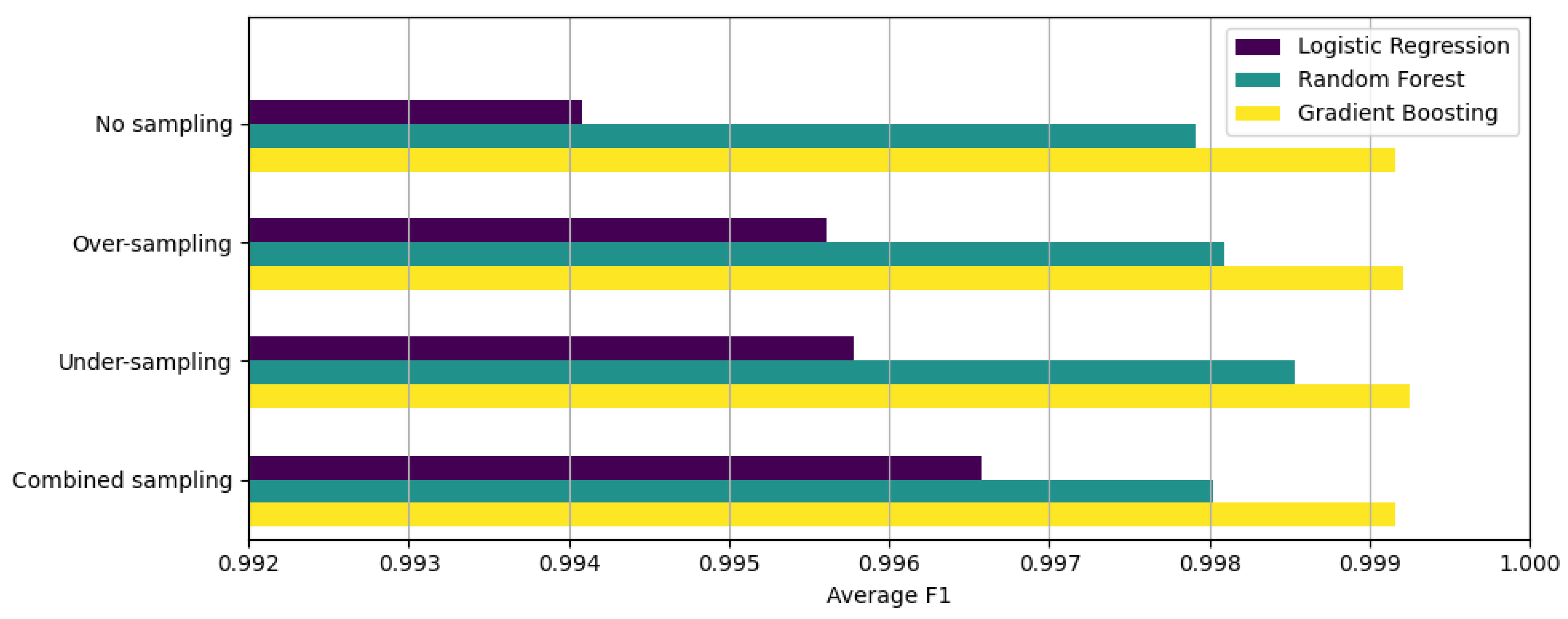
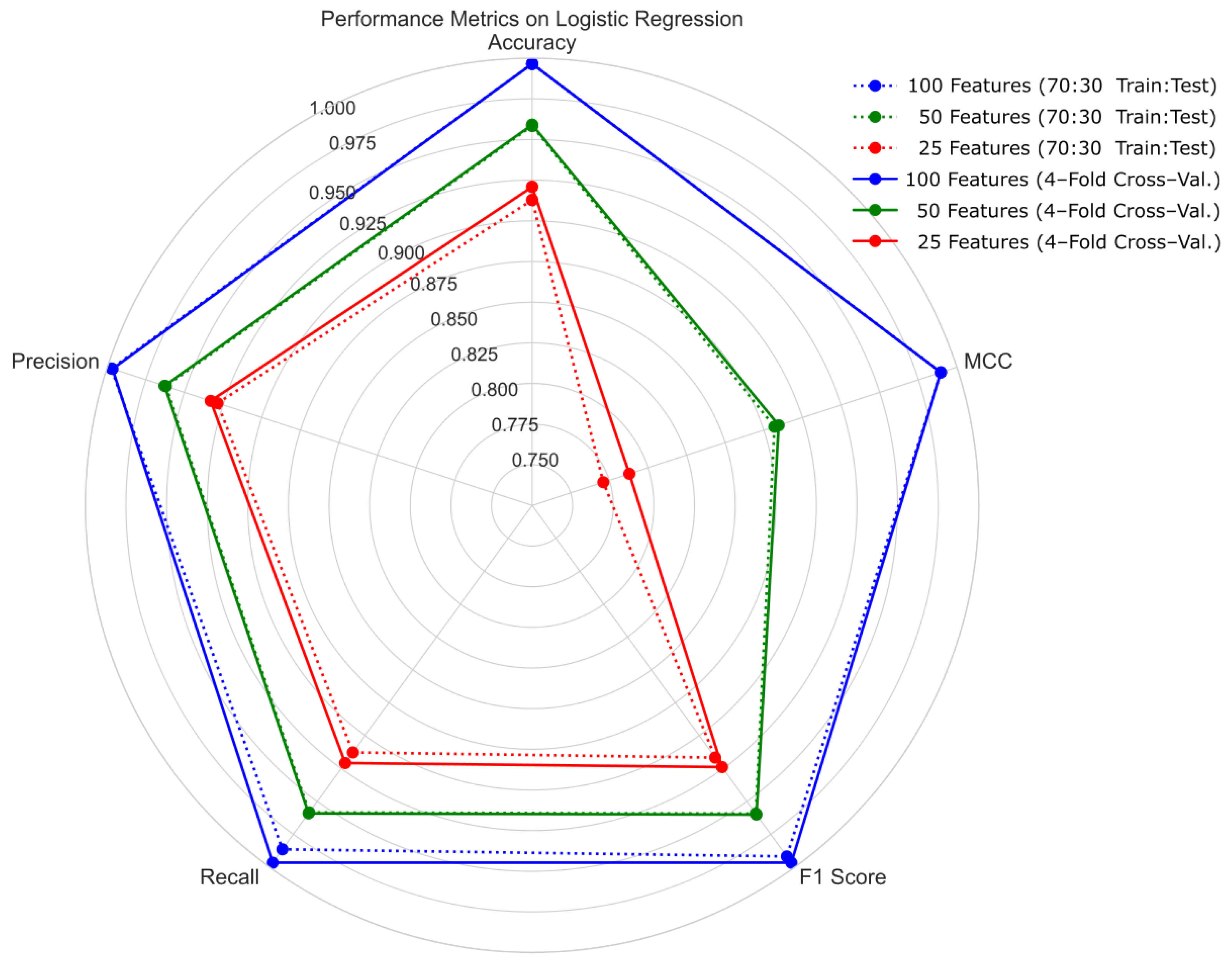
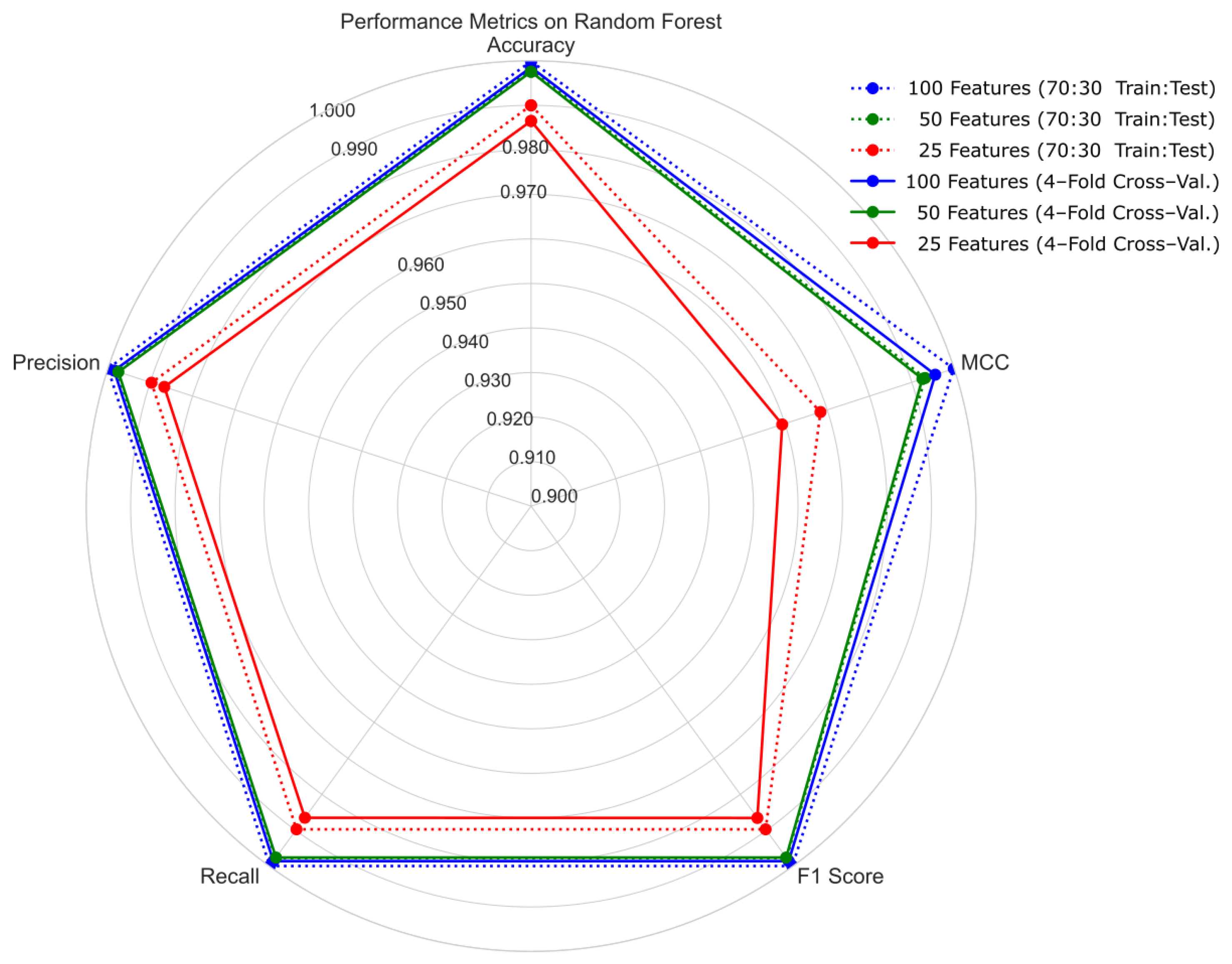
4.2. Four-Fold Cross-Validation
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Noriega, J.P.; Rivera, L.A.; Herrera, J.A. Machine Learning for Credit Risk Prediction: A Systematic Literature Review. Data 2023, 8, 169. [Google Scholar] [CrossRef]
- Gjeçi, A.; Marinč, M.; Rant, V. Non-performing loans and bank lending behaviour. Risk Manag. 2023, 25, 7. [Google Scholar] [CrossRef]
- Liu, H.; Qiao, H.; Wang, S.; Li, Y. Platform Competition in Peer-to-Peer Lending Considering Risk Control Ability. Eur. J. Oper. Res. 2019, 274, 280–290. [Google Scholar] [CrossRef]
- Sulastri, R.; Janssen, M. Challenges in Designing an Inclusive Peer-to-Peer (P2P) Lending System. In Proceedings of the 24th Annual International Conference on Digital Government Research, DGO ‘23, New York, NY, USA, 11–14 July 2023; pp. 55–65. [Google Scholar] [CrossRef]
- Ko, P.C.; Lin, P.C.; Do, H.T.; Huang, Y.F. P2P Lending Default Prediction Based on AI and Statistical Models. Entropy 2022, 24, 801. [Google Scholar] [CrossRef]
- Kurniawan, R. Examination of the Factors Contributing To Financial Technology Adoption in Indonesia using Technology Acceptance Model: Case Study of Peer to Peer Lending Service Platform. In Proceedings of the 2019 International Conference on Information Management and Technology (ICIMTech), Denpasar, Indonesia, 19–20 August 2019; Volume 1, pp. 432–437. [Google Scholar] [CrossRef]
- Wang, Q.; Xiong, X.; Zheng, Z. Platform Characteristics and Online Peer-to-Peer Lending: Evidence from China. Financ. Res. Lett. 2021, 38, 101511. [Google Scholar] [CrossRef]
- Ma, Z.; Hou, W.; Zhang, D. A credit risk assessment model of borrowers in P2P lending based on BP neural network. PLoS ONE 2021, 16, e0255216. [Google Scholar] [CrossRef]
- Moscato, V.; Picariello, A.; Sperlí, G. A benchmark of machine learning approaches for credit score prediction. Expert Syst. Appl. 2021, 165, 113986. [Google Scholar] [CrossRef]
- Liu, W.; Fan, H.; Xia, M. Credit scoring based on tree-enhanced gradient boosting decision trees. Expert Syst. Appl. 2022, 189, 116034. [Google Scholar] [CrossRef]
- Kriebel, J.; Stitz, L. Credit default prediction from user-generated text in peer-to-peer lending using deep learning. Eur. J. Oper. Res. 2022, 302, 309–323. [Google Scholar] [CrossRef]
- Uddin, N.; Uddin Ahamed, M.K.; Uddin, M.A.; Islam, M.M.; Talukder, M.A.; Aryal, S. An ensemble machine learning based bank loan approval predictions system with a smart application. Int. J. Cogn. Comput. Eng. 2023, 4, 327–339. [Google Scholar] [CrossRef]
- Yin, W.; Kirkulak-Uludag, B.; Zhu, D.; Zhou, Z. Stacking ensemble method for personal credit risk assessment in Peer-to-Peer lending. Appl. Soft Comput. 2023, 142, 110302. [Google Scholar] [CrossRef]
- Muslim, M.A.; Nikmah, T.L.; Pertiwi, D.A.A.; Dasril, Y. New model combination meta-learner to improve accuracy prediction P2P lending with stacking ensemble learning. Intell. Syst. Appl. 2023, 18, 200204. [Google Scholar] [CrossRef]
- Niu, K.; Zhang, Z.; Liu, Y.; Li, R. Resampling ensemble model based on data distribution for imbalanced credit risk evaluation in P2P lending. Inf. Sci. 2020, 536, 120–134. [Google Scholar] [CrossRef]
- Li, X.; Ergu, D.; Zhang, D.; Qiu, D.; Cai, Y.; Ma, B. Prediction of loan default based on multi-model fusion. Procedia Comput. Sci. 2022, 199, 757–764. [Google Scholar] [CrossRef]
- He, H.; Bai, Y.; Garcia, E.A.; Li, S. ADASYN: Adaptive synthetic sampling approach for imbalanced learning. In Proceedings of the 2008 IEEE International Joint Conference on Neural Networks (IEEE World Congress on Computational Intelligence), Hong Kong, 1–6 June 2008; pp. 1322–1328. [Google Scholar] [CrossRef]
- Chen, Y.R.; Leu, J.S.; Huang, S.A.; Wang, J.T.; Takada, J.I. Predicting Default Risk on Peer-to-Peer Lending Imbalanced Datasets. IEEE Access 2021, 9, 73103–73109. [Google Scholar] [CrossRef]
- Kumar, V.L.; Natarajan, S.; Keerthana, S.; Chinmayi, K.M.; Lakshmi, N. Credit Risk Analysis in Peer-to-Peer Lending System. In Proceedings of the 2016 IEEE International Conference on Knowledge Engineering and Applications (ICKEA), Singapore, 28–30 September 2016; pp. 193–196. [Google Scholar] [CrossRef]
- Setiawan, N. A Comparison of Prediction Methods for Credit Default on Peer to Peer Lending using Machine Learning. Procedia Comput. Sci. 2019, 157, 38–45. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Z.; Yang, H.; Wang, G.; Xu, Z. An innovative model fusion algorithm to improve the recall rate of peer-to-peer lending default customers. Intell. Syst. Appl. 2023, 20, 200272. [Google Scholar] [CrossRef]
- Ziemba, P.; Becker, J.; Becker, A.; Radomska-Zalas, A.; Pawluk, M.; Wierzba, D. Credit Decision Support Based on Real Set of Cash Loans Using Integrated Machine Learning Algorithms. Electronics 2021, 10, 2099. [Google Scholar] [CrossRef]
- Dong, H.; Liu, R.; Tham, A.W. Accuracy Comparison between Five Machine Learning Algorithms for Financial Risk Evaluation. J. Risk Financ. Manag. 2024, 17, 50. [Google Scholar] [CrossRef]
- Stoltzfus, J.C. Logistic regression: A brief primer. Acad. Emerg. Med. 2011, 18, 1099–1104. [Google Scholar] [CrossRef]
- Manglani, R.; Bokhare, A. Logistic Regression Model for Loan Prediction: A Machine Learning Approach. In Proceedings of the 2021 Emerging Trends in Industry 4.0 (ETI 4.0), Raigarh, India, 19–21 May 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Kadam, E.; Gupta, A.; Jagtap, S.; Dubey, I.; Tawde, G. Loan Approval Prediction System using Logistic Regression and CIBIL Score. In Proceedings of the 2023 4th International Conference on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, 7–9 August 2023; pp. 1317–1321. [Google Scholar] [CrossRef]
- Zhu, X.; Chu, Q.; Song, X.; Hu, P.; Peng, L. Explainable prediction of loan default based on machine learning models. Data Sci. Manag. 2023, 6, 123–133. [Google Scholar] [CrossRef]
- Lin, M.; Chen, J. Research on Credit Big Data Algorithm Based on Logistic Regression. Procedia Comput. Sci. 2023, 228, 511–518. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Zhu, L.; Qiu, D.; Ergu, D.; Ying, C.; Liu, K. A study on predicting loan default based on the random forest algorithm. Procedia Comput. Sci. 2019, 162, 503–513. [Google Scholar] [CrossRef]
- Rao, C.; Liu, M.; Goh, M.; Wen, J. 2-stage modified random forest model for credit risk assessment of P2P network lending to “Three Rurals” borrowers. Appl. Soft Comput. 2020, 95, 106570. [Google Scholar] [CrossRef]
- Reddy, C.S.; Siddiq, A.S.; Jayapandian, N. Machine Learning based Loan Eligibility Prediction using Random Forest Model. In Proceedings of the 2022 7th International Conference on Communication and Electronics Systems (ICCES), Coimbatore, India, 12–14 November 2022; pp. 1073–1079. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Zhou, L.; Fujita, H.; Ding, H.; Ma, R. Credit risk modeling on data with two timestamps in peer-to-peer lending by gradient boosting. Appl. Soft Comput. 2021, 110, 107672. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, J. Risk Prediction of P2P Credit Loans Overdue Based on Gradient Boosting Machine Model. In Proceedings of the 2021 IEEE International Conference on Power, Intelligent Computing and Systems (ICPICS), Shenyang, China, 29–31 July 2021; pp. 212–216. [Google Scholar] [CrossRef]
- Miaojun Bai, Y.Z.; Shen, Y. Gradient boosting survival tree with applications in credit scoring. J. Oper. Res. Soc. 2022, 73, 39–55. [Google Scholar] [CrossRef]
- Qian, H.; Wang, B.; Yuan, M.; Gao, S.; Song, Y. Financial distress prediction using a corrected feature selection measure and gradient boosted decision tree. Expert Syst. Appl. 2022, 190, 116202. [Google Scholar] [CrossRef]
- Chawla, N.V.; Bowyer, K.W.; Hall, L.O.; Kegelmeyer, W.P. SMOTE: Synthetic Minority over-Sampling Technique. J. Artif. Int. Res. 2002, 16, 321–357. [Google Scholar] [CrossRef]
- Bach, M.; Werner, A.; Palt, M. The Proposal of Undersampling Method for Learning from Imbalanced Datasets. Procedia Comput. Sci. 2019, 159, 125–134. [Google Scholar] [CrossRef]
- Batista, G.E.A.P.A.; Prati, R.C.; Monard, M.C. A Study of the Behavior of Several Methods for Balancing Machine Learning Training Data. SIGKDD Explor. Newsl. 2004, 6, 20–29. [Google Scholar] [CrossRef]
- Ethon0426. Lending Club 2007–2020Q3. Available online: https://www.kaggle.com/datasets/ethon0426/lending-club-20072020q1 (accessed on 17 January 2024).
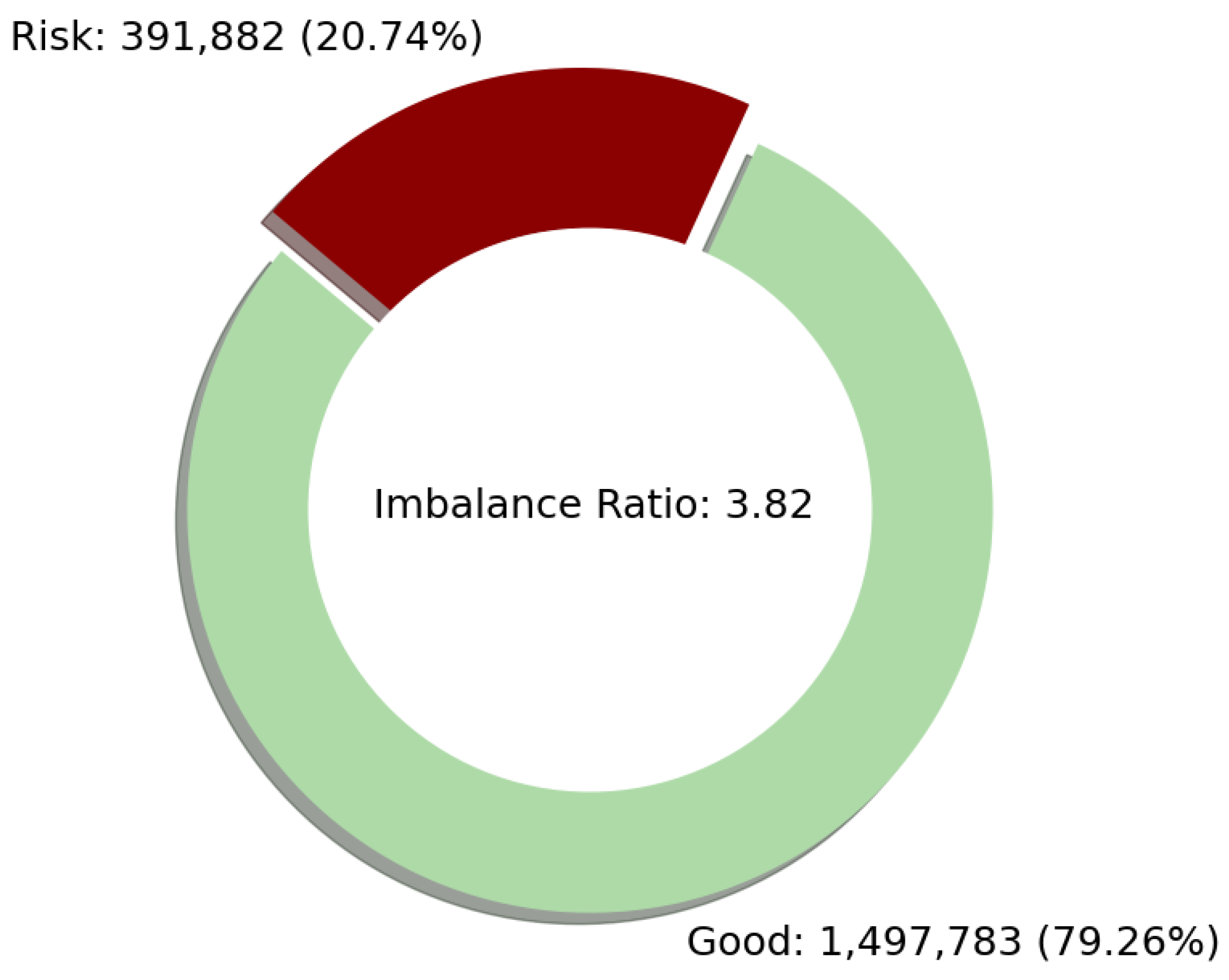
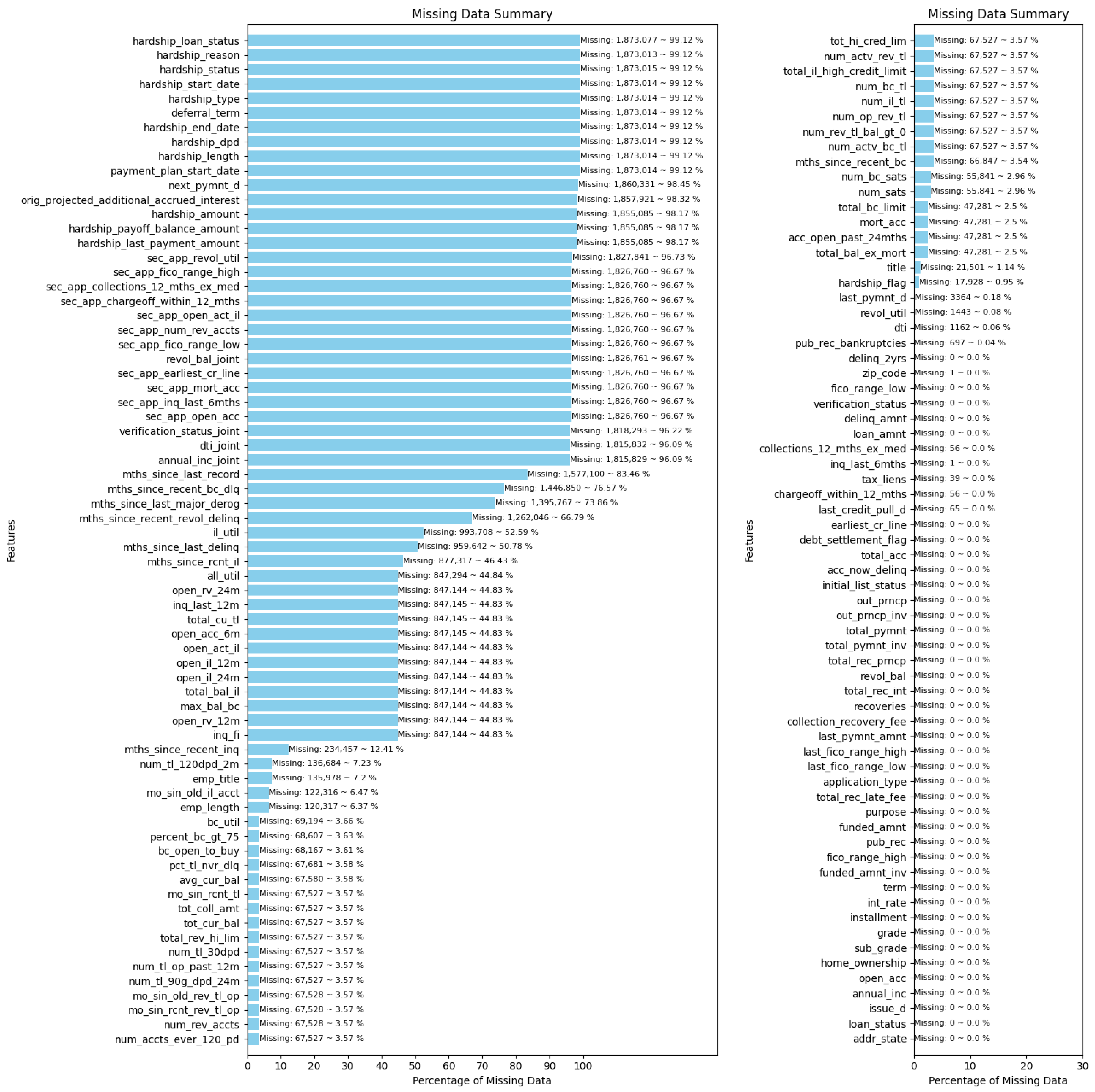
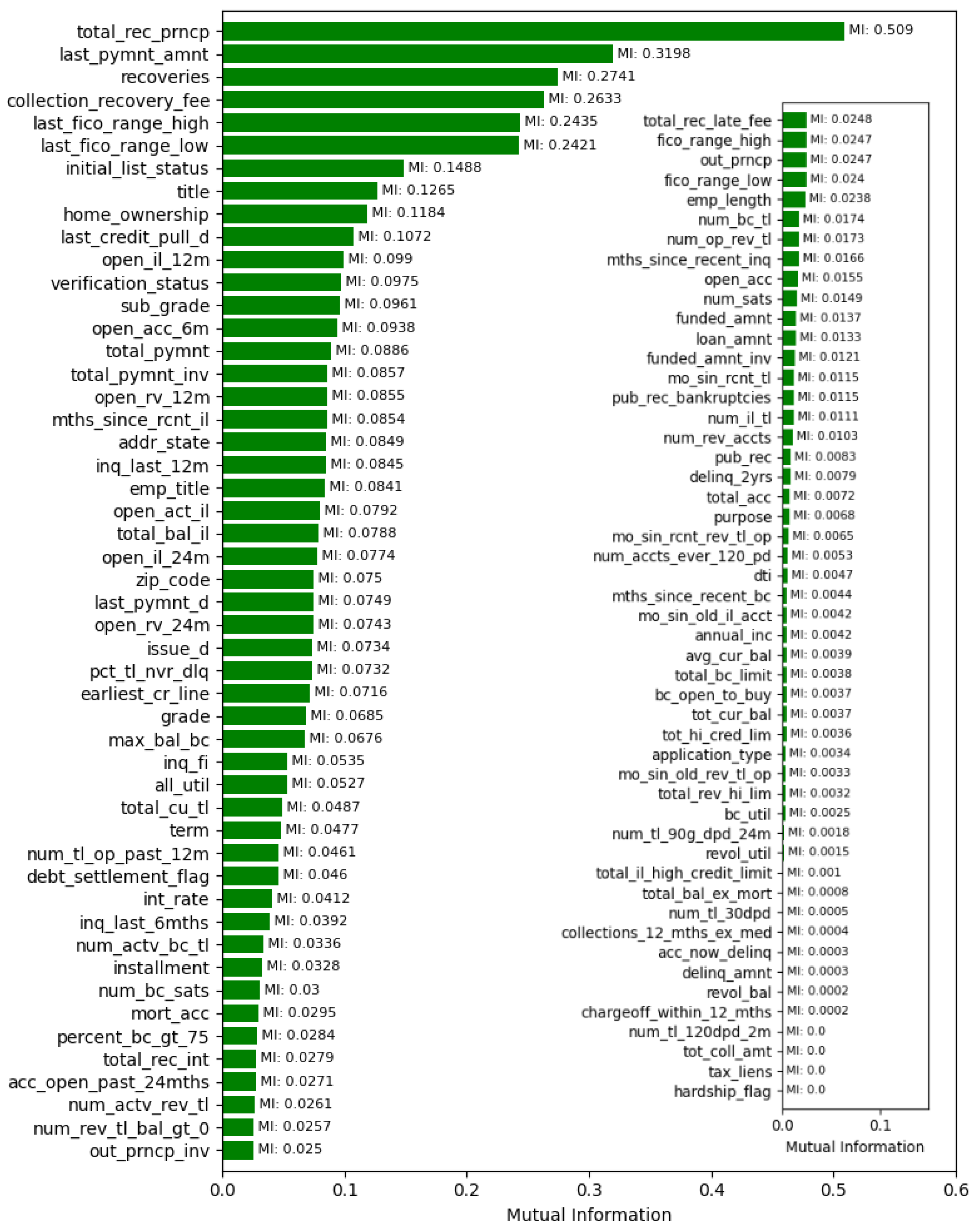
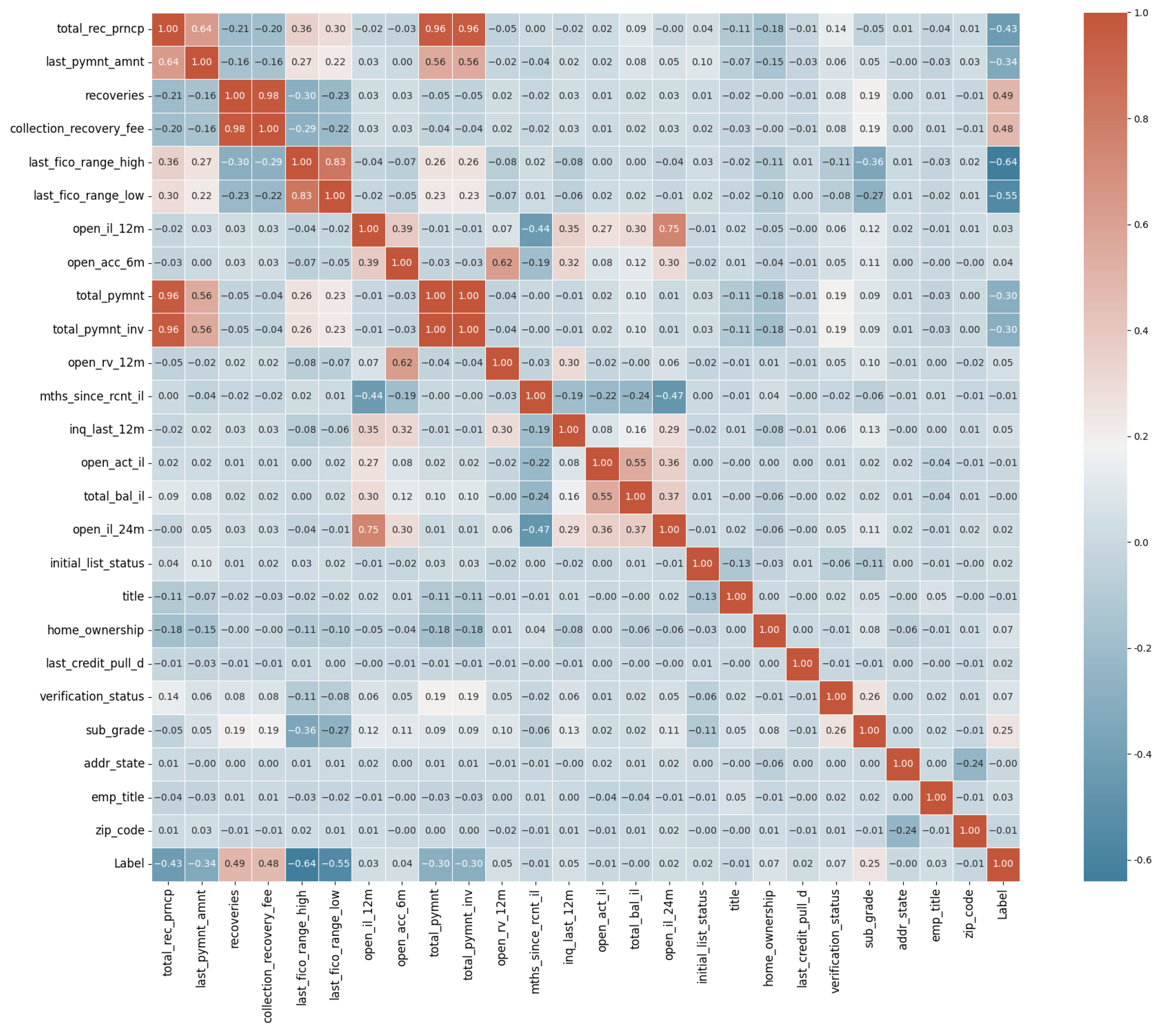

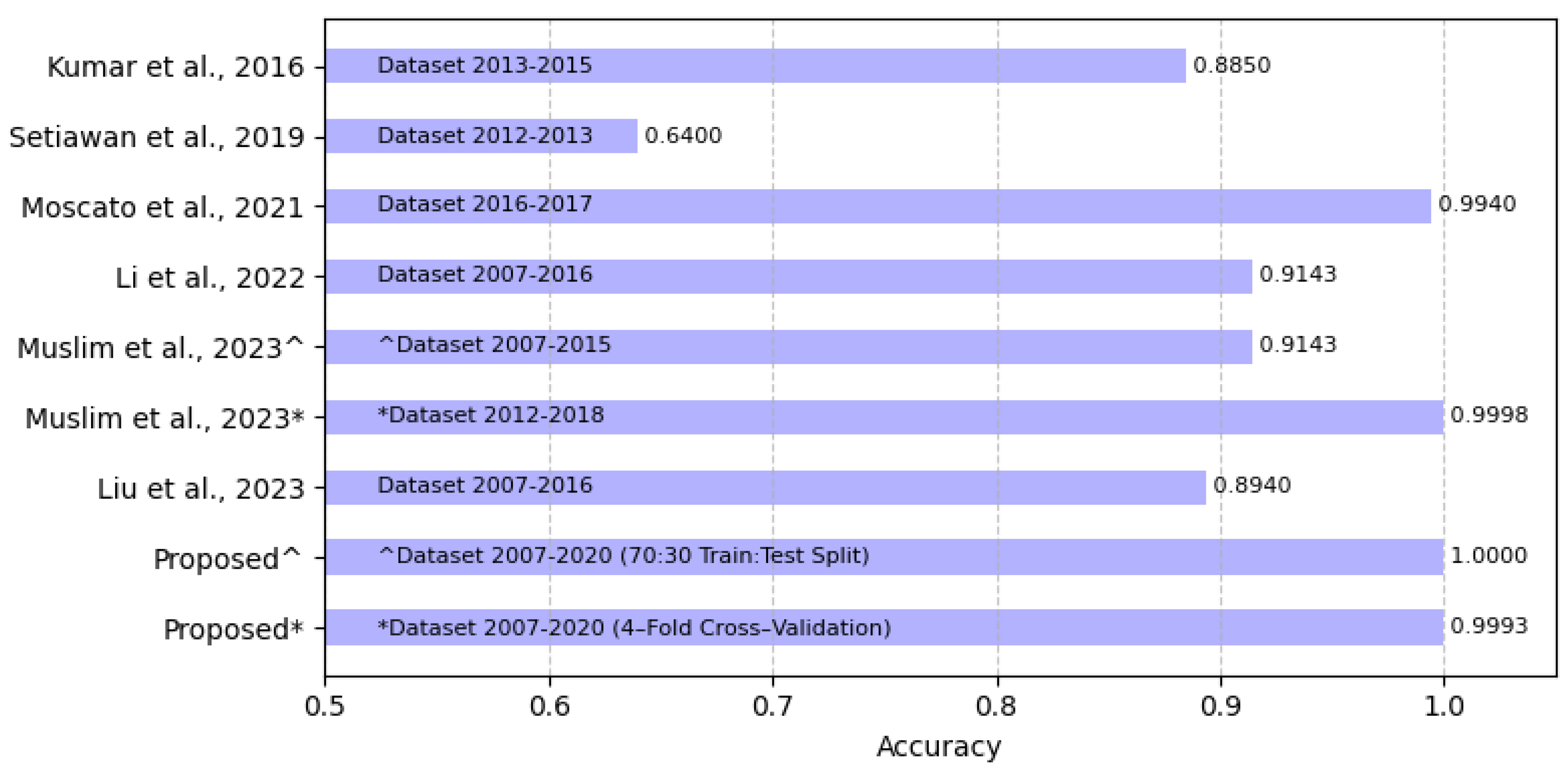
| Research | LendingClub Data | Imbalance Solving | ML | Best Performance |
|---|---|---|---|---|
| [19] | Year: 2013–2015 | - | Random forest | : 0.885 |
| Samples: 656,724 | Decision tree | |||
| Features: 115 | Bagging | |||
| Classes: 2 ({good}; {bad}) | ||||
| [20] | Year: 2012–2013 | - | BPSOSVM + | : 0.64 |
| Samples: 164,620 | Extremely randomized tree | : 062 | ||
| Features: 34 | : 0.65 | |||
| Classes: 2 ({Charged Off, | : 0.61 | |||
| Late (31–120 days), | ||||
| Default}; {Fully Paid}) | ||||
| [9] | Year: 2016–2017 | Under-sampling | Logistic regression | : 0.64 |
| Samples: 877,956 | Over-sampling | Random forest | : 0.71 | |
| Features: 151 | Hybrid | MLP | : 0.66 | |
| Classes: 2 ({Fully Paid}; | : 0.64 | |||
| {Charged Off}) | ||||
| [16] | Year: 2019 | ADASYN | Fusion model | : 0.994 |
| Samples: 128,262 | (logistic regression, | : 0.99 | ||
| Features: 150 | random forest, | : 0.99 | ||
| Classes: no details | and CatBoost) | |||
| [14] | Year: 2007–2015 | SMOTE | LGBFS | : 0.9143 |
| Samples: 9578 | + StackingXGBoos | : 0.9151 | ||
| Features: 14 | : 0.9165 | |||
| Classes: 2 ({not.fully.paid}; | ||||
| {fully.paid}) | ||||
| [14] | Year: 2012–2018 | SMOTE | LGBFS | : 0.99982 |
| Samples: 2,875,146 | + StackingXGBoos | : 0.9999 | ||
| Features: 18 | : 0.9999 | |||
| Classes: 2 | ||||
| loan_status | ||||
| [21] | Year: 2007–2016 | SMOTE | LGB-XGB-Stacking | : 0.8940 |
| Samples: 396, 030 | : 0.7131 | |||
| Features: 27 | : 0.7975 | |||
| Classes: 2 ({Fully Paid}; | ||||
| {Charged Off}) |
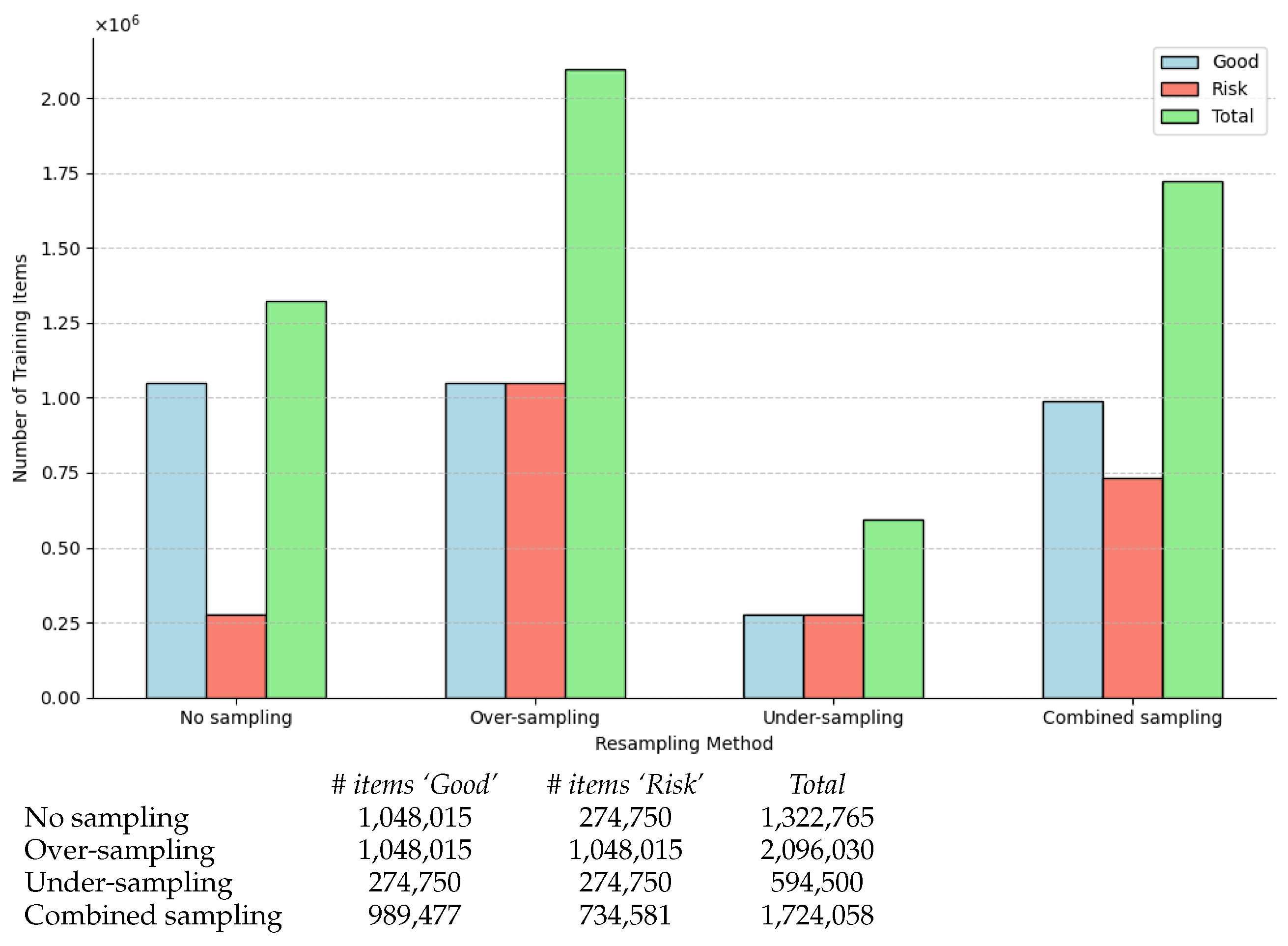
| Loan Status | Count | Label |
|---|---|---|
| “Fully Paid” | 1,497,783 | “Good” |
| “Charged Off” | 362,548 | “Risk” |
| “In Grace Period” | 10,028 | “Risk” |
| “Late (16–30 days)” | 2719 | “Risk” |
| “Late (31–120 days)” | 16,154 | “Risk” |
| “Default” | 433 | “Risk” |
| “Current” | 1,031,016 | - |
| “Issued” | 2062 | - |
| “Does not meet the credit policy. Status: Fully Paid” | 1988 | - |
| “Does not meet the credit policy. Status: Charged Off” | 761 | - |
| Total | 2,925,493 |
| Imbalanced Data Handling Technique | Model | Accuracy | Precision | Recall | F1 Score | MCC |
|---|---|---|---|---|---|---|
| No sampling (original data) | Logistic regression | 0.9882 | 0.9920 | 0.9506 | 0.9709 | 0.9639 |
| Random forest | 0.9979 | 0.9999 | 0.9902 | 0.9951 | 0.9938 | |
| Gradient boosting | 0.9961 | 0.9999 | 0.9812 | 0.9905 | 0.9882 | |
| Over-sampling | Logistic regression | 0.9914 | 0.9895 | 0.9685 | 0.9789 | 0.9736 |
| Random forest | 0.9999 | 1.0000 | 0.9999 | 0.9999 | 0.9999 | |
| Gradient boosting | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | |
| Under-sampling | Logistic regression | 0.9950 | 0.9900 | 0.9856 | 0.9878 | 0.9847 |
| Random forest | 0.9986 | 0.9989 | 0.9940 | 0.9965 | 0.9956 | |
| Gradient boosting | 0.9979 | 0.9992 | 0.9908 | 0.9950 | 0.9937 | |
| Combined sampling | Logistic regression | 0.9966 | 0.9973 | 0.9864 | 0.9918 | 0.9897 |
| Random forest | 0.9979 | 0.9994 | 0.9907 | 0.9950 | 0.9937 | |
| Gradient boosting | 0.9972 | 0.9997 | 0.9866 | 0.9931 | 0.9914 |
| Method | 4-Fold cv | Accuracy | Precision | Recall | F1 Score | MCC |
|---|---|---|---|---|---|---|
| Logistic regression: No sampling | Fold 1 | 0.993637 | 0.993660 | 0.993637 | 0.993607 | 0.980512 |
| Fold 2 | 0.994283 | 0.994302 | 0.994283 | 0.994258 | 0.982578 | |
| Fold 3 | 0.993988 | 0.994015 | 0.993988 | 0.993960 | 0.981772 | |
| Fold 4 | 0.994526 | 0.994546 | 0.994526 | 0.994503 | 0.983267 | |
| Average | 0.994108 | 0.994131 | 0.994108 | 0.994082 | 0.982032 | |
| Logistic regression: Over-sampling | Fold 1 | 0.995970 | 0.995972 | 0.995970 | 0.995960 | 0.987666 |
| Fold 2 | 0.996202 | 0.996201 | 0.996202 | 0.996196 | 0.988435 | |
| Fold 3 | 0.995349 | 0.995352 | 0.995349 | 0.995337 | 0.985900 | |
| Fold 4 | 0.994964 | 0.994964 | 0.994964 | 0.994951 | 0.984602 | |
| Average | 0.995621 | 0.995622 | 0.995621 | 0.995611 | 0.986651 | |
| Logistic regression: Under-sampling | Fold 1 | 0.996188 | 0.996185 | 0.996188 | 0.996182 | 0.988336 |
| Fold 2 | 0.995838 | 0.995836 | 0.995838 | 0.995831 | 0.987324 | |
| Fold 3 | 0.995170 | 0.995165 | 0.995170 | 0.995161 | 0.985355 | |
| Fold 4 | 0.995948 | 0.995945 | 0.995948 | 0.995943 | 0.987621 | |
| Average | 0.995786 | 0.995783 | 0.995786 | 0.995779 | 0.987159 | |
| Logistic regression: Combined sampling | Fold 1 | 0.997049 | 0.997050 | 0.997049 | 0.997044 | 0.990975 |
| Fold 2 | 0.996418 | 0.996421 | 0.996418 | 0.996411 | 0.989094 | |
| Fold 3 | 0.996833 | 0.996833 | 0.996833 | 0.996828 | 0.990406 | |
| Fold 4 | 0.996016 | 0.996012 | 0.996016 | 0.996011 | 0.987829 | |
| Average | 0.996579 | 0.996579 | 0.996579 | 0.996573 | 0.989576 |
| Method | 4-Fold cv | Accuracy | Precision | Recall | F1 Score | MCC |
|---|---|---|---|---|---|---|
| Random forest: No sampling | Fold 1 | 0.997993 | 0.997998 | 0.997993 | 0.997990 | 0.993868 |
| Fold 2 | 0.997949 | 0.997954 | 0.997949 | 0.997945 | 0.993762 | |
| Fold 3 | 0.997818 | 0.997823 | 0.997818 | 0.997813 | 0.993395 | |
| Fold 4 | 0.997919 | 0.997924 | 0.997919 | 0.997915 | 0.993651 | |
| Average | 0.997920 | 0.997925 | 0.997920 | 0.997916 | 0.993669 | |
| Random forest: Over-sampling | Fold 1 | 0.998114 | 0.998118 | 0.998114 | 0.998111 | 0.994237 |
| Fold 2 | 0.998167 | 0.998171 | 0.998167 | 0.998164 | 0.994425 | |
| Fold 3 | 0.998050 | 0.998055 | 0.998050 | 0.998047 | 0.994100 | |
| Fold 4 | 0.998042 | 0.998047 | 0.998042 | 0.998039 | 0.994026 | |
| Average | 0.998093 | 0.998098 | 0.998093 | 0.998090 | 0.994197 | |
| Random forest: Under-sampling | Fold 1 | 0.998567 | 0.998568 | 0.998567 | 0.998566 | 0.995621 |
| Fold 2 | 0.998548 | 0.998548 | 0.998548 | 0.998547 | 0.995583 | |
| Fold 3 | 0.998478 | 0.998478 | 0.998478 | 0.998477 | 0.995393 | |
| Fold 4 | 0.998525 | 0.998525 | 0.998525 | 0.998523 | 0.995497 | |
| Average | 0.998529 | 0.998530 | 0.998529 | 0.998528 | 0.995523 | |
| Random forest: Combined sampling | Fold 1 | 0.998076 | 0.998079 | 0.998076 | 0.998073 | 0.994120 |
| Fold 2 | 0.997987 | 0.997990 | 0.997987 | 0.997984 | 0.993877 | |
| Fold 3 | 0.998059 | 0.998063 | 0.998059 | 0.998056 | 0.994125 | |
| Fold 4 | 0.997985 | 0.997989 | 0.997985 | 0.997981 | 0.993851 | |
| Average | 0.998027 | 0.998030 | 0.998027 | 0.998023 | 0.993993 |
| Method | 4-Fold cv | Accuracy | Precision | Recall | F1 Score | MCC |
|---|---|---|---|---|---|---|
| Gradient boosting: No sampling | Fold 1 | 0.999172 | 0.999173 | 0.999172 | 0.999172 | 0.997471 |
| Fold 2 | 0.999130 | 0.999130 | 0.999130 | 0.999130 | 0.997355 | |
| Fold 3 | 0.999217 | 0.999217 | 0.999217 | 0.999216 | 0.997630 | |
| Fold 4 | 0.999107 | 0.999107 | 0.999107 | 0.999106 | 0.997275 | |
| Average | 0.999156 | 0.999157 | 0.999156 | 0.999156 | 0.997433 | |
| Gradient boosting: Over-sampling | Fold 1 | 0.999280 | 0.999281 | 0.999280 | 0.999280 | 0.997801 |
| Fold 2 | 0.999179 | 0.999179 | 0.999179 | 0.999178 | 0.997503 | |
| Fold 3 | 0.999208 | 0.999209 | 0.999208 | 0.999208 | 0.997605 | |
| Fold 4 | 0.999174 | 0.999175 | 0.999174 | 0.999174 | 0.997482 | |
| Average | 0.999210 | 0.999211 | 0.999210 | 0.999210 | 0.997598 | |
| Gradient boosting: Under-sampling | Fold 1 | 0.999285 | 0.999284 | 0.999285 | 0.999284 | 0.997814 |
| Fold 2 | 0.999276 | 0.999276 | 0.999276 | 0.999276 | 0.997799 | |
| Fold 3 | 0.999257 | 0.999257 | 0.999257 | 0.999257 | 0.997752 | |
| Fold 4 | 0.999166 | 0.999166 | 0.999166 | 0.999166 | 0.997456 | |
| Average | 0.999246 | 0.999246 | 0.999246 | 0.999246 | 0.997705 | |
| Gradient boosting: Combined sampling | Fold 1 | 0.999164 | 0.999164 | 0.999164 | 0.999163 | 0.997446 |
| Fold 2 | 0.999177 | 0.999177 | 0.999177 | 0.999176 | 0.997496 | |
| Fold 3 | 0.99913 | 0.99913 | 0.99913 | 0.999129 | 0.997367 | |
| Fold 4 | 0.999181 | 0.999181 | 0.999181 | 0.99918 | 0.997501 | |
| Average | 0.999163 | 0.999163 | 0.999163 | 0.999162 | 0.997453 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wattanakitrungroj, N.; Wijitkajee, P.; Jaiyen, S.; Sathapornvajana, S.; Tongman, S. Enhancing Supervised Model Performance in Credit Risk Classification Using Sampling Strategies and Feature Ranking. Big Data Cogn. Comput. 2024, 8, 28. https://doi.org/10.3390/bdcc8030028
Wattanakitrungroj N, Wijitkajee P, Jaiyen S, Sathapornvajana S, Tongman S. Enhancing Supervised Model Performance in Credit Risk Classification Using Sampling Strategies and Feature Ranking. Big Data and Cognitive Computing. 2024; 8(3):28. https://doi.org/10.3390/bdcc8030028
Chicago/Turabian StyleWattanakitrungroj, Niwan, Pimchanok Wijitkajee, Saichon Jaiyen, Sunisa Sathapornvajana, and Sasiporn Tongman. 2024. "Enhancing Supervised Model Performance in Credit Risk Classification Using Sampling Strategies and Feature Ranking" Big Data and Cognitive Computing 8, no. 3: 28. https://doi.org/10.3390/bdcc8030028
APA StyleWattanakitrungroj, N., Wijitkajee, P., Jaiyen, S., Sathapornvajana, S., & Tongman, S. (2024). Enhancing Supervised Model Performance in Credit Risk Classification Using Sampling Strategies and Feature Ranking. Big Data and Cognitive Computing, 8(3), 28. https://doi.org/10.3390/bdcc8030028






