Novel Complex Wave Solutions of the (2+1)-Dimensional Hyperbolic Nonlinear Schrödinger Equation
Abstract
:1. Introduction
2. General Properties of -Expansion Method
3. Application of Projected Method
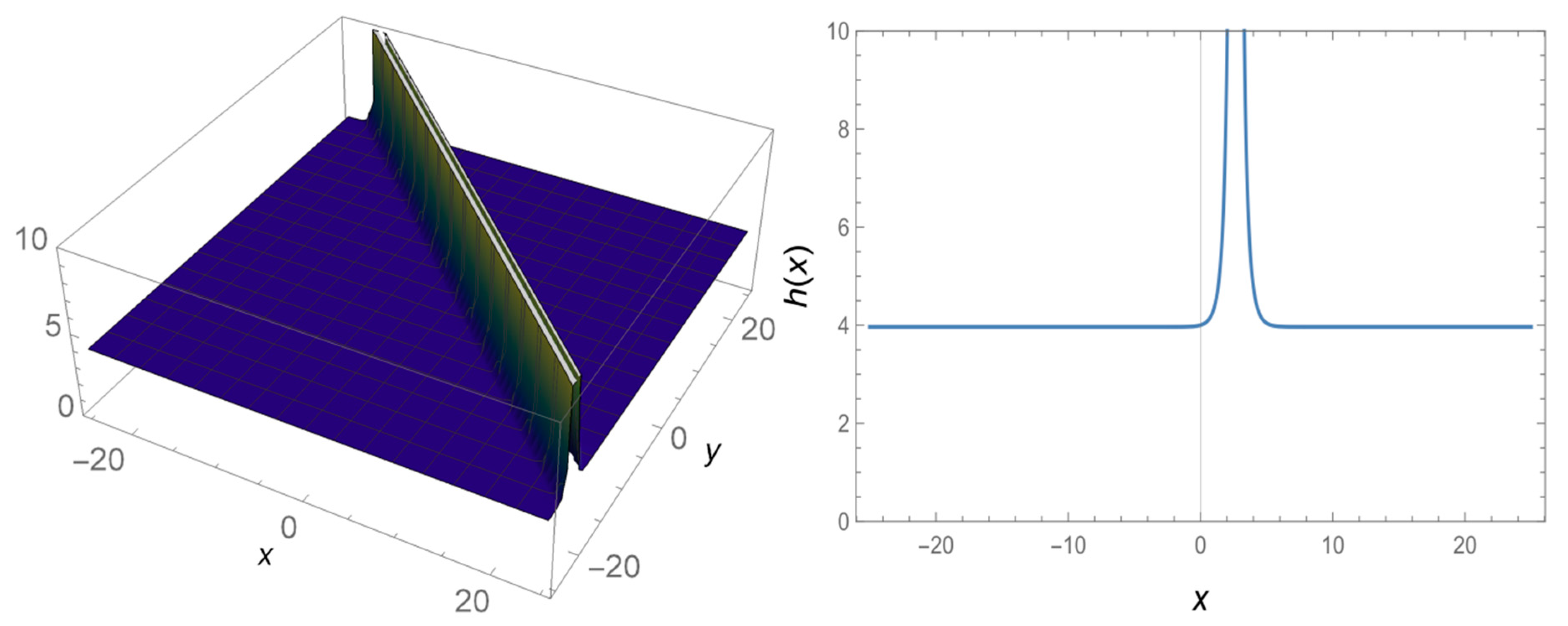
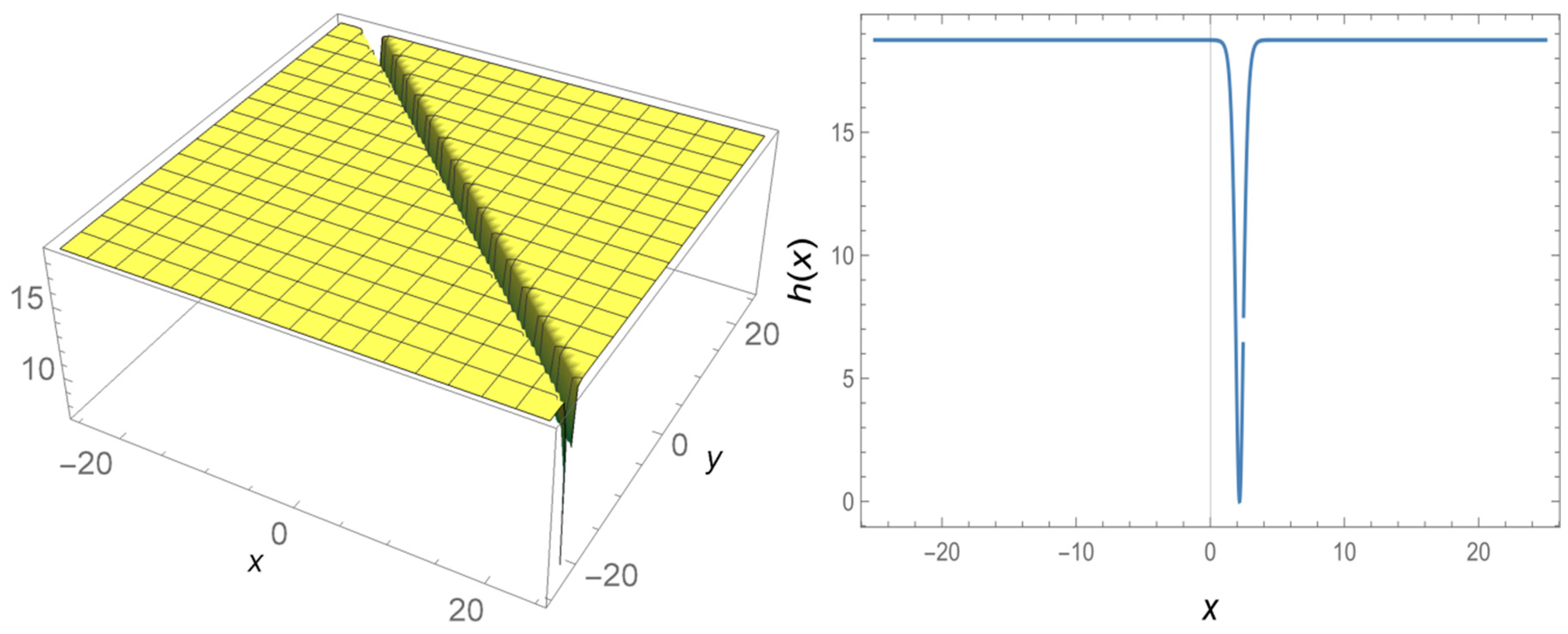
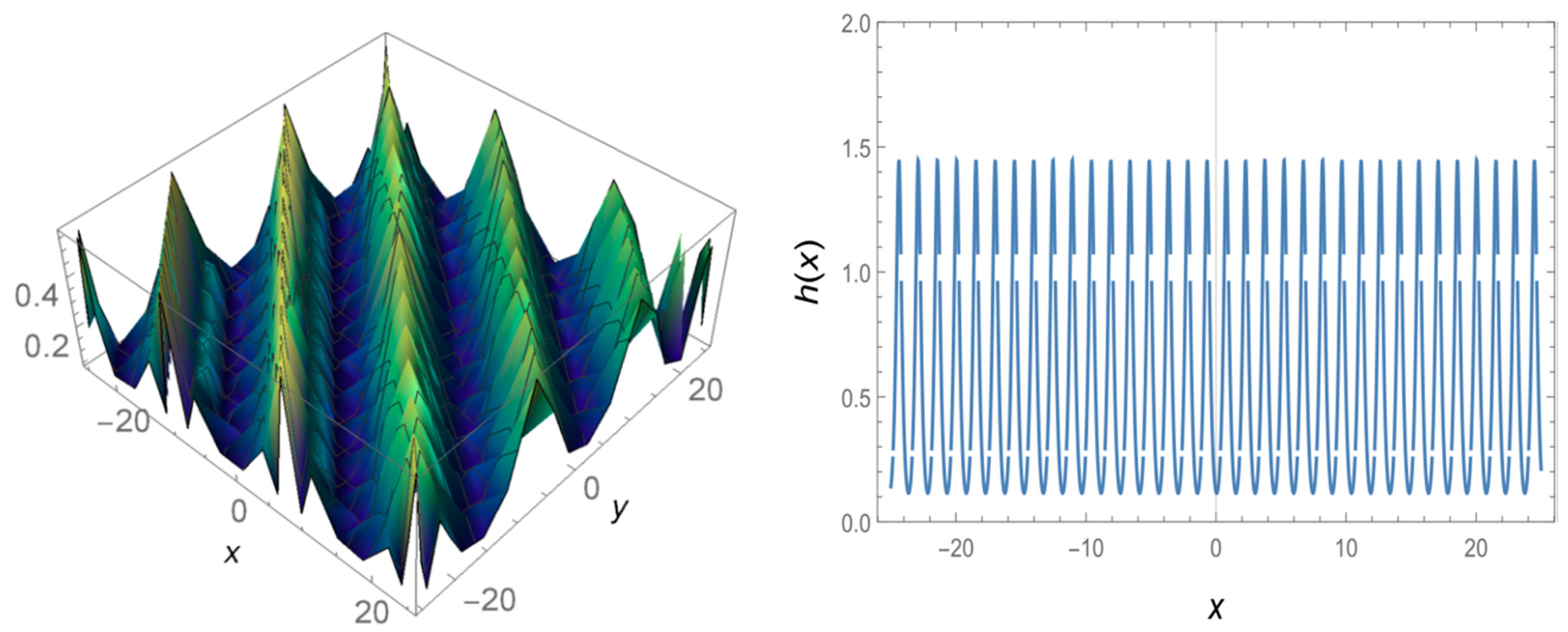
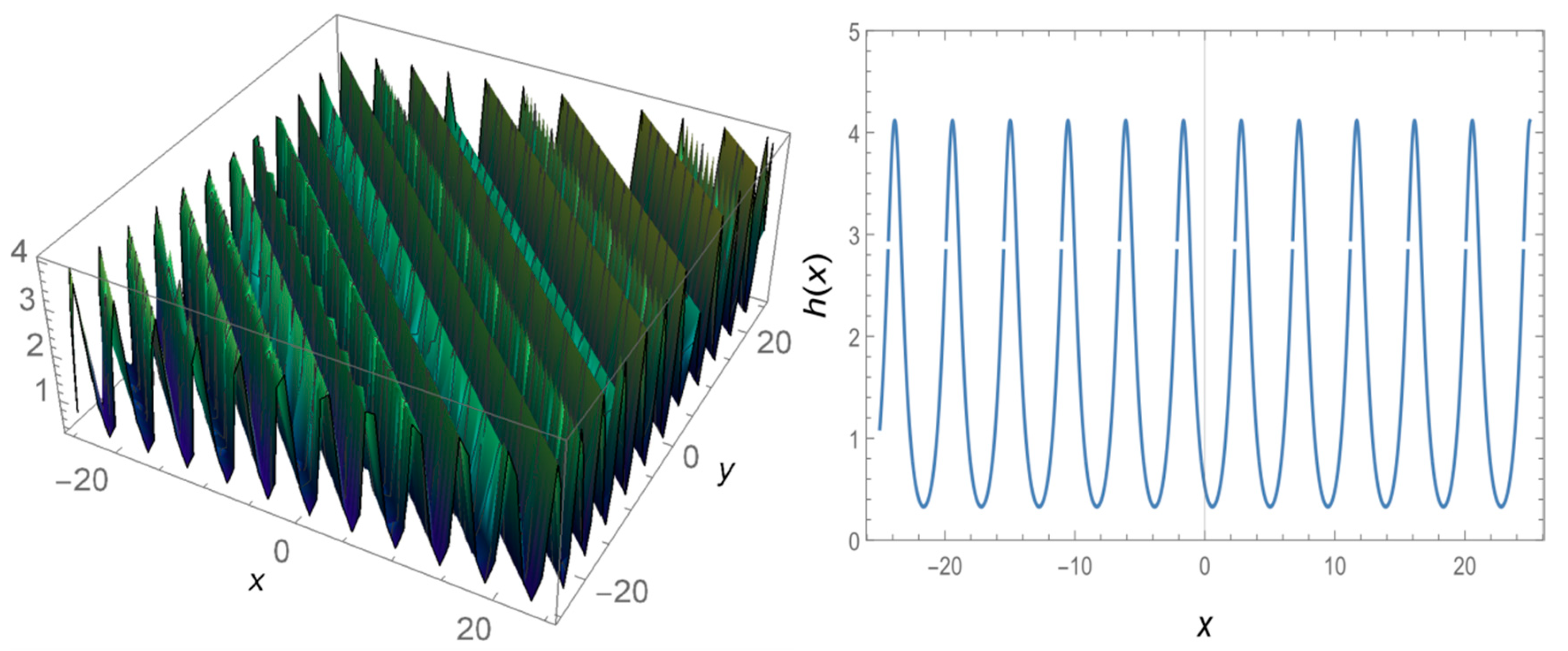
4. Results and Discussions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ismael, H.F.; Bulut, H.; Baskonus, H.M. Optical soliton solutions to the Fokas–Lenells equation via sine-Gordon expansion method and (m + (G′/G))-expansion method. Pramana 2020, 94, 35. [Google Scholar] [CrossRef]
- Gao, W.; Ismael, H.F.; Husien, A.M.; Bulut, H.; Baskonus, H.M. Optical soliton solutions of the cubic-quartic nonlinear Schrödinger and resonant nonlinear Schrödinger equation with the parabolic law. Appl. Sci. 2020, 10, 219. [Google Scholar] [CrossRef] [Green Version]
- Yokus, A.; Durur, H.; Ahmad, H. Hyperbolic Type solutions for the couple Boiti-Leon-Pempinelli system. Facta Univ. Ser. Math. Inform. 2020, 35, 523–531. [Google Scholar]
- Ali, K.K.; Dutta, H.; Yilmazer, R.; Noeiaghdam, S. On the new wave behaviors of the Gilson-Pickering equation. Front. Phys. 2020, 8, 54. [Google Scholar] [CrossRef]
- Durur, H.; Yokuş, A. Analytical solutions of Kolmogorov–Petrovskii–Piskunov equation. J. Balikesir Univ. Inst. Sci. Technol. 2020, 22, 628–636. [Google Scholar]
- Darvishi, M.T.; Najafi, M.; Wazwaz, A.M. Construction of exact solutions in amagneto-electro-elastic circular rod. Waves Random Complex Media 2020, 30, 340–353. [Google Scholar] [CrossRef]
- Gao, W.; Silambarasan, R.; Baskonus, H.M.; Anand, R.V.; Rezazadeh, H. Periodic waves of the nondissipative double dispersive micro strain wave in the micro structured solids. Phys. A Stat. Mech. Appl. 2020, 545, 123772. [Google Scholar] [CrossRef]
- Su-Ping, Q.; Li-Xin, T. Modification of the Clarkson–Kruskal Direct method for a coupled system. Chin. Phys. Lett. 2007, 24, 2720. [Google Scholar] [CrossRef]
- Durur, H. Different types analytic solutions of the (1+1)-dimensional resonant nonlinear Schrödinger’s equation using (G′/G)-expansion method. Mod. Phys. Lett. B 2020, 34, 2050036. [Google Scholar] [CrossRef]
- Rezazadeh, H.; Kumar, D.; Neirameh, A.; Eslami, M.; Mirzazadeh, M. Applications of three methods for obtaining optical soliton solutions for the Lakshmanan–Porsezian–Daniel model with Kerr law nonlinearity. Pramana 2020, 94, 39. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H.; Atangana, A. On the complex and hyperbolic structures of the longitudinal wave equation in a magneto-electro-elastic circular rod. Smart Mater. Struct. 2016, 25, 035022. [Google Scholar] [CrossRef]
- Liu, H.; Bai, C.L.; Xin, X. Painlevé analysis, group classification and exact solutions to the nonlinear wave equations. Eur. Phys. J. B 2020, 93, 26. [Google Scholar] [CrossRef]
- Yokus, A.; Durur, H.; Ahmad, H.; Yao, S.W. Construction of different types analytic solutions for the Zhiber-Shabate quation. Mathematics 2020, 8, 908. [Google Scholar] [CrossRef]
- Yavuz, M.; Sulaiman, T.A.; Usta, F.; Bulut, H. Analysis and numerical computations of the fractional regularized long-wave equation with damping term. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Guan, X.; Liu, W.; Zhou, Q.; Biswas, A. Some lump solutions for a generalized (3+1)-dimensional Kadomtsev–Petviashvili equation. Appl. Math. Comput. 2020, 366, 124757. [Google Scholar] [CrossRef]
- El-Labany, S.K.; El-Taibany, W.F.; Behery, E.E.; Fouda, S.M. Collision of dustion acoustic multi solitons in a non-extensive plasma using Hirota bilinear method. Phys. Plasmas 2018, 25, 013701. [Google Scholar] [CrossRef]
- Sharma, B.; Kumar, S.; Cattani, C.; Baleanu, D. Nonlinear dynamics of Cattaneo–Christov heat flux model for third-grade power-law fluid. J. Comput. Nonlinear Dyn. 2020, 15, 011009. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Baleanu, D.; Machado, J.A.T.; Osman, M.S.; Rezazadeh, H.; Arshed, S.; Günerhan, H. Traveling wave solutions to nonlinear directional couplers by modified Kudryashov method. Phys. Scr. 2020. [Google Scholar] [CrossRef]
- Ali, K.K.; Wazwaz, A.M.; Mehanna, M.S.; Osman, M.S. On short-range pulse propagation described by (2+1)-dimensional Schrödinger’s hyperbolic equation in nonlinear optical. Phys. Scr. 2020, 95, 075203. [Google Scholar] [CrossRef]
- Zayed, E.M.E.; Al-Nowehy, A.G. Exact solutions and optical soliton solutions for the (2 + 1)-dimensional hyperbolic nonlinear Schrödinger equation. Optik 2016, 127, 4970–4983. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Kumar, D.; Chakrabarty, A.K. Dispersive optical soliton solutions for the hyperbolic and cubic-quintic nonlinear Schrödinger equations via the extended sinh-Gordon equation expansion method. Eur. Phys. J. Plus 2018, 133, 182. [Google Scholar] [CrossRef]
- Ahmed, I.; Chunlai, M.; Zheng, P. Exact solution of the (2+1)-dimensional hyperbolic nonlinear Schrödinger equation byAdomian decomposition method. Malaya J. Mat. 2014, 2, 160–164. [Google Scholar]
- El-Ganaini, S.I.A. The first integral method to the nonlinear Schrodinger equations in higher dimensions. Abst. Appl. Anal. 2013, 2013, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Pelinovsky, D.E.; Rouvinskaya, E.A.; Kurkina, O.E.E.; Deconinck, B. Short-wave transverse instabilities of line solitons of the two-dimensional hyperbolic nonlinear Schrödinger equation. Theor. Math. Phys. 2014, 179, 452–461. [Google Scholar] [CrossRef] [Green Version]
- Yokuş, A.; Durur, H. Complex hyperbolic traveling wave solutions of Kuramoto-Sivashinsky equation using (1/G′)expansion method for nonlinear dynamic theory. J. Balikesir Univ. Inst. Sci. Technol. 2019, 21, 590–599. [Google Scholar]
- Durur, H.; Yokuş, A. Hyperbolic traveling wave solutions for Sawada–Kotera equation using (1/G′)-expansion method. Afyon Kocatepe Univ. J. Sci. Eng. Sci. 2019, 19, 615–619. [Google Scholar]
- Yokuş, A. Comparison of Caputo and conformable derivatives for time-fractional Korteweg–deVries equation via the finite difference method. Int. J. Mod. Phys. B 2018, 32, 1850365. [Google Scholar] [CrossRef]
- Yavuz, M.; Yokus, A. Analytical and numerical approaches to nerve impulse model of fractional-order. Numer. Methods Part. Differ. Equ. 2020. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Tenkam, H.M.; Khumalo, M. A behavioral analysis of KdVB equation under the law of Mittag–Leffler function. Chaos Solitons Fractals 2019, 125, 139–145. [Google Scholar] [CrossRef]
- Khan, Z.H.; Hussain, S.T.; Hammouch, Z. Flow and heat transfer analysis of water and ethyleneglycol based Cunano particles between two parallel disks with suction/injection effects. J. Mol. Liq. 2016, 221, 298–304. [Google Scholar]
- Guedda, M.; Hammouch, Z. On similarity and pseudo-similarity solutions of Falkner–Skan boundary layers. Fluid Dyn. Res. 2006, 38, 211–223. [Google Scholar] [CrossRef]
- Goufo, E.F.D.; Atangana, A. Dynamics of traveling waves of variable order hyperbolic Liouville equation: Regulation and control. Discret. Contin. Dyn. Syst. S 2019, 13, 645–662. [Google Scholar] [CrossRef] [Green Version]
- Seadawy, A.R. Stability analysis solutions for nonlinear three-dimensional modified Korteweg–de Vries–Zakharov–Kuznetsov equation in a magnetized electron–positron plasma. Phys. A Stat. Mech. Appl. 2016, 455, 44–51. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.; Lu, D.; Wang, J. Travelling wave solutions of generalized coupled Zakharov–Kuznetsov and dispersive long wave equations. Results Phys. 2016, 6, 1136–1145. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Seadawy, A.R.; Arshad, M.; Wang, J. New solitary wave solutions of (3+1)-dimensional nonlinear extended Zakharov-Kuznetsov and modified KdV-Zakharov-Kuznetsov equations and their applications. Results Phys. 2017, 7, 899–909. [Google Scholar] [CrossRef]
- Özkan, Y.S.; Yaşar, E.; Seadawy, A.R. A third-order nonlinear Schrödinger equation: The exact solutions, group-invariant solutions and conservation laws. J. Taibah Univ. Sci. 2020, 14, 585–597. [Google Scholar] [CrossRef]
- Ahmad, H.; Seadawy, A.R.; Khan, T.A.; Thounthong, P. Analytic approximate solutions for some nonlinear Parabolic dynamical wave equations. J. Taibah Univ. Sci. 2020, 14, 346–358. [Google Scholar] [CrossRef] [Green Version]
- Arnous, A.H.; Seadawy, A.R.; Alqahtani, R.T.; Biswas, A. Optical solitons with complex Ginzburg–Landau equation by modified simple equation method. Optik 2017, 144, 475–480. [Google Scholar] [CrossRef]
- Seadawy, A.R.; Jun, W. Mathematical methods and solitary wave solutions of three-dimensional Zakharov-Kuznetsov-Burgers equation in dusty plasma and its applications. Results Phys. 2017, 7, 4269–4277. [Google Scholar]
- Durur, H.; Tasbozan, O.; Kurt, A. New analytical solutions of conformable time fractional bad and good modified Boussinesq equations. Appl. Math. Nonlinear Sci. 2020, 5, 447–454. [Google Scholar] [CrossRef]
- Durur, H.; Kurt, A.; Tasbozan, O. New travelling wave solutions for KdV6 equation using sub equation method. Appl. Math. Nonlinear Sci. 2020, 5, 455–460. [Google Scholar] [CrossRef]
- Kaya, D.; Yokuş, A.; Demiroğlu, U. Comparison of exact and numerical solutions for the Sharma–Tasso–Olver equation. In Numerical Solutions of Realistic Nonlinear Phenomena; Springer: Cham, Switzerland, 2020; pp. 53–65. [Google Scholar]
- Apeanti, W.O.; Seadawy, A.R.; Lu, D. Complex optical solutions and modulation instability of hyperbolic Schrödinger dynamical equation. Results Phys. 2019, 12, 2091–2097. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Bright–dark solitary wave solutions of generalized higher-order nonlinear Schrödinger equation and its applications in optics. J. Electromagn. Waves Appl. 2017, 31, 1711–1721. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D. Exact bright–dark solitary wave solutions of the higher-order cubic–quintic nonlinear Schrödinger equation and its stability. Optik 2017, 138, 40–49. [Google Scholar] [CrossRef]
- Arshad, M.; Seadawy, A.R.; Lu, D.; Jun, W. Modulation instability analysis of modify unstable nonlinear schrodinger dynamical equation and its optical soliton solutions. Results Phys. 2017, 7, 4153–4161. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Cattani, C.; Ciancio, A. Periodic, complex and kink-type solitons for the nonlinear model in microtubules. J. Appl. Sci. 2019, 21, 34–45. [Google Scholar]
- Conte, R.; Musette, M. Elliptic general analytic solutions. Stud. Appl. Math. 2009, 123, 63–81. [Google Scholar] [CrossRef]
- Conte, R.; Ng, T.W. Meromorphic solutions of a third order nonlinear differential equation. J. Math. Phys. 2010, 51, 033518. [Google Scholar] [CrossRef] [Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Durur, H.; Ilhan, E.; Bulut, H. Novel Complex Wave Solutions of the (2+1)-Dimensional Hyperbolic Nonlinear Schrödinger Equation. Fractal Fract. 2020, 4, 41. https://doi.org/10.3390/fractalfract4030041
Durur H, Ilhan E, Bulut H. Novel Complex Wave Solutions of the (2+1)-Dimensional Hyperbolic Nonlinear Schrödinger Equation. Fractal and Fractional. 2020; 4(3):41. https://doi.org/10.3390/fractalfract4030041
Chicago/Turabian StyleDurur, Hulya, Esin Ilhan, and Hasan Bulut. 2020. "Novel Complex Wave Solutions of the (2+1)-Dimensional Hyperbolic Nonlinear Schrödinger Equation" Fractal and Fractional 4, no. 3: 41. https://doi.org/10.3390/fractalfract4030041



