Journal Description
Fractal and Fractional
Fractal and Fractional
is an international, scientific, peer-reviewed, open access journal of fractals and fractional calculus and their applications in different fields of science and engineering published monthly online by MDPI.
- Open Access— free for readers, with article processing charges (APC) paid by authors or their institutions.
- High Visibility: indexed within Scopus, SCIE (Web of Science), Inspec, and other databases.
- Journal Rank: JCR - Q1 (Mathematics, Interdisciplinary Applications) / CiteScore - Q1 (Analysis)
- Rapid Publication: manuscripts are peer-reviewed and a first decision is provided to authors approximately 23.7 days after submission; acceptance to publication is undertaken in 2.7 days (median values for papers published in this journal in the second half of 2024).
- Recognition of Reviewers: reviewers who provide timely, thorough peer-review reports receive vouchers entitling them to a discount on the APC of their next publication in any MDPI journal, in appreciation of the work done.
Impact Factor:
3.6 (2023);
5-Year Impact Factor:
3.5 (2023)
Latest Articles
Discrete Memristive Hindmarsh-Rose Neural Model with Fractional-Order Differences
Fractal Fract. 2025, 9(5), 276; https://doi.org/10.3390/fractalfract9050276 - 24 Apr 2025
Abstract
Discrete systems can offer advantages over continuous ones in certain contexts, particularly in terms of simplicity and reduced computational costs, though this may vary depending on the specific application and requirements. Recently, there has been growing interest in using fractional differences to enhance
[...] Read more.
Discrete systems can offer advantages over continuous ones in certain contexts, particularly in terms of simplicity and reduced computational costs, though this may vary depending on the specific application and requirements. Recently, there has been growing interest in using fractional differences to enhance discrete models’ flexibility and incorporate memory effects. This paper examines the dynamics of the discrete memristive Hindmarsh-Rose model by integrating fractional-order differences. Our results highlight the complex dynamics of the fractional-order model, revealing that chaotic firing depends on both the fractional-order and magnetic strength. Notably, certain magnetic strengths induce a transition from periodic firing in the integer-order model to chaotic behavior in the fractional-order model. Additionally, we explore the dynamics of two coupled discrete systems, finding that electrical coupling leads to the synchronization of chaotic dynamics, while chemical coupling ultimately results in a quiescent state.
Full article
(This article belongs to the Special Issue Advances in Fractional-Order Chaotic and Complex Systems)
Open AccessArticle
On the Laplace Residual Series Method and Its Application to Time-Fractional Fisher’s Equations
by
Rawya Al-deiakeh, Sharifah Alhazmi, Shrideh Al-Omari, Mohammed Al-Smadi and Shaher Momani
Fractal Fract. 2025, 9(5), 275; https://doi.org/10.3390/fractalfract9050275 - 24 Apr 2025
Abstract
In this paper, we develop an analytical approximate solution for the nonlinear time-fractional Fisher’s equation using a right starting space function and a unique analytic-numeric technique referred to as the Laplace residual power series approach. The generalized Taylor’s formula and the Laplace transform
[...] Read more.
In this paper, we develop an analytical approximate solution for the nonlinear time-fractional Fisher’s equation using a right starting space function and a unique analytic-numeric technique referred to as the Laplace residual power series approach. The generalized Taylor’s formula and the Laplace transform operator are coupled in the aforementioned method, where the coefficients, obtained through fractional expansion in the Laplace space, are determined by applying the limit concept. In order to validate and illustrate the theoretical methodology of the LRPS technique, as well as to show its effectiveness, adaptability, and superiority in solving various types of nonlinear time and space fractional differential equations, numerical experiments are generated. The obtained analytical solutions are compatible with the precise solutions and concur with those proposed by the other approaches. The outcomes show that the Laplace residual power series strategy is incredibly successful, straightforward to implement, and well suited for handling the complexity of nonlinear problems.
Full article
(This article belongs to the Special Issue Fractional Differential Equations: Computation and Modelling with Applications)
►▼
Show Figures
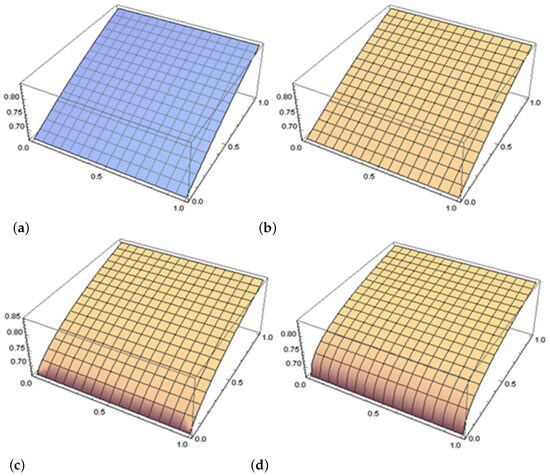
Figure 1
Open AccessArticle
Duality Revelation and Operator-Based Method in Viscoelastic Problems
by
Zelin Liu, Xiaobin Yu and Yajun Yin
Fractal Fract. 2025, 9(5), 274; https://doi.org/10.3390/fractalfract9050274 - 23 Apr 2025
Abstract
Viscoelastic materials are commonly used in civil engineering, biomedical sciences, and polymers, where understanding their creep and relaxation behaviors is essential for predicting long-term performance. This paper introduces an operator-based method for modeling viscoelastic materials, providing a unified framework to describe both creep
[...] Read more.
Viscoelastic materials are commonly used in civil engineering, biomedical sciences, and polymers, where understanding their creep and relaxation behaviors is essential for predicting long-term performance. This paper introduces an operator-based method for modeling viscoelastic materials, providing a unified framework to describe both creep and relaxation functions. The method utilizes stiffness and compliance operators, offering a systematic approach for analyzing viscoelastic problems. The operator-based method enhances the mathematical duality between the creep and relaxation functions, providing greater physical intuition and understanding of time-dependent material behavior. It directly reflects the intrinsic properties of materials, independent of input and output conditions. The method is extended to dynamic problems, with complex modulus and compliance derived through operator representations. The fractal tree model, with its constant loss factor across the frequency spectrum, demonstrates potential engineering applications. By incorporating a damage-based variable coefficient, the model now also accounts for the accelerated creep phase of rocks, capturing damage evolution under prolonged loading. While promising, the current method is limited to one-dimensional problems, and future research will aim to extend it to three-dimensional cases, integrate experimental validation, and explore broader applications.
Full article
(This article belongs to the Special Issue Fractal Analysis and Its Applications in Materials Science)
►▼
Show Figures
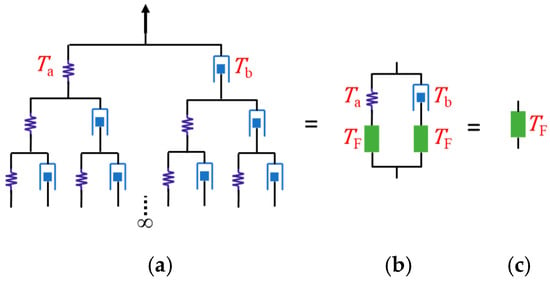
Figure 1
Open AccessArticle
Comparison Principle Based Synchronization Analysis of Fractional-Order Chaotic Neural Networks with Multi-Order and Its Circuit Implementation
by
Rongbo Zhang, Kun Qiu, Chuang Liu, Hongli Ma and Zhaobi Chu
Fractal Fract. 2025, 9(5), 273; https://doi.org/10.3390/fractalfract9050273 - 23 Apr 2025
Abstract
This article investigates non-fragile synchronization control and circuit implementation for incommensurate fractional-order (IFO) chaotic neural networks with parameter uncertainties. In this paper, we explore three aspects of the research challenges, i.e., theoretical limitations of uncertain IFO systems, the fragility of the synchronization controller,
[...] Read more.
This article investigates non-fragile synchronization control and circuit implementation for incommensurate fractional-order (IFO) chaotic neural networks with parameter uncertainties. In this paper, we explore three aspects of the research challenges, i.e., theoretical limitations of uncertain IFO systems, the fragility of the synchronization controller, and the lack of circuit implementation. First, we establish an IFO chaotic neural network model incorporating parametric uncertainties, extending beyond conventional commensurate-order architectures. Second, a novel, non-fragile state-error feedback controller is designed. Through the formulation of FO Lyapunov functions and the application of inequality scaling techniques, sufficient conditions for asymptotic synchronization of master–slave systems are rigorously derived via the multi-order fractional comparison principle. Third, an analog circuit implementation scheme utilizing FO impedance units is developed to experimentally validate synchronization efficacy and accurately replicate the system’s dynamic behavior. Numerical simulations and circuit experiments substantiate the theoretical findings, demonstrating both robustness against parameter perturbations and the feasibility of circuit realization.
Full article
(This article belongs to the Topic Fractional Calculus: Theory and Applications, 2nd Edition)
►▼
Show Figures
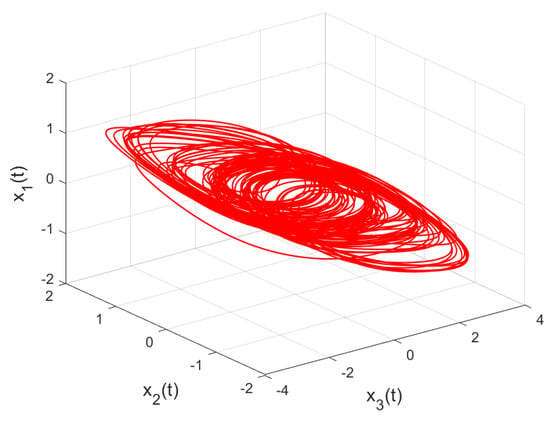
Figure 1
Open AccessArticle
Fractional Heat Conduction with Variable Thermal Conductivity of Infinite Annular Cylinder Under Thermoelasticity Theorem of Moore–Gibson–Thompson
by
Eman A. N. Al-Lehaibi
Fractal Fract. 2025, 9(5), 272; https://doi.org/10.3390/fractalfract9050272 - 23 Apr 2025
Abstract
To discuss the fractional order heat conduction based on Youssef’s model, a new mathematical model of a thermoelastic annular cylinder with variable thermal conductivity will be constructed in this work. The Moore–Gibson– Thompson theorem of generalized thermoelasticity will be considered and the governing
[...] Read more.
To discuss the fractional order heat conduction based on Youssef’s model, a new mathematical model of a thermoelastic annular cylinder with variable thermal conductivity will be constructed in this work. The Moore–Gibson– Thompson theorem of generalized thermoelasticity will be considered and the governing equations will be derived in dimensionless forms. The Laplace transform technique will be used for a one-dimensional thermoelastic, isotropic, and homogeneous annular cylinder in which the interior surrounded surface is thermally shocked and there is an axial traction-free environment, while the outer surrounded surface has neither heat increment nor cubical deformation. The numerical results will be computed for the Laplace transform inversions by using Tzou’s iteration approach. The distributions of the cubical deformation, invariant average stress, axial stress, and temperature increment will be represented in figures to analyze and discuss. The results show that the fractional-order and variable thermal conductivity parameters have significant effects on all the studied functions. The physical behaviour of the thermal conductivity is closely aligned with the classification of thermal conductivity into weak, normal, and strong categories, which is essential.
Full article
(This article belongs to the Special Issue Analysis of Heat Conduction and Anomalous Diffusion in Fractional Calculus)
►▼
Show Figures
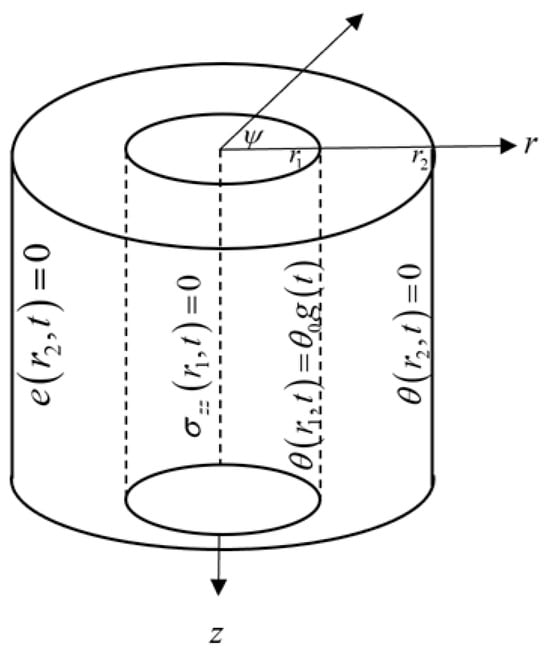
Figure 1
Open AccessArticle
Some Results Related to Booth Lemniscate and Integral Operators
by
Bilal Khan, Zahra Orouji and Ali Ebadian
Fractal Fract. 2025, 9(5), 271; https://doi.org/10.3390/fractalfract9050271 - 22 Apr 2025
Abstract
►▼
Show Figures
In this work, we explore the impact of integral operators such as the Libera and Alexander operators on specific families of analytic functions introduced in the literature and find some of their remarkable results. Using techniques from differential subordination and convolution theory, we
[...] Read more.
In this work, we explore the impact of integral operators such as the Libera and Alexander operators on specific families of analytic functions introduced in the literature and find some of their remarkable results. Using techniques from differential subordination and convolution theory, we establish results concerning the radius of convexity and convolution properties for these function classes. Additionally, we investigate how these integral operators influence the geometric properties of functions in
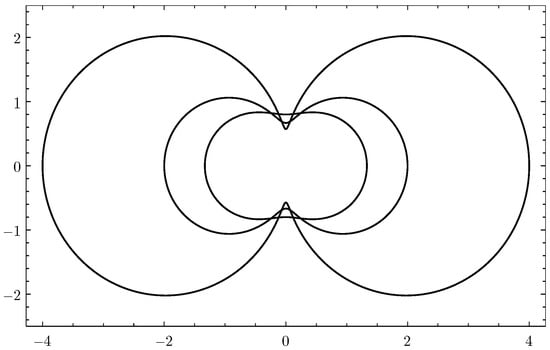
Figure 1
Open AccessArticle
A Study of Fuzzy Fixed Points and Their Application to Fuzzy Fractional Differential Equations
by
Nawal Alharbi and Nawab Hussain
Fractal Fract. 2025, 9(5), 270; https://doi.org/10.3390/fractalfract9050270 - 22 Apr 2025
Abstract
This study investigates fuzzy fixed points and fuzzy best proximity points for fuzzy mappings within the newly introduced framework
This study investigates fuzzy fixed points and fuzzy best proximity points for fuzzy mappings within the newly introduced framework
(This article belongs to the Special Issue Fixed Point Theory and Fractals)
Open AccessArticle
Approximation of Fractional Caputo Derivative of Variable Order and Variable Terminals with Application to Initial/Boundary Value Problems
by
Paulina Stempin and Wojciech Sumelka
Fractal Fract. 2025, 9(5), 269; https://doi.org/10.3390/fractalfract9050269 - 22 Apr 2025
Abstract
This article presents a method for the approximate calculation of fractional Caputo derivatives, including a crucial aspect of the ability to handle arbitrary—even variable—terminals and order. The proposed method involves rearranging the fractional operator as a series of higher-order derivatives considered at a
[...] Read more.
This article presents a method for the approximate calculation of fractional Caputo derivatives, including a crucial aspect of the ability to handle arbitrary—even variable—terminals and order. The proposed method involves rearranging the fractional operator as a series of higher-order derivatives considered at a specific point. We demonstrate the effect of the number of terms included in the series expansion on the solution accuracy and error analysis. The advantage of the method is its simplicity and ease of implementation. Additionally, the method allows for a quick estimation of the fractional derivative by using a few first terms of the expansion. The elaborated algorithm is tested against a comprehensive series of illustrative examples, providing very good agreement with the exact/reference solutions. Furthermore, the application of the proposed method to fractional boundary/initial value problems is included.
Full article
(This article belongs to the Special Issue Contemporary Methods of Fractional Order Differential and Differential-Operator Equations)
►▼
Show Figures
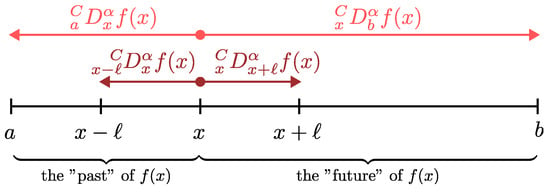
Figure 1
Open AccessArticle
Fractal Sturm–Liouville Theory
by
Alireza Khalili Golmankhaneh, Zoran Vidović, Hüseyin Tuna and Bilender P. Allahverdiev
Fractal Fract. 2025, 9(5), 268; https://doi.org/10.3390/fractalfract9050268 - 22 Apr 2025
Abstract
►▼
Show Figures
This paper provides a short summary of fractal calculus and its application to generalized Sturm–Liouville theory. It presents both the fractal homogeneous and non-homogeneous Sturm–Liouville problems and explores the theory’s applications in optics. We include examples and graphs to illustrate the effect of
[...] Read more.
This paper provides a short summary of fractal calculus and its application to generalized Sturm–Liouville theory. It presents both the fractal homogeneous and non-homogeneous Sturm–Liouville problems and explores the theory’s applications in optics. We include examples and graphs to illustrate the effect of fractal support on the solutions and propose new models for fractal structures.
Full article
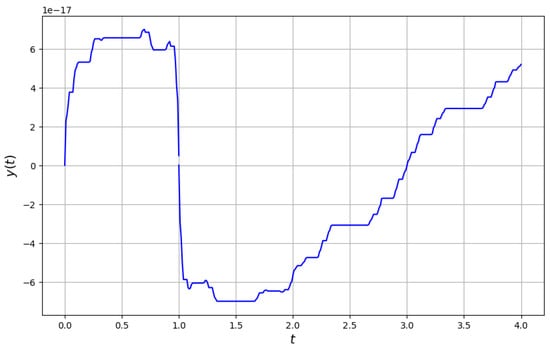
Figure 1
Open AccessArticle
Application of Fractional Fourier Transform and BP Neural Network in Prediction of Tumor Benignity and Malignancy
by
Xuanyu Liu, Nan Gao, Shuoran He and Lizhen Wang
Fractal Fract. 2025, 9(5), 267; https://doi.org/10.3390/fractalfract9050267 - 22 Apr 2025
Abstract
To address the limitations of traditional tumor diagnostic methods in image feature extraction and model generalization, this study innovatively proposes a synergistic diagnostic model that integrates fractional Fourier transform (FrFT) and error back-propagation (BP) neural networks. The model leverages the time–frequency analysis capability
[...] Read more.
To address the limitations of traditional tumor diagnostic methods in image feature extraction and model generalization, this study innovatively proposes a synergistic diagnostic model that integrates fractional Fourier transform (FrFT) and error back-propagation (BP) neural networks. The model leverages the time–frequency analysis capability of FrFT and incorporates the fractal characteristics observed during tumor proliferation, effectively enhancing multi-scale feature extraction and representation. Experimental results show that the proposed model achieves an accuracy of 93.177% in classifying benign and malignant tumors, outperforming the support vector machine (SVM) method. The integration of FrFT improves feature distinguishability and reduces dependence on manual extraction. This study not only represents a breakthrough in tumor diagnostic technology but also paves new avenues for the application of fractional calculus and fractal geometry in medical image analysis. The findings show great potential for clinical application and future development.
Full article
(This article belongs to the Special Issue Fractal and Fractional Analysis in Biomedical Sciences and Engineering)
►▼
Show Figures
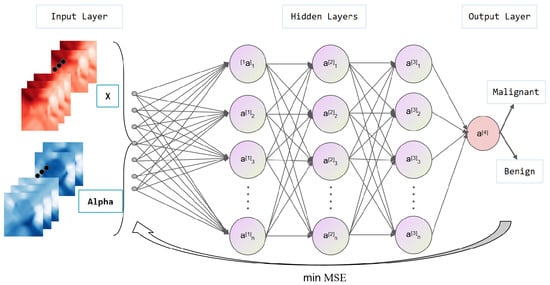
Figure 1
Open AccessArticle
Pore Fractal and Structure Analysis of Pore-Filling Chlorite in Continental Shales: A Case Study from the Qingshankou Formation in the Gulong Sag
by
Yuan Kang, Rukai Zhu, Kouqi Liu, Jingya Zhang and Chang Liu
Fractal Fract. 2025, 9(4), 266; https://doi.org/10.3390/fractalfract9040266 - 21 Apr 2025
Abstract
The successful exploration and development of shale oil in the clay-rich Gulong shale have sparked increased research into the influence of clay minerals on shale reservoirs. However, compared to chlorite in sandstones, limited studies have focused on the occurrence of chlorite in continental
[...] Read more.
The successful exploration and development of shale oil in the clay-rich Gulong shale have sparked increased research into the influence of clay minerals on shale reservoirs. However, compared to chlorite in sandstones, limited studies have focused on the occurrence of chlorite in continental shales and its effects on shale reservoir properties. This study offers a comprehensive analysis of chlorite in Gulong shale samples from three wells at different diagenetic stages. Four primary chlorite occurrences are identified in the Gulong shale: Type I, which is chlorite filling dissolved pores in carbonate; Type II, which is isolated chlorite; Type III, which is chlorite filling organic matter; and Type IV, which is chlorite filling authigenic microquartz. Types I and III chlorites exhibit higher porosity, offering more storage space for shale reservoirs. Chlorites of Types I, III, and IV, filled with other substances, display higher fractal dimensions, indicating more complex pore structures. These complex pores are favorable for oil adsorption but hinder oil seepage. The processes of organic matter expulsion and dissolution, which intensify with increasing diagenesis, promote the development of Types I and III chlorites, thereby positively influencing the shale reservoir porosity of Gulong shale. This study underscores the influence of chlorite occurrences on shale reservoir properties, providing valuable insights for the future exploration and development of shale oil and gas.
Full article
(This article belongs to the Special Issue Pore Structure and Fractal Characteristics in Unconventional Oil and Gas Reservoirs)
►▼
Show Figures
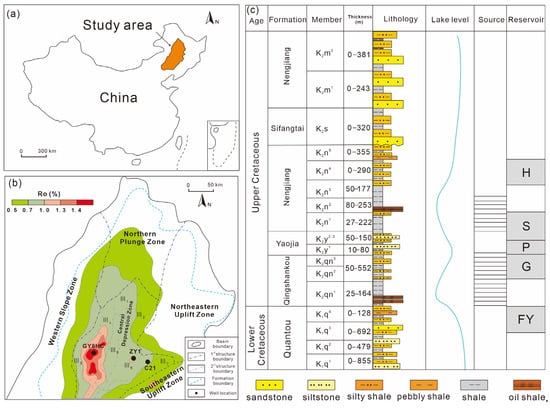
Figure 1
Open AccessArticle
Characterization of Pore Heterogeneity in Lacustrine Shale Based on MIP, LTNA, NMR, and Multifractal Characteristics: A Case Study of the Jurassic Dongyuemiao Member, China
by
Xu Wu, Yifan Gu, Yuqiang Jiang, Zhanlei Wang and Yonghong Fu
Fractal Fract. 2025, 9(4), 265; https://doi.org/10.3390/fractalfract9040265 - 21 Apr 2025
Abstract
Pore structure plays a critical role in evaluating shale “sweet spots”. Compared to marine shale, lacustrine shale has more diverse lithofacies types and greater heterogeneity in pore structure due to frequently changing environmental conditions. Using methods such as mercury intrusion porosimetry (MIP), field
[...] Read more.
Pore structure plays a critical role in evaluating shale “sweet spots”. Compared to marine shale, lacustrine shale has more diverse lithofacies types and greater heterogeneity in pore structure due to frequently changing environmental conditions. Using methods such as mercury intrusion porosimetry (MIP), field emission scanning electron microscopy (FE-SEM), nuclear magnetic resonance (NMR), and X-ray diffraction (XRD), this study investigates the micropore structures and heterogeneity of different lithofacies in the Jurassic Dongyuemiao Member lacustrine shale. Image processing and multifractal theory were employed to identify the controlling factors of pore structure heterogeneity. The key findings are as follows. (1) Based on mineral content and laminae types, the lithofacies types of Dongyuemiao lacustrine shale are classified into four types: shell–laminae mixed shale (SLMS), silty–laminae clay shale (SLCS), clast–laminae clay shale (CLCS), and clay shale (CS). (2) Based on genesis, shale reservoirs’ pore and permeability space are categorized into inorganic pores, organic pores, and micro-fractures. Inorganic pores consist of inter-particle pores and intra-particle pores. Pore size distribution curves for all four lithofacies exhibit two main peaks, with pore sizes concentrated in the ranges of 2–10 nm and 50–80 nm. Mesopores and macropores dominate, accounting for over 80% of the total pore volume. Mesopores are most developed in CLCS, representing 56.3%. (3) Quartz content is positively correlated with the multifractal dimension, while clay content shows a negative correlation. Higher quartz content, coupled with lower clay content, weakens pore structure heterogeneity. A negative correlation exists between total organic carbon (TOC) and the multifractal dimension, indicating that higher organic matter content enhances organic pore development and increases microscopic heterogeneity. (4) Porosity heterogeneity in SLMS is effectively characterized by D0-Dmax, while in the other three lithofacies, it is characterized by Dmin-D0. Permeability across all lithofacies correlates with D0-Dmax. In CS, SLMS, and SLCS, permeability is positively correlated with D0-Dmax, with higher values indicating greater permeability heterogeneity. In CLCS, permeability is negatively correlated with D0-Dmax, such that lower values reflect stronger heterogeneity.
Full article
(This article belongs to the Special Issue Pore Structure and Fractal Characteristics in Unconventional Oil and Gas Reservoirs)
►▼
Show Figures
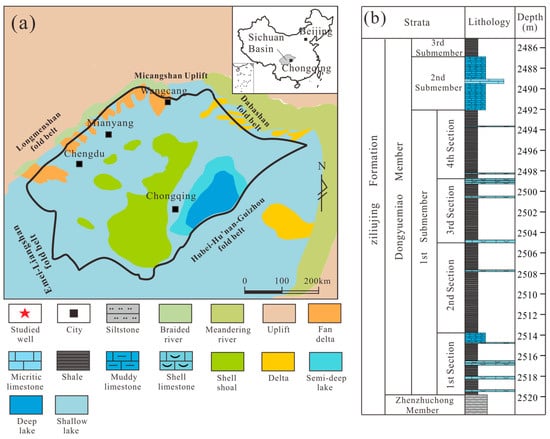
Figure 1
Open AccessArticle
A Simple Fractional Model with Unusual Dynamics in the Derivative Order
by
Guillermo Fernández-Anaya, Francisco A. Godínez, Rogelio Valdés, Luis Alberto Quezada-Téllez and M. A. Polo-Labarrios
Fractal Fract. 2025, 9(4), 264; https://doi.org/10.3390/fractalfract9040264 - 21 Apr 2025
Abstract
Fractional variable order systems with unusual dynamics in the order are a little-studied topic. In this study, we present three examples of very simple fractional systems with unusual dynamics in the derivative order. These cases involve different approaches to define the variable-order dynamics:
[...] Read more.
Fractional variable order systems with unusual dynamics in the order are a little-studied topic. In this study, we present three examples of very simple fractional systems with unusual dynamics in the derivative order. These cases involve different approaches to define the variable-order dynamics: (1) an integer-order differential equation that includes the state variable, (2) a differential equation that incorporates the state variable and features both integer- and fractional-order derivatives, and (3) fractional variable-order differential equations nested in the derivative orders. We prove a result that shows how the extended recursion of the last case is generalized. These examples illustrate the richness that simple dynamical systems can reveal through the order of their derivatives.
Full article
(This article belongs to the Special Issue Applications of Fractional Calculus in Modern Mathematical Modeling)
►▼
Show Figures
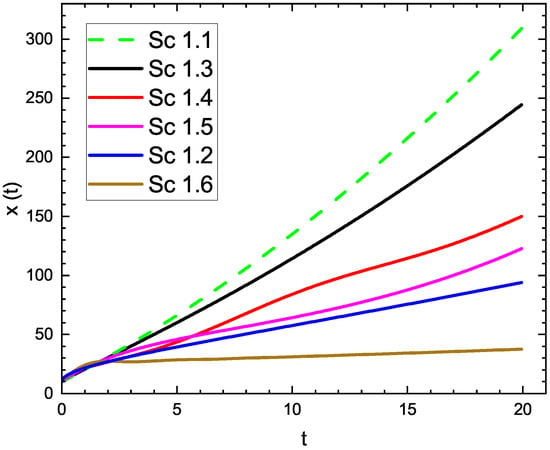
Figure 1
Open AccessArticle
Pore–Fracture Structure and Fractal Features of Carboniferous Taiyuan Formation Hydrocarbon Source Rocks as Investigated Using MICP, LFNMR, and FESEM
by
Dun Wu, Liu Zhao, Guangqing Hu and Wenyong Zhang
Fractal Fract. 2025, 9(4), 263; https://doi.org/10.3390/fractalfract9040263 - 20 Apr 2025
Abstract
The pore structure of reservoir rocks was a crucial factor affecting hydrocarbon production. Accurately characterized the micropore structure of different types of rock reservoirs was of great significance for unconventional natural gas exploration. In this study, multiple observation methods (field emission scanning electron
[...] Read more.
The pore structure of reservoir rocks was a crucial factor affecting hydrocarbon production. Accurately characterized the micropore structure of different types of rock reservoirs was of great significance for unconventional natural gas exploration. In this study, multiple observation methods (field emission scanning electron microscope (FESEM) and low-field nuclear magnetic resonance (LFNMR)) and physical tests (mercury injection capillary pressure (MICP)) were employed, and double logarithmic plots for fractal fitting were illustrated. The fractal dimension of 15 samples was calculated using fractal theory to systematically investigate the pore–fracture structure and fractal characteristics of hydrocarbon source rock (limestone, mudstone, and sandstone) samples from the Late Carboniferous Taiyuan Formation in the Huainan coalfield. MICP experiments revealed that sandstone reservoirs had larger and more uniformly distributed pore throats compared to mudstone and limestone, exhibiting superior connectivity and permeability. The T2 spectrum characteristic maps obtained using LFNMR were also consistent with the pore distribution patterns derived from MICP experiments, particularly showed that sandstone types exhibited excellent signal intensity across different relaxation time periods and had a broader T2 spectrum width, which fully indicated that sandstone types possess superior pore structures and higher connectivity. FESEM experiments demonstrated that sandstone pores were highly developed and uniform, with sandstone fractures dominated by large fractures above the micrometer scale. Meanwhile, the FESEM fractal dimension results indicated that sandstone exhibits good fractal characteristics, validating its certain oil storage capacity. Furthermore, the FESEM fractal dimension exhibited a good correlation with the porosity and permeability of the hydrocarbon source rock reservoirs, suggesting that the FESEM fractal dimension can serve as an important parameter for evaluating the physical properties of hydrocarbon source rock reservoirs. This study enriched the basic geological theories for unconventional natural gas exploration in deep coal-bearing strata in the Huainan coalfield.
Full article
(This article belongs to the Special Issue Pore Structure and Fractal Characteristics in Unconventional Oil and Gas Reservoirs)
►▼
Show Figures
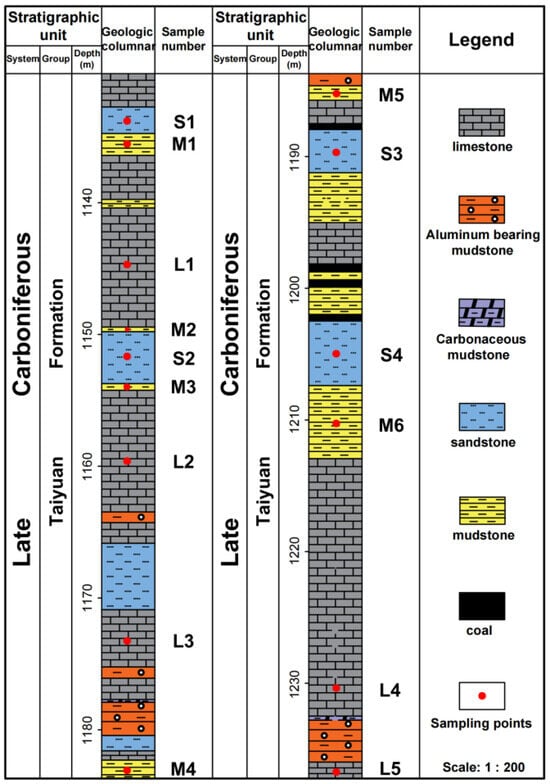
Figure 1
Open AccessArticle
Fractional Order Grey Model of Optimization Investment Allocation for Maximum Value Addition in Beijing’s High-Tech Industries
by
Zhenxiu Liu, Lukang Jia and Lifeng Wu
Fractal Fract. 2025, 9(4), 262; https://doi.org/10.3390/fractalfract9040262 - 19 Apr 2025
Abstract
High-tech industries are of strategic importance to the national economy, and Beijing has been designated as a science and technology innovation center by the State Council. Accurate analysis of its added value is crucial for technological development. While recent data enhance prediction accuracy,
[...] Read more.
High-tech industries are of strategic importance to the national economy, and Beijing has been designated as a science and technology innovation center by the State Council. Accurate analysis of its added value is crucial for technological development. While recent data enhance prediction accuracy, its limited volume poses challenges. The cumulative grey Lotka–Volterra model and grey differential dynamic multivariate model address this by leveraging short-term data effectively. This study applies these two models to analyze influencing factors and predict Beijing’s high-tech industry growth. Results show a competitive relationship with four systems, lacking synergy. In the next five years, a mutually beneficial trend is expected. The Mean Absolute Percentage Error (MAPE) remains within 10%, confirming the model’s reliability.
Full article
(This article belongs to the Special Issue Applications of Fractional-Order Grey Models)
►▼
Show Figures
Figure 1
Open AccessArticle
Positive Properties of Green’s Function for Fractional Dirichlet Boundary Value Problem with a Perturbation Term and Its Applications
by
Yongqing Wang
Fractal Fract. 2025, 9(4), 261; https://doi.org/10.3390/fractalfract9040261 - 19 Apr 2025
Abstract
In this article, we study a fractional lower-order differential equation,
[...] Read more.
In this article, we study a fractional lower-order differential equation,
(This article belongs to the Special Issue Advances in Boundary Value Problems for Fractional Differential Equations, 3rd Edition)
Open AccessArticle
A Comparative Analysis of Different Fractional Optimal Control Strategies to Eradicate Bayoud Disease in Date Palm Trees
by
Muhammad Imran, Azhar Iqbal Kashif Butt, Brett Allen McKinney, Muneerah Al Nuwairan, Fatemah H. H. Al Mukahal and Saira Batool
Fractal Fract. 2025, 9(4), 260; https://doi.org/10.3390/fractalfract9040260 - 18 Apr 2025
Abstract
►▼
Show Figures
Bayoud disease, caused by Fusarium oxysporum f. sp. albedinis, is a major threat to date palm trees. It leads to lower crop yields, financial losses, and decreased biodiversity. The complexity of the disease presents challenges to effective disease management. This study introduces a
[...] Read more.
Bayoud disease, caused by Fusarium oxysporum f. sp. albedinis, is a major threat to date palm trees. It leads to lower crop yields, financial losses, and decreased biodiversity. The complexity of the disease presents challenges to effective disease management. This study introduces a mathematical model comprising six compartments for palm trees: susceptible trees, resistant varieties, exposed trees, infected trees, isolated trees under treatment, and recovered trees, along with a contaminant water compartment. The model emphasizes the role of resistant varieties, contamination of irrigation water, and the treatment of infected trees in disease control. Theoretical analyses guarantee positivity, boundedness, and the existence of a unique solution. The existence of equilibrium points (disease-free and endemic) and the reproduction number (
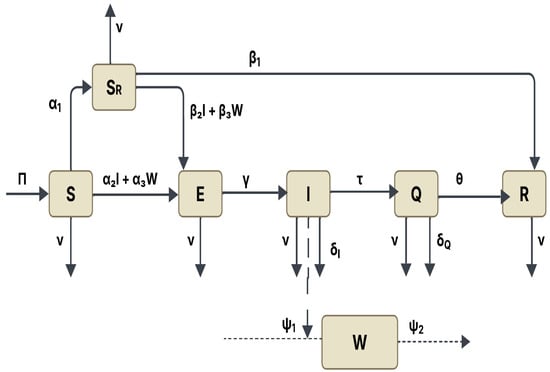
Figure 1
Open AccessArticle
Qualitative Analysis of a Three-Dimensional Dynamical System of Fractal-Fractional-Order Evolution Differential Equations with Terminal Boundary Conditions
by
F. Gassem, Arshad Ali, Khaled Aldwoah, Ria H. Egami, Osman Osman, Bakri Younis and Amel Touati
Fractal Fract. 2025, 9(4), 259; https://doi.org/10.3390/fractalfract9040259 - 18 Apr 2025
Abstract
In this research article, we investigate a three-dimensional dynamical system governed by fractal-fractional-order evolution differential equations subject to terminal boundary conditions. We derive existence and uniqueness results using Schaefer’s and Banach’s fixed-point theorems, respectively. Additionally, the Hyers–Ulam stability approach is employed to analyze
[...] Read more.
In this research article, we investigate a three-dimensional dynamical system governed by fractal-fractional-order evolution differential equations subject to terminal boundary conditions. We derive existence and uniqueness results using Schaefer’s and Banach’s fixed-point theorems, respectively. Additionally, the Hyers–Ulam stability approach is employed to analyze the system’s stability. We employ vector terminology for the proposed problem to make the analysis simple. To illustrate the practical relevance of our findings, we apply the derived results to a numerical example and graphically illustrate the solution for different fractal-fractional orders, emphasizing the effect of the derivative’s order on system behavior.
Full article
(This article belongs to the Special Issue Boundary Value Problems for Nonlinear Fractional Differential Equations: Theory, Methods and Application)
►▼
Show Figures
Figure 1
Open AccessArticle
ϑ-Fractional Stochastic Models for Simulating Tumor Growth and Chemical Diffusion in Biological Tissues
by
Ahmed Ghezal and Najmeddine Attia
Fractal Fract. 2025, 9(4), 258; https://doi.org/10.3390/fractalfract9040258 - 18 Apr 2025
Abstract
This paper presents an advanced simulation-based investigation of tumor growth and chemical diffusion in biological tissues, using
This paper presents an advanced simulation-based investigation of tumor growth and chemical diffusion in biological tissues, using
(This article belongs to the Special Issue Fractal and Fractional Analysis in Biomedical Sciences and Engineering)
►▼
Show Figures
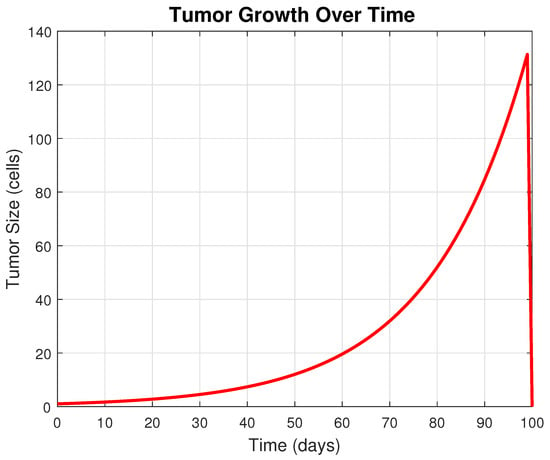
Figure 1
Open AccessArticle
Fractal Analysis of Organic Matter Nanopore Structure in Tectonically Deformed Shales
by
Mingliang Liang, Min Dong, Zongxiu Wang, Kaixun Zhang, Xiaoshi Li and Xingqiang Feng
Fractal Fract. 2025, 9(4), 257; https://doi.org/10.3390/fractalfract9040257 - 18 Apr 2025
Abstract
Fractal analysis was used to characterize the organic matter nanopore structure in tectonically deformed shales, providing insights into the heterogeneity and complexity of the pore network. Shale samples from different tectonic deformation styles (undeformed, brittle deformed, and ductile deformed) in the Lower Cambrian
[...] Read more.
Fractal analysis was used to characterize the organic matter nanopore structure in tectonically deformed shales, providing insights into the heterogeneity and complexity of the pore network. Shale samples from different tectonic deformation styles (undeformed, brittle deformed, and ductile deformed) in the Lower Cambrian Niutitang Formation in western Hunan, South China, were collected. By comprehensively applying techniques such as low-temperature gaseous (CO2 and N2) adsorption (LTGA), scanning electron microscopy (SEM), and ImageJ analysis, we accurately obtained key parameters of the pore structure. The results show ductile deformation reduces fractal dimension (DM) by ~0.2 compared to brittle deformed shale, reflecting the homogenization of organic nanopore structures. Brittle deformation leads to a more complex pore network, while ductile deformation reduces the complexity of the organic nanopore structure. The fractal dimensions are affected by various factors, with micropore development being crucial for undeformed shale, clay and pore length–width ratio dominating in brittle deformed shale, and all-scale pores being key for ductile deformed shale. This study provides the first comparative analysis of fractal dimensions across undeformed, brittle deformed, and ductile deformed shales, revealing distinct pore structure modifications linked to deformation styles. These findings not only enhance our understanding of the influence mechanism of tectonic deformation on shale pore structure and fractal characteristics but also provide a theoretical basis for optimizing shale gas exploration and production strategies. These findings offer a framework for predicting gas storage and flow dynamics in tectonically complex shale reservoirs. For instance, in areas with different tectonic deformation styles, we can better evaluate the gas storage capacity and production potential of shale reservoirs according to the obtained fractal characteristics, which is of great significance for efficient shale gas development.
Full article
(This article belongs to the Special Issue Pore Structure and Fractal Characteristics in Unconventional Oil and Gas Reservoirs)
►▼
Show Figures

Figure 1

Journal Menu
► ▼ Journal Menu-
- Fractal Fract Home
- Aims & Scope
- Editorial Board
- Reviewer Board
- Topical Advisory Panel
- Instructions for Authors
- Special Issues
- Topics
- Sections
- Article Processing Charge
- Indexing & Archiving
- Editor’s Choice Articles
- Most Cited & Viewed
- Journal Statistics
- Journal History
- Journal Awards
- Editorial Office
Journal Browser
► ▼ Journal BrowserHighly Accessed Articles
Latest Books
E-Mail Alert
News
Topics
Topic in
AppliedMath, Axioms, Fractal Fract, MCA, Mathematics, Symmetry
Fractional Calculus, Symmetry Phenomenon and Probability Theory for PDEs, and ODEs
Topic Editors: Renhai Wang, Junesang ChoiDeadline: 30 April 2025
Topic in
Axioms, Computation, Fractal Fract, Mathematics, Symmetry
Fractional Calculus: Theory and Applications, 2nd Edition
Topic Editors: António Lopes, Liping Chen, Sergio Adriani David, Alireza AlfiDeadline: 31 May 2025
Topic in
Algorithms, Axioms, Fractal Fract, Mathematics, Symmetry
Fractal and Design of Multipoint Iterative Methods for Nonlinear Problems
Topic Editors: Xiaofeng Wang, Fazlollah SoleymaniDeadline: 30 June 2025
Topic in
Atmosphere, Earth, Encyclopedia, Entropy, Fractal Fract, MAKE, Meteorology
Revisiting Butterfly Effect, Multiscale Dynamics, and Predictability Using Ai-Enhanced Modeling Framework (AEMF) and Chaos Theory
Topic Editors: Bo-Wen Shen, Roger A. Pielke Sr., Xubin ZengDeadline: 31 July 2025

Conferences
Special Issues
Special Issue in
Fractal Fract
Applications of Fractals and Fractional Calculus in Nuclear Reactors
Guest Editor: Gilberto Espinosa ParedesDeadline: 25 April 2025
Special Issue in
Fractal Fract
Fractional-Order Controllers in Electronics and Automation Engineering
Guest Editors: Allan G. Soriano-Sánchez, Didier López-MancillaDeadline: 30 April 2025
Special Issue in
Fractal Fract
Enhancing Pain Assessment and Anesthesia Management: Fractional Modeling with AI
Guest Editor: Martine NeckebroekDeadline: 30 April 2025
Special Issue in
Fractal Fract
Fractal Analysis and Its Applications in Materials Science
Guest Editor: Zine El Abiddine FellahDeadline: 30 April 2025





