Utilizing Fractals for Modeling and 3D Printing of Porous Structures
Abstract
:1. Introduction
2. Settings of IFS-Based Fractals
| Algorithm 1 The main processes of the IFS |
 |
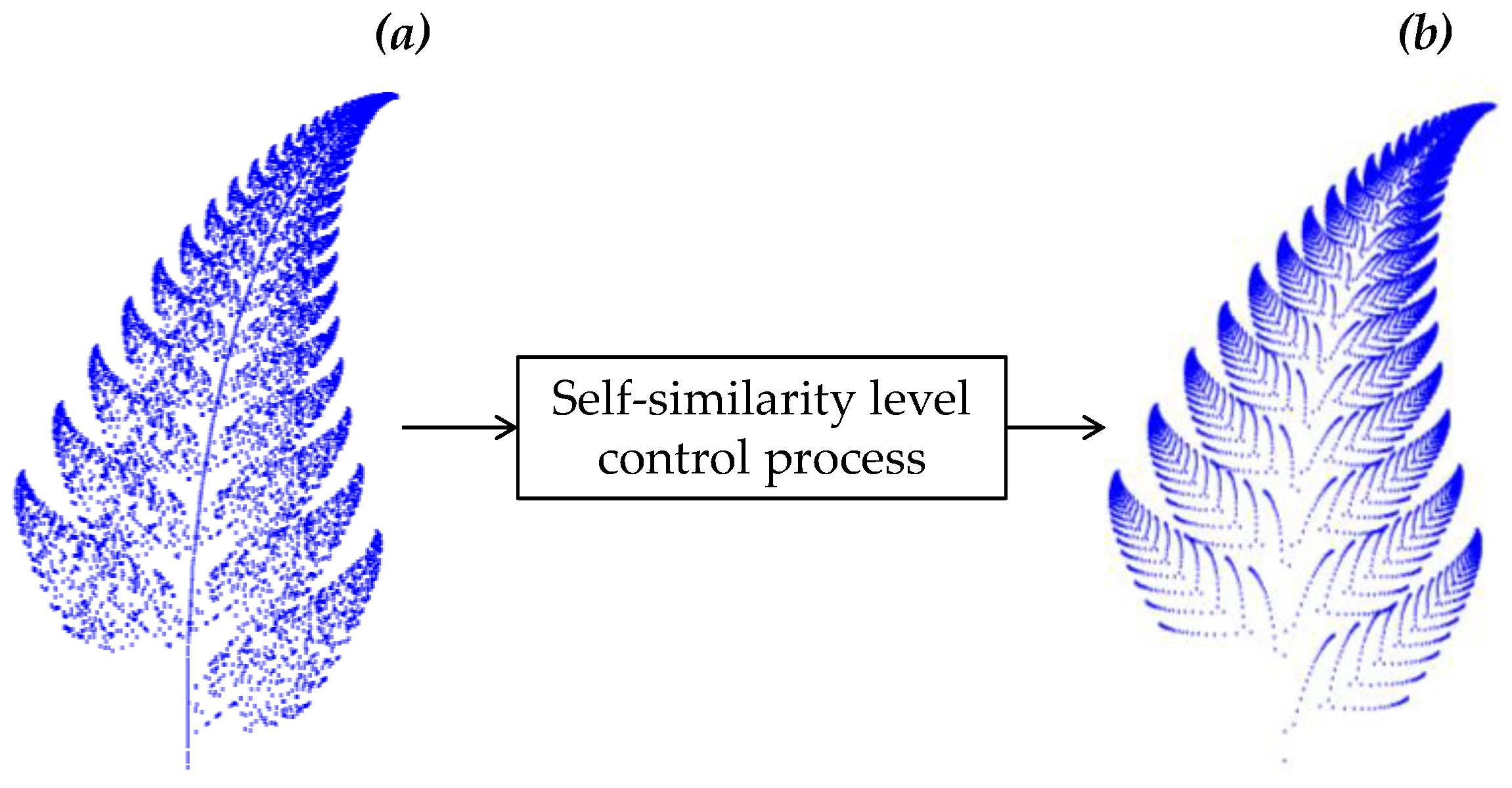
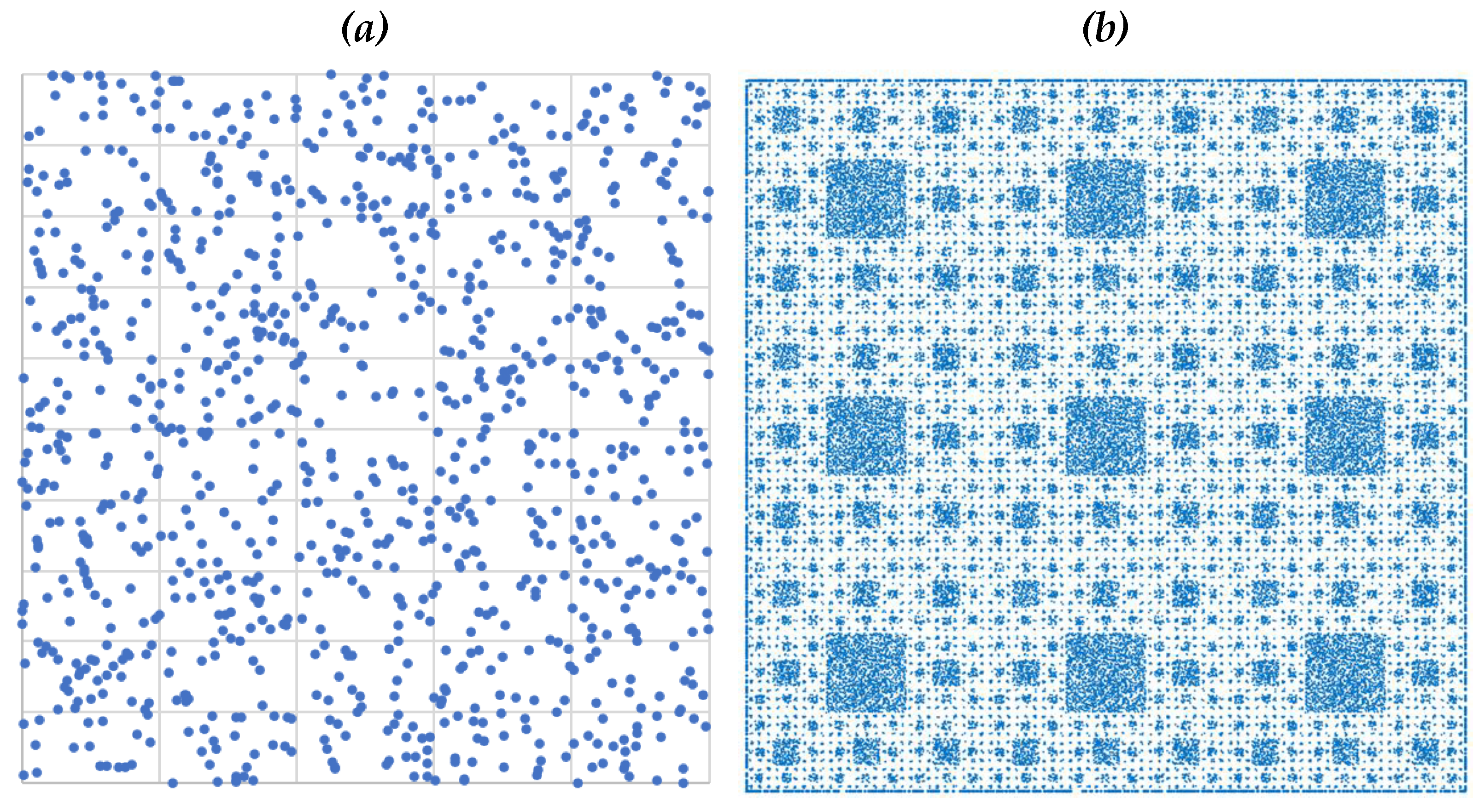
3. Controlling Self-Similarity Levels
| Algorithm 2 IFS-inspired mapping |
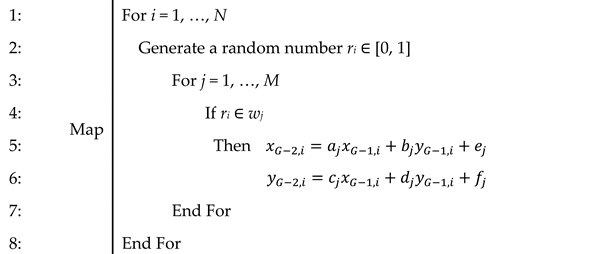 |
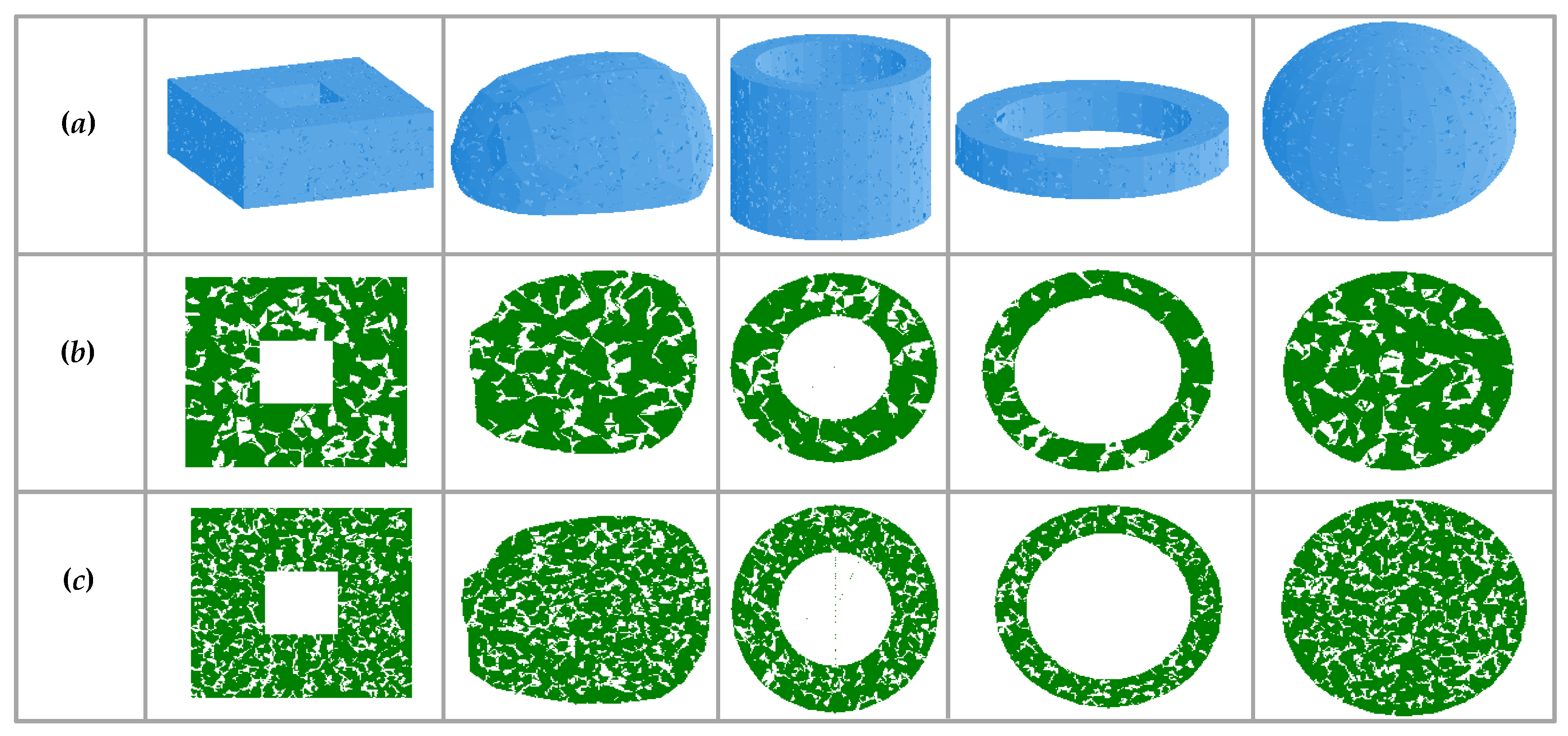
4. Modeling Porous Structures Using Sierpinski Carpet
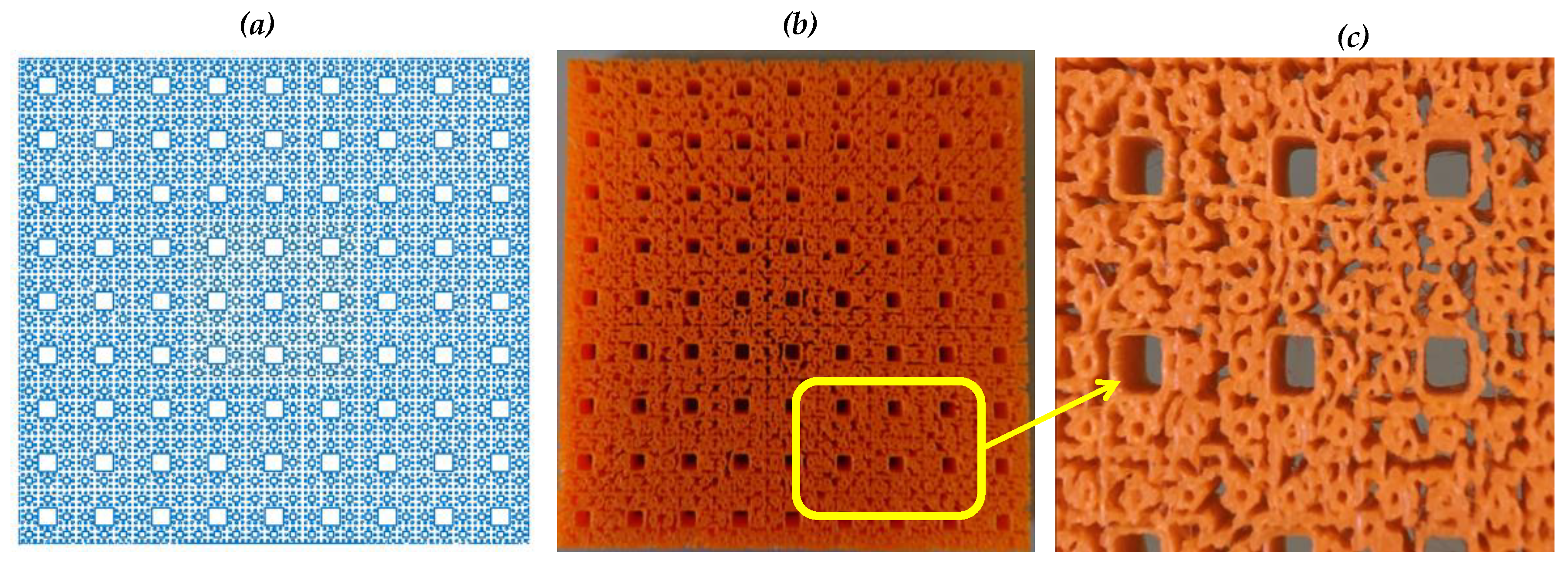
5. Solid Modeling and 3D Printing
6. Concluding Remarks
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman: New York, NY, USA, 1983. [Google Scholar]
- Frame, M.; Urry, A. Fractal Worlds: Grown, Built, and Imagined; Yale University Press: New Haven, CT, USA, 2016. [Google Scholar]
- Alan, F. Applications of fractal geometry to biology. Bioinformatics 1992, 8, 359–366. [Google Scholar]
- Otaki, J.M. The Fractal Geometry of the Nymphalid Groundplan: Self-Similar Configuration of Color Pattern Symmetry Systems in Butterfly Wings. Insects 2021, 12, 39. [Google Scholar] [CrossRef] [PubMed]
- Werner, D.H.; Haupt, R.L.; Werner, P.L. Fractal antenna engineering: The theory and design of fractal antenna arrays. IEEE Antennas Propag. Mag. 1999, 41, 37–58. [Google Scholar] [CrossRef] [Green Version]
- Mohanty, A.; Behera, B.R. Insights on radiation modes and pattern diversity of two element UWB fractal MIMO antenna using theory of characteristics modes analysis. AEU Int. J. Electron. Commun. 2021, 135, 153726. [Google Scholar] [CrossRef]
- Rmili, H.; Oueslati, D.; Ladhar, L.; Sheikh, M. Design of a chipless RFID tags based on natural fractal geometries for security applications. Microw. Opt. Technol. Lett. 2016, 58, 75–82. [Google Scholar] [CrossRef]
- Çalışkan, A.; Çevik, U. Three-dimensional modeling in medical image processing by using fractal geometry. J. Comput. 2017, 12, 479–485. [Google Scholar] [CrossRef]
- Goel, B.D.; Kwatra, S.C. A Data Compression Algorithm for Color Images Based on Run-Length Coding and Fractal Geometry. In Proceedings of the IEEE International Conference on Communications, Spanning the Universe, Philadelphia, PA, USA, 12–15 June 1988; Volume 3, pp. 1253–1256. [Google Scholar]
- Ludlow, D.K. Fractal Geometry Applications. In Particle Technology and Applications, 1st ed.; Lee, S., Henthorn, K.H., Eds.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Zhou, Z.; Su, Y.; Wang, W.; Yan, Y. Application of the fractal geometry theory on fracture network simulation. J. Petrol. Explor. Prod. Technol. 2017, 7, 487–496. [Google Scholar] [CrossRef] [Green Version]
- Katona, V. Relief Method: The Analysis of Architectonic Façades by Fractal Geometry. Buildings 2021, 11, 16. [Google Scholar] [CrossRef]
- Lee, M.S. Application of Fractal Geometry to Architectural Design. Archit. Res. 2014, 16, 175–183. [Google Scholar] [CrossRef] [Green Version]
- Mandelbrot, B.B. How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science 1967, 156, 636–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Avnir, D.; Farin, D.; Pfeifer, P. Molecular fractal surfaces. Nature 1984, 308, 261–263. [Google Scholar] [CrossRef]
- Pfeifer, P.; Avnir, D. Chemistry in noninteger dimensions between two and three: I. Fractal theory of heterogeneous surface. J. Chem. Phys. 1983, 79, 3558–3565. [Google Scholar] [CrossRef]
- Stewart, E. Towards numerically estimating Hausdorff dimensions. ANZIAM J. 2001, 42, 451–461. [Google Scholar] [CrossRef] [Green Version]
- Yong, H.; Changsong, S.; Xin, Y. Fractal signal processing method of acoustic emission monitoring for seismic damage of concrete columns. Int. J. Lifecycle Perform. Eng. 2019, 3, 59–76. [Google Scholar]
- Teti, R.; Segreto, T.; Caggiano, A.; Nele, L. Smart Multi-Sensor Monitoring in Drilling of CFRP/CFRP Composite Material Stacks for Aerospace Assembly Applications. Appl. Sci. 2020, 10, 758. [Google Scholar] [CrossRef] [Green Version]
- Namazi, H.; Qadri, M.O. Fractal-based analysis of the relation between tool wear and machine vibration in milling operations. Fractals 2020, 28, 2050101. [Google Scholar]
- Jiří, M.; Vladimír, B. Surface Roughness and Fractal Dimension. J. Text. Inst. 2001, 92, 91–113. [Google Scholar]
- Adcock, J.L.; Fulvio, P.F.; Dai, S. Towards the selective modification of soft-templated mesoporous carbon materials by elemental fluorine for energy storage devices. J. Mater. Chem. A 2013, 1, 9327–9331. [Google Scholar] [CrossRef]
- Xia, Y.; Yanga, Z.; Zhua, Y. Porous carbon-based materials for hydrogen storage: Advancement and challenges. J. Mater. Chem. A 2013, 1, 9365–9381. [Google Scholar] [CrossRef]
- Kalimuldina, G.; Nurpeissova, A.; Adylkhanova, A.; Issatayev, N.; Adair, D.; Bakenov, Z. 3D Hierarchical Nanocrystalline CuS Cathode for Lithium Batteries. Materials 2021, 14, 1615. [Google Scholar] [CrossRef] [PubMed]
- Pehlivan, E.; Džugan, J.; Fojt, J.; Sedláček, R.; Rzepa, S.; Daniel, M. Post-Processing Treatment Impact on Mechanical Properties of SLM Deposited Ti-6Al-4 V Porous Structure for Biomedical Application. Materials 2020, 13, 5167. [Google Scholar] [CrossRef]
- Hong, J.-Y.; Ko, S.-Y.; Lee, W.; Chang, Y.-Y.; Kim, S.-H.; Yun, J.-H. Enhancement of Bone Ingrowth into a Porous Titanium Structure to Improve Osseointegration of Dental Implants: A Pilot Study in the Canine Model. Materials 2020, 13, 3061. [Google Scholar] [CrossRef]
- Song, K.; Wang, Z.; Lan, J.; Ma, S. Porous structure design and mechanical behavior analysis based on TPMS for customized root analogue implant. J. Mech. Behav. Biomed. Mater. 2021, 115. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Mao, J.; Zhou, Y.; Ji, F.; Chen, X. Mechanical properties and osteoblast proliferation of complex porous dental implants filled with magnesium alloy based on 3D printing. J. Biomater. Appli. Sept. 2020. [Google Scholar] [CrossRef]
- Marco, M.; Belda, R.; Miguélez, M.H.; Giner, E. Numerical analysis of mechanical behaviour of lattice and porous structures. Compos. Struct. 2021, 261, 113292. [Google Scholar] [CrossRef]
- Ishibashi, S.; Shimada, K.; Kanetaka, H.; Tsukuda, M.; Mizoi, T.; Chuzenji, M.; Kikuchi, S.; Mizutani, M.; Kuriyagawa, T. Porosity and Tensile Properties of Rhizoid Porous Structure Fabricated Using Selective Laser Melting. Int. J. Autom. Technol. 2020, 14, 582–591. [Google Scholar] [CrossRef]
- Seto, Y.; Ullah, A.S.; Kubo, A.K.; D’Addona, D.M.; Teti, R. On the Porous Structuring using Unit Cells. Procedia CIRP 99C 2021. in print. [Google Scholar] [CrossRef]
- Zeng, Q.; Luo, M.; Pang, X.; Li, L.; Li, K. Surface fractal dimension: An indicator to characterize the microstructure of cement-based porous materials. Appl. Surface Sci. 2013, 282, 302–307. [Google Scholar] [CrossRef]
- Kim, J.; Choi, S. A fractal-based approach for reconstructing pore structures of GGBFS-blended cement pastes. Constr. Build. Mater. 2020, 265, 120350. [Google Scholar] [CrossRef]
- Gao, Y.; Wu, K.; Yuan, Q. Limited fractal behavior in cement paste upon mercury intrusion porosimetry test: Analysis and models. Constr. Build. Mater. 2021, 276, 122231. [Google Scholar] [CrossRef]
- Yang, J.; Liao, X.; Wang, G.; Chen, J.; Song, P.; Tang, W.; Guo, F.; Liu, F.; Li, G. Heterogeneous silicon rubber composite foam with gradient porous structure for highly absorbed ultra-efficient electromagnetic interference shielding. Compos. Sci. Technol. 2021, 206, 108663. [Google Scholar] [CrossRef]
- Neimark, A. A new approach to the determination of the surface fractal dimension of porous solids. Physica A Stat. Mechan. Appl. 1992, 191, 258–262. [Google Scholar] [CrossRef]
- Friesen, W.I.; Mikula, R.J. Fractal dimensions of coal particles. J. Colloid Interface Sci. 1987, 120, 263–271. [Google Scholar] [CrossRef]
- Zhang, B.; Li, S. Determination of the surface fractal dimension for porous media by mercury porosimetry. Ind. Eng. Chem. Res. 1995, 34, 1383–1386. [Google Scholar] [CrossRef]
- Zeng, Q.; Li, K.; Fen-Chong, T.; Dangla, P. Surface fractal analysis of pore structure of high-volume fly-ash cement pastes. Appl. Surface Sci. 2010, 257, 762–768. [Google Scholar] [CrossRef]
- Tang, S.; Huang, J.; Duan, L.; Yu, P.; Chen, E. A review on fractal footprint of cement-based materials. Powder Technol. 2020, 370, 237–250. [Google Scholar] [CrossRef]
- Wang, L.; Jin, M.; Wu, Y.; Zhou, Y.; Tang, S. Hydration, shrinkage, pore structure and fractal dimension of silica fume modified low heat Portland cement-based materials. Constr. Build. Mater. 2021, 272, 121952. [Google Scholar] [CrossRef]
- Wang, L.; Guo, F.; Yang, H. Comparison of fly ash, PVA fiber, MgO and shrinkage-reducing admixture on the frost resistance of face slab concrete via pore structural and fractal analysis. Fractals 2021, 29, 2140002. [Google Scholar] [CrossRef]
- Wang, L.; Luo, R.; Zhang, W. Effects of fineness and content of phosphorus slag on cement hydration, permeability, pore structure and fractal dimension of concrete. Fractals 2021, 29, 2140004. [Google Scholar] [CrossRef]
- Wang, L.; Jin, W.; Guo, F. Pore structural and fractal analysis of the influence of fly ash and silica fume on the mechanical property and abrasion resistance of concrete. Fractals 2021, 29, 2140003. [Google Scholar] [CrossRef]
- Ullah, A.S.; Tashi; Kubo, A.; Harib, K.H. Tutorials for Integrating 3D Printing in Engineering Curricula. Educ. Sci. 2020, 10, 194. [Google Scholar] [CrossRef]
- Liu, L.; Yang, X.; Bhandari, B.; Meng, Y.; Prakash, S. Optimization of the Formulation and Properties of 3D-Printed Complex Egg White Protein Objects. Foods 2020, 9, 164. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Awad, A.; Yao, A.; Trenfield, S.J.; Goyanes, A.; Gaisford, S.; Basit, A.W. 3D Printed Tablets (Printlets) with Braille and Moon Patterns for Visually Impaired Patients. Pharmaceutics 2020, 12, 172. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tao, Y.; Li, Z.; Li, P. A Design and Fabrication Method for Wood-Inspired Composites by Micro X-Ray Computed Tomography and 3D Printing. Appl. Sci. 2020, 10, 1400. [Google Scholar] [CrossRef] [Green Version]
- Tashi; Ullah, A.S. Symmetrical Patterns of Ainu Heritage and Their Virtual and Physical Prototyping. Symmetry 2019, 11, 985. [Google Scholar] [CrossRef] [Green Version]
- Takeuchi, Y. 3D Printable Hydroponics: A Digital Fabrication Pipeline for Soilless Plant Cultivation. IEEE Access 2019, 7, 35863–35873. [Google Scholar] [CrossRef]
- Saleh, M.S.; Li, J.; Park, J.; Panat, R. 3D printed hierarchically-porous microlattice electrode materials for exceptionally high specific capacity and areal capacity lithium ion batteries. Addit. Manuf. 2018, 23, 70–78. [Google Scholar] [CrossRef]
- Beecroft, M. 3D printing of weft knitted textile based structures by selective laser sintering of nylon powder. IOP Conf. Ser. Mater. Sci. Eng. 2016, 137, 012017. [Google Scholar] [CrossRef]
- Melnikova, R.; Ehrmann, A.; Finsterbusch, K. 3D printing of textile-based structures by Fused Deposition Modelling (FDM) with different polymer materials. IOP Conf. Ser. Mater. Sci. Eng. 2014, 62, 012018. [Google Scholar] [CrossRef] [Green Version]
- Skylar-Scott, M.A.; Gunasekaran, S.; Lewis, J.A. Laser-assisted direct ink writing of planar and 3D metal architectures. Proc. Natl. Acad. Sci. USA 2016, 113, 6137–6142. [Google Scholar] [CrossRef] [Green Version]
- Huber, T.; Clucas, D.; Vilmay, M.; Pupkes, B.; Stuart, J.; Dimartino, S.; Fee, C. 3D Printing Cellulose Hydrogels Using LASER Induced Thermal Gelation. J. Manuf. Mater. Process. 2018, 2, 42. [Google Scholar] [CrossRef] [Green Version]
- Elsayed, H.; Chmielarz, A.; Potoczek, M.; Fey, T.; Colombo, P. Direct ink writing of three dimensional Ti2AlC porous structures. Addit. Manuf. 2019, 28, 365–372. [Google Scholar]
- Barile, G.; Leoni, A.; Muttillo, M.; Paolucci, R.; Fazzini, G.; Pantoli, L. Fused-Deposition-Material 3D-Printing Procedure and Algorithm Avoiding Use of Any Supports. Sensors 2020, 20, 470. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.; Liu, K.; Yu, Z. Tetrahedron-Based Porous Scaffold Design for 3D Printing. Designs 2019, 3, 16. [Google Scholar] [CrossRef] [Green Version]
- Domínguez-Robles, J.; Mancinelli, C.; Mancuso, E.; García-Romero, I.; Gilmore, B.F.; Casettari, L.; Larrañeta, E.; Lamprou, D.A. 3D Printing of Drug-Loaded Thermoplastic Polyurethane Meshes: A Potential Material for Soft Tissue Reinforcement in Vaginal Surgery. Pharmaceutics 2020, 12, 63. [Google Scholar] [CrossRef] [Green Version]
- Vaneker, T.; Bernard, A.; Moroni, G.; Gibson, I.; Zhang, Y. Design for additive manufacturing: Framework and methodology. CIRP Annals 2020, 69, 578–599. [Google Scholar] [CrossRef]
- Sharif Ullah, A.M.M. Design for additive manufacturing of porous structures using stochastic point-cloud: A pragmatic approach. Comput. Aided Design Appl. 2018, 15, 138–146. [Google Scholar] [CrossRef]
- Sharif Ullah, A.M.M.; Hiroki, K.; Akihiko, K.; D’Addona, D.M. A system for designing and 3D printing of porous structures. CIRP Annals 2020, 69, 113–116. [Google Scholar] [CrossRef]
- Ambekar, R.S.; Mohanty, I.; Kishore, S.; Das, R.; Pal, V.; Kushwaha, B.; Roy, A.K.; Kumar Kar, S.; Tiwary, C.S. Atomic Scale Structure Inspired 3D-Printed Porous Structures with Tunable Mechanical Response. Adv. Eng. Mater. 2021, 2001428. [Google Scholar] [CrossRef]
- Sultan, S.; Mathew, A.P. 3D Printed Porous Cellulose Nanocomposite Hydrogel Scaffolds. J. Vis. Exp. 2019, 146, e59401. [Google Scholar] [CrossRef] [PubMed]
- Hui, M.; Yuanfu, T.; Weizhao, H.; Peng, C.; Yuntian, F.; Laifei, C. Structure design influencing the mechanical performance of 3D printing porous ceramics. Ceram. Int. 2021, 47, 8389–8397. [Google Scholar]
- Ming, L.; Liangchao, Z.; Jingzhi, L.; Kai, Z. Design optimization of interconnected porous structures using extended triply periodic minimal surfaces. J. Comput. Phys. 2021, 425, 109909. [Google Scholar]
- Zhang, X.-Y.; Fang, G.; Zhou, J. Additively Manufactured Scaffolds for Bone Tissue Engineering and the Prediction of their Mechanical Behavior: A Review. Materials 2017, 10, 50. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Fu, J.; Shang, C.; Lin, Z.; Li, B. Porous scaffold design by solid T-splines and triply periodic minimal surfaces. Comput. Methods Appl. Mechan. Eng. 2018, 336, 333–352. [Google Scholar] [CrossRef]
- King, P.; Masihi, M. Percolation in Porous Media. In Encyclopedia of Complexity and Systems Science; Meyers, R., Ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Ghouse, S.; Babu, S.; Nai, K.; Hooper, P.A.; Jeffers, J.R.T. The influence of laser parameters, scanning strategies and material on the fatigue strength of a stochastic porous structure. Addit. Manuf. 2018, 22, 290–301. [Google Scholar] [CrossRef]
- Barnsley, M.F.; Demko, S. Iterated function systems and the global construction of fractals. Proc. Royal Soc. London A Math. Phys. Sci. 1985, 399, 243–275. [Google Scholar]
- Ullah, A.M.M.S.; D’Addona, D.M.; Harib, K.H.; Lin, T. Fractals and Additive Manufacturing. Int. J. Autom. Technol. 2016, 10, 222–230. [Google Scholar] [CrossRef]
- Sharif Ullah, A.M.M.; Sato, Y.; Kubo, A.; Tamaki, J. Design for Manufacturing of IFS Fractals from the Perspective of Barnsley’s Fern-leaf. Comput. Aided Design Appl. 2015, 12, 241–255. [Google Scholar] [CrossRef]
- Riddle, L.; Sierpinski, C. 2020. Available online: http://larryriddle.agnesscott.org/ifs/carpet/carpet.htm (accessed on 27 February 2019).
- Yicha, Z.; Zhiping, W.; Yancheng, Z.; Samuel, G.; Alain, B. Bio-inspired generative design for support structure generation and optimization in Additive Manufacturing (AM). CIRP Annals 2020, 69, 117–120. [Google Scholar]
- Zhu, L.; Feng, R.; Li, X.; Xi, J.; Wei, X. Design of lightweight tree-shaped internal support structures for 3D printed shell models. Rapid Prototyp. J. 2019, 25, 1552–1564. [Google Scholar] [CrossRef]
- Sharif Ullah, A.M.M.; Omori, R.; Nagara, Y.; Kubo, A.; Tamaki, J. Toward Error-free Manufacturing of Fractals. Procedia CIRP 2013, 12, 43–48. [Google Scholar] [CrossRef]











| Parameters | Affine Maps | |||||||
|---|---|---|---|---|---|---|---|---|
| j = | ||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| aj | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 |
| bj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| cj | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| di | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 | 1/3 |
| ej | 0 | 0 | 0 | 1/3 | 1/3 | 2/3 | 2/3 | 2/3 |
| fj | 0 | 1/3 | 2/3 | 0 | 2/3 | 0 | 1/3 | 2/3 |
| pj | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 | 1/8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ullah, A.S.; D’Addona, D.M.; Seto, Y.; Yonehara, S.; Kubo, A. Utilizing Fractals for Modeling and 3D Printing of Porous Structures. Fractal Fract. 2021, 5, 40. https://doi.org/10.3390/fractalfract5020040
Ullah AS, D’Addona DM, Seto Y, Yonehara S, Kubo A. Utilizing Fractals for Modeling and 3D Printing of Porous Structures. Fractal and Fractional. 2021; 5(2):40. https://doi.org/10.3390/fractalfract5020040
Chicago/Turabian StyleUllah, AMM Sharif, Doriana Marilena D’Addona, Yusuke Seto, Shota Yonehara, and Akihiko Kubo. 2021. "Utilizing Fractals for Modeling and 3D Printing of Porous Structures" Fractal and Fractional 5, no. 2: 40. https://doi.org/10.3390/fractalfract5020040
APA StyleUllah, A. S., D’Addona, D. M., Seto, Y., Yonehara, S., & Kubo, A. (2021). Utilizing Fractals for Modeling and 3D Printing of Porous Structures. Fractal and Fractional, 5(2), 40. https://doi.org/10.3390/fractalfract5020040








