Exact Traveling Wave Solutions of the Local Fractional Bidirectional Propagation System Equations
Abstract
:1. Introduction
2. Brief of the Local Fractional Derivative
3. Exact Traveling Wave Solutions of Bidirectional Wave Equations
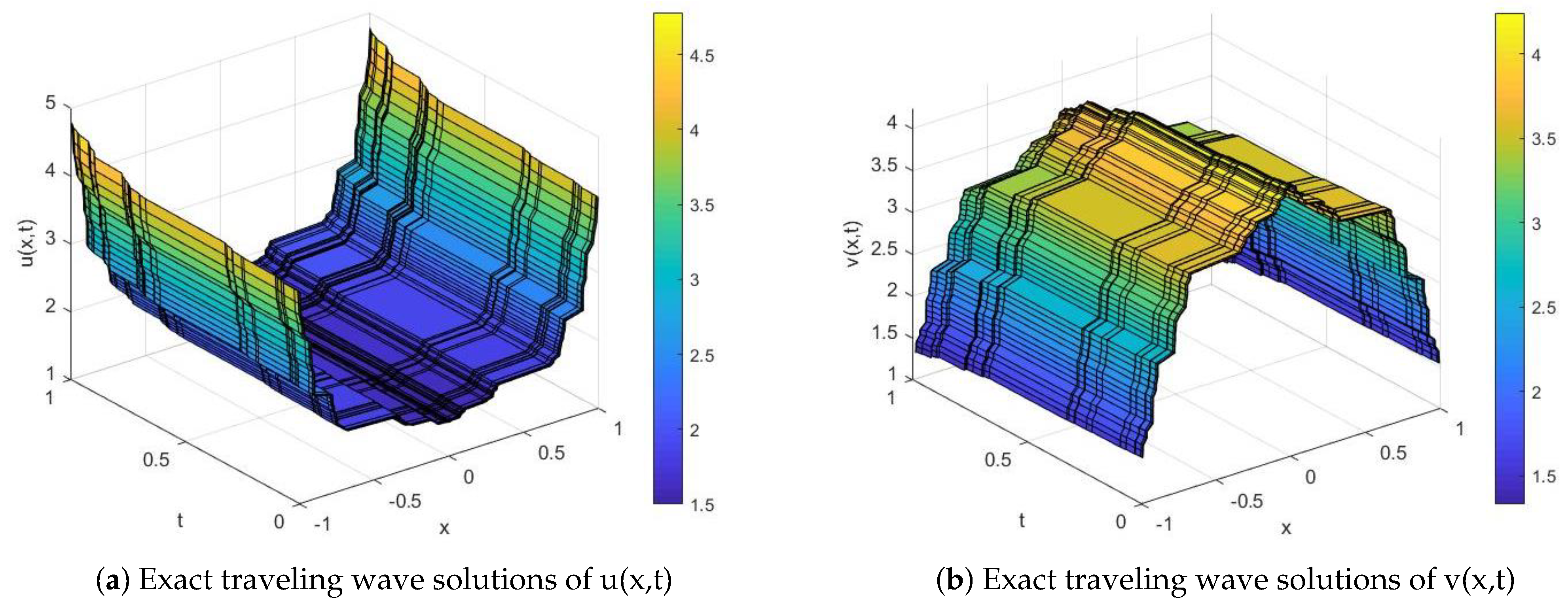
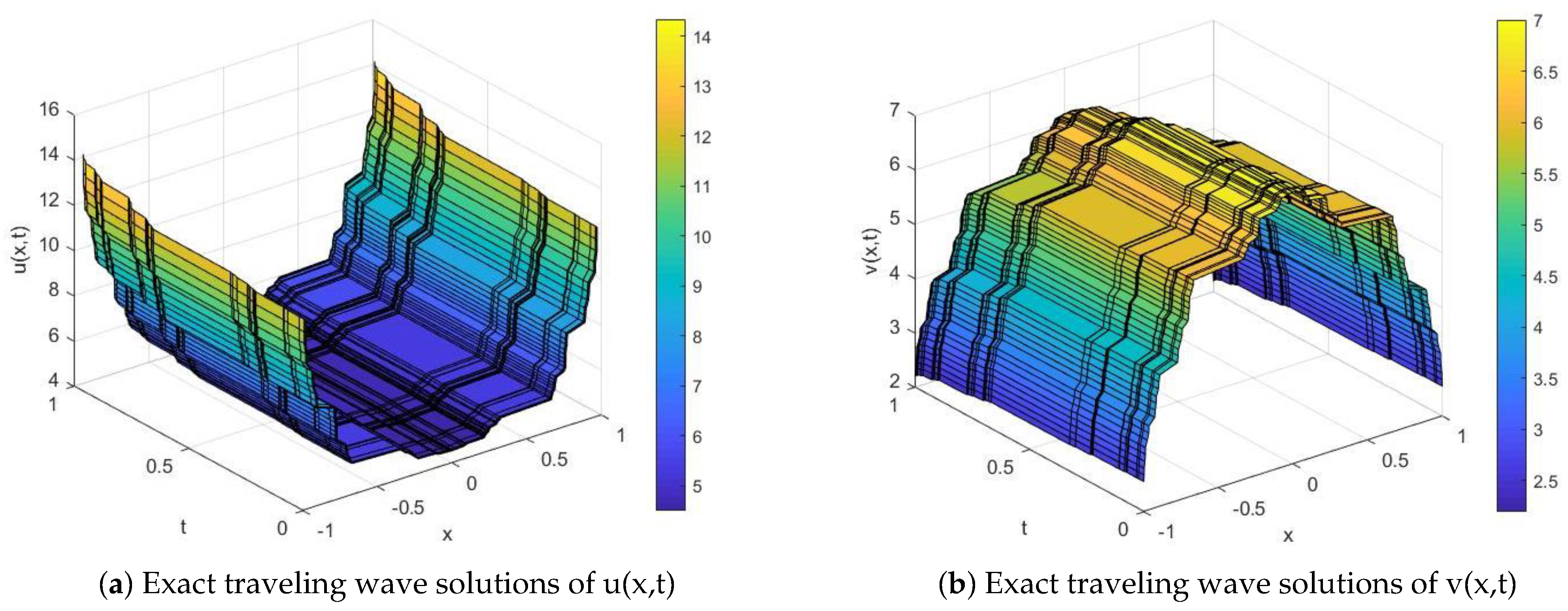
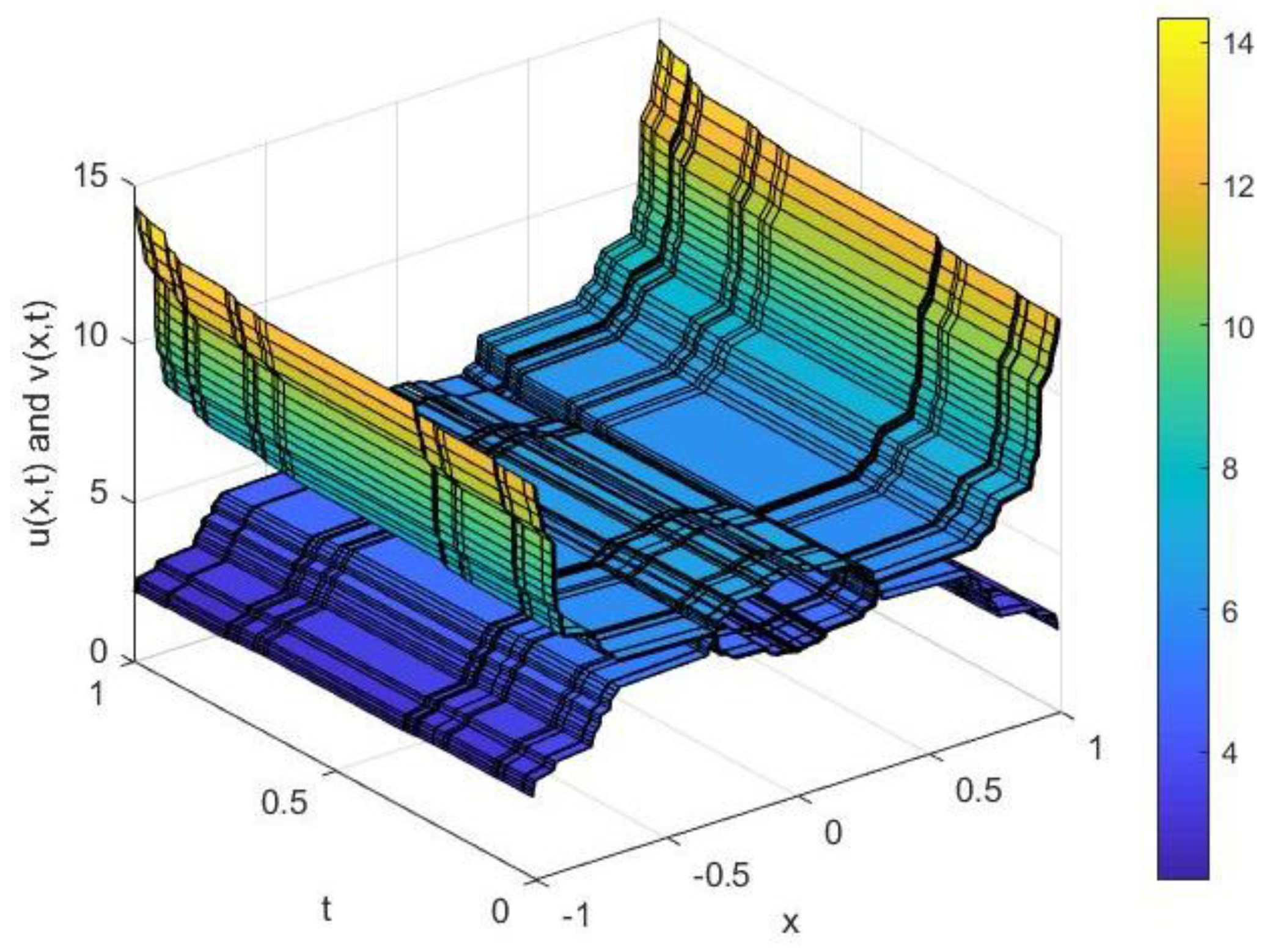
4. Discussion of the Solutions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer Science and Business Mediaew: New York, NY, USA, 2011; pp. 9–10. ISBN 978-3-642-14002-0. [Google Scholar]
- Momani, S.; Odibat, Z.; Alawneh, Z. Variational iteration method for solving the spaceand time-fractional KdV equation. Numer. Methods Partial. Differ. Equ. Int. J. 2008, 24, 262–271. [Google Scholar] [CrossRef]
- West, B.; Bologna, M.; Grigolini, P. Physics of fractal operators. In Institute for Nonlinear Science; Springer: New York, NY, USA, 2003; pp. 34–40. ISBN 978-0-387-21746-8. [Google Scholar]
- Mohyud-Din, S.T.; Yıldırım, A.; Yülüklü, E. Homotopy analysis method for space-and time-fractional KdV equation. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 928–941. [Google Scholar] [CrossRef]
- Yang, X.J. Advanced Local Fractional Calculus and Its Applications; World Science: New York, NY, USA, 2012; pp. 29–30. ISBN 978-1-938576-01-0. [Google Scholar]
- Kolwankar, K.M.; Gangal, A.D. Fractional differentiability of nowhere differentiable functions and dimensions. Chaos 1996, 6, 505–513. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractionaldifferential Equations North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006; Volume 204. [Google Scholar]
- Wang, K.L.; Wang, K.J.; He, C.H. Physical insight of local fractional calculus and its application to fractional KdV-Burgers-Kuramoto equation. Fractals 2019, 27, 1950122. [Google Scholar] [CrossRef]
- Iftikhar, S.; Kumam, P.; Erden, S. Newton’s-type integral inequalities via local fractiona integrals. Fractals 2020, 28, 20500372. [Google Scholar] [CrossRef]
- Yong, Z. Basic Theory of Fractional Differential Equations; World Scientific: Singapore, 2014; pp. 19–25. ISBN 978-8-813148-16-1. [Google Scholar]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Adomian, G. A review of the decomposition method and some recent results for nonlinear equations. J. Appl. Math. Comput. 1991, 21, 101–127. [Google Scholar] [CrossRef] [Green Version]
- Liao, S. On the homotopy analysis method for nonlinear problems. J. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Odibat, Z.; Sami Bataineh, A. An adaptation of homotopy analysis method for reliable treatment of strongly nonlinear problems: Construction of homotopy polynomials. Math. Methods Appl. Sci. 2015, 38, 991–1000. [Google Scholar] [CrossRef]
- Singh, J.; Ahmadian, A.; Rathore, S. An efficient computational approach for local fractional Poisson equation in fractal media. Numer. Methods Partial. Differ. Equ. 2020, 37, 1439–1448. [Google Scholar] [CrossRef]
- Yang, X.J.; Baleanu, D.; Srivastava, H.M. Local Fractional Integral Transforms and Their Applications; Academic Press: Cambridge, MA, USA, 2015; pp. 39–50. ISBN 978-0-12-804002-7. [Google Scholar]
- Gao, F.; Yang, X.J.; Ju, Y. Exact traveling-wave solutions for one-dimensional modified Korteweg-de Vries equation defined on Cantor sets. Fractals 2019, 27, 1940010. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.T.; Baleanu, D. Exact traveling-wave solution for local fractional Boussinesq equation in fractal domain. Fractals 2017, 25, 1740006. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J.; Gao, F.; Srivastava, H.M. Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations. Comput. Math. Appl. 2017, 73, 203–210. [Google Scholar] [CrossRef]
- Yang, X.J.; Machado, J.T.; Baleanu, D.; Cattani, C. On exact traveling-wave solutions for local fractional Korteweg-de Vries equation. Chaos Interdiscip. J. Nonlinear Sci. 2016, 26, 084312. [Google Scholar] [CrossRef]
- Chen, M. Exact traveling-wave solutions to bidirectional wave equations. Int. J. Theor. Phys. 1998, 37, 1547–1567. [Google Scholar] [CrossRef]
- Gorenflo, R.; Mainardi, F. Fractional Calculus: Integral and Differential Equations of Fractional Order. Mathematics 2008, 49, 277–290. [Google Scholar]
- Krni, M.; Vukovi, P. Multidimensional Hilbert-Type Inequalities Obtained via Local Fractional Calculus. Acta Appl. Math. 2020, 169, 667–680. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F.; Srivastava, H.M. Non-differentiable exact solutions for the nonlinear odes defined on fractal sets. Fractals 2017, 25, 1740002. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J.; Srivastava, H.M.; Torres, D.F.M.; Zhang, Y.D. Non-differentiable solutions for local fractional nonlinear Riccati differential equations. Fund. Inform. 2016, 145, 55–63. [Google Scholar] [CrossRef] [Green Version]
- Yang, X.J.; Gao, F.; Srivastava, H.M. New rheological models within local fractional derivative. Rom. Rep. Phys. 2017, 69, 113. [Google Scholar]
- Bona, J.L.; Saut, J.C.; Toland, J.F. Boussinesq equations for small-amplitude long wavelength water waves. Preprint 1997. [Google Scholar]
- Bona, J.L.; Smith, R. A model for the two-way propagation of water waves in a channel. MAthematical Proc. Camb. Philos. Soc. 1976, 79, 167–182. [Google Scholar] [CrossRef]
- Boussinesq, J. TheÂorie de l’intumescence liquide appeleÂe onde solitaire ou de translationse propageant dans un canal rectangulaire. Comptes Rendus L’Acadmie Sci. 1871, 72, 755–759. [Google Scholar]
- Newell, A.C. Finite amplitude instabilities of partial difference equations. SIAM J. Appl. Math. 1977, 33, 133–160. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sang, X.; Zhang, Z.; Yang, H.; Han, X. Exact Traveling Wave Solutions of the Local Fractional Bidirectional Propagation System Equations. Fractal Fract. 2022, 6, 653. https://doi.org/10.3390/fractalfract6110653
Sang X, Zhang Z, Yang H, Han X. Exact Traveling Wave Solutions of the Local Fractional Bidirectional Propagation System Equations. Fractal and Fractional. 2022; 6(11):653. https://doi.org/10.3390/fractalfract6110653
Chicago/Turabian StyleSang, Xue, Zongguo Zhang, Hongwei Yang, and Xiaofeng Han. 2022. "Exact Traveling Wave Solutions of the Local Fractional Bidirectional Propagation System Equations" Fractal and Fractional 6, no. 11: 653. https://doi.org/10.3390/fractalfract6110653





