Anomalous Thermally Induced Deformation in Kelvin–Voigt Plate with Ultrafast Double-Strip Surface Heating

Abstract

The Jeffreys-type heat conduction equation with flux precedence describes the temperature of diffusive hot electrons during the electron–phonon interaction process in metals. In this paper, the deformation resulting from ultrafast surface heating on a “nanoscale” plate is considered. The focus is on the anomalous heat transfer mechanisms that result from anomalous diffusion of hot electrons and are characterized by retarded thermal conduction, accelerated thermal conduction, or transition from super-thermal conductivity in the short-time response to sub-thermal conductivity in the long-time response and described by the fractional Jeffreys equation with three fractional parameters. The recent double-strip problem, Awad et al., Eur. Phy. J. Plus 2022, allowing the overlap between two propagating thermal waves, is generalized from the semi-infinite heat conductor case to thermoelastic case in the finite domain. The elastic response in the material is not simultaneous (i.e., not Hookean), rather it is assumed to be of the Kelvin–Voigt type, i.e., $\sigma =E\left(\epsilon +{\tau }_{\epsilon }\dot{\epsilon }\right)$, where $\sigma$ refers to the stress, $\epsilon$ is the strain, $E$ is the Young modulus, and ${\tau }_{\epsilon }$ refers to the strain relaxation time. The delayed strain response of the Kelvin–Voigt model eliminates the discontinuity of stresses, a hallmark of the Hookean solid. The immobilization of thermal conduction described by the ordinary Jeffreys equation of heat conduction is salient in metals when the heat flux precedence is considered. The absence of the finite speed thermal waves in the Kelvin–Voigt model results in a smooth stress surface during the heating process. The temperature contours and the displacement vector chart show that the anomalous heat transfer characterized by retardation or crossover from super- to sub-thermal conduction may disrupt the ultrafast laser heating of metals.

1. Introduction

In many physical situations, thermal conduction may encounter anomalous behavior deviating from the classical diffusive “Fourier” behavior, e.g., heat transfer in fractals, heterogeneous materials, metals with distributed impurities, and nanoscale materials [1,2,3,4,5,6]. Fractional kinetic equations are effective mathematical tools for modeling such anomalous behaviors [7,8,9,10,11,12,13,14,15,16,17,18,19]. A recent fractional version of the Jeffreys equation has been proposed in [20], and under certain circumstances, it can be connected to the continuous-time random walk scheme [21]. The fractional Jeffreys equation with three fractional parameters is a versatile mathematical tool describing many anomalous heat/mass transition behaviors, e.g., acceleration, retardation, and crossover from super- to subdiffusion.

The stresses generated in elastic materials due to thermal effects may cause the material to reach the yield point. Before the yield point, the linearized thermal stress theories with different heat conduction models [6,22,23,24] present successful initial engineering assessments for predicting the stresses and deformations in different types of thermal loadings and heat conductors. One of the earliest studies which presented a prediction of stress distribution induced by anomalous heat/mass transfer is the study of Povstenko [25]; see also the comprehensive monograph by the same author [26]. In [27,28,29,30], different forms of anomalous heat conduction models are adopted and the corresponding thermal stresses are computed. The main feature in most well known fractional heat conduction models is the disappearance of the finite thermal wave speed, with some exceptions to the Atangana–Baleanu fractional derivative [31,32].

The Kelvin–Voigt model is a crucial tool for defining and studying the viscoelastic behavior of certain solid materials in which there is a retardation time in the material response [33]. It differs from the Hookean solid in the retarded response of strain to an applied stress, namely, $\sigma =E\left(\epsilon +{\tau }_{\epsilon }\dot{\epsilon }\right)$, where ${\tau }_{\epsilon }$ is the retardation time, or the strain relaxation time [34]. When ${\tau }_{\epsilon }\to 0$, the Hookean response is recovered, i.e., $\sigma =E\epsilon$. The Kelvin–Voigt thermoelasticity has been considered in a variety of viscoelastic applications, e.g., unbounded thermoviscoelastic domain with spherical cavity [35], vibration of an Euler Bernoulli beam [36,37], and micropolar thermoelasticity [38], and has been extended to the second-gradient media [39].

In order to generalize the Danilovskaya problem in hyperbolic thermoelasticity [40,41] to the finite domains, El-Maghraby [42] solved the Lord–Shulman equations for a thick plate with an internal heat source, and the same author [43] solved the Green–Lindsay equations for a thick plate with body force. A similar setting of the thick plate problem in thermoelasticity has been solved for a transversely isotropic medium [44] and has been considered in Kelvin–Voigt medium when a specific form of the fractional dual-phase lag is considered [45]. For ultrafast thermal heating of metals, the deformation resulting from the electronic conduction was considered in [46] for a one-dimension metal film. The authors considered in their formulation that the driving force describes the effect of free carriers on the lattice [47], mathematically described by the term $T_e\nabla T_e$, where $T_e$ is the electron temperature. In the linearized version, the nonlinear term $T_e\nabla T_e$ is neglected; thus, the coupling factor is lost. A generalized version of ultrafast thermoelasticity was considered in [48], where the stress includes the lattice temperature and the lattice conduction equation is inserted. If the lattice conduction is neglected and the force describing the effect of free carriers on the lattice is neglected, the resulting ultrafast thermoelasticity corresponds to the dual-phase-lag thermoelasticity with flux precedence [6]; see also [49].

In the present article, we consider a Kelvin–Voigt nanoscale two-dimensional plate with infinite extension subject to an ultrafast surface heating on its upper surface taking the double-strip shape [50,51]. The delayed strain response underlying the Kelvin–Voigt assumption, the nanoscale thickness of the plate, and the ultrafast heating method can be considered as reasoning causes for adopting non-Fourier heat transfer mechanisms such as accelerating, retarding, and crossover from super- to sub-thermal conduction. The Laplace–Fourier transform technique is used to obtain exact solutions in the transformed domain. Then, double infinite summations are numerically implemented to obtain the solutions in the physical domain. The relation between the heat flux and the temperature gradient is shown graphically in different critical instants. We organize the paper as follows: In Section 2, we present the governing equations for the Kelvin–Voigt thermoelasticity with the fractional Jeffreys equation with three fractional parameters. The two-dimensional formulation of the Kelvin–Voigt thermoelastic plate problem is given in Section 3. In Section 4, we derive exact solutions for the temperature, hydrostatic stress, and displacement components in the transformed domain. A suitable numerical technique is adopted in Section 5 to obtain the solution to the physical domain numerically. Lastly, we summarize the work findings in Section 6.

2. Mathematical Model

The governing equations for a homogeneous isotropic thermoviscoelastic material of Kelvin–Voigt type [23,33,34] in the context of the fractional Jeffreys heat conduction equation [20,21] consist of the following:

(i)

Stress–strain constitutive relation

$${\sigma }_{ij}=2\mu e_{ij}+\lambda e{\delta }_{ij}-\left(3\lambda +2\mu \right){\alpha }_T\theta {\delta }_{ij}$$

(1)

where $\lambda ={\lambda }_0\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)$,$\mu ={\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right)$, ${\lambda }_0$ and ${\mu }_0$ are the standard Lamé constants, ${\lambda }_v$ and ${\mu }_v$ are viscoelastic relaxation times pertinent to the Kelvin–Voigt solid, ${\alpha }_T$ is the coefficient of linear thermal expansion, ${\sigma }_{ij}={\sigma }_{ji}$ are the components of the Cauchy stress tensor, $e_{ij}$ is the linear strain tensor, ${\delta }_{ij}$ is the Kronecker delta, $\theta =T-T_0$ is the temperature of the medium, $T$ is the absolute temperature, and $T_0$ is the temperature of the medium in its natural state; $\theta$ is assumed to satisfy the linearized condition $\left|\theta /T_0\right|\ll 1$.

(ii)

The strain–displacement relation

$$e_{ij}=\frac{1}{2}\left(u_{i,j}+u_{j,i}\right),$$

(2)

where $e_{ij}=e_{ji}$ is the linear strain tensor, $e=e_{ii}=u_{i,i}$ is the cubical dilation, and $u_i$ is the component of the displacement vector. The subscript $i$ refers to the component of the vector in the $x_i$-direction, the standard notation ${\left(·\right)}_{,i}=\left(\partial /\partial x_i\right)\left(·\right)$ has been employed, and $x_i$ is the i-th system coordinate.

(iii)

Conservation of momentum

$${\sigma }_{ij,j}+\rho F_i=\rho \frac{{\partial }^2{u}_i}{\partial t^2},$$

(3)

where $\rho$ is the material density, assumed to be constant; $F_i$ is the body force component in the $x_i$-direction; and the tensor convention of summing over repeated indices is used.

Substituting Equation (1) into Equation (3), and using the relations $\lambda ={\lambda }_0\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)$ and $\mu ={\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right)$, we obtain

$$\left({\lambda }_0+{\mu }_0\right)\left(1+{\delta }_v\frac{\partial }{\partial t}\right)e_{,i}+{\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right)u_{i,jj}-\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T\left(1+{\gamma }_v\frac{\partial }{\partial t}\right){\theta }_{,i}+\rho F_i=\rho \frac{{\partial }^2{u}_i}{\partial t^2},$$

(4)

where ${\gamma }_v=\frac{3{\lambda }_0{\lambda }_v+2{\mu }_0{\mu }_v}{3{\lambda }_0+2{\mu }_0}$ and ${\delta }_v=\frac{{\lambda }_0{\lambda }_v+{\mu }_0{\mu }_v}{{\lambda }_0+{\mu }_0}$.

(iv)

The balance equation for the entropy

$$-q_{i,i}+Q=\rho T_0\frac{\partial S}{\partial t},$$

(5)

where $q_i$ is the heat flux generalized component, $Q$ is the strength of the heat source inside the body, and $S$ is the entropy per unit mass.

Starting from the assumption that for a thermally conducting Kelvin–Voigt solid subject to small strain and small temperature changes [23,38], we have

$$\rho T_{0}S=\rho c_E\theta +\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T{T}_0\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)e,$$

(6)

where $c_E$ is the specific heat at constant strain.

Hence, the energy balance equation is given from (5) and (6) as

$$\rho c_E\frac{\partial \theta }{\partial t}+\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T{T}_0\left(\frac{\partial }{\partial t}+{\gamma }_v\frac{{\partial }^2}{\partial t^2}\right)e=-q_{i,i}+Q.$$

(7)

The above equations are supplemented with the fractional Jeffery’s heat conduction equation [20,21], namely,

$$\left(1+{\tau }_q^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)q_i=-\check{K}\frac{{\partial }^{1-\gamma }}{\partial t^{1-\gamma }}\left(1+{\tau }_{\theta }^{\beta }\frac{{\partial }^{\beta }}{\partial t^{\beta }}\right){\theta }_{,i}, \check{K}=K{\tau }_q^{1-\gamma },$$

(8)

where ${\tau }_q\ge 0$ and ${\tau }_{\theta }\ge 0$ are the heat flux and the temperature gradient phase lags [6], respectively, $K$ is the thermal conductivity, and $0<\alpha ,\beta ,\gamma \le 1$. The assumption $\check{K}=K{\tau }_q^{1-\gamma }$ is adopted to keep the dimension in order [7,52]. The fractional derivative in (8) is defined in the Riemann–Liouville sense [53]:

$$\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}f\left(t\right)=\left\{\begin{array}{cc}\frac{1}{\mathsf{\Gamma }\left(1-\alpha \right)}\frac{\partial }{\partial t}{\int }_0^t\frac{f\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha }}d\tau ,\hfill & \hfill 0<\alpha <1,\\ \frac{\partial }{\partial t}f\left(t\right),\hfill & \hfill \alpha =1.\end{array}\right.$$

Substituting Equation (8) into Equation (7), we obtain the energy equation:

$$K{\tau }_q^{1-\gamma }\frac{{\partial }^{1-\gamma }}{\partial t^{1-\gamma }}\left(1+{\tau }_{\theta }^{\beta }\frac{{\partial }^{\beta }}{\partial t^{\beta }}\right){\theta }_{,ii}=\left(1+{\tau }_q^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\left[\rho c_E\frac{\partial \theta }{\partial t}+\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T{T}_0\left(\frac{\partial }{\partial t}+{\gamma }_v\frac{{\partial }^2}{\partial t^2}\right)e-Q\right].$$

(9)

3. Problem Formulation

We consider a plate made of a homogeneous isotropic solid occupying the region $\mathsf{\Omega }$ defined by $\mathsf{\Omega }=\left\{\left(x,y,z\right):-\infty <x,z<\infty , 0\le y\le l\right\}$. The $y$-axis is taken perpendicular to the plate plane and pointing inwards, such that $y=0$ refers to the upper surface and $y=l$ refers to the lower surface. The body is assumed to be initially quiescent. Furthermore, we assume that there are no body forces or heat sources. The upper surface of the plate is assumed to be traction-free and subjected to ultrafast double-strip heating [50], which decays exponentially with time, while the lower surface is assumed to be traction-free and thermally insulated; see Figure 1.

From the above settings, all the considered functions should depend on $x, y,$ and $t$. Also, the displacement vector is given in the form

$$\mathbf{u}=〈u,v,0〉, u=u\left(x,y,t\right), v=v\left(x,y,t\right).$$

(10)

Hence, the governing equations for Kelvin–Voigt thermoelastic plate on the domain $\left(x,y, t\right)\in \left(-\infty ,\infty \right)\times \left[0,l\right]\times \left(0,\infty \right)$ consist of the following:

(i)

The non-vanishing components of the stress tensor

$${\sigma }_{xx}=2{\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right)\frac{\partial u}{\partial x}+{\lambda }_0\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)e-\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\theta ,$$

(11)

$${\sigma }_{yy}=2{\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right)\frac{\partial v}{\partial y}+{\lambda }_0\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)e-\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\theta ,$$

(12)

$${\sigma }_{zz}={\lambda }_0\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)e-\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\theta ,$$

(13)

$${\sigma }_{xy}={\sigma }_{yx}={\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right)\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right).$$

(14)

(ii)

The non-vanishing components of the strain tensor

$$e_{xx}=\frac{\partial u}{\partial x},$$

(15)

$$e_{yy}=\frac{\partial v}{\partial y},$$

(16)

$$e_{xy}=e_{yx}=\frac{1}{2}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right).$$

(17)

Also, the cubical dilation $e$ is given by

$$e=e_{xx}+e_{yy}=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}.$$

(18)

(iii)

The equations of motion in the absence of body forces along the x- and y-directions, respectively,

$$\left({\lambda }_0+{\mu }_0\right)\left(1+{\delta }_v\frac{\partial }{\partial t}\right)\frac{\partial e}{\partial x}+{\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right){\nabla }^{2}u-\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\frac{\partial \theta }{\partial x}=\rho \frac{{\partial }^{2}u}{\partial t^2},$$

(19)

$$\left({\lambda }_0+{\mu }_0\right)\left(1+{\delta }_v\frac{\partial }{\partial t}\right)\frac{\partial e}{\partial y}+{\mu }_0\left(1+{\mu }_v\frac{\partial }{\partial t}\right){\nabla }^{2}v-\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\frac{\partial \theta }{\partial y}=\rho \frac{{\partial }^{2}v}{\partial t^2},$$

(20)

By differentiating Equations (19) and (20) with respect to $x$ and $y$, respectively, adding the resulting equations and utilizing Equation (18), we obtain

$$\left[\left({\lambda }_0+2{\mu }_0\right)+\left(\left({\lambda }_0+{\mu }_0\right){\delta }_v+{\mu }_0{\mu }_v\right)\frac{\partial }{\partial t}\right]{\nabla }^{2}e-\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_t\left(1+{\gamma }_v\frac{\partial }{\partial t}\right){\nabla }^2\theta =\rho \frac{{\partial }^{2}e}{\partial t^2},$$

(21)

where ${\nabla }^2=\left(\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}\right)$ is the Laplace operator in Cartesian coordinates.

(i)

The heat conduction equation in the absence of a heat source

$$K{\tau }_q^{1-\gamma }\frac{{\partial }^{1-\gamma }}{\partial t^{1-\gamma }}\left(1+{\tau }_{\theta }^{\beta }\frac{{\partial }^{\beta }}{\partial t^{\beta }}\right){\nabla }^2\theta =\left(1+{\tau }_q^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\left[\rho c_E\frac{\partial \theta }{\partial t}+\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T{T}_0\left(\frac{\partial }{\partial t}+{\gamma }_v\frac{{\partial }^2}{\partial t^2}\right)e\right],$$

(22)

associated with the following thermal and mechanical boundary conditions:

$$\theta (x,0,t)={\mathsf{\Theta }}_0(x,t),\hspace{1em}\hspace{1em}{\left.\frac{\partial \theta (x,y,t)}{\partial y}\right|}_{y=l}=0,$$

(23)

$${\sigma }_{yy}(x,0,t)={\sigma }_{yy}(x,l,t)=0,$$

(24)

$${\sigma }_{xy}(x,0,t)={\sigma }_{xy}(x,l,t)=0,$$

(25)

where ${\mathsf{\Theta }}_0(x,t)$ is a given time-dependent thermal boundary condition, disturbed spatially on the upper surface.

Additionally, it is assumed that the system initiates the experiment in a state of rest with no accelerations, namely,

$$\begin{array}{c}{\left.u(x,y,t)\right|}_{t=0}={\left.\frac{\partial u(x,y,t)}{\partial t}\right|}_{t=0}=0,{\left. v(x,y,t)\right|}_{t=0}={\left.\frac{\partial v(x,y,t)}{\partial t}\right|}_{t=0}=0,\\ {\left.\theta (x,y,t)\right|}_{t=0}={\left.\frac{\partial \theta (x,y,t)}{\partial t}\right|}_{t=0}=0,\end{array}$$

(26)

The governing equations can be put in a more convenient form by using the following non-dimensional variables:

$$\begin{array}{c}\left(x^{*},y^{*}\right)=c_1\eta \left(x,y\right), \left(u_{ }^{*}, v_{ }^{*}\right)=c_1\eta \frac{\rho c_1^3\eta }{\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T{T}_0}\left(u, v\right),\\ e_{ij}^{*}=\frac{{\rho }^2{c}_1^2}{\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T{T}_0}{e}_{ij}^{ }, {\theta }^{*}=\frac{\theta }{T_0}, {\mathsf{\Theta }}_0^{\mathrm{*}}=\frac{{\mathsf{\Theta }}_0}{T_0}, {\sigma }_{ij}^{*}=\frac{{\sigma }_{ij}^{ }}{\left(3{\lambda }_0+2{\mu }_0\right){\alpha }_T{T}_0},\\ \left(t^{*},t_p^{*},{\tau }_q^{*},{\tau }_{\theta }^{*},{\lambda }_v^{*},{\mu }_v^{*}\right)=c_1^2\eta \left(t,t_p{\tau }_q^{ },{\tau }_{\theta }^{ },{\lambda }_v,{\mu }_v\right),\end{array}$$

(27)

where $c_1=\sqrt{\frac{{\lambda }_0+2{\mu }_0}{\rho }}$ and $\eta =\frac{\rho c_E}{K}$.

Using the above non-dimensional variables, Equations (11)–(14), (21), and (22) take the following forms (the asterisks were omitted to avoid confusion):

$${\sigma }_{xx}=2{\beta }^2\left(1+{\mu }_v\frac{\partial }{\partial t}\right)\frac{\partial u}{\partial x}+\left(1-2{\beta }^2\right)\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)e-\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\theta ,$$

(28)

$${\sigma }_{yy}=2{\beta }^2\left(1+{\mu }_v\frac{\partial }{\partial t}\right)\frac{\partial v}{\partial y}+\left(1-2{\beta }^2\right)\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)e-\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\theta ,$$

(29)

$${\sigma }_{zz}=\left(1-2{\beta }^2\right)\left(1+{\lambda }_v\frac{\partial }{\partial t}\right)e-\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\theta ,$$

(30)

$${\sigma }_{xy}={\beta }^2\left(1+{\mu }_v\frac{\partial }{\partial t}\right)\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right),$$

(31)

$$\left[1+\left(\left(1-{\beta }^2\right){\delta }_v+{\alpha }_1{\beta }^2\right)\frac{\partial }{\partial t}\right]{\nabla }^{2}e-\left(1+{\gamma }_v\frac{\partial }{\partial t}\right){\nabla }^2\theta =\frac{{\partial }^{2}e}{\partial t^2},$$

(32)

$${\tau }_q^{1-\gamma }\frac{{\partial }^{1-\gamma }}{\partial t^{1-\gamma }}\left(1+{\tau }_{\theta }^{\beta }\frac{{\partial }^{\beta }}{\partial t^{\beta }}\right){\nabla }^2\theta =\left(1+{\tau }_q^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\left[\frac{\partial \theta }{\partial t}+\epsilon \left(\frac{\partial }{\partial t}+{\gamma }_v\frac{{\partial }^2}{\partial t^2}\right)e\right],$$

(33)

where ${\beta }^2=\frac{{\mu }_0}{{\lambda }_0+2{\mu }_0}$ and $\epsilon =\frac{{\left(3{\lambda }_0+2{\mu }_0\right)}^2{\alpha }_T^2{T}_0}{\rho c_E\left({\lambda }_0+2{\mu }_0\right)}$.

We shall consider the hydrostatic stress as the mean value of the normal stresses ${\sigma }_{xx},{\sigma }_{yy}$, and ${\sigma }_{zz}$, namely,

$${\sigma }_H=\frac{{\sigma }_{xx}+{\sigma }_{yy}+{\sigma }_{zz}}{3}.$$

(34)

By using Equations (28)–(30), we obtain

$${\sigma }_H=\left[\left(1-\frac{4}{3}{\beta }^2\right)+\left(\frac{2}{3}{\beta }^2{\mu }_v+\left(1-2{\beta }^2\right){\lambda }_v\right)\frac{\partial }{\partial t}\right]e-\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\theta ,$$

(35)

associated with the following non-dimensional thermal and mechanical boundary conditions

$$\theta (x,0,t)={\mathsf{\Theta }}_0(x,t),\hspace{1em}\hspace{1em}{\left.\frac{\partial \theta (x,y,t)}{\partial y}\right|}_{y=l}=0,$$

(36)

$${\sigma }_{yy}(x,0,t)={\sigma }_{yy}(x,l,t)=0,$$

(37)

$${\sigma }_{xy}(x,0,t)={\sigma }_{xy}(x,l,t)=0,$$

(38)

and non-dimensional homogeneous initial conditions

$$\begin{array}{c}{\left.u(x,y,t)\right|}_{t=0}={\left.\frac{\partial u(x,y,t)}{\partial t}\right|}_{t=0}=0,{\left. v(x,y,t)\right|}_{t=0}={\left.\frac{\partial v(x,y,t)}{\partial t}\right|}_{t=0}=0,\\ {\left.\theta (x,y,t)\right|}_{t=0}={\left.\frac{\partial \theta (x,y,t)}{\partial t}\right|}_{t=0}=0,\end{array}$$

(39)

4. Solutions in the Integral-Transform Domain

We shall now define the Laplace transform (denoted by a bar) with respect to a function $h\left(x,y,t\right)$ by the relation [54]

$$\overline{h}\left(x,y,s\right)=\mathcal{L}\left\{h\left(x,y,t\right);t\right\}\left(x,y,s\right)={\int }_0^{\infty }h\left(x,y,t\right)e^{-st}dt,$$

(40)

where $h\left(x,y,t\right)$ is a continuous function over time, $s$ is the Laplace parameter, and the inverse Laplace’s transform is defined as

$${\mathcal{L}}^{-1}\left(\overline{h}\left(x,y,s\right)\right)=\frac{1}{2\pi i}\underset{\beta \to \infty }{\lim }\underset{\alpha -i\beta }{\overset{\alpha +i\beta }{\int }}\overline{h}\left(x,y,s\right)e^{st}ds=h\left(x,y,t\right),$$

(41)

where $i=\sqrt{-1},$ and the Fourier exponential transform (denoted by a hat) to a function $\overline{h}\left(x,y,s\right)$ with respect to the variable $x$ is defined by the relation

$$\widehat{\overline{h}}\left(q,y,s\right)=\mathcal{F}\left\{\overline{h}\left(x,y,s\right);x\right\}\left(q,y,s\right)={\int }_0^{\infty }\overline{h}\left(x,y,s\right)e^{-iqx}dx,$$

(42)

with its corresponding inversion

$${\mathcal{F}}^{-1}\left(\widehat{\overline{h}}\left(q,y,s\right)\right)=\frac{1}{2\pi }\underset{-\infty }{\overset{\infty }{\int }}\widehat{\overline{h}}\left(q,y,s\right)e^{iqx}dq=\overline{h}\left(x,y,s\right),$$

(43)

We assume that all the relevant functions are sufficiently smooth on the real line such that the Fourier transform of these functions exists. According to the homogeneous initial conditions (39), upon applying the Laplace transform on both sides of Equations (32) and (33), we arrive at

$$\left[\left(1+\varsigma s\right){\nabla }^2-s^2\right]\overline{e}-\left(1+{\gamma }_{0}s\right){\nabla }^2\overline{\theta }=0,$$

(44)

$$\left({\nabla }^2-sL\right)\overline{\theta }-\epsilon s\left(1+{\gamma }_{0}s\right)L\overline{e}=0,$$

(45)

where

$$\varsigma =\left(1-{\beta }^2\right){\delta }_v+{\mu }_v{\beta }^2, L\left(s\right)=\frac{1+{\tau }_q^{\alpha }{s}^{\alpha }}{{\tau }_q^{1-\gamma }{s}^{1-\gamma }\left(1+{\tau }_{\theta }^{\beta }{s}^{\beta }\right)}.$$

(46)

Eliminating $\bar{\theta }$ between Equations (44) and (45), we obtain

$$\left[\left(1+\varsigma s\right){\nabla }^4-\left(s\left(1+\varsigma s\right)L+s^2+\epsilon s{\left(1+{\gamma }_{v}s\right)}^{2}L\right){\nabla }^2+s^{3}L\right]\bar{e}=0,$$

(47)

which can be factorized as

$${\prod }_{i=1}^2\left({\nabla }^2-k_i^2\right)\bar{e}=0,$$

(48)

where $k_i^2,\left(i=1, 2\right)$ are the roots with positive real parts of the characteristic equation

$$\left(1+\varsigma s\right)k^4-\left[s\left(1+\varsigma s\right)L+s^2+\epsilon s{\left(1+{\gamma }_{v}s\right)}^{2}L\right]k^2+s^{3}L=0.$$

(49)

Upon applying the exponential Fourier transform on Equation (48), we obtain

$${\prod }_{i=1}^2\left({\mathfrak{D}}^2-m_i^2\right)\widehat{\overline{e}}=0,$$

(50)

where $m_i^2=q^2+k_i^2$, $i=1, 2$, and $\mathfrak{D}=\partial /\partial y$. The general solution of Equation (50), bounded for the region $0\le y\le l$, is given as

$$\widehat{\overline{e}}=\sum _{i=1}^2\left(k_{\mathrm{i}}^2-sL\right)\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right],$$

(51)

where $A_i, B_i$, $i=1, 2$, are parameters depending on $s$ and $q$. Similarly, eliminating $\bar{e}$ between Equations (44) and (45) leads to the characteristic equation

$$\left[\left(1+\varsigma s\right){\nabla }^4-\left(s\left(1+\varsigma s\right)L+s^2+\epsilon s{\left(1+{\gamma }_{v}s\right)}^{2}L\right){\nabla }^2+s^{3}L\right]\bar{\theta }=0.$$

(52)

Therefore, the general solution of (52) for $y\in \left[0,l\right]$ can be written as

$$\widehat{\overline{\theta }}=\epsilon s\left(1+{\gamma }_{v}s\right)L\sum _{i=1}^2\left[A_i^{\prime }{e}^{-m_{i}y}+B_i^{\prime }{e}^{m_{i}y}\right],$$

(53)

where $A_i^{\prime }, B_i^{\prime }$, $i=1, 2$, are parameters depending on $s$ and $q$. In view of Equations (51), (53) and (45), one can deduce the following relations for $A_i^{\prime }$ and $B_i^{\prime }$

$$A_i^{\prime }\left(q,s\right)=A_i\left(q,s\right), B_i^{\prime }\left(q,s\right)=B_i\left(q,s\right), i=\mathrm{1,2}.$$

(54)

Using the above relations in Equation (53), we obtain

$$\widehat{\overline{\theta }}=\epsilon s\left(1+{\gamma }_{v}s\right)L\sum _{i=1}^2\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right].$$

(55)

On the other hand, Equations (17) and (19) can be written in the non-dimensional form as

$$e=\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}.$$

(56)

$${\beta }^2\left(1+{\mu }_v\frac{\partial }{\partial t}\right){\nabla }^{2}v+\left(1-{\beta }^2\right)\left(1+{\delta }_v\frac{\partial }{\partial t}\right)\mathfrak{D}e-\left(1+{\gamma }_v\frac{\partial }{\partial t}\right)\mathfrak{D}\theta =\frac{{\partial }^{2}v}{\partial t^2},$$

(57)

Taking the Laplace–Fourier transforms for Equations (56) and (57), we obtain

$$\widehat{\overline{u}}=\frac{1}{iq}\left(\widehat{\overline{e}}-\frac{\partial \widehat{\overline{v}}}{\partial y}\right),$$

(58)

$$\left({\mathfrak{D}}^2-m^2\right)\widehat{\overline{v}}=\frac{1}{{\beta }^2\left(1+{\mu }_{v}s\right)}\left(\left(1+{\gamma }_{v}s\right)\mathfrak{D}\widehat{\overline{\theta }}-\left(1-{\beta }^2\right)\left(1+{\delta }_{v}s\right)\mathfrak{D}\widehat{\overline{e}}\right)$$

(59)

where $m^2=q^2+\frac{s^2}{{\beta }^2\left(1+{\mu }_{v}s\right)}$.

Next, substituting Equations (51) and (55) into the right-hand side of Equation (59), we obtain

$$\widehat{\overline{v}}=C_1{e}^{-my}+C_2{e}^{my}+\sum _{i=1}^2{\psi }_i\left[-A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right],$$

(60)

where ${\psi }_i=\frac{m_i\left({\epsilon s\left(1+{\gamma }_{v}s\right)}^{2}L-\left(1-{\beta }^2\right)\left(1+{\delta }_{v}s\right)\left(k_{\mathrm{i}}^2-sL\right)\right)}{{\beta }^2\left(1+{\mu }_{v}s\right)(m_i^2-m^2)},$ and $C_i$, $i=1, 2$, are parameters depending on $s$ and $q$.

To determine the tangential component of the velocity, utilizing Equations (51) and (60) in the right-hand side of Equation (58), we obtain

$$\widehat{\overline{u}}=\frac{i}{q}\left(m\left(-C_1{e}^{-my}+C_2{e}^{my}\right)+\sum _{i=1}^2\left({\psi }_i{m}_i-k_{\mathrm{i}}^2+sL\right)\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right]\right).$$

(61)

Finally, we combine Equations (51), (55), (60) and (61) with the Laplace and Fourier transforms of Equations (28), (31) and (35), and perform some straightforward calculations; the results are

$${\widehat{\overline{\sigma }}}_{xx}=2{m\beta }^2\left(1+{\mu }_{v}s\right)\left[C_1{e}^{-my}-C_2{e}^{my}\right]+\sum _{i=1}^2{\phi }_i\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right],$$

(62)

$${\widehat{\overline{\sigma }}}_{yy}=2{m\beta }^2\left(1+{\mu }_{v}s\right)\left[-C_1{e}^{-my}+C_2{e}^{my}\right]+\sum _{i=1}^2{\varpi }_i\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right],$$

(63)

$${\widehat{\overline{\sigma }}}_{zz}=\sum _{i=1}^2{\chi }_i\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right],$$

(64)

$$\begin{array}{cc}{\widehat{\overline{\sigma }}}_{xy}=\hfill & \frac{i{\beta }^2\left(1+{\mu }_{v}s\right)}{q}(\left(q^2+m^2\right)[C_1{e}^{-my}+C_2{e}^{my}]\hfill \\ & \hspace{1em}\hspace{1em} +\sum _{i=1}^2\left(q^2{\psi }_i+m_i\left({\psi }_i{m}_i-k_{\mathrm{i}}^2+sL\right)\right)\left[-A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right]),\hfill \end{array}$$

(65)

$${{\widehat{\overline{\sigma }}}_H}_{ }=\sum _{i=1}^2{\zeta }_i\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right],$$

(66)

where

$$\begin{array}{c}\hfill {\phi }_i=-2{\beta }^2\left(1+{\mu }_{v}s\right){\psi }_i{m}_i+\left(k_{\mathrm{i}}^2-Ls\right)\left(2{\beta }^2\left(1+{\mu }_{v}s\right)+\left(1-2{\beta }^2\right)\left(1+{\lambda }_{v}s\right)\right)-\epsilon s{\left(1+{\gamma }_{v}s\right)}^{2}L,\hfill \\ \hfill {\varpi }_i=2{\beta }^2\left(1+{\mu }_{v}s\right){\psi }_i{m}_i+\left(1-2{\beta }^2\right)\left(1+{\lambda }_{v}s\right)\left(k_{\mathrm{i}}^2-sL\right)-{\epsilon s{\left(1+{\gamma }_{v}s\right)}^{2}L}^{ },\hfill \\ {\chi }_i=\left(1-2{\beta }^2\right)\left(1+{\lambda }_{v}s\right)\left(k_{\mathrm{i}}^2-sL\right)-\epsilon s{\left(1+{\gamma }_{v}s\right)}^{2}L,\\ \hfill {\zeta }_i=\left(\left(1-\frac{4}{3}{\beta }^2\right)+\left(\frac{2}{3}{\beta }^2{\mu }_v+\left(1-2{\beta }^2\right){\lambda }_v\right)s\right)\left(k_{\mathrm{i}}^2-sL\right)-\epsilon s{\left(1+{\gamma }_{v}s\right)}^{2}L.\hfill \end{array}$$

The boundary conditions (36)–(38) in the Laplace–Fourier domain read

$$\widehat{\overline{\theta }}(q,0,s)={\widehat{\overline{\mathsf{\Theta }}}}_0(q,s),\hspace{1em}\hspace{1em}{\left.\frac{\partial \widehat{\overline{\theta }}(q,y,s)}{\partial y}\right|}_{y=l}=0,$$

(67)

$${\widehat{\overline{\sigma }}}_{yy}(q,0,s)={\widehat{\overline{\sigma }}}_{yy}(q,l,s)=0,$$

(68)

$${\widehat{\overline{\sigma }}}_{xy}(q,0,s)={\widehat{\overline{\sigma }}}_{xy}(q,l,s)=0.$$

(69)

Without loss of generality, we specify the condition of double-strip heating [50,51]:

$${\mathsf{\Theta }}_0\left(x,t\right)=\left[H\left(b-\left|x\right|\right)-H\left(a-\left|x\right|\right)\right]\exp \left(-\frac{t}{t_p}\right),$$

(70)

where $H(·)$ is the Heaviside unit step function, and $t_p$ is a temporal parameter characterizing the thermalization time, or alternatively, the heating rate. In other words, if we take a dimensional thermalization parameter $t_p=1$ femtosecond, then at the physical time $t=1$ picosecond, the surface reaches zero temperature difference $\theta \left(x,0,t\right)=0$, or alternatively, the absolute surface temperature becomes identical with the room temperature, $T\left(x,0,t\right)=T_0$. The double-strip heating parameters $a$ and $b$ are taken as nonzero constants such that ($a<b$). The boundary surface temperature in the Laplace–Fourier domain is determined by

$${\widehat{\overline{\mathsf{\Theta }}}}_0\left(q,s\right)=\frac{2t_p}{q(1+t_{p}s)}\left[\sin \left(bq\right)-\mathrm{s}\mathrm{i}\mathrm{n}\left(aq\right)\right].$$

(71)

Equations (67)–(69) immediately give the following system of six linear equations in the unknown parameters $A_i\left(q,s\right),B_i\left(q,s\right), \left(i=1, 2\right)$ and $C_i\left(q,s\right), \left(i=1, 2\right)$.

$$\epsilon sL\left(1+{\gamma }_{v}s\right)\sum _{i=1}^2\left[A_i+B_i\right]=\frac{t_p}{q(1+t_{p}s)}\left(\sin \left(bq\right)-\mathrm{s}\mathrm{i}\mathrm{n}\left(aq\right)\right),$$

(72)

$$\sum _{i=1}^2{m}_i\left[-A_i{e}^{-m_{i}l}+B_i{e}^{m_{i}l}\right]=0,$$

(73)

$$2{m\beta }^2\left(1+{\mu }_{v}s\right)\left[-C_1+C_2\right]+\sum _{i=1}^2{\varpi }_i\left[A_i+B_i\right]=0,$$

(74)

$$2{m\beta }^2\left(1+{\mu }_{v}s\right)\left[-C_1{e}^{-ml}+C_2{e}^{ml}\right]+\sum _{i=1}^2{\varpi }_i\left[A_i{e}^{-m_{i}l}+B_i{e}^{m_{i}l}\right]=0,$$

(75)

$$\left(q^2+m^2\right)\left[C_1+C_2\right]+\sum _{i=1}^2\left(q^2{\psi }_i+m_i\left({\psi }_i{m}_i-k_{\mathrm{i}}^2+sL\right)\right)\left[-A_i+B_i\right]=0,$$

(76)

$$\left(q^2+m^2\right)\left[C_1{e}^{-ml}+C_2{e}^{ml}\right]+\sum _{i=1}^2\left(q^2{\psi }_i+m_i\left({\psi }_i{m}_i-k_{\mathrm{i}}^2+sL\right)\right)\left[-A_i{e}^{-m_{i}l}+B_i{e}^{m_{i}l}\right]=0.$$

(77)

This completes the solution of the problem in the Laplace–Fourier-transformed domain.

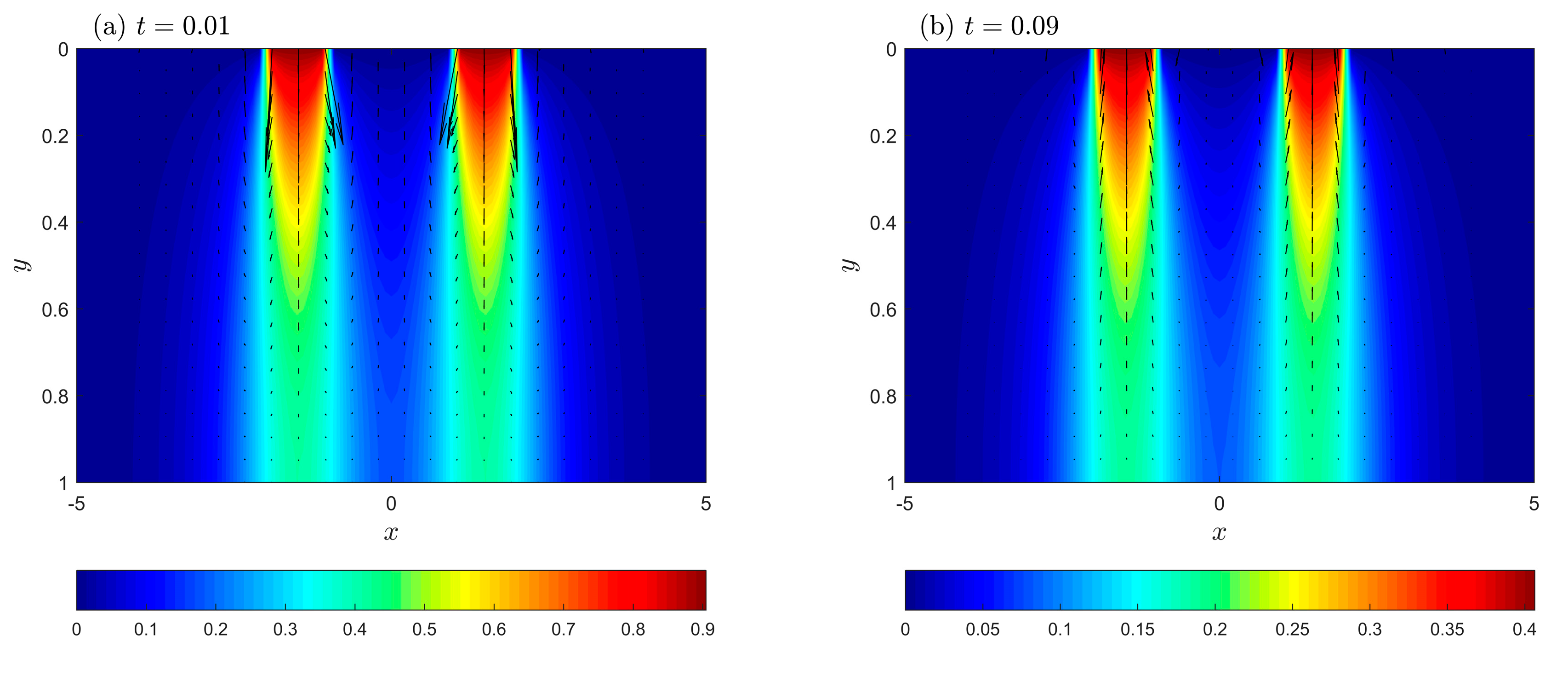
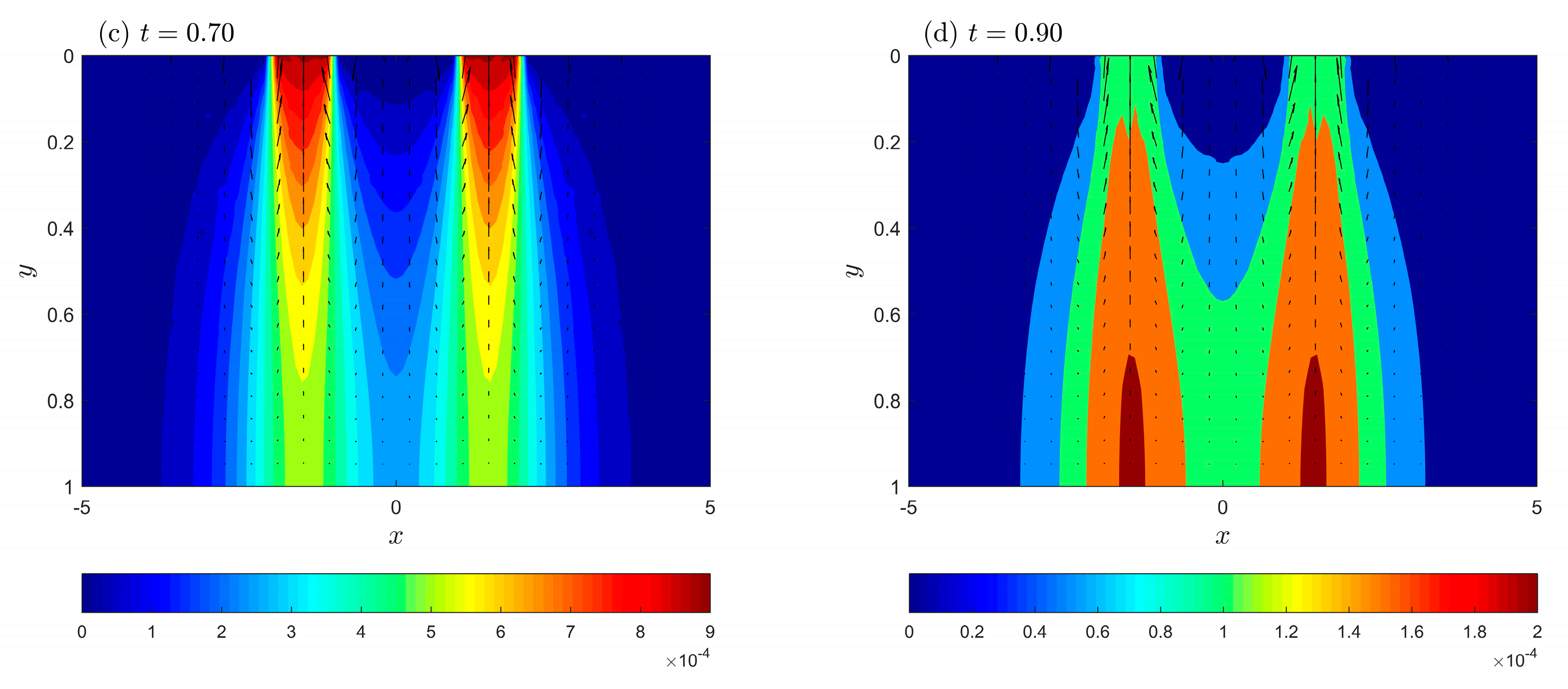
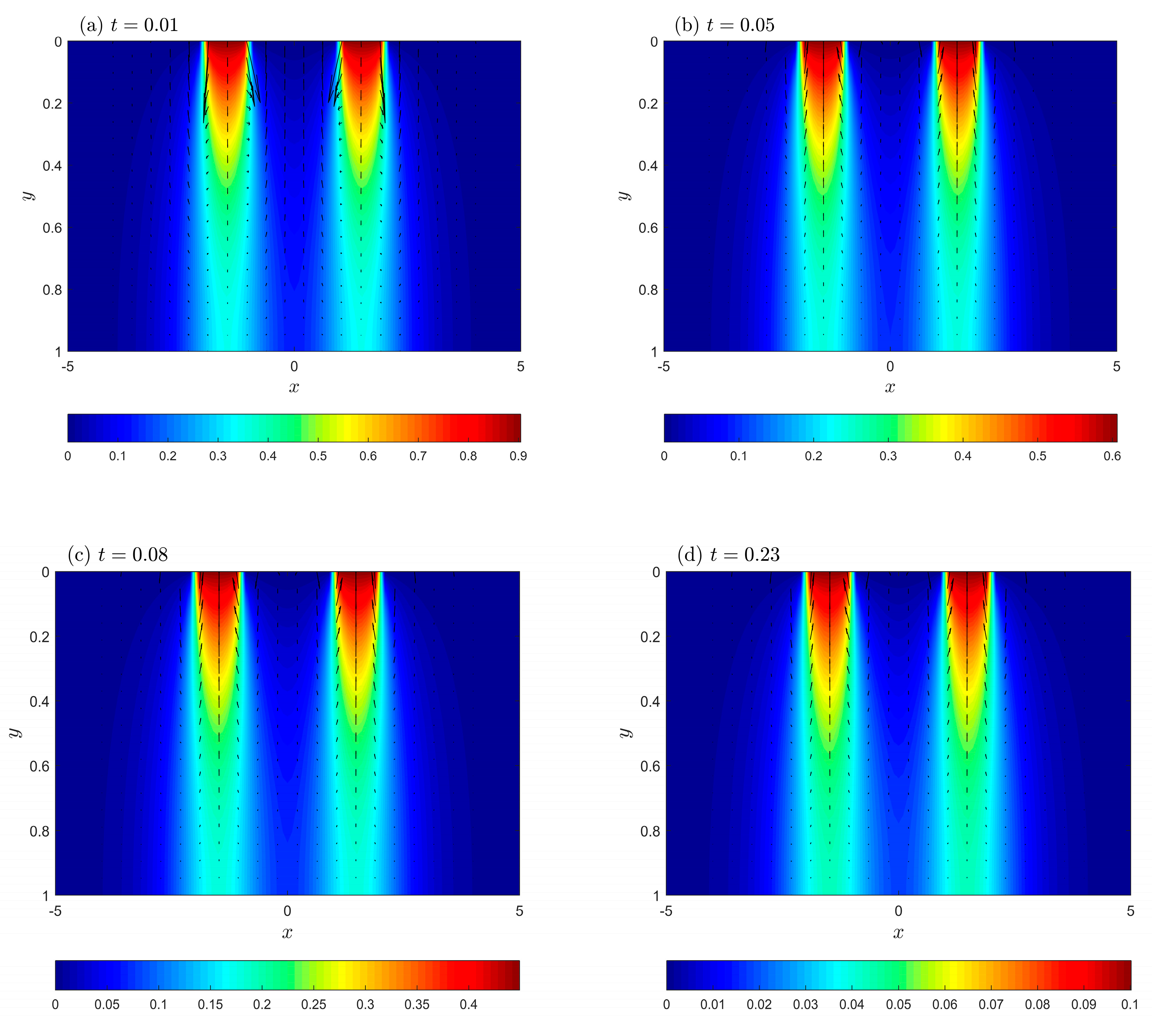
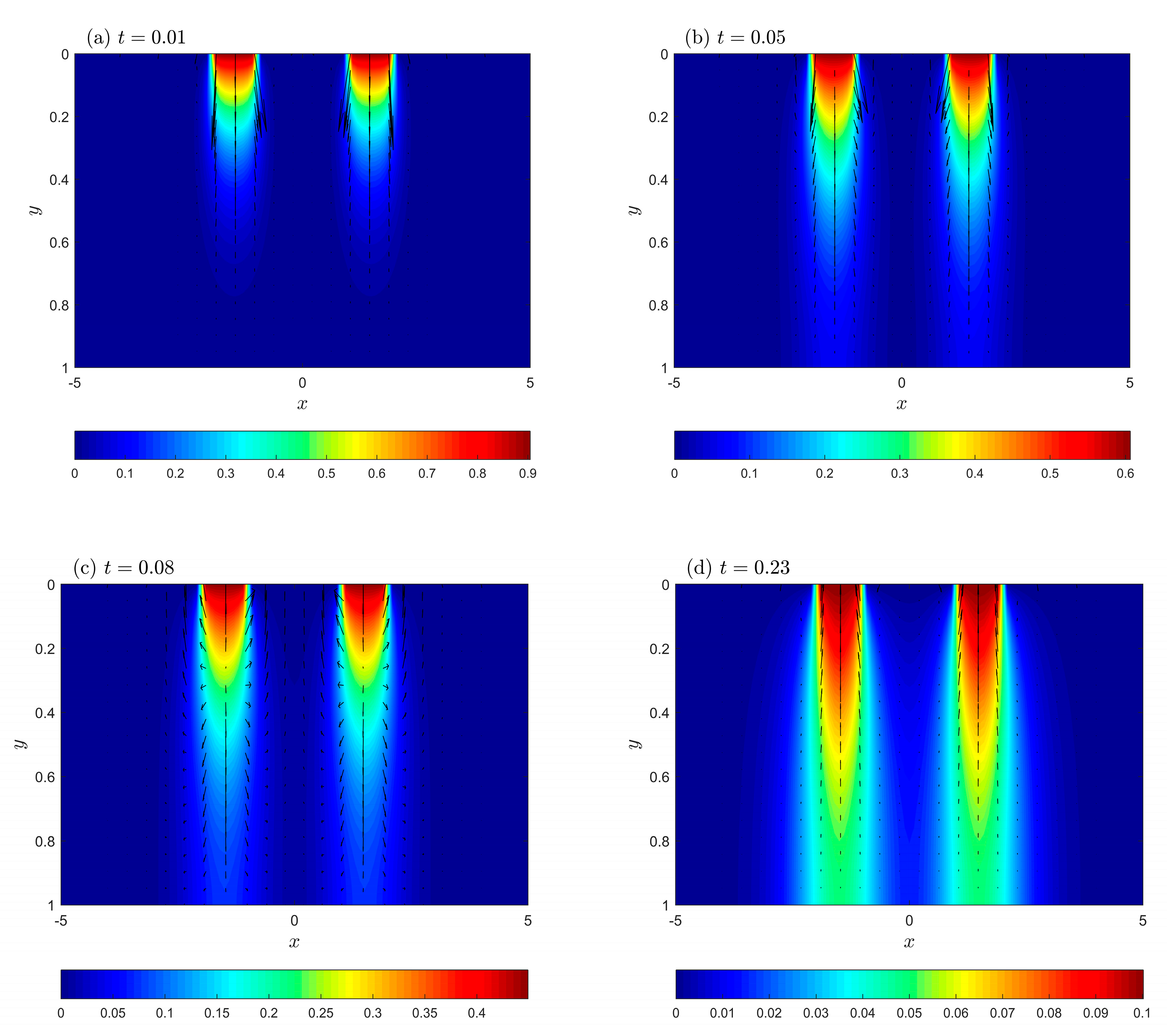
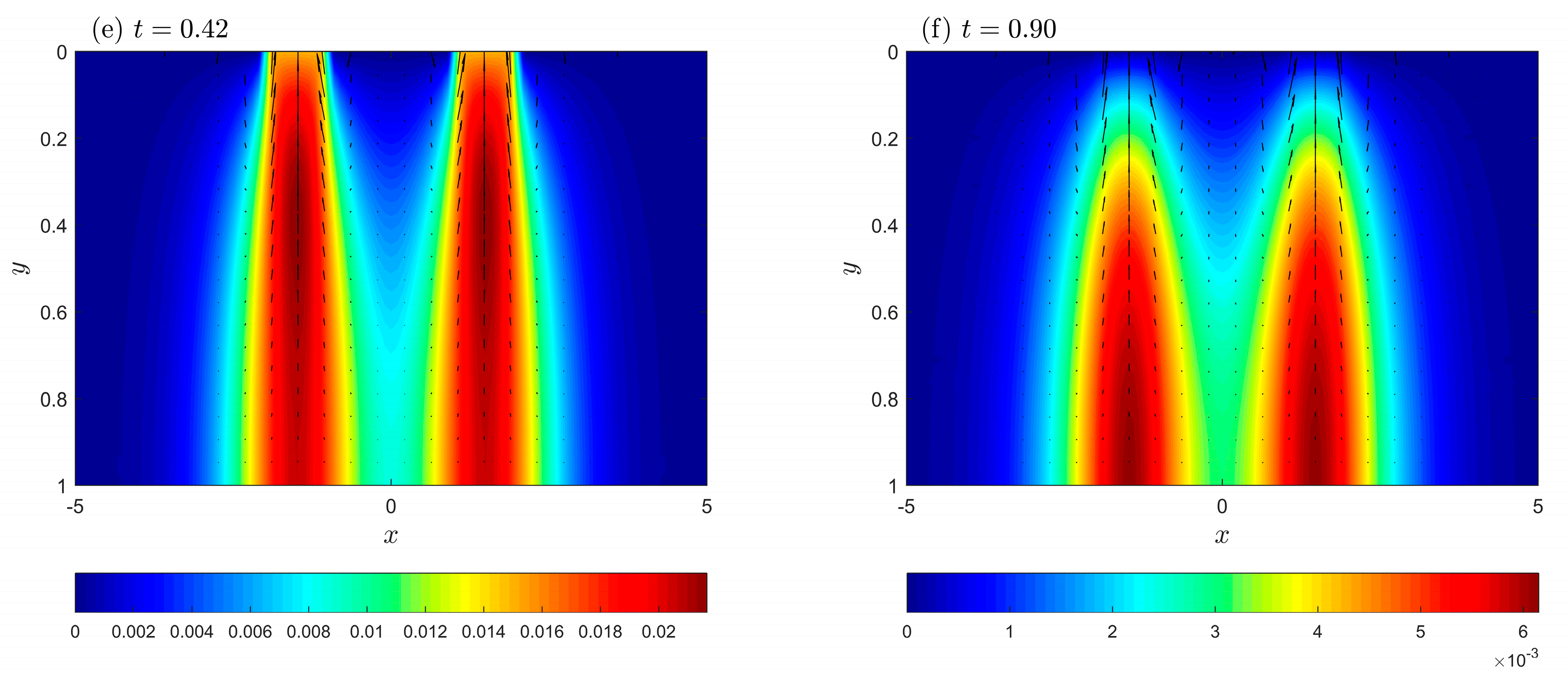
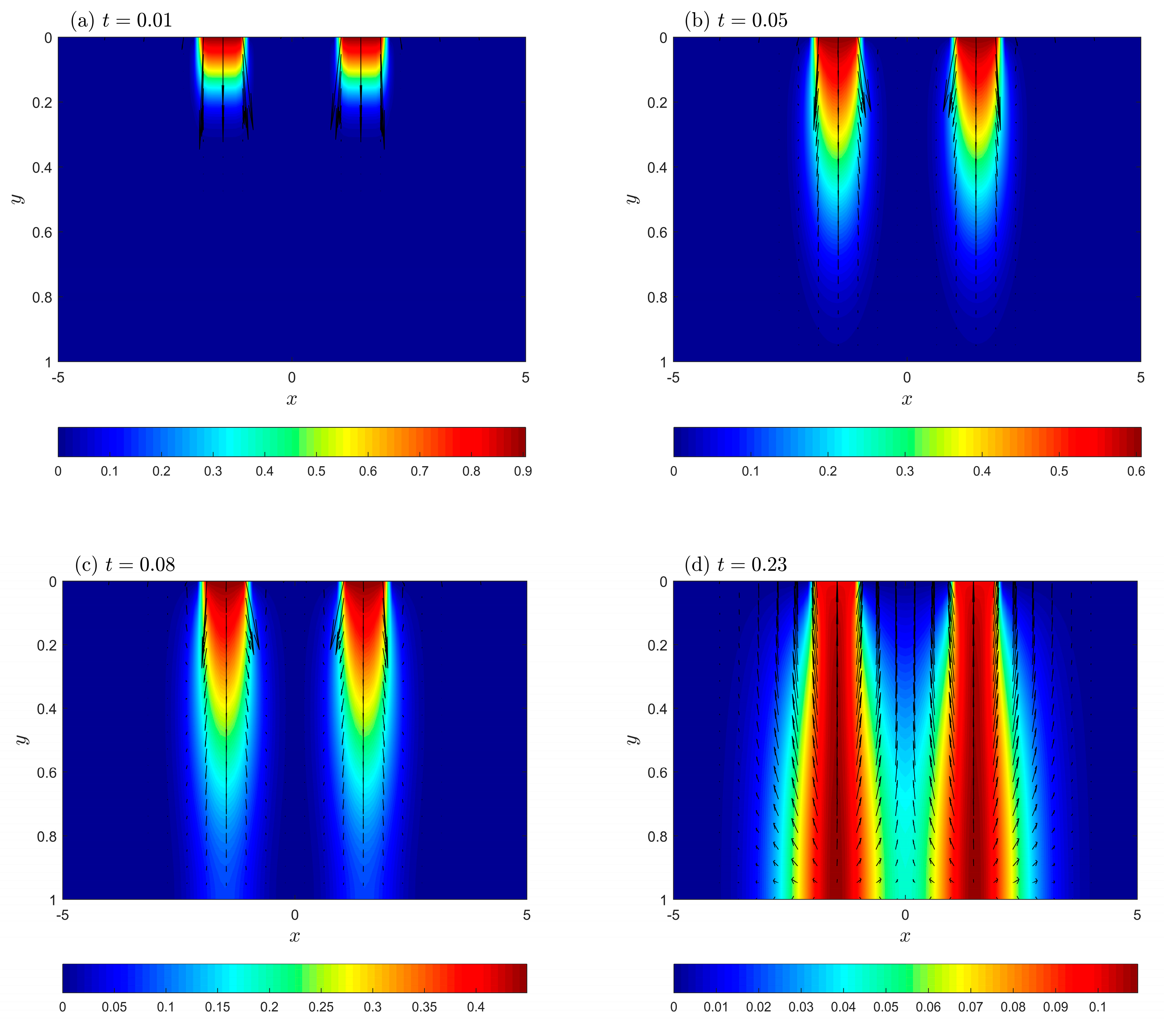
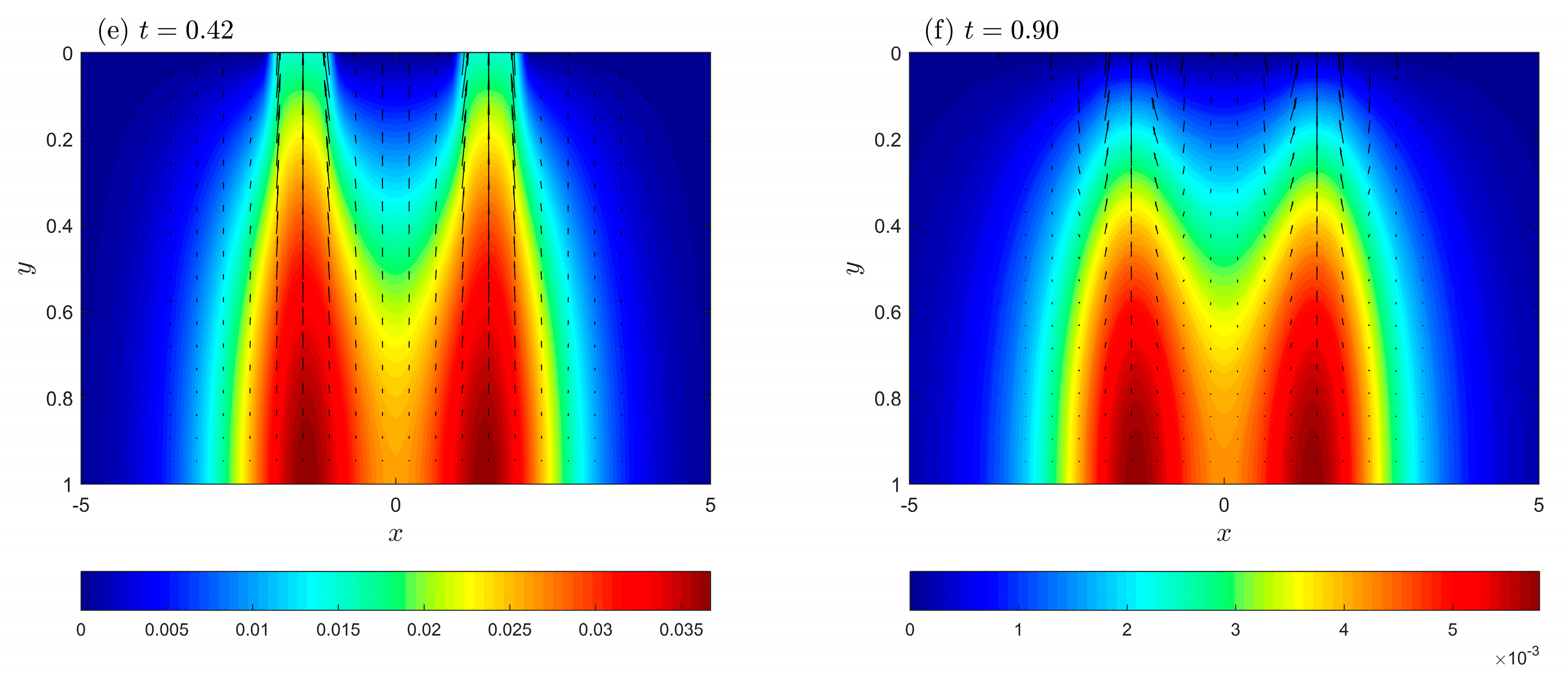
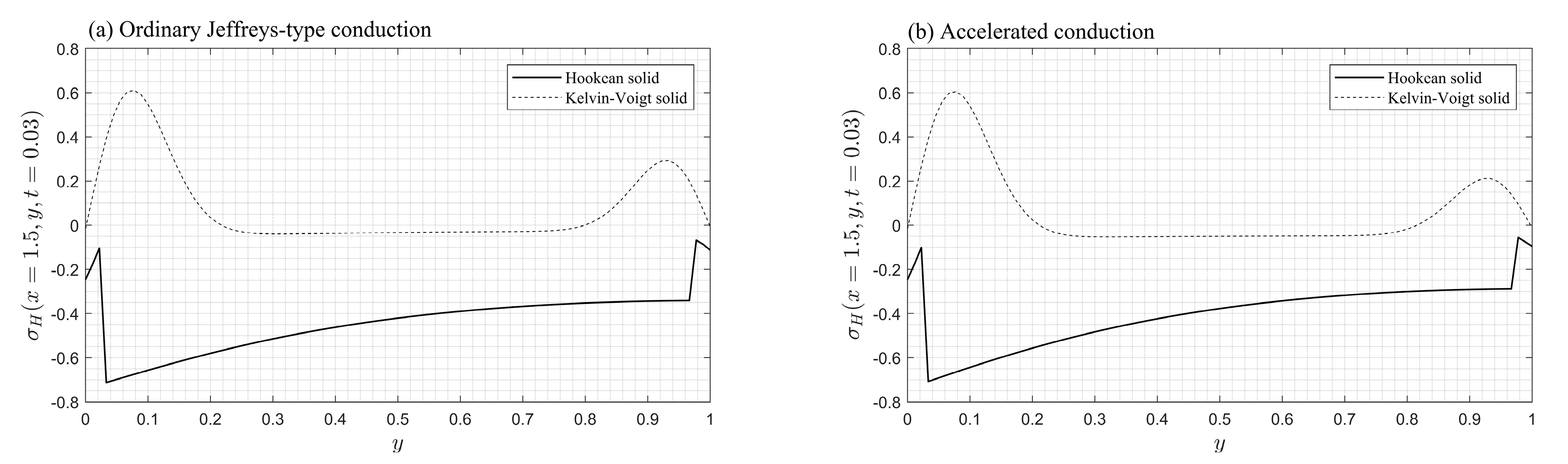
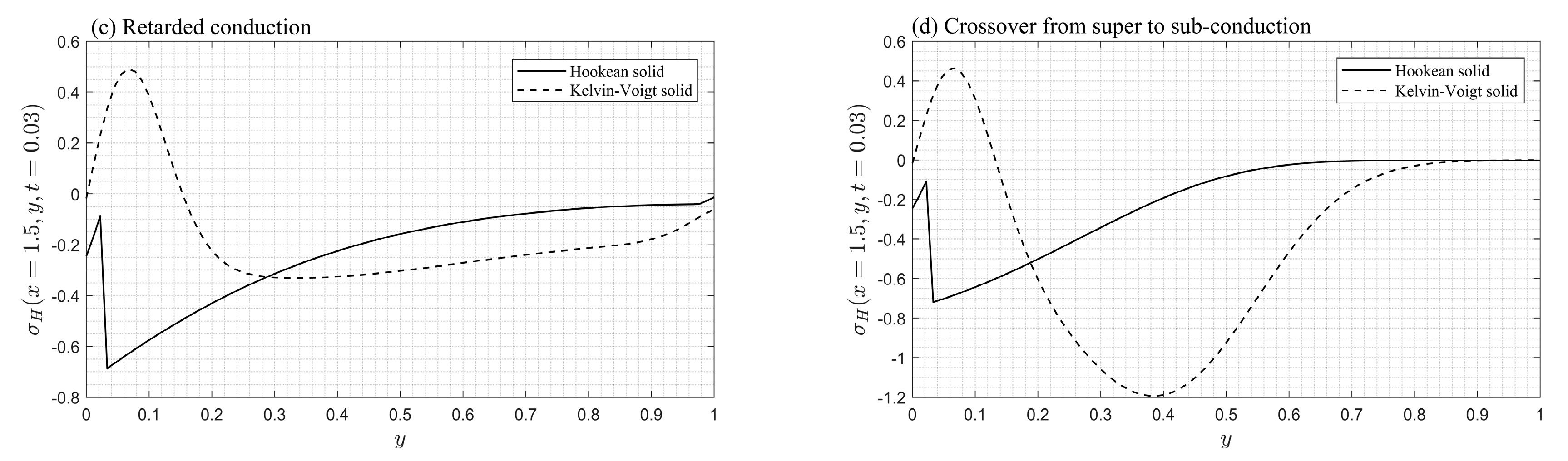
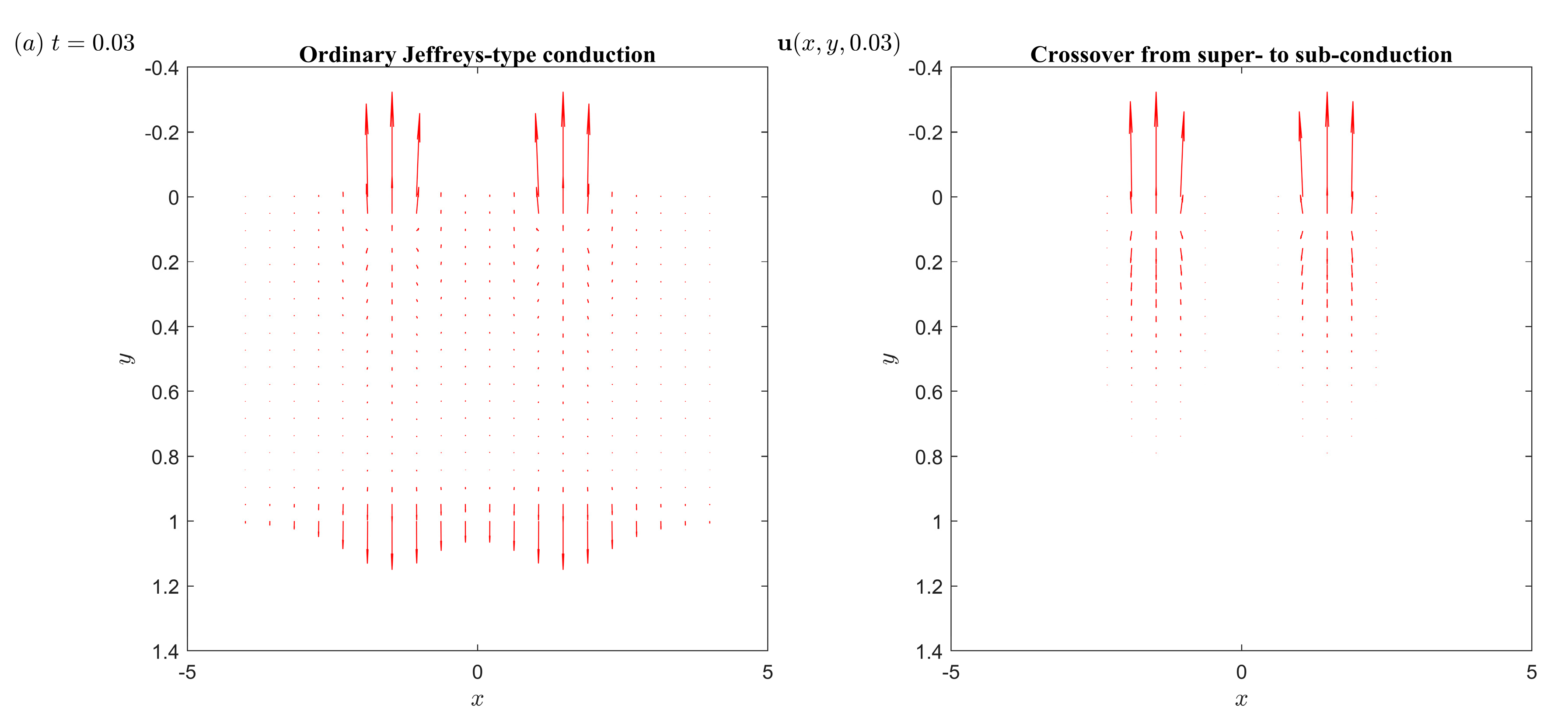
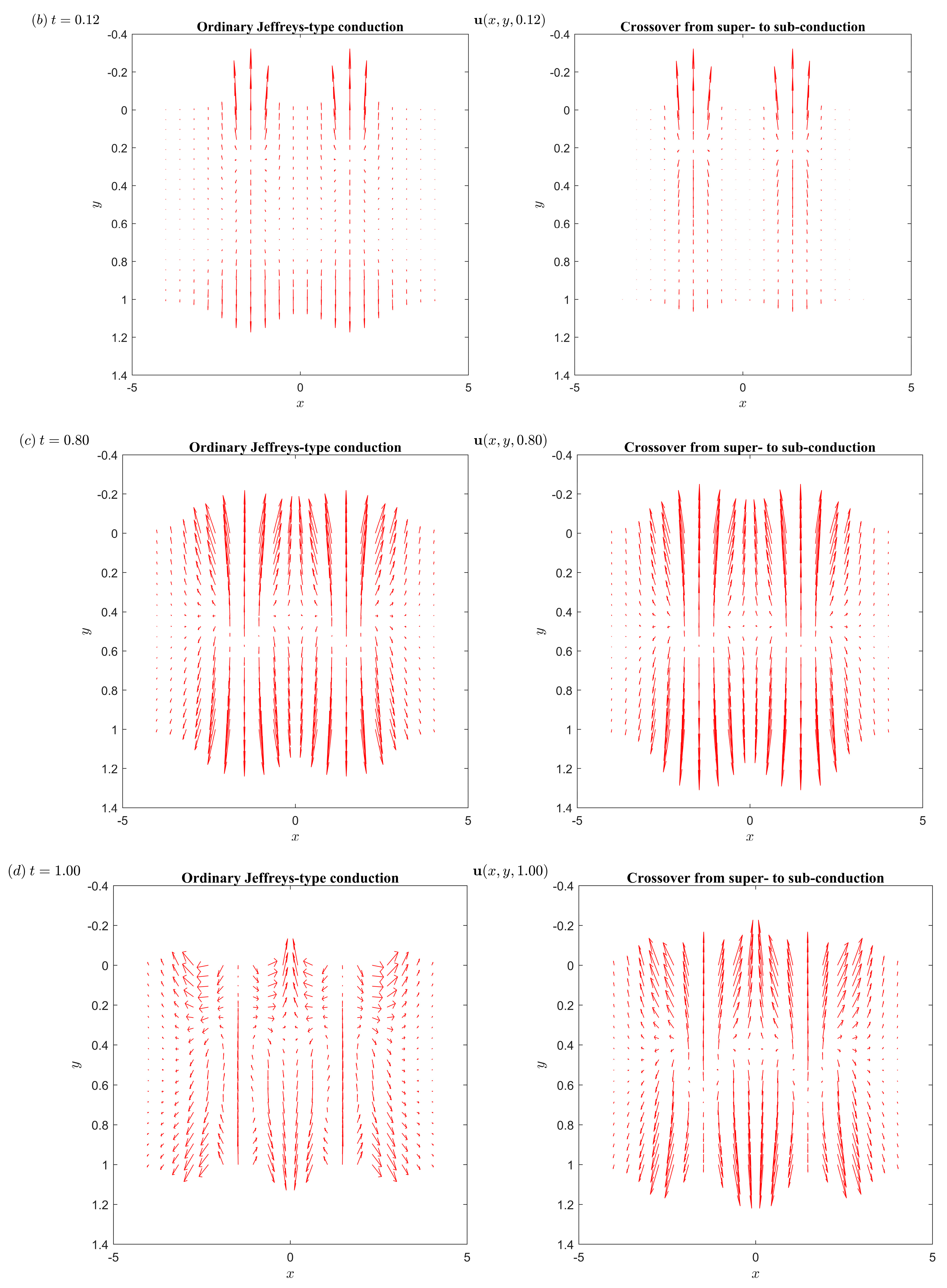
5. Numerical Results and Discussion

In order to present numerical results, copper material [6,55,56] is chosen for the purposes of numerical evaluation, with the parameters in SI units listed in

Table 1. Mechanical and thermal properties of copper at reference temperature $T_0=293 °\mathrm{K}$.

Property	${\mathit{\lambda }}_0$	${\mathit{\mu }}_0$	$\mathit{\rho }$	${\mathit{c}}_{\mathit{E}}$	${\mathit{\alpha }}_{\mathit{T}}$	$\mathit{k}$	${\mathit{\tau }}_{\mathit{q}}$	${\mathit{\tau }}_{\mathit{\theta }}$	${\mathit{\lambda }}_{\mathit{v}}={\mathit{\mu }}_{\mathit{v}}$
Value	$7.76\times {10}^{10}$	$3.86\times {10}^{10}$	8954	$383.1$	$1.78\times {10}^{-5}$	$386.0$	$0.4648$	70.833	$0.68831$
SI unit	$\mathrm{K}\mathrm{g}\cdot {\mathrm{m}}^{-1}\cdot {\mathrm{s}}^{-2}$	$\mathrm{K}\mathrm{g}\cdot {\mathrm{m}}^{-1}\cdot {\mathrm{s}}^{-2}$	$\mathrm{K}\mathrm{g}\cdot {\mathrm{m}}^{-3}$	$\mathrm{J}·{\mathrm{K}\mathrm{g}}^{-1}·{\mathrm{K}}^{-1}$	${\mathrm{K}}^{-1}$	$\mathrm{W}·{\mathrm{m}}^{-1}·{\mathrm{K}}^{-1}$	picoseconds	picoseconds	picoseconds

.

In addition, we choose the dimensionless plate thickness and the double-strip parameters as

$$l=1, a=1, b=2, t_p=0.1.$$

(78)

According to the choice of the dimensionless thickness, $l=1$, and the dimensionless thermalization parameter, $t_p=0.1$, the real thickness of the plate is $1/{(c}_1\eta )=27.063 \mathrm{n}\mathrm{a}\mathrm{n}\mathrm{o}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{e}\mathrm{r}\mathrm{s},$ and the real thermalization parameter equals $0.1/\left(c_1^2\eta \right)=1.302 \mathrm{p}\mathrm{i}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{e}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{s}$; refer to Equation (27), and also see [57].

In this section, we implement two infinite series to calculate the integrals (41) and (43). Thereby, we will bring the temperature, displacement, and hydrostatic stress to the physical domain. Inversion of the Laplace parameter $s$ to the physical time $t$ requires the implementation of Durbin formula, which is the approximation of the integral (41); see [58,59].

$$\begin{array}{c}\widehat{h}\left(q,y,t\right)=\frac{2\exp \left(\gamma \right)}{T_1}\left\{-\frac{1}{2}\widehat{\overline{h}}\left(q,y,\frac{\gamma }{t}\right)+\mathfrak{R}\left[{\displaystyle \sum _{j=0}^{NSum1}}\widehat{\overline{h}}\left(q,y,\frac{\gamma }{t}+\frac{2\pi ij}{T_1}\right)\cos \left(\frac{2\pi jt}{T_1}\right)\right]\right.\hfill \\ \hfill -\left.\mathfrak{I}\left[{\displaystyle \sum _{j=0}^{NSum1}}\widehat{\overline{h}}\left(q,y,\frac{\gamma }{t}+\frac{2\pi ij}{T_1}\right)\sin \left(\frac{2\pi jt}{T_1}\right)\right]\right\},\hfill \end{array}$$

(79)

where $\gamma \cong 4.7 ~ 10$ and $T_1$ is chosen so that $0<t\le 2T_1$. For accelerating the computations time, we use a FORTRAN subroutine [60] for the series with $Nsum1$ $\cong {10}^6$. Inversion of the Fourier transform, i.e., transforming $q$ into $x$, requires implementing another integral (refer to (43)), which can be approximated by the following Riemann sum

$${\mathcal{F}}^{-1}\left(\widehat{h}\left(q,y,t\right)\right)=\frac{1}{\pi }\left\{\begin{array}{c}{\displaystyle \sum _{n=0}^{Nsum2}}\widehat{h}\left(q_n,y,t\right)\cos \left(q_{n}x\right)∆q_n, \mathrm{for} \mathrm{even} \mathrm{function},\\ i{\displaystyle \sum _{n=0}^{Nsum2}}\widehat{h}\left(q_n,y,t\right)\sin \left(q_{n}x\right)∆q_n, \mathrm{for} \mathrm{odd} \mathrm{function}. \end{array}\right.$$

(80)

Using a suitable numerical approach, such as a trapezoidal approach, or a nested approach using the Bulirsch–Stoer step method, the rational function extrapolation, and modified midpoint method [61], the series (80) can be implemented. The parameter $Nsum2$ takes a value from 100 to 500. The computation time for 100 points ranges from 30 to 180 s depending on the mathematical model, the numerical technique used for inverting the Fourier transform, and the Intel Core processor version. Because of the evanescence of discontinuities in the stresses of the Kelvin–Voigt model and in the temperature of the fractional Jeffreys equation, the running time of the program is much less than that for the elastic case with finite thermal wave speed [57]. The computation was carried out on two Intel Core processors, Core i5-9600K and Core i7-1165G7. MATLAB R2019a was utilized for graphical representations on an NVIDIA Geforce MX330 graphics card.

The heat flux $\mathbf{q}=〈q_x,q_y,0〉$ is an important physical vector quantity predicting the actual heat direction inside the conductor. Using the following non-dimensional transformation:

$$\left(\begin{array}{c}{q}_x\\ q_y\end{array}\right)\to k{T}_0{c}_1\eta \left(\begin{array}{c}{q}_x\\ q_y\end{array}\right),$$

(81)

along with the dimensionless quantities (27) and the fractional Jeffreys Equation (8), the dimensionless heat flux components are given in terms of the temperature gradient as

$$\left(1+{\tau }_q^{\alpha }\frac{{\partial }^{\alpha }}{\partial t^{\alpha }}\right)\left\{\begin{array}{c}{q}_x\\ q_y\end{array}\right\}=-{\tau }_q^{1-\gamma }\frac{{\partial }^{1-\gamma }}{\partial t^{1-\gamma }}\left(1+{\tau }_{\theta }^{\beta }\frac{{\partial }^{\beta }}{\partial t^{\beta }}\right)\left\{\begin{array}{c}\frac{\partial \theta }{\partial x}\\ \frac{\partial \theta }{\partial y}\end{array}\right\}.$$

(82)

When the combined Laplace–Fourier transform (40) and (42) is invoked, the heat flux components (82) have the following exact formulas in the transformed domain:

$$\left\{\begin{array}{c}{\widehat{\overline{q}}}_x\\ {\widehat{\overline{q}}}_y\end{array}\right\}=-\frac{1}{L\left(s\right)}\left\{\begin{array}{c}iq\widehat{\overline{\theta }}\\ \mathfrak{D}\widehat{\overline{\theta }}\end{array}\right\},$$

(83)

and $L\left(s\right)=\frac{1+{\tau }_q^{\alpha }{s}^{\alpha }}{{\tau }_q^{1-\gamma }{s}^{1-\gamma }\left(1+{\tau }_{\theta }^{\beta }{s}^{\beta }\right)}$. In view of the temperature (55), the heat flux components (83) are given as

$$\begin{gathered} {\widehat{\overline{q}}}_x=-iq\epsilon s\left(1+{\gamma }_{v}s\right)\sum _{i=1}^2\left[A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right], \\ {\widehat{\overline{q}}}_y=-\epsilon s\left(1+{\gamma }_{v}s\right)\sum _{i=1}^2{m}_i\left[-A_i{e}^{-m_{i}y}+B_i{e}^{m_{i}y}\right]. \end{gathered}$$

(84)

In what follows, we will concentrate on four heat transfer models: the ordinary Jeffreys equation with flux precedence, known as the parabolic dual-phase-lag (DPL) model with ${\tau }_{\theta }>{\tau }_q$, the fractional Jeffreys equation with accelerated heat transfer, the fractional Jeffreys equation with retarded transfer, and the fractional Jeffreys equation with crossover from super- to sub-thermal conduction.

In Figure 2, we represent the temporal evolution of the temperature distribution governed by the flux-precedence DPL thermoelasticity and propagating from the upper surface to the lower surface. The heat flux components (84) are also inserted into the figure as a vector plot for anticipating the direction of heat. Before the dimensionless time instant $t=0.09$, the heat flux is directed from the upper surface to the lower surface which precedes and stimulates the temperature gradient. In the case of a semi-infinite conductor [50], the temperature peak diffuses with time progress, leaving the boundary surface. Here, in the finite domain setting, because of the presence of the reflecting boundary condition on the lower boundary (36) and the acute heat flux precedence, ${\tau }_{\theta }\gg {\tau }_q$, the heat flux vector reverses its direction between the dimensionless instants $t=0.08$ and $t=0.09$, so that the upper surface always has the highest temperature though the overall dissipation of heat (i.e., the decrease in temperature value with time). This behavior is also attributed to the immobilization characteristic of the Jeffreys “DPL” equation referred to in the literature; see [2,21,62]. Because of the cooling of the upper surface, the hot portion begins to move from the upper to the lower surface at a late instant $t=0.7$ and $0.9$; see recent studies on the ultrafast heating of micro- and nanostructures [63,64]. Some numerical results for the temperature at dimensionless time instants $t=0.05$ and $t=0.5$ are given in

Table 2. Numerical values of the temperature profile at the dimensionless instant $t=0.05$.

		Ordinary Jeffreys Heat Conduction			The Fractional Jeffreys-Type Heat Conduction
					Accelerated Conduction			Retarded Conduction			Crossover from Super- to Sub-Conduction
	x	$0.5$	$1.5$	$2.5$	$0.5$	$1.5$	$2.5$	$0.5$	$1.5$	$2.5$	$0.5$	$1.5$	$2.5$
y
$0.0$		$0.000017$	$0.606626$	0.000009	$0.000017$	$0.606626$	$0.000009$	$0.000017$	$0.606626$	$0.000009$	$0.000017$	$0.606626$	$0.000009$
$0.1$		$0.032830$	$0.538056$	$0.028552$	$0.027667$	$0.528095$	$0.024501$	$0.008853$	$0.487462$	$0.008775$	$0.007961$	$0.546885$	$0.007959$
$0.2$		$0.062894$	$0.475297$	$0.054399$	$0.052757$	$0.457417$	$0.046500$	$0.015883$	$0.381876$	$0.015723$	$0.013360$	$0.469591$	$0.013353$
$0.3$		$0.088464$	$0.421706$	$0.076011$	$0.073675$	$0.397627$	$0.064506$	$0.020156$	$0.293778$	$0.019925$	$0.014976$	$0.382421$	$0.014957$
$0.4$		$0.109023$	$0.378412$	$0.092930$	$0.090061$	$0.349397$	$0.078216$	$0.021814$	$0.223230$	$0.021540$	$0.013300$	$0.292004$	$0.013327$
$0.5$		$0.124909$	$0.344735$	$0.105599$	$0.102339$	$0.311841$	$0.088122$	$0.021502$	$0.168625$	$0.021190$	$0.009705$	$0.205164$	$0.009689$
$0.6$		$0.136780$	$0.319396$	$0.114740$	$0.111189$	$0.283509$	$0.094984$	$0.020134$	$0.127722$	$0.019788$	$0.005969$	$0.129459$	$0.005976$
$0.7$		$0.145297$	$0.301096$	$0.121077$	$0.117327$	$0.262969$	$0.099543$	$0.018390$	$0.098306$	$0.017996$	$0.003056$	$0.071513$	$0.003064$
$0.8$		$0.150998$	$0.288772$	$0.125192$	$0.121319$	$0.249104$	$0.102376$	$0.016819$	$0.078572$	$0.016355$	$0.001299$	$0.033724$	$0.001296$
$0.9$		$0.154272$	$0.281676$	$0.127501$	$0.123560$	$0.241099$	$0.103910$	$0.015675$	$0.067243$	$0.015253$	$0.000497$	$0.013852$	$0.000474$
$1.0$		$0.155339$	$0.279372$	$0.128245$	$0.124284$	$0.238483$	$0.104395$	$0.015274$	$0.063551$	$0.014875$	$0.000294$	$0.007668$	$0.000260$

and

Table 3. Numerical values of the temperature profile at the dimensionless instant $t=0.5$.

		Ordinary Jeffreys Heat Conduction			The Fractional Jeffreys-Type Heat Conduction
					Accelerated Conduction			Retarded Conduction			Crossover from Super- to Sub-Conduction
	x	$0.5$	$1.5$	$2.5$	$0.5$	$1.5$	$2.5$	$0.5$	$1.5$	$2.5$	$0.5$	$1.5$	$2.5$
y
$0.0$		0.000019	$0.006720$	$0.000020$	$0.000019$	$0.006720$	$0.000020$	$0.000019$	$0.006720$	$0.000020$	$0.000019$	$0.006720$	$0.000020$
$0.1$		$0.000376$	$0.006006$	$0.000330$	$0.000535$	$0.006319$	$0.000456$	$0.001648$	$0.010298$	$0.001426$	$0.003184$	$0.010157$	$0.002406$
$0.2$		$0.000722$	$0.005325$	$0.000619$	$0.001032$	$0.005914$	$0.000862$	$0.003188$	$0.012555$	$0.002742$	$0.006230$	$0.013075$	$0.004709$
$0.3$		$0.001020$	$0.004735$	$0.000872$	$0.001470$	$0.005515$	$0.001225$	$0.004562$	$0.013864$	$0.003915$	$0.009065$	$0.015561$	$0.006847$
$0.4$		$0.001252$	$0.004269$	$0.001063$	$0.001830$	$0.005192$	$0.001515$	$0.005728$	$0.014572$	$0.004878$	$0.011628$	$0.017672$	$0.008755$
$0.5$		$0.001443$	$0.003896$	$0.001211$	$0.002132$	$0.004929$	$0.001749$	$0.006678$	$0.014898$	$0.005662$	$0.013871$	$0.019431$	$0.010401$
$0.6$		$0.001583$	$0.003611$	$0.001321$	$0.002366$	$0.004728$	$0.001929$	$0.007430$	$0.015017$	$0.006280$	$0.015748$	$0.020859$	$0.011785$
$0.7$		$0.001683$	$0.003419$	$0.001395$	$0.002540$	$0.004603$	$0.002060$	$0.007996$	$0.015054$	$0.006726$	$0.017237$	$0.021988$	$0.012872$
$0.8$		$0.001752$	$0.003287$	$0.001445$	$0.002664$	$0.004520$	$0.002152$	$0.008393$	$0.015067$	$0.007040$	$0.018316$	$0.022795$	$0.013656$
$0.9$		$0.001791$	$0.003215$	$0.001473$	$0.002736$	$0.004478$	$0.002204$	$0.008630$	$0.015080$	$0.007225$	$0.018970$	$0.023293$	$0.014129$
$1.0$		$0.001803$	$0.003192$	$0.001482$	$0.002760$	$0.004465$	$0.002221$	$0.008706$	$0.015088$	$0.007286$	$0.019190$	$0.023462$	$0.014287$

.

The time evolution of the temperature distribution and the heat flux vector governed by the fractional Jeffreys equation with different transport situations are represented in Figure 3, Figure 4 and Figure 5 for accelerated, retarded, and crossover from super- to sub-thermal conductivity, respectively, at six instants. The terminologies “accelerated”, “retarded” and “crossover from super- to sub-” were named based on their deviation from the linear behavior of the mean squared displacement in the case of particle transfer being considered [21]. When the temperature distribution is resulting from anomalous diffusion of hot electrons within the lattice, then the thermal behavior might inherit a similar attitude. As Figure 3 shows, the accelerated case is not dissimilar from the ordinary DPL model in the short time response. The temperature distribution arrives at the lower surface at a very early instant, and the heat flux vector changes its direction to become from the lower surface to the upper surface very fast between the instants $t=0.01$ and $0.02$. Again, the direction reverse of the heat flux vector keeps the peak temperature at the upper surface for a relatively long time; see Figure 3c,d. The cooling of the upper surface due to the exponential function $\exp \left(-t/t_p\right)$ enforces the movement of the temperature peak from the upper to the lower surface as the subfigures Figure 3e,f show.

In Figure 4, the retarded heat conduction case represented by the fractional Jeffreys equation is drawn. In comparison with the ordinary Jeffreys equation and the fractional Jeffreys equation of accelerated type, the retardation case moves slower than the accelerated case such that the thermal waves have not yet reached the lower surface at $t=0.01$. In contrast to the rapid change in the direction of the heat flux in Figure 2 and Figure 3, the heat flux vector spends a longer interval from $t=0.05$ to $t=0.1$ to change its direction. The retardation in heat transfer causes lower values for the temperature at the lower surface compared with the ordinary Jeffreys and the acceleration case; compare the instants $t=0.01$ and $0.05$ in Figure 2, Figure 3 and Figure 4.

The crossover from super- to sub-thermal conduction is represented in Figure 5. Because of its affinity in the temporal behavior to the Cattaneo equation, the temperature distribution of such crossover moves slower than all flux-precedence Jeffreys models (ordinary and fractional), but there is no explicit form for its speed from a mathematical point of view. The heat flux reverses its direction between the instants $t=0.14$ and $t=0.3$, i.e., during a longer interval compared with all flux-precedence (ordinary and fractional) Jeffreys models.

In Figure 6, the hydrostatic stress, for the four models of thermoelasticity based on the ordinary and fractional flux-precedence Jeffreys heat conduction equations, is illustrated. At the early instant $t=0.01$, in Figure 6a, it is salient that the thermal waves resulting from the crossover from super- to sub-thermal conduction are the slowest ones among the four models, followed by those of the retarded heat transfer model. The two peaks near the upper surface are attributed to the mechanical waves of the Kelvin–Voigt model. At the subsequent instant $t=0.14$, all the thermal waves are reflected from the lower surface and are ready to overlap with the mechanical waves coming from the upper surface; see Figure 6c. It is clear that the Kelvin–Voigt model diminishes the discontinuities of stresses; see the elastic case [57]. To emphasize this merit in the Kelvin–Voigt solid, we compare it with the Hookean response excited by the four thermal transport mechanisms in Figure 7. In the interval $y\in \left[\mathrm{0,0.2}\right]$, the curves for both Hookean and Kelvin–Voigt solids are not affected by the thermal transport mechanism, and the discontinuity in the Hookean solid is due to the dominated mechanical wave. The interval $y\in \left[\mathrm{0.2,1}\right]$, however, contains the dominated thermal wave, and thus there is a significant difference among the Jeffreys-type conduction models for the single elastic/viscoelastic model. The stresses of Kelvin–Voigt solid record higher values for all models of heat transfer compared with the Hookean elastic case.

In Figure 8, we represent the displacement vector induced by the ordinary Jeffreys-type heat conduction and the crossover from super- to sub-thermal conduction. We do not attach the other models due to the resemblance between their effects on the displacement with the Jeffreys-type heat conduction and crossover from super- to sub-thermal conduction model. The early arrival of the thermal wave to the lower surface, in the case of a Jeffreys-type heat conductor, is very clear in instant $t=0.01$; see Figure 8a. At the instant $t=1$, the displacement of the Jeffreys-type heat conduction is on a position of cutting at the double-strip, while the crossover from super- to sub-thermal conduction model is delayed. The contour figures, stress surfaces and displacement vectors are screenshots from full videos in the Supplementary Material section.

6. Summary

In this work, we have studied the effect of anomalous heat transfer inherited from the anomalous diffusion of thermal energy carriers throughout the material lattice. The material response is assumed to follow the Kelvin–Voigt assumption in which the stress–strain relation is not instantaneous; however, there is a retardation in the material strain compared with the elastic “Hookean” response. The Kelvin–Voigt hypothesis may be a reason for the occurrence of anomalies during the diffusion of thermal energy carriers and thus anomalous heat transfer. We have considered a two-dimensional plate with nanoscale thickness, heated by an ultrafast double-strip on its upper surface. The Laplace and Fourier transforms have been used to obtain the solution in the transformed domain. A numerical method based on accelerating the implementation of two infinite sums has been used to obtain the solutions in the proper time–space domain.

The thermal wave resulting from the crossover from super- to sub-thermal conduction is slower than that resulting from the retarded conduction, which in turn is slower than that resulting from the accelerated conduction. The ordinary flux-precedence Jeffreys-type heat conduction has the fastest thermal waves among the models considered in this work. The faster models transport thermal energy to the other surface during a short time interval and record the maximum temperature value on the lower surface. The displacement vector chart of the accelerated and ordinary Jeffreys-type heat conduction evolves faster than those in retarded and crossover models.