A New Technique to Achieve Torsional Anchor of Fractional Torsion Equation Using Conservation Laws

Abstract

The main idea in this research is introducing another approximate method to calculate solutions of the fractional Torsion equation, which is one of the applied equations in civil engineering. Since the fractional order is closed to an integer, we convert the fractional Torsion equation to a perturbed ordinary differential equation involving a small parameter epsilon. Then we can find the exact solutions and approximate symmetries for the alternative approximation equation. Also, with help of the definition of conserved vector and the concept of nonlinear self-adjointness, approximate conservation laws(ACL) are obtained without approximate Lagrangians by using their approximate symmetries. In order to apply the presented theory, we apply the Lie symmetry analysis (LSA) and concept of nonlinear self-adjoint Torsion equation, which are very important in mathematics and engineering sciences, especially civil engineering.

1. Introduction

Fractional calculus is a rapidly developing discipline within mathematics that has gained significant attention in recent years due to its ability to model and understand nonlinear phenomena to various scientific and engineering disciplines. Using new aspects of fractional calculus, researchers can further expand its applications across different disciplines [1]. Over the course of several decades, Lie symmetry analysis (LSA) has been widely applied and demonstrated its significance in various fields, including mathematics, mechanics, dynamics, control theory, and modeling. LSA has proven to be a valuable tool for studying and solving partial differential equations (PDEs) and fractional differential equations (FDEs) [2,3,4]. Recently, many scientists have been applied various methods to obtain analytical solutions of FDEs in different papers such as, the sine-Gordon expansion method [5], first integral method [6], Lie symmetry method [7], Bäcklund transformation method [8], fractional sub-equation method [9], $\frac{G^{\prime }}{G}$-expansion method [10], extended unified method [11], Yang’s special function method [12] and so on. However, this paper is devoted of approximating FDEs to corresponding ODEs when including small epsilon parameter the fractional order is closed to an integer value [13,14,15,16,17,18]. Solutions of the FDEs can be obtained based on the solutions of the perturbed equations by substituting the original FDE into the approximate differential equation and by approximate $D_x^{\alpha }\phi$ with integer order derivative with epsilon parameter.

Conservation laws play a crucial role in the investigation and interpretation of PDEs within the realms of mathematical and engineering sciences. The conserved vectors of conservation laws using LSA can be obtained by new Noether’s operators [19,20,21,22,23,24].

In view of the fact that it is not possible to calculate all the group-invariant solutions, all these invariant solutions can be classified into different classes. By explaining that under the symmetry group, a solution from one class can be transformed to another from the same class. So that the answers of different classes are not the same. This classification of solutions is called the optimal system under the subalgebra [25,26,27].

In solid mechanics, torsion is defined as the twisting of a body due to the applied torque. We consider a uniform rod that is fixed at one end and subjected to torque at the other end. This torque is typically applied about its axis, and it twists the rod to a specific angle. It is assumed that the rod cannot be subjected to compression beyond its elastic limit. In this article, we focus on studying the following Torsion equation with the aim of calculating the applied torsional anchor on edge steel beams in connection with the joist roof and block.

$${}_0{D}_x^{\alpha }\left(G_J{}_0{D}_x^{\alpha }\phi \right)+m=0,$$

(1)

Here $G_J$ is torsional hardness constant and m is torsional anchor constant that cross-sectional area of the beam is in the distance x from the support, and it creates a rotational as much $\phi$. Since edge beams in steel buildings are affected by bending and torsion anchors due to the load bearing wall and the one-way roof slab attached thereto, it can be assumed that the girder is fully integrated with the roof slab and its lateral period is dependent on the roof slab support period.

The torsional anchor of the wall load can be calculated according to the position on the wing of the edge beam and its deviation from its axis. However, the torsion due to the load of the roof slab connected to the edge beam due to the uncertainty of the exact position of the slab support relative to the weak axis of the beam can not be easily calculated. Therefore, according to the principle of conformity of the deformation between the bending period of the end of the slab and the torsion of the edge beam, it is possible to calculate the period of the slab roof support based on the slab and load characteristics. One can then calculate the torsion anchor on an edge beam whose period is like the roof slab. Obviously, the higher the slab ceiling size, the greater the bending hardness, the lower the slab end time and consequently the edge beam torsion and the torsion on the beam is also reduced.

Our main purpose for this article is to investigate the LSA and solutions to the FTE. We can construct the conservation laws using modified Noether’s theorem [28,29,30,31].

In sequel, we construct the optimal system of subalgebras of the found symmetries for Torsion FDE. This article is organized as follows.

In Section 2, the basic results to convert an FDE to an approximate equation and some definitions are presented. The determining equations and the infinitesimal transformations are obtained in Section 3. In Section 4, some reduced equations and optimal system are obtained. ACL of equation are introduced through the concept of nonlinear self adjointness, and methodology to obtain the ACL of Torsion perturbed FDEs is illustrated in Section 5. Finally, conclusion is given in Section 6.

2. Converting the FDE to Approximate ODE

In the past few decades, FDEs have gained significant popularity as a modeling tool for various physical phenomena. They have found widespread application, particularly in situations where classical calculus fails to efficiently describe uncommon phenomena and complex natural processes. FDEs provide a more flexible and accurate framework for capturing the behavior of these systems, allowing researchers to better understand and predict their dynamics. The first note about fractional derivatives history dates back about 300 years ago. Since then, many mathematicians studied the fractional calculus like Fourier, Liouville, Lacroix, Riemann, Letnikov, Abel, Caputo and many others have all contributed to the advancement of this discipline [32,33,34,35].

We present briefly some definitions and properties of the Caputo and Riemann-Liouville fractional operators which will be used in the further of our work.

There are several different type fractional derivatives. However, we use the right and left hand sides fractional derivatives in the Riemann-Liouville and Caputo sense as follows [17,36,37,38].

Definition 1. 

The left and right-sided Caputo fractional partial derivative are defined by

$$\left({}_a^C{D}_{x^1}^{\alpha +j}\phi \right)\left(x\right)=\frac{1}{\Gamma (1-\alpha )}{\int }_a^{x^1}\frac{1}{{(x^1-\xi )}^{\alpha }}\frac{{\partial }^{j+1}\phi (\xi ,x^2,\dots ,x^n)}{\partial {\xi }^{j+1}}d\xi ,$$

(2)

$$\left({}_{x^1}^C{D}_b^{\alpha +j}\phi \right)\left(x\right)=\frac{{(-1)}^{j+1}}{\Gamma (1-\alpha )}{\int }_{x^1}^b\frac{1}{{(\xi -x^1)}^{\alpha }}\frac{{\partial }^{j+1}\phi (\xi ,x^2,\dots ,x^n)}{\partial {\xi }^{j+1}}d\xi .$$

(3)

Definition 2. 

The left and right-sided Riemann-Liouville fractional partial derivative are defined by

$$\left({}_a{D}_{x^1}^{\alpha +j}\phi \right)\left(x\right)=\frac{1}{\Gamma (1-\alpha )}{\left(\frac{\partial }{\partial x^1}\right)}^{j+1}{\int }_a^{x^1}\frac{\phi (\xi ,x^2,\dots ,x^n)}{{(x^1-\xi )}^{\alpha }}d\xi ,$$

(4)

$$\left({}_{x^1}{D}_b^{\alpha +j}\phi \right)\left(x\right)=\frac{{(-1)}^{j+1}}{\Gamma (1-\alpha )}{\left(\frac{\partial }{\partial x^1}\right)}^{j+1}{\int }_{x^1}^b\frac{\phi (\xi ,x^2,\dots ,x^n)}{{(x^1-\xi )}^{\alpha }}d\xi .$$

(5)

Here $\alpha \in (0,1)j=0,1,\dots ,m$ and $\Gamma (·)$ denotes Gamma function.

Let us consider a multi orders FDE as follows:

$$Q\left(x,\phi \left(x\right),{\phi }_{\left(1\right)},\dots ,{\phi }_{\left(k\right)}{,}_a{D}_{x^1}^{{\alpha }_0}\phi {,}_a{D}_{x^1}^{{\alpha }_1}\phi ,\dots {,}_a{D}_{x^1}^{{\alpha }_m}\phi {,}_{x^1}{D}_b^{{\beta }_0}\phi {,}_{x^1}{D}_b^{{\beta }_1}\phi ,\dots {,}_{x^1}{D}_b^{{\beta }_l}\phi \right)=0,$$

(6)

where ${\left\{{\alpha }_i\right\}}_{i=0}^m$ and ${\left\{{\beta }_j\right\}}_{j=0}^l$ are positive increasing sequences and $l,k,m\in \mathbb{N}$. Also, $\phi \left(x\right)=\phi (x^1,x^2,\dots ,x^n)$ is a function of $x\in {\mathbb{R}}^n,x^1\in (a,b)$ and

$${\phi }_{\left(s\right)}\equiv \left\{{\phi }_{i_1\dots i_s}\right\}=\left\{\frac{{\partial }^s\phi \left(x\right)}{\partial x^{i_1}\dots \partial x^{i_s}}\right\};i_1,\dots i_s=1,\dots n,s=1,\dots ,k,$$

are successive derivatives of $\phi$ w.r.t $x^i$.

We can approximate the Equation (6) into following perturbed equation when all the orders ${\alpha }_i$ and ${\beta }_j$ are so close to integer values [31].

$$Q\left(x,\phi ,{\phi }_{\left(s\right)}{,}_a{D}_{x^1}^{\alpha +i}\phi {,}_{x^1}{D}_b^{\alpha +j}\phi \right)=0,s=1,\dots ,k,i=0,\cdots ,m,j=0,\cdots ,m,\alpha \in (0,1).$$

(7)

Considering the $\alpha =\epsilon +1$ or $\alpha =\epsilon$ in Equation (7), then for each derivative ${}_a{D}_{x^1}^{j+\epsilon }\phi {,}_{x^1}{D}_b^{j+\epsilon }\phi (j=0,1,\dots )$ or ${}_a{D}_{x^1}^{j-\epsilon }\phi {,}_{x^1}{D}_b^{j-\epsilon }\phi (j=1,2,\dots )$ at arbitrary point $x^1\in (a,b)$, by using Taylor expansion with $0<\epsilon \ll 1$ we have

$$\begin{array}{cc}\hfill {}_a{D}_{x^1}^{j\pm \epsilon }\phi & =\sum _{s=0}^{\infty }\left(\genfrac{}{}{0pt}{}{j\pm \epsilon }{s}\right)\frac{{(x^1-a)}^{s\pm \epsilon -j}}{\Gamma (1+s\pm \epsilon -j)}\frac{{\partial }^s\phi (\xi ,x^2,\dots ,x^n)}{\partial {\xi }^s}\hfill \\ & =\frac{{\partial }^j\phi }{\partial {\left(x^1\right)}^j}\pm \epsilon ([\chi (j+1)-ln(x^1-a)]\frac{{\partial }^j\phi }{\partial {\left(x^1\right)}^j}\hfill \\ & -\sum _{s=0,s\ne j}^{\infty }\frac{j!{(a-x^1)}^{s-j}}{s!(s-j)}\frac{{\partial }^s\phi }{\partial {\left(x^1\right)}^s})+o\left(\epsilon \right),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {}_{x^1}{D}_b^{j\pm \epsilon }\phi & =\frac{{\partial }^j\phi }{\partial {\left(x^1\right)}^j}\pm \epsilon ([\chi (1+j)-ln(b-x^1)]\frac{{\partial }^j\phi }{\partial {\left(x^1\right)}^j}\hfill \\ & -\sum _{s=0,s\ne j}^{\infty }\frac{j!{(x^1-b)}^{s-j}}{s!(s-j)}\frac{{\partial }^s\phi }{\partial {\left(x^1\right)}^s})+o\left(\epsilon \right),\hfill \end{array}$$

(9)

and for Caputo fractional derivative

$$\begin{array}{c}\hfill {}_a^C{D}_{x^1}^{j\pm \epsilon }\phi {=}_a{D}_{x^1}^{j\pm \epsilon }\phi \mp \epsilon \sum _{s=0}^{j-1}{(-1)}^{s-j}(j-s-1)!{(x^1-a)}^{s-j}\frac{{\partial }^s\phi }{\partial {\left(x^1\right)}^s}{|}_{x^1=a}+p(x,a),\end{array}$$

(10)

$$\begin{array}{c}\hfill {}_{x^1}^C{D}_b^{j\pm \epsilon }\phi {=}_{x^1}{D}_b^{j\pm \epsilon }\phi \mp \epsilon \sum _{s=0}^{j-1}{(-1)}^{s-j}(j-s-1)!{(b-x^1)}^{s-j}\frac{{\partial }^s\phi }{\partial {\left(x^1\right)}^s}{|}_{x^1=b}+q(x,b).\end{array}$$

(11)

where

$$\begin{array}{c}\hfill p(x,a)=\left\{\begin{array}{cc}-[1+\epsilon (\chi \left(1\right)-ln(x^1-a))]\frac{{\partial }^j\phi }{\partial {\left(x^1\right)}^j}{|}_{x^1=a},\hfill & {}_a^C{D}_{x^1}^{j+\epsilon }\phi ;\hfill \\ 0,\hfill & {}_a^C{D}_{x^1}^{j-\epsilon }\phi ,\hfill \end{array}\right.\end{array}$$

$$\begin{array}{c}\hfill q(x,b)=\left\{\begin{array}{cc}-[1+\epsilon (\chi \left(1\right)-ln(b-x^1))]\frac{{\partial }^j\phi }{\partial {\left(x^1\right)}^j}{|}_{x^1=b},\hfill & {}_{x^1}^C{D}_b^{j+\epsilon }\phi ;\hfill \\ 0,\hfill & {}_{x^1}^C{D}_b^{j-\epsilon }\phi .\hfill \end{array}\right.\end{array}$$

Proposition 1. 

If the function Q is differentiable continuously in Equation (7) w.r.t ${}_a{D}_{x^1}^{\alpha +j}\phi$ and ${}_{x^1}{D}_b^{\alpha +j}\phi$$(j=0,1,\dots ,m)$, then we can approximate Equation (7) using perturbed integer-order equation for $\alpha =1-\epsilon$ or $\alpha =\epsilon$ as

$$\begin{array}{c}\hfill Q_{\left(0\right)}(x,\phi ,{\phi }_{\left(1\right)},\dots ,{\phi }_{\left(l\right)})+\epsilon Q_{\left(1\right)}(x,\phi ,{\phi }_{\left(1\right)},\dots ,{\phi }_{\left(l\right)},D_{x^1}^{l+1}\phi ,D_{x^1}^{l+2}\phi ,\dots )\approx 0,\end{array}$$

(12)

where for $\alpha =\epsilon$ l is $max\{m-1,k\}$ and for $\alpha =1-\epsilon$ l is $max\{m,k\}$.

3. Lie Group Analysis for Perturbed Equation (12)

Inasmuch as Lie group analysis is an efficient algorithmic approach to study symmetric properties of differential equations so many researchers investigated how to construct approximate symmetries for perturbed equations via this method. Such as Baikov et al., Johnpillai et al. [13,22,23], have applied standard methods of perturbation operator symmetry and dependent variables to obtain approximate symmetries. The first order differential operator is

$$\begin{array}{cc}\hfill X& \approx X_{\left(0\right)}+\epsilon X_{\left(1\right)}\hfill \\ & \equiv \left({\xi }_{\left(0\right)}^h(x,\phi )+\epsilon {\xi }_{\left(1\right)}^h(x,\phi )\right)\frac{\partial }{\partial x^h}+\left({\eta }_{\left(0\right)}(x,\phi )+\epsilon {\eta }_{\left(1\right)}(x,\phi )\right)\frac{\partial }{\partial \phi },\hfill \end{array}$$

(13)

where

$$\begin{array}{c}{\xi }_{\left(0\right)}^h(x,\phi )=\frac{\partial {\theta }_{\left(0\right)}^h(x,\phi ,a)}{\partial a}{{|}_{a=0},{\xi }_{\left(1\right)}^h(x,\phi )=\frac{\partial {\theta }_{\left(1\right)}^h(x,\phi ,a)}{\partial a}|}_{a=0},h=1,\dots ,n;\hfill \\ {\eta }_{\left(0\right)}(x,\phi )=\frac{\partial {\mu }_{\left(0\right)}(x,\phi ,a)}{\partial a}{{|}_{a=0},{\eta }_{\left(1\right)}(x,\phi )=\frac{\partial {\mu }_{\left(1\right)}(x,\phi ,a)}{\partial a}|}_{a=0}.\hfill \end{array}$$

By computing the solutions of the characteristic equation

$$\begin{array}{c}\hfill X\left(Q_{\left(0\right)}+\epsilon Q_{\left(1\right)}\right){|}_{\left(12\right)}\approx 0,\end{array}$$

(14)

exact symmetries will be achieved for the perturbed Equation (7).

The approximate point transformations are

$$\begin{array}{cc}\hfill {\overline{x}}^i& \approx {\theta }^i(x,\phi ,a,\epsilon )\equiv {\theta }_{\left(0\right)}^i(x,\phi ,a)+\epsilon {\theta }_{\left(1\right)}^i(x,\phi ,a),i=1,\dots ,n,\hfill \\ \hfill \overline{\phi }& \approx \mu (x,\phi ,a,\epsilon )\equiv {\mu }_{\left(0\right)}(x,\phi ,a)+\epsilon {\mu }_{\left(1\right)}(x,\phi ,a),\hfill \end{array}$$

(15)

that satisfied in

$$\begin{array}{c}\hfill {\overline{x}}^i{|a=0\approx x^i,\overline{\phi }|}_{a=0}=\phi ,\end{array}$$

are a one-parameter approximate Lie-point transformation group when the group properties

$$\begin{array}{ccc}\hfill & & {\theta }^i\left({\theta }^1(x,\phi ,a,\epsilon ),\dots ,{\theta }^n(x,\phi ,a,\epsilon ),\mu (x,\phi ,a,\epsilon ),b,\epsilon \right)\approx {\theta }^i(x,b+a,\epsilon ),i=1,\cdots ,n,\hfill \\ & & \mu \left({\theta }^1(x,\phi ,a,\epsilon ),\dots ,{\theta }^n(x,\phi ,a,\epsilon ),\mu (x,\phi ,a,\epsilon ),b,\epsilon \right)\approx \mu (x,b+a,\epsilon ).\hfill \end{array}$$

are satisfied with the accuracy $o\left(\epsilon \right)$.

4. Classification of Group-Invariant Solution

The construction of optimal system for one dimensional subalgebras reduce to the classification of the orbits for the adjoint representation (AR) [18]. If we know the infinitesimal adjoint action $ad\mathbf{g}$ of a Lie algebra $\mathbf{g}$ on itself, we can reconstruct the adjoint representation $AdG$ of the underlying Lie group, either by integrating the system of linear ordinary differential equations.

$$\begin{array}{c}\hfill \frac{dX}{dϵ}{=adY|}_X,X\left(0\right)=X_0,\end{array}$$

with solution

$$\begin{array}{c}\hfill X\left(ϵ\right)=Ad\left(\exp \left(ϵY\right)\right)X_0,\end{array}$$

where

$$\begin{array}{c}\hfill Ad\left(\exp \left(ϵY\right)\right)X_0=\sum _{n=0}^{\infty }\frac{{ϵ}^n}{n!}{\left(adY\right)}^n\left(X_0\right)=X_0-ϵ[Y,X_0]+\frac{{ϵ}^2}{2}[Y,[Y,X_0]]-\dots .\end{array}$$

Here $ϵ$ is a parameter and $[X_i,X_j]$ denotes the usual commutator.

4.1. Optimal System of Perturbed Fractional Torsion Equation

Consider perturbed fractional torsion equation

$$\begin{array}{c}\hfill {}_0{D}_x^{2\alpha }\phi \left(x\right)=-\frac{m}{G_J}-\frac{3}{2}\epsilon {\phi }_{xx}\left(x\right),\alpha \in (0,1).\end{array}$$

(16)

We must first apply extension (8) for Equation (16) in order to estimate the symmetries of the above perturbed fractional equation.

Let $\alpha =1-\epsilon$, it leads the approximation of Equation (16) as follows

$$\begin{array}{cc}\hfill Q_{\left(0\right)}+\epsilon Q_{\left(1\right)}={\phi }_{xx}& +\frac{m}{G_J}-\epsilon [(\frac{3}{2}-\gamma -lnx){\phi }_{xx}+\frac{\phi }{x^2}\hfill \\ & -2\frac{{\phi }_x}{x}-\sum _{k=3}^{\infty }\frac{2!}{k!(k-2)!}{(-x)}^{k-2}\frac{{\partial }^k\phi }{\partial x^k}]+\frac{3}{2}\epsilon {\phi }_{xx}=0.\hfill \end{array}$$

(17)

For this purpose, we should to obtain symmetries of perturbed Equation (17), that results are as follows using Maple 2021.1 software.

$$\begin{array}{cc}\hfill X_1& ={\partial }_x,X_2={\partial }_{\phi },X_3=x{\partial }_{\phi },X_4=(\phi +\frac{m}{G_J}{x}^2){\partial }_{\phi },\hfill \\ \hfill X_5& =x{\partial }_x-\frac{m}{G_J}{x}^2{\partial }_{\phi },X_6=\frac{x^2}{2}{\partial }_x-\frac{1}{2}(\frac{m}{2G_J}{x}^3-x\phi ){\partial }_{\phi },\hfill \\ \hfill X_7& =\phi {\partial }_x-\frac{m}{2G_J}(\frac{m}{2G_J}{x}^3+3x\phi ){\partial }_{\phi },\hfill \\ \hfill X_8& =(\frac{m}{2G_J}{x}^3+x\phi ){\partial }_x-(\frac{m^2}{4{G_J}^2}{x}^4-{\phi }^2){\partial }_{\phi },\hfill \\ \hfill Y_1& =\epsilon \left(x{B}_7-x{B}_{7}lnx-B_{8}lnx\right){\partial }_{\phi },\hfill \\ \hfill Y_2& =-\frac{x^2}{6}{\partial }_x+(\frac{G_J{x}^3}{12m}-\frac{1}{6}x\phi ){\partial }_{\phi }+\epsilon [(\frac{5}{12}-\frac{\gamma }{2}-\frac{lnx}{2})x^2{\partial }_x\hfill \\ & +(\frac{-x\phi }{2lnx}-\frac{1}{2}x\phi (\gamma -\frac{1}{3})-\frac{1}{6}{x}^{3}lnx{\phi }_{xx}+\frac{5}{36}{x}^3{\phi }_{xx}+\frac{G_J}{4m}{x}^{3}ln\hfill \\ & +\frac{G_J\gamma }{4m}{x}^3+\frac{1}{2160}{x}^6{\phi }_{xxxxx}-\frac{1}{240}{x}^5{\phi }_{xxxx}+\frac{1}{24}{x}^4{\phi }_{xxx}-\frac{1}{6}\gamma x^3{\phi }_{xx}\hfill \\ & +x{B}_7-x{B}_{7}lnx-B_{8}lnx{\displaystyle )}{\partial }_{\phi }{\displaystyle ]},\hfill \\ \hfill Y_3& =(2\phi +\frac{G_J}{m}{x}^2){\partial }_{\phi }+\epsilon [2\phi lnx+(2\gamma -1)\phi +\frac{G_J}{m}{x}^{2}lnx+\frac{1}{1200}{x}^5{\phi }_{xxxxx}\hfill \\ & -\frac{1}{144}{x}^4{\phi }_{xxxx}+\frac{1}{18}{x}^3{\phi }_{xxx}+\frac{G_J}{m}\gamma x^2+x{B}_7-x{B}_{7}lnx-B_{8}lnx]{\partial }_{\phi },\hfill \\ \hfill Y_4& =\epsilon \left[\frac{x^4}{720}{\phi }_{xxxxx}-\frac{x^3}{72}{\phi }_{xxxx}+\frac{x^2}{6}{\phi }_{xxx}+x{B}_7-x{B}_{7}lnx-B_{8}lnx-\frac{1}{x}\phi \right]{\partial }_{\phi },\hfill \\ \hfill Y_5& =-(\frac{G_J{x}^2}{2m}+\phi ){\partial }_x-\epsilon \left[x\phi lnx+\gamma \phi +\frac{G_J}{m}\gamma x^2-x{B}_7+x{B}_{7}lnx+B_{8}lnx\right]{\partial }_{\phi }.\hfill \end{array}$$

(18)

In Table 1, Table 2, Table 3 and Table 4, the ARs are given for unperturbed part of (17) By using the infinitesimal generators (18),

Table 1. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_1$	${\mathit{X}}_2$
$X_1$	$X_1$	$X_2$
$X_2$	$X_1$	$X_2$
$X_3$	$X_1+ϵX_2$	$X_2$
$X_4$	$X_1+H\frac{G_J}{m}{X}_3$	$H{X}_2$
$X_5$	$H{X}_1-P\frac{G_J}{m}{X}_3$	$X_2$
$X_6$	$X_1+\frac{ϵ}{2}{X}_4+ϵX_5+\frac{{ϵ}^2}{2}{X}_6$	$X_1+\frac{ϵ}{2}{X}_2$
$X_7$	$X_1-\frac{3ϵG_J}{2m}{X}_4-\frac{3{ϵ}^2{G_J}^2}{4m^2}{X}_6-\frac{3{ϵ}^2{G}_J}{4m}{X}_7+\frac{{ϵ}^3{G_J}^2}{8m^2}{X}_8$	$ϵX_1+X_2-\frac{3ϵG_J}{2m}{X}_3-\frac{3{ϵ}^2{G}_J}{4m}{X}_5+\frac{{ϵ}^3{G_J}^2}{2m^2}{X}_6+\frac{{ϵ}^3{G}_J}{4m}{X}_7-\frac{{ϵ}^4{G_J}^2}{16m^2}{X}_8$
$X_8$	$X_1+\frac{3ϵG_J}{m}{X}_6+ϵX_7$	$X_2+2ϵX_4+ϵX_5+{ϵ}^2{X}_8$

Table 1. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_1$	${\mathit{X}}_2$
$X_1$	$X_1$	$X_2$
$X_2$	$X_1$	$X_2$
$X_3$	$X_1+ϵX_2$	$X_2$
$X_4$	$X_1+H\frac{G_J}{m}{X}_3$	$H{X}_2$
$X_5$	$H{X}_1-P\frac{G_J}{m}{X}_3$	$X_2$
$X_6$	$X_1+\frac{ϵ}{2}{X}_4+ϵX_5+\frac{{ϵ}^2}{2}{X}_6$	$X_1+\frac{ϵ}{2}{X}_2$
$X_7$	$X_1-\frac{3ϵG_J}{2m}{X}_4-\frac{3{ϵ}^2{G_J}^2}{4m^2}{X}_6-\frac{3{ϵ}^2{G}_J}{4m}{X}_7+\frac{{ϵ}^3{G_J}^2}{8m^2}{X}_8$	$ϵX_1+X_2-\frac{3ϵG_J}{2m}{X}_3-\frac{3{ϵ}^2{G}_J}{4m}{X}_5+\frac{{ϵ}^3{G_J}^2}{2m^2}{X}_6+\frac{{ϵ}^3{G}_J}{4m}{X}_7-\frac{{ϵ}^4{G_J}^2}{16m^2}{X}_8$
$X_8$	$X_1+\frac{3ϵG_J}{m}{X}_6+ϵX_7$	$X_2+2ϵX_4+ϵX_5+{ϵ}^2{X}_8$

Table 2. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_3$	${\mathit{X}}_4$
$X_1$	$-ϵX_2+X_3$	$\frac{{ϵ}^2{G}_J}{2m}{X}_2-\frac{G_J}{m}ϵX_3+X_4$
$X_2$	$X_3$	$-ϵX_2+X_4$
$X_3$	$X_3$	$-ϵX_3+X_4$
$X_4$	$H{X}_3$	$X_4$
$X_5$	$\tilde{H}{X}_3$	$X_4$
$X_6$	$X_3$	$X_4$
$X_7$	$X_3-ϵX_4+ϵX_5-\frac{3{ϵ}^2{G}_J}{2m}{X}_6-{ϵ}^2{X}_7+\frac{{ϵ}^3{G}_J}{4m}{X}_8$	$X_4+\frac{ϵG_J}{m}{X}_6+ϵX_7-\frac{{ϵ}^2{G}_J}{4m}{X}_8$
$X_8$	$X_3+2ϵX_6$	$X_4$

Table 2. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_3$	${\mathit{X}}_4$
$X_1$	$-ϵX_2+X_3$	$\frac{{ϵ}^2{G}_J}{2m}{X}_2-\frac{G_J}{m}ϵX_3+X_4$
$X_2$	$X_3$	$-ϵX_2+X_4$
$X_3$	$X_3$	$-ϵX_3+X_4$
$X_4$	$H{X}_3$	$X_4$
$X_5$	$\tilde{H}{X}_3$	$X_4$
$X_6$	$X_3$	$X_4$
$X_7$	$X_3-ϵX_4+ϵX_5-\frac{3{ϵ}^2{G}_J}{2m}{X}_6-{ϵ}^2{X}_7+\frac{{ϵ}^3{G}_J}{4m}{X}_8$	$X_4+\frac{ϵG_J}{m}{X}_6+ϵX_7-\frac{{ϵ}^2{G}_J}{4m}{X}_8$
$X_8$	$X_3+2ϵX_6$	$X_4$

Table 3. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_5$	${\mathit{X}}_6$
$X_1$	$-ϵX_1-\frac{{ϵ}^2{G}_J}{m}{X}_2+\frac{2ϵG_j}{m}{X}_3+X_5$	$\frac{{ϵ}^2}{2}{X}_1+\frac{{ϵ}^3{G}_J}{4m}{X}_2-\frac{3{ϵ}^2{G}_J}{4m}{X}_3-\frac{ϵ}{2}{X}_4-ϵX_5+X_6$
$X_2$	$X_5$	$-\frac{ϵ}{2}{X}_2+X_6$
$X_3$	$ϵX_3+X_5$	$X_6$
$X_4$	$X_5$	$X_6$
$X_5$	$X_5$	$\tilde{H}{X}_6$
$X_6$	$X_5+ϵX_6$	$X_6$
$X_7$	$X_5-\frac{2ϵG_J}{m}{X}_6-ϵX_7+\frac{{ϵ}^2{G}_J}{2m}{X}_8$	$X_6-\frac{ϵ}{2}{X}_8$
$X_8$	$X_5$	$X_6$

Table 3. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_5$	${\mathit{X}}_6$
$X_1$	$-ϵX_1-\frac{{ϵ}^2{G}_J}{m}{X}_2+\frac{2ϵG_j}{m}{X}_3+X_5$	$\frac{{ϵ}^2}{2}{X}_1+\frac{{ϵ}^3{G}_J}{4m}{X}_2-\frac{3{ϵ}^2{G}_J}{4m}{X}_3-\frac{ϵ}{2}{X}_4-ϵX_5+X_6$
$X_2$	$X_5$	$-\frac{ϵ}{2}{X}_2+X_6$
$X_3$	$ϵX_3+X_5$	$X_6$
$X_4$	$X_5$	$X_6$
$X_5$	$X_5$	$\tilde{H}{X}_6$
$X_6$	$X_5+ϵX_6$	$X_6$
$X_7$	$X_5-\frac{2ϵG_J}{m}{X}_6-ϵX_7+\frac{{ϵ}^2{G}_J}{2m}{X}_8$	$X_6-\frac{ϵ}{2}{X}_8$
$X_8$	$X_5$	$X_6$

Table 4. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_7$	${\mathit{X}}_8$
$X_1$	$\frac{{ϵ}^3{G_J}^2}{4m^2}{X}_2-\frac{3{ϵ}^2{G_J}^2}{4m^2}{X}_3+\frac{3ϵG_J}{2m}{X}_4+X_7$	$-\frac{{ϵ}^3{G}_J}{2m}{X}_1-\frac{{ϵ}^4{G_J}^2}{4m^2}{X}_2+\frac{{ϵ}^3{G_J}^2}{m^2}{X}_3+\frac{3{ϵ}^2{G}_J}{2m}{X}_5-\frac{3ϵG_J}{m}{X}_6-ϵX_7+X_8$
$X_2$	$-ϵX_1+\frac{3ϵG_J}{2m}{X}_3+X_7$	${ϵ}^2{X}_2-2ϵX_4-ϵX_5+X_8$
$X_3$	$-{ϵ}^2{X}_3+ϵX_4-ϵX_5+X_7$	$-2ϵX_6+X_8$
$X_4$	$\tilde{H}(X_6+X_7)$	$\tilde{H}{X}_8$
$X_5$	$P\frac{G_j}{m}{X}_6+H{X}_7$	$X_8$
$X_6$	$X_7+\frac{ϵ}{2}{X}_8$	$X_8$
$X_7$	$X_7$	$X_8$
$X_8$	$X_7$	$X_8$

Table 4. AR for unperturbed part of Equation (17).

Ad[Xi, Xj]	${\mathit{X}}_7$	${\mathit{X}}_8$
$X_1$	$\frac{{ϵ}^3{G_J}^2}{4m^2}{X}_2-\frac{3{ϵ}^2{G_J}^2}{4m^2}{X}_3+\frac{3ϵG_J}{2m}{X}_4+X_7$	$-\frac{{ϵ}^3{G}_J}{2m}{X}_1-\frac{{ϵ}^4{G_J}^2}{4m^2}{X}_2+\frac{{ϵ}^3{G_J}^2}{m^2}{X}_3+\frac{3{ϵ}^2{G}_J}{2m}{X}_5-\frac{3ϵG_J}{m}{X}_6-ϵX_7+X_8$
$X_2$	$-ϵX_1+\frac{3ϵG_J}{2m}{X}_3+X_7$	${ϵ}^2{X}_2-2ϵX_4-ϵX_5+X_8$
$X_3$	$-{ϵ}^2{X}_3+ϵX_4-ϵX_5+X_7$	$-2ϵX_6+X_8$
$X_4$	$\tilde{H}(X_6+X_7)$	$\tilde{H}{X}_8$
$X_5$	$P\frac{G_j}{m}{X}_6+H{X}_7$	$X_8$
$X_6$	$X_7+\frac{ϵ}{2}{X}_8$	$X_8$
$X_7$	$X_7$	$X_8$
$X_8$	$X_7$	$X_8$

where

$$H=\sum _{n=1}^8\frac{1}{n!}{ϵ}^n,\tilde{H}=\sum _{n=1}^8{(-1)}^n\frac{1}{n!}{ϵ}^n,P=\sum _{n=1}^4\frac{2}{(2n-1)!}{ϵ}^{2n-1}.$$

Let $V={\sum }_{i=1}^8{X}_i+{\sum }_{i=1}^5{Y}_i$ be the most general element, and then we will simplify it by applying suitable adjoint maps. Finally, we can obtain the one-dimensional optimal system of (18). The following symmetries are just a few of the members of the one-dimensional optimal system of the perturbed torsion equation, that is given by:

$$\begin{array}{cc}\hfill V_1& =X_1,V_2=X_2,V_3=X_3,V_4=X_4,V_5=X_5,\hfill \\ \hfill V_6& =X_6,V_7=X_7,V_8=X_8,V_9=X_3+a{X}_6+b{X}_7,V_{10}=X_1+X_6,\hfill \\ \hfill V_{11}& =X_2+a{X}_4+b{X}_8,V_{12}=X_1+X_2+a{X}_4+b{X}_6+c{X}_8,\dots .\hfill \end{array}$$

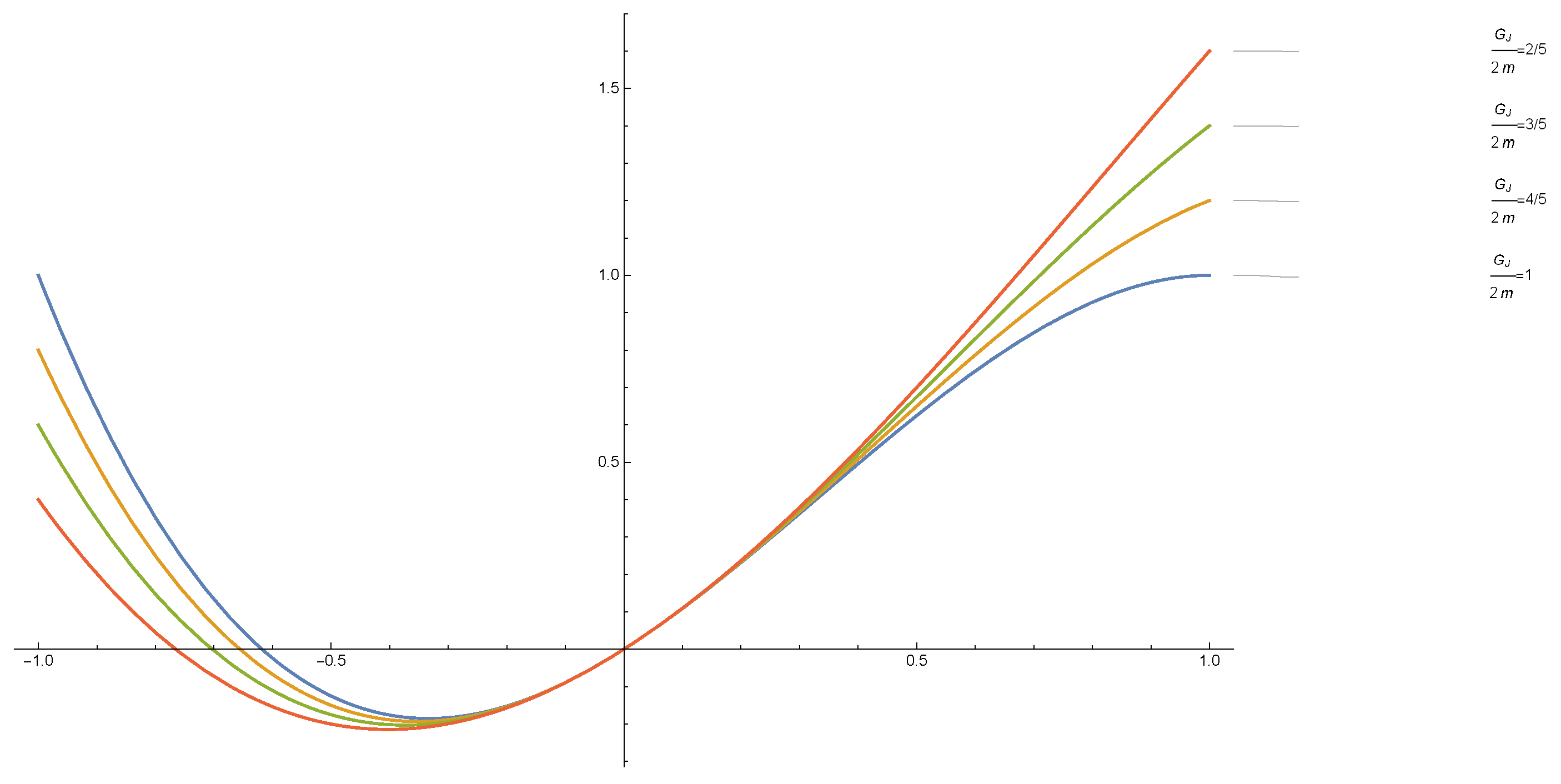
4.2. Reduction and Exact Solution of Perturbed Torsion Equation (18)

Case 1: For the symmetry of $V_1=X_1$, solution of unperturbed part of reduced equation will be in the form

$$\phi \left(x\right)=c_{1}x+c_2-\frac{G_J}{2m}{x}^2.$$

Case 2: For $V_5=X_5$, By using corresponding characteristic equation

$$\begin{array}{c}\hfill \frac{dx}{x}=\frac{d\phi }{-\frac{G_J}{m}{x}^2},\end{array}$$

and integration of that, invariant solution and reduced equation of unperturbed torsional equation will be in the form:

$$\begin{array}{c}\hfill Q=Q(\phi +\frac{G_J}{2m}{x}^2),{\phi }_{xx}+2\frac{G_J}{m}=0.\end{array}$$

$\phi \left(x\right)=c_{1}x+c_2-\frac{G_J}{m}{x}^2$ is solution of above reduced equation.

Case 3: For $V_6=X_6$ the reduced equation is:

$$\begin{array}{c}\hfill x^2{\phi }_{xx}-2x{\phi }_x+2\phi +\frac{G_J}{m}{x}^3=0,\end{array}$$

where $\phi \left(x\right)=c_{1}x+c_2{x}^2-\frac{G_J}{2m}{x}^3$ is solution of unperturbed equation of the above equation.

Case 4: Symmetry $V_7=X_7$, with invariant function

$Q=Q(\frac{\frac{G_J}{m}{x}^2+2\phi }{\sqrt{\frac{G_J}{m}{x}^2+2\phi }})=Q(\frac{A}{\sqrt{A}})$, and reduced equation

$$\begin{array}{c}\hfill \frac{\frac{{G_J}^3}{m^3}{x}^4\sqrt{A}+8\frac{{G_J}^2}{m^2}{x}^2\phi \sqrt{A}+4\frac{G_J}{m}{x}^2\phi {\phi }_{xx}+4\frac{G_J}{m}{x}^2{\phi }_x^2-24\frac{G_J}{m}x\phi {\phi }_x+16\frac{G_J}{m}\sqrt{A}{\phi }^2+24\frac{G_J}{m}{\phi }^2}{{\sqrt{A}}^5}=0,\end{array}$$

have two solutions in the form:

$$\begin{array}{cc}\hfill {\phi }_1\left(x\right)=& -1/4\frac{G_J}{m}{x}^2\left(-1/2\frac{G_J}{m}{x}^2-4c_{1}x+4c_2-1/2\sqrt{D}\right)\hfill \\ & -1/2\frac{G_J}{m}{x}^2-2c_{1}x\left(-1/2\frac{G_J}{m}{x}^2-4c_{1}x+4c_2-1/2\sqrt{D}\right)\hfill \\ & +2c_2\left(-1/2\frac{G_J}{m}{x}^2-4c_{1}x+4c_2-1/2\sqrt{D}\right),\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\phi }_2\left(x\right)=& -1/4\frac{G_J}{m}{x}^2\left(-1/2\frac{G_J}{m}{x}^2-4c_{1}x+4c_2+1/2\sqrt{K}\right)\hfill \\ & -1/2\frac{G_J}{m}{x}^2-2c_{1}x\left(-1/2\frac{G_J}{m}{x}^2-4c_{1}x+4c_2+1/2\sqrt{K}\right)\hfill \\ & +2c_2\left(-1/2\frac{G_J}{m}{x}^2-4c_{1}x+4c_2+1/2\sqrt{K}\right),\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill D& =\frac{{G_J}^2}{m^2}{x}^4+16\frac{G_J}{m}{c}_1{x}^3-16\frac{G_J}{m}{c}_2{x}^2\hfill \\ & +64{{\mathit{c}}_{\mathit{1}}}^2{x}^2-4\frac{G_J}{m}{x}^2-128{\mathit{c}}_{\mathit{1}}{\mathit{c}}_{\mathit{2}}x+64{{\mathit{c}}_{\mathit{2}}}^2,\hfill \end{array}$$

$$K=16\frac{G_J}{m}{c}_2{x}^2+64{c_1}^2{x}^2-4\frac{G_J}{m}{x}^2-128c_1{c}_{2}x+64{c_2}^2.$$

$c_1$ and $c_2$ are arbitrary constants.

Case 5: Finally for symmetry $V_8=X_8$, with invariant function and solution similar to case 3.

The curve of solutions are shown in Figure 1 and Figure 2 for different torsional hardness and torsional anchor constants.

5. ACL for Equation (12)

We know that the connection between conservation laws and symmetries of the differential equations can be expressed with the Noether’s theorem.

Johnpillai et al. [23] studied about ACL via approximate Noether type symmetry operators.

5.1. Construction of Conservation Laws

Here, we remind the aim of nonlinear self-adjointness of perturbed equations for inducing approximate nonlinear self-adjointness.

For Equation (12), consider formal Lagrangian as follows

$$\mathbf{L}\approx {\mathbf{L}}_{\left(0\right)}+\epsilon {\mathbf{L}}_{\left(1\right)}\equiv v{Q}_{\left(0\right)}+\epsilon v{Q}_{\left(1\right)}.$$

(19)

Adjoint equations are defined for Equation (12) as follows:

$$\begin{array}{cc}\hfill \frac{\delta \mathbf{L}}{\delta \phi }& \approx Q_{\left(0\right)}^{*}(x,\phi ,v,{\phi }_{\left(1\right)},v_{\left(1\right)},\dots ,{\phi }_{\left(l\right)},v_{\left(l\right)})\hfill \\ & +\epsilon Q_{\left(1\right)}^{*}(x,\phi ,v,{\phi }_{\left(1\right)},v_{\left(1\right)},\dots ,{\phi }_{\left(l\right)},v_{\left(l\right)},D_{x^1}^{l+1}\phi ,D_{x^1}^{l+1}v,D_{x^1}^{l+2}\phi ,D_{x^1}^{l+2}v,\dots )\hfill \\ & \approx 0\hfill \end{array}$$

(20)

where $v_{\left(i\right)}$ denotes i th-derivatives of v w.r.to x, $\frac{\delta }{\delta \phi }$ is the variational derivative written as

$$\frac{\delta }{\delta \phi }=\frac{\partial }{\partial \phi }+\sum _{s=1}^{\infty }{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial }{\partial {\phi }_{i_1\dots i_s}},$$

and

$$D_i=\frac{\partial }{\partial x^i}+{\phi }_i\frac{\partial }{\partial \phi }+v_i\frac{\partial }{\partial v}+\sum _{s=1}^{\infty }\left[{\phi }_{i{i}_1\dots i_s}\frac{\partial }{\partial {\phi }_{i_1\dots i_s}}+v_{i{i}_1\dots i_s}\frac{\partial }{\partial v_{i_1\dots i_s}}\right].$$

If assume

$$v\approx p_{\left(0\right)}(x,\phi )+\epsilon p_{\left(1\right)}(x,\phi )\ne 0,$$

(21)

we write

$$\mathbf{L}\approx p_{\left(0\right)}{Q}_{\left(0\right)}+\epsilon \left(p_{\left(0\right)}{Q}_{\left(1\right)}+p_{\left(1\right)}{Q}_{\left(0\right)}\right),$$

and if Equation (12) satisfies following condition then we called it approximately nonlinearly self adjoint equation

$$Q_0^{*}{{|}_{v\approx p_{\left(0\right)}+\epsilon p_{\left(1\right)}}+\epsilon Q_{\left(1\right)}^{*}|}_{v\approx p_{\left(0\right)}}\approx {\omega }_{\left(0\right)}{Q}_{\left(0\right)}+\epsilon \left({\omega }_{\left(0\right)}{Q}_{\left(1\right)}+{\omega }_{\left(1\right)}{Q}_{\left(0\right)}\right).$$

(22)

In (22), those parameters ${\omega }_{\left(0\right)}$ and ${\omega }_{\left(1\right)}$ are unknown.

For Equation (12), any approximate symmetry (13) eventually leads to a conservation law

$$D_i\left(C^i\right)=0,C^i\approx C_{\left(0\right)}^i+\epsilon C_{\left(1\right)}^i,$$

with

$$\begin{array}{cc}\hfill C_{\left(0\right)}^i& =W_{\left(0\right)}\left(\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_i}+\sum _{s=1}^{l-1}{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_{i{i}_1\dots i_s}}\right)\hfill \\ & +\sum _{r=1}^{l-1}{D}_{k_1}\dots D_{k_r}\left(W_{\left(0\right)}\right)\left[\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_{i{k}_1\dots k_r}}+\sum _{s=1}^{l-r-1}{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_{i{k}_1\dots k_r{i}_1\dots i_s}}\right],\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill C_{\left(1\right)}^i& =W_{\left(1\right)}\left(\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_i}+\sum _{s=1}^{l-1}{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_{i{i}_1\dots i_s}}\right)\hfill \\ & +\sum _{r=1}^{l-1}{D}_{k_1}\dots D_{k_r}\left(W_{\left(1\right)}\right)\left[\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_{i{k}_1\dots k_r}}+\sum _{s=1}^{l-r-1}{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial {\mathbf{L}}_{\left(0\right)}}{\partial {\phi }_{i{k}_1\dots k_r{i}_1\dots i_s}}\right]\hfill \\ & +W_{\left(0\right)}\left(\frac{\partial {\mathbf{L}}_{\left(1\right)}}{\partial {\phi }_i}+\sum _{s=1}^{\infty }{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial {\mathbf{L}}_{\left(1\right)}}{\partial {\phi }_{i{i}_1\dots i_s}}\right)\hfill \\ & +\sum _{r=1}^{\infty }{D}_{k_1}\dots D_{k_r}\left(W_{\left(0\right)}\right)\left[\frac{\partial {\mathbf{L}}_{\left(1\right)}}{\partial {\phi }_{i{k}_1\dots k_r}}+\sum _{s=1}^{\infty }{(-1)}^s{D}_{i_1}\dots D_{i_s}\frac{\partial {\mathbf{L}}_{\left(1\right)}}{\partial {\phi }_{i{k}_1\dots k_r{i}_1\dots i_s}}\right].\hfill \end{array}$$

(24)

where $W_{\left(i\right)}={\eta }_{\left(i\right)}-{\xi }_{\left(i\right)}^i{\phi }_i,i=0,1$ and ${\mathbf{L}}_{\left(0\right)}$, ${\mathbf{L}}_{\left(1\right)}$ were given in (19) upon the substitution (21).

5.2. ACL for Torsion Perturbed Fractional Equation

According to approximate formal Lagrangian

$$\begin{array}{cc}\hfill \mathbf{L}\approx v(x,\phi ){\displaystyle [}{\phi }_{xx}& +\frac{m}{G_J}+\epsilon [(\gamma +lnx){\phi }_{xx}-\frac{\phi }{x^2}\hfill \\ & +2\frac{{\phi }_x}{x}+\sum _{k=3}^{\infty }\frac{2!}{k!(k-2)!}{(-x)}^{k-2}\frac{{\partial }^k\phi }{\partial x^k}\left]\right],\hfill \end{array}$$

(25)

using Equation (20), we obtain adjoint equation as follows:

$$\begin{array}{cc}\hfill Q^{*}\approx v_{2x}& +\epsilon [-(3+\nu +lnx)v_{2x}-5x{v}_{3x}-\frac{11}{4}{x}^2{v}_{4x}\hfill \\ & -\frac{37}{60}{x}^3{v}_{5x}-\frac{7}{120}{x}^4{v}_{6x}-\frac{1}{504}{x}^5{v}_{7x}],\hfill \end{array}$$

(26)

here

$$v=p_0(x,\phi )+\epsilon p_1(x,\phi ).$$

(27)

We can obtain an approximate formal Lagrangian by placing (27) into (26) and studying Equation (22), so we get

$$v=c_{3}x+c_4+\epsilon \left[\left(\frac{m}{2G_J}+\phi \right){\lambda }_1+c_{1}x+c_2\right],$$

(28)

where $c_i(i=1,2,3,4)$ and ${\lambda }_1$ are arbitrary constants.

Then

$$\mathbf{L}\approx {\mathbf{L}}_{\left(0\right)}+\epsilon {\mathbf{L}}_{\left(1\right)},$$

(29)

where

$$\begin{array}{cc}\hfill {\mathbf{L}}_{\left(0\right)}& =p_0{Q}_0=(c_{3}x+c_4)({\phi }_{xx}+\frac{m}{G_J}),\hfill \\ \hfill {\mathbf{L}}_{\left(1\right)}& =p_1{Q}_0+p_0{Q}_1=\left(\left(\frac{m}{2G_J}+\phi \right){\lambda }_1+c_{1}x+c_2\right)\left({\phi }_{xx}+\frac{m}{G_J}\right)\hfill \\ & -(c_{3}x+c_4)\left((-\gamma -lnx){\phi }_{xx}+\frac{\phi }{x^2}-2\frac{{\phi }_x}{x}-\sum _{k=3}^{\infty }\frac{2!}{(k-2)!k!}{(-x)}^{k-2}\frac{{\partial }^k\phi }{\partial x^k}\right).\hfill \end{array}$$

(30)

$c_1,c_2,c_3,c_4,c_5,a$ and b are arbitrary constants.

By using the Formulas (23) and (24) and perform all necessary computations, the conserved vector for Equation (16) can be obtained as follows

$$C_{\left(0\right)}^x=-c_3{W}_{\left(0\right)}+(c_{3}x+c_4)D_x\left(W_{\left(0\right)}\right),$$

$$\begin{array}{cc}\hfill C_{\left(1\right)}^x=& -c_3{W}_{\left(1\right)}+(c_{3}x+c_4)D_x\left(W_{\left(1\right)}\right)+D_x\left(W_{\left(0\right)}\right)\left[p_1-p_0+p_0(\gamma +lnx)\right]\hfill \\ & +W_{\left(0\right)}\left[(c_{3}x+c_4)\frac{2}{x}-D_x(p_1+p_0(\gamma +lnx))-\sum _{k=3}^{\infty }\frac{2!}{k!(k-2)!}{D}_{(k-1)x}\left(x^{k-2}{p}_0\right)\right]\hfill \\ & +\sum _{i=1}^{\infty }{(-1)}^{i-1}{D}_{ix}{W}_{\left(0\right)}\left[\sum _{k=i+1}^{\infty }\frac{2!}{k!(k-2)!}{D}_{(k-2)x}\left(p_0{x}^{k-2}\right)\right],\hfill \end{array}$$

where

$$C^x=C_{\left(0\right)}^x+\epsilon C_{\left(1\right)}^x.$$

(I)

For $X_1={\partial }_x$, $W_{\left(0\right)}=-{\phi }_x$, $W_{\left(1\right)}=0$ and component of ACL is:

$$C^x=c_3{\phi }_x-(c_{3}x+c_4){\phi }_{xx}+\epsilon \left[A{\phi }_x-B{\phi }_{xx}\right].$$

(II)

Symmetry $X_2={\partial }_{\phi }$, yields $W_{\left(0\right)}=1$ and $W_{\left(1\right)}=0$, therefore

$$C^x=c_3+A\epsilon .$$

(III)

For unperturbed symmetry $X_3=x{\partial }_{\phi }$, we obtain $W_{\left(0\right)}=x$ and $W_{\left(1\right)}=0$, so we have

$$C^x=c_4+\epsilon \left[-xA+B\right].$$

(IV)

Consider the symmetry $X_4=(\frac{m}{2G_J}{x}^2+\phi ){\partial }_{\phi }$, with $W_{\left(0\right)}=\frac{m}{2G_J}{x}^2+\phi$ and $W_{\left(1\right)}=0$, we have

$$C^x=-c_3(\frac{m}{2G_J}{x}^2+\phi )+(c_{3}x+c_4)(\frac{m}{G_J}x+{\phi }_x)+\epsilon \left[-(\frac{m}{2G_J}{x}^2+\phi )A+(\frac{m}{G_J}x+{\phi }_x)B\right].$$

(V)

For $X_5=x{\partial }_x-\frac{m}{G_J}{x}^2{\partial }_{\phi }$, $W_{\left(0\right)}=-\frac{m}{G_J}{x}^2-x\phi$, $W_{\left(1\right)}=0$, we have

$$\begin{array}{cc}\hfill C^x=& +c_3(\frac{m}{G_J}{x}^2+x{\phi }_x)-(c_{3}x+c_4)(\frac{2m}{G_J}x+x{\phi }_{xx}+{\phi }_x)\hfill \\ & +\epsilon \left[(\frac{m}{G_J}{x}^2+x{\phi }_x)A-(\frac{2m}{G_J}x+x{\phi }_{xx}+{\phi }_x)B\right].\hfill \end{array}$$

(VI)

For $X_6=\frac{x^2}{2}{\partial }_x-(\frac{m}{4G_J}{x}^3-\frac{1}{2}x\phi ){\partial }_{\phi }$, $W_{\left(0\right)}=\frac{1}{2}x\phi -\frac{m}{4G_J}{x}^3-\frac{x^2}{2}{\phi }_x$ and $W_{\left(1\right)}=0$, we conclude

$$\begin{array}{cc}\hfill C^x=& -c_3(\frac{1}{2}x\phi -\frac{m}{4G_J}{x}^3-\frac{x^2}{2}{\phi }_x)+(c_{3}x+c_4)(\frac{1}{2}\phi -\frac{3m}{4G_J}{x}^2-\frac{x}{2}{\phi }_x-\frac{x^2}{2}{\phi }_{xx})\hfill \\ & +\epsilon \left[(\frac{1}{2}x\phi -\frac{m}{4G_J}{x}^3-\frac{x^2}{2}{\phi }_x)A+(\frac{1}{2}\phi -\frac{3m}{4G_J}{x}^2-\frac{x}{2}{\phi }_x-\frac{x^2}{2}{\phi }_{xx})B\right].\hfill \end{array}$$

(VII)

For $X_7=\phi {\partial }_x-(\frac{m^2}{4G_J^2}{x}^3+\frac{3m}{2G_J}x\phi ){\partial }_{\phi }$, $W_{\left(0\right)}=-(\frac{m^2}{4G_J^2}{x}^3+\frac{3m}{2G_J}x\phi +\phi {\phi }_x)$ and $W_{\left(1\right)}=0$, we obtain

$$\begin{array}{cc}\hfill C^x=& +c_3(\frac{m^2}{4G_J^2}{x}^3+\frac{3m}{2G_J}x\phi +\phi {\phi }_x)\hfill \\ & -(c_{3}x+c_4)\left(\frac{3m^2}{4G_J^2}{x}^2+\frac{3m}{2G_J}\phi +(\frac{3m}{2G_J}x-{\phi }_x){\phi }_x-\phi {\phi }_{xx}\right)\hfill \\ & +\epsilon \left[(\frac{m^2}{4G_J^2}{x}^3+\frac{3m}{2G_J}x\phi +\phi {\phi }_x)A-(\frac{3m^2}{4G_J^2}{x}^2+\frac{3m}{2G_J}\phi +(\frac{3m}{2G_J}x+{\phi }_x){\phi }_x+\phi {\phi }_{xx})B\right].\hfill \end{array}$$

(VIII)

Symmetry $X_8=(x\phi +\frac{m}{2G_J}{x}^3){\partial }_x-(\frac{m^2}{4G_J^2}{x}^4-{\phi }^2){\partial }_{\phi }$, gives $W_{\left(0\right)}=({\phi }^2-\frac{M^2}{4G_J^2}{x}^4)-(x\phi +\frac{m}{2G_J}{x}^3){\phi }_x$ and $W_{\left(1\right)}=0$, we get

$$\begin{array}{cc}\hfill C^x=& -c_3\left(({\phi }^2-\frac{M^2}{4G_J^2}{x}^4)-(x\phi +\frac{m}{2G_J}{x}^3){\phi }_x\right)\hfill \\ & -(c_{3}x+c_4)\left(\frac{m^2}{G_J^2}{x}^3+(\phi +\frac{3m}{2G_J}{x}^2){\phi }_x-(2\phi -x{\phi }_x){\phi }_x+(x\phi +\frac{m}{2G_J}{x}^3){\phi }_{xx}\right)\hfill \\ & +\epsilon [({\phi }^2-\frac{M^2}{4G_J^2}{x}^4-(x\phi +\frac{m}{2G_J}{x}^3){\phi }_x)A\hfill \\ & -\left(\frac{m^2}{G_J^2}{x}^3+(3\phi +\frac{3m}{2G_J}{x}^2+x{\phi }_x){\phi }_x+(x\phi +\frac{m}{2G_J}{x}^3){\phi }_{xx}\right)B].\hfill \end{array}$$

(VIIII)

The approximate symmetry $Y_1=\epsilon (B_{7}x-B_{7}xlnx-B_{8}lnx){\partial }_{\phi }$ with $W_{\left(0\right)}=0$ and $W_{\left(1\right)}=B_{7}x-B_{7}xlnx-B_{8}lnx$, yields

$$C^x=-c_3(B_{7}x-B_{7}xlnx-B_{8}lnx)-(c_{3}x+c_4)\left(B_{7}lnx+\frac{1}{x}{B}_8\right).$$

(X)

Similarly for $Y_4=\epsilon \left[\frac{x^4}{720}{\phi }_{xxxxx}-\frac{x^3}{72}{\phi }_{xxxx}+\frac{x^2}{6}{\phi }_{xxx}+x{B}_7-x{B}_{7}lnx-B_{8}lnx-\frac{1}{x}\phi \right]{\partial }_{\phi }$, $W_{\left(0\right)}=0$ and $W_{\left(1\right)}=\left[\frac{x^4}{720}{\phi }_{xxxxx}-\frac{x^3}{72}{\phi }_{xxxx}+\frac{x^2}{6}{\phi }_{xxx}+x{B}_7-x{B}_{7}lnx-B_{8}lnx-\frac{1}{x}\phi \right]$, we derive

$$\begin{array}{cc}\hfill C^{\left(x\right)}=& -c_3\left(\frac{x^4}{720}{\phi }_{xxxxx}-\frac{x^3}{72}{\phi }_{xxxx}+\frac{x^2}{6}{\phi }_{xxx}-x{B}_7-x{B}_{7}lnx-B_{8}lnx-\frac{1}{x}\phi \right)\hfill \\ & +(c_{3}x+c_4)(-\frac{1}{120}{x}^3{\phi }_{xxxxx}+\frac{1}{8}{x}^2{\phi }_{xxxx}+\frac{1}{3}x{\phi }_{xxx}+\frac{1}{720}{x}^4{\phi }_{xxxxxx}\hfill \\ & -B_{7}lnx-\frac{1}{x}{B}_8+\frac{\phi }{x^2}-\frac{{\phi }_x}{x}).\hfill \end{array}$$

(XI)

Finally, for $Y_5=-(\frac{G_J{x}^2}{2m}+\phi ){\partial }_{\phi }-\epsilon \left[x\phi lnx+\gamma \phi +\frac{G_J}{m}\gamma x^2-x{B}_7+x{B}_{7}lnx+B_{8}lnx\right]{\partial }_{\phi }$, $W_{\left(0\right)}=-(\frac{G_J{x}^2}{2m}+\phi )$ and $W_{\left(1\right)}=x\phi lnx+\gamma \phi +\frac{G_J}{m}\gamma x^2-x{B}_7+x{B}_{7}lnx+B_{8}lnx$, we obtain

$$\begin{array}{cc}\hfill C^x=& +c_3(\frac{G_J}{2m}{x}^2+\phi )+(c_{3}x+c_4)(\frac{G_J}{m}x+{\phi }_x)\hfill \\ & -\epsilon (c_3{W}_{\left(1\right)}+(c_{3}x+c_4)(\phi lnx+\phi +\frac{G_J}{m}\gamma x+\frac{G_J}{m}xlnx+\frac{G_J}{2m}x\hfill \\ & +B_{7}lnx+\frac{B_8}{x}+(xlnx+\gamma ){\phi }_x)+(\frac{G_J{x}^2}{2m}+\phi )A+(\frac{G_J}{m}x+{\phi }_x)B).\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill A& =-\left[-\frac{1}{x}(c_{3}x+c_4)+\frac{{\lambda }_1{G}_J}{m}x+(\gamma +lnx)c_3+{\lambda }_1{u}_x+\frac{59}{60}{c}_3+c_1\right]\hfill \\ \hfill B& =\frac{1}{2}{\lambda }_1(\frac{G_J}{m}{x}^2+2\phi )+c_{1}x+c_2+(\gamma +lnx-1)(c_{3}x+c_4)\hfill \end{array}$$

The torsion constant J for the IPE(a standard related to narrow-flange I-beams) and 2IPE sections is given in

Table 5. The torsion constant J.

PE	J	2PE	J
140	$2/450$	$2\times 140$	$4/900$
160	$3/620$	$2\times 160$	$7/240$
180	$4/810$	$2\times 180$	$9/620$
200	$7/010$	$2\times 200$	$14/02$
220	$9/100$	$2\times 220$	$18/20$
240	$12/900$	$2\times 240$	$25/80$
270	$18/00$	$2\times 270$	$36/00$
300	$20/20$	$2\times 300$	$40/40$
330	$28/30$	$2\times 330$	$56/60$
370	$37/50$	$2\times 370$	$75/00$
400	$51/30$	$2\times 400$	$102/60$

.

6. Conclusions

In this paper, we investigated a method in which a term containing a small epsilon parameter should be replaced the fractional expression of an FDE. Using these terms that approximate with a small parameter, new approximate symmetries, conservation laws of reduced partial differential equations have been found. And then followed by with the help of Lie transformations, analytical solutions, perturbed symmetry and conservation laws of fractional Torsion equation are obtained.