Evolving Patterns in Irrational Numbers Using Waiting Times between Digits
Abstract
:1. Introduction
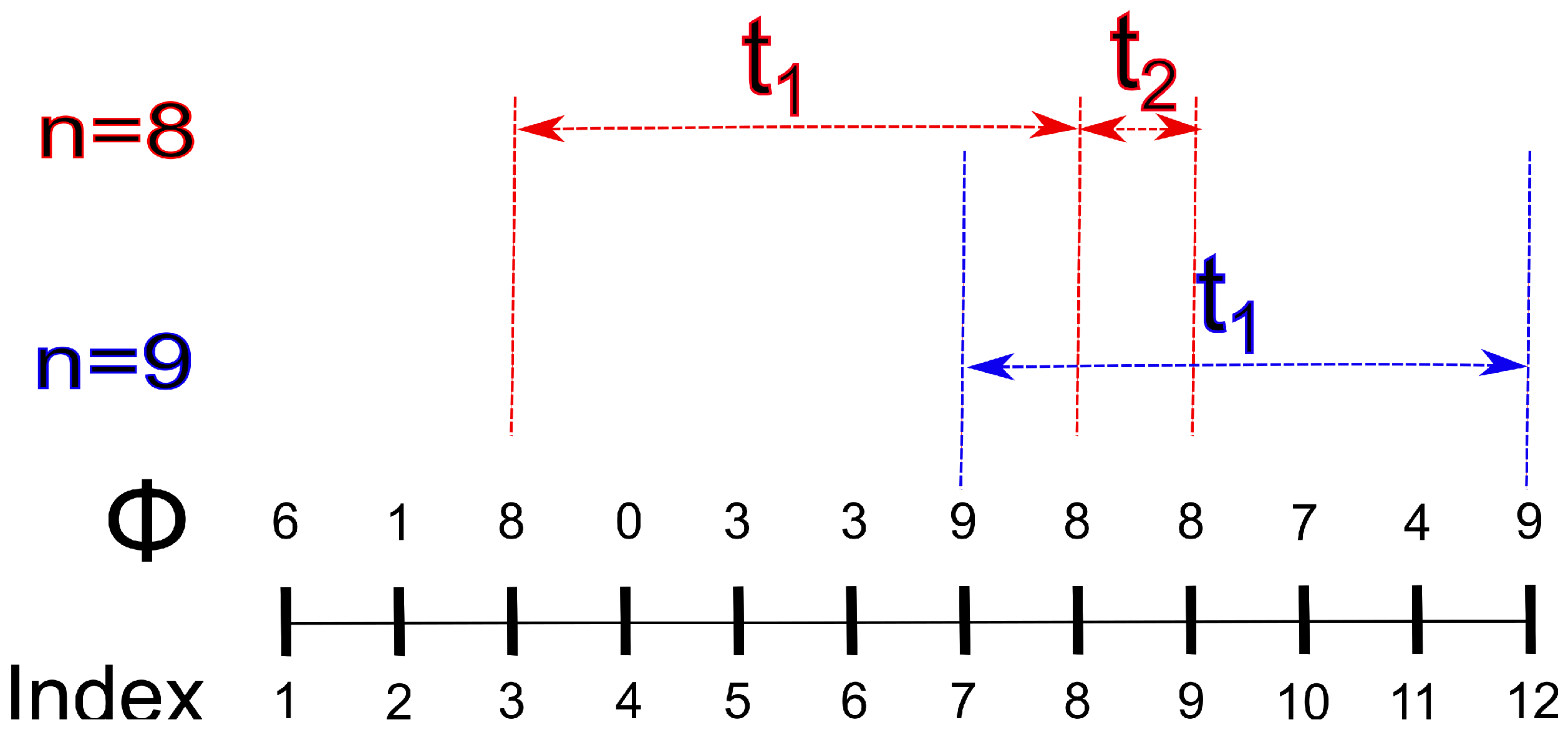
2. Methods
2.1. Irrational Numbers
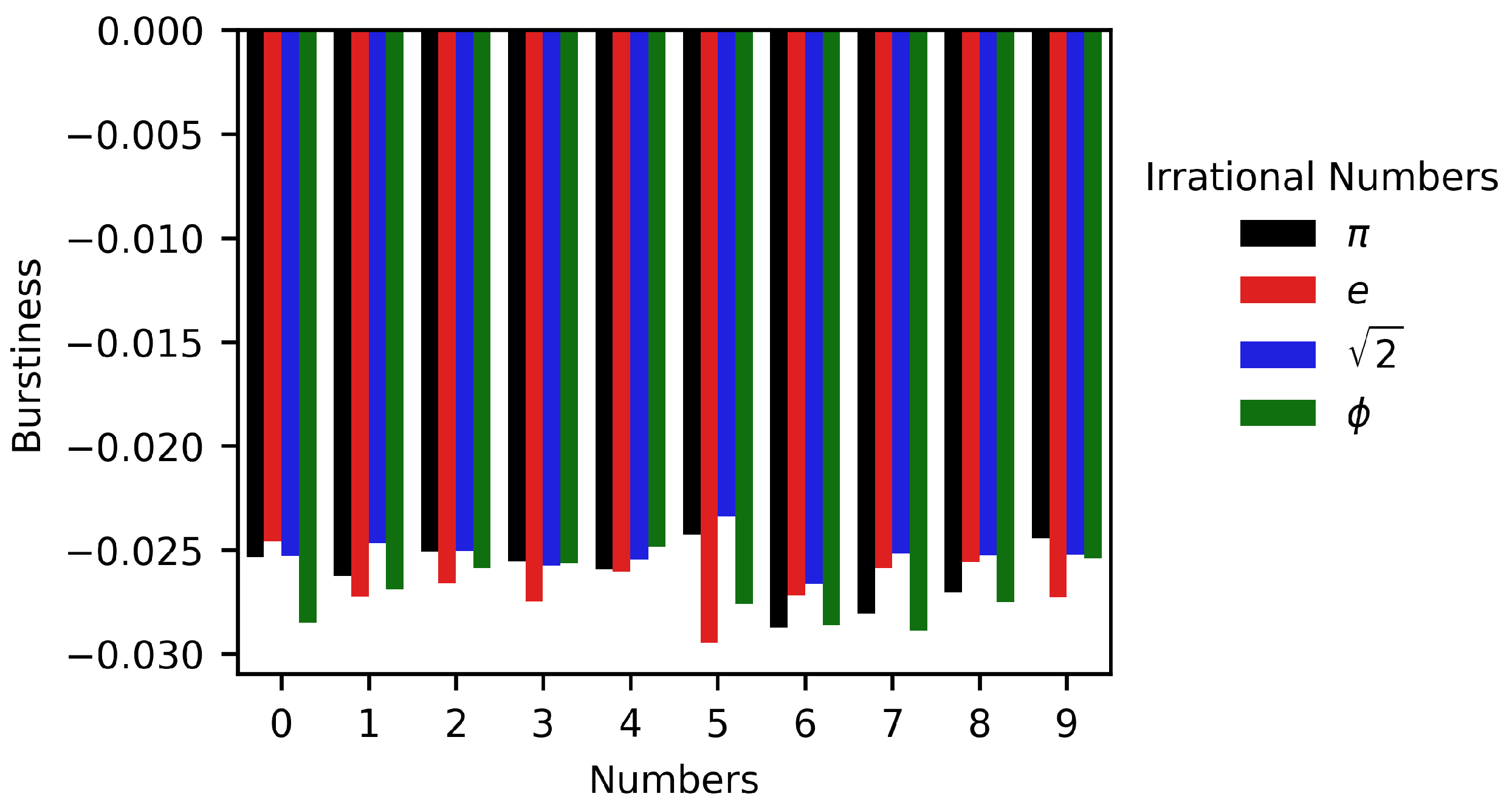
2.2. Burstiness Index
2.3. Complexity–Entropy Plane
3. Results
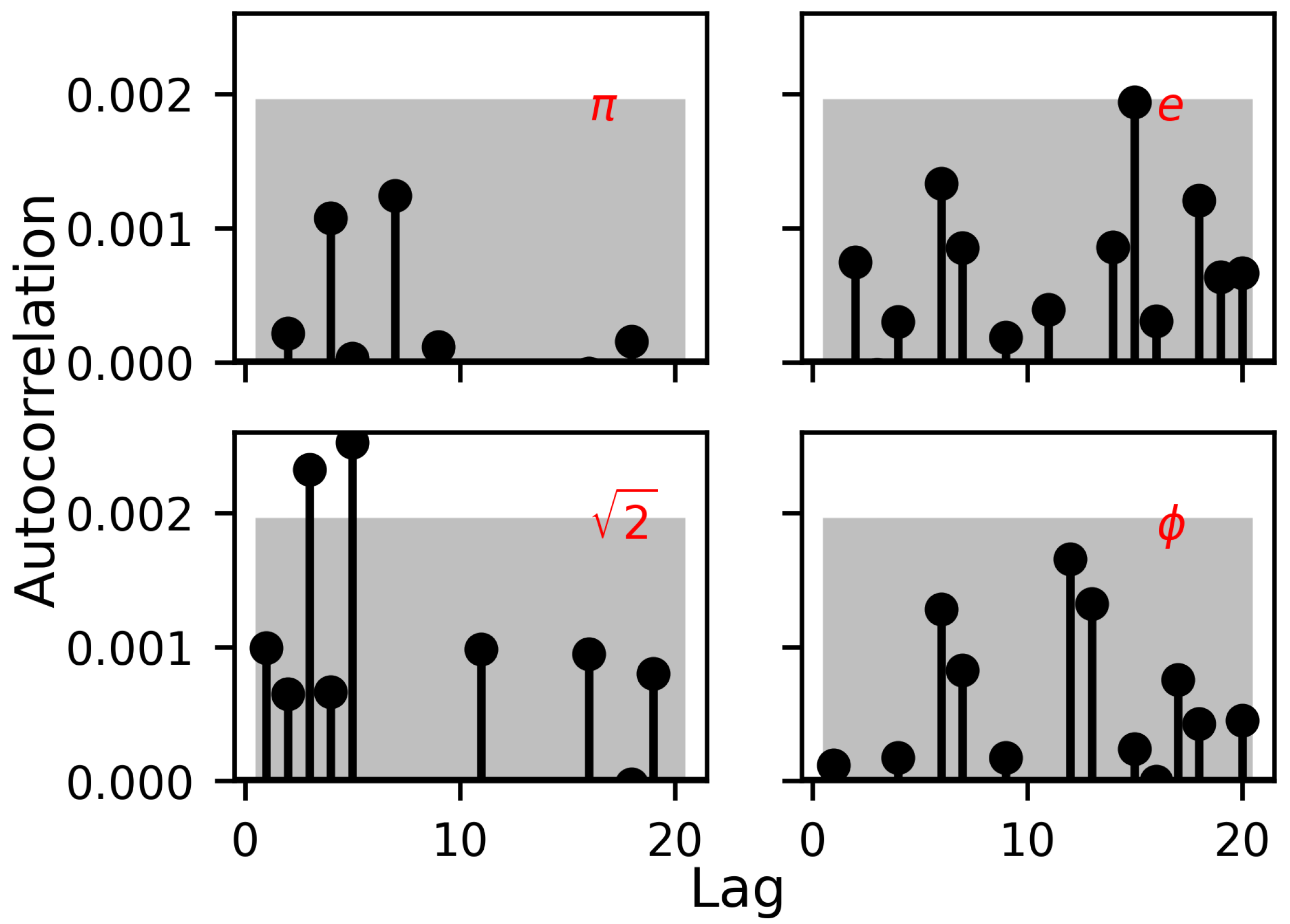
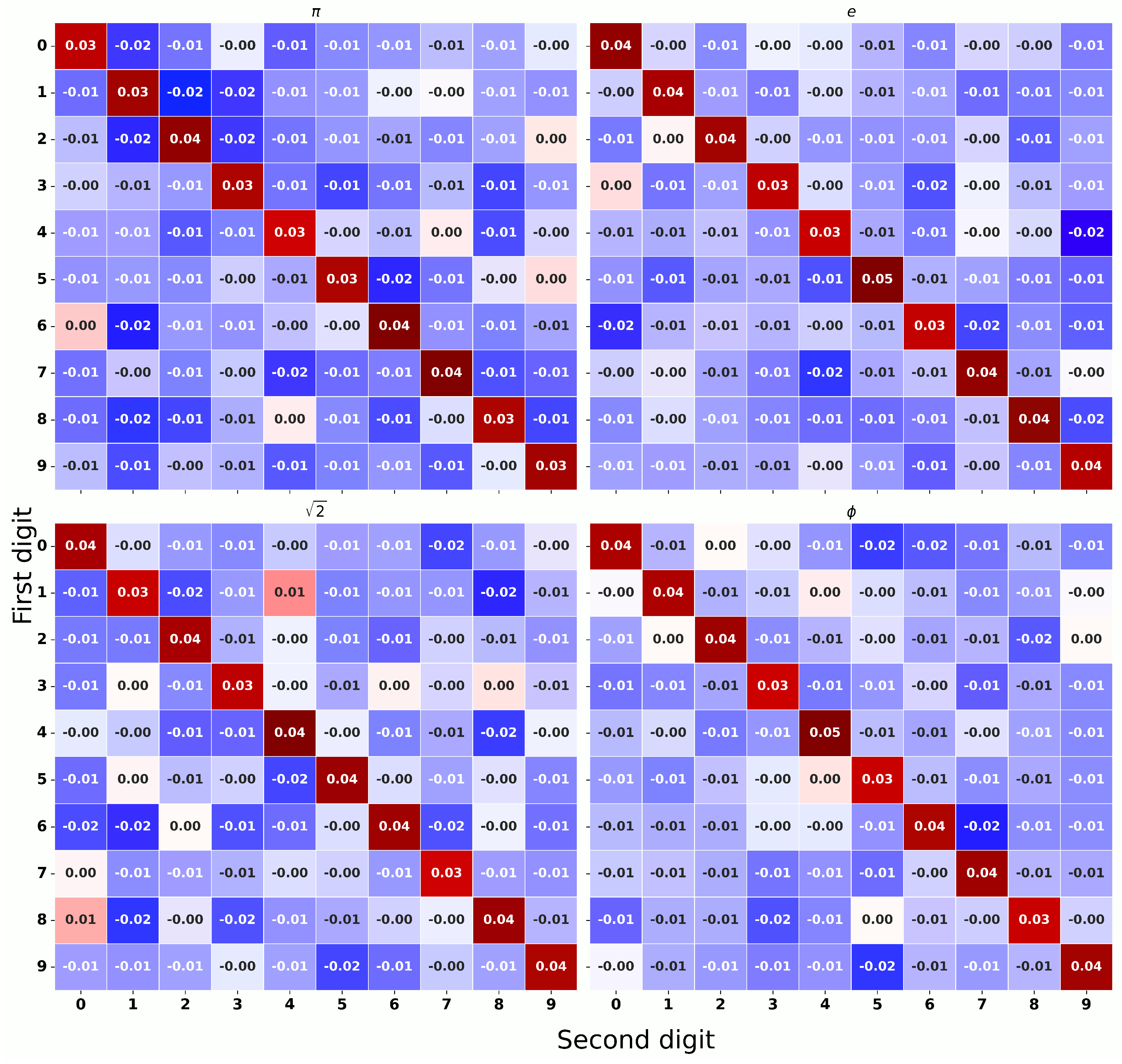
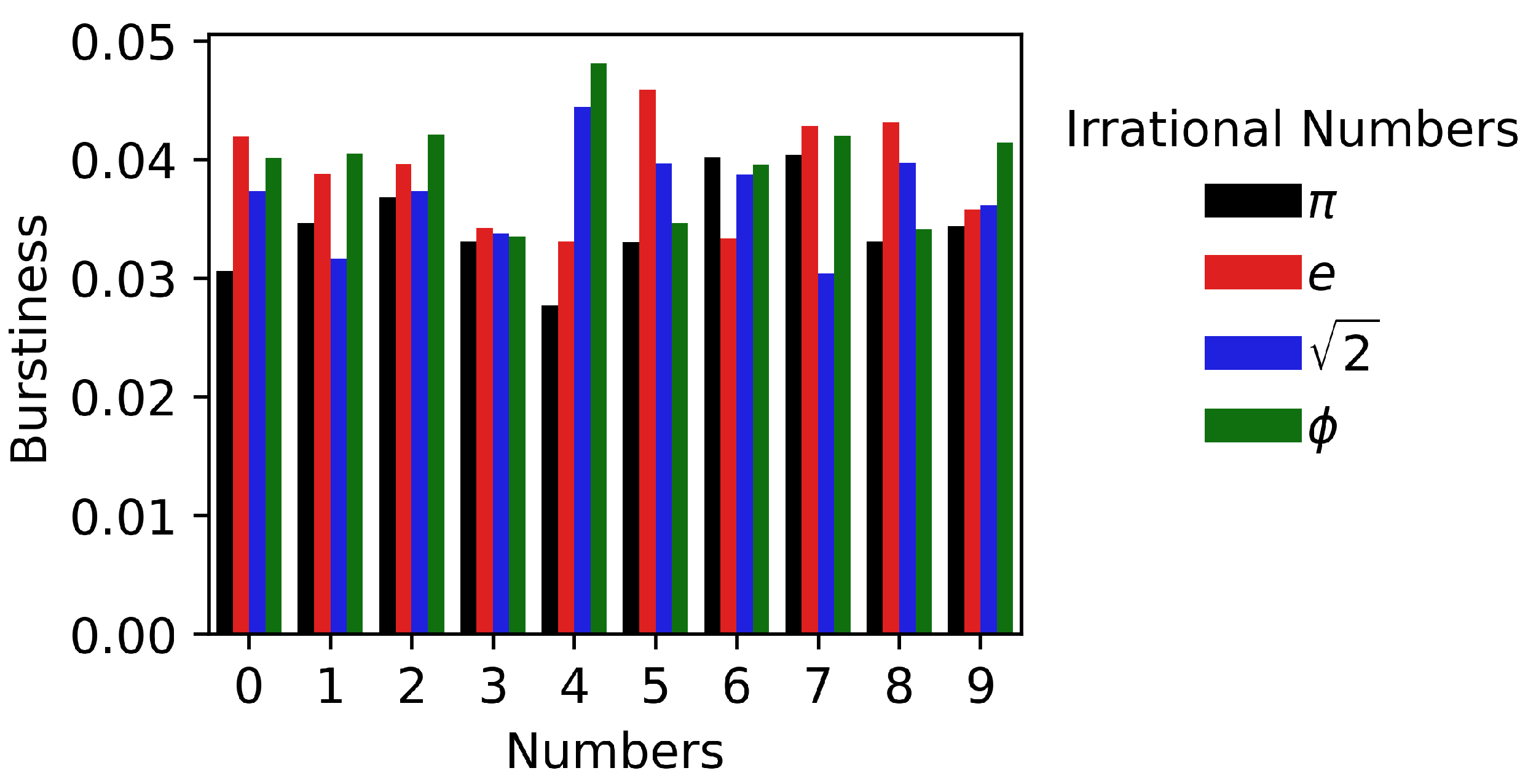
3.1. Autocorrelation and Burstiness Analysis
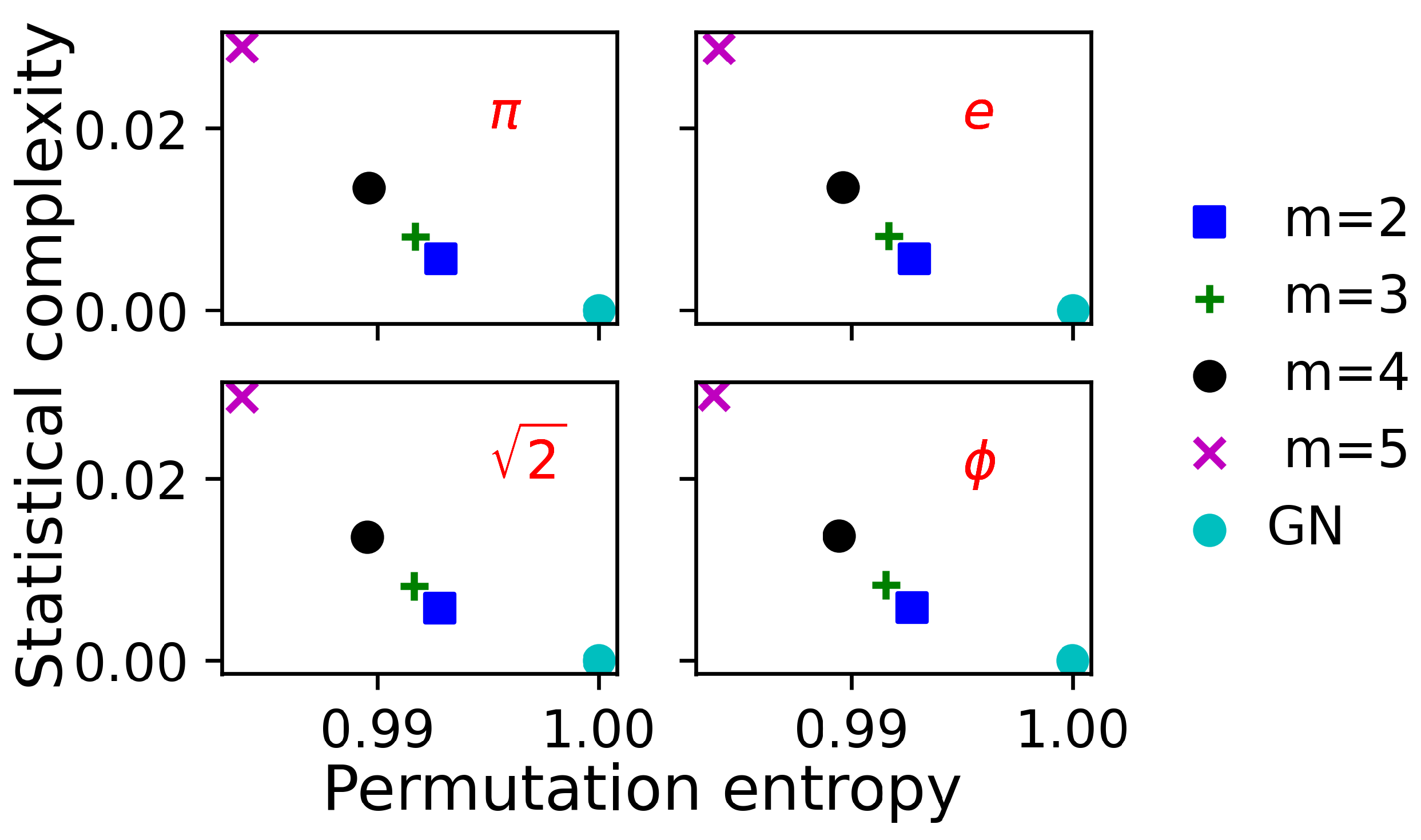
3.2. Complexity–Entropy Plane Analysis
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bollman, M. Basic Gambling Mathematics: The Numbers Behind the Neon; CRC Press: Boca Raton, FL, USA, 2023. [Google Scholar]
- Wang, J.; Jiang, G.p.; Yang, H. Improved DES algorithm based on irrational numbers. In Proceedings of the 2008 International Conference on Neural Networks and Signal Processing, Nanjing, China, 7–11 June 2008; pp. 628–631. [Google Scholar]
- Van Niel, K.; Laffan, S.W. Gambling with randomness: The use of pseudo-random number generators in GIS. Int. J. Geogr. Inf. Sci. 2003, 17, 49–68. [Google Scholar] [CrossRef]
- Knuth, D.E. The Art of Computer Programming; Pearson Education: London, UK, 1997; Volume 3. [Google Scholar]
- Yavari, A. A practical research on randomness of digits of binary expansion of irrational numbers. In Proceedings of the 2009 7th International Conference on Information, Communications and Signal Processing (ICICS), Macau, China, 8–10 December 2009; pp. 1–5. [Google Scholar]
- Yu, F.; Li, L.; Tang, Q.; Cai, S.; Song, Y.; Xu, Q. A survey on true random number generators based on chaos. Discret. Dyn. Nat. Soc. 2019, 2019, 2545123. [Google Scholar] [CrossRef]
- Stojanovski, T.; Pihl, J.; Kocarev, L. Chaos-based random number generators. Part II: Practical realization. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2001, 48, 382–385. [Google Scholar] [CrossRef]
- Herrero-Collantes, M.; Garcia-Escartin, J.C. Quantum random number generators. Rev. Mod. Phys. 2017, 89, 015004. [Google Scholar] [CrossRef]
- Jeong, Y.S.; Oh, K.J.; Cho, C.K.; Choi, H.J. Pseudo-random number generation using LSTMs. J. Supercomput. 2020, 76, 8324–8342. [Google Scholar] [CrossRef]
- Overmars, A.; Venkatraman, S. A new method of golden ratio computation for faster cryptosystems. In Proceedings of the 2017 Cybersecurity and Cyberforensics Conference (CCC), London, UK, 21–23 November 2017; pp. 9–15. [Google Scholar]
- Ott, E. Chaos in Dynamical Systems; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Fernie, E. The ground plan of Norwich Cathedral and the square root of two. J. Br. Archaeol. Assoc. 1976, 39, 77–86. [Google Scholar] [CrossRef]
- Houston, K. The Book: A Cover-to-Cover Exploration of the Most Powerful Object of Our Time; WW Norton & Company: New York, NY, USA, 2016. [Google Scholar]
- Dunlap, R.A. The Golden Ratio and Fibonacci Numbers; World Scientific: Singapore, 1997. [Google Scholar]
- Liu, X.; Lu, P.; Shao, J.; Cao, H.; Zhu, Z. Information hiding technology and application analysis based on decimal expansion of irrational numbers. In Proceedings of the AOPC 2017: Fiber Optic Sensing and Optical Communications, Beijing, China, 4–6 June 2017; Volume 10464, pp. 46–52. [Google Scholar]
- Dodge, Y. A natural random number generator. Int. Stat. Rev./Rev. Int. Stat. 1996, 64, 329–344. [Google Scholar] [CrossRef]
- Rosso, O.A.; Larrondo, H.; Martin, M.T.; Plastino, A.; Fuentes, M.A. Distinguishing noise from chaos. Phys. Rev. Lett. 2007, 99, 154102. [Google Scholar] [CrossRef] [PubMed]
- Vogl, M.; Roetzel, P.G. Chaoticity versus stochasticity in financial markets: Are daily S&P 500 return dynamics chaotic? Commun. Nonlinear Sci. Numer. Simul. 2022, 108, 106218. [Google Scholar]
- Chan, H.H.; Chan, S.H.; Liu, Z. Domb’s numbers and Ramanujan–Sato type series for 1/π. Adv. Math. 2004, 186, 396–410. [Google Scholar] [CrossRef]
- Levine, M.W.; Shefner, J.M. A model for the variability of interspike intervals during sustained firing of a retinal neuron. Biophys. J. 1977, 19, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Parsons, T. Monte Carlo method for determining earthquake recurrence parameters from short paleoseismic catalogs: Example calculations for California. J. Geophys. Res. Solid Earth 2008, 113, B03302. [Google Scholar] [CrossRef]
- Goh, K.I.; Barabási, A.L. Burstiness and memory in complex systems. Europhys. Lett. 2008, 81, 48002. [Google Scholar] [CrossRef]
- Kim, E.K.; Jo, H.H. Measuring burstiness for finite event sequences. Phys. Rev. E 2016, 94, 032311. [Google Scholar] [CrossRef] [PubMed]
- Lamberti, P.W.; Martin, M.; Plastino, A.; Rosso, O. Intensive entropic non-triviality measure. Phys. A Stat. Mech. Appl. 2004, 334, 119–131. [Google Scholar] [CrossRef]
- Lai, D.; Danca, M.F. Fractal and statistical analysis on digits of irrational numbers. Chaos Solitons Fractals 2008, 36, 246–252. [Google Scholar] [CrossRef]
- Croll, G.J. Bientropy-the approximate entropy of a finite binary string. arXiv 2013, arXiv:1305.0954. [Google Scholar]
- Zhao, Y.; Gao, Y.; Huang, J. Mathematical irrational numbers not so physically irrational. arXiv 2009, arXiv:0901.0768. [Google Scholar]
- Johnson, B.R.; Leeming, D.J. A study of the digits of π, e and certain other irrational numbers. Sankhyā Indian J. Stat. Ser. B 1990, 52, 183–189. [Google Scholar]
- Zunino, L.; Olivares, F.; Scholkmann, F.; Rosso, O.A. Permutation entropy based time series analysis: Equalities in the input signal can lead to false conclusions. Phys. Lett. A 2017, 381, 1883–1892. [Google Scholar] [CrossRef]



| Number | Symbol | Approximations | Expression |
|---|---|---|---|
| Euler number | e | 2.781828 | |
| Pi | [19] | 3.141592 | |
| Square root of 2 | 1.414213 | ||
| Golden ratio | 1.618033 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ogunjo, S.; Kantz, H. Evolving Patterns in Irrational Numbers Using Waiting Times between Digits. Fractal Fract. 2024, 8, 197. https://doi.org/10.3390/fractalfract8040197
Ogunjo S, Kantz H. Evolving Patterns in Irrational Numbers Using Waiting Times between Digits. Fractal and Fractional. 2024; 8(4):197. https://doi.org/10.3390/fractalfract8040197
Chicago/Turabian StyleOgunjo, Samuel, and Holger Kantz. 2024. "Evolving Patterns in Irrational Numbers Using Waiting Times between Digits" Fractal and Fractional 8, no. 4: 197. https://doi.org/10.3390/fractalfract8040197






